5점이 원뿔을 결정한다.

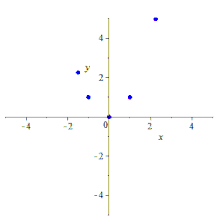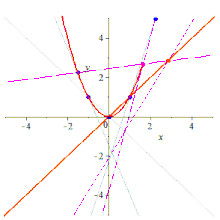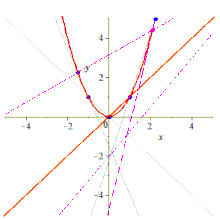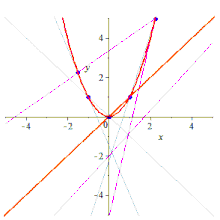
유클리드 기하학 및 투영 기하학에서 두 개의 (구분이 있는) 점이 선을 결정하는 것처럼(도 1 평면 곡선), 5개의 점이 원뿔(도 2 평면 곡선)을 결정합니다.선에는 존재하지 않는 원뿔에 대한 추가 섬세함이 있기 때문에 원뿔에 대한 문장과 증명은 모두 선에 대한 것보다 더 기술적입니다.

형식적으로, 평면의 어떤 5개의 점(공직선이 3개 없음)이 주어지면, 그것들을 통과하는 독특한 원뿔이 존재하며, 이것은 유클리드 평면과 파피안 투영 평면 모두에 해당된다.실제로, 임의의 5개의 점을 통과하는 원뿔이 있지만, 3개의 점을 공선화하면 원뿔은 퇴화(직선을 포함하기 때문에 축소 가능)되어 고유하지 않을 수 있습니다. 자세한 내용은 설명을 참조하십시오.

증명서

이 결과는 여러 가지 방법으로 입증될 수 있습니다. 차원 계산 논거는 가장 직접적이고 더 높은 수준으로 일반화되지만 다른 증명은 원뿔형에게 특별합니다.

치수 계산

직관적으로 일반적인 선형 위치에서 5개의 점을 통과하면 원뿔의 (투영적인) 선형 공간에 5개의 독립적인 선형 구속조건이 지정되므로 이 간단한 문장은 섬세함을 무시하지만 고유한 원뿔을 지정합니다.

보다 정확하게는 다음과 같습니다.

• 원뿔은 5차원 투영 $공간{\displaystyle {\mathbf{}}^{}}$ ${\displaystyle {}^{}}$5$$; {\$displaystyle \mathbf {P}$^{$5};}$의 점에 해당합니다.
• 원뿔이 점을 통과해야 하는 경우 좌표에 선형 조건이 부과됩니다$.{\displaystyle }$$고정식{\displaystyle }$${\displaystyle (x}$,${\displaystyle y}$ $),\style (x , y$ ),\style (x , y ),\style$$ (${\displaystyle x}$ , y${\displaystyle }$) + ${\displaystyle {}^{}}$ y${\displaystyle {}^{}{2\mathrm{}}^{}{}^{}}$+ ${\displaystyle Dx}$ + ${\displaystyle Ey}$ + ${\displaystyle F}$ ${\displaystyle =}$ { $display$ ${\displaystyle {}^{}}$ $^{2}$ +$$Bxy + F = 0 ($xy$ + y )$Cy^{2}+Dx+Ey$+$F=0}$은 (${\displaystyle A,}$ ${\displaystyle B,}$ ${\displaystyle C,}$ ${\displaystyle D,}$ $);({displaystyle (A, B, C,$D, D, E, F$)}$의 선형 방정식입니다$.$
• 치수 계수에 의해, 각 제약조건이 가능성의 치수를 1씩 절단하고 하나는 5차원으로 시작하기 때문에, 원뿔을 지정하기 위해 5개의 제약조건이 필요하다.
• 5차원에서 5개의 (독립된) 초평면의 교점은 단일 지점(공식적으로 베주트 정리에 의해)이다.
• 점의 일반적인 선형 위치는 구속조건이 독립적이라는 것을 의미하며, 따라서 고유한 원뿔을 지정한다.
• 결과 원뿔은 곡선이기 때문에 (1개 이상의 점을 가지고 있기 때문에) 퇴화되지 않으며 선을 포함하지 않으므로(즉, 적어도 5개 점 중 3개를 포함해야 하는) 축소할 수 없다.

위의 분석에서 두 가지 미묘한 점은 결과점이 2차 방정식(선형 방정식이 아님)이고 제약조건이 독립적이라는 것이다.첫 번째는 간단합니다.A, B 및 $C$가 모두 사라지면${\displaystyle D}$ x${\displaystyle }$+ E ${\displaystyle y}$ + F$=$ ${\displaystyle 0}$ { $displaystyle Dx$+ $Ey$ + F $=$0 } defines$$, a, a a3개의 점(실제로 임의의 수의 점)이 선상에 놓입니다.따라서 일반적인 선형 위치는 원뿔형을 보장합니다.두 번째는 구속조건이 독립적이라는 점에서 상당히 미묘하다. 즉, 평면에서 일반적인 선형 위치에 있는 5개의 점을 지정하면 Veronese 지도 아래의 P$$(\$style \mathbf {P}$^{$5})$에 $있는{\displaystyle {\mathbf{}}^{}}$ 이미지가 일반적인 선형 위치에 있다는 사실에 해당하며, 이는 Veronese 맵이 birgular: i이기 때문이다.5개의 점의 이미지가 관계를 만족하면 관계가 풀백될 수 있으며 원래 점 또한 관계를 만족해야 합니다.Veronese 맵에는 [${\displaystyle {x\mathrm{}}^{}2}$ : x${\displaystyle }$y : ${\displaystyle y}$ ${\displaystyle {2\mathrm{}}^{}}$: ${\displaystyle x}$z : ${\displaystyle y}$z : ${\displaystyle {}^{}}$ $],$ {\$displaystyle [x^{2}:xz:yz^{2}},}$의${\displaystyle }$좌표가 있으며 타겟 $(\$는 [${\displaystyle A}$:${\displaystyle B}$ : ${\displaystyle C}$ :${\displaystyle D}$ : D : D : D : 2 : 2 : 2 ] : ] : 2${\displaystyle }$。$C:D:E:F]}$ ${\displaystyle {}^{}}$ 5 (\$displaystyle \mathbf {P}$^{$5$$})$ 원뿔형.Veronese 지도는 "점에서의 원뿔의 평가"에 해당하며, 제약의 독립성에 대한 문장은 이 지도에 대한 기하학적 진술이다.

합성 증명

5개의 점이 원뿔을 결정한다는 것은 위에 제시된 해석적(대칭) 증거에 더해 합성 기하학(즉, 평면 내의 선과 점)에 의해 입증될 수 있다.이러한 증거는 다음과 같은 Jakob Steiner의 ^[1]정리를 사용하여 제시될 수 있다.

X점을 통과하는 선연필과 Y점을 통과하는 선연필 사이에 투영 변환 f가 주어졌을 때 선x와 그 $화상{\displaystyle }$ f$(x)$ 사이의$$ 교점 집합 C가 원뿔을 형성한다.

XY 선(각각 X를 통과하는 선과 Y를 통과하는 선)의 초기 이미지와 이미지를 고려하여 X와 Y가 이 원뿔 위에 있다는 점에 유의하십시오.

이는 X 및 Y 포인트를 표준 포인트${\displaystyle }$[${\displaystyle 1}$: ${\displaystyle 0}$ : 0${\displaystyle }$$]\{{\displaystyle }$ $displaystyle$[ 1 : 0 : 0$]$${\displaystyle \mathrm{및}}$[ ${\displaystyle 0}$ :${\displaystyle 0}$ $]{$ $displaystyle$$$[ 0 : 1 : 0 ]{ displaystyle $[ 0$ : $0$]}{ displaystyle [ 0 : 0 : 0 ]}{ displaystyle [ 0 : 0 : 0 : 0 }}}을$$$$ 투영 변환함으로써 나타낼 수 있습니다.함수의 ph(표시해야 함)는 쌍곡선이므로 원뿔형이며, 따라서 원곡선 C는 원뿔형입니다.

5개의 점 X, Y, A, B, C를 지정하면 ${\displaystyle \mathrm{XA},}$ ${\displaystyle \mathrm{XB},}$ $(\displaystyle$ XA,$XB, XC)$의 3개의 ${\displaystyle \mathrm{라인}}$에 XA${\displaystyle ,}$ ${\displaystyle \mathrm{YB},}$ $(\displaystyle$YA, $YBY, XC$)를 사용할 수 있습니다$.$y는 회선상에서 3-transitive입니다).이 지도에서 X는 Y에 매핑되는데, 이는 이 선들의 고유한 교차점이기 때문에 스타이너의 정리 가설을 만족시키기 때문이다.따라서 결과 원추형에는 5개의 포인트가 모두 포함되어 있으며 원하는 원추형 고유의 원추형입니다.

건설

5점이 주어지면, 그것들을 포함한 원뿔을 다양한 방법으로 구성할 수 있다.

해석적으로$,{\displaystyle }$ 5개의 점의 ${\displaystyle {}_{}}$(${\displaystyle {}_{}{}_{}{}_{}{}_{yi}}$) ${\displaystyle {\mathrm{i}}_{}}$ ${\displaystyle {=1}_{}}$,${\displaystyle 2_{}}$,${\displaystyle 3_{}}$, 4, $5({$style ($x_{i$},$y_{i$})_${i=$1, 2, 3, 4,5$$})_{i}_{i}_{i})_${i=$1, 2, 3, 4,$5}$_i}_{i}_{style}_{i}_{i}_{i}_{style}_{i}_{i}_{i}_{i}}_{i}_{i}_{i}_{i}_________음이온, 6개의 알 수 없지만 균질하므로 스케일링이 한 차원을 제거합니다. 구체적으로는 계수 중 하나를 1로 설정하면 이 작업이 수행됩니다.

이것은 다음과 같은 결정 방정식으로 매우 직접적으로 달성될 수 있다.

$}&x_{5}y_{5}&, y_{5}^{2}&, x_{5}&, y_{5}&, 1\end{bmatrix}}=0}$

이 행렬은 첫 번째 행에 변수가 있고 다른 모든 행에 숫자가 있으므로 행렬식은 최대 2의 6개 단수의 선형 조합입니다.또한 행렬이 반복되는 행을 가지므로 결과 다항식은 5개의 입력점$({\displaystyle x}$ ${\displaystyle ,y}$ ) $=$ (${\displaystyle x_{}}$i , ${\displaystyle y_{}}$i$$) { $displaystyle (x$, y )=($x_{i$,$y_{i})$에서 분명하게 사라집니다.

종합적으로, 원뿔은 파스칼 정리의 역수인 브라이켄리지-맥로린 정리를 적용하여 브라이켄리지-맥로린 ^[2][3][4][5]구조에 의해 구성될 수 있다.파스칼의 정리는 원뿔에 6개의 점이 주어졌을 때, 반대편에 의해 정의된 선은 세 개의 공선 점에서 교차한다고 말한다.5개의 기존 점이 주어진 경우 6번째 점에 대해 가능한 위치를 구성하기 위해 이 값을 반대로 할 수 있습니다.

일반화

자연 일반화는 n-공간에서 k점(일반 위치)의 구성이 열거형 기하학의 기본 질문인 다양한 정도 d와 차원 m을 결정하는 k의 값을 묻는 것이다.

단순한 예는 평면 곡선이 예인 하이퍼서페이스(코디멘션 1 하위 변수, 단일 다항식의 0, $대문자{\displaystyle }$ m ${\displaystyle =\mathrm{n}}$ -$$1(\$displaystyle$ m$=n-1))$에 대한 것이다.

하이퍼서페이스의 경우 다중 집합 계수, 보다 친숙하게 이항 계수 또는 보다 우아하게 상승 요인 측면에서 다음과 같이 답변이 제공됩니다.

$\displaystyle k=\left(\!\!{n+1 \choose d}\!\!\right)-1={n+d \choose d}-1=subscfrac {1}{n!}(d+1)^{(n)}-1.}$

이는 Veronese 맵의 유사한 분석을 통해 확인할 수 있다. 일반적인 위치의 k개 점들은 다양성에 k개의 독립적인 선형 조건을 부과하며(Veronese 맵은 이중규격이기 때문에${\displaystyle ),}$ n +$$(\$style n+1$} 변수$$(n차원 투영 $공간$은${\displaystyle \mathrm{n}}$+ 1\$style n+$1)의 균질한 균질성을 갖는다.rdinates)는${\displaystyle }$( ${\displaystyle n\genfrac{}{}{0ex}{}{}{}}$+ ${\displaystyle \genfrac{}{}{0ex}{}{1}{}\genfrac{}{}{0ex}{}{}{}}$)$$, \ $displaystyle$\ $text$style \$$$left$ ( \ ! \ ) $。{\displaystyle }$${n+1 \choose d}\!$투영으로$$ $인해$ 1을 뺀 \!\right$)}:$ 다항식에 상수를 곱해도 0은 변경되지 않습니다$.$

위의 공식에서 포인트 수 k는 d of degree n의 다항식이며, $선행{\displaystyle \mathrm{}계수}$는 1/n$!$ {\$displaystyle$1/$n!}$입니다.

$평면$ 곡선의 경우, 여기서 $n{\displaystyle }$ $=$, {\$displaystyle$ n=$2,}$ 공식은 다음과 같습니다.

${\displaystyle \textstyle {1}{2}}(d+1)-1=\textstyle {{1}{2}(d^{2}+3d)}$

$d{\displaystyle }$ ${\displaystyle =}$ ${\displaystyle 0,1}$,${\displaystyle 2}$,${\displaystyle 3}$, 4$({displaystyle$ d$=0,1,2,3,4})$의 $값$은 0${\displaystyle ,2}$,$({displaystyle$ 0$,2,5,9,14$)$$입니다. 0도 곡선은 없습니다(단일 점이 점이며 따라서 코드텐션 2인 점에 의해 결정됨), 2점은 9점을 결정합니다.4등분 등을 하다

관련 결과

5개의 점이 원뿔형을 결정하는 반면, 원뿔형 위의 6개 이상의 점 집합은 일반적인 위치에 있지 않다. 즉, 파스칼의 정리에 나타난 것처럼 구속된다.

마찬가지로, 9개의 점이 입방체를 결정하지만, 9개의 점이 1개 이상의 입방체 위에 있다면(즉, 2개의 입방체의 교집합), 그것들은 일반적인 위치에 있지 않으며, 실제로 케일리-바차라크 정리에 명시된 추가 제약을 만족한다.

4개의 점은 원뿔이 아니라 연필로, 모두 4개의 점을 통과하는 원뿔의 1차원 선형 시스템(공식적으로 4개의 점을 기저 궤적으로 함)을 결정합니다.마찬가지로 3점은 2차원 선형계(net), 2점은 3차원 선형계(web), 1점은 4차원 선형계를, 0점은 모든 원뿔의 5차원 선형계에 제약을 두지 않는다.

잘 알려진 바와 같이, 세 개의 비선점은 유클리드 기하학에서 원을 결정하고 두 개의 뚜렷한 점은 아폴로 원과 같은 원의 연필을 결정합니다.원추형의 특수한 경우이기 때문에 이러한 결과는 일반적인 결과와 배치되는 것으로 보인다.단, 파피안 투영 평면에서 원뿔은 무한대의 선상의 2개의 특정 점을 통과할 경우에만 원이기 때문에 원뿔은 아핀 평면에 3개, 그리고 이 2개의 특수점에 의해 5개의 비공선점에 의해 결정된다.비슷한 고려 사항으로 원의 연필을 정의하는 데 필요한 점의 수가 예상보다 적은 것이 설명됩니다.

접선

점을 통과하는 대신, 곡선의 다른 조건이 주어진 선에 접해 있습니다.주어진 5개의 선에 접하는 것도 투영적 이중성에 의해 원뿔을 결정하지만, 대수적 관점에서 선에 대한 접선은 2차 제약이므로, nair한 차원 계수는 5개의 주어진 선에 접하는 2 = 32개의 원뿔을 산출한다⁵.그 중 31개는 열거형 기하학의 퍼지 인자로 설명되어야 한다.이 직관을 공식화하는 것은 정당화하기 위해 상당한 발전이 필요하다.

Another classic problem in enumerative geometry, of similar vintage to conics, is the Problem of Apollonius: a circle that is tangent to three circles in general determines eight circles, as each of these is a quadratic condition and 23 = 8. As a question in real geometry, a full analysis involves many special cases, and the actual number of circles7을 제외한 0에서 8 사이의 임의의 숫자입니다.

「 」를 참조해 주세요.

• n차 평면 곡선으로 일반화하기 위한 크레이머의 정리(대수 곡선)

레퍼런스

외부 링크

• 원뿔 단면을 결정하는 5가지 점, Wolfram 대화형 시연