리만-로흐 정리

리만-로흐 정리

들판	대수기하학과 복소해석학
첫 번째 증명:	구스타프 록
첫번째 증거	1865
일반화	아티야-가수지수 정리 그로텐디크-리만-로흐 정리 히르제브루흐-리만-로흐 정리 표면에 대한 리만-로흐 정리 리만-로흐형 정리
결과들	특수분수에 관한 클리포드 정리 리만-후르비츠 공식

리만-로흐 정리(Riemann-Roch theorem)는 수학, 특히 복소해석학과 대수기하학에서 규정된 0과 허용된 극을 사용하여 메로모픽 함수의 공간의 차원을 계산하는 데 중요한 정리입니다. 그것은 연결된 콤팩트 리만 표면의 복잡한 분석과 그 표면의 순수한 위상학적 속 g를 순수한 대수적 설정으로 전달할 수 있는 방법을 연관시킵니다.

처음에 리만(1857)에 의해 리만의 부등식으로 증명된 이 정리는 리만의 단명한 제자인 구스타프 로흐(1865)의 연구를 거쳐 리만 표면에 대한 결정적인 형태에 도달했습니다. 나중에 대수적 곡선, 고차원 다양성, 그 이상으로 일반화되었습니다.

예비개념

리만 곡면 $X{\displaystyle }$ ${\displaystyle X}$는 복소수 집합인$$$C{\displaystyle \mathbb{}}$ ${\$의 열린 부분 집합과 국소적으로 동형인 위상 공간입니다. 또한 이러한 열린 부분 집합 사이의 전이 맵은 완전형이어야 합니다. 후자의 조건은 $C{\displaystyle \mathbb{}}$ ${\$의 복소형 함수와 복소형 함수를 다루는 복소 분석의 개념과 방법을 $표면{\displaystyle }$ X ${\displaystyle$ X$}$로 옮길 수 있습니다$.$ 리만-로흐 정리의 목적을 위해 표면 $X{\displaystyle }$ ${\displaystyle X}$는 항상 콤팩트하다고 가정합니다$$. 구어적으로 말하면, 리만 곡면의$$ $g{\displaystyle }$ ${\displaystyle g}$ 속은 그 손잡이 수이다. 예를 들어 오른쪽에 표시된 리만 곡면의 g 속은 3입니다. 보다 정확하게는 속은 첫 번째 베티 수의 절반, 즉 $복잡한{\displaystyle \mathbb{}}$ 계수를 가진$$ 첫 번째 단일 상동성 그룹 $H1(X,$ C${\displaystyle )}$의 C ${\$$displaystyle \mathbb {C}$ 차원의$$ 절반으로 정의됩니다$.$ 속은 콤팩트 리만 표면을 동형까지 분류합니다. 즉, 두 개의 그러한 표면은 그들의 속이 동일한 경우에만 동형입니다. 따라서 이 속은 리만 표면의 중요한 위상 불변량입니다. 반면 호지 이론은 $속$이 X ${\displaystyle X}$의 홀로모픽 단일 형태 $공간$의 C ${\$ 차원과 일치한다는$$것을 보여주므로 속은 리만 표면에 대한 복잡한 분석 정보도 인코딩합니다.^[1]

분할자 $D{\displaystyle }$ ${\displaystyle D}$는 지표면의 점에 있는 자유 아벨 군의 요소입니다. 마찬가지로, 약수는 정수 계수를 갖는 표면의 점들의 유한 선형 조합입니다.

$임의$의 동형 함수 f ${\displaystyle f}$는 다음과 같이 정의되는${\displaystyle }$(${\displaystyle f)}$ ${\displaystyle (f)}$로 표시되는 약수를 생성합니다$$.

${\displaystyle(f):=\sum _{z_{\nu}\in R(f)}s_{\nu}z_{\nu}}$

$여기$서 R${\displaystyle (f)}$ ${\displaystyle R(f)}$는 f ${\displaystyle$ f$}$의 모든 영점과 극점의 집합이고$,$ $s$ν {\displaystyle s_{\n$u}}$은(는)

${\displaystyles_{\nu }:={\begin{cases}a&{\text{if }}z_{\nu }{\text{ is a zero of order }}a\\-a&{\text{if }}z_{\nu}{\text{는 순서의 극입니다}}a.\end{case}}}$

집합 $R{\displaystyle (f)}$ ${\displaystyle R(f)}$은 유한한 것으로 알려져$$ 있습니다. 이는 $X{\displaystyle }$ ${\displaystyle$ X$}$가 콤팩트하고 (0이 아닌) 홀로포머 함수의 0이 누적점을 갖지 않기 때문입니다. 따라서${\displaystyle }$(${\displaystyle f)}$ ${\displaystyle (f)}$은(는) 잘 정의되어 있습니다. 이 형태의 모든 나눗셈을 주 나눗셈이라고 합니다. 주 나눗셈에 따라 다른 두 나눗셈을 선형 동치라고 합니다. 동형 1-형태의 약수는 유사하게 정의됩니다. 전역 동형 1-형태의 약수를 표준 약수($일반적$으로 K ${\displaystyle$ K$}$로 표시)라고 합니다.$$ 임의의 두 개의 동형 1-형태는 선형 등가 약수를 산출하므로, 표준 약수는 선형 등가까지 고유하게 결정됩니다(따라서 "표준 약수").

${\displaystyle \mathrm{기호}}$ ${\displaystyle \mathrm{deg}}$ ⁡ (D) ${\displaystyle$\deg(D)}는 $분주기$ D $displaystyle$D}의 차수(때로는 $인덱스라고도 함),$즉 D {\displaystyle D}에서$발생$하는 계수의 합을 의미합니다. 글로벌 메로모픽 함수의 약수는 항상 차수가 0임을 알 수 있습니다. 따라서 나눗셈의 정도는 선형 동치 클래스에만 의존합니다.

숫자$$ℓ (D) ${\displaystyle$\ell (D)}은 ($)$ + D${\displaystyle$ (h)+D${\displaystyle \}}$의$$모든 계수가 음수가 아닌 표면의 동형$함수$ h${\displaystyle$ h}의 벡터 $공간$의 치수$(C {\displaystyle \mathbb${C} 위)입니다. 직관적으로, 우리는 이것을 모든 점의 극이 $D{\displaystyle }${\$displaystyle$ D$}$의 해당 계수보다 나쁘지 않은 모든 동형 함수라고 생각할 수 있습니다$.$ $z{\displaystyle }$ ${\displaystyle z}$에서 $D{\displaystyle }$ ${\displaystyle$ D$}$의 계수가 음수이면$$, $그런{\displaystyle }$ 다음 $h{\displaystyle }$ ${\displaystyle$ h$}$가 z ${\displaystyle z}$에서 최소 해당 다중도의 0을 가져야$$ 합니다.$$ D ${\displaystyle D}$의 계수가 양수이면$$ $h{\displaystyle }$ ${\displaystyle h}$는 최대 해당 순서의 극을 가질$$ 수 있습니다. 선형 등가 약수의 벡터 공간은 스칼라까지 잘 정의된 전역 동형 함수와의 곱셈을 통해 자연스럽게 동형입니다.

정리문

$정준{\displaystyle }$ 약수 $K{\displaystyle }$ ${\displaystyle$ K$}$를 갖는 속$$ g$$ ${\displaystyle$ g$}$의 콤팩트 리만 곡면에 대한 리만-로흐 정리

${\displaystyle \ell (D)-\ell (K-D)=\deg (D)-g+1.}$

일반적으로 숫자$$ℓ (D) ${\displaystyle \$ell (D)}가 관심있는 것인${\displaystyle \mathrm{반면}}$,$$ℓ (K - D)${\displaystyle$ \ell (K - D)}는 수정항(특이도 지수라고도 함)으로 생각되므로 정리는 대략 다음과 같이 비유할 수 있습니다.

치수 - 보정 = 정도 - 속 + 1.

벡터 공간의 차원이므로 보정항${\displaystyle }$ℓ ${\displaystyle (}$K$$- D) ${\displaystyle$ \$ell$(K - D)}은 항상 음수가 아니므로,

${\displaystyle \ell(D)\geq \deg(D)-g+1.}$

이것을 리만의 부등식이라고 합니다. Roch의 진술 중 일부는 부등식의 양변 사이의 가능한 차이에 대한 설명입니다. 속 $g{\displaystyle }$ ${\displaystyle$ g$}$의 일반적인 리만 $표면$에서$$K {\$displaystyle$$$K$}$는 약수를 나타내기 위해 선택된 메로모픽 형태와 무관하게 차수 ${\displaystyle 2}$$g{\displaystyle \mathrm{}}$- 2 ${\displaystyle 2g-2}$를 갖습니다. 이것은 정리에 $D$ = ${\displaystyle K}$ ${\$displaystyle D = K}를 넣는 것으로부터 이어집니다. $특히{\displaystyle }$ D ${\displaystyle D}$가 ${\displaystyle \mathrm{2g}}$- ${\displaystyle 1}$ ${\displaystyle 2g$ - 1$}$ 이상의$$도를$$ 가지는 한 보정항은 0이므로,

${\displaystyle \ell(D)=\deg(D)-g+1.}$

이 정리는 이제 낮은 속의 표면에 대해 설명될 것입니다. 또한 선다발을 사용한 이 정리의 등가 공식과 대수 곡선에 대한 이 정리의 일반화 등 여러 밀접하게 관련된 정리들이 있습니다.

예

이 정리는 문제의 표면 위에$$ $있는{\displaystyle }$ 점$$P {\$displaystyle$P}를 선택하고 수열에 관한 것으로 설명됩니다.

${\displaystyle \ell(n\cdot P),n\geq 0}$

즉, 함수가 최대 $n$ ${\displaystyle$ $n$$}$의 순서 극을 가질 수 있는 $P$ ${\displaystyle$ P$}$를 제외한 모든 곳에서 동형인 함수 공간의 차원입니다$.$ $따라서$ n = ${\displaystyle 0}$ ${\displaystyle$n=0}인 경우, 함수는 전체여야 합니다. $전체면{\displaystyle }$X {\$displaystyle$ X$}$ 위에 홀로포름이 있습니다$.$ 리우빌의 정리에 의하면, 그러한 함수는 반드시 일정합니다. 따라서${\displaystyle }$ℓ (0) = 1 ${\displaystyle$\ell (0) = 1} 입니다. 일반적으로 시퀀스 ℓ (n ⋅ P) {\displaystyle \ell (n\cdot P)}은 증가하는 시퀀스입니다.

속 0

리만 구(복소 사영선이라고도 함)는 단순히 연결되어 있으므로 첫 번째 특이 호몰로지는 0입니다. 특히 그 속은 0입니다. 구면은 $C{\displaystyle \mathbb{}}$ ${\$의 두 복사본으로 덮일 수 있으며$,$ 전이 맵은 다음에 의해 제공됩니다.

${\displaystyle \mathbb {C} \setminus \{0\}\ni z\mapsto {\frac {1}{z}}\in \mathbb {C} \setminus \{0\}.}$

따라서 C {\displaystyle \mathbb {C}의 한 복사본에서 ω = dz$$${\$displaystyle \omega = dz} 형식은 리만 구면에서 동형으로 확장됩니다. 무한대의 이중 극을 가지므로

${\displaystyle d\left ({\frac {1}{z}}\right)=-{\frac {1}{z^{2}}\, dz.}$

따라서, 그 약수 $K$:= ${\displaystyle \mathrm{div}}$⁡${\displaystyle (}$ω) = - 2 P {\$displaystyle K:$=$\operatorname${$div$}(\$omega$)=-$2P$}(여기서 $P${\displaystyle P}는 무한대의 점입니다).

따라서, 이 정리는 ${\displaystyle \mathrm{수열}}$⋅ (n ℓ P$) {\displaystyle$ \ell (n\cdot P)}가 다음과 같이 읽습니다.

1, 2, 3, ... .

이 수열은 부분 분수 이론에서도 읽을 수 있습니다. 반대로 이 시퀀스가 이러한 방식으로 시작되는 경우 g$${\$displaystyle$ g$}$은(는) 0이어야 합니다.

1속

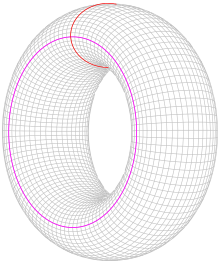
다음 경우는 토러스 C / λ {\displaystyle \mathbb {C} /\Lambda }와 같은 $속$ g = ${\displaystyle 1}$ ${\$$displaystyle$ g=1$}$의 리만 표면이며, 여기서 λ {\displaystyle \Lambda }는 2차원 격자(Z 2 {\displaystyle \mathbb {Z} ^{2}와 동형)입니다. 첫 번째 단일 상동성 그룹은 오른쪽 그림과 같이 두 개의 루프에 의해 자유롭게 생성됩니다. $C$ ${\displaystyle C}$의 표준 복소 좌표 $z$ ${\displaystyle$ z$}$는 X {\displaystyle X}의 단일 형태 ω = d z ${\$displaystyle \omega = dz}을(를) 생성하며, 이는 어디에서나 홀로포밍(holomy), 즉 극이 전혀 없습니다. 따라서$$ω${\displaystyle$ \omega}의 약수인$K$ ${\displaystyle$ K$}$는 0입니다.

이 표면에서 이 시퀀스는

1, 1, 2, 3, 4, 5 ... ;

그리고 이것은 ${\displaystyle \mathrm{케이스}}$ g = 1$${\$displaystyle$ g = 1$}$을 특징으로 합니다. 실제로 D = 0 {\displaystyle D = ${\displaystyle 0}$}의 경우 위에서 언급한 대로 ℓ (K - D) = ℓ (0) = 1 {\displaystyle \ell (K - D) =\ell (0) = 1}입니다. $n$ > 0 {\displaystyle n > 0}인 D$$= $n$ ⋅ P {\displaystyle D= n\cdot P}의 경우 K - D {\displaystyle K-D}의 정도가 엄격하게 음수이므로 보정항은 0입니다. 차원의 순서는 타원 함수 이론에서도 유도될 수 있습니다.

2속 이상

${\displaystyle \mathrm{g}}$ = 2${\$displaystyle g = 2}의 경우 위에서 언급한 순서는

1, 1, ?, 2, 3, ... .

이를 통해 2도의 ?항은 점에 따라 1 또는 2임을 알 수 있습니다. 어떤 속 2의 곡선에서도 정확히 6개의 점이 있다는 것을 증명할 수 있는데, 그 점들의 수열은 1, 1, 2, ...이고 나머지 점들은 일반 수열 1, 1, 1, 2, ...입니다. 특히, 속 2 곡선은 과립성 곡선입니다. > ${\display g> 2}$의 경우 대부분의 점에서 시퀀스가 ${\displaystyle \mathrm{g}}$+ 1 ${\display g+1}$으로 시작하고 다른 시퀀스와 함께 점이 유한하게 많다는 것이 항상 사실입니다(Weierstrass 점 참조).

선다발에 대한 Riemann–Roch

리만 곡면 위의 나눗셈과 복소형 선다발 사이의 밀접한 대응 관계를 이용하여, 이 정리는 X 위의 복소형 선다발 L이라고 하는 다른, 그러나 동등한 방법으로도 표현할 수 있습니다. $H{\displaystyle {}^{}}$ ${\displaystyle {0\mathrm{}}^{}}$(${\displaystyle X,}$ L${\displaystyle )}$ ${\displaystyle H^{0}$ ($X, L)}$ 이 L의 홀로모픽 절들의 공간을 나타낸다고$$ 하자. ${\displaystyle {이\mathrm{}}^{}}$ 공간은 유한 차원이며, 차원은 $0{\displaystyle {}^{}}$(${\displaystyle X,}$ ${\displaystyle L)}$ ${\displaystyle$ h$^{0}(X,$ L$)}$로 표시됩니다$.$ K를 X의 표준 번들이라고 하자. 그렇다면 리만-로흐 정리는 다음과 같습니다.

${\displaystyle h^{0}(X,L)-h^{0}(X,L^{-1}\otimes K)=\deg(L)+1-g.}$

앞 절의 정리는 L이 점다발일 때의 특수한 경우입니다.

이 정리는 다음과 같이 K의 g개의 선형 독립적인 홀로모픽 절편 또는 X 위의 한 형태가 있음을 보여주기 위해 적용될 수 있습니다. L을 자명한 다발이라고 할 때, X 위의 유일한 홀로모픽 함수는 상수이므로 h ${\displaystyle 0^{}}$ ${\displaystyle {}^{}X,}$ ${\displaystyle L)}$ = ${\displaystyle 1}$ ${\displaystyle$h^{0} (X, L) = 1}이다. L의 차수는 0이고, ${\$ L$^{-1}}$은 사소 묶음입니다. 따라서,

${\displaystyle 1-h^{0}(X,K)=1-g.}$

$따라서$ ${\displaystyle h}$ ${\displaystyle 0^{}}$(${\displaystyle X,}$ ${\displaystyle K)}$ = g ${\displaystyle$h^{0} (X, K) = g} 이므로, 홀로모픽 일 형태가 있음을 증명할 수 있습니다.

표준다발의 정도

표준 번들 $K$ ${\displaystyle$ K$}$가 ${\displaystyle h^{}}$ 0${\displaystyle {}^{}X,}$ K${\displaystyle )}$ = g ${\displaystyle$ h$^{$0}(X, K) = ${\displaystyle g}$}이므로, L = K {\displaystyle L = K}에 리만-로흐를 적용하면 다음과 같은 결과를 얻을 수 있습니다.

${\displaystyle h^{0}(X,K)-h^{0}(X,K^{-1}\otimes K)=\deg(K)+1-g}$

로 다시 쓸 수 있는

${\displaystyle g-1=\deg(K)+1-g}$

따라서 표준 번들의 차수는 ${\displaystyle \mathrm{deg}}$⁡(${\displaystyle \mathrm{K}}$) =$2g$- 2 {\displaystyle \deg(K) = 2g-2}입니다.

대수곡선에 대한 리만-로흐 정리

위의 리만 표면의 약수에 대한 리만-로흐 정리 공식의 모든 항목은 대수기하학에서 유사체를 갖습니다. 리만 곡면의 아날로그는 k장에 대한 비특이 대수 곡선 C입니다. 용어의 차이(곡선 대 표면)는 실제 다양체로서의 리만 곡면의 차원이 2개이지만 복소 다양체로서의 차원은 1개이기 때문입니다. 리만 곡면의 조밀성은 사영과 동일한 대수 곡선이 완전하다는 조건과 유사합니다. 일반적인 필드 k에 대해서는 단일 (공)호몰로지에 대한 좋은 개념이 없습니다. 이른바 기하학적 속은 다음과 같이 정의됩니다.

${\displaystyle g(C):=\dim _{k}\Gamma (C,\Omega _{C}^{1})}$

즉, 전역적으로 정의된 (대수적인) 단일 형식의 공간의 차원으로서(Kähler 미분 참조). 마지막으로, 리만 표면의 메로모픽 함수는 홀로모픽 함수의 분수로 국소적으로 표현됩니다. 따라서 이들은 정규 함수의 국소적인 부분인 유리 함수로 대체됩니다. 따라서 모든 점에서 극이 D의 해당 계수보다 나쁘지 않은 곡선의 유리 함수 공간의 차원(오버 k)에 대한$$ℓ (D)${\displaystyle$\ell (D)}을 작성하면 위와 매우 동일한 공식이 유지됩니다.

${\displaystyle \ell (D)-\ell (K-D)=\deg (D)-g+1.}$

여기서 C는 대수적으로 닫힌 장 k에 대한 사영 비특이 대수적 곡선입니다. 사실, 동일한 공식은 기본 필드의 가능한 확장과 나눗셈을 지지하는 점의 잔차 필드에서 오는 다중성을 고려해야 한다는 점을 제외하고는 모든 필드에 대한 투영 곡선을 나타냅니다.^[4] 마지막으로, 아르티니아 링 위의 적절한 곡선의 경우, 제수와 관련된 선다발의 오일러 특성은 제수의 정도(적절하게 정의됨)에 구조적인 $쉬프트{\displaystyle \mathcal{}}$O {\$displaystyle$ {\$mathcal${$O}}$의 오일러 특성으로 주어집니다$.$^[5]

정리의 매끄러움 가정도 완화될 수 있습니다: 대수적으로 닫힌 장 위의 (투영) 곡선에 대해, 모든 국소환이 고렌슈타인 고리이며, 위에서 정의된 기하 속이 다음과 같이 정의된 산술 속 g로_a 대체되는 경우 위와 같은 문장이 성립합니다.

${\displaystyle g_{a}:=\dim_{k}H^{1}(C,{\mathcal {O}}_{C}).}$^[6]

(평활한 곡선의 경우 기하학적 속은 산술적 속과 일치합니다.) 이 정리는 일반적인 단일 곡선(그리고 고차원 다양성)으로도 확장되었습니다.^[7]

적용들

힐베르트 다항식

리만-로흐의 중요한 결과 중 하나는 곡선 위의 선다발의 힐베르트 다항식을 계산하는 공식을 제공한다는 것입니다. 만약 $선다발$ L$${\$displaystyle${\$mathcal {L}}$이 충분하다면, 힐베르트 다항식은 사영 공간에 임베딩을 제공하는 첫 번째 ${\displaystyle {\mathrm{차수}}^{}}$ L ⊗ n${\displaystyle$ {\$mathcal {L}}^{\otimes$ n}을 제공할 것입니다. For example, the canonical sheaf ${\displaystyle \omega _{C}}$ has degree ${\displaystyle 2g-2}$, which gives an ample line bundle for genus ${\displaystyle g\geq 2}$.^[8] If we set ${\displaystyle \omega _{C}(n)=\omega _{C}^{\otimes n}}$ then the Riemann–Roch formula reads

${\displaystyle {\begin{aligned}\chi (\omega _{C}(n))&=\deg(\omega _{C}^{\otimes n})-g+1\\&=n(2g-2)-g+1\\&=2ng-2n-g+1\\&=(2n-1)(g-1)\end{aligned}}}$

차수 $1$ ${\displaystyle$ 1$}$$$ω C {\displaystyle $\omega_{$C}의 힐베르트 다항식 부여

${\displaystyle H_{\omega _{C}}(t)=2(g-1)t-g+1}$

삼원정규${\displaystyle {}_{}^{}}$ω C ⊗ 3 {\$displaystyle$ \$omega_{$C}^{\otimes 3}}이 곡선을 포함하는 데 사용되므로 힐베르트 다항식

${\displaystyle H_{C}(t)=H_{\omega _{C}^{\otimes 3}}(t)}$

일반적으로 곡선의 힐베르트 체계(및 대수 곡선의 모듈리 공간)를 구성할 때 고려됩니다. 이 다항식은

${\displaystyle {\begin{aligned}H_{C}(t)&=(6t-1)(g-1)\\&=6(g-1)t+(1-g)\end{aligned}}}$

그리고 g속 곡선의 힐베르트 다항식이라고 합니다.

플뤼리카노니컬 임베딩

이 방정식을 더 분석하면 오일러 특성은 다음과 같이 읽힙니다.

${\displaystyle {\begin{aligned}\chi(\omega_{C}^{\otimes n})&=h^{0}\left(C,\omega_{C}^{\otimes n}\right)-h^{0}\left(C,\omega_{C}\otimes n}\right)\times \left(\omega_{C}^{\otimes n}\right)\\&=h^{0}\left(C,\omega_{C}^{\otimes n}\right)-h^{0}\left(C,\left(\omega_{C}^{\otimes (n-1)}\right)^{\vee}\right)\end{aligned}}$

${\displaystyle {deg}_{}^{}}$⁡(ω C ⊗ n${\displaystyle )}$ = n ($2g$ - 2) {\displaystyle \deg$(\$omega _{C}^{\otimes n}) = n(2g - 2)}

${\displaystyle h^{0}\left(C,\omega_{C}^{\otimes (n-1)}\right)^{\vee}\right)=0}$

$n$≥ 3 {\$displaystyle$$$n\geq 3}의 경우, 그 정도는 모든 g ≥ 2 {\displaystyle g\geq 2}에 대해 음수이므로 전역 섹션이 없음을 의미하므로 ω C ⊗ n {\displaystyle \omega_{C}^{\otimes n}의 전역 섹션에서 일부 투영 공간에 임베딩됩니다. 특히, $ω$C${\displaystyle {}_{}^{}}$⊗ 3 {\$displaystyle$ \omega_{C}^{\otimes 3}}는 PN$$≅ P$(H$ ${\displaystyle 0_{}^{}}$(C,${\displaystyle {}_{}^{}}$ω C ⊗ 3) {\displaystyle \mathbb {P} ^{N}\cong \mathbb {P}(H^{0}(C,$\omega_{C}^{\otimes$ 3$})}$ 여기서 $n$ $=$ ${\displaystyle \mathrm{5g}}$-$5$- 1 $=$ ${\displaystyle 5g}$-$$6 {\displaystyle N $=$ 5g-5-1 $=$ 5g-6} h 0 이후($ω$ C $⊗$ 3) $=$ 6g - 6g + 1 {\displaystyle h^{0}(\omega_{C}^{\otimes 3}) $=$ 6g - 6-g+1}입니다. 이는 힐베르트 다항식 ${\displaystyle {HC}_{}t)}$ ${\displaystyle H_{C}(t)}$를 갖는 힐베르트 스킴을 구성하기 위한 사영 공간으로 사용될 수 있기 때문에 대수 곡선의 모듈리 공간 구성에 유용합니다$.$^[9]

특이점이 있는 평면 곡선의 속

d의 축소 불가능한 평면 대수 곡선은 적절하게 계산될 때 (d - 1)(d - 2)/2 - g 특이점을 갖습니다. 따라서 곡선이 (d - 1)(d - 2)/2개의 다른 특이점을 가지면 유리 곡선이므로 유리 모수화를 인정합니다.

리만-후르비츠 공식

리만-리만-로흐 정리의 결과는 리만 표면 또는 대수 곡선 사이의 (적층화된) 지도에 관한 후르비츠 공식입니다.

특수분수에 관한 클리포드 정리

특수분수에 대한 클리포드의 정리도 리만-로흐 정리의 결과입니다. ℓ(D > 0, {\$displaystyle$\ell $(K-D)$> 0,}을 만족하는 특수한 나눗셈(즉, ℓ (K-D$)$ > 0,{\displaystyle \ell (D) > 0,}에 대해 다음 부등식이 성립함을 나타냅니다.

${\displaystyle \ell (D)\leq {\frac {\deg D}{2}}+1.}$

증명

대수곡선에 대한 증명

대수적 곡선에 대한 문장은 Serreduality를 사용하여 증명할 수 있습니다. 정수$$ℓ (D) ${\displaystyle$\ell (D)}는 D(cf)와 연관된 선${\displaystyle \mathrm{번들}}$ L$(D$) ${\displaystyle {\mathcal${L}}(D)}의 전역 섹션 공간의 차원입니다. 카르티에 나눗셈). In terms of sheaf cohomology, we therefore have ${\displaystyle \ell (D)=\mathrm {dim} H^{0}(X,{\mathcal {L}}(D))}$, and likewise ${\displaystyle \ell ({\mathcal {K}}_{X}-D)=\dim H^{0}(X,$$\omega_{X}\otimes {\mathcal {L}}(D)^{\vee$ 그러나 곡선의 특정한 경우에서 비특이 사영 다양체에 대한 수직 이중성은 H ${\displaystyle 0^{}}$ ${\displaystyle {}^{}X,}$$ω$ ${\displaystyle X}$ $⊗$ L (D) $∨$) {\displaystyle H^{0$}(X,\omega_{X}\otimes {\$mathcal {L}}(D)^{\vee }는 ${\displaystyle \mathrm{이중}}$ H 1${\displaystyle }$(X,$L$ {\$displaystyle$ H^{1}(X$,{\mathcal$ {L$}}(D$vee}}. 따라서 좌변은 나눗셈 D의 오일러 특성과 같습니다. D = 0일 때, 우리는 정의에 의해 구조 쉬프에 대한 오일러 특성이 $1{\displaystyle }$- ${\displaystyle g}$ ${\displaystyle 1-g}$임을 발견합니다. 일반적인 나눗셈에 대한 정리를 증명하려면 나눗셈에 점을 하나씩 추가하여 진행하고 오일러 특성이 오른쪽에 따라 변환되도록 할 수 있습니다.

콤팩트 리만 곡면에 대한 증명

콤팩트 리만 곡면에 대한 정리는 Chow's Theorem과 GAGA 원리를 사용하여 대수적 버전에서 추론할 수 있습니다. 사실 모든 콤팩트 리만 곡면은 어떤 복잡한 사영 공간에서 대수 방정식으로 정의됩니다. (Chow's Theorem은 사영 공간의 닫힌 분석 하위 변이체는 대수 방정식으로 정의된다고 말하고, GAGA 원리는 대수 변이체의 두상 코호몰로지가 동일한 방정식으로 정의되는 분석 변이체의 두상 코호몰로지와 동일하다고 말합니다.)

대수적 곡선의 경우 증명과 동일하게 주장함으로써 Chow의 정리의 사용을 피할 수 있습니다. $그러나{\displaystyle \mathcal{}}$ L${\displaystyle (D)}$ ${\displaystyle {\$$mathcal$${L}}(D)}$을 (${\displaystyle h)}$+ ${\displaystyle D}$ ${\displaystyle(h)+D}$의 모든 계수가 음수가$$ 되지 않도록 동형 함수 h의 $쉬프{\displaystyle {\mathcal{}}_{}}$ ${\displaystyle {OD}_{}}${\$displaystyle$ {$O}_{D}$로 대체합니다. 여기서 오일러 특성이 나눗셈에 한 점을 더할 때 원하는 대로 변환된다는 사실은 짧은 정확한 수열에 의해 유도된 긴 정확한 수열에서 읽을 수 있습니다.

${\displaystyle 0\to {\mathcal {O}}_{D}\to {\mathcal {O}}_{D+P}\to \mathbb {C} _{P}\to 0}$

여기서 ${\displaystyle {}_{}}$ ${\displaystyle \mathbb {C} _{P}$는 마천루 판재 P이고, 지도 ${\displaystyle {OD}_{}}$+ ${\displaystyle P_{}}$ → ${\displaystyle {}_{}}$ ${\displaystyle {\mathcal {O}_{D+$$P}\to \mathbb {C} _{P}}$ -${\displaystyle \mathrm{k}}$- 1 ${\displaystyle -k-1}$번째 로랑 계수를 반환합니다. 여기서 $k$ $=$ ${\displaystyle D}$ (${\displaystyle }$P${\displaystyle }$)${\$displaystyle k $=$ D (P)}.

산술 리만-로흐 정리

산술 리만-로흐 정리의 버전은 만약 k가 전역장이고, f가 k의 아델들 중 적합하게 허용되는 함수라면, 모든 아이디얼에 대하여 포아송 합 공식을 갖는다고 말합니다.

${\displaystyle {\frac {1}{ a }}\sum _{x\in k}{\hat {f}}(x/a)=\sum _{x\in k}f(ax).}$

k가 유한장 위의 대수 곡선의 함수장이고 f가 k 위에서 사소한 임의의 문자일 때, 이것은 기하학적 리만-로흐 정리를 복구합니다.^[12]

산술 리만-로흐 정리의 다른 버전들은 전통적인 리만-로흐 정리와 더 정확히 비슷하게 하기 위해 아라켈로프 이론을 사용합니다.

리만-로흐 정리의 일반화

곡선에 대한 리만-로흐 정리는 1850년대에 리만과 로흐에 의해, 1931년에 프리드리히 카를 슈미트가 유한한 성질의 완벽한 분야를 연구하면서 대수적 곡선에 대해 증명되었습니다. 피터 로케트가 ^[13]말했듯이

F. K. 슈미트의 첫 번째 주요 업적은 콤팩트 리만 표면에 대한 리만-로흐의 고전 정리가 유한한 기본 장을 갖는 함수장으로 전이될 수 있다는 발견입니다. 사실, 리만-로흐 정리에 대한 그의 증명은 반드시 유한한 것이 아니라 임의의 완벽한 기본 장에 대해서도 적용됩니다.

곡선에 대한 후속 이론이 (예를 들어 브릴-노에테르 이론에서) 산출되는 정보를 정교화하려고 노력한다는 점에서 기초가 됩니다.

(나눗셈이나 선다발의 적절한 개념을 위해) 더 높은 차원의 버전이 있습니다. 그들의 일반적인 공식은 정리를 두 부분으로 나누는 것에 달려 있습니다. 이제 세레 이중성이라고 할 수 있는 ${\displaystyle \mathrm{하나}}$는${\displaystyle }$ℓ $($K - D)${\displaystyle \$ell (K - D)}항을 첫 번째 쉬프 $코호몰로지$ 그룹의 차원으로 해석합니다$.$ ℓ ($D$) ${\displaystyle$ \ell ( D${\displaystyle )\}}$인 경우 정리의 왼쪽은 오일러 특성이 됩니다. 그리고 우변은 그것을 리만 표면의 위상에 따라 보정된 차수로 계산합니다.

2차원 대수기하학에서 그러한 공식은 이탈리아 학파의 기하학자들에 의해 발견되었습니다. 표면에 대한 리만-로흐 정리가 증명되었습니다. (몇 가지 버전이 있는데, 첫 번째는 막스 노에테르 때문일 가능성이 있습니다.)

N차원 일반화인 히르제브루흐-리만-로흐 정리는 프리드리히 히르제브루흐에 의해 대수 위상수학의 특징적인 수업의 적용으로 발견되고 증명되었습니다. 그는 고다이라 쿠니히코의 연구에 많은 영향을 받았습니다. 장 피에르 세레는 오늘날 우리가 알고 있는 것처럼 일반적인 형태의 세레 이중성을 제공하고 있었습니다.

알렉산더 그로텐디크는 1957년에 그로텐디크-리만-로흐 정리로 알려진 광범위한 일반화를 증명했습니다. 그의 작품은 리만-로흐를 다양성에 관한 정리가 아니라 두 다양성 사이의 형태론에 관한 것으로 재해석합니다. 증명의 세부 사항은 1958년 Armand Borel과 Jean-Pierre Serre에 의해 출판되었습니다.^[14] 나중에 그로텐디크와 그의 공동 연구자들은 증명을 단순화하고 일반화했습니다.^[15]

마침내 대수 위상학에서도 일반적인 버전이 발견되었습니다. 이러한 개발은 본질적으로 모두 1950년에서 1960년 사이에 수행되었습니다. 그 후 Atiyah-Singer 지수 정리는 일반화로 가는 또 다른 길을 열었습니다. 결과적으로 일관성 있는 쉬프의 오일러 특성은 합리적으로 계산 가능합니다. 교대합 내에서 단 하나의 합에 대해서는 정리 소멸과 같은 추가 인수를 사용해야 합니다.

참고 항목

• 아라켈로프 이론
• 그로텐디크-리만-로흐 정리
• 히르제브루흐-리만-로흐 정리
• 가와사키의 리만-로흐 공식
• 힐베르트 다항식
• 대수곡선의 모듈리

메모들

참고문헌

• Serre, Jean-Pierre; Borel, Armand (1958). "Le théorème de Riemann-Roch". Bulletin de la Société Mathématique de France. 79: 97–136. doi:10.24033/bsmf.1500.
• Griffiths, Phillip; Harris, Joseph (1994), Principles of algebraic geometry, Wiley Classics Library, New York: John Wiley & Sons, doi:10.1002/9781118032527, ISBN 978-0-471-05059-9, MR 1288523
• Grothendiek, Alexander, et al. (1966/67), Théoréme de Riemann–Roch (SGA 6), LNM 225, Springer-Verlag, 1971.
• Fulton, William (1974). Algebraic Curves (PDF). Mathematics Lecture Note Series. W.A. Benjamin. ISBN 0-8053-3080-1.
• Jost, Jürgen (2006). Compact Riemann Surfaces. Berlin, New York: Springer-Verlag. ISBN 978-3-540-33065-3. 복잡한 상황에서의 증명은 208-219페이지를 참조하십시오. Jost는 약간 다른 표기법을 사용합니다.
• Hartshorne, Robin (1977). Algebraic Geometry. Berlin, New York: Springer-Verlag. ISBN 978-0-387-90244-9. MR 0463157. OCLC 13348052.Hartshorne, Robin (1977). Algebraic Geometry. Berlin, New York: Springer-Verlag. ISBN 978-0-387-90244-9. MR 0463157. OCLC 13348052.에는 대수적으로 닫힌 필드 위의 곡선에 대한 문장이 포함됩니다. 섹션 IV.1을 참조하십시오.
• "Riemann–Roch theorem", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
• Hirzebruch, Friedrich (1995). Topological methods in algebraic geometry. Classics in Mathematics. Berlin, New York: Springer-Verlag. ISBN 978-3-540-58663-0. MR 1335917..
• Miranda, Rick (1995). Algebraic Curves and Riemann Surfaces. Graduate Studies in Mathematics. Vol. 5. doi:10.1090/gsm/005. ISBN 9780821802687.
• Shigeru Mukai (2003). An Introduction to Invariants and Moduli. Cambridge studies in advanced mathematics. Vol. 81. William Oxbury (trans.). New York: Cambridge University Press. ISBN 0-521-80906-1.
• 콤팩트 리만 표면의 벡터 다발, M. S. 나라심한, pp. 5-6.
• Riemann, Bernhard (1857). "Theorie der Abel'schen Functionen". Journal für die reine und angewandte Mathematik. 1857 (54): 115–155. doi:10.1515/crll.1857.54.115. hdl:2027/coo.31924060183864. S2CID 16593204.
• Roch, Gustav (1865). "Ueber die Anzahl der willkurlichen Constanten in algebraischen Functionen". Journal für die reine und angewandte Mathematik. 1865 (64): 372–376. doi:10.1515/crll.1865.64.372. S2CID 120178388.
• Schmidt, Friedrich Karl (1931), "Analytische Zahlentheorie in Körpern der Charakteristik p", Mathematische Zeitschrift, 33: 1–32, doi:10.1007/BF01174341, S2CID 186228993, Zbl 0001.05401, archived from the original on 2017-12-22, retrieved 2020-05-16
• Stichtenoth, Henning (1993). Algebraic Function Fields and Codes. Springer-Verlag. ISBN 3-540-56489-6.
• 미샤 카포비치, 리만-로흐 정리(강의 노트) 기초개론
• J. 그레이, 리만-로흐 정리와 기하학, 1854-1914.
• 임의의 장 위에 매끄러운 사영 곡선을 위한 리만-로흐가 있습니까? Math Overflow에서