피라미드(기하학)

규칙 기반 오른쪽 피라미드
예: 정사각형 피라미드
얼굴	n삼각형 1 n면 폴리곤
가장자리	2n
꼭지점	n + 1
슐레플리 기호	( ) ∨ {n}
콘웨이 표기법	Yn
대칭군	Cnv, [1,n], (*nnn), 주문 2n
로테이션 그룹	Cn, [1,n],+ (nn), 순서 n
이중 다면체	자기 인식의
특성.	볼록한

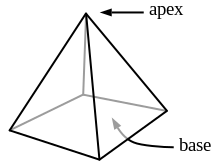
기하학에서, 피라미드(그리스어 ^[1][2]δαμμα)는 다각형 밑면과 꼭지점이라고 불리는 점을 연결한 다면체이다.각각의 밑부분과 끝부분은 측면이라고 불리는 삼각형을 형성합니다.이것은 다각형 밑면을 가진 원뿔 모양 솔리드입니다.면 베이스가 n개인 피라미드는 꼭지점 n개 + 1개, 면 n개 및 모서리 2n개를 가집니다.모든 피라미드는 자기 이중화이다.

오른쪽 피라미드는 밑면의 중심 바로 위에 정점이 있다.오른쪽이 아닌 피라미드는 사선 피라미드라고 불린다.정다각형은 정다각형 밑면을 가지며 보통 오른쪽 ^[3][4]피라미드임을 암시한다.

지정되지 않았을 때, 피라미드는 보통 물리적 피라미드 구조처럼 정사각형 피라미드로 추정됩니다.삼각형 기반 피라미드는 종종 사면체라고 불린다.

사선형 피라미드 중 예각 삼각형과 둔각 삼각형과 같이 피라미드의 정점이 기저부 내부 위에 있으면 예각이라고 할 수 있고, 정점이 기저부 외부 위에 있으면 둔각이라고 할 수 있다.직각 피라미드는 밑면의 가장자리 또는 정점 위에 정점이 있습니다.사면체에서 이러한 한정자는 어떤 면이 밑면으로 간주되는지에 따라 변화한다.

피라미드는 프리즘의 한 종류이다.피라미드는 베이스 평면의 다른 쪽에 두 번째 오프셋 점을 추가하여 2개의 평면으로 이중화할 수 있습니다.

정기저를 가진 오른쪽 피라미드

정기저를 가진 오른쪽 피라미드는 대칭이 C 또는 [1,n]이고_nv 차수가 2n인 이등변 삼각형 변을 가진다.점을 나타내는 확장 Schléfli 기호 ( ) { {n}, (정규 오프셋)을 정규 폴리곤 {n}에 결합할 수 있습니다.결합 연산은 결합된 ^[5]두 그림의 모든 정점 쌍 사이에 새 에지를 생성합니다.

모든 정삼각형 면이 있는 삼각뿔 또는 삼각뿔은 정사면체가 되는데, 정사면체는 플라톤 고체 중 하나입니다.삼각형 피라미드의 하부 대칭 케이스는_3v 등변 삼각형 밑면을 가진 C와 3개의 동일한 이등변 삼각형 변을 가진다.정사각형과 오각형의 피라미드는 또한 정다각형으로 구성될 수 있는데, 이 경우 그것들은 존슨의 고체이다.

정사각형 피라미드(또는 볼록 다면체)의 모든 모서리가 구에 접해 접점의 평균 위치가 구 중심에 있다면 피라미드는 정준이며 정팔면체의 절반을 형성한다고 한다.

밑면이 육각형 이상인 피라미드는 이등변 삼각형으로 구성되어야 한다.정삼각형이 있는 육각형 피라미드는 완전히 평탄한 도형이 될 것이고, 칠각형 이상은 삼각형이 전혀 만나지 않을 것이다.

일반 피라미드
디지털	삼각형의	광장	오각형의	육각형	칠각형의	팔각형의	에네오갈	십각형...
부적절한	규칙적인.	등변		이등분

오른쪽 별 피라미드

규칙적인 다각형 밑면을 가진 오른쪽 피라미드는 별 ^[6]피라미드라고 불린다.예를 들어 오각형 피라미드는 오각형 베이스와 5개의 교차하는 삼각형 변을 가진다.

기저가 불규칙한 오른쪽 피라미드

오른쪽 피라미드는 ( )pP로 명명할 수 있다.여기서 ( )는 정점, θ는 결합 연산자, P는 기저 폴리곤이다.

이등변 삼각형의 직교하는 2개의 세그먼트, 즉 4개의 이등변 삼각면을 포함한 이등변 삼각형의 결합(직교 오프셋)으로서 이등변 삼각형의 밑면에 대한 점의 결합으로서 [( ) )( )]∨ { }{ { }{ { }로 쓸 수 있다.두 개의 서로 다른 베이스-아펙스 방향에서 C 대칭을 가지며_1v 전체_2v 대칭에서 C 대칭을 갖습니다.

( )[ [ { } × { } ) 로 표기된 직사각형 오른쪽 피라미드와 ( )[ [ { } + { }) 로 표기된 마름모꼴 피라미드는 둘 다 대칭_2v C를 가진다.

오른쪽 피라미드

직사각형 피라미드	마름모꼴

용량

피라미드(또는 원뿔)의 부피는 $V{\displaystyle }$ ${\displaystyle =}$ ${\displaystyle \frac{1}{}}$ 3 ${\displaystyle b}$ (\$displaystyle$ V=$$t tfrac ${1}{3}$이다. 여기서 b는 베이스의 면적이고 h는 베이스에서 꼭대기까지의 높이이다.이는 h가 밑면을 포함하는 평면으로부터의 수직 거리로 측정되는 경우, 정규 또는 비정규 폴리곤 및 정점의 모든 위치에 대해 작동합니다.서기 499년 인도 수학과 인도 천문학의 고전 시대의 수학자이자 천문학자 아리아바타는 아리아바티야에서 이 방법을 사용했다.

그 공식은 미적분을 사용하여 정식으로 증명될 수 있다.유사성에 의해 베이스와 평행한 단면의 선형 치수는 정점에서 베이스로 직선적으로 증가한다.스케일링 계수(비례 계수)는 1${\displaystyle }$- ${\displaystyle y\frac{}{}}$ ${\displaystyle \frac{h}{}}$$(\$$displaystyle$1-${\$$tfrac$ ${y}{$h$\})$ ${\displaystyle \frac{\mathrm{또는}}{}}$h - ${\displaystyle \frac{}{}}$ $h(\$displaystyle {$tfrac {h-y$}{h$\}\})$입니다. 여기서 h는 베이스 평면으로부터 단면까지의 수직 거리입니다.단면의 면적은 형상의 스케일 팩터의 제곱에 비례하므로 높이 y에서의 단면의${\displaystyle \frac{\mathrm{면적}}{}}$은${\displaystyle \frac{}{}}$b$($${\displaystyle \frac{{h\mathrm{}}^{}}{}}$ ${\displaystyle \frac{{}^{}}{}}$ y) ${\displaystyle \frac{{2h\mathrm{}}^{}}{}}$2$({\tfrac${($h-y)}{h^{$2$\}\}\})$이다.또는 b와 h가 모두 ${\displaystyle \frac{{}^{}}{}}$이므로 b${\displaystyle \frac{{}^{}}{}\mathrm{h2}(h}$ - $)$ $디스플레이$ {$bfrac}.$$$볼륨은 적분에 의해 주어집니다.

${\displaystyle {\frac {b} {h^{2}\int _{0}^{h}(h-y)^{2},dy=paramfrac {-b}{3h^{2}}(h-y)^{3}_{0}=paramtfrac {3}{3}{3}.$

같은 $방정식{\displaystyle }$ ${\displaystyle V\frac{\mathrm{}}{}}$ ${\displaystyle =}$ ${\displaystyle 1}$ ${\displaystyle \frac{3}{}}$ h (\$displaystyle$ V =$tfrac {1}$ {$3}{}$}} }$$})는 베이스가 있는 원뿔에도 적용된다.이것은 위의 것과 유사한 논거에 의해 증명될 수 있다; 원뿔의 부피를 참조하라.

예를 들어, 밑면이 변 길이가 s인 n변 정다각형이고 높이가 h인 피라미드의 부피는 다음과 같다.

${\displaystyle V=svfrac {n}{12}}hs^{2}\cot {frac {pi }{n}.}$

직사각형의 밑면을 가진 피라미드에 대한 미적분 없이 이 공식은 정확하게 도출될 수 있다.단위 입방체를 고려합니다.정육면체 중심에서 8개의 정점 각각에 이르는 선을 그립니다.이렇게 하면 입방체가 베이스 영역 1과 높이 1/2의 6개의 동일한 정사각형 피라미드로 분할됩니다.각 피라미드는 분명히 1/6의 부피를 가지고 있다.이로부터 피라미드 부피 = 높이 × 베이스 면적 / 3을 추론한다.

다음으로 입방체를 3방향으로 균등하게 부피 abc를 갖는 직사각형 입체 모서리가 a, b, c가 되도록 균등하게 확장한다.안에 있는 6개의 피라미드 각각도 마찬가지로 확장되어 있다.그리고 각 피라미드는 같은 부피 abc/6을 가지고 있습니다.피라미드 쌍의 높이가 a/2, b/2 및 c/2이므로 피라미드 부피 = 높이 × 베이스 면적 / 3을 다시 볼 수 있습니다.

변삼각형이 등변일 때 부피의 공식은 다음과 같습니다.

${\displaystyle V=black {1}{12}ns^{3}\cot \leftfrac {\pi }{n}}}{\flac {1-{\flac {1}{4\sin ^2}{\tfrac {{pi }}}}}}}}}}}.}$

이 공식은 n = 2, 3, 4, 5에만 적용되며, 부피가 0인 경우 n = 6에도 적용됩니다(즉, 피라미드 높이는 0).^{[citation needed]}

표면적

피라미드의 표면적은 ${\displaystyle S}$ A ${\displaystyle =B}$ + ${\displaystyle 1\frac{\mathrm{}}{}}$ ${\displaystyle 2}$P ${\displaystyle L}$({$displaystyle$ SA$=B+{\tfrac {1}{2})$이다.$PL$ 여기서 B는 베이스 면적, P는 베이스 둘레, $경사{\displaystyle }$ 높이 ${\displaystyle L\sqrt{{}^{}}}$ ${\displaystyle =}$ ${\displaystyle \sqrt{{h\mathrm{}}^{}{}^{}}}$ +$$ 2 ({$displaystyle$ L =$sqrt {h^{$2} + $r^{2$})$\}\}\}\}\}.$ 여기서 h는 피라미드 고도, r은 베이스의 반지름입니다.

중심

피라미드의 중심은 정점과 베이스의 중심을 연결하는 선분에 있습니다.솔리드 피라미드의 경우 중심은 베이스에서 정점까지의 거리의 1/4입니다.

n차원 피라미드

2차원 피라미드는 꼭대기라고 불리는 비선형의 점으로 연결된 바닥 모서리에 의해 형성된 삼각형이다.

4차원 피라미드는 다면체 피라미드라고 불리며, 4공간 초평면의 3공간 초평면에 있는 다면체에 의해 그 초평면에서 다른 점이 떨어져 있습니다.

고차원 피라미드도 비슷하게 구성되어 있다.

심플화 패밀리는 삼각형, 사면체, 5셀, 5심플렉스 등에서 증가하는 모든 차원의 피라미드를 나타냅니다.n차원 심플렉스는 가장자리에 의해 연결된 모든 정점 쌍, 면을 정의하는 정점의 모든 3배, 사면체 셀을 정의하는 점의 모든 4배 등을 갖는 최소 n+1 정점을 가진다.

다면체 피라미드

4차원 기하학에서 다면체 피라미드는 베이스 다면체 셀과 정점으로 구성된 4개의 폴리토프이다.측면 면은 피라미드 셀로, 각각 기본 다면체와 정점으로 구성됩니다.다면체 피라미드의 정점과 가장자리는 평면 그래프(기반의 그래프)에 하나의 정점(정점)을 추가하여 형성된 그래프인 정점 그래프의 예를 형성합니다.

규칙 5셀(4-단순)은 사면체 피라미드의 한 예이다.외주반경이 1 미만인 균일한 다면체는 정사면체 변을 가진 다면체 피라미드를 만들 수 있다.v 정점, e 엣지 및 f 면을 가진 다면체는 v+1 정점, e+v 엣지, f+e 면 및 1+f 셀을 가진 다면체 피라미드 상의 밑면이 될 수 있다.

축 대칭을 가진 4D 다면체 피라미드는 Schlegel 다이어그램(기본 다면체의 중심에 정점을 배치하는 3D 투영)을 사용하여 3D로 시각화할 수 있습니다.

등변 균일한 다면체 기반 피라미드(슐레겔 다이어그램)

대칭	[1,1,4]	[1,2,3]	[1,3,3]	[1,4,3]		[1,5,3]
이름.	정사각형 피라미달 피라미드	삼각 프리즘 피라미드	사면체 피라미드	입방체 피라미드	팔면체 피라미드	이십면체 피라미드
세그먼트코라 색인[7]	K4.4	K4.7	K4.1	K4.26.1	K4.3	K4.84
높이	0.707107	0.645497	0.790569	0.500000	0.707107	0.309017
이미지 (베이스)
기초	광장 피라미드	삼각형의 프리즘	사면체	큐브	팔면체	이십면체

볼록한 4-폴리토프는 내부점을 더해 각 패싯에서 중심점까지 1개의 피라미드를 생성함으로써 다면체 피라미드로 분할할 수 있다.이것은 볼륨을 계산하는 데 유용할 수 있습니다.

다면체 피라미드의 4차원 하이퍼볼륨은 기본 다면체 부피의 1/4에 수직 높이를 곱한 반면 삼각형의 부피는 기본 다면체 부피의 1/2 길이 곱하기 높이의 1/3이고 피라미드디어 피라미드의 부피는 기본 다면체 부피의 1/3이다.

다면체 피라미드의 3차원 표면적은 S ${\displaystyle V}$ ${\displaystyle =B}$ + ${\displaystyle 1\frac{\mathrm{}}{}}$ ${\displaystyle 3}$ A$$ {\$display style$ SV =$B+{\tfrac {1}{$$3$}}이다.$AL$ 여기서 B는 베이스 부피, A는 베이스 표면적, L은 경사 높이(가로쪽 피라미드 셀의 높이) $L{\displaystyle }$ ${\displaystyle =}$ ${\displaystyle h\sqrt{{}^{}{2\mathrm{}}^{}}}$ + ${\displaystyle \sqrt{{r\mathrm{}}^{}}}$2({$displaystyle$ L$=sqrt {h^{$2}+$r^{2$})$\}\}\}\}\}:$ 여기서 h는 높이, r은 반지름입니다.

「 」를 참조해 주세요.

• 이원체
• 원뿔(기하학)
• 삼각뿔 (화학)
• 좌절.

레퍼런스

외부 링크

• Weisstein, Eric W. "Pyramid". MathWorld.