표면장력

물방울을 자르기 위한 이 시도에서 표면 장력과 소수성이 상호작용합니다.

비누를 이용한 표면장력 실험실증

표면 장력은 정지해 있는 액체 표면이 가능한 최소 표면적으로 줄어드는 경향입니다.표면장력은 면도날이나 곤충(물거미)과 같이 물보다 밀도가 높은 물체가 부분적으로 물에 잠기지 않고 수면에 떠오를 수 있도록 하는 것입니다.

액체-공기 계면에서 표면 장력은 공기 중 분자보다 액체 분자가 서로에게 더 많이 끌리는 것(응집으로 인해)에서 기인합니다.^[1]

게임에는 두 가지 주요 메커니즘이 있습니다.하나는 액체를 수축시키는 표면 분자의 안쪽 힘입니다.^[2]^[3]두 번째는 액체 표면에 평행한 접선력입니다.^[3]이러한 접선력을 일반적으로 표면장력이라고 합니다.순 효과는 액체가 마치 표면이 늘어진 탄성막으로 덮여 있는 것처럼 행동한다는 것입니다.그러나 표면 장력이 액체-공기 또는 액체-증기 계면의 고유 특성인 반면 탄성막의 장력은 막의 변형량에 따라 달라지므로 이 비유를 너무 멀리 해서는 안 됩니다.^[4]

물 분자가 수소 결합의 그물을 통해 서로 상대적으로 높은 인력을 받기 때문에, 물은 대부분의 다른 액체보다 높은 표면 장력(20°C에서 미터당 72.8 밀리뉴톤(mN)을 가집니다.표면장력은 모세혈관 현상에서 중요한 요소입니다.

표면 장력은 단위 길이당 힘 또는 단위 면적당 에너지 차원을 갖습니다.^[4]이 둘은 동등하지만, 면적 단위당 에너지를 언급할 때 표면 에너지라는 용어를 사용하는 것이 일반적인데, 이는 고체에도 적용된다는 점에서 더 일반적인 용어입니다.

재료 과학에서 표면 장력은 표면 응력 또는 표면 에너지에 사용됩니다.

원인들

응집력 때문에, 표면에서 떨어진 곳에 위치한 분자는 이웃한 액체 분자에 의해 모든 방향으로 똑같이 끌어당겨져 순 힘이 0이 됩니다.표면에 있는 분자들은 모든 면에 같은 분자를 가지고 있지 않기 때문에 안쪽으로 당겨집니다.이로 인해 일부 내부 압력이 발생하고 액체 표면이 최소 면적으로 수축됩니다.^[2]

또한 액체-공기 계면에서 표면과 평행한 장력이 있는데, 이는 물 분자의 응집 특성 때문에 외부 힘에 저항하게 됩니다.^[2]^[3]

같은 종류의 분자 사이에 작용하는 인력을 응집력이라고 하고, 다른 종류의 분자 사이에 작용하는 인력을 접착력이라고 합니다.액체의 응집력과 용기의 재질과의 접착력 사이의 균형에 따라 습윤 정도, 접촉각, 메니스커스의 형태가 결정됩니다.응집력이 지배적일 때(특히 접착 에너지가 응집 에너지의 절반 미만) 습윤이 적고 메니스커스는 수직 벽에서 볼록합니다(유리 용기의 수은과 같이).반면, 접착력이 우세할 때(접착 에너지가 응집 에너지의 절반 이상일 때), 습윤이 높고 유사한 메니스커스가 오목합니다(유리 안의 물에서처럼).

표면 장력은 액체 방울의 모양에 책임이 있습니다.쉽게 변형되지만, 물방울은 표면층의 응집력의 불균형에 의해 구형으로 당겨지는 경향이 있습니다.다른 힘이 없다면, 사실상 모든 액체의 방울은 대략적으로 구형일 것입니다.구형은 라플라스의 법칙에 따라 표면층의 필요한 "벽장 장력"을 최소화합니다.

표면장력을 보는 또 다른 방법은 에너지에 관한 것입니다.이웃과 접촉하는 분자는 혼자일 때보다 낮은 에너지 상태에 있습니다.내부 분자는 가능한 한 많은 이웃을 가지고 있지만, 경계 분자는 (내부 분자에 비해) 누락된 이웃을 가지고 있으므로 더 높은 에너지를 가지고 있습니다.액체가 에너지 상태를 최소화하려면 더 높은 에너지 경계 분자의 수가 최소화되어야 합니다.경계 분자의 수가 최소화되면 표면적이 최소화됩니다.^[5]표면적을 최소화하기 때문에 표면은 매끄러운 모양을 취할 것입니다.

물리학

물리 단위

기호 γ(또는 σ 또는 T)로 표시되는 표면 장력은 단위 길이당 힘으로 측정됩니다.SI 단위는 m당 뉴턴이지만 cgs 단위인 cm당 다이네 단위도 사용됩니다.예를 들면.^[6]

\gamma =1~\mathrm {\frac {dyn}{cm}} =1~\mathrm {\frac {erg}{cm^{2}} =1~\mathrm {\frac {10^{-7}\,m\cdot N}{10^{-4}\,m^{2}} =0.001~\mathrm {\frac {N}{m} =0.001~\frac {J}{m^{2}} .

정의.

표면장력은 힘이나 에너지로 정의할 수 있습니다.

힘으로 따지면

액체의 $표면장력$ γ은 단위 길이당 힘입니다.오른쪽 그림에서 직사각형 프레임은 "U"자 모양을 이루는 세 개의 움직이지 않는 면(검은색)과 오른쪽으로 미끄러질 수 있는 네 번째 움직일 수 있는 면(파란색)으로 구성되어 있습니다.표면 장력은 파란색 막대를 왼쪽으로 당깁니다. 이동식 측면을 유지하는 데 필요한 힘 $F$ 는 이동식 측면의 길이 $L$ 에 비례합니다. $따라서$ F $/ L$ 비율은 액체의 고유 특성(성분, 온도 등)에만 의존하며 형상에는 의존하지 않습니다.예를 들어, 프레임의 형상이 더 복잡했다면, 이동 가능한 변의 길이 $L$ 과 슬라이딩을 멈추기 위해 필요한 힘 $F$ 를 갖는 비율 $F / L$ 은 모든 형상에서 동일한 것으로 나타났습니다.따라서 표면 장력을 다음과 같이 정의합니다.

\gamma ={\frac {F}{2L}}

12의 이유는 필름에 두 개의 면(두 개의 면)이 있고 각각의 면은 힘에 동일하게 기여하므로 단일 면이 기여하는

힘

은 γL =

F / 2

입니다.

에너지면에서

액체의 $표면장력$ γ은 액체의 표면적 변화에 대한 액체의 에너지 변화의 비율입니다.이것은 힘의 관점에서 이전의 정의와 쉽게 관련될 수 있습니다:^[7] 만약 $F$ 가 변이 미끄러지기 시작하는 것을 멈추기 위해 필요한 힘이라면, 이것은 또한 변이 일정한 속도로 미끄러지는 상태를 유지하는 힘입니다. (뉴턴의 제2법칙에 의해)그러나 (힘이 가해진 방향으로) 측면이 오른쪽으로 움직이고 있다면, 가해진 힘이 액체에 작용하는 동안 늘어난 액체의 표면적이 증가하고 있는 것입니다.이는 표면적이 증가하면 필름의 에너지가 증가한다는 것을 의미합니다.δ $x$ 가 측면을 거리만큼 이동할 때 힘 $F$ 가 하는 일은 W = $F$ δ $x$ 입니다. 동시에 필름의 전체 면적은 δ $A$ = 2L δx만큼 증가합니다(액체는 두 측면, 두 표면을 가지므로 계수 2가 여기에 있음).따라서 γ = $1 / 2F / L$ 의 분자와 분모 모두에 δx를 곱하면 다음을 얻을 수 있습니다.

\gamma ={\frac {F}{2L}}={\frac {F\Deltax}{2L\Delta x}}={\frac {W}{\Delta A}}

이 작업

W

는, 일반적인 주장에 의해, 퍼텐셜 에너지로 저장된 것으로 해석됩니다.따라서 표면장력은 SI 시스템에서 제곱미터당 줄과 cgs 시스템에서 cm당² ergs로 측정할 수도 있습니다.기계 시스템은 최소 위치 에너지의 상태를 찾으려고 노력하기 때문에, 자유 액체 방울은 자연스럽게 주어진 부피에 대해 최소 표면적을 갖는 구 모양을 가정합니다.단위 면적당 에너지 측정과 단위 길이당 힘의 등가성은 치수 분석을 통해 입증될 수 있습니다.^[8]

영향들

물.

일반 물에서는 표면 장력의 몇 가지 영향을 볼 수 있습니다.

나뭇잎과 같은 밀랍 모양의 표면에 빗물을 비딩하는 것.물은 왁스에 약하게 달라붙고 스스로 강하게 달라붙기 때문에, 물은 물방울로 뭉쳐집니다.표면 장력은 구면의 부피 대비 표면적이 가장 작기 때문에 구면에 가까운 모양을 제공합니다.
액체 덩어리가 늘어나면 방울이 형성됩니다.(아래) 애니메이션은 수도꼭지에 달라붙은 물이 표면 장력이 더 이상 수도꼭지에 연결된 물방울을 유지할 수 없을 정도로 늘어날 때까지 질량을 증가시키는 것을 보여줍니다.그리고 나서 그것은 분리되고 표면 장력은 방울을 구체로 형성합니다.만약 수도꼭지에서 물줄기가 흘러나온다면, 그 물줄기는 떨어지는 동안 방울로 쪼개질 것입니다.중력은 물줄기를 뻗고, 표면 장력은 그것을 구체로 꼬집습니다.^[9]
물보다 밀도가 높은 물체의 부유는 물체가 젖지 않을 때 발생하며, 표면 장력에 의해 발생하는 힘에 의해 물체의 무게가 견딜 수 있을 정도로 충분히 작을 때 발생합니다.^[5]예를 들어, 물거미들은 다음과 같은 방식으로 연못의 표면을 걸을 때 표면장력을 사용합니다.물거미 다리의 비침투성은 다리 분자와 물 분자 사이에 인력이 없다는 것을 의미하기 때문에 다리가 물 위로 내려올 때 물의 표면장력은 다리에 의한 변형으로 평탄성을 회복하려 할 뿐입니다.물의 이러한 행동은 물의 질량이 물이 지탱할 수 있을 정도로 충분히 작은 한 물의 표면에 서 있을 수 있도록 물거미를 위쪽으로 밀어 올립니다.물의 표면은 탄성 필름처럼 행동합니다: 곤충의 발은 물의 표면에 움푹 패인 부분을 발생시키고, 표면적을^[10] 증가시키고 물의 표면 곡률을 최소화하는 경향이 곤충의 발을 위로 밀어 올립니다.
오일과 물(이 경우 물과 액체 왁스)의 분리는 이종 액체 사이의 표면에 장력이 발생하여 발생합니다.이러한 형태의 표면장력은 "계면장력"이라고 불리지만, 그 화학적 성질은 동일합니다.
와인의 눈물은 알코올 음료가 들어있는 잔의 측면에 방울과 지류가 형성되는 것입니다.그 원인은 물과 에탄올의 상이한 표면 장력 사이의 복잡한 상호 작용입니다. 에탄올에 의한 물의 표면 장력 수정과 물보다 빠르게 증발하는 에탄올의 조합에 의해 유도됩니다.

가. 나뭇잎에 물비딩
나. 수도꼭지에서 물이 뚝뚝 떨어지는 것
다. 물거미는 표면장력 때문에 액체의 꼭대기에 머무름
라. 이종 액체간의 상호작용이 있는 용암램프: 물과 액체 왁스
E. '와인의 눈물' 현상을 보여주는 사진.

계면활성제

표면장력은 다른 일반적인 현상에서 볼 수 있는데, 특히 계면활성제를 사용하여 표면장력을 감소시킬 때 더욱 그렇습니다.

비눗방울의 표면적은 매우 넓으며 질량은 매우 적습니다.순수한 물속의 기포는 불안정합니다.그러나 계면활성제의 첨가는 기포에 대한 안정화 효과를 가질 수 있습니다(마랑고니 효과 참조).계면활성제는 실제로 물의 표면장력을 3배 이상 감소시킵니다.
에멀젼은 표면 장력이 작용하는 콜로이드의 한 종류입니다.순수한 물에 매달린 작은 기름 조각들은 자발적으로 훨씬 더 큰 덩어리로 모이게 될 것입니다.그러나 계면활성제가 있으면 표면 장력이 감소하여 물 속의 미세한 기름 방울을 안정적으로 유지할 수 있습니다(또는 그 반대도 마찬가지입니다.

표면곡률 및 압력

표면 장력은 표면의 작은(차분) 부분에 작용합니다. $δθ$ 와 $δθ$ 는 $패치$ 치수에 대한 휘어진 정도를 나타냅니다.장력과 압력의 균형은 영-라플라스 방정식으로 이어집니다.

인장된 표면에 정상적인 힘이 작용하지 않으면 표면이 평평한 상태를 유지해야 합니다.그러나 표면의 한쪽 면의 압력과 다른 쪽 면의 압력이 다를 경우 압력 차이의 곱셈 표면적은 정상적인 힘이 됩니다.표면 장력이 압력에 의해 힘을 상쇄하려면 표면이 휘어져야 합니다.이 다이어그램은 작은 표면 조각의 표면 곡률이 어떻게 그 조각의 중심에 정상적으로 작용하는 표면 장력의 순 성분으로 이어지는지를 보여줍니다.모든 힘이 균형을 이룰 때 결과 방정식은 영-라플라스 방정식으로 알려져 있습니다.^[11]

\Deltap=\gamma \left ({\frac {1}{R_{x}}+{\frac {1}{R_{y}}\right)

여기서:

$δp$ 는 라플라스 압력으로 알려진 압력 차이입니다.
$γ$ 은 표면장력입니다.
$R$ 과_x $R$ 은_y 표면에 평행한 각 축의 곡률 반경입니다.

오른쪽 괄호 안의 양은 (정규화에 따라) 실제로 표면의 평균 곡률의 두 배입니다.이 방정식에 대한 해는 물방울, 웅덩이, 메니시, 비눗방울, 그리고 표면장력에 의해 결정되는 다른 모든 모양들(예를 들어 물거미의 발이 연못의 표면에 내는 인상들의 모양)을 결정합니다.아래 표는 물방울의 내부 압력이 반지름이 감소함에 따라 어떻게 증가하는지를 보여줍니다.아주 작은 방울은 효과가 미세하지만, 방울 크기가 분자 크기에 가까워지면 압력 차이가 엄청납니다.(단일 분자의 한계에서는 개념이 무의미해집니다.)

STP에서 서로 다른 반경의 물방울에 대한

δp

액적반경	1mm	0.1mm	1 μm	10nm
$δp$ (atm)	0.0014	0.0144	1.436	143.6

부동 객체

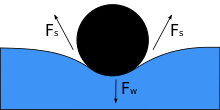
물체가 액체 위에 놓였을 때, 물체의 $무게 w$ F는 표면을 짓누르고, 표면 장력과 아래쪽 힘이 같아지면 물체와 접촉하는 지점에서 물의 표면과 평행한 양쪽 $F$ 의_s 표면 장력으로 균형을 잡습니다.신체의 작은 움직임으로 인해 물체가 가라앉을 수 있습니다.접촉각이 줄어들면 표면장력이 감소합니다.두 $F s$ 화살표의 수평 성분은 서로 반대 방향을 가리키므로 서로 취소하지만 수직 성분은 같은 방향을 가리키므로 $F$ 의_w 균형을 맞추기 위해 합산됩니다^[5].이러한 현상이 발생하기 위해서는 물체의 표면이 젖지 않아야 하며, 물체의 무게는 표면 장력이 이를 지탱할 수 있을 만큼 충분히 낮아야 합니다.만약 $m$ 이 바늘의 질량과 중력에 의한 g $가속도$ 를 나타낸다면, 우리는

F_{\mathrm {w} = 2F_{\mathrm {s}}\sin \theta \quad \좌측 화살표 \quad mg=2\gamma L\sin \theta

액체표면

엄격한 수학적 방법을 사용하여 임의의 모양 틀에 의해 경계를 이루는 최소 표면의 모양을 찾는 것은 어려운 일이 될 수 있습니다.그러나 철사로 틀을 만들고 비누 용액에 담궈 놓으면 몇 초 안에 결과적인 비누 필름에 국소적으로 최소 표면이 나타날 것입니다.^[8]^[13]

그 이유는 영-라플라스 방정식에서 볼 수 있듯이 유체 인터페이스 전체의 압력 차이가 평균 곡률에 비례하기 때문입니다.개방형 연속막의 경우 압력 차이가 0이므로 평균 곡률이 0이고 최소 표면은 평균 곡률이 0인 특성을 갖습니다.

접촉각

액체의 표면은 그 액체와 다른 매질 사이의 경계면입니다.^{[note 1]}예를 들어 연못의 꼭대기 표면은 연못 물과 공기 사이의 경계면입니다.그렇다면 표면장력은 액체만의 특성이 아니라 액체가 다른 매질과 접촉하는 특성입니다.액체가 용기 안에 있는 경우, 상부 표면에 있는 액체/공기 인터페이스 외에 액체와 용기 벽 사이에도 인터페이스가 있습니다.액체와 공기 사이의 표면 장력은 보통 용기 벽과의 표면 장력과 다릅니다.그리고 두 표면이 만나는 곳에서 그들의 기하학적 구조는 모든 힘이 균형을 이루도록 해야 합니다.^[8]^[11]

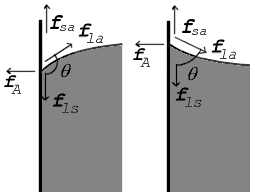두 표면이 만나는 곳에서 $접촉각$ 인 θ을 형성하는데, 이는 표면의 접선이 고체 표면과 이루는 각도입니다.위의 다이어그램에 표시된 것처럼 액체를 통해 각도를 측정합니다.오른쪽 그림은 두 가지 예를 보여 줍니다.액체-공기 인터페이스, 액체-고체 인터페이스 및 고체-공기 인터페이스에 대한 장력이 표시됩니다.왼쪽의 예는 액체-고체와 고체-공기 표면 장력의 $차이$ 인 γ $-$ γ가 액체-공기 표면 장력인 γ보다 작지만, 그럼에도 불구하고 양의 값을 갖는 경우입니다.

\gamma _{\mathrm {la}}>\gamma _{\mathrm {ls}}-\gamma _{\mathrm {sa}>0

이 다이어그램에서 수직력과 수평력 모두 평형이라고 하는 접촉점에서 정확하게 상쇄되어야 합니다. $f la$ 의 $수평 A$ 성분은 접착력 f 에 의해 상쇄됩니다.^[8]

f_{\mathrm {A} = f_{\mathrm {la}}\sin \theta

그러나 힘의 균형을 더 잘 보여주는 것은 수직 방향입니다.f 의 $수직 la$ 성분은 솔리드 표면을 따라 작용하는 힘의 차이, $f ls$ - f 를_sa 정확하게 상쇄해야 합니다.^[8]

f_{\mathrm {ls}}-f_{\mathrm {sa} =-f_{\mathrm {la}}\cos \theta

일부 액체-고체 접촉각^[8]

액체.

단단한

연락
각

물.

소다석회 유리

납유리

0°

파라핀 왁스

107°

실버

90°

요오드화메틸

소다석회 유리

29°

납유리

30°

융해 석영

33°

수성.

소다석회 유리

140°

힘은 각각의 표면 장력에 정비례하기 때문에 다음과 같은 결과도 얻을 ^[11]수 있습니다.

\gamma _{\mathrm {ls}}-\gamma _{\mathrm {sa} =-\gamma _{\mathrm {la}}\cos \theta

어디에

$γ$ 은 액체-고체 표면 장력이며,
$γ$ 은 액체-공기 표면 장력입니다.
$γ$ 은 고체-공기 표면 장력입니다.
$θ$ 는 접촉각으로 오목한 메니스커스는 접촉각이 90° 미만이고 볼록한 메니스커스는 접촉각이 90° 이상입니다.

이는 액체-고체 및 고체-공기 표면 장력, γ $-$ γ의차이가 직접 측정하기는 어렵지만 액체-공기 표면 장력, γ 및 쉽게 측정 가능한 전진 및 후퇴 접촉각의 함수인 평형 접촉각, θ에서 추론할 수 있음을 의미합니다(본조 접촉각 참조).

이와 같은 관계는 오른쪽 다이어그램에 존재합니다.그러나 이 경우 접촉 각도가 90° 미만이므로 액체-고체/고체-공기 표면 장력 차이는 음이어야 합니다.

\gamma _{\mathrm {la}}>0>\gamma _{\mathrm {ls}}-\gamma _{\mathrm {sa}}

특수 접촉각

접촉 각도가 90°인 물-은 계면의 특수한 경우 액체-고체/고체-공기 표면 장력 차이는 정확히 0입니다.

접촉 각도가 정확히 180°인 경우도 특별합니다.특별하게 준비된 테프론이 들어간 물이 이에 접근합니다.^[11]접촉각 180°는 액체-고체 표면 장력이 액체-공기 표면 장력과 정확히 같을 때 발생합니다.

\gamma _{\mathrm {la}}=\gamma _{\mathrm {ls}}-\gamma _{\mathrm {sa}}>0\qquad \theta =180^{\circ}

수직관내 액체

오래된 스타일의 수은 기압계는 수은이 부분적으로 채워진 직경 약 1cm의 수직 유리관과 채워지지 않은 부피에 진공(Torricelli's vacuum)이 있는(오른쪽 그림 참조) 수직 유리관으로 구성되어 있습니다.튜브 중앙의 수은 레벨이 가장자리보다 높아 수은 돔의 상부 표면을 형성합니다.수은의 상부 표면이 관의 전체 단면에 걸쳐 평평하다면 수은의 전체 기둥의 질량 중심은 약간 더 낮을 것입니다.하지만 돔 모양의 꼭대기는 수은 덩어리 전체에 비해 표면적이 약간 적습니다.다시 두 효과를 결합하여 총 위치 에너지를 최소화합니다.이와 같은 표면 형상을 볼록한 반월상(半月狀)이라고 합니다.

우리는 수은이 유리에 전혀 달라붙지 않기 때문에 유리와 접촉하는 표면 부분을 포함하여 수은의 전체 질량의 표면적을 고려합니다.따라서 수은의 표면장력은 유리와 접촉하는 부분을 포함한 전체 표면적에 작용합니다.유리가 아닌 구리로 만든 튜브라면 상황은 매우 달라질 것입니다.수은은 구리에 공격적으로 달라붙습니다.따라서 구리 튜브에서는 튜브 중앙의 수은 수준이 가장자리보다 낮을 것입니다(즉, 오목한 반월상이 될 것입니다).액체가 용기의 벽에 달라붙는 상황에서, 우리는 용기와 접촉하는 유체의 표면적 부분이 음의 표면장력을 갖는다고 생각합니다.그러면 유체가 접촉 표면적을 극대화하기 위해 작동합니다.따라서 이 경우 컨테이너와 접촉하는 면적을 늘리면 위치 에너지가 증가하기보다는 감소합니다.이러한 감소는 용기 벽 근처에서 유체를 들어올리는 것과 관련된 증가된 전위 에너지를 보상하기에 충분합니다.

모세관 상승 및 하강 그림.적색=접촉각 90°미만, 청색=접촉각 90°초과

튜브가 충분히 좁고 벽에 액체 접착력이 충분히 강하면 표면 장력이 모세관 작용으로 알려진 현상으로 액체를 끌어 올릴 수 있습니다.기둥이 들어올려지는 높이는 주린의 법칙에 따라 다음과 같습니다.^[8]

h={\frac {2\gamma {{\mathrm {la}}\cos \theta}{\rhogr}

어디에

$액체$ 가 들어올려진 높이,
$γ$ 은 액체-공기 표면 장력입니다.
$ρ$ 은 액체의 밀도이고,
$r$ 은 모세관의 반지름이고,
$g$ 는 중력에 의한 가속도,
$θ$ 는 위에서 설명한 접촉각입니다.유리 용기의 수은과 $같이$ θ이 90°보다 크면 액체가 들뜨기 보다는 눌려집니다.

표면의 웅덩이

접촉 각도가 180°인 웅덩이 가장자리의 종단 곡선.곡선은 다음과 같은 공식으로 나타납니다.^[11] ${\displaystyle x-x_{0}={\frac {1}{2}}H\cosh ^{-1}\left({\frac {H}}\right)-H{\sqrt {1-{\frac {h^{2}}{H^{2}}}}}.$ 여기서 ${\textstyle H=2{\sqrt {{\gamma }/{g\rho }}}}$ = ${\textstyle H=2{\sqrt {{\gamma }/{g\rho }}}}$ γ ${\textstyle H=2{\sqrt {{\gamma }/{g\rho }}}}$ / ${\textstyle H=2{\sqrt {{\gamma }/{g\rho }}}}$ ρ ${\textstyle$ H = $2{\sqrt {\$ gamma }/{ $g\rho}}}}$

수평의 평평한 유리 시트에 수은을 붓으면 눈에 띄는 두께의 웅덩이가 생깁니다.물웅덩이는 두께가 0.5cm가 조금 안 될 정도로만 펼쳐져 있을 것이고, 시너는 없을 것입니다.다시 이것은 수은의 강한 표면장력의 작용 때문입니다.액체 질량은 최대한 많은 수은을 낮은 수준으로 끌어내기 때문에 평평해지지만 표면장력은 동시에 전체 표면적을 감소시키는 작용을 합니다.타협의 결과는 거의 고정된 두께의 웅덩이입니다.

동일한 표면 장력 시연은 물, 석회수 또는 심지어 식염수를 사용할 수 있지만 물이 달라붙지 않는 물질로 구성된 표면에서만 수행할 수 있습니다.왁스는 그런 물질입니다.매끄럽고 평평하며 수평인 왁스 표면에 붓는 물은, 왁스를 바른 유리판이 유리에 붓는 수은과 비슷하게 행동할 것이라고 말합니다.

접촉각이 180°인 표면의 액체 웅덩이의 두께는 다음과 같습니다.^[11]

h=2{\sqrt {\frac {\gamma }{g\rho}}}

어디에

$그$ 웅덩이의 깊이는 센티미터 또는 미터입니다.
$γ$ 는 $액체$ 의 표면장력을 센티미터당 다인 또는 미터당 뉴톤 단위로 나타낸 것입니다.
$g$ 는 중력에 의한 가속도이며 980cm/s² 또는 9.8m/s와² 같습니다.
$ρ$ 는 $세제곱$ 센티미터 당 그램 또는 세제곱 미터 당 킬로그램 단위의 액체의 밀도입니다.

접촉각이 낮아지면 퍼들의 깊이가 감소함을 보여주는 그림

실제로는 어떤 액체와도 180°의 접촉각을 갖는 표면이 거의 없기 때문에 웅덩이의 두께는 위 공식에 의해 예측된 것보다 약간 적을 것입니다.접촉 각도가 180° 미만일 경우 두께는 다음과 같습니다.^[11]

h = {\sqrt {\frac {2\gamma {{\mathrm {la}}\left(1-\cos \theta \right)}{g\rho }}}

유리의 수은의 경우 γ = 487 dyn/cm, ρ = 13.5 g/cm, θ = 140°로 $h$ = 0.36cm입니다.25°C의 파라핀에 있는 물의 경우 γ = 72 dyn/cm, ρ = 1.0 g/cm, θ = 107°로 $h$ = 0.44cm입니다.

이 공식은 또한 접촉각이 0°일 때 액체가 표면 위로 미세한 얇은 층으로 퍼질 것이라고 예측합니다.그러한 표면은 액체에 의해 완전히 젖을 수 있다고 합니다.

시냇물이 방울로 갈라지는 것.

우리 모두는 일상 생활에서 수도꼭지에서 나오는 물줄기가 아무리 부드럽게 수도꼭지에서 뿜어져 나오더라도 물방울로 쪼개질 것이라는 것을 관찰합니다.이것은 플래토-레일리 불안정성이라고 불리는 현상 때문인데,^[11] 이는 전적으로 표면장력의 영향의 결과입니다.

이 불안정성에 대한 설명은 시냇물에 작은 섭동이 존재하는 것으로 시작됩니다.이런 것들은 시냇물이 아무리 부드럽게 흐르더라도 항상 존재합니다.섭동이 정현파 성분으로 해결되면 일부 성분은 시간에 따라 증가하고 다른 성분은 시간에 따라 감소한다는 것을 알 수 있습니다.시간이 지남에 따라 성장하는 것 중 일부는 다른 것보다 더 빠른 속도로 성장합니다.구성 요소가 쇠퇴하거나 성장하는지, 그리고 얼마나 빨리 성장하는지는 전적으로 해당 요소의 파수(센티미터당 몇 개의 정점과 수조를 측정하는 척도)와 원래 원통형 스트림의 반경에 의해 결정됩니다.

갤러리

숟가락에서 튕겨져 나오는 움직이는 물의 시트가 깨지는 것.
흐르는 물이 손에 달라붙는 사진.표면 장력은 흐름과 손 사이에 한 장의 물을 만듭니다.
비누 거품은 표면 장력과 내부 공압의 균형을 유지합니다.
표면 장력은 동전이 가라앉는 것을 막습니다: 동전은 분명히 물보다 밀도가 높기 때문에, 질량 균형을 맞추기 위해 부력이 자신보다 더 큰 부피를 이동시켜야 합니다.
알루미늄 동전은 10°C의 물 표면에 떠 있습니다.여분의 무게는 동전을 바닥으로 떨어뜨릴 것입니다.
데이지.꽃 전체가 (방해받지 않는) 자유 표면의 수준 아래에 놓여 있습니다.물은 가장자리를 중심으로 부드럽게 솟아오릅니다.표면 장력은 물이 꽃잎 사이의 공기를 이동시켜 꽃을 잠기게 하는 것을 방지합니다.
금속 종이 클립이 물 위에 떠있습니다.보통 물이 넘치지 않고 조심스럽게 몇 개를 추가할 수 있습니다.
물 위에 떠있는 금속 종이 클립.조명 앞 그릴은 '컨투어 라인'을 형성하여 메탈 페이퍼 클립으로 인한 수면의 변형을 보여줍니다.

열역학

표면장력의 열역학적 이론

J.W. 깁스는 불연속면에 대한 개념을 바탕으로 열역학적 모세혈관 이론을 개발했습니다.^[14]깁스는 두 동형 물질 사이에 존재하는 미세하게 흐릿한 물리적 계면 어딘가에 날카로운 수학적 표면이 놓여 있는 경우를 고려했습니다.그는 표면의 위치를 정확히 선택하는 것이 다소 자의적이라는 것을 깨닫고 표면을 유연하게 두었습니다.계면은 주변 물질(온도 $T$ , 화학 $퍼텐셜$ μ)과 열 및 화학적 평형 상태로 존재하기 때문에, 깁스는 표면이 과잉 에너지, 과잉 엔트로피 및 과잉 입자를 가질 수 있는 경우를 고려하여 이 경우의 자연 자유 에너지 함수는 $U-TS-\mu _{1}N_{1}-\mu _{2}N_{2}\cdots$ $U-TS-\mu _{1}N_{1}-\mu _{2}N_{2}\cdots$ $U-TS-\mu _{1}N_{1}-\mu _{2}N_{2}\cdots$ - $U-TS-\mu _{1}N_{1}-\mu _{2}N_{2}\cdots$ $U-TS-\mu _{1}N_{1}-\mu _{2}N_{2}\cdots$ $U-TS-\mu _{1}N_{1}-\mu _{2}N_{2}\cdots$ $U-TS-\mu _{1}N_{1}-\mu _{2}N_{2}\cdots$ - $U-TS-\mu _{1}N_{1}-\mu _{2}N_{2}\cdots$ 2 $U-TS-\mu _{1}N_{1}-\mu _{2}N_{2}\cdots$ $U-TS-\mu _{1}N_{1}-\mu _{2}N_{2}\cdots$ ⋯ ${\display$ . $스타일 U-TS-\mu _{1}N_{1}-\mu _{2}N_{2}\cdots$ $U-TS-\mu _{1}N_{1}-\mu _{2}N_{2}\cdots$ 나중에 그랜드 퍼텐셜로 명명되고 기호 $ω$ ${\displaystyle$ \ $Omega}$ 이(가 $\Omega$ 지정된 수량입니다.

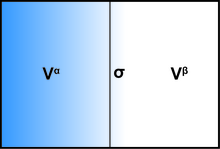
불연속면을 포함하는 $V$ 주어진 하위 볼륨 V $V$ 을(를) 고려하면, 볼륨은 수학적 표면에 의해 두 부분 A와 B로 분할되며, 볼륨 $V_{\text{A}}$ 는 ${\$ $A}}$ 및 $V_{\text{A}}$ $V_{\text{B}}$ {\ $displaystyle V_$ {\ $text}$ $B}},$ $V=V_{\text{A}}+V_{\text{B}}$ $=$ $V=V_{\text{A}}+V_{\text{B}}$ $V=V_{\text{A}}+V_{\text{B}}$ + V $V=V_{\text{A}}+V_{\text{B}}$ ${\displaystyle$ V $=$ $V_{\text{$ $A}}+V_{\text{$ $B}}$ 정확합니다 $V=V_{\text{A}}+V_{\text{B}}$ .이제, 두 부분 A와 B가 균질 유체(압력 $p_{\text{A}}$ ${\$ 인 경우 $A}},$ $p_{\text{B}}$ ${\$ $B$ 와 수학적 경계까지 완전한 균질성을 유지했으며, 표면 효과 없이 이 볼륨의 총 거대 퍼텐셜은 $-p_{\text{A}}V_{\text{A}}-p_{\text{B}}V_{\text{B}}$ $-p_{\text{A}}V_{\text{A}}-p_{\text{B}}V_{\text{B}}$ A $-p_{\text{A}}V_{\text{A}}-p_{\text{B}}V_{\text{B}}$ - $-p_{\text{A}}V_{\text{A}}-p_{\text{B}}V_{\text{B}}$ $-p_{\text{A}}V_{\text{A}}-p_{\text{B}}V_{\text{B}}$ ${\$ { $A}}V_{\text{$ $A}}-p_{\text{$ $B}}V_{\text{$ $B$ 관심 표면효과는 이를 수정한 것으로 $\Omega _{\text{S}}$ $ω$ $\Omega _{\text{S}}$ ${\displaystyle \Omega$ _ ${\text{$ $S}}:$ 따라서 $\Omega _{\text{S}}$ 볼륨의 총 그랜드 퍼텐셜은 다음과 같습니다.

{\displaystyle \Omega =-p_{\text{A}}V_{\text{A}}-p_{\text{B}}V_{\text{B}}+\Omega _{\text{S}}}.

충분히 거시적이고 완만한 곡면의 경우, 표면 자유 에너지는 단순히 표면적에 비례해야 합니다.^[14]^[15]

\Omega _{\text{S}}=\gamma A,

표면 장력 γ

\gamma

및 표면

A

A

{\displaystyle A

위에서 설명한 바와 같이, 각 면의 부피가 변하지 않는다고 가정할 때 표면적 A를 $dW$ = γ dA로 늘리는 데 필요한 기계적 작업을 의미합니다.열역학은 일정한 화학적 퍼텐셜과 온도를 가진 시스템의 경우 모든 자발적인 상태 변화는 이 자유 에너지 ω $\Omega$ 의 감소를 동반할 것을 요구합니다 $\Omega$ 즉,표면에서 주변 유체로 에너지와 입자의 이동 가능성을 고려한 총 엔트로피 증가이를 통해 액체 덩어리의 표면적을 줄이는 것이 다른 에너지 변화와 연결되지 않는 한 항상 자발적인 이유를 쉽게 이해할 수 있습니다.표면적을 넓히기 위해서는 일정량의 에너지를 더해야 한다는 것입니다.

깁스와 다른 과학자들은 표면의 정확한 미세한 위치에서의 임의성과 씨름해왔습니다.^[16]매우 촘촘한 곡률을 가진 미세한 표면의 경우 표면 장력이 크기와 무관하다고 가정하는 것은 옳지 않으며, 톨만 길이와 같은 주제가 작용합니다.거시적인 크기의 표면(그리고 평면 표면)의 경우 표면 $배치$ 는 γ에 큰 영향을 미치지 않지만 표면 장력 함수 γ $\gamma (T,\mu _{1},\mu _{2},\cdots )$ $\gamma (T,\mu _{1},\mu _{2},\cdots )$ $\gamma (T,\mu _{1},\mu _{2},\cdots )$ ⋯ $\gamma (T,\mu _{1},\mu _{2},\cdots )$ 의 부분 도함수인 표면 엔트로피, 표면 초과 질량 밀도 및 표면 내부 에너지 값에는 매우 강한 영향을 미칩니다. $displaystyle \gamma (T,\mu$ _ ${1},\mu _{2},\cdots )}.$

깁스는 고체의 경우 표면 자유 에너지는 표면 응력(그가 표면 장력이라고 부르는 것)과 완전히 다를 수 있다고 강조했습니다.^[14]^{: 315} 표면 자유 에너지는 표면을 형성하는 데 필요한 일이고 표면 응력은 표면을 늘이는 데 필요한 일입니다.2액체 계면의 경우 표면이 늘어나면 유체와 표면이 자연을 완전히 재생시키기 때문에 형성과 신축의 구분이 없습니다.고체의 경우, 표면을 탄력적으로 늘일 경우, 근본적으로 표면이 변화합니다.또한 고체의 표면 응력은 방향성 양(응력 텐서)인 반면 표면 에너지는 스칼라입니다.

깁스 이후 15년 후, J.D. 반데르발스는 밀도의 연속적인 변화에 대한 가설을 바탕으로 모세혈관 효과에 대한 이론을 개발했습니다.^[17]그는 에너지 밀도에 항 $c(\nabla \rho )^{2},$ ( ∇ ρ ) $c(\nabla \rho )^{2},$ {\ $displaystyle$ c $(\nabla \rho)^{2}$ 를 추가했습니다. 여기서 c는 모세관 계수이고 ρ는 밀도입니다.다상 평형의 경우, 반데르발스 접근법의 결과는 깁스 공식과 실질적으로 일치하지만, 상전이 역학의 모델링을 위해서는 반데르발스 접근법이 훨씬 더 편리합니다.^[18]^[19]반데르발스 모세관 에너지는 이제 다상 흐름의 위상장 모델에 널리 사용됩니다.이러한 용어는 비평형 가스의 역학에서도 발견됩니다.^[20]

기포의 열역학

이상적인 구형 버블 내부의 압력은 열역학적 자유 에너지 고려에서 도출될 수 있습니다.^[15]위의 자유 에너지는 다음과 같이 쓸 수 있습니다.

\Omega =-\Delta PV_{\text{A}}-p_{\text{B}}V+\gamma A

여기서 δ

\Delta P=p_{\text{A}}-p_{\text{B}}

=

\Delta P=p_{\text{A}}-p_{\text{B}}

A

\Delta P=p_{\text{A}}-p_{\text{B}}

-

\Delta P=p_{\text{A}}-p_{\text{B}}

\Delta P=p_{\text{A}}-p_{\text{B}}

{\displaystyle \Delta

P =

p_{\text{

A}}-p_{\text{

B}}

는

\Delta P=p_{\text{A}}-p_{\text{B}}

버블 내부(A)와 외부(B)의 압력차이며,

V_{\text{A}}

{\

A}}}

은

V_{\text{A}}

버블 부피입니다.평형상태에서 D ω = 0

등

,

\Delta P\,dV_{\text{A}}}=\gamma \,dA.

구형 버블의 경우 부피와 표면적은 단순히 다음과 같이 주어집니다.

V_{\text{A}}={\tfrac {4}{3}}\pi R^{3}\quad \rightarrow \quad dV_{\text{A}}=4\pi R^{2}\,dR,

그리고.

A=4\pi R^{2}\quad \rightarrow \quad dA=8\pi R\,dR.

이 관계들을 앞의 표현에 대입하면, 우리는

\Delta P={\frac {2}{R}}\gamma,

R

=

R일

때 영-라플라스 방정식과 동등합니다.

온도의 영향

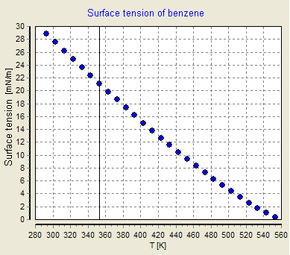
표면 장력은 온도에 따라 달라집니다.따라서 인터페이스의 표면장력에 대한 값이 주어지면 온도를 명시적으로 표시해야 합니다.일반적인 추세는 표면 장력이 온도가 증가함에 따라 감소하여 임계 온도에서 0의 값에 도달하는 것입니다.자세한 내용은 외트뵈시 규칙을 참조하십시오.표면 장력과 온도를 연관시키는 경험적 방정식은 다음과 같습니다.

외트뵈시:^[21]^[22]^[23] $\gamma V^{2/3}=k(T_{\mathrm {C}-T)$ 여기서 $V$ 는 물질의 몰 부피, $T$ 는_C 임계 온도, $k$ 는 거의 모든 물질에 대해 유효한 상수입니다.^[21]일반적인 값은 $k$ = 2.1 x 10 J K mol입니다.물의 경우 $V$ = 18ml/mol, $T$ = 647K(374°C)를 추가로 사용할 수 있습니다.라메이와 쉴즈는 외트뵈시에 대한 변형을 다음과 같이 설명합니다.^[25] $\gamma V^{2/3}=k\left(T_{\mathrm {C}}-T-6\,\mathrm {K} \right)$ 여기서 온도 오프셋이 6K인 경우 더 낮은 온도에서 실제에 더 잘 맞는 공식을 제공합니다.
구겐하임-카타야마:^[22] $\gamma =\gamma ^{\circ}\left(1-{\frac {T}{T_{\mathrm {C}}}\right)^{n$ $γ °$ 는 각 액체의 상수이고 $n$ 은 경험적 요인으로 유기 액체의 경우 11/9입니다.이 방정식은 또한 반데르발스에 의해 제안되었으며, 그는 γ $°$ 가 식을 통해 주어질 수 있다고 제안했습니다. $K_{2}T_{\mathrm {C}^{1/3}P_{\mathrm {C}^{2/3},$ 여기서 K는 $모든 2$ 액체에 대한 보편 상수이고, $P$ 는_C 액체의 임계 압력입니다.(후의 실험에서 $K$ 는₂ 액체마다 어느 정도의 차이가 있음이 밝혀졌습니다.)^[22]

구겐하임-카타야마와 외트뵈 모두 임계 온도에서 표면 장력이 0에 도달하는 반면, 라메이와 쉴즈는 이 끝점에서 현실과 일치하지 않는다는 사실을 고려합니다.

용질농도의 영향

용질은 표면의 성질과 용질에 따라 표면 장력에 다른 영향을 미칠 수 있습니다.

영향이 거의 없거나 전혀 없음, 예를 들어 물 공기에서 설탕, 기름/공기에서 대부분의 유기 화합물
대부분의 무기염이 물 공기에서 표면 장력을 증가시킵니다.
비단조성 변화, 대부분의 무기산은 물 공기에서 발생합니다.
대부분의 앰피 파일(예: 물 공기에서 알코올)과 같이 표면 장력을 점진적으로 감소시킵니다.
일정한 임계농도까지 표면장력을 감소시키고, 그 후에는 영향이 없음: 미셀을 형성하는 계면활성제

결과를 복잡하게 만드는 것은 용질이 용매 표면에서 그것의 부피에서와는 다른 농도로 존재할 수 있다는 것입니다.이 차이는 용질-용매 조합마다 다릅니다.

깁스 등온선은 다음과 같이 말합니다.

\Gamma =-{\frac {1}{RT}}\left({\frac {\partial \gamma}{\partial \ln C}\right)_{T,P

$γ$ 은 표면 농도로 알려져 있으며, 표면까지 벌크 농도가 우세할 경우 표면의 단위 면적당 용질의 초과를 나타냅니다.mol/m² 단위입니다.
$C$ 는 벌크 용액 내 물질의 농도입니다.
$R$ 은 기체상수이고 T는 온도입니다.

특정 가정이 추론에 적용되므로 깁스 등온선은 두 성분이 있는 이상적인(매우 희박한) 용액에만 적용할 수 있습니다.

입도가 증기압에 미치는 영향

클라우지우스-클라페이론 관계는 켈빈 방정식이라는 또 다른 방정식으로 이어집니다.표면 장력 때문에 현탁액의 작은 액적에 대한 증기압이 계면이 평평할 때 동일한 액체의 표준 증기압보다 큰 이유를 설명합니다.즉, 액체가 작은 물방울을 형성할 때 주변에 있는 증기의 평형 농도가 더 높다는 것입니다.이는 액적 내부의 압력이 외부의 압력보다 크기 때문에 발생합니다.^[25]

P_{\mathrm {v} ^{\mathrm {fog} = P_{\mathrm {v} ^{\circ}e^{V2\gamma /(RTR_{\mathrm {k})}

작은 물방울의 표면(왼쪽)에 있는 분자는 평평한 표면(오른쪽)에 있는 분자보다 평균적으로 더 적은 이웃을 갖습니다.따라서 그들은 평평한 표면 분자보다 물방울에 더 약하게 결합되어 있습니다.

$P v °$ 는 해당 온도와 압력에서 해당 액체의 표준 증기압입니다.
$V$ 는 어금니 부피입니다.
$R$ 은 기체 상수입니다.
$r$ 은_k 켈빈 반지름으로 물방울의 반지름입니다.

그 효과는 증기의 초포화 상태를 설명합니다.핵분열 장소가 없을 때 작은 물방울이 형성되어야만 더 큰 물방울로 진화할 수 있습니다.이를 위해서는 상전이점의 증기압보다 몇 배나 많은 증기압이 필요합니다.^[25]

이 식은 고체에 대한 메조 다공성을 평가하기 위해 촉매 화학에서도 사용됩니다.^[26]

효과는 표면 분자의 평균 분자 이웃 수 측면에서 볼 수 있습니다(도표 참조).

표에는 다양한 물방울 크기의 물에 대한 이 효과의 일부 계산값이 나와 있습니다.

STP에서^[22] 서로 다른 반경의 물방울에 $대한$ P $/ P 0$
액적반경(nm)	1000	100	10	1
$P / P 0$	1.001	1.011	1.114	2.95

그 효과는 매우 작은 방울 크기에서 명확해지는데, 1 nm 반경의 방울 안에 약 100개의 분자가 들어 있기 때문인데, 이는 양자역학 분석이 필요할 정도로 작은 양입니다.

측정방법

표면 장력은 다양한 효과로 나타나기 때문에 측정에 여러 경로를 제공합니다.어떤 방법이 최적인지는 측정되는 액체의 성질, 장력을 측정해야 하는 조건, 그리고 액체가 변형되었을 때 표면의 안정성에 달려 있습니다.표면 장력을 측정하는 기구는 텐시오미터라고 불립니다.

뒤누이 링 방법:표면 또는 계면 장력을 측정하기 위해 사용되는 전통적인 방법.표면 또는 인터페이스의 습윤 특성은 이 측정 기법에 거의 영향을 미치지 않습니다.표면에 의해 링에 가해지는 최대 당김을 측정합니다.^[21]
윌헬미 플레이트 방식: 장시간에 걸쳐 표면장력을 확인하는 데 특히 적합한 보편적인 방식입니다.둘레가 알려진 수직판을 저울에 부착하고 습윤에 의한 힘을 측정합니다.
스피닝 드롭 방식:이 기술은 낮은 계면 장력을 측정하는 데 이상적입니다.무거운 위상 내 낙하의 직경은 둘 다 회전한 상태에서 측정됩니다.
펜던트 낙하 방법: 표면 및 계면 장력은 온도 및 압력이 상승한 경우에도 이 기술로 측정할 수 있습니다.낙하물의 형상은 광학적으로 분석됩니다.펜던트 드롭의 경우 최대 직경과 드롭 정점에서 최대 직경 거리에 있는 이 파라미터와 직경 사이의 비율은 표면 장력을 결정하기 위해 크기 및 형상 파라미터를 평가하는 데 사용되었습니다.
버블 압력법(재거법):짧은 표면 에이징에서의 표면 장력을 측정하기 위한 측정 방법.각 버블의 최대 압력을 측정합니다.
적하 부피법: 계면 연령의 함수로서 계면 장력을 결정하기 위한 방법.한 밀도의 액체는 다른 밀도의 두 번째 액체로 펌핑되고 생성된 방울 사이의 시간이 측정됩니다.
모세관 상승 방법:모세관의 끝은 용액에 담깁니다.용액이 모세관 내부에 도달하는 높이는 아래에 논의된 방정식에 의해 표면 장력과 관련이 있습니다.^[27]
스테라그메트릭법: 액체 방울을 가중하여 판독하는 방법.
세실드롭법: 기판 위에 낙하물을 놓고 접촉각을 측정하여 표면장력과 밀도를 측정하는 방법(세실드롭법 참조).^[28]
Du Nouy–Padday 방법:Du Nouy 방법의 최소화된 버전은 링 대신 작은 직경의 금속 바늘을 사용하며, 최대 당김을 기록하기 위해 고감도 마이크로밸런스와 결합합니다.이 방법의 장점은 매우 작은 샘플 부피(수십 마이크로리터 이하)를 매우 높은 정밀도로 측정할 수 있다는 것입니다. 부력을 보정할 필요가 없습니다(적절한 형상의 바늘 또는 막대용).또한 약 20초 안에 최소로 매우 빠르게 측정을 수행할 수 있습니다.
공중부양 낙하의 진동 주파수:초유체 He의 표면장력을 측정하기 위해 자기적으로 부상된 방울의 진동 진동 진동의 고유주파수가 사용되었습니다. $이$ 값은 T = 0 K에서 0.375 dyn/cm로 추정됩니다.
구형 및 반구형 액체 낙하의 공진 진동:이 기술은 변조된 전기장에 의해 진동으로 구동되는 구형 및 반구형 펜던트 액적의 공진 주파수를 측정하는 것을 기반으로 합니다.표면 장력과 점도는 획득된 공진 곡선으로부터 평가될 수 있습니다.^[30]^[31]^[32]
드롭바운스 방법:이 방법은 공기역학적 공중부양과 분할 가능한 노즐 설계를 기반으로 합니다.안정적으로 공중부양된 액적을 플랫폼에 떨어뜨린 후 샘플은 표면적을 최소화하기 위해 공기 중에서 진동하면서 변형되고 튕겨집니다.이러한 진동 거동을 통해 액체의 표면장력과 점도를 측정할 수 있습니다.^[33]
스마트폰 기준:어떤 스마트폰들은 투명한 액체의 표면장력을 측정하는데 사용될 수 있습니다.이 방법은 알려진 주파수의 모세관 파동의 파장을 측정하는 것을 기반으로 합니다.스마트폰은 액체와 함께 컵 위에 놓여있습니다.그러면 스마트폰의 진동 모터가 액체 표면에 있는 모세관의 잔물결을 자극하고, 이것은 스마트폰의 카메라에 의해 포착됩니다.^[34]

가치

자료표

공기에^[35] 대한 dyn/cm 단위의 다양한 액체 표면 장력
"%"로 표시된 혼합물 조성은 질량 기준입니다.
dyn/cm는 mN/m(미터당 밀리뉴톤)의 SI 단위와 같습니다.
액체.	온도(°C)	표면장력, ,
아세트산	20	27.60
초산(45.1%) + 물	30	40.68
초산(10.0%) + 물	30	54.56
아세톤	20	23.70
피	22	55.89
디에틸에테르	20	17.00
에탄올	20	22.27
에탄올(40%) + 물	25	29.63
에탄올(11.1%) + 물	25	46.03
글리세롤	20	63.00
n-헥산	20	18.40
염산 17.7M 수용액	20	65.95
이소프로판올	20	21.70
액체 헬륨 II	−273	0.37^[36]
액체질소	−196	8.85
액체산소	−182	13.2
수성.	15	487.00
메탄올	20	22.60
용융 염화은	650	163^[37]
용융염화나트륨/염화칼슘(47/53몰%)	650	139^[38]
n-옥탄	20	21.80
염화나트륨 6.0M 수용액	20	82.55
수크로스(55%) + 물	20	76.45
물.	0	75.64
물.	25	71.97
물.	50	67.91
물.	100	58.85
톨루엔	25	27.73

물의 표면장력

순수한 액체 물이 증기와 접촉하는 표면 장력은 IAPWS에^[39] 의해 다음과 같이 주어졌습니다.

\gamma _{\text{w}}=235.8\left(1-{\frac {T}{T_{\text{C}}}}\right)^{1.256}}\left[1-0.625\left(1-{\frac {T}{T_{\text{C}}}}\right)\right]~{\text{m}N/m}},

여기서 $T$ 와 임계 $온도$ T = 647.096 K는 모두 켈빈 단위로 표현됩니다.삼중점(0.01°C)에서 임계점까지 전체 증기-액체 포화 곡선의 유효 영역.또한 최소 -25°C까지 준안정(과냉각) 조건으로 외삽했을 때 합리적인 결과를 제공합니다.이 공식은 1976년 IAPWS에 의해 처음 채택되었으며, 1990년의 국제 온도 척도에 부합하도록 1994년에 조정되었습니다.

이 제형의 불확실성은 IAPWS에 의해 온도의 전체 범위에 걸쳐 제공됩니다.^[39]온도가 100°C 미만인 경우 불확실성은 ±0.5%입니다.

해수 표면장력

Nayar 등은 ^[40]대기압에서 염도 범위 20 ≤ $S$ ≤ 131 g/kg, 온도 범위 1 ≤ $t$ ≤ 92 °C에 대한 해수의 표면장력에 대한 참고자료를 발표하였다.온도와 염도의 범위는 해양학적 범위와 열 담수화 기술에서 만나는 조건의 범위를 모두 포함합니다.측정값의 불확실성은 0.18~0.37mN/m로 다양했고 평균 불확실성은 0.22mN/m이었습니다.

Nayar et al. 는 데이터와 다음 방정식의 상관관계를 나타냈습니다.

\gamma _{\mathrm {sw} =\gamma _{\mathrm {w}}\left(1+3.766\times 10^{-4}S+2.347\times 10^{-6}St\right)

여기

서 γ은 mN/m 단위의 해수 표면장력, γ은 mN/m 단위의 물 표면장력,

S

는 g/kg 단위의 기준 염도,

t

는 섭씨 온도입니다.측정값과 상관 관계 사이의 평균 절대 백분율 편차는 0.19%인 반면 최대 편차는 0.60%입니다.

국제 물 및 증기 특성 협회(IAPWS)는 이 상관 관계를 국제 표준 가이드라인으로 채택했습니다.^[42]

참고 항목

안개방지
모세관파 — 수면에서 표면장력과 관성에 의해 조절되는 단파
Cheerio 효과 — 젖은 물에 젖은 작은 부유 물체가 서로 끌어당기는 경향.
응집력
무차원수
- 채권번호 또는 외트뵈스 번호
- 모세관 번호
- 마랑고니 수
- 베버수
도르트문트 데이터 뱅크 — 실험 온도에 따른 표면 장력 포함
전기 침지력
전기습윤
전기 캐퍼시
외트뵈스 규칙 — 온도에 따라 표면장력을 예측하는 규칙
유동관
유체정역학적 평형—중력이 물질을 둥글게 끌어당기는 효과
계면(화학)
메니스커스 — 용기 내 액체에 의해 형성되는 표면 곡률
수은이 심장을 뛰게 함 – 균일하지 않은 표면 장력의 결과
미세유체학
세실드롭 기술
천소신
특정 표면 에너지 - 등방성 물질의 표면 장력과 동일.
방사낙하법
석순측량법
표면압
표면과학
표면장력 생체모방법
표면장력값
계면활성제 — 표면장력을 감소시키는 물질.
Szyszkowski 방정식 — 수용액의 표면장력 계산
와인의 눈물 — 알코올 음료가 들어있는 잔의 측면에서 표면 장력이 유발되는 현상
Tolman 길이 — 곡면의 표면 장력을 보정하기 위한 선행 용어입니다.
습윤 및 탈습윤

해설서

^ 수은 기압계에서 상부 액체 표면은 액체와 일부 증발된 액체 분자를 포함하는 진공 사이의 계면입니다.

참고문헌

^ "Surface Tension - an overview ScienceDirect Topics". www.sciencedirect.com. Archived from the original on 2021-12-30. Retrieved 2021-12-30.
^ ^a ^b ^c "Surface Tension (Water Properties) – USGS Water Science School". US Geological Survey. July 2015. Archived from the original on October 7, 2015. Retrieved November 6, 2015.
^ ^a ^b ^c Berry, M V (1971). "The molecular mechanism of surface tension" (PDF). Physics Education. 6 (2): 79–84. Bibcode:1971PhyEd...6...79B. doi:10.1088/0031-9120/6/2/001. S2CID 250797804. Archived (PDF) from the original on 31 December 2021. Retrieved 8 July 2020.
^ ^a ^b Halliday, David; Resnick, Robert; Krane, Kenneth S. (2010-04-20). Physics, Volume 2. John Wiley & Sons. p. 342. ISBN 978-0-471-40194-0. Archived from the original on 2022-09-22. Retrieved 2021-03-19.
^ ^a ^b ^c White, Harvey E. (1948). Modern College Physics. van Nostrand. ISBN 978-0-442-29401-4.
^ Bush, John W. M. (April 2004). "MIT Lecture Notes on Surface Tension, lecture 1" (PDF). Massachusetts Institute of Technology. Archived (PDF) from the original on March 8, 2022. Retrieved April 1, 2007.
^ "Mechanical definition of surface tension". MIT. Archived from the original on April 12, 2013. Retrieved Dec 16, 2013.
^ ^a ^b ^c ^d ^e ^f ^g ^h Sears, Francis Western; Zemanski, Mark W. (1955) 대학 물리학 제2판.애디슨 웨슬리
^ Bush, John W. M. (May 2004). "MIT Lecture Notes on Surface Tension, lecture 5" (PDF). Massachusetts Institute of Technology. Archived (PDF) from the original on February 26, 2007. Retrieved April 1, 2007.
^ Bush, John W. M. (May 2004). "MIT Lecture Notes on Surface Tension, lecture 3" (PDF). Massachusetts Institute of Technology. Archived (PDF) from the original on February 26, 2007. Retrieved April 1, 2007.
^ ^a ^b ^c ^d ^e ^f ^g ^h Pierre-Gilles de Gennes; Françoise Brochard-Wyart; David Quéré (2002). Capillarity and Wetting Phenomena—Drops, Bubbles, Pearls, Waves. Alex Reisinger. Springer. ISBN 978-0-387-00592-8.
^ Butt, Hans-Jürgen; Graf, Karlheinz; Kappl, Michael (2006). Physics and Chemistry of Interfaces. Wiley. p. 9. ISBN 978-3-527-60640-5.
^ 아론슨, 스콧 (2005년 3월) NP-완전 문제와 물리적 현실 보관 2018-02-23 웨이백 머신에서 보관.ACM SIGACT 뉴스
^ ^a ^b ^c ^d Gibbs, J.W. (2002) [1876–1878], "On the Equilibrium of Heterogeneous Substances", in Bumstead, H.A.; Van Nameeds, R.G. (eds.), The Scientific Papers of J. Willard Gibbs, vol. 1, Woodbridge, CT: Ox Bow Press, pp. 55–354, ISBN 978-0918024770
^ ^a ^b Landau; Lifshitz (1980). Course of Theoretical Physics Volume 5: Statistical Physics I (3 ed.). Pergamon. pp. 517–537.
^ Rusanov, A (2005). "Surface thermodynamics revisited". Surface Science Reports. 58 (5–8): 111–239. Bibcode:2005SurSR..58..111R. doi:10.1016/j.surfrep.2005.08.002. ISSN 0167-5729.
^ van der Waals, J.D. (1979) [1893], translated by Rowlinson, J.S., "The thermodynamic theory of capillarity under the hypothesis of a continuous variation of density", J. Stat. Phys., 20 (2): 197–200, Bibcode:1979JSP....20..197R, doi:10.1007/BF01011513, S2CID 122954999
^ Cahn, J.W.; Hilliard, J.E. (1958), "Free energy of a nonuniform system. I. Interfacial free energy", J. Chem. Phys., 28 (2): 258–266, Bibcode:1958JChPh..28..258C, doi:10.1063/1.1744102
^ Langer, J.S.; Bar-On, M.; Miller, H.D. (1975), "New computational method in the theory of spinodal decomposition", Phys. Rev. A, 11 (4): 1417–1429, Bibcode:1975PhRvA..11.1417L, doi:10.1103/PhysRevA.11.1417
^ Gorban, A.N.; Karlin, I. V. (2016), "Beyond Navier–Stokes equations: capillarity of ideal gas", Contemporary Physics (Review article), 58 (1): 70–90, arXiv:1702.00831, Bibcode:2017ConPh..58...70G, doi:10.1080/00107514.2016.1256123, S2CID 55317543
^ ^a ^b ^c ^d "Surface Tension by the Ring Method (Du Nouy Method)" (PDF). PHYWE. Archived (PDF) from the original on 2007-09-27. Retrieved 2007-09-08.
^ ^a ^b ^c ^d Adam, Neil Kensington (1941). The Physics and Chemistry of Surfaces, 3rd ed. Oxford University Press.
^ ^a ^b "Physical Properties Sources Index: Eötvös Constant". Archived from the original on 2011-07-06. Retrieved 2008-11-16.
^ Vargaftik, N. B.; Volkov, B. N.; Voljak, L. D. (1983). "International Tables of the Surface Tension of Water" (PDF). Journal of Physical and Chemical Reference Data. 12 (3): 817. Bibcode:1983JPCRD..12..817V. doi:10.1063/1.555688. Archived from the original (PDF) on 2016-12-21. Retrieved 2017-07-13.
^ ^a ^b ^c Moore, Walter J. (1962). Physical Chemistry, 3rd ed. Prentice Hall.
^ Ertl, G.; Knözinger, H. and Weitkamp, J. (1997).이종 촉매학 핸드북, Vol. 2, p. 430와일리-VCH, 와인하임.ISBN 3-527-31241-2
^ Calvert, James B. "Surface Tension (physics lecture notes)". University of Denver. Archived from the original on 2007-09-15. Retrieved 2007-09-08.
^ "Sessile Drop Method". Dataphysics. Archived from the original on August 8, 2007. Retrieved 2007-09-08.
^ Vicente, C.; Yao, W.; Maris, H.; Seidel, G. (2002). "Surface tension of liquid 4He as measured using the vibration modes of a levitated drop". Physical Review B. 66 (21): 214504. Bibcode:2002PhRvB..66u4504V. doi:10.1103/PhysRevB.66.214504.
^ Zografov, Nikolay (2014). "Droplet oscillations driven by an electric field". Colloids and Surfaces A: Physicochemical and Engineering Aspects. 460: 351–354. doi:10.1016/j.colsurfa.2013.12.013.
^ Tankovsky, N. (2013). "Electrically Driven Resonant Oscillations of Pendant Hemispherical Liquid Droplet and Possibility to Evaluate the Surface Tension in Real Time". Zeitschrift für Physikalische Chemie. 227 (12): 1759–1766. doi:10.1524/zpch.2013.0420. S2CID 101722165.
^ Tankovsky, Nikolay (2011). "Oscillations of a Hanging Liquid Drop, Driven by Interfacial Dielectric Force". Zeitschrift für Physikalische Chemie. 225 (4): 405–411. doi:10.1524/zpch.2011.0074. S2CID 101625925.
^ Sun, Yifan; Muta, Hiroaki; Ohishi, Yuji (June 2021). "Novel Method for Surface Tension Measurement: the Drop-Bounce Method". Microgravity Science and Technology. 33 (3): 32. Bibcode:2021MicST..33...32S. doi:10.1007/s12217-021-09883-7.
^ Yue, Shichao; Katabi, Dina (2021). "Liquid testing with your smartphone". Communications of the ACM. 64 (10): 75–83. doi:10.1145/3481038. ISSN 0001-0782.
^ Lange's Handbook of Chemistry(1967) 10판. pp 1661–1665 ISBN 0-07-016190-9(11판)
^ Brouwer, W; Pathria, R. K (1967). "On the Surface Tension of Liquid Helium II". Physical Review. 163 (1): 200–205. Bibcode:1967PhRv..163..200B. doi:10.1103/PhysRev.163.200.
^ Moser, Z; Gasior, W; Rzyman, K (1982). "Activities and Surface Tension of Liquid AgCl-KCl Solutions". Journal of the Electrochemical Society. 129 (3): 502–506. doi:10.1149/1.2131529.
^ Addison, C; Coldrey, J (1960). "Influence of Surface Reactions on the Interface Between Liquid Sodium and Molten Sodium Chloride + Calcium Chloride Mixtures". Transactions of the Faraday Society. 56: 840–845. doi:10.1039/tf9605600840.
^ ^a ^b International Association for the Properties of Water and Steam (June 2014). "Revised Release on Surface Tension of Ordinary Water Substance". Archived from the original on 2016-04-04. Retrieved 2016-02-20.
^ Nayar, K. G; Panchanathan, D; McKinley, G. H; Lienhard, J. H (November 2014). "Surface tension of seawater" (PDF). J. Phys. Chem. Ref. Data. 43 (4): 43103. Bibcode:2014JPCRD..43d3103N. doi:10.1063/1.4899037. hdl:1721.1/96884. Archived from the original on 2022-09-22. Retrieved 2018-04-20.
^ Millero, Frank J; Feistel, Rainer; Wright, Daniel G; McDougall, Trevor J (January 2008). "The composition of Standard Seawater and the definition of the Reference-Composition Salinity Scale". Deep-Sea Research Part I. 55 (1): 50. Bibcode:2008DSRI...55...50M. doi:10.1016/j.dsr.2007.10.001.
^ Guideline on the Surface Tension of Seawater (PDF) (Technical report). International Association for the Properties of Water and Steam. October 2019. IAPWS G14-19. Archived (PDF) from the original on 2020-03-26. Retrieved 2020-03-26.

외부 링크

"왜 표면 장력이 계면과 평행합니까?"물리적 스택 교환.2021-03-19 검색.
베리, MV (1971-03-01)."표면장력의 분자적 메커니즘."물리학 교육. 6 (2): 79–84. 도이: 10.1088/0031-9120/6/2/001ISSN 0031-9120.
3월달, 안토닌;Weijs, Joost H.; Snoweijer, Jacco H.; Andreoti, Bruno (2011-09-26)."왜 표면장력이 계면에 평행한 힘인가요?"American Journal of Physics. 79(10): 999-1008. Doi: 10.1119/1.3619866ISSN 0002-9505. arXiv: https://arxiv.org/abs/1211.3854
표면장력과 흥미로운 실제 사례에 대하여
다양한 액체의 표면장력
일부 공통 구성요소에 대한 온도 의존적 표면장력
이온 H⁺, NH⁺
₄, Na⁺, K⁺, Mg²⁺, Ca²⁺, SO²⁻
₄, NO⁻
₃, Cl⁻, CO²⁻
₃, Br⁻ 및 OH를⁻ 포함하는 수용액용 표면장력 계산기
T. Proctor Hall (1893) 액체의 표면장력을 측정하는 새로운 방법, Philosophical Magazine (시리즈 5, 36: 385–415), 생물다양성 유산 도서관 링크
버블 월^{[permanent dead link]}(응집력, 표면 장력 및 수소 결합에 대해 설명하는 국립 고자기장 연구소의 오디오 슬라이드 쇼)
C. 피스터: 인터페이스 자유 에너지. Scholarpedia 2010 (통계역학 제1원리로부터)
표면 및 계면 장력
"Molten salts mixture surface tension". The Journal of Chemical Thermodynamics. 3 (2): 259–265. March 1971. doi:10.1016/S0021-9614(71)80111-8.

[14] 수은 기압계에서 상부 액체 표면은 액체와 일부 증발된 액체 분자를 포함하는 진공 사이의 계면입니다.

[1] "Surface Tension - an overview ScienceDirect Topics". www.sciencedirect.com. Archived from the original on 2021-12-30. Retrieved 2021-12-30.

[usgs-2] "Surface Tension (Water Properties) – USGS Water Science School". US Geological Survey. July 2015. Archived from the original on October 7, 2015. Retrieved November 6, 2015.

[berry-3] Berry, M V (1971). "The molecular mechanism of surface tension" (PDF). Physics Education. 6 (2): 79–84. Bibcode:1971PhyEd...6...79B. doi:10.1088/0031-9120/6/2/001. S2CID 250797804. Archived (PDF) from the original on 31 December 2021. Retrieved 8 July 2020.

[:0-4] Halliday, David; Resnick, Robert; Krane, Kenneth S. (2010-04-20). Physics, Volume 2. John Wiley & Sons. p. 342. ISBN 978-0-471-40194-0. Archived from the original on 2022-09-22. Retrieved 2021-03-19.

[white-5] White, Harvey E. (1948). Modern College Physics. van Nostrand. ISBN 978-0-442-29401-4.

[MIT1-6] Bush, John W. M. (April 2004). "MIT Lecture Notes on Surface Tension, lecture 1" (PDF). Massachusetts Institute of Technology. Archived (PDF) from the original on March 8, 2022. Retrieved April 1, 2007.

[MIT_Non-Newtonian-7] "Mechanical definition of surface tension". MIT. Archived from the original on April 12, 2013. Retrieved Dec 16, 2013.

[s_z-8] ^ ^a ^b ^c ^d ^e ^f ^g ^h Sears, Francis Western; Zemanski, Mark W. (1955) 대학 물리학 제2판.애디슨 웨슬리

[MIT5-9] Bush, John W. M. (May 2004). "MIT Lecture Notes on Surface Tension, lecture 5" (PDF). Massachusetts Institute of Technology. Archived (PDF) from the original on February 26, 2007. Retrieved April 1, 2007.

[MIT3-10] Bush, John W. M. (May 2004). "MIT Lecture Notes on Surface Tension, lecture 3" (PDF). Massachusetts Institute of Technology. Archived (PDF) from the original on February 26, 2007. Retrieved April 1, 2007.

[cwp-11] ^ ^a ^b ^c ^d ^e ^f ^g ^h Pierre-Gilles de Gennes; Françoise Brochard-Wyart; David Quéré (2002). Capillarity and Wetting Phenomena—Drops, Bubbles, Pearls, Waves. Alex Reisinger. Springer. ISBN 978-0-387-00592-8.

[Physics_and_Chemistry_of_Interfaces-12] Butt, Hans-Jürgen; Graf, Karlheinz; Kappl, Michael (2006). Physics and Chemistry of Interfaces. Wiley. p. 9. ISBN 978-3-527-60640-5.

[13] 아론슨, 스콧 (2005년 3월) NP-완전 문제와 물리적 현실 보관 2018-02-23 웨이백 머신에서 보관.ACM SIGACT 뉴스

[gibbseq-15] Gibbs, J.W. (2002) [1876–1878], "On the Equilibrium of Heterogeneous Substances", in Bumstead, H.A.; Van Nameeds, R.G. (eds.), The Scientific Papers of J. Willard Gibbs, vol. 1, Woodbridge, CT: Ox Bow Press, pp. 55–354, ISBN 978-0918024770

[landaulifshitz-16] Landau; Lifshitz (1980). Course of Theoretical Physics Volume 5: Statistical Physics I (3 ed.). Pergamon. pp. 517–537.

[Rusanov2005-17] Rusanov, A (2005). "Surface thermodynamics revisited". Surface Science Reports. 58 (5–8): 111–239. Bibcode:2005SurSR..58..111R. doi:10.1016/j.surfrep.2005.08.002. ISSN 0167-5729.

[18] van der Waals, J.D. (1979) [1893], translated by Rowlinson, J.S., "The thermodynamic theory of capillarity under the hypothesis of a continuous variation of density", J. Stat. Phys., 20 (2): 197–200, Bibcode:1979JSP....20..197R, doi:10.1007/BF01011513, S2CID 122954999

[19] Cahn, J.W.; Hilliard, J.E. (1958), "Free energy of a nonuniform system. I. Interfacial free energy", J. Chem. Phys., 28 (2): 258–266, Bibcode:1958JChPh..28..258C, doi:10.1063/1.1744102

[20] Langer, J.S.; Bar-On, M.; Miller, H.D. (1975), "New computational method in the theory of spinodal decomposition", Phys. Rev. A, 11 (4): 1417–1429, Bibcode:1975PhRvA..11.1417L, doi:10.1103/PhysRevA.11.1417

[21] Gorban, A.N.; Karlin, I. V. (2016), "Beyond Navier–Stokes equations: capillarity of ideal gas", Contemporary Physics (Review article), 58 (1): 70–90, arXiv:1702.00831, Bibcode:2017ConPh..58...70G, doi:10.1080/00107514.2016.1256123, S2CID 55317543

[phywe-22] "Surface Tension by the Ring Method (Du Nouy Method)" (PDF). PHYWE. Archived (PDF) from the original on 2007-09-27. Retrieved 2007-09-08.

[adam-23] Adam, Neil Kensington (1941). The Physics and Chemistry of Surfaces, 3rd ed. Oxford University Press.

[Physical_Properties_Sources_Index_(PPSI)-24] "Physical Properties Sources Index: Eötvös Constant". Archived from the original on 2011-07-06. Retrieved 2008-11-16.

[25] Vargaftik, N. B.; Volkov, B. N.; Voljak, L. D. (1983). "International Tables of the Surface Tension of Water" (PDF). Journal of Physical and Chemical Reference Data. 12 (3): 817. Bibcode:1983JPCRD..12..817V. doi:10.1063/1.555688. Archived from the original (PDF) on 2016-12-21. Retrieved 2017-07-13.

[moore-26] Moore, Walter J. (1962). Physical Chemistry, 3rd ed. Prentice Hall.

[Handbook-27] Ertl, G.; Knözinger, H. and Weitkamp, J. (1997).이종 촉매학 핸드북, Vol. 2, p. 430와일리-VCH, 와인하임.ISBN 3-527-31241-2

[calvert-28] Calvert, James B. "Surface Tension (physics lecture notes)". University of Denver. Archived from the original on 2007-09-15. Retrieved 2007-09-08.

[dp-29] "Sessile Drop Method". Dataphysics. Archived from the original on August 8, 2007. Retrieved 2007-09-08.

[30] Vicente, C.; Yao, W.; Maris, H.; Seidel, G. (2002). "Surface tension of liquid 4He as measured using the vibration modes of a levitated drop". Physical Review B. 66 (21): 214504. Bibcode:2002PhRvB..66u4504V. doi:10.1103/PhysRevB.66.214504.

[31] Zografov, Nikolay (2014). "Droplet oscillations driven by an electric field". Colloids and Surfaces A: Physicochemical and Engineering Aspects. 460: 351–354. doi:10.1016/j.colsurfa.2013.12.013.

[32] Tankovsky, N. (2013). "Electrically Driven Resonant Oscillations of Pendant Hemispherical Liquid Droplet and Possibility to Evaluate the Surface Tension in Real Time". Zeitschrift für Physikalische Chemie. 227 (12): 1759–1766. doi:10.1524/zpch.2013.0420. S2CID 101722165.

[33] Tankovsky, Nikolay (2011). "Oscillations of a Hanging Liquid Drop, Driven by Interfacial Dielectric Force". Zeitschrift für Physikalische Chemie. 225 (4): 405–411. doi:10.1524/zpch.2011.0074. S2CID 101625925.

[34] Sun, Yifan; Muta, Hiroaki; Ohishi, Yuji (June 2021). "Novel Method for Surface Tension Measurement: the Drop-Bounce Method". Microgravity Science and Technology. 33 (3): 32. Bibcode:2021MicST..33...32S. doi:10.1007/s12217-021-09883-7.

[35] Yue, Shichao; Katabi, Dina (2021). "Liquid testing with your smartphone". Communications of the ACM. 64 (10): 75–83. doi:10.1145/3481038. ISSN 0001-0782.

[36] Lange's Handbook of Chemistry(1967) 10판. pp 1661–1665 ISBN 0-07-016190-9(11판)

[37] Brouwer, W; Pathria, R. K (1967). "On the Surface Tension of Liquid Helium II". Physical Review. 163 (1): 200–205. Bibcode:1967PhRv..163..200B. doi:10.1103/PhysRev.163.200.

[38] Moser, Z; Gasior, W; Rzyman, K (1982). "Activities and Surface Tension of Liquid AgCl-KCl Solutions". Journal of the Electrochemical Society. 129 (3): 502–506. doi:10.1149/1.2131529.

[39] Addison, C; Coldrey, J (1960). "Influence of Surface Reactions on the Interface Between Liquid Sodium and Molten Sodium Chloride + Calcium Chloride Mixtures". Transactions of the Faraday Society. 56: 840–845. doi:10.1039/tf9605600840.

[IAPWS-40] International Association for the Properties of Water and Steam (June 2014). "Revised Release on Surface Tension of Ordinary Water Substance". Archived from the original on 2016-04-04. Retrieved 2016-02-20.

[Nayar-41] Nayar, K. G; Panchanathan, D; McKinley, G. H; Lienhard, J. H (November 2014). "Surface tension of seawater" (PDF). J. Phys. Chem. Ref. Data. 43 (4): 43103. Bibcode:2014JPCRD..43d3103N. doi:10.1063/1.4899037. hdl:1721.1/96884. Archived from the original on 2022-09-22. Retrieved 2018-04-20.

[42] Millero, Frank J; Feistel, Rainer; Wright, Daniel G; McDougall, Trevor J (January 2008). "The composition of Standard Seawater and the definition of the Reference-Composition Salinity Scale". Deep-Sea Research Part I. 55 (1): 50. Bibcode:2008DSRI...55...50M. doi:10.1016/j.dsr.2007.10.001.

[43] Guideline on the Surface Tension of Seawater (PDF) (Technical report). International Association for the Properties of Water and Steam. October 2019. IAPWS G14-19. Archived (PDF) from the original on 2020-03-26. Retrieved 2020-03-26.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[13]

[note 1]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]

[25]

[26]

[27]

[28]

[30]

[31]

[32]

[33]

[34]

[35]

[36]

[37]

[38]

[39]

[40]

[42]

v t 물리학의 주요 분야
사단	순수하다 응용의 공학 기술
어프로치	실험적인 이론적 계산
고전적인	고전역학 뉴턴식의 분석적 천상의 연속체 음향학 고전 전자기학 고전 광학 광선 파도. 열역학 통계적 비평형
현대의	상대론적 역학 스페셜 일반적 핵물리학 양자역학 입자물리학 원자, 분자, 광학 물리학 아토믹 분자의 현대 광학 응축물질물리학
학제간	천체물리학 대기 물리학 생물물리학 화학물리학 지구물리학 재료과학 수리물리학 의학물리학 해양물리학 양자정보과학
관련된	물리학의 역사 노벨 물리학상 물리학 철학 물리학 교육 물리학 발견 연대표

Search

표면장력

네임스페이스

더

목차

원인들

물리학

물리 단위

정의.

힘으로 따지면

에너지면에서

영향들

물.

계면활성제

표면곡률 및 압력

부동 객체

액체표면

접촉각

특수 접촉각

수직관내 액체

표면의 웅덩이

시냇물이 방울로 갈라지는 것.

갤러리

열역학

표면장력의 열역학적 이론

기포의 열역학

온도의 영향

용질농도의 영향

입도가 증기압에 미치는 영향

측정방법

가치

자료표

물의 표면장력

해수 표면장력

참고 항목

해설서

참고문헌

외부 링크