This is a good article. Click here for more information.

수학과 건축

Mathematics and architecture

2003년 완공된 런던 세인트 메리 액스(30)[1]는 파라메트릭적으로 설계된 혁명의 고체다.
인도 카주라호주 칸다리야 마하데바 사원(c. 1030)은 프랙탈과 같은 구조를 가진 종교 건축의 사례로, 전체와 유사한 부분이 많다.[2]

다른 예술과 마찬가지로 건축가들이 수학을 몇 가지 이유로 사용하기 때문에 수학과 건축은 관련이 있다.건축가들은 건축물을 엔지니어링할 때 필요한 수학과는 별도로 기하학을 사용한다. 건물의 공간적 형태를 정의하기 위해; 기원전 6세기 피타고라스로부터, 조화롭게 여겨지는 형태를 창조하기 위해, 그리고 수학적, 미학적, 그리고 때로는 종교적 원칙에 따라 건물과 그 주변을 배치한다.테셀레이션과 같은 수학적 객체로 건물을 장식하고, 높은 빌딩의 기단 주위의 풍속을 최소화하는 것과 같은 환경 목표를 달성하기 위해.

고대 이집트, 고대 그리스, 인도, 이슬람 세계에서는 피라미드, 사원, 모스크, 궁전, 묘지 등을 포함한 건물들이 종교적인 이유로 특정한 비율로 배치되었다.이슬람 건축에서는 기하학적 모양과 기하학적 타일 무늬가 건물 내외부를 장식하는데 사용된다.일부 힌두교 사원은 일부가 전체를 닮은 프랙탈과 같은 구조를 가지고 있어 힌두교 우주론의 무한대에 대한 메시지를 전달하고 있다.중국 건축에서 푸젠 성의 튤루는 원형, 공동 방어 구조다.21세기에, 수학적인 장식이 공공건물을 덮기 위해 다시 사용되고 있다.

르네상스 건축에서는 레온 바티스타 알베르티, 세바스티아노 셀리오, 안드레아 팔라디오 등의 건축가들이 의도적으로 대칭과 비율을 강조하였는데, 고대 로마 출신의 비트루비우스의 드 아스트라투라와 고대 그리스 출신의 피타고라스의 산수의 영향을 받았다.19세기 말에 러시아의 블라디미르 슈호프와 바르셀로나의 안토니 가우디는 하이퍼볼로이드 구조의 사용을 개척했다. 사그라다 파밀리아에서 가우디는 또한 쌍곡선 파라볼로이드, 테셀레이션, 카트리네이드, 헬리코이드, 지배 표면도 통합했다.20세기에, 현대 건축과 해체주의 같은 스타일들은 원하는 효과를 얻기 위해 다른 기하학적 구조를 탐구했다.최소한의 표면은 덴버 국제공항에서처럼 텐트처럼 생긴 지붕 덮개에 이용되었고, 리처드 버크민스터 풀러는 지오데틱 돔으로 알려진 강한 얇은 껍질 구조의 사용을 개척했다.

연결된 필드

르네상스 시대에는 레온 바티스타 알베르티와 같은 건축가가 산술과 기하학 등 많은 학문 분야에 정통할 것으로 기대되었다.

건축가 마이클 오스왈드와 킴 윌리엄스는 건축과 수학의 관계를 고려했을 때 건축은 건물을 만드는 실제적인 문제와 관련된 직업인 반면 수학은 숫자와 다른 것에 대한 순수한 연구이기 때문에 일반적으로 이해되는 분야들은 단지 약하게 연관되어 있는 것처럼 보일 수 있다는 점에 주목한다.골절된 물건그러나 그들은 이 두 가지가 강하게 연결되어 있으며, 오래전부터 이어져 왔다고 주장한다.고대 로마에서 비트루비우스는 건축가를 석공이나 목수와 같은 다른 필요한 모든 영역에서 숙련된 장인들을 감독할 수 있도록 하기 위해 주로 기하학 같은 다른 학문들을 충분히 알고 있는 사람으로 묘사했다.졸업생들이 많은 장인을 지도해 온 명인 건설업자들이 만든 우아한 홀에서 문법, 논리, 수사(삼두법)의 기본 요강과 함께 산술, 기하학, 미학을 배운 중세 시대에도 마찬가지였다.그의 직업의 최상위에 있는 건축가에게는 건축가나 기술자라는 칭호가 주어졌다.르네상스 시대에는 산술, 기하학, 음악, 천문학이라는 4가지 강점이 레온 바티스타 알베르티와 같은 르네상스 시대의 남성에게 기대되는 추가적인 강의요강이 되었다.영국에서 비슷하게, 오늘날 건축가로 알려진 크리스토퍼 렌 경은 처음에 유명한 천문학자였다.[3]

윌리엄스와 오스왈드는 독일 사회학자 테오도르 아도르노의 접근에 따라 1500년 이후 수학과 건축의 상호작용을 더욱 개괄적으로 고찰하면서 건축가들 사이에서 세 가지 경향 즉, 혁명적으로 되는 것, 완전히 새로운 사상을 도입하는 것, 반동적인 것, 변화를 도입하는 데 실패하는 것, 또는 실제로 부흥론자가 돌아가는 것 등을 파악한다.그들은 건축가들이 부활주의 시대에 영감을 얻기 위해 수학을 찾는 것을 피했다고 주장한다.이것은 왜 19세기 영국의 고딕 부흥과 같은 부흥주의 시대에 건축이 수학과는 거의 관련이 없었는지를 설명해 줄 것이다.마찬가지로, 그들은 1520년에서 1580년 사이의 이탈리아 매너리즘이나 17세기 바로크와 팔라디아 운동과 같은 반동시대에는 수학이 거의 상담되지 않았다는 점에 주목한다.이와는 대조적으로 퓨처리즘과 구성주의 같은 혁명적인 20세기 초 운동은 수학을 수용하고 모더니즘 건축으로 이어지며 낡은 사상을 적극적으로 배척했다.또한 20세기 말에 프랙탈 기하학은 건축가들에 흥미롭고 매력적인 덮개를 제공하기 위해 시대적 타일링과 마찬가지로 건축가들에 의해 빠르게 점령되었다.[4]

건축가들은 건물의 공학에서 수학의 필수적 용도를 제쳐두고 몇 가지 이유로 수학을 사용한다.[5]첫째로, 그들은 건물의 공간적 형태를 정의하기 때문에 기하학을 사용한다.[6]둘째로, 그들은 수학을 아름답고 조화롭다고 여겨지는 형태를 디자인하는데 사용한다.[7]는 피타 고라스 학파의 고대 그리스, 고대 로마, 이슬람 세계와 이탈리아 르네상스에서 number,[8]의 건축가들이 그들의 종교적 철학과 함께 그 때부터 –뿐만 아니라 심미적 그리고 때때로 종교적인 수학적 원칙에 따라 인위적인 환경– 건물과 지정된 주변 환경의 비율 선택했다..[9][10][11][12]세 번째로, 그들은 건물을 장식하기 위해 테셀레이션과 같은 수학적 물체를 사용할 수 있다.[13][14]넷째, 그들은 높은 빌딩의 기슭에서 휘몰아치는 기류를 최소화하는 것과 같은 환경 목표를 달성하기 위해 컴퓨터 모델링의 형태로 수학을 사용할 수 있다.[1]

세속 미학

고대 로마

비트루비우스의 그리스 주택 계획

비트루비우스

추가 정보:비트루비우스, 비트루비우스 모듈 및 데아스터라
조반니 파올로 파니니의 판테온 내부, 1758년

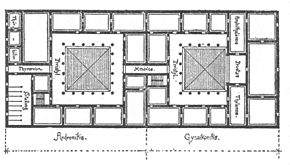
영향력 있는 고대 로마의 건축가 비트루비우스는 신전과 같은 건물의 설계는 비례와 대칭이라는 두 가지 특성에 달려 있다고 주장했다.비율은 건물의 각 부분이 다른 모든 부분과 조화롭게 연관되도록 보장한다.비트루비우스의 사용에서 대칭은 거울 대칭보다 영어 용어 모듈화에 더 가까운 것을 의미하며, 다시 말해 전체 건물로 (모형) 부품을 조립하는 것과 관련이 있다.파노에 있는 바실리카에서 그는 작은 정수의 비율을 사용하며, 특히 삼각형 숫자(1, 3, 6, 10, ...)를 사용하여 구조를 (비트루비아) 모듈로 비례시킨다.[a]따라서 바실리카의 너비는 1:2이고, 그 주변의 통로는 넓이만큼 높으며, 1:1이고, 기둥은 5피트 두께로 50피트 높이로 1:10이다.[9]

판테온의 평면도

비트루비우스는 기원전 15년 자신의 드 아스트라투라에서 건축에 필요한 세 가지 자질, 즉 확고함, 유용성(또는 헨리 워튼의 16세기 영어에서 "Commodity"), 그리고 기쁨이라고 명명했다.이것들은 건축에서 수학이 사용되는 방법을 분류하기 위한 범주로 사용될 수 있다.견고성은 건축물이 일어설 수 있도록 하기 위해 수학의 사용을 포함하며, 따라서 예를 들어 안정성을 보장하고 성능을 모델링하기 위해 설계에 사용되는 수학적 도구와 건축을 지원하기 위해 사용된다.유용성은 부분적으로 수학의 효과적인 적용, 설계의 공간 및 기타 관계에 대한 추론 및 분석에서 비롯된다.기쁨은 건물 안에 수학적 관계가 구현된 데서 기인하는 결과물의 속성이다; 그것은 미적, 관능적, 지적 자질을 포함한다.[16]

파리에 있는 생트 주느비에브 성당Church of Sainte-Geneviève

주요기사 : 판테온(롬)

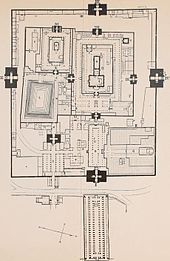
로마의 판테온은 로마의 고전적인 구조와 비례, 장식을 보여주면서 온전하게 살아남았다.주요 구조물은 돔형이고, 빛이 들어오게 하기 위해 원형으로 남겨진 꼭지점이다; 삼각형의 페디멘트를 가진 짧은 대장으로 정면에 있다.내부 서클의 높이와 직경이 43.3m(142ft)로 같아 내부 전체가 큐브 안에 정확히 들어갈 수 있고, 내부에는 같은 직경의 구형이 들어갈 수 있다.[17]이러한 치수는 고대 로마의 측정 단위로 표현했을 때 더 타당하다.그 돔은 150 로마 피트에[b] 걸쳐 있다.); 오큘러스 지름은 30 로마 피트로 되어 있고, 문간은 40 로마 피트의 높이로 되어 있다.[18]판테온은 세계에서 가장 큰 비강제 콘크리트 돔으로 남아 있다.[19]

르네상스

추가 정보:르네상스 건축
1470년 피렌체 산타 마리아 노벨라의 파사드프리제(사각형 포함) 이상은 레온 바티스타 알베르티가 맡았다.

건축에 관한 최초의 르네상스 논문은 레온 바티스타 알베르티의 1450년 작품(건축술에 관하여)으로, 1485년 건축에 관한 최초의 인쇄 책이 되었다.그것은 부분적으로 비트루비우스의 드 아스트라투라와 니코마쿠스를 통해 피타고라스의 산수를 기초로 했다.Alberti는 큐브에서 시작해서 그것으로부터 비율을 얻는다.따라서 얼굴의 대각선은 비율을 1:152인 반면, 정육면체의 둘레를 이루는 구의 직경은 1:153이다.[20][21]알베르티는 또한 필리포 브루넬레스치의 선형 원근법의 발견을 기록했는데, 편리한 거리에서 볼 때 아름답게 비례하는 건물 설계를 가능하게 하기 위해 개발되었다.[12]

세바스티아노 셀리오(1569년[22])가 세운 무대의 건축적 관점

다음 주요 내용은 세바스티아노 설리오의 레골레 제너럴리 다르치테투라(건축총칙)로, 1537년 제1권이 베니스에 등장했고, 1545권(1권과 2권)은 기하와 원근법을 다뤘다.설리오의 관점 구성 방법 중 두 가지는 잘못되었지만, 이것이 그의 작품이 널리 사용되는 것을 멈추지는 못했다.[23]

안드레아 팔라디오의 빌라 피사니 계획과 고도

1570년 안드레아 팔라디오는 베니스에서 영향력 있는 I quattro libri 델'architettura(The Four Books of Architecture)를 출판했다.이 널리 인쇄된 책은 1624년 <건축의 요소들>로 영국 외교관 헨리 워튼과 같은 지지자들의 도움을 받아 이탈리아 르네상스의 사상을 유럽 전역에 전파하는 데 크게 기여했다.[24]별장 내 각 방의 비율은 3:4와 4:5와 같이 간단한 수학 비율로 계산되었고, 집 안의 서로 다른 방은 이 비율에 의해 상호 연관되어 있었다.초기 건축가들은 대칭적인 한 면의 균형을 맞추기 위해 이러한 공식을 사용했지만 팔라디오의 디자인은 보통 정사각형의 빌라 전체와 관련이 있었다.[25]팔라디오는 [26][27]콰트로 리브리에 다음과 같은 비율을 허용했다.

7가지 종류의 방이 가장 아름답고 잘 비례하여 더 잘 만들어진다: 그것들은 드물지만; 또는 사각형이 될 수 있다; 또는 사각형이 될 수 있다; 또는 그 길이가 넓이의 사각형의 대각선과 같을 것이다; 또는 1/3정사각형과 1/2정사각형; 또는 1/2정사각형과 1/2정사각형; 또는 2/3정사각형; 또는 2/2정사각형이다.[c]

1615년 빈첸초 스마모찌는 르네상스 후기 논문 리데아 델라르치테투라 우니베르살레(The Idea of a Universal Architetura Universale)를 발표하였다.[28]그는 도시와 건물의 디자인을 비트루비우스와 피타고라스의 사상, 그리고 팔라디오의 보다 최근의 사상과 연관시키려 했다.[29]

19세기

1911년 우크라이나의 블라디미르 슈호프에 의한 하이퍼볼로이드 래티스텔 8위

하이퍼볼로이드 구조물은 19세기 말부터 블라디미르 슈호프에 의해 돛대, 등대, 냉각탑에 사용되었다.그들의 두드러진 모양은 미적으로 흥미롭기도 하고, 구조적인 재료를 경제적으로 사용하기도 한다.슈호프의 첫 번째 하이퍼볼로이드 탑은 1896년 니즈니노브고로드에서 전시되었다.[30][31][32]

20세기

추가 정보:현대 건축과 현대 건축
드 스티글의 미끄럼틀, 교차하는 평면: 리에트벨드 슈뢰더 하우스, 1924년

20세기 초반의 운동 러시아 구성주의에 의해[d] 개척된 근대 건축은 직선으로 된 유클리드 기하학을 사용했다.[33]드 스티글 운동에서는 수평과 수직이 보편성을 구성하는 것으로 보였다.건축 양식은 게리트 리에트벨트의 1924년 리에트 슈뢰더 하우스에서처럼 미끄러지거나 서로 교차하는 지붕 평면, 벽면, 발코니를 이용하여 이 두 방향성 경향을 한데 모으는 것으로 구성된다.[34]

1920년 다이 프랑제 알스 에르파인더에서 나온 라울 하인리히 프랑세의 양귀비와 페퍼팟(바이오메틱스) 이미지

모더니즘 건축가들은 평면뿐만 아니라 곡선을 자유롭게 활용할 수 있었다.찰스 홀든의 1933년 아르노스 역에는 콘크리트 지붕이 평평한 벽돌로 된 원형 매표소가 있다.[35]1938년 바우하우스 화가 라슬로 모홀리-나기는 라울 하인리히 프랑세의 일곱 가지 생명공학 요소, 즉 결정, 구체, 원뿔, 평면, (큐보이드) 스트립, (실린지) 막대, 나선형을 자연에서 영감을 받은 건축의 기본 구성 요소로 채택했다.[36][37]

Le Corbusier는 인간의 키에 기초하여 건축에서 인체측정학적으로 비례하는 Modulor를 제안했다.[38]Le Corbusier의 1955년 Chapelle Noter-Dame du Haut은 수학적 공식에서 설명할 수 없는 자유형 곡선을 사용한다.[e]그 모양은 배의 배회나 기도하는 손과 같은 자연적인 형태를 연상시킨다고 한다.[41]설계는 가장 큰 규모에 불과하다. 더 작은 규모에서는 디테일의 서열도 없고, 따라서 프랙탈 차원도 없다. 시드니 오페라 하우스, 덴버 국제공항, 구겐하임 박물관, 빌바오 등과 같은 다른 20세기 유명한 건물에도 적용된다.[39]

현대 건축은 2010년 세계 건축 조사에 응답한 90명의 주요 건축가들의 의견에 따라 매우 다양하다. 최고의 건축가는 프랭크 게리의 구겐하임 박물관인 빌바오라고 평가되었다.[42]

1995년 완공된 덴버 국제공항 원단 지붕의 최소 표면은 콜로라도의 눈 덮인 산과 아메리카 원주민들의 티피 텐트를 연상시킨다.

1995년에 완공된 덴버 국제공항의 터미널 건물에는 최소 표면(즉, 평균 곡률 0)으로 지지되는 직물 지붕이 강철 케이블로 설치되어 있다.콜로라도의 눈 덮인 산과 아메리카 원주민들의 티피 텐트를 연상시킨다.[43][44]

건축가 리처드 버크민스터 풀러는 지오데틱 돔으로 알려진 강한 얇은 껍질 구조를 디자인한 것으로 유명하다.몬트레알 바이오세르 돔의 높이는 61m(200ft)이며 지름은 76m(249ft)이다.[45]

시드니 오페라하우스는 배의 돛을 연상시키는 솟아오르는 하얀 금고로 이루어진 극적인 지붕을 가지고 있으며, 표준화된 구성품을 이용하여 건축할 수 있도록 금고는 모두 같은 반경의 구형 쉘의 삼각형 부분으로 구성되어 있다.이것들은 모든 방향에서 요구되는 균일한 곡률을 가지고 있다.[46]

20세기 후반의 운동 탈구축주의는 프랭크 게리의 디즈니 콘서트 홀과 빌바오 구겐하임 미술관에서처럼 건축 이론의 니코스 살링가로스(Nikos Salingaros)가 비병렬 벽, 중첩된 격자, 복잡한 2-D 표면을 사용함으로써 고도로[48] 복잡성의 임의적인 형태라고[47] 부르는 것으로 의도적인 장애를 일으킨다.[49][50]20세기까지 건축학과 학생들은 수학의 기초를 닦을 의무가 있었다.살링가로스는 처음에는 "지나치게 단순하고 정치적으로 주도적인" 모더니즘과 그 다음에는 "반과학적인" 해체주의가 건축과 수학의 구분을 효과적으로 분리시켰다고 주장한다.그는 비수학적 건축의 "퍼베이시브 미학"이 사람들에게 "건축된 환경에서 수학적 정보를 거부하도록" 훈련시키기 때문에 이러한 "수학적 가치의 역전"은 해롭다고 믿는다; 그는 이것이 사회에 부정적인 영향을 미친다고 주장한다.[39]

종교적 원칙

고대 이집트

참고 항목: 황금 비율 § 이집트 피라미드
베이스:기자대 피라미드와 같은 피라미드의 히포테누스(b:a) 비율은 1:103(케플러 삼각형), 3:5(3:4:5 삼각형) 또는 1:4/105일 수 있다.

고대 이집트의 피라미드는 수학적인 비율로 만들어진 무덤이지만, 이것들이 무엇이었는지, 그리고 피타고라스의 정리가 사용되었는지가 논의되고 있다.기자의 피라미드 기저길이의 절반에 이르는 경사 높이의 비율은 황금비율에서 1%도 안 된다.[51]이것이 설계법이었다면 케플러의 삼각형(면각 51°49')[51][52]의 사용을 암시하는 것이겠지만, 많은 과학사학자들에 따르면 황금비율은 피타고라스 시대에 이르러서야 알 수 있었다.[53]그레이트 피라미드는 또한 베이스 대 하이포텐 사용 비율이 1:4/³(면각 51°50')[54]인 삼각형을 기반으로 했을 수도 있다.

일부 피라미드의 비율은 또한 Rhind Mathematical Papyrus (기원전 1650–1550년)에서 알려진 3:4:5 삼각형 (면각 53°8')에 기초했을지도 모른다; 이것은 1882년 역사학자 Moritz Cantor에 의해 처음 추측되었다.[55]고대 이집트에서는 치수를 위해 매듭을 지은 줄을 이용하여 직각이 정확하게 배치되었고,[55] 플루타르크가 이시스와 오시리스(c. 100 AD)에서 이집트인들이 3:4:5 삼각형을 동경한다고 기록했으며,[55] 기원전 1700년 이전의 두루마기가 기본적인 사각 공식을 증명했다고 알려져 있다.[56][f]역사학자 로저 L.쿡은 "피타고라스의 정리를 모르는 상태에서 그런 조건에 관심을 갖는 사람은 상상하기 어렵다"고 관찰하면서도 기원전 300년 이전에는 실제로 삼각형의 옆면 길이를 찾기 위한 정리의 사용을 언급하는 이집트 문헌은 없으며, 직각을 구성하는 더 간단한 방법이 있다는 점에 주목한다.쿡은 칸토르의 추측이 여전히 불확실하다고 결론짓는다; 그는 고대 이집트인들이 아마도 피타고라스의 정리를 알고 있었을 것이라고 추측하지만, "직각구성을 만들기 위해 그것을 사용했다는 증거는 없다"[55]고 추측한다.

고대 인도

추가 정보:인도와 바스투 샤스트라의 건축물
힌두비루팍샤 사원의 고푸람은 프랙탈과 같은 구조를 가지고 있는데, 그 부분은 전체적으로 닮았다.

인도의 고대 건축과 도시 계획 협곡인 바스투 샤스트라는 만다라라고 불리는 대칭적인 그림을 사용한다.복잡한 계산은 건물과 그 구성요소의 치수에 도달하기 위해 사용된다.설계는 건축과 자연과의 통합, 구조물의 다양한 부분의 상대적 기능, 기하학적 패턴(얀트라), 대칭, 방향 맞춤을 활용한 고대 신앙을 통합하기 위한 것이다.[57][58]그러나, 초기 건설자들은 우연히 수학적인 비율에 도달했을지도 모른다.수학자 조르주 이프라 씨는 줄과 말뚝을 가진 단순한 '트릭'을 타원이나 직각과 같은 기하학적 모양을 배치하는 데 사용할 수 있다고 지적한다.[12][59]

마두라이 미낙시 암만사 7세기 이후 계획.4개의 관문(번호 I-IV)은 키가 큰 고뿌람이다.

프랙탈의 수학은 기존 건물들이 보편적인 매력을 가지고 있고 시각적으로 만족하는 이유는 시청자들에게 다른 시야 거리에서 스케일의 감각을 제공하기 때문이다.예를 들어 7세기에 지어진 함피의 비루팍샤 사원과 카주라호의 칸다리야 마하데프 사원과 같은 힌두 사원의 키 큰 고푸람 문고집에서는 부분과 전체가 동일한 성격을 띠며 프랙탈 치수는 1.7~1.8이다.시바 경의 거주지인 신성한 카일라시 산을 대표하는 가장 높고 중심적인 탑에 대한 작은 탑들의 군집(시하라, 점등. '산')은 힌두 우주론에서 우주의 끝없는 반복을 묘사하고 있다.[2][60]종교학자인 William J. Jackson은 작은 탑들 사이에 그룹화된 탑들의 패턴을 관찰했는데, 그 자체는 여전히 더 작은 탑들 사이에 그룹화되어 있다.

우아하게 예술화된 이상적 형태는 무한한 존재와 의식의 상승 수준을 암시하고, 위로는 초월을 향해 솟아오르는 크기를 확장하며, 동시에 신성한 것을 내면 깊숙이 수용한다.[60][61]

미낙시 암만사는 사당이 여러 개 있는 대규모 단지로, 마두라이 거리는 샤스트라에 따라 그 주변에 동심원적으로 배치되어 있다.네 개의 관문은 함피에서와 같이 프랙탈과 같은 반복 구조를 가진 높은 탑(고푸람)이다.각 사당 주변의 외함은 직사각형이며 높은 돌담으로 둘러싸여 있다.[62]

고대 그리스

추가 정보:그리스 건축, 황금비율, 피타고라스주의, 유클리드 기하학
파르테논 신전은 피타고라스 비율을 이용하여 설계되었다.

피타고라스 (기원전 569년 – 475년)와 그의 추종자들인 피타고라스는 "모든 것은 숫자"라고 주장했다.그들은 주파수의 특정한 작은 정수의 비율을 가진 주석에 의해 생성된 하모니를 관찰했고, 건물 역시 그러한 비율로 설계되어야 한다고 주장했다.그리스어 대칭은 원래 건물의 가장 작은 디테일에서부터 전체 디자인에 이르기까지 정확한 비율의 건축 형태의 조화를 나타낸다.[12]

파르테논 신전은 길이 69.5m (228ft), 폭 30.9m (101ft), 높이 13.7m (45ft)이다.이것은 너비 대 길이 대 9의 비율을 제공하며, 높이 대 너비의 경우에도 마찬가지다.이것들을 합치면 높이: 너비:길이 16:36:81 또는 피타고라스의 42:62:9가2 된다[63].이것은 모듈을 0.858m로 설정한다. 4:9 사각형은 3:4 비율의 옆면이 있는 3개의 연속 직사각형으로 구성될 수 있다.각각의 반직각은 편리한 3:4:5 직각 삼각형이 되어 각도와 측면을 적절히 매듭을 지은 로프로 점검할 수 있다.내부 면적(나오)도 마찬가지로 4:9 비율(21.44m(70.3ft) 너비 48.3m)을 가지며, 외부 기둥의 지름 1.905m(6.25ft)와 중심 간격 4.293m(14.08ft)의 비율도 4:9이다.[12]

파르테논 신전의 평면도

파르테논 신전은 존 줄리어스 노리치와 같은 작가들에 의해 "가장 완벽한 도리아 사원"으로 여겨지고 있다.[64]그것의 정교한 건축적 정교함에는 "기단의 곡률, 나오스의 벽의 테이퍼, 기둥의 얽힘 사이의 미묘한 일치"가 포함된다.[64]결속은 기둥들이 올라갈 때 지름이 미세하게 줄어드는 것을 말한다.기단은 기둥이 서 있는 플랫폼이다.다른 고대 그리스 사원에서와 마찬가지로 승강장은 약간의 포물선 위쪽으로 굴곡이 있어 빗물을 흘리고 지진에 대비하여 건물을 보강한다.[65]따라서 기둥들은 바깥쪽으로 기울어져야 할지도 모르지만, 실제로는 약간 안쪽으로 기울어져 있어서, 그들이 계속하면 건물의 중심으로부터 약 1킬로미터 반을 만날 수 있다; 그것들이 모두 같은 높이이기 때문에, 외부 기단 가장자리의 곡률은 아치트레이브와 위 지붕으로 전달된다: "모두 r을 따른다.섬세한 곡선에 건설되는 것"이라고 말했다.[66]

황금비율은 기원전 300년에 유클리드(Eucleid)가 기하학적 구조법을 기술하면서 알려졌다.[67]황금비율은 파르테논 신전을 비롯한 고대 그리스 건축물의 설계는 물론 조각, 그림, 화병 등에도 사용됐다는 주장이 제기됐다.[68]그러나 니코스 살링가로스 같은 보다 최근의 저자들은 이 모든 주장을 의심하고 있다.[69]컴퓨터 과학자 조지 마코우스키의 실험은 황금 직사각형에 대한 어떤 선호도 찾지 못했다.[70]

이슬람 건축

추가 정보:이슬람 건축과 황금비율 § 건축
에딘, 셀리미예 모스크, 1569–1575

이슬람 미술사 안토니오 페르난데스-푸에르타스는 코르도바의 대 모스크와 [71]같은 알함브라가 약 0.62m(2.0ft)의 히스파노-무슬림 발이나 코도를 사용하여 설계되었다고 주장한다.궁전의 사자 궁정에서는 그 비율이 일련의 추문을 따른다.면 1과 √2가 있는 직사각형에는 (피타고라스의 정리로는) √3의 대각선이 있는데, 이는 궁중 양쪽에서 만든 직각 삼각형을 묘사하고 있다; 시리즈는 √4 (1:2 비율 부여), √5 등으로 이어진다.장식 패턴은 원 안에 정사각형을 생성하는 √2와 8개의 점이 있는 별을 생성하는 33과 6개의 점이 있는 별을 생성하는 √2와 유사하게 비례한다.황금비율이 알함브라에서 사용되었다는 이전의 주장을 뒷받침할 증거가 없다.[10][72]사자의 법정은 두 자매의 전당과 아벤서라제스의 전당에 의해 분류된다. 이 두 개의 홀의 중심과 사자 법정의 안쪽 구석에서 규칙적인 육각형을 그릴 수 있다.[73]

터키 에디른에 있는 셀리미예 모스크는 미마르 시난이 건물 내부 어디에서나 미흐랩을 볼 수 있는 공간을 제공하기 위해 지은 것이다.매우 큰 중심 공간은 이에 따라 8개의 거대한 기둥으로 이루어진 팔각형으로 배열되며, 지름 31.25m(102.5ft)와 높이 43m(141ft)의 원형 돔으로 덮여 있다.팔각형은 4개의 세미돔이 있는 정사각형으로 형성되며, 외부적으로는 83m(272ft)의 키에 예외적으로 키가 큰 4개의 미니트(minaret)가 있다.따라서 이 건물의 계획은 8각형 안, 사각형 안쪽에 원을 그리는 것이다.[74]

무굴 건축

주요 기사:무굴 건축, 파테푸르 식리, 타지마할의 기원과 건축
아그라 단지의 정원의 일부가 있는 타지마할 묘지

버려진 제국 도시 파테푸르 식리와 타지마할 콤플렉스에서 볼 수 있는 무굴 건축은 독특한 수학적 질서와 대칭성과 조화를 바탕으로 한 강한 미학을 가지고 있다.[11][75]

타지마할은 그 규모와 대칭성, 값비싼 장식을 통해 파라다이스를[76] 대표하고 무굴 황제 샤 자한의 힘을 보여주는 무굴 건축의 예다.피에트라두라, 대문(Darwaza-i rauza), 다른 건물, 정원, 길이 함께 통일된 위계적 디자인을 이루고 있다.건물들은 서쪽의 붉은 사암에 있는 모스크와 거의 동일한 건물인 자와브 또는 동쪽의 '답변'이 복합체의 양쪽 대칭을 유지하도록 되어 있다.형식적인 샤르바그('4배 정원')는 네 부분으로 되어 있으며, 낙원의 4강을 상징하며, 묘지의 조망과 반성을 제공한다.이것들은 차례로 16파르터로 나뉜다.[77]

타지마할 단지 부지 계획.대문은 우측에 있고, 중앙에는 묘소가 있으며, 모스크(아래)와 자와브가 있다.그 계획에는 정사각형과 옥타곤이 포함되어 있다.

타지마할 단지는 그리드에 배치되었고, 작은 그리드로 세분되었다.건축학자인 코흐와 바르크라우드는 단지의 폭을 374 무굴야드 또는 가스로 부여하고 있으며,[g] 주요 면적은 374 가즈 광장 3개다.이것들은 바자회와 카라반세라이와 같은 지역에서 17개 가즈 모듈로 나뉘었다; 정원과 테라스는 23개 가즈 모듈로 되어 있고, 넓이는 368개 가즈(16 x 23)이다.묘소, 모스크, 게스트하우스는 7가즈 격자 위에 배치되어 있다.코흐와 바러드는 단지에서 반복적으로 사용되는 8각형이 7개의 면으로 주어질 경우 폭 17개의 면으로 되어 [h]있어 단지 내 비율의 선택을 설명하는 데 도움이 될 수 있다고 관찰한다.[78]

기독교 건축

추가 정보:교회건축

비잔티움(현 이스탄불)에 있는 하히아 소피아(현 이스탄불)의 기독교 가부장적 성당은 537년에 처음 지어졌다(그리고 두 번 다시 지어졌다)는 천 년 동안[i] 지어진 성당 중 가장 큰 규모였다.그것은 술탄 아흐메드와 그 도시의 다른 모스크를 포함한 많은 후기 건물들에 영감을 주었다.비잔틴 건축물은 원형 돔과 같은 직경(31m(102ft)인 두 개의 반쪽 돔에 의해 왕관을 씌운 나브를 포함하고 있으며, 더 작은 반쪽 돔 5개가 apse를 형성하고 광대한 직사각형 실내의 네 모서리를 둥글게 만들었다.[79]이것은 평범한 건축가들에 의해 아래(사각형 베이스)의 일상과 위(높아 오르는 구형 돔)의 신성한 하늘을 나타내는 것으로 해석되었다.[80]황제 쥐스티니아누스는 밀레투스의 이시도레와 트랄레스의 안테미우스라는 두 가지 기하학을 건축가로서 사용하였으며, 이시도레는 아르키메데스의 작품을 고체 기하학에 편찬하여 그의 영향을 받았다.[12][81]

이스탄불, 하히아 소피아
a) 갤러리 계획(반쪽 위)
b) 1층 평면도(하반부)

기독교에서 물 세례의 중요성은 세례 건축의 규모에 반영되었다.440년에 지어진 로마에서 가장 오래된, 라테란 침례교에서는 팔각 침례교 유행을 세웠다;[82] 이 건물들 내부의 세례문자는 1152년에서 1363년 사이에 지어진 이탈리아 최대의 침례교인 피사의 8각형 서체는 원형이고, 팔각형 서체로 되어 있다.높이는 54.86m(180.0ft)로 직경은 34.13m(112.0ft)(8:5)이다.[83]성 암브로스는 서체와 침례는 [j]"8일째 되는 날 그리스도가 부활함으로써 죽음의 속박을 느슨하게 하고 죽은 자를 무덤에서 영접하기 때문"이라고 썼다.[84][85]성 아우구스티누스는 비슷하게 8일째를 "영원한"이라고 묘사했다.그리스도의 부활로 거룩해진"[85][86]1059년에서 1128년 사이에 지어진 플로렌스 성 요한의 팔각 침례는 그 도시에서 가장 오래된 건물 중 하나이며, 고전 고대의 직접적인 전통에서 마지막 건물 중 하나이다. 프란체스코 탤런티, 알베르티, 브루넬레스치 등 주요 건축가들이 사용했던 것처럼 이후의 플로렌타인 르네상스에 매우 큰 영향을 미쳤다.e 클래식 건축의 [87]모델

숫자 5는 얀 블라제 산티니 아이첼이 설계한 체코 republic아나 사사보우 인근의 젤레나호라에 있는 네포무크 성 요한 1721 순례교회에서 "[88]훌륭하게"나브는 원형이며, 다섯 쌍의 기둥과 다섯 개의 타원형의 돔으로 둘러싸여 있고, 오기벌 유인원과 교대로 있다.교회에는 5개의 성문, 5개의 채플, 5개의 제단, 5개의 별들이 있다; 한 전설은 네포묵의 세인트 존이 순교했을 때 그의 머리 위로 5개의 별이 나타났다고 주장한다.[88][89]다섯 개의 건축물은 또한 그리스도의 다섯 개의 상처와 "타쿠이"의 다섯 글자를 상징할지도 모른다. (라틴어: "나는 침묵을 지켰다" [고백의 비밀에 대하여])[90]

안토니 가우디는 1882년 (2015년 현재 완성되지 않은) 바르셀로나의 사그라다 파밀리아에서 아주 다양한 기하학적 구조를 사용했으며, 일부는 최소 표면이었다.여기에는 쌍곡선 파라볼로이드와 혁명의 하이퍼볼로이드,[91] 테셀레이션, 카트리네이드 아치, 카티노이드, 헬리코이드, 지배 표면 등이 포함된다.이 다양한 기하학적 조합은 교회 주위에서 다른 방식으로 창조적으로 결합된다.예를 들어 사그라다 파밀리아의 '패션 파사드'에서 가우디는 어느 지점에서 만나지 않고도 윗부분(디렉토리)에서 겹치는 쌍곡 포물선 모양의 돌 '브랜치'를 조립했다.이와는 대조적으로, 대장에는 다른 구조물과 부드럽게 결합하여 결합되지 않은 표면을 형성하는 쌍곡선 포물선 표면이 있다.또한 가우디는 나무의 모양에서 파생된 기둥과 변형되지 않은 현무암으로 만들어진 인텔을 자연적으로 갈라(용융된 바위에서 식힘으로써) 육각형 기둥으로 만드는 자연적인 무늬를 스스로 수학적으로 이용한다.[92][93][94]

1971년 가정 성모 대성당 샌프란시스코에는 안장 지붕이 8개의 쌍곡 포물선 모양으로 구성되어 있으며, 지붕의 아래쪽 수평 단면이 정사각형이고 위쪽 단면이 기독교 십자가가 되도록 배치되어 있다.이 건물은 측면의 평방 77.7m (255ft), 높이 57.9m (190ft)이다.[95]오스카 니메이어가 만든 1970년 브라질리아 성당은 하이퍼볼로이드 구조를 다르게 사용한다; 그것은 각각 90톤의 무게가 나가는 16개의 동일한 콘크리트 빔으로 구성되어 있고, 혁명의 하이퍼볼로이드를 형성하기 위해 원형으로 배열되어 있으며,[k] 하얀 빔은 하늘에 기도하는 손과 같은 모양을 만들고 있다.오직 돔만이 밖에서 보인다: 건물의 대부분은 땅 아래에 있다.[96][97][98][99]

스칸디나비아의 몇몇 중세 교회는 덴마크의 본홀름 섬에 있는 4개를 포함하여 원형이다.그 중 가장 오래된 것 중 하나인 1160년의 외스테를라스 교회는 거대한 원형 돌기둥 둘레에 원형 나브를 두르고, 아치를 뚫고 프레스코로 장식했다.그 원형 구조물은 3층이고, 분명히 방어를 위한 최상층 건물인 강화되어 있었다.[100][101]

수학적 장식

이슬람 건축 장식

주요 기사:이슬람 기하학적 패턴

이슬람 건물들은 보통 여러 가지 수학적 테셀레이션을 사용하는 기하학적 무늬로 장식되는데, 세라믹 타일(기리, 젤리그)로 이루어져 있으며, 그 자체는 평범하거나 줄무늬로 장식되어 있을 수 있다.[12]이슬람 문양에는 6개, 8개, 8개 점의 배수로 이루어진 별과 같은 대칭이 사용된다.이 중 일부는 '카템 술레마니' 또는 솔로몬의 물개 모티브를 바탕으로 한 것으로, 두 개의 사각형으로 이루어진 여덟 개의 점으로 이루어진 별이며, 하나는 같은 중심에서 다른 쪽으로부터 45도 회전했다.[102]이슬람 패턴은 17개의 가능한 벽지 그룹들 중 많은 것을 이용한다; 1944년에 이르면, 에디스 뮐러는 알함브라가 11개의 벽지 그룹을 장식에 사용했다는 것을 보여주었고, 1986년에 브란코 그룬바움은 알함브라에서 13개의 벽지 그룹을 발견했다고 주장하면서 나머지 4개 그룹은 이스 어디에서도 발견되지 않는다고 논쟁의 여지가 있다.라미 [102]장식

현대 건축 장식

추가 정보:장식(예술) 및 현대 건축

20세기 말에 프랙탈 기하학, 주기적 타일링과 같은 새로운 수학적 구조들이 건축가들에 흥미롭고 매력적인 덮개를 제공하기 위해 건축가들에 의해 압수되었다.[4]1913년, 모더니즘 건축가 아돌프 로스는 20세기의 나머지 기간 동안 건축 사고에 영향을 주면서 [103]"오르나멘트는 범죄"라고 선언했었다.21세기에 건축가들은 다시 장식의 사용을 탐구하기 시작했다. 21세기 장식은 매우 다양하다.헤닝 라센의 2011년 하파 콘서트 겸 컨퍼런스 센터인 레이캬비크는 커다란 유리 덩어리로 만들어진 암석의 크리스탈 벽처럼 생긴 것을 가지고 있다.[103]영국 런던 소재 외국 사무소 건축가들의 2010년 라벤스본 칼리지(Ravensbourne College)는 테셀링을 장식적으로 하고 있으며, 빨간색, 흰색, 갈색에 아노다이징 알루미늄 타일 2만8000개로 크기가 다른 원형 유리창을 연결했다.테셀레이션은 세 종류의 기와, 정삼각형 기와 두 개의 불규칙한 펜타곤을 사용한다.[104][105][l]쿠도 가즈미의 가나자와 우미미라이 도서관은 평탄한 콘크리트 벽에 설치된 작은 원형 유리 블록으로 장식 격자를 만든다.[103]

디펜스

유럽

추가 정보:별자리

요새의 건축은 높은 석조 벽을 가진 중세 요새에서 15세기 중반에서 19세기 사이에 포격을 견딜 수 있는 낮고 대칭적인 요새로 진화했다.별 모양의 기하학적 구조는 공격 보병들이 방어 화재를 피할 수 있는 데드 존을 피할 필요성에 따라 결정되었다. 투사 지점의 측면은 각도를 이루어 그러한 화력이 지면을 쓸 수 있도록 했고, 각 투사 지점을 넘어 (양쪽에서) 십자 포화를 제공하도록 했다.그러한 방어시설을 설계한 유명한 건축가로는 미켈란젤로, 발다사레 페루찌, 빈첸초 스마모찌, 세바스티앙 르 프레스트레 드 바우반이 있다.[106][107]

건축사학자 지그프리드 기디온은 "르네상스는 한 도시 유형에 의해 최면에 걸렸고, 필라레테에서 스캐모찌에 이르기까지 1세기 반 동안 모든 유토피아적 계획에 감명을 받았다"고 항성모양의 요새화가 르네상스 이상도시에 영향을 미쳤다고 주장했다.[108]

중국

푸젠 성 융딩 현의 튤루

중국 건축에서 푸젠 성의 튤루는 주로 빈 벽과 단 하나의 철제 도금된 나무 문을 가진 원형 공동의 방어 구조물이며, 일부는 16세기부터 시작되었다.벽에는 바깥과 안쪽으로 완만하게 경사져 있는 지붕이 얹혀 있어 고리를 이루고 있다.원의 중심은 자갈이 깔린 열린 뜰로, 종종 우물이 있고, 5층 높이까지 시계가 달린 갤러리들로 둘러싸여 있다.[109]

환경목표

이란 야흐찰의 야크찰

건축가들은 또한 환경 목표를 충족시키기 위해 건물의 형태를 선택할 수도 있다.[88]예를 들어, 오이처럼 생긴 모양으로 '게르킨'으로 알려진 포스터 앤 파트너스의 30세 세인트 메리 액스 런던은 파라메트릭 모델링(parametric modeling)을 사용하여 설계된 혁명의 고체다.그것의 기하학은 단순히 미적인 이유 때문이 아니라, 그것의 기초에서 휘몰아치는 기류를 최소화하기 위해 선택되었다.건물의 외관상 곡면임에도 불구하고, 상단의 렌즈를 제외하고는 피부를 형성하는 유리 패널이 모두 평평하다.삼각 패널보다 폐기량이 적은 직사각형 유리로 절단할 수 있어 대부분의 패널은 사변측정감시다.[1]

페르시아의 전통적인 야크찰은 증발 냉각기 역할을 했다.지상에서는 돔 모양의 구조물이 있었지만, 얼음과 때로는 음식을 보관할 수 있는 지하 저장공간이 있었다.지하공간과 두꺼운 내열공사로 1년 내내 수납공간을 단열했다.내부 공간은 종종 풍차들로 더욱 냉각되었다.[110]

참고 항목

메모들

  1. ^ De Architectura 제3장 제4권에서는 모듈을 직접 논한다.[15]
  2. ^ 로마의 발은 약 0.296미터(0.97피트)이었다.
  3. ^ 현대 대수 표기법에서 이 비율은 각각 1:1, √2:1, 4:3, 3:2, 5:3, 2:1이다.
  4. ^ 예를 들어 구성주의는 바우하우스와 르 코르뷔지에에게 영향을 주었다.[33]
  5. ^ 반대 의견을 제시하는 페이스 니코스 살링가로스(Pace Nikos Salingaros)는 그러나 르 꼬르뷔지에의 예배당의 곡선에 수학이 어떤 형태로 구현될지는 정확히 알 수 없다.[39][40]
  6. ^ 중왕국의 베를린 파피루스 6619는 "100 평방 면적이 두 개의 작은 정사각형과 같다"고 말했다.한 쪽은 ½ + 다른 쪽은 ½."
  7. ^ 1가지는 약 0.86미터(2.8피트)이다.
  8. ^ 대체 변을 연장하여 팔각형 주위에 그려진 사각형에는 7의 하이포텐스를 가진 직각 삼각형 4개와 and49/2 또는 4.9497의 다른 두 변이 거의 5개씩 추가된다.따라서 광장의 옆면은 5+7+5로 17이다.
  9. ^ 1520년 세비야 대성당이 완공되기 전까지.
  10. ^ 성주간 엿새째 되는 날은 좋은 금요일이었고, 그 다음 일요일은 이렇게 여덟째 날이었다.[84]
  11. ^ 이는 90톤(장탄 89톤, 단탄 99톤)이다.
  12. ^ 구조 격자의 리듬을 피하기 위해 주기적인 타일링을 고려했지만 실제로는 펜로즈 타일링이 너무 복잡해 가로 2.625m, 세로 4.55m의 격자를 선택했다.[105]

참조

  1. ^ a b c Freiberger, Marianne (1 March 2007). "Perfect buildings: the maths of modern architecture". Plus magazine. Retrieved 5 October 2015.
  2. ^ a b Rian, Iasef Md; Park, Jin-Ho; Ahn, Hyung Uk; Chang, Dongkuk (2007). "Fractal geometry as the synthesis of Hindu cosmology in Kandariya Mahadev temple, Khajuraho". Building and Environment. 42 (12): 4093–4107. doi:10.1016/j.buildenv.2007.01.028.
  3. ^ Williams, Kim; Ostwald, Michael J., eds. (2015). Architecture and Mathematics from Antiquity to the Future: Volume I: from Antiquity to the 1500s. Birkhäuser. pp. chapter 1. 1–24. ISBN 978-3-319-00136-4.
  4. ^ a b Williams, Kim; Ostwald, Michael J., eds. (2015). Architecture and Mathematics from Antiquity to the Future: Volume II: The 1500s to the Future. Birkhäuser. pp. chapter 48. 1–24. ISBN 978-3-319-00142-5.
  5. ^ "Architectural Engineering Overview" (PDF). Sloan Career Cornerstone Center. Archived from the original (PDF) on 14 July 2015. Retrieved 11 October 2015.
  6. ^ Leyton, Michael (2001). A Generative Theory of Shape. Springer. ISBN 978-3-540-42717-9.
  7. ^ Stakhov, Alexey; Olsen, Olsen (2009). The Mathematics of Harmony: From Euclid to Contemporary Mathematics and Computer Science. World Scientific. ISBN 978-981-277-582-5.
  8. ^ Smith, William (1870). Dictionary of Greek and Roman Biography and Mythology. Little, Brown. p. 620.
  9. ^ a b Vitruvius (2009). On Architecture. Penguin Books. pp. 8–9. ISBN 978-0-14-193195-1.
  10. ^ a b Tennant, Raymond (July 2003). "International Joint Conference of ISAMA, the International Society of the Arts, Mathematics, and Architecture, and BRIDGES. Mathematical Connections in Art Music, and Science, University of Granada, Spain, July, 2003. Islamic Constructions: The Geometry Needed by Craftsmen" (PDF). International Joint Conference of ISAMA, the International Society of the Arts, Mathematics, and Architecture, and BRIDGES, Mathematical Connections in Art Music, and Science.
  11. ^ a b Rai, Jaswant (1993). "Mathematics and Aesthetics in Islamic Architecture: Reference to Fatehpur Sikri". Journal of King Saud University, Architecture & Planning. 5 (1): 19–48.[영구적 데드링크]
  12. ^ a b c d e f g O'Connor, J. J.; Robertson, E. F. (February 2002). "Mathematics and Architecture". University of St Andrews. Retrieved 4 October 2015.
  13. ^ van den Hoeven, Saskia; van der Veen, Maartje (2010). "Muqarnas: Mathematics in Islamic Arts" (PDF). Utrecht University. Archived from the original (PDF) on 4 March 2016. Retrieved 30 September 2015.
  14. ^ Cucker, Felipe (2013). Manifold Mirrors: The Crossing Paths of the Arts and Mathematics. Cambridge University Press. pp. 103–106. ISBN 978-0-521-72876-8.
  15. ^ Vitruvius. "VITRUVIUS, BOOK IV, CHAPTER 3 On the Doric order". Vitruvius.be. Retrieved 6 October 2015.
  16. ^ Williams, Kim; Ostwald, Michael J. (9 February 2015). Architecture and Mathematics from Antiquity to the Future: Volume I: Antiquity to the 1500s. Birkhäuser. pp. 42, 48. ISBN 978-3-319-00137-1.
  17. ^ Roth, Leland M. (1992). Understanding Architecture: Its Elements, History, And Meaning. Boulder: Westview Press. p. 36. ISBN 0-06-438493-4.
  18. ^ Claridge, Amanda (1998). Rome. Oxford Archaeological Guides. Oxford Oxfordshire: Oxford University Press. pp. 204–5. ISBN 0-19-288003-9.
  19. ^ Lancaster, Lynne C. (2005). Concrete Vaulted Construction in Imperial Rome: Innovations in Context. Cambridge: Cambridge University Press. pp. 44–46. ISBN 0-521-84202-6.
  20. ^ March, Lionel (1996). "Renaissance mathematics and architectural proportion in Alberti's De re aedificatoria". Architectural Research Quarterly. 2 (1): 54–65. doi:10.1017/S135913550000110X.
  21. ^ "Sphere circumscribing a cube". Mathalino.com Engineering Math Review. Retrieved 4 October 2015.
  22. ^ 하버드 대학교 Houghton Library의 타이프 525.69.781
  23. ^ Andersen, Kirsti (2008). The Geometry of an Art: The History of the Mathematical Theory of Perspective from Alberti to Monge. Springer. pp. 117–121. ISBN 978-0-387-48946-9.
  24. ^ Ruhl, Carsten (7 April 2011). "Palladianism: From the Italian Villa to International Architecture". European History Online. Retrieved 3 October 2015.
  25. ^ Copplestone, Trewin (1963). World Architecture. Hamlyn. p. 251.
  26. ^ Wassell, Stephen R. "The Mathematics Of Palladio's Villas: Workshop '98". Nexus Network Journal. Retrieved 3 October 2015.
  27. ^ Palladio, Andrea; Tavernor, Robert; Schofield, Richard (trans.) (1997) [1570]. I quattro libri dell'architettura. MIT Press. p. book I, chapter xxi, page 57.{{cite book}}: CS1 maint : 복수이름 : 작성자 목록(링크)
  28. ^ Scamozzi, Vincenzo; Vroom, W. H. M. (trans.) (2003) [1615]. The Idea of a Universal Architecture. Architectura & Natura.
  29. ^ Borys, Ann Marie (28 March 2014). Vincenzo Scamozzi and the Chorography of Early Modern Architecture. Ashgate Publishing. pp. 140–148 and passim. ISBN 978-1-4094-5580-6.
  30. ^ Beckh, Matthias (2015). Hyperbolic Structures: Shukhov's Lattice Towers – Forerunners of Modern Lightweight Construction. John Wiley & Sons. pp. 75 and passim. ISBN 978-1-118-93268-1.
  31. ^ "The Nijni-Novgorod exhibition: Water tower, room under construction, springing of 91 feet span". The Engineer: 292–294. 19 March 1897.
  32. ^ Graefe, Rainer; et al. (1990). Vladimir G. Suchov 1853–1939. Die Kunst der sparsamen Konstruktion. Deutsche Verlags-Anstalt. pp. 110–114. ISBN 3-421-02984-9.
  33. ^ a b Hatherley, Owen (4 November 2011). "The Constructivists and the Russian Revolution in Art and Architecture". The Guardian. Retrieved 6 June 2016.
  34. ^ "Rietveld Schröderhuis (Rietveld Schröder House)". World Heritage Centre. UNESCO. Retrieved 13 December 2012.
  35. ^ Historic England. "Details from listed building database (1358981)". National Heritage List for England. Retrieved 5 October 2015.
  36. ^ Moholy-Nagy, Laszlo; Hoffman, Daphne M. (trans.) (1938). The New Vision: Fundamentals of Design, Painting, Sculpture, Architecture. New Bauhaus Books. p. 46.
  37. ^ Gamwell, Lynn (2015). Mathematics and Art: A Cultural History. Princeton University Press. p. 306. ISBN 978-0-691-16528-8.
  38. ^ Le Corbusier (2004) [1954 and 1958]. The Modulor: A Harmonious Measure to the Human Scale, Universally Applicable to Architecture and Mechanics. Birkhäuser. ISBN 3-7643-6188-3.
  39. ^ a b c Salingaros, Nikos. "Architecture, Patterns, and Mathematics". Nexus Network Journal. Retrieved 9 October 2015. 의 업데이트된 버전
  40. ^ Greene, Herb. "Le Corbusier: Notre Dame du Haut at Ronchamp". Archived from the original on 7 September 2015. Retrieved 5 October 2015.
  41. ^ Hanser, David A. (2006). Architecture of France. Greenwood Publishing Group. p. 211. ISBN 978-0-313-31902-0.
  42. ^ "Vanity Fair's World Architecture Survey: the Complete Results". Vanity Fair. 30 June 2010. Archived from the original on 8 November 2014. Retrieved 22 July 2010.
  43. ^ "Denver International Airport Press Kit" (PDF). Denver International Airport. 2014. Archived from the original (PDF) on 12 April 2015. Retrieved 5 October 2015.
  44. ^ "Denver International Airport". Fenstress Architects. Retrieved 5 October 2015.
  45. ^ "Biosphere". A view on cities. Archived from the original on 27 September 2007. Retrieved 1 October 2015.
  46. ^ Hahn, Alexander J. (4 February 2013). "Mathematical Excursions To Architecture". Inside Science. Retrieved 5 October 2015.
  47. ^ Salingaros, Nikos (2006). A Theory of Architecture. Umbau. pp. 139–141. ISBN 9783937954073.
  48. ^ Salingaros, Nikos (2006). A Theory of Architecture. Umbau. pp. 124–125. ISBN 9783937954073.
  49. ^ Gehry, Frank O.; Mudford, Grant; Koshalek, Richard (2009). Symphony: Frank Gehry's Walt Disney Concert Hall. Five Ties. ISBN 9780979472749.
  50. ^ Garcetti, Gil (2004). Iron: Erecting the Walt Disney Concert Hall. Princeton Architectural Press. ISBN 9781890449285.
  51. ^ a b Bartlett, Christopher (2014). "The Design of The Great Pyramid of Khufu". Nexus Network Journal. 16 (2): 299–311. doi:10.1007/s00004-014-0193-9.
  52. ^ Markowsky, George (January 1992). "Misconceptions About the Golden Ratio" (PDF). The College Mathematics Journal. 23 (1): 2–19. doi:10.1080/07468342.1992.11973428. Archived from the original (PDF) on 2008-04-08. Retrieved 2015-10-01.
  53. ^ Livio, Mario (2003) [2002]. The Golden Ratio: The Story of Phi, the World's Most Astonishing Number (First trade paperback ed.). New York City: Broadway Books. p. 61. ISBN 0-7679-0816-3.
  54. ^ Gazalé, Midhat (1999). Gnomon: From Pharaohs to Fractals. Princeton University Press.[페이지 필요]
  55. ^ a b c d Cooke, Roger L. (2011). The History of Mathematics: A Brief Course (2nd ed.). John Wiley & Sons. pp. 237–238. ISBN 978-1-118-03024-0.
  56. ^ Gillings, Richard J. (1982). Mathematics in the Time of the Pharaohs. Dover. p. 161.
  57. ^ 크람리쉬, 스텔라 (1976년), 힌두사원 제1권 2권 ISBN 81-208-0223-3
  58. ^ Vibhuti Sachdev, Giles Tillotson (2004). Building Jaipur: The Making of an Indian City. pp. 155–160. ISBN 978-1-86189-137-2.
  59. ^ Ifrah, Georges (1998). A Universal History of Numbers. Penguin.
  60. ^ a b "Fractals in Indian Architecture". Yale University. Archived from the original on 6 February 2012. Retrieved 1 October 2015.
  61. ^ Jackson, William J. "For All Fractal Purposes ... an introduction". Indiana University-Purdue University Indianapolis. Archived from the original on 14 September 2015. Retrieved 1 October 2015.
  62. ^ King, Anthony D. (2005). Buildings and Society: Essays on the Social Development of the Built Environment. Taylor & Francis. p. 72. ISBN 0-203-48075-9.
  63. ^ Maor, Eli (2007). The Pythagorean Theorem: A 4,000-year History. Princeton University Press. p. 19. ISBN 978-0-691-12526-8.
  64. ^ a b Norwich, John Julius (2001). Great Architecture of the World. Artists House. p. 63.
  65. ^ Penrose, Francis (1973) [1851]. Principles of Athenian Architecture. Society of Dilettanti. p. ch. II.3, plate 9.
  66. ^ Stevens, Gorham P. (July 1962). "Concerning the Impressiveness of the Parthenon". American Journal of Archaeology. 66 (3): 337–338. doi:10.2307/501468. JSTOR 501468.
  67. ^ 유클리드, 원소제6권, 발의안 제30호
  68. ^ Archibald, R. C. "Notes on the Logarithmic Spiral, Golden Section and the Fibonacci Series". Retrieved 1 October 2015.
  69. ^ 건축에 있어서 황금평균의 적용
  70. ^ Markowsky, George (January 1992). "Misconceptions about the Golden Ratio" (PDF). The College Mathematics Journal. 23 (1): 2–19. doi:10.1080/07468342.1992.11973428. Archived from the original (PDF) on 2008-04-08. Retrieved 2015-10-01.
  71. ^ Gedal, Najib. "The Great Mosque of Cordoba: Geometric Analysis". Islamic Art & Architecture. Archived from the original on 2 October 2015. Retrieved 16 October 2015.
  72. ^ Irwin, Robert (26 May 2011). The Alhambra. Profile Books. pp. 109–112. ISBN 978-1-84765-098-6.
  73. ^ Robertson, Ann (2007). "Revisiting the Geometry of the Sala de Dos Hermanas" (PDF). BRIDGES. Retrieved 11 October 2015.
  74. ^ Blair, Sheila; Bloom, Jonathan M. (1995). The Art and Architecture of Islam 1250–1800. Yale University Press. ISBN 0-300-06465-9.
  75. ^ Michell, George; Pasricha, Amit (2011). Mughal Architecture & Gardens. Antique Collectors Club. ISBN 978-1-85149-670-9.
  76. ^ Parker, Philip (2010). World History. Dorling Kindersley. p. 224. ISBN 978-1-4053-4124-0.
  77. ^ Koch, Ebba (2006). The Complete Taj Mahal: And the Riverfront Gardens of Agra (1st ed.). Thames & Hudson. pp. 24 and passim. ISBN 0-500-34209-1.
  78. ^ Koch, Ebba (2006). The Complete Taj Mahal: And the Riverfront Gardens of Agra (1st ed.). Thames & Hudson. pp. 104–109. ISBN 0-500-34209-1.
  79. ^ Fazio, Michael; Moffett, Marian; Wodehouse, Lawrence (2009). Buildings Across Time (3rd ed.). McGraw-Hill Higher Education. ISBN 978-0-07-305304-2.
  80. ^ Gamwell, Lynn (2015). Mathematics and Art: A Cultural History. Princeton University Press. p. 48. ISBN 978-0-691-16528-8.
  81. ^ Kleiner, Fred S.; Mamiya, Christin J. (2008). Gardner's Art Through the Ages: Volume I, Chapters 1–18 (12th ed.). Wadsworth. p. 329. ISBN 978-0-495-46740-3.
  82. ^ Menander, Hanna; Brandt, Olof; Appetechia, Agostina; Thorén, Håkan (2010). "The Lateran Baptistery in Three Dimensions" (PDF). Swedish National Heritage Board. Retrieved 30 October 2015.
  83. ^ "The Baptistery". The Leaning Tower of Pisa. Retrieved 30 October 2015.
  84. ^ a b Huyser-Konig, Joan. "Theological Reasons for Baptistry Shapes". Calvin Institute of Christian Worship. Retrieved 30 October 2015.
  85. ^ a b Kuehn, Regina (1992). A Place for Baptism. Liturgy Training Publications. pp. 53–60. ISBN 978-0-929650-00-5.
  86. ^ Augustine of Hippo (426). The City of God. p. Book 22, Chapter 30.
  87. ^ Kleiner, Fred (2012). Gardner's Art through the Ages: A Global History. Cengage Learning. pp. 355–356. ISBN 978-1-133-71116-2.
  88. ^ a b c Simitch, Andrea; Warke, Val (2014). The Language of Architecture: 26 Principles Every Architect Should Know. Rockport Publishers. p. 191. ISBN 978-1-62788-048-0.
  89. ^ "Zelená hora near Žďár nad Sázavou". Czech Tourism. Retrieved 10 November 2015.
  90. ^ "Attributes of Saint John of Nepomuk". Saint John of Nepomuk. Archived from the original on 4 March 2016. Retrieved 10 November 2015.
  91. ^ Burry, M.C., J.R. Burry, G.M. Dunlop and A. Maher (2001). "Drawing Together Euclidean and Topological Threads (pdf)" (PDF). Presented at SIRC 2001 – the Thirteenth Annual Colloquium of the Spatial Information Research Center. Dunedin, New Zealand: University of Otago. Archived from the original (PDF) on 2007-10-31. Retrieved 2007-11-28.
  92. ^ "The Geometry of Antoni Gaudi". Math & the Art of MC Escher. Saint Louis University Mathematics and Computer Science. Retrieved 4 October 2015.
  93. ^ Usvat, Liliana. "Antony Gaudi and Mathematics". Mathematics Magazine. Retrieved 4 October 2015.
  94. ^ M.C. Burry; J.R. Burry; G.M. Dunlop; A. Maher (2001). "Drawing Together Euclidean and Topological Threads" (PDF). The 13th Annual Colloquium of the Spatial Information Research Centre, University of Otago, Dunedin, New Zealand. Archived from the original (PDF) on 25 June 2008. Retrieved 5 August 2008. {{cite journal}}:Cite 저널은 필요로 한다. journal=(도움말)
  95. ^ Nervi, Pier Luigi. "Cathedral of Saint Mary of the Assumption". Architectuul. Retrieved 12 October 2015.
  96. ^ "Brasilia Cathedral". About Brasilia. Retrieved 13 November 2015.
  97. ^ Behrends, Ehrhard; Crato, Nuno; Rodrigues, Jose Francisco (2012). Raising Public Awareness of Mathematics. Springer Science & Business Media. p. 143. ISBN 978-3-642-25710-0.
  98. ^ Emmer, Michele (2012). Imagine Math: Between Culture and Mathematics. Springer Science & Business Media. p. 111. ISBN 978-88-470-2427-4.
  99. ^ Mkrtchyan, Ruzanna (2013). "Cathedral of Brasilia". Building.AM. Retrieved 13 November 2015.
  100. ^ "Østerlars kirke" (in Danish). Nordens kirker. Retrieved 2 December 2016.
  101. ^ "Østerlars kirke" (in Danish). Natur Bornholm. Archived from the original on 19 July 2011. Retrieved 2 December 2016.
  102. ^ a b Rønning, Frode. "Islamic Patterns And Symmetry Groups" (PDF). University of Exeter. Retrieved 18 April 2014.
  103. ^ a b c Gibberd, Matt; Hill, Albert (20 August 2013). "The Return of Ornamentation". The Telegraph. Archived from the original on 18 October 2014. Retrieved 12 October 2015.
  104. ^ "Ravensbourne College by Foreign Office Architects". de zeen magazine. 13 September 2010. Retrieved 12 October 2015.
  105. ^ a b Bizley, Graham. "FOA's peninsula patterns for Ravensbourne College". bdonline.co.uk. Retrieved 16 October 2015.
  106. ^ Duffy, C. (1975). Fire & Stone, The Science of Fortress Warfare 1660–1860. Booksales. ISBN 978-0-7858-2109-0.
  107. ^ Chandler, David (1990). The Art of Warfare in the Age of Marlborough. Spellmount. ISBN 978-0-946771-42-4.
  108. ^ Giedion, Siegfried (1962) [1941]. Space, Time and Architecture. Harvard University Press. p. 43.
  109. ^ O'Neill, Tom (4 January 2015). "China's Remote Fortresses Lose Residents, Gain Tourists". National Geographic. Retrieved 6 January 2017.
  110. ^ Ayre, James (28 April 2018). "Yakhchāls, Āb Anbārs, & Wind Catchers — Passive Cooling & Refrigeration Technologies Of Greater Iran (Persia)". CleanTechnica. Archived from the original on 1 May 2018. Retrieved 25 February 2022.

외부 링크