새로운 유도 수수께끼

그뤼와 블리엔은 넬슨 굿맨 인 팩트, 픽션, 그리고 예측이 흄의 원래 문제의 계승자인 "유도의 새로운 수수께끼"를 설명하기 위해 만든 논리 술어의 예들이다. 이러한 술어는 응용이 시간에 의존하기 때문에 특이하다. 많은 사람들이 이 새로운 수수께끼를 풀려고 노력했지만 힐러리 푸트남과 다른 사람들은 그러한 시간에 의존하는 것이 채택된 언어에 달려 있다고 주장해 왔고, 어떤 언어에서는 "녹색"과 같은 자연적으로 들리는 술어에도 똑같이 적용된다. Goodman에게 있어서 그들은 실행 가능한 술어와 궁극적으로는 어떤 경험적 일반화가 법률과 유사하고 그렇지 않은지에 대한 문제를 설명한다.^[1][2] 굿맨의 구성과 그루와 블랑의 사용은 철학자들이 개념 분석에서 간단한 예를 어떻게 사용하는지를 보여준다.

그뤼 앤 블랑

Goodman은 임의적이지만 고정된 시간 t에 상대적인 "회색"을 정의했다:^{[note 1]} 물체는 t 전에 관찰되고 녹색인 경우와 그렇지 않은 경우만 회색으로 정의된다. 물체가 t보다 먼저 관찰되고 파란색이거나, 그렇지 않으면 그렇게 관찰되지 않고 녹색인 경우에만 "블렌"이다.^[3]

2031년 1월 1일, 임의의 미래 시간 t에 대해 에메랄드나 잘 물든 풀과 같이 t 이전에 관찰된 모든 녹색에 대해 녹색과 그루가 모두 적용된다. 푸른 새나 푸른 꽃과 같이 t 이전에 관찰된 모든 푸른 색에도 푸른 색과 흰 색이라는 술어가 모두 적용된다. 그러나 2031년 1월 2일 에메랄드나 잘 물든 풀은 퇴색하고 푸른 새나 푸른 꽃들은 퇴색한다. 술어는 일상생활이나 과학에서 사용되는 술어의 종류가 아니라 미래의 어느 시간 t까지 녹색과 청록색으로 술어와 똑같이 적용된다. 관찰자의 관점에서 볼 때, 어떤 술어가 미래로 구현될 수 있는지는 확실치 않다.

유도의 새로운 수수께끼

이 절에서 굿맨의 새로운 유도 수수께끼는 술어를 도입하기 위한 맥락을 설정하고 그에 따라 그들의 철학적 중요성을 설명하기 위해 윤곽을 드러낸다.^[2][4]

인덕션과 그 해체의 오래된 문제

굿맨은 흄의 유도 문제를 우리가 하는 예측의 타당성에 대한 문제로 제기한다. 예측은 아직 관찰되지 않은 것과 관찰된 것과 관찰될 것 사이에 필요한 연관성이 없기 때문에, 이러한 예측에 대한 객관적 정당성은 없다. 연역논리는 그러한 추론에 대한 유효한 연역논리의 규칙이 없기 때문에 과거 관측에 근거한 미래 관측에 대한 예측을 추론하는데 사용될 수 없다. 흄의 대답은 한 종류의 사건을 다른 종류의 사건 이후에 관찰하는 것은 규칙성의 습관(즉, 한 종류의 사건을 다른 종류의 사건과 연관시키는 것)을 낳는다는 것이었다. 그리고 나서 예측은 이러한 규칙성이나 마음의 습관에 기초한다.

굿맨은 흄의 대답을 진지하게 받아들인다. 그는 흄이 단지 우리의 예측의 근원을 설명하고 있을 뿐 그들의 정당성을 설명하고 있지 않다는 다른 철학자들의 반대를 거부한다. 그의 견해는 흄이 뭔가 더 깊은 것을 확인했다는 것이다. 이를 설명하기 위해 굿맨은 공제 제도의 정당화 문제로 눈을 돌린다. 굿맨에게 연역제도의 타당성은 좋은 연역관행에 대한 적합성에 의해 정당화된다. 연역체계 규칙의 정당성은 구체적인 연역추론을 거부할 것인지 아니면 받아들일 것인지에 대한 우리의 판단에 달려 있다. 따라서 굿맨에게 있어서 유도의 문제는 연역체계를 정당화하는 것과 같은 문제로 용해되고 굿맨에 따르면 흄은 마음의 습관으로 올바른 궤도에 오른 반면 문제는 흄이 깨달은 것보다 더 복잡하다.

유도 규칙을 정당화하는 맥락에서 이것은 굿맨에 대한 일반화 확인의 문제가 된다. 그러나 이번 확인은 정당성의 문제가 아니라 증거가 일반화를 어떻게 검증하는지를 정확히 규정하는 문제가 있다. 굿맨의 인덕션 관점에 있어서 그들의 철학적 역할을 하는 것은 이 차례와 함께다.

투영 가능한 술어

굿맨에게 있어서 새로운 유도의 수수께끼는 법률과 비법률적인 일반화를 구별하는 우리의 능력에 달려 있다. 합법적인 일반화는 확인할 수 있지만 비법률적인 일반화는 확인할 수 없다. 예측을 하려면 합법적인 일반화가 필요하다. 굿맨의 예를 들어, 모든 구리가 전기를 전도한다는 일반화는 특정한 구리 조각으로 확인할 수 있는 반면, 주어진 방에 있는 모든 사람이 3남이라는 일반화는 법률적인 것이 아니라 우연적인 것이다. 모든 구리가 전기를 전도한다는 일반화는 이 구리 조각이 전기를 전도할 것이라는 예측의 근거다. 그러나 주어진 방에 있는 모든 사람이 셋째 아들이라는 일반화는 그 방에 있는 주어진 사람이 셋째 아들이라는 것을 예측할 수 있는 근거는 아니다.

그러므로 문제는 무엇이 어떤 일반화를 법처럼 만들고 다른 것들은 우연한 것으로 만드는가 하는 것이다. 이것은 굿맨에게 있어 어떤 술어가 실행 가능한지(즉, 예측의 역할을 하는 법률적 일반화에 사용될 수 있는지)와 그렇지 않은지를 결정하는 문제가 된다. 굿맨은 이것이 근본적인 문제가 있는 곳이라고 주장한다. 이 문제는 굿맨의 역설로 알려져 있다: 지금까지 조사된 모든 에메랄드가 녹색이었다는 명백한 유력한 증거로부터, 사람들은 미래의 모든 에메랄드가 녹색일 것이라는 귀납적인 결론을 내릴 수 있다. 그러나 이 예측이 합법적인지 아닌지는 이 예측에 사용된 술어에 달려 있다. 굿맨은 (t가 아직 지나가지 않았다고 가정하면) 관찰된 모든 에메랄드가 그루라는 것은 똑같이 사실이라고 관찰했다. 따라서, 같은 증거에 의해 우리는 미래의 모든 에메랄드가 그루가 될 것이라는 결론을 내릴 수 있다. 유도의 새로운 문제는 녹색과 파란색과 같은 투사 가능한 술어와 회색과 같은 투사 불가능한 술어를 구별하는 것 중 하나가 된다.

흄, 굿맨은 이 문제를 놓쳤다고 Goodman은 주장한다. 우리는 습관에 의해 우리가 관찰한 모든 사건들의 연관성으로부터 일반화를 형성하지 않는다. 다만 그것들 중 일부만. 과거에 관찰된 에메랄드는 모두 초록색이고, 우리는 다음 에메랄드가 초록색이 될 것이라고 생각하는 습관을 형성했지만, 그것들은 똑같이 회색이었고, 우리는 그름에 관한 습관을 형성하지 않는다. 법률과 같은 예측(또는 예상)은 궁극적으로 우리가 사용하는 술어로 구별할 수 있다. 굿맨의 해결책은 법 같은 예측은 녹색과 파란색과 같은 투사 가능한 술어에 기초하고, 투사 불가능한 술어에 근거하지 않으며 술어를 투사할 수 있게 만드는 것은 그들의 긴축이며, 이는 그들의 성공적인 과거 예측에 달려있다. 그러므로 굿맨의 주장에서 그루와 블랭은 둘 다 유도의 새로운 수수께끼를 설명하고, 상대적 긴축을 통해 실현 가능한 술어와 실현 불가능한 술어의 구별을 설명하기 위한 기능이다.

응답

한 가지 대응은 인위적으로 분리된 그루 정의에 호소하는 것이다. 술어적 긴축의 개념은 필요하지 않다. 굿맨은 이것이 성공하지 못한다고 말했다. 만약 우리가 그루와 블리엔을 원시 술어로 받아들인다면, 우리는 초록색을 "t 전에 처음 관찰된 회색과 그렇지 않은 경우"로 정의할 수 있고, 그리고 마찬가지로 파란색을 나타낼 수 있다. 녹색에 대한 이러한 이분법적 정의의 수용가능성을 부정하는 것은 질문을 구걸하는 것일 것이다.

술어를 긴축할 필요가 없는 또 다른 제안된 결의안은 "x is grue"는 x의 단순한 술어가 아니라 x와 시간 t의 술어라는 것이다. 우리는 물체가 시간 t를 알지 않아도 녹색이라는 것을 알 수 있지만 우리는 그것이 grue라는 것을 알 수 없다. 이런 상황이라면 시대가 바뀌어도 'x is grue'가 그대로 유지되리라고 기대해서는 안 된다. 그러나 "x는 녹색"이 특정 시간 t의 술어로 간주되지 않는 이유를 물을 수 있다. 즉, 녹색의 보다 일반적인 정의는 시간 t에 대한 어떠한 언급도 필요하지 않지만, 정의는 그렇다. Goodman은 또한 시간을 명시적으로 언급하는 Grue와 bleen의 관점에서 파란색은 정의될 수 있기 때문에 이 제안된 해결책을 구걸하는 질문으로 다루고 거부한다.^[5]

스윈번

리차드 스윈번은 특정한 경우에 술어의 적용가능성을 시험하는 방법에 기초하여 구분을 함으로써 녹색의 정의가 그르륵과 블랑의 관점에서 다시 정의될 수 있다는 반대 의견을 지나친다. 그는 질적 술어와 위치적 술어를 구별한다. 질적 술어는 녹색과 마찬가지로 x와 특정 시간, 장소 또는 사건 사이의 공간적 또는 시간적 관계를 알지 못하고 평가할 수 있다. 위치 술어는 grue와 같이 x가 특정 시간, 장소 또는 사건에 대한 공간적 또는 시간적 관계를 알지 못하면 평가할 수 없다. 이 경우 x가 시간 t 이전 또는 이후에 관찰되고 있는지 여부. 녹색은 위치 술어의 관점에서 정의될 수 있지만, 녹색은 질적 술어가 되는 기준을 충족하지만, 녹색은 위치 술어에 불과하다는 사실과는 무관하다. 그는 일부 x가 에메랄드처럼 검사 중이지만 이 두 술어를 투영하면 질적 술어와 위치적 술어 둘 다 만족하지만, 상충되는 예측, 즉 시간 후에 검사한 에메랄드가 grue로 나타날지 녹색으로 나타날지 여부에 상관없이 이 경우 질적 술어를 투영해야 한다고 결론짓는다.^[6]

카르나프

루돌프 카르납은 굿맨의 1946년 기사에 응답했다^[7]. Carnap의 귀납적 논리에 대한 접근법은 주어진 증거 e에 의한 가설 h의 확인 c(h,e)의 개념에 기초한다.^{[note 2]} h와 e 모두 다음과 같은 간단한 언어 L로 표현된 논리 공식이다.

• 다중 정량화("모든 x에 대해 그러한 y가 있다..."),
• 단항 및 이항 술어 기호(수동 및 관계)
• 평등 관계 「=」.

담론의 우주는 불명예스러울 정도로 많은 개인들로 구성되는데, 각각은 그 자신의 상수 기호에 의해 지정된다; 그러한 개인은 확장된 육체적 신체가 아니라 ("실제 세계의 시공간과 같은") 위치로 간주되어야 한다.^[8] 상태 설명은 부정되거나 무절제한 모든 가능한 지상 원자 문장을 포함하는 (대개 무한) 접속사로서, 그러한 접속사는 전 우주의 가능한 상태를 설명한다.^[9] 카르나프는 다음과 같은 의미 속성을 요구한다.

• 원자 문장은 서로 논리적으로 독립되어 있어야 한다.^[10] 특히 상수 기호가 서로 다르고 완전히 분리된 개인을 지정해야 한다.^{[note 3]} 더구나 서로 다른 술어는 논리적으로 독립적이어야 한다.^{[note 4][note 5]}
• 술어가 지정한 품질과 관계는 단순해야 한다. 즉, 술어를 단순한 구성 요소로 분석해서는 안 된다.^[11] 분명히 카르납은 불손하고 편파적이며 근거가^{[note 6]} 충분한 질서가^{[note 7]} 보다 간단하다는 것을 염두에 두고 있었다.
• L에서 원시 술어의 집합은 완전해야 한다. 즉, 우주의 두 위치가 직접 관찰에 의해 다르게 발견될 수 있는 모든 존중은 L에서 표현 가능해야 한다.^[12]

카르나프는 세 가지 성질을 구분한다.

1. 순수하게 질적인 속성, 즉 개별 상수를 사용하지 않고 표현할 수 있는 속성, 원시 술어가 없는 속성,
2. 순전히 위치적 특성, 즉 원시 술어 없이 표현 가능한 특성
3. 혼합 특성, 즉 나머지 모든 표현 가능한 특성.

이 분류법을 밝히려면 x를 변수와 상수 기호로 하고, 그 다음 1.의 예는 "x는 파란색이고 x는 따뜻하지 않다", 2. "x = a" 및 3. "x는 빨간색이고 x = a는 아니다"가 될 수 있다.

카르납은 위에서 스케치한 그의 귀납 논리 이론을 바탕으로 굿맨의 속성 W의 실현가능성 개념을 다음과 같이 공식화한다: 관찰된 샘플에서 W의 상대적 빈도가 높을수록 관찰되지 않은 개인이 굿맨에게 "잠정적인 답변으로서" 제안하는 속성을 가질 확률이 높다.소송 특성은 투영 가능하며, 모든 순전히 위치적 특성은 투영할 수 없으며, 혼합 특성은 추가 조사가 필요하다.^[13]

퀴네

Willard Van Orman Quine은 "자연적인 종류"만을 실행 가능한 술어로 간주하는 접근법에 대해 논한다.^[14] 그는 먼저 모든 공유 사례가 "각각 F는 G"라는 주장을 확인하는 데 도움이 될 경우 두 술어 F와 G를 (동시에) 투영할 수 있도록 정의함으로써 굿맨의 Grue 역설과 Hempel의 까마귀 역설을 연관시킨다.^[15] 그렇다면 헴펠의 역설은 단지 투영 가능한 술어(예: "까마귀", "검은 색")의 보완은 투영할 필요가 없다는 것을 보여주는 반면,^{[note 8]} 굿맨의 역설은 "초록색"은 투영할 수 있지만 "그루"는 투영할 수 없다는 것을 보여준다.

다음으로, Quine은 유사성의 주관적인 개념으로 투영가능성을 감소시킨다. 두 개의 녹색 에메랄드는 보통 두 개의 녹색 에메랄드보다 더 유사한 것으로 간주된다. 초록색 에메랄드를 관찰하면 다음에 비슷한 관찰(즉, 초록색 에메랄드)을 기대할 수 있다. 녹색 에메랄드는 자연적인 종류지만, 그뤼 에메랄드는 그렇지 않다. Quine은 "유사성 또는 종류의 일반적인 개념의 의심스러운 과학적 지위"^[16]를 조사한다. 둘 다 사상과 언어에 있어서 기본적인 것으로서, 예를 들어 정체성, 부정, 분리 등의 논리적 관념과 같다. 그러나 논리적 개념을 유사성이나 종류와 어떻게 연관시킬 것인지는 여전히 불분명하다.^{[note 9]} 따라서 Quine은 적어도 후자의 두 가지 개념을 서로 연관시키려 한다.

굿맨이 카르납에 근거한 "자연적인 종류"의 정의에 대해 반례하는 것

기하학에서 원 영역의 정의와 유사하게 p보다 "패러다임" 개체 p가 "포일" 개체와 더 유사한 모든 개체 x의 집합으로 종류를 정의하지 못함

유사성과 종류 사이의 관계

유사성의 개념은 미세하게 많은 종류만 가정할 때, A와 B가 A와 C보다 더 많은^{[note 10]} 종류에 공동으로 속한다면 C보다는 A라는 물체가 B와 더 유사하다.^{[17][note 11]}

반대로, 유사성에 의해 종류를 어떻게 정의해야 하는지는 다시 불분명하다. 예를 들어, 붉은 사물의 종류를 고정된 "파라디그마틱" 붉은 사물과 더 유사한 모든 사물의 집합으로 정의하는 것은 또 다른 고정된 "포일" 비 적색 개체(cf)와 같다. 왼쪽 그림)은 만족스럽지 않은데, 모양, 무게 등 전체적인 유사성의 정도는 붉은 색의 정도를 나타내는 증거가 거의 없기 때문이다.^[17] (사진에서 노란색 파프리카는 오렌지색보다 빨간 색과 더 유사한 것으로 간주될 수 있다.)

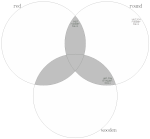
Carnap에서 영감을 받은 대안적 접근법은 비회원 각각에 비해 서로 더 유사한 구성원을 적어도 한 명의 구성원으로 정의한다.^{[18][note 12]} 그러나 굿맨은^[19] 이 정의가 모든 붉은 둥근 것, 붉은 나무로 된 것, 둥근 나무로 된 것(cf. right picture)의 집합을 자연종류의 제안된 정의에 부합하게 하는 반면,^{[note 13]} "분명히 그것은 그 누구도 어떤 종류로 의미하지는 않는다"^{[note 14][20]}고 주장했다.

유사성과 종류에 대한 개념은 다른 개념에 의해 정의될 수 없지만, 그것들은 적어도 함께 다양하다: 만약 A가 다른 방식이 아닌 B보다 C와 더 유사한 것으로 재평가된다면, A, B, C의 종류 배정은 그에 상응하는 방식으로, 그리고 반대로 순서가 바뀔 것이다.^[20]

유사성과 종류에 대한 기본적인 중요성

언어에서, 모든 일반 용어는 언급된 것들의 어떤 유사성 때문에 일반화되었다. 단어 사용법을 배우는 것은 단어가 사용된 현재와 과거의 상황과 현재와 과거의 음성적 표현 사이의 이중 유사성, 즉 viz.에 달려 있다.^[21]

모든 합리적인 기대는 비슷한 원인이 비슷한 영향을 미칠 것으로 기대하는 우리의 성향과 함께 상황의 유사성에 달려 있다.^[16] 이것은 유사하지만 완전히 동일한 환경에서는 재현될 수 없기 때문에 모든 과학적 실험을 포함한다. 이미 헤라클리투스의 유명한 속담 "어떤 사람도 같은 강에 두 번 발을 디디지 않는다"는 것은 비슷한 상황과 동일한 상황의 구분을 강조하였다.

새의 유사성 관계
틴베르겐과 로렌츠는 경험이 없는 칠면조 병아리의 거친 유사성 관계를 보여주었다.[22][23][24] 위쪽 줄: 진짜 매(왼쪽)와 거위(오른쪽)가 날아간다. 아래쪽 행: 판지 더미가 원문과 유사한 반응을 보인다.

유사성과 종류의 기원

행동적 의미에서 인간과 다른 동물들은 선천적인 유사성 기준을 가지고 있다. 그것은 우리의 동물 생득권의 일부분이며, 수학이나 논리에 대한 이질성,^[25] cf. 새의 예와 같은 지적 지위의 결여에서 특징적으로 동물적인 것이다.

습관성형성

유도 그 자체는 본질적으로 동물적인 기대나 습관 형성이다. 허세적 학습은^[26] 유도의 한 예로서, 사람마다 자질이나 친절의 간격을 두고 이웃과 같이 하면 충분하기 때문에, 신기하게도 편안한 것이다.^[27] 이와는 대조적으로, "우리의 유사성 감각의 교묘한 불합리성"은 우리가 결코 만들지 않았던 만장일치적인 자연과 어떻게든 조화를 이루기를 기대할 이유를 거의 제시하지 않는다.^{[note 15]} 그것에 관한 이론들을 귀납적으로 얻은 이유는 유도의 영원한 철학적 문제다. 와타나베에 이어 콰인은 다윈의 이론을 설명으로 제시한다:^[28] 사람들의 선천적인 자질 간격은 유전자와 연계된 특성이라면, 가장 성공적인 인지를 위해 만든 간격은 자연 선택을 통해 우세해지는 경향이 있었을 것이다.^[29] 그러나 이것은 새로운 영역에 익숙해지는 과정에서 자신의 자질 간격을 역동적으로 다듬는 인간의 능력을 설명할 수는 없다.^{[note 16]}

철학적 분석에 사용되는 유사한 술어

퀘우스

사울 크립케는 그의 저서 비트겐슈타인의 규칙과 개인언어에 관한 논문에서 사울 크립케의 개인적인 해석(일부^[30] 사람들에 의한 "크립켄슈타인"이라는 별칭)의 일환으로 유도에 대한 회의론보다는 의미에 대한 회의론으로 이어지는 관련 주장을 제안했다. 그는 새로운 형태의 덧셈을 제안했는데, quus라고 불렀는데, quus는 추가된 숫자 중 하나가 57과 같거나 그 이상인 것을 제외한 모든 경우에 "+"와 동일하다. 이 경우 답은 5가 된다. 즉, 다음과 같다.

${\displaystyle x{\text{{}y={\case}x}x+y&{{{}x,y<57\\[12pt]5&{\text{}}}}}x\geq 57{} 또는 }y\geq 57\end{case}}}}}}$

그리고 나서 그는 내가 "+"를 의미한다고 생각했을 때, 이전에 내가 실제로 쿼스를 의미하지 않았다고 생각했을 때, 어떻게 모든 사람이 그것을 알 수 있었는지를 묻는다. 그러자 크립케는 비트겐슈타인의 해석에 대해 단어의 의미가 개별적으로 정신적 실체를 포함하고 있지 않다고 주장한다.

참고 항목

• N-유니버설스
• 유도 문제
• 솔로몬노프의 귀납 추론 - 정보 이론 관점

메모들

참조

추가 읽기

• 굿맨, 넬슨(1955) 팩트, 픽션, 그리고 예측. 매사추세츠 주 캠브리지: 하버드 UP, 1955년 제2판 인디애나폴리스: 1965년 3월호 인디애나폴리스: 밥스-메릴, 1973년 매사추세츠주 캠브리지 4판: 하버드 UP, 1983.
• Kripke, Saul (1982). Wittgenstein on Rules and Private Language. Basil Blackwell Publishing. ISBN 0-631-13521-9.
• Wolpert, David (1996). "The Lack of A Priori Distinctions between Learning Algorithms". Neural Computation. 8 (7): 1341–1390. doi:10.1162/neco.1996.8.7.1341. S2CID 207609360.
• Stalker, Douglas (1994). Grue! The New Riddle of Induction. Open Court Publishing. ISBN 0-8126-9218-7.
• 프란체스키, 폴, 유네 솔루션 pour paradise de Goodman, Dialogue, vol.40, 2001, 페이지 99–123, 영어 번역.
• 엘긴, 캐서린, 에드(1997) 넬슨 굿맨의 철학: 선택된 에세이. 제2권, 넬슨 굿맨의 새로운 유도 수수께끼. 뉴욕: 갈랜드. ISBN 0-8153-2610-6
• 굿맨의 원래 정의 그뤼