양자점 세포자동화

Quantum dot cellular automaton

양자점 셀룰러 오토마타(QDCA, 때로는 양자 셀룰러 오토마타, QCA)는 존 폰 노이만이 도입한 셀룰러 오토마타의 기존 모델과 유사하게 고안된 기존의 컴퓨터 설계(CMOS)의 개선안이다.

배경

데이터를 나타내고 연산을 수행하도록 설계된 모든 기기는, 그것이 이용하는 물리 원리와 그것을 구축하는 데 사용되는 재료에 관계없이, 구별성과 조건부 상태 변화라는 두 가지 기본적인 속성을 가져야 하며, 후자는 전자를 암시한다.이는 그러한 장치가 국가를 구별할 수 있게 하는 장벽을 가지고 있어야 하며, 조건부 상태 변화를 수행하기 위해서는 이러한 장벽을 제어할 수 있는 능력이 있어야 한다는 것을 의미한다.예를 들어 디지털 전자 시스템에서 트랜지스터는 그러한 제어 가능한 에너지 장벽의 역할을 수행하므로 트랜지스터와 함께 컴퓨팅을 수행하는 것이 매우 실용적이다.

셀룰러 오토마타

셀룰러 오토매틱(CA)은 균일한(핀라이트 또는 무한) 셀 그리드로 구성된 이산형 동적 시스템이다.각 셀은 이산 시간에서 제한된 수의 상태 중 하나에만 있을 수 있다.시간이 전진함에 따라 그리드 내 각 셀의 상태는 이전 상태의 인자와 바로 인접한 셀의 상태(셀의 "근접")에 의해 결정된다.셀룰러 오토매틱의 가장 잘 알려진 예는 1970년에 그가 묘사한 존 호튼 콘웨이의 "Game of Life"이다.

양자점세포

기원

셀룰러 오토마타는 일반적으로 소프트웨어 프로그램으로 구현된다.그러나 1993년 사순절 외에서는 양자점 세포를 이용한 자동화의 물리적 구현을 제안했다.이 자동차는 빠르게 인기를 얻었고 1997년에 처음으로 제작되었다.사순절은 세포 자동화와 양자 역학의 별개의 특성을 결합하여 매우 높은 전환 속도(테라헤르츠 순서)에서 연산을 수행하고 극히 적은 양의 전력을 소비할 수 있는 나노 스케일 소자를 만들었다.

현대 세포

오늘날 표준 고체상태 QCA 세포 설계에서는 양자점 사이의 거리가 약 20nm, 셀 간 거리는 약 60nm로 간주하고 있다.여느 CA와 마찬가지로 Quantum(-dot) Cellular Automata는 그리드에 배치된 셀들 간의 단순한 상호작용 규칙을 기반으로 한다.QCA 셀은 사각형 패턴으로 배열된 네 개의 양자 점으로 구성된다.이 양자점들은 전자가 그들에게 터널을 뚫음으로써 차지할 수 있는 사이트들이다.

셀 디자인

그림 2 - 4점 QCA 셀의 간단한 도표
그림 3 - 4점 QCA 셀의 가능한 두 가지 상태

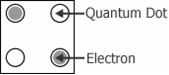
그림 2는 양자점 셀의 단순화된 도표를 보여준다.[1]만약 세포가 두 개의 전자로 충전된다면, 각각은 세포의 어떤 부위로 자유롭게 터널링할 수 있고, 이 전자들은 상호 정전기적 반발로 인해 서로에 관해서 가장 먼 부지를 차지하려고 할 것이다.따라서 두 가지 구별 가능한 세포 상태가 존재한다.그림 3은 양자점 셀의 가능한 최소 에너지 상태를 나타낸다.세포의 상태는 그것의 양극화라고 불리며, P로 표시된다.임의로 선택했지만, 논리 "0"을 나타내기 위해 세포 양극화 P = -1을 사용하고 논리 "1"을 나타내기 위해 P = +1을 사용하는 것이 표준 관행이 되었다.

QCA 와이어

그림 4 - 퀀텀 도트 셀의 와이어셀과 셀의 점 사이의 상대적 거리는 스케일링되지 않는다(셀은 셀 내부의 점보다 훨씬 멀리 떨어져 있다).

양자점 셀의 그리드 배열은 연산을 허용하는 방식으로 동작한다.가장 간단한 실제적인 세포 배치는 양자점 세포를 직렬로, 서로 옆으로 배치함으로써 주어진다.그림 4는 그러한 4개의 양자점 셀의 배열을 보여준다.그림의 경계 상자는 물리적 구현을 나타내는 것이 아니라 개별 셀을 식별하는 수단으로 표시된다.

그림 4에 나타낸 배열에서 어느 세포의 양극화가 ("드라이버 셀"에 의해) 변경될 경우, 나머지 세포는 그들 사이의 쿨롱 상호작용으로 인한 새로운 양극화와 즉시 동기화될 것이다.이렇게 해서 양극화 상태를 전달하는 양자점 세포의 '와이어'를 만들 수 있다.그러한 와이어의 구성은 계산을 위한 완전한 논리 관문을 형성할 수 있다.

QCA에는 그림 4와 같이 단순한 2진 와이어와 인버터 체인으로, 45도 반전 QCA 셀을 나란히 배치해 구성된다.

논리 관문

과반수 관문

대다수 관문과 인버터(NOT) 관문은 QCA의 가장 기본적인 두 가지 구성 요소로 간주된다.그림 5는 3개의 입력과 1개의 출력을 가진 다수 관문을 보여준다.이 구조에서 출력에 대한 각 입력의 전기장 효과는 동일하고 가법적이며, 그 결과 대다수의 입력 상태("이진 0" 또는 "이진 1")가 출력 셀의 상태가 되고, 따라서 게이트의 이름이 된다.예를 들어 입력 A와 B가 "이진 0" 상태로 존재하고 입력 C가 "이진 1" 상태로 존재한다면, 입력 A와 B의 조합된 전기장 효과가 입력 C의 그것보다 크기 때문에 출력은 "이진 0" 상태로 존재할 것이다.

그림 5 - QCA 과반수 관문

다른 관문

다른 유형의 관문, 즉 AND 관문과 OR 관문은 그 입력 중 하나에 고정된 양극화가 있는 다수 관문을 사용하여 건설할 수 있다.반면에 NOT 게이트는 그림 6과 같이 근본적으로 다수 게이트와 다르다.이 설계의 핵심은 입력이 분할되고 결과 입력이 출력물에 비스듬히 임팩트 있다는 것이다.직교 배치와 대조적으로, 이 입력 구조의 전기장 효과는 출력에서 양극화의 반전을 강요한다.

그림 6 - NOT 게이트의 표준 구현입력 및 출력 값의 라벨링은 이 문서의 나머지 부분과 정반대되는 규약을 따른다는 점에 유의하십시오.

국가전환

그림 7 - QCA 시계, 단계 및 세포 에너지 장벽에 미치는 영향

양자점 세포와 세포 자동자 사이에는 연관성이 있다.세포는 오직 2개의 상태 중 하나에 있을 수 있고 세포의 조건부 상태 변화는 인접한 이웃의 상태에 의해 결정된다.단, 데이터 흐름을 제어하는 방법은 QCA 셀에서 상태 전환이 일어나는 방향을 규정하는 것이 필요하다.QCA 시스템의 클럭은 자동 전원 공급과 데이터 흐름 방향 제어라는 두 가지 목적을 제공한다.QCA 시계는 자동자의 격자 아래 전도성 물질의 영역으로, 그 위 QCA 세포의 전자 터널링 장벽을 변조한다.

4단계

QCA 시계는 그 위에 있는 세포의 터널링 장벽에서 4단계를 유도한다.1단계에서는 터널링 장벽이 높아지기 시작한다.두 번째 단계는 터널링 장벽이 전자 터널링을 방지할 수 있을 정도로 높을 때 도달한다.세 번째 단계는 높은 장벽이 낮아지기 시작할 때 발생한다.그리고 마지막으로 4단계에서는 터널링 장벽이 전자가 다시 자유롭게 터널을 뚫을 수 있게 한다.간단히 말해서, 시계 신호가 높을 때, 전자는 터널에 자유롭다.시계 신호가 낮으면 셀이 걸리게 된다.

그림 7은 4단계의 클럭 신호와 각 클럭 단계에서 셀에 미치는 영향을 보여준다.일반적인 QCA 설계에는 4개의 클럭이 필요하며, 각 클럭은 이전 클럭과 주기적으로 90도 위상 이탈이다.만약 수평 와이어가 8개의 셀과 각 연속 쌍으로 구성된다면, 왼쪽부터 시작하여 각 연속 클럭에 연결된다면, 데이터는 자연스럽게 왼쪽에서 오른쪽으로 흐를 것이다.첫 번째 한 쌍의 셀은 두 번째 한 쌍의 셀이 래치될 때까지 래치 상태를 유지할 것이다.이러한 방식으로 데이터 흐름 방향을 클럭 존을 통해 제어할 수 있다.

와이어크로싱

그림 8 - 기본 와이어-크로싱 기술이것은 도식적이고 거리는 스케일링되지 않는다; 세포는 세포 내의 점보다 훨씬 더 멀리 떨어져 있다.

QCA 셀에서의 와이어 교차 작업은 두 개의 다른 양자점 방향(한 개는 45도 방향)을 사용하여 수행할 수 있으며, 그림 8에서 도식적으로 나타낸 것처럼 한 유형으로 구성된 와이어가 다른 유형의 와이어를 수직으로 "통과"할 수 있다.두 종류의 세포에서 점 사이의 거리는 정확히 동일하며, 각 세포의 전자들 사이에 동일한 쿨롱 상호작용을 생성한다.그러나 이 두 종류의 세포로 구성된 전선은 서로 다르다. 한 종류는 변화 없이 양극화를 전파하고, 다른 종류는 인접한 하나의 세포에서 다른 종류로 양극화를 역전시킨다.교차점에서 서로 다른 와이어 유형 간의 상호작용으로 두 와이어의 순 편광 변화가 발생하지 않으므로 양쪽 와이어의 신호가 보존될 수 있다.

제작 문제

이 기술은 다소 간단하지만, 엄청난 조작 문제를 나타낸다.새로운 종류의 세포 패턴은 잠재적으로 제작 비용과 기반 구조의 두 배 정도의 양을 도입할 수 있다; 중간 격자망에서 가능한 양자점 위치의 수는 두 배가 되며 기하학적 설계 복잡성의 전반적인 증가는 불가피하다.그러나 이 기술이 제시하는 또 다른 문제는 같은 방향의 세포들 사이의 추가 공간이 세포의 지상 상태와 세포의 첫 흥분 상태 사이의 에너지 장벽을 감소시킨다는 것이다.이는 최대 작동 온도, 엔트로피 저항성 및 전환 속도 측면에서 기기의 성능을 저하시킨다.

크로스바 네트워크

QCA 기기 제작을 보다 실용적으로 만드는 다른 와이어 크로싱 기법이 크리스토퍼 그라운키, 데이비드 휠러, 더글러스 터보, 제프리 D에 의해 제시되었다.Will, 논문 "퀀텀닷 셀룰러 오토마타를 이용한 크로스바 네트워크 구현"이 논문은 와이어크로싱 구현의 새로운 방법을 제시할 뿐만 아니라 QCA 클럭링에 대한 새로운 시각을 제시한다.

이들의 와이어크로싱 기법은 동기화의 함수로서 연산을 수행할 수 있는 QCA 장치를 구현하는 개념을 도입한다.이는 장치를 물리적으로 변경하지 않고 클럭 시스템을 통해 장치의 기능을 수정할 수 있는 능력을 의미한다.따라서 앞에서 언급한 제작 문제는 a) 퀀텀 도트 패턴의 한 유형만을 사용하는 것과, b) 적절한 복잡성의 범용 QCA 빌딩 블록을 만드는 능력으로 완전히 해결되며, 이 기능은 타이밍 메커니즘(즉, 시계)에 의해서만 결정된다.

그러나 준유아적 스위칭은 QCA의 고유 스위칭 속도에 비해 셀의 터널링 장벽이 상대적으로 느리게 전환될 것을 요구한다.이는 셀이 갑자기 전환될 때 관찰되는 벨 소리 및 측정 가능한 상태를 방지한다.따라서 QCA의 스위칭 속도는 셀이 양극화를 변화시키는 데 걸리는 시간이 아니라 사용 중인 시계의 적절한 준 부차적 스위칭 시간에 의해 제한된다.

직렬과 병렬

컴퓨팅이 가능한 장치를 설계할 때는 병렬 데이터 라인을 직렬 데이터 스트림으로 변환해야 하는 경우가 많다.이 변환은 서로 다른 데이터 조각을 단일 와이어에서 시간에 의존하는 값의 시리즈로 줄일 수 있게 한다.그림 9는 이와 같은 병렬 변환 QCA 장치를 보여준다.음영 구역의 숫자는 연속적인 90도 단계에서 서로 다른 시계 구역을 나타낸다.모든 입력이 동일한 클럭 지정 영역에 어떻게 배치되는지 주목하십시오.병렬 데이터를 입력 A, B, C 및 D에서 구동하고 최소한 나머지 15개 직렬 전송 단계에서는 더 이상 구동하지 않는 경우 출력 X는 3, 7, 11 및 15단계에서 D, C, B 및 A의 값을 순서대로 나타낼 것이다.출력에서 새로운 클럭링 영역을 추가해야 하는 경우 적절한 상태 잠금 기간을 올바르게 선택하여 입력에 해당하는 값을 래치하도록 클럭을 설정할 수 있다.

새로운 래칭 클럭 영역은 그림 9에 표시된 다른 네 개의 클럭 영역으로부터 완전히 독립적일 것이다.예를 들어, 새로운 래칭 영역에 대한 관심 값이 D가 16번째 단계마다 제시하는 값이라면, 새로운 영역의 클럭링 메커니즘은 4번째 단계와 그 이후 16번째 단계마다 값을 래치하도록 구성되어야 하므로 D를 제외한 모든 입력을 무시해야 할 것이다.

그림 9 - 직렬 변환과 평행

추가 시리얼 라인

장치에 두 번째 시리얼 라인을 추가하고 다른 래칭 영역을 추가하면 서로 다른 두 출력에서 두 입력 값을 래칭할 수 있다.계산을 수행하기 위해 각 출력에서 두 직렬 라인을 모두 입력하는 게이트가 추가된다.게이트는 직렬 회선 끝에 있는 두 래치 영역이 동시에 관심 값을 가질 때만 데이터를 처리하도록 구성된 새로운 래치 영역 위에 배치된다.그림 10은 그러한 약정을 보여준다.올바르게 구성된 경우, 지역 5와 6은 각각 지역 7에 대한 관심 입력 값을 보유하게 된다.이 순간 래칭 영역 7은 영역 5와 6에서 AND 게이트를 통해 래칭 값을 래칭할 수 있으므로, 래칭 영역 5, 6, 7을 구성하기만 하면 출력이 임의의 두 입력(즉, R 및 Q)의 AND 결과로 구성될 수 있다.

이는 물리적 설계를 그대로 둔 채 16가지 기능을 구현할 수 있는 유연성을 나타낸다.추가 직렬 회선과 병렬 입력은 분명히 실현 가능한 기능의 수를 증가시킬 것이다.그러나 이러한 장치의 중요한 단점은 실현 가능한 기능의 수가 증가함에 따라 클럭링 영역의 수가 증가해야 한다는 것이다.결과적으로, 이 기능 구현 방법을 이용하는 기기는 기존의 기기보다 상당히 느린 성능을 발휘할 수 있다.

그림 10 – 다기능 QCA 장치

제작

일반적으로 QCA 구현에는 금속 섬, 반도체, 분자, 자기 등 4가지 등급이 있다.

금속 섬

금속 섬 구현은 QCA의 개념을 입증하기 위해 만들어진 최초의 제작 기술이었다.기존에는 구조적인 특성이 확장 가능한 설계에 적합하지 않아 속도와 실용성 측면에서 기존 기술과 경쟁하려는 의도는 아니었다.방법은 알루미늄 섬을 이용해 양자점을 만드는 것으로 구성된다.초기 실험은 1마이크로미터 크기의 금속 섬에서 실시되었다.상대적으로 큰 섬들 때문에 양자 효과(전자기 전환)를 관측하기 위해서는 금속 섬나라 장치를 극도로 낮은 온도로 유지해야 했다.

반도체

반도체(또는 솔리드 스테이트) QCA 구현은 CMOS 장치 구현에 사용된 것과 동일한 고도로 발전된 반도체 제작 프로세스를 가진 QCA 장치를 구현하는 데 잠재적으로 사용될 수 있다.셀 양극화는 충전 위치로 암호화되며, 양자점 상호작용은 정전 커플링에 의존한다.그러나 현재 반도체 공정은 아직 이토록 작은 특징(20나노미터)을 가진 소자의 대량생산이 가능한 지경에 이르지 못했다.[citation needed]그러나 연속적인 석판화 방법은 QCA 솔리드 스테이트 구현을 달성할 수 있게 하지만 반드시 실용적이지는 않다.직렬 석판화는 느리고 비싸며 솔리드 스테이트 QCA 장치의 양산에 적합하지 않다.오늘날 대부분의 QCA 프로토타이핑 실험은 이 구현 기술을 사용하여 수행된다.[citation needed]

분자의

제안되었지만 아직 구현되지 않은 방법은 단일 분자로 QCA 장치를 만드는 것으로 구성된다.[2]그러한 방법의 예상되는 장점은 대칭성이 높은 QCA 세포 구조, 매우 높은 스위칭 속도, 극도로 높은 장치 밀도, 상온에서의 작동 및 심지어 자가 조립을 통한 장치 양산의 가능성이다.분자의 선택, 적절한 인터페이스 메커니즘의 설계 및 시계 기술을 포함한 많은 기술적 난제가 이 방법을 구현하기 전에 해결되어야 한다.

자석

일반적으로 MQCA(또는 QCA: M)라고 불리는 자기 QCA는 자기 나노입자 사이의 상호작용을 기반으로 한다.이들 나노입자의 자기화 벡터는 다른 모든 구현에서 양극화 벡터와 유사하다.MQCA에서 "퀀텀"이라는 용어는 전자 터널링 효과가 아닌 자기 교환 상호작용의 양자-기계적 특성을 가리킨다.이런 방식으로 제작된 기기는 실온에서 작동할 수 있다.

CMOS 대비 개선

보완금속산화반도체(CMOS) 기술은 지난 40년간 VLSI(Very Large Scale Integrated) 장치의 구현을 위한 산업 표준으로 주로 이러한 장치의 소형화(즉, 전환 속도 증가, 복잡성 증가, 전력 소비 감소)의 결과 때문이다.Quantum Cellular Automata(QCA)는 CMOS 기술이 앞으로 부과할 근본적인 한계에 대한 대체 솔루션으로 제안된 많은 대안 기술 중 하나에 불과하다.

QCA는 CMOS 기술의 한계를 대부분 해결하지만, 자체도 가지고 있다.연구에 따르면 QCA 셀의 고유 스위칭 시간은 기껏해야 테라헤르츠 정도라고 한다.단, 적절한 준 부차 클럭 전환 주파수 설정 때문에 솔리드 스테이트 QCA의 경우 메가헤르츠, 분자 QCA의 경우 기가헤르츠 순으로 실제 속도는 훨씬 더 낮을 수 있다.

참조

  1. ^ Roy, S. S. (September 2016). "Simplification of master power expression and effective power detection of QCA device (Wave nature tunneling of electron in QCA device". 2016 IEEE Students' Technology Symposium (TechSym). pp. 272–277. doi:10.1109/techsym.2016.7872695. ISBN 978-1-5090-5163-2. S2CID 45731602.
  2. ^ Sinha Roy, Soudip (2017-12-25). Generalized Quantum Tunneling Effect and Ultimate Equations for Switching Time and Cell to Cell Power Dissipation Approximation in QCA Devices. doi:10.13140/rg.2.2.23039.71849.
  • Debashis De, Sitanshu Bhattacharaya 및 K. P. Ghatak, Quantum Dots 및 Quantum Cellular Automata:최신 동향 및 애플리케이션, Nova, 2013
  • Srivastava, S.; Asthana, Bhanja, S., S., S., "QCA 회로 설계를 위한 QCAPro - QCA 회로 설계를 위한 오류 전력 추정 도구", 2011년 회로 및 시스템(ISCAS), 2011년 IEEE 국제 심포지엄 on, vol, pp. 2377-2380, 15–18.
  • V.V. 지르노프, R.K. 캐빈, J.A.Hutchby와 G.I. Bourianoff, "이진 로직 스위치 스케일링 - 게단켄 모델" Proc.IEEE, 제91권, 1934 페이지, 2003년 11월.
  • S. Bhanja, S.사르카르, "베이지안 네트워크를 이용한 QCA 회로의 확률론적 모델링", IEEE 나노기술 거래, Vol. 5(6), 페이지 657-670, 2006.
  • S. 스리바스타바와 S.Bhanja, "Hierarchical Probabilistic Macromodeling for QCA 회로", IEEE Transactions on Computers, Vol. 56(2), 페이지 174-190, 2007년 2월.
  • 베스, 티 프로시저"양적 컴퓨팅: 소개"2000 IEEE 회로 및 시스템에 관한 국제 심포지엄, 2000.2000년 5월 735-736 vol.1
  • 빅터 V. 지르노프, 제임스 A.허치비, 조지 1세부리아노프와 조 E.Brewer "신흥 연구 논리 장치" IEEE 회로 & 장치 매거진 2005년 5월 4일 오후 4시
  • 울프람, 스티븐 "A New Kind of Science", 울프람 미디어 메이, 2002 p. ix (Preface
  • C.S. 사순절, P.Tubaw, W. Porod, G. Bernstein, "퀀텀 셀룰러 오토마타" 나노기술, 1993 페이지 49-57.
  • 빅터 V. 지르노프, 제임스 A.허치비, 조지 1세부리아노프와 조 E.Brewer "신흥 연구 논리 장치" IEEE 회로 & 장치 매거진 2005년 5월 7일 오후 7시
  • 콘래드 월러스와 G. A. 줄리엔 "퀀텀닷 셀룰러 오토마타 애더즈" 전기 & 컴퓨터 Eng 부서.캘거리 캘거리 대학교, AB, 캐나다 페이지 4 - 6
  • S. 헨더슨, E. 존슨, Janulis, D.Turnaw, "표준 CMOS 설계 프로세스 방법론을 QCA 로직 설계 프로세스에 통합" IEEE Trans.나노기술, 제3권, 제1권, 2004년 3월. 페이지 2 - 9
  • 크리스토퍼 그라운키, 데이비드 휠러, 더글러스 터보, 제프리 D.유언. "퀀텀닷 셀룰러 오토마타를 이용한 크로스바 네트워크 구축" 2005년 7월 1~6일자 나노기술 관련 IEEE 거래
  • G. T'oth 및 C. S. S. 사순절, "금속-섬 양자점 셀룰러 자동화를 위한 준방사선 전환", 제85권, 제5권, 1999 페이지 2977호 - 2984호
  • G. T'oth, C. S. S. 사순절, "퀀텀닷 셀룰러 오토마타를 이용한 수량 컴퓨팅", 물리학 A. 63, 2000 페이지 1 - 9
  • C. S. 사순절, B.이삭센, M. 리버만, "분자 양자점 셀룰러 오토마타", J. Am.Chem. Soc, vol. 125, 2003 페이지 1056 - 1063
  • K. 월러스, G. A. 줄리엔, V. S. 디미트로프, "퀀텀 셀룰러 오토마타를 위한 컴퓨터 산술 구조" 전기 & 컴퓨터 Eng 부서.캘거리 대학교, 캘거리, AB, 캐나다 페이지 1 - 4
  • 루이 장, 팔라브 굽타, 니라즈 K.Jha "다수 네트워크와 소수 네트워크의 합성 및 QCA, TPL, SET 기반 나노기술의 응용" 2005년 제4차 임베디드 시스템 설계 국제회의 229-234 페이지와 공동으로 개최된 제18차 VLSI 설계 국제회의의 진행
  • Quantum Automaton의 개념을 소개하는 첫 번째 보고서:
  • 바이아누, I. 1971a."카테고리, 펑커스, 양자 오토마타 이론".제4인터울.의회 LMPS, 1971년 8월-9월
  • 바이아누, I.1971b."조직적 슈퍼카테고리 및 시스템의 질적 역학"황소. 수학.바이오피스,[permanent dead link] 339-353: http://cogprints.ecs.soton.ac.uk/archive/00003674/01/ORganismic_supercategories_and_qualitative_dynamics_of_systems_final3.pdf
  • 니미에, M. 2004.노트르담 대학교의 박사학위 논문인 양자 세포 오토마타의 디지털 시스템 설계
  • 최근 업데이트:
  • Quantum Transversible Automata: http://cogprints.org/3697/
  • 양자 나노 오토마타.: http://doc.cern.ch/archive/electronic/other/ext/ext-2004-125/Quantumnanoautomata.doc
  • Quantum Automata 범주.: http://fs512.fshn.uiuc.edu/QAuto.pdf.[permanent dead link]

외부 링크

  • [1] – 노트르담의 QCA 홈 페이지