램지-카스-쿠프만 모형

시리즈의 일부
거시경제학
기본개념 총수요 총공급량 경기순환 디플레 수요충격 소독 유효수요 기대들 적응형 합리적인 금융위기 성장 인플레 수요를 끌어모으다 비용밀당 이자율 투자. 유동성트랩 국민소득과 산출량 측정 GDP GNI NNI 마이크로 파운데이션 돈. 내생적 화폐창조 화폐수요 유동성선호 통화공급 국민계정 SNA 공칭강성 물가수준 불경기 수축팽창 스태그플레이션 공급충격 저장중 실업
정책들 재정 화폐의 상업의 중앙은행 보편기본소득
모델들 IS–LM AD–AS 케인즈 십자가 승수 액셀러레이터 필립스 곡선 Arrow–Debreu 해로드도마르 솔로-스완 램지-카스-쿱만스 중복세대 일반균형 DSGE 내생적 성장 매칭이론 먼델플레밍 오버슈팅 나이루
관련분야 계량경제학 경제통계 화폐경제학 개발경제학 국제경제학
학교 주류 케인즈어 네오- 신규 화폐론 뉴클래식 실물경기순환이론 스톡홀름 공급측 신고전학적 합성 소금물과 담수 헤테로독스 오스트리아어 샤탈리즘 현대 화폐론 생태학 포스트 케인지안 서킷리즘 부등식 마르크스주의자 시장통화주의
사람 프랑수아 케스나이 아담 스미스 토머스 로버트 맬서스 카를 마르크스 레옹 왈라스 크누트 위크셀 어빙 피셔 웨슬리 클레어 미첼 존 메이나드 케인스 앨빈 한센 미차우 칼레키 군나르 미르달 시몬 쿠즈네츠 조안 로빈슨 프리드리히 하이에크 존 힉스 리처드 스톤 하이만 민스키 밀턴 프리드먼 폴 새뮤얼슨 로렌스 클라인 에드먼드 펠프스 로버트 루카스 주니어 에드워드 C. 프레스콧 피터 다이아몬드 윌리엄 노르트하우스 조셉 스티글리츠 토머스 서전트 폴 크루그먼 N. 그레고리 맨큐
참고 항목 거시경제모형 거시경제학 출판물 경제학 응용의 미시경제학 정치경제 수리경제학
머니포털 비즈니스포털
v t

Ramsey–Cass–Koopmans 모델, 또는 Ramsey 성장 모델은 주로 Frank P. Ramsey의 연구에 기반을 둔 신고전학파 경제 성장 모델이며,^[1] David Cass와 Tjalling Koopmans에 의해 상당한 확장이 이루어졌습니다.^[2][3] Ramsey-Cass-Koopmans 모델은 한 시점에서 소비의 선택이 명시적으로 마이크로 기반이 되어 저축률을 내생화한다는 점에서 Solow-Swan 모델과 다릅니다. 결과적으로 Solow-Swan 모델과 달리 장기 정상 상태로의 전환에 따라 절약률이 일정하지 않을 수 있습니다. 모형의 또 다른 함의는 결과가 Pareto 최적 또는 Pareto 효율적이라는 것입니다.^{[note 1]}

원래 램지는 이 모델을 다음 세대에 걸쳐 소비 수준을 극대화하는 소셜 플래너의 문제로 설정했습니다.^[4] 나중에야 카스와 쿠프만스가 대표적인 대리인과 함께 탈중앙화된 역동적 경제를 묘사하는 모델을 채택했습니다. Ramsey-Cass-Koopmans 모델은 경기 순환 변동이 아닌 장기적인 경제 성장을 설명하는 것만을 목표로 하며, 시장 불완전성, 가계 간 이질성 또는 외생적 충격과 같은 교란 요인을 포함하지 않습니다. 따라서 후속 연구자들은 모델을 확장하여 정부 구매 충격, 고용 변화 및 기타 교란 요인을 허용했으며, 이를 실제 경기 순환 이론이라고 합니다.

수학적 기술

모델설정

일반적인 설정에서 시간은 $단순화$를 위해 ${\displaystyle \mathrm{t}}$ = 0${\$displaystyle t = 0}에서 연속적으로 시작되어 영원히 계속됩니다. 가정에 따르면 생산적 요소는 $자본{\displaystyle }$ K ${\displaystyle K}$와 노동 $L{\displaystyle }$ ${\displaystyle L}$이며$$둘 다 음이 아니어야 합니다. $전체$ 모집단을 구성하는 노동력은 일정한 $속도$로 n ${\displaystyle$$n{\displaystyle \stackrel{}{\},}}$ 즉 ${\displaystyle L}$ ˙ ${\displaystyle }$= ${\displaystyle \frac{d}{}}$ L d $t$= n L {\$displaystyle$ {\dot {L}}= {\$tfrac {\$mathrm {d} L$}{\mathrm$ {d} t}}= nL}, implying that ${\displaystyle L=L_{0}e^{nt}}$ with initial level ${\displaystyle L_{0}>0}$ at ${\displaystyle t=0}$. Finally, let ${\displaystyle Y}$ denote aggregate production, and ${\displaystyle C}$ denote aggregate consumption.

Ramsey-Cass-Koopmans 모델이 궁극적으로 설명하고자 하는 변수는 $c$ = ${\displaystyle$ c = {\frac$${C}{$L}},$ 1인당(또는 보다 정확하게는 노동력당) 소비량$$및 k = CL {\displaystyle k = {\frac {K}{L}}, 소위 자본 강도입니다. 먼저 자본 ${\displaystyle \frac{}{}}$을 뉴턴 표기법의 K ˙ = d K ${\displaystyle \frac{dt}{}}$ ${\displaystyle$ {\dot {K}}={\tfrac {\mathrm {d} K}{\mathrm {d} t}}를 소비 C {\displaystyle C}와 연결하여 소비-투자 균형을 설명합니다. 좀 더 구체적으로, 기존 자본스톡은 $감가상각률$δ {\displaystyle$$\delta}(일정하다고 가정)에 의해 하락하므로, 당기 생산$생산량$ Y ${\displaystyle$Y}의 투자가 필요합니다. 따라서,

생산요소와 총생산량의 관계는 총생산함수 $Y$ = F $,$ L${\displaystyle }$) $displaystyle$ Y = F ($K,$L)}로 설명됩니다. 일반적인 선택은 Cobb-Douglas 생산함수 F (K, L ) = A K 1 - α {\displaystyle F (K, L) =$AK^{1-\alpha }L^{\alpha$ 그러나 일반적으로 Inada 조건을 만족하는 생산 함수는 허용됩니다. 그러나 중요한 것은 $F{\displaystyle }$ ${\displaystyle F}$가 1도 동차여야 한다는 것이며$$, 이는 경제적으로 규모에 대한 일정한 수익을 의미합니다. 이 가정을 사용하면 1인당 총 생산량을 다시 표시할 수 있습니다.

예를 들어, $A$ = 1${\displaystyle ,}$ ${\displaystyle \alpha }$ =${\displaystyle }$0${\displaystyle .5}$ {\$displaystyle$ A = $1,\alpha$ = 0.$5}$로 Cobb-Douglas 생산 함수를 사용하면 f${\displaystyle (}$k$)$ = k 0.5 {\displaystyle f(k) = k^{0.5}}입니다.

Ramsey-Cass-Koopmans 모형의 첫 번째 핵심 방정식을 얻기 위해서는 자본 스톡에 대한 동태 방정식을 1인당 용어로 표현해야 합니다. ${\displaystyle \frac{\mathrm{}}{}}$ ${\displaystyle \frac{t}{}}$ (${\displaystyle \frac{\mathrm{KL}}{})}$ ${\$ t$}\left({\tfrac {K}{L}\right)}$에 대한 몫 규칙을 참고하면$,$ 다음과 같습니다.

Solow-Swan 모형과 유사한 비선형 미분방정식

복지 극대화

소비가 분배되는 방식에 대한 문제를 무시하면 효용 $U{\displaystyle }$ ${\displaystyle$ U$}$의 비율은 총 소비의 함수입니다$$. $즉$, U = U${\displaystyle }$($,$ t) ${\displaystyle$ U = U (C,$$t)}입니다$.$ 무한대의 문제를 피하기 위해, 우리는 할인율 ∞ (0, ρ ∈) {\displaystyle \rho \in (0,\infty)}에서 미래의 효용을 지수 함수적으로 할인합니다. 높은 ρ {\displaystyle \rho }는 높은 조급함을 반영합니다.

${\displaystyle {}_{}^{}}$ 계획자의 문제는 사회 복지 함수 U ${\displaystyle 0_{}}$ = ∫ 0$$∞ ${\displaystyle e^{}}$ - ρ t U (C, t) d {\displaystyle U_{0}=\int _{0}^{\infty}e^{-\rhot}U(C, t)\,\mathrm {d} t}를 극대화하는 것입니다.

경제가 변하지 않는 효용 $함수{\displaystyle }$ u${\displaystyle (c)}$ ${\displaystyle$ u$(c)}($대표 에이전트)를 가진 동일한 불멸의 개인들로 채워졌다고 가정하면 총 효용은 다음과 같습니다.

$유틸리티$ 함수는 엄격하게 증가(즉, 블리스 포인트가 $없음$)하고 c ${\$displaystyle $c}$에서 오목한 것으로 가정되며$,$ ${\displaystyle \underset{}{lim}}$ → $0$ u = ∞$${\displaystyle \lim_{c\to 0}u_{c} =\infty}, $여기$서 ${\displaystyle u_{}}$ ${\displaystyle u_{c}}$는 ${\displaystyle \frac{\mathrm{소비}}{}}$ ∂ u$$∂$$c${\displaystyle$ {\partial$$u$\}\{\backslash$partial c}}의 한계 유틸리티입니다.

그래서 우리는 소셜 플래너의 문제를 가지고 있습니다.

${\displaystyle \max _{c}\int _{0}^{\infty }e^{-(\rho -n)t}u(c)\,\mathrm {d} t}$

${\displaystyle {\text{subject}}\quad c=f(k)-(n+\delta)k-{\dot {k}}$

여기서 0이 아닌 초기 자본 k = $k$0 > 0 {\displaystyle k (0) = k_{0} > 0이 주어집니다.

적분이 잘 정의되었는지 확인하기 위해ρ > n ${\displaystyle$rho > n}을(를) 부과합니다.

해

해는 보통 해밀턴 함수를 사용하여 구할 수 있으며,^{[note 3][note 4]} 소비의 최적 진화를 설명하는 미분방정식입니다.

케인스-램지의 [5]법칙

$f$ ${\displaystyle k_{}}$( k${\displaystyle }$)${\displaystyle }$-$$δ - ρ ${\$displaystyle f_${k$}(k$)$-\delta -\rho }${\displaystyle {}_{}}$은 f$k$ = ∂$$k f {\$displaystyle f_${k} =\partial _{k}f}가 자본의 한계 생산물인 경우, 자본 감가상각과 시간 할인을 설명하는 순 투자의 한계 수익률을 반영합니다.

여기서$$σ (c) ${\displaystyle \sigma$ (c$)}$는 다음과 같이 정의되는 시간간 대체의 탄력성입니다.

공식적으로 상대적 위험 회피의 역수에 해당합니다. 수량은 유틸리티 함수의 곡률을 반영하며 시간이 지남에 따라 대표 에이전트가 소비를 원활하게 하고자 하는 정도를 나타냅니다. 에이전트가 상대적 위험 회피도가 높으면 EIS가 낮으므로 시간이 지남에 따라 소비를 원활하게 할 의향이 더 높습니다.

$종종$ u$${\$display$ u$}$가 엄격하게 단조적으로 증가하고 σ > 0 ${\displaystyle$sigma >0}이라고 가정합니다. 특히 유틸리티가 로그인 경우 다음과 같이 일정합니다.

우리는 램지 규칙을 다시 쓸 수 있습니다.$t$ ${\displaystyle \ln }$ ⁡ c${\displaystyle {\frac {d}{dt$}}\ln c}를 "consum 지연율"로 $해석$했는데, 이는 높은 경우 에이전트가 나중에 비해 훨씬 더 적게 소비하고 있음을 의미하며, 이는 근본적으로 지연 소비에 대한 것입니다.

위상 공간에서의 그래픽 분석

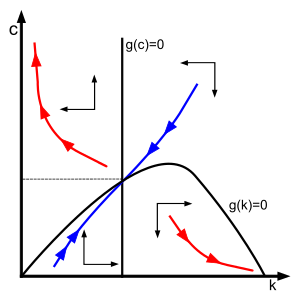
$k{\displaystyle }$ ${\displaystyle k}$와 $c{\displaystyle }$ ${\displaystyle$ c$}$에 대한 두 결합 미분 방정식은 램지-카스-쿱만 역학 시스템을 형성합니다$$.

$시스템에 대한$ 정상 상태($k$ ∗${\displaystyle {}^{}}$ c$$∗$)$${\displaystyle$(k^{\$ast},$c^{\ast})}는 k ˙ {\dot {k}} 및 c ˙ {\displaystyle {\dot {c}}을 0으로 설정하여${\displaystyle \stackrel{}{}}찾을$ 수 있습니다$.$ 세 가지 솔루션이 있습니다.

${\displaystyle f_{k}\left(k^{\ast}\right)=\delta +\rho \quad {\text{and}}\quad c^{\ast}=f\left(k^{\ast}\right)-(n+\delta )k^{\ast}}$

${\displaystyle (0,0)}$

${\displaystyle f(k^{*})=(n+\delta )k^{*}{\text{ with }}k^{*}>0,c^{*}=0}$

첫 번째는 상부 사분면 내부의 유일한 해결책입니다. 안장 지점입니다(아래와 같이). 두 번째는 반발 지점입니다. 세 번째는 퇴화된 안정적인 균형입니다.

기본적으로 첫 번째 솔루션을 의미하지만, 다른 두 솔루션은 추적해야 합니다.

최적의 궤적은 동적 시스템을 따라야 합니다. 그러나 변수 $c{\displaystyle }$ ${\displaystyle$ $c$$}$가 각 자본 강도 $k{\displaystyle }$ ${\displaystyle$ k$}$에서 제어 변수이므로$,$ 우리는 해당 최적 궤적을 찾기 위해 시작 소비율 $c{\displaystyle }$(${\displaystyle 0)}$ ${\displaystyle c(0)}$을 찾아야 합니다$.$ 밝혀진 바에 따르면, 최적의 궤적은 내부 평형점으로 수렴하는 고유한 궤적입니다. 궤적은 ∗> 0, $c$ ∗ = 0 ${\display$ k^{*}> 0,$$c$^\{*\}$= 0}인 완전 절약 평형으로 수렴하거나 k → 0, c → ∞ {\display k\ to 0, c\to \infty}로 발산하는데, 이는 경제가 유한한 시간에 모든 자본을 소비한다는 것을 의미합니다. 둘 다 내부 평형점을 향한 궤적보다 전반적으로 낮은 효용을 달성합니다.

$해$의 안정성$($k ∗${\displaystyle {}^{}}$c ∗) {\$displaystyle(k^{\$ast}, c^{\ast})}에 대한 정성적 문장은 1차 테일러 다항식에 의한 선형화를 필요로 합니다.

${\displaystyle {\begin{bmatrix}{\dot {k}}\\{\dot {c}}\end{bmatrix}}\approx \mathbf {J} (k^{\ast },c^{\ast }){\begin{bmatrix}(k-k^{\ast })\\(c-c^{\ast })\end{bmatrix}}}$

여기서 $J{\displaystyle }$($k$∗,$c$ ∗)${\displaystyle \mathbf {J}$ ($k^{\$ast},c^{\ast})}는 정상 상태에서 평가된 자코비안 행렬로 다음과 같이 주어집니다.

${\displaystyle \mathbf {J} \left(k^{\ast},c^{\ast}\right)={\begin{bmatrix}\rho -n&-1\{\frac {1}{\sigma }f_{kk}(k)\cdot c^{\ast}&0\end{bmatrix}}}$

which has determinant ${\displaystyle \left \mathbf {J} \left(k^{\ast },c^{\ast }\right)\right ={\frac {1}{\sigma }}f_{kk}(k)\cdot c^{\ast }<0}$ since ${\displaystyle c^{*}>0}$ , ${\displaystyle \sigma }$ is positive by assumption, $f{\displaystyle }$ ${\displaystyle f}$이(이나다 조건) 오목이므로$$ < ${\displaystyle f_{kk}<0}$입니다. 행렬식은 고유값의 곱과 같으므로 고유값은 부호에서 실제와 반대여야 합니다.^[6]

따라서 안정 다양체 정리에 의해 평형은 안장점이고 위상 다이어그램에서 파란색 곡선으로 표시된 평형에 수렴하는 고유한 안정 팔, 즉 "안장 경로"가 존재합니다.

이 시스템은 "슬래들 경로 안정적"이라고 불리는데, 이는 모든 불안정한 궤적들이 "노 폰지 스킴" 조건에 의해 배제되기 때문입니다.^[7]

${\displaystyle \lim_{t\to \infty}k\cdote^{-\int_{0}^{t}\left(f_{k}-n-\delta \right)\mathrm {d}s}\geq 0}$

자본 스톡의 현재 가치가 마이너스가 될 수 없음을 암시합니다.^{[note 6]}

역사

이 섹션에는 여러 가지 문제가 있습니다. 개선을 도와주시거나 토크 페이지에서 이러한 문제에 대해 논의해 주시기 바랍니다. (이러한 템플릿 메시지를 제거하는 방법 및 시기에 대해 알아보기) 이 섹션은 검증을 위해 추가 인용이 필요합니다. 이 섹션의 신뢰할 수 있는 출처에 인용문을 추가하여 이 기사를 개선하는 데 도움을 주시기 바랍니다. 출처가 없는 재료는 문제가 발생하여 제거될 수 있습니다. 출처 찾기 : "Ramsey–Cass–Koopmans 모델" – 뉴스 · 신문 · 책 · 학자 · JSTOR (2017년 12월) (본 템플릿 메시지 제거 방법 및 시기에 대해 알아보기) 이 섹션에는 독창적인 연구가 포함되어 있을 수 있습니다. 청구 내용을 확인하고 인라인 인용을 추가하여 개선해 주시기 바랍니다. 독창적인 연구로만 구성된 진술은 제거되어야 합니다. (2017년 12월) (이 템플릿 메시지를 제거하는 방법과 시기에 대해 알아봅니다) 이 섹션은 특정 아이디어, 사건 또는 논란에 과도한 비중을 부여할 수 있습니다. 서로 다른 관점을 상황에 맞게 균형 있게 다시 작성하여 개선할 수 있도록 도와주시기 바랍니다. (2017년 12월) (본 템플릿 메시지의 삭제 방법 및 시기에 대해 학습) (이 템플릿 메시지를 제거하는 방법과 시기에 대해 알아보기)

Spear and Young은 Cass의 "자본 축적의 집합적 모델에서 최적의 성장"이라는 주장의 동시적이고 독립적인 발전의 진실성에 부분적으로 초점을 ^[8]맞추어 1950년대와 1960년대의 최적 성장의 역사를 재조명하고, 그리고 Tjalling Koopman의 "최적의 경제 성장 개념에 대하여"(개발계획에 대한 계량경제학적 접근에 관한 연구 주간, 1965, 로마: 교황청 과학 아카데미).

일생 동안 Cass와 Koopmans 모두 단일 부문 연속 시간 성장 모델에서 최적의 성장을 특징짓는 결과가 "동시적이고 독립적인" 것이 아니라고 제안하지 않았습니다. 우선순위에 대한 문제가 논의점이 된 것은 출판된 버전의 쿠프만스의 작품에서 나중에 RES 논문이 된 카스의 논문에 나오는 챕터를 인용했기 때문입니다. 쿠프만스는 논문에서 카스가 독립적으로 쿠프만스가 발견하는 것과 유사한 조건을 얻었으며, 카스도 논문에서 할인율이 0이 되는 제한적인 경우를 고려한다고 각주에서 밝혔습니다. 카스는 "이 논문의 원본이 완성된 후, 쿠프만스의 매우 유사한 분석이 우리의 관심을 끌게 되었습니다. 우리는 사회적 할인율이 0이 되는 제한적인 경우에 대해 논의할 때 그의 결과를 이용합니다." 캐스가 거시경제역학에 건넨 인터뷰에서 그는 쿠프만스가 프랭크 램지의 이전 작품을 지목한 것에 공을 돌리면서도 그 사실을 몰랐다는 사실에 당황했다고 주장하면서도 자신의 작품과 쿠프만스의 작품이 사실상 독립적이었다는 기본적인 주장을 불식시키기 위해 아무 말도 하지 않습니다.

스피어와 영은 1963년 10월 교황청 과학 아카데미가 개최한 회의에서 쿠프만의 자주 인용되는 발표의 기초가 ^[9]된 이전에 간과되었던 쿠프만의 논문의 작업지 버전에 근거하여 이러한 역사에 대해 논쟁을 제기합니다.^[10] 이 카울즈 토론 논문에는 오류가 있습니다. 쿠프만스는 그의 주요 결과에서 오일러 방정식이 최적의 정상 상태에 수렴하지 않는 오일러 방정식의 해가 유한 시간에 제로 소비 또는 제로 자본 경계에 부딪힐 것이기 때문에 모델에서 최적의 궤적을 특성화하는 데 필요하고 충분하다고 주장합니다. 이 오류는 분명히 바티칸 회의에서 제시된 것이지만, 쿠프만스가 발표할 당시에는 이 문제에 대해 논평한 참가자가 없었습니다. 이것은 바티칸 학회에서 각 논문 발표 후의 토론이 학술대회 분량에서 그대로 유지되기 때문으로 유추할 수 있습니다.

Edmond Malinvaud의 논문 발표에 이어 바티칸 볼륨 토론에서, Malinvaud가 그의 논문에 소위 "횡단성 조건"(Malinvaud가 조건 I이라고 부르는)을 명시적으로 포함시켰기 때문에 문제가 발생합니다. 프레젠테이션 마지막에 쿠프만스는 Malinvaud에게 최적의 정상 상태에 수렴하지 않는 오일러 방정식에 대한 해가 유한 시간에 경계에 도달하는 것을 조건 I이 단순히 보장하는 경우가 아닌지 질문합니다. Malinvaud는 그렇지 않다고 대답하고, Koopmans가 로그 유틸리티 함수와 Cobb-Douglas 생산 함수로 예제를 살펴보라고 제안합니다.

이 시점에서, 쿠프만스는 분명히 자신에게 문제가 있다는 것을 인식하고 있지만, 바티칸 회의 이후에 작성된 논문의 나중 버전에 대한 혼란스러운 부록에 근거하여, 그는 Malinvaud의 조건 1에 의해 제기된 문제를 어떻게 다룰지 결정할 수 없는 것 같습니다.

카스와의 거시경제역학 인터뷰에서 쿠프만스는 1964년 1월 계량경제학회의 겨울 회의에서 카스의 논문 고문인 우자와 히로후미를 만났고, 우자와는 그의 제자인 [카스]가 이미 이 문제를 해결했다고 조언했습니다. 그 후 Uzawa는 Koopmans에게 Cass의 논문 챕터 사본을 제공했을 것입니다. 그는 Koopmans가 자신의 논문의 공개 버전에서 인용한 IMSSSS 기술 보고서를 가장하여 보낸 것으로 보입니다. 쿠프만스의 인용에 나열된 TR 번호는 보고서의 발행일을 1950년대 초로 지정했을 것이지만 분명히 그렇지 않았기 때문에 "게이즈"라는 단어는 여기에 적합합니다.

쿠프만스의 논문의 공개된 버전에서 그는 오일러 방정식 외에 새로운 조건 알파를 부과하며 오일러 방정식을 만족하는 궤적 중에서 유일하게 허용되는 궤적은 모델의 최적의 정상 상태 평형으로 수렴하는 궤적이라고 말합니다. 이 결과는 카스가 레프 폰트랴긴의 책의 관련 부분에서 추론한 횡단성 조건의 부과를 통해 카스의 논문에서 도출되었습니다.^[11] 스피어와 영은 쿠프만스가 멀린보나 카스의 횡단성 기술을 "빌리는" 것처럼 보이고 싶지 않았기 때문에 이 길을 택했다고 추측합니다.

1950년대의 Malinvaud의 기여에 대한 이것과 다른 검토에 기초하여, 특히 횡단성 조건의 중요성에 대한 그의 직관인 Spear와 Young은 신고전적 성장 모델이 기존의 Ramsey-Cass-Koopmans 경칭보다는 Ramsey-Malinvaud-Cass 모델로 더 잘 불릴 수 있음을 시사합니다.

메모들

참고문헌

더보기

• Acemoglu, Daron (2009). "The Neoclassical Growth Model". Introduction to Modern Economic Growth. Princeton: Princeton University Press. pp. 287–326. ISBN 978-0-691-13292-1.
• Barro, Robert J.; Sala-i-Martin, Xavier (2004). "Growth Models with Consumer Optimization". Economic Growth (Second ed.). New York: McGraw-Hill. pp. 85–142. ISBN 978-0-262-02553-9.
• Bénassy, Jean-Pascal (2011). "The Ramsey Model". Macroeconomic Theory. New York: Oxford University Press. pp. 145–160. ISBN 978-0-19-538771-1.
• Blanchard, Olivier Jean; Fischer, Stanley (1989). "Consumption and Investment: Basic Infinite Horizon Models". Lectures on Macroeconomics. Cambridge: MIT Press. pp. 37–89. ISBN 978-0-262-02283-5.
• Miao, Jianjun (2014). "Neoclassical Growth Models". Economic Dynamics in Discrete Time. Cambridge: MIT Press. pp. 353–364. ISBN 978-0-262-02761-8.
• Novales, Alfonso; Fernández, Esther; Ruíz, Jesús (2009). "Optimal Growth: Continuous Time Analysis". Economic Growth: Theory and Numerical Solution Methods. Berlin: Springer. pp. 101–154. ISBN 978-3-540-68665-1.
• Romer, David (2011). "Infinite-Horizon and Overlapping-Generations Models". Advanced Macroeconomics (Fourth ed.). New York: McGraw-Hill. pp. 49–77. ISBN 978-0-07-351137-5.

외부 링크

• Orazio Attanasio가 YouTube에서 램지의 원본 논문에 대한 토론