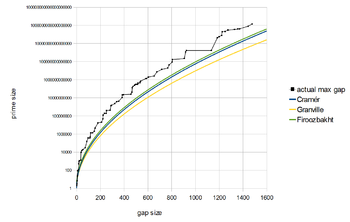
프라임 갭

소수점 갭은 연속된 두 소수 사이의 차이입니다.g 또는 g(p_n)로 표시된_n n번째 소수 간격은 (n + 1)번째 소수와 n번째 소수 사이의 차이이다.

$\displaystyle g_{n}=p_{n+1}-p_{n}.\ }$

g₁₂ = 1, g = g₃ = 2, g = 4가 있습니다₄.주요 격차의 순서(g_n)는 광범위하게 연구되어 왔지만, 많은 의문과 추측이 답하지 않은 채로 남아 있다.

처음 60개의 주요 격차는 다음과 같습니다.

1, 2, 4, 4, 6, 2, 6, 6, 6, 6, 4, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 4, 4, 4, 2, 2, 2, 4, 2, 2, 6, 6, 6, 6, 6, 6, 6, 10, 6, 6, 6, 2, 12, 12, 12, 12, 14, 4, 14, 14, 14, 14, 14, 14, 14, 4, 14, 14, 6, 6, 6, 12, 24, 14, 14, 14, 14, 14, 4, 4, 14, 4, 14, 4, 14, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4,

g의 정의에_n 따르면 모든 소수는 다음과 같이 쓸 수 있다.

${\displaystyle p_{n+1}=2+\sum _{i=1}^{n}g_{i}.}$

단순한 관찰

첫 번째, 가장 작고 홀수인 소수 간격은 유일한 짝수인 2와 첫 번째 홀수인 3 사이의 크기 1의 간격입니다.다른 모든 소수 격차는 동일하다.길이가 2인 연속되는 간격 쌍은 소수 3, 5, 7 사이의 간격₂ g와 g뿐입니다₃.

모든 정수 n에 대해 요인 n!은 n을 포함한 모든 양의 정수의 곱입니다.그리고 순서대로

$\displaystyle n!+2,n!+3,\ldots,n!+n}$

첫 번째 항은 2로 나누어지며 두 번째 항은 3으로 나누어집니다.따라서 이것은 n - 1의 연속 합성 정수의 수열이며 길이가 n 이상인 소수점 사이의 간격에 속해야 합니다.따라서 임의의 큰 소수점 사이에 간격이 존재한다. 즉, 임의의 정수 N에 대해 g ≤ N의 정수_m m이 존재한다.

그러나 n개의 소수 갭은 n!보다 훨씬 작은 숫자로 발생할 수 있습니다.예를 들어, 크기가 14보다 큰 첫 번째 소수 갭은 소수 523과 541 사이에 발생하며, 15!는 매우 큰 숫자 1307674368000입니다.

소수점 사이의 평균 간격은 이러한 소수점의 자연 로그와 함께 증가하며, 따라서 관련된 소수점에 대한 소수점 간 간격의 비율이 감소한다(그리고 점근적으로 0).이것은 소수 정리의 결과이다.경험적 관점에서 자연대수에 대한 갭 길이의 비율이 고정 양수 k보다 크거나 같을 확률이 e가 될 것으로^−k 예상되며, 결과적으로 그 비율은 임의로 커질 수 있다.실제로 관련된 정수의 자릿수에 대한 간격의 비율은 제한 없이 증가합니다.이것은 Westzynthius에 ^[2]의한 결과의 결과이다.

반대 방향에서, 쌍둥이 소수 추측은 무한히 많은 정수 n에 대해 g = 2라고_n 가정한다.

수치 결과

보통g의 비율 n나는 n(pn){\textstyle{\frac{g_{n}}{ln(p_{n})}}}그 격차가 gn의 장점. 4월 16일 2022[업데이트]처럼 확인된 가능성 있는 주요 격차들과 알려진 가장 큰 주요 격차208095-digit 가능성 있는 최고급 제품과 공적 M=14.9985, 미힐 얀센은 pr 체를 사용하여 발견되는 작업대와 길이 7186572,이라 불린다.ogram devJ. K.^[3][4] 안데르센에 의해 도망쳤다.갭 엔드로 확인된 확인된 소수와 가장 큰 소수의 차이는 길이가 1113106이고 25.90이며, 18662자리의 소수가 P에 의해 발견되었다.카미, M. 얀센, J. K.^[5][6] 안데르센.

2017년 12월^[update] 현재, 갭코인 네트워크에서 발견된 가장 큰 성과 값 및 40 이상의 성과는 41.93878373으로, 87자리 소수 2937032340680225908723766104464646434705748117620582178957287283222이다.그것과 다음 소수의 차이는 8350이다.^[7]

알려진 최대 성과 값(2020년 ^{[7][8][9][10]}10월^[update] 기준)

메리트	ᄀn	숫자	pn.	날짜.	디스커버
41.938784	8350	87	위 참조	2017	갭코인
39.620154	15900	175	3483347771 × 409#/30 − 7016	2017	다나 야콥슨
38.066960	18306	209	650094367 × 491#/2310 − 8936	2017	다나 야콥슨
38.047893	35308	404	100054841 × 953#/210 − 9670	2020	세스 트로이시
37.824126	8382	97	512950801 × 229#/5610 − 4138	2018	다나 야콥슨

크라메르-상크-그랑빌 비율은 g/(ln(p_n))^2[7]의_n 비율이다.소수점 2, 3, 7에 대해 비정상적으로 높은 비율 값을 폐기하면 이 비율의 가장 큰 값은 소수점 1693182318746371에 대해 0.9206386이 됩니다.기타 기록 용어는 OEIS: A111943에서 확인할 수 있습니다.

모든 m < n에 대해 g < g일_n 경우_m g는 최대 간격이라고 한다_n. 2018년 8월^[update] 현재 가장 큰 것으로 알려진 최대 소수 간격의 길이는 Bertil Nyman이 발견했다.이것은 80번째 최대 격차로, 18361375334787046697 ^[11]프라임 이후에 발생합니다.기타 레코드(최대) 갭사이즈는 OEIS: A005250, 대응하는 소수_n p는 OEIS: A002386, n 값은 OEIS: A005669로 확인할 수 있습니다.n번째 소수점까지의 최대 간격 시퀀스는 약 ${\displaystyle 2}$ $ln$ ${\displaystyle †}$ n$(아래$ 표 참조) 항을$$^[12] 갖는 것으로 추측됩니다.

80개의 알려진 최대 소수 간격

1번부터 27번까지 # ᄀn pn. n 1 1 2 1 2 2 3 2 3 4 7 4 4 6 23 9 5 8 89 24 6 14 113 30 7 18 523 99 8 20 887 154 9 22 1,129 189 10 34 1,327 217 11 36 9,551 1,183 12 44 15,683 1,831 13 52 19,609 2,225 14 72 31,397 3,385 15 86 155,921 14,357 16 96 360,653 30,802 17 112 370,261 31,545 18 114 492,113 40,933 19 118 1,349,533 103,520 20 132 1,357,201 104,071 21 148 2,010,733 149,689 22 154 4,652,353 325,852 23 180 17,051,707 1,094,421 24 210 20,831,323 1,319,945 25 220 47,326,693 2,850,174 26 222 122,164,747 6,957,876 27 234 189,695,659 10,539,432

28번부터 54번까지 # ᄀn pn. n 28 248 191,912,783 10,655,462 29 250 387,096,133 20,684,332 30 282 436,273,009 23,163,298 31 288 1,294,268,491 64,955,634 32 292 1,453,168,141 72,507,380 33 320 2,300,942,549 112,228,683 34 336 3,842,610,773 182,837,804 35 354 4,302,407,359 203,615,628 36 382 10,726,904,659 486,570,087 37 384 20,678,048,297 910,774,004 38 394 22,367,084,959 981,765,347 39 456 25,056,082,087 1,094,330,259 40 464 42,652,618,343 1,820,471,368 41 468 127,976,334,671 5,217,031,687 42 474 182,226,896,239 7,322,882,472 43 486 241,160,624,143 9,583,057,667 44 490 297,501,075,799 11,723,859,927 45 500 303,371,455,241 11,945,986,786 46 514 304,599,508,537 11,992,433,550 47 516 416,608,695,821 16,202,238,656 48 532 461,690,510,011 17,883,926,781 49 534 614,487,453,523 23,541,455,083 50 540 738,832,927,927 28,106,444,830 51 582 1,346,294,310,749 50,070,452,577 52 588 1,408,695,493,609 52,302,956,123 53 602 1,968,188,556,461 72,178,455,400 54 652 2,614,941,710,599 94,906,079,600

55~80번 # ᄀn pn. n 55 674 7,177,162,611,713 251,265,078,335 56 716 13,829,048,559,701 473,258,870,471 57 766 19,581,334,192,423 662,221,289,043 58 778 42,842,283,925,351 1,411,461,642,343 59 804 90,874,329,411,493 2,921,439,731,020 60 806 171,231,342,420,521 5,394,763,455,325 61 906 218,209,405,436,543 6,822,667,965,940 62 916 1,189,459,969,825,483 35,315,870,460,455 63 924 1,686,994,940,955,803 49,573,167,413,483 64 1,132 1,693,182,318,746,371 49,749,629,143,526 65 1,184 43,841,547,845,541,059 1,175,661,926,421,598 66 1,198 55,350,776,431,903,243 1,475,067,052,906,945 67 1,220 80,873,624,627,234,849 2,133,658,100,875,638 68 1,224 203,986,478,517,455,989 5,253,374,014,230,870 69 1,248 218,034,721,194,214,273 5,605,544,222,945,291 70 1,272 305,405,826,521,087,869 7,784,313,111,002,702 71 1,328 352,521,223,451,364,323 8,952,449,214,971,382 72 1,356 401,429,925,999,153,707 10,160,960,128,667,332 73 1,370 418,032,645,936,712,127 10,570,355,884,548,334 74 1,442 804,212,830,686,677,669 20,004,097,201,301,079 75 1,476 1,425,172,824,437,699,411 34,952,141,021,660,495 76 1,488 5,733,241,593,241,196,731 135,962,332,505,694,894 77 1,510 6,787,988,999,657,777,797 160,332,893,561,542,066 78 1,526 15,570,628,755,536,096,243 360,701,908,268,316,580 79 1,530 17,678,654,157,568,189,057 408,333,670,434,942,092 80 1,550 18,361,375,334,787,046,697 423,731,791,997,205,041

기타 결과

상한

1852년에 증명된 Bertrand의 공식은 k와 2k 사이에 항상 소수가 존재하며, 특히_n+1 p < 2p는_n g < p를_n 의미합니다_n.

1896년에 증명된 소수 정리는 충분히 큰 소수에서 소수 p와 다음 소수 사이의 간격의 평균 길이가 점근적으로 p의 자연 로그인 ln(p)에 근접할 것이라고 말한다.갭의 실제 길이는 이보다 훨씬 크거나 적을 수 있습니다.그러나 소수 정리로부터 소수 간격의 길이에 대한 상한을 추론할 수 있다.

$(\displaystyle \epsilon$> $0$마다 N$(\displaystyle N)$이라는 $숫자$가 있습니다

n< $>$ { $displaystyle$ g$_$ { $n$} < $p$_ { $n$} \ $silon$ }。

또한 소수점에 비례하여 격차가 임의로 작아진다는 것을 추론할 수 있다.

$\displaystyle \lim _{n\to \infty}{\frac {g_{n}}{p_{n}}=0.}$

Hoheisel(1930)은 다음과 같은 상수 θ < 1이 존재한다는 것을 최초로 보여준 사람이다^[13].

$\displaystyle \pi (x+x^{\theta })\pi (x)\sim {\log(x)}}{\text {as }x\to \infty ,}$

이 때문에, 라는 것을 알 수 있다

${\displaystyle g_{n}<p_{n}^{\theta},}$

충분히 큰 n에 대해서.

Hoheisel은 θ의 가능한 값 32999/33000을 구했다.이것은 Heilbronn에 ^[14]의해 249/250으로 개선되었고, Chudakov에 ^[15]의해 θ > 0에 대해 θ = 3/4 + θ로 개선되었다.

큰 개선은 잉햄에 의한 것이다.잉햄은 ^[16]어떤 양의 상수 c에 대해 다음과 같은 것을 보여주었다.

$t$$$$(t^{c}),$ 그$$ $후{\displaystyle }$ ${\displaystyle (}$ (${\displaystyle }$ + ${\displaystyle {}^{}}$) - ${\displaystyle (}$ (${\displaystyle x}$) - ${\displaystyle \frac{\log }{}}$ ${\displaystyle \frac{（}{}}$x$$) \ $displaystyle \pi ( x$ + $x^$ { \$theta$} ) - \$pi ( x$ ) \$sim$ { $x ^$ { \ theta } { \ $log$( )} ( 1$$+ )$）$ 。$}$

여기서 O는 빅 O 표기법, θ는 리만 제타 함수, θ는 소수계수 함수이다.임의의 c > 1/6이 허용되므로 θ는 5/8보다 큰 임의의 수임을 알 수 있습니다.

잉햄 결과의 직접적인 결과는 n이 충분히 클 경우 ^[17]항상 n과 (n + 1) 사이에^{3 3}소수가 있다는 것입니다.린델뢰프 가설은 잉햄의 공식은 어떤 양수라도 유지한다는 것을 암시할 것이다. 그러나 이것조차도 충분히 큰 n과 (n + ²1) 사이에² 소수가 있다는 것을 암시하기에는 충분하지 않을 것이다(레전드르의 추측 참조).이를 검증하기 위해서는 크라메르의 추측과 같은 더 강력한 결과가 필요할 것이다.

1972년 헉슬리는 θ = 7/12 = 0.58(3)^[18]을 선택할 수 있음을 보여주었다.

2001년의 Baker, Harman 및 Pintz에 의한 결과, θ는 0.525로 ^[19]간주될 수 있습니다.

2005년 다니엘 골드스턴, 야노스 핀츠, 켐 이드롬은 다음과 같은 사실을 증명했다.

$\displaystyle \liminf _{n\to \infty }{\frac {g_{n}}{\log p_{n}}=0}$

그리고 2년 후 이것을 개선하여^[20]

${\displaystyle \liminf _{n\to \infty }{\frac {g_{n}}{\fracrt {\log p_{n}}(\log \log p_{n})^{2}}<\infty .}$

2013년, 장이탕은 다음과 같은 것을 증명했다.

$\displaystyle \liminf _{n\to \infty }g_{n} <7\cdot 10^{7}$

7천만 ^[21]개를 넘지 않는 격차가 무한히 많다는 것을 의미합니다.Zhang의 한계를 최적화하기 위한 Polymath Project의 공동 노력으로 2013년 ^[22]7월 20일 한계를 4680으로 낮출 수 있었습니다.2013년 11월 제임스 메이나드는 GPY 체의 새로운 정교함을 도입하여 결합을 600으로 줄이고 m에 대해 각각 m개의 ^[23]소수를 포함하는 변환 수가 무한히 많은 유계 구간이 존재한다는 것을 보여주었다.Maynard의 아이디어를 사용하여, Polymath 프로젝트는 경계를 246으로 ^[22][24]개선했습니다. 엘리엇-할버스탐 추측과 그 일반화 형태를 가정하면,^[22] N은 각각 12와 6으로 감소했습니다.

하한

1931년, 에릭 웨스틴티우스는 최대 소수 격차가 로그보다 더 커진다는 것을 증명했다.즉,^[2]

$\displaystyle \limsup _{n\to \infty}{\frac {g_{n}}{\log p_{n}}=\infty .}$

1938년 로버트 랭킨은 c > 0의 상수의 존재를 증명하여 부등식이

${\displaystyle g_{n}>{\frac {c\log n\log \log n\log \log \log n}{(\log \log \log n)^2}}}$

는 무한히 많은 값 n을 유지하며 Westzynthius 및 Paul Erd's의 결과를 개선합니다.그는 나중에 어떤 상수 c < e도^γ 취할 수 있다는 것을 보여주었다. 여기서 θ는 오일러-마셰로니 상수이다.상수 c 값은 1997년에 2e ^[25]미만의^γ 값으로 개선되었습니다.

Paul Erd's는 상기의 부등식에서의 상수 c가 임의로 ^[26]클 수 있다는 것을 증명하거나 반증하는 것에 대해 10,000달러의 상금을 걸었다.이것은 2014년에 포드-그린-코냐긴-에 의해 옳다는 것이 증명되었다.타오와 제임스 ^[27][28]메이나드입니다

결과는 더욱 개선되었다

${\displaystyle g_{n}>{\frac {c\log n\log \log n\log \log n}}$

Ford-Green-Konyagin-Maynard-Tao의 ^[29]무한히 많은 n 값에 대해.

Erdés의 원래 상금의 정신에 따라 Terence Tao는 ^[30]이 불평등에서 c가 임의로 크게 받아들여질 수 있다는 증거로 미화 10,000달러를 제시했습니다.

소수점 사슬의 하한도 결정되었다.^[31]

소수점 사이의 간격에 대한 추측

리만 가설에서는 훨씬 더 좋은 결과가 나올 수 있다.Harald Cramér은^[32] 갭 g가_n 다음을 만족한다는 것을 리만 가설이 암시한다는 것을 증명했다.

$({displaystyle g_{n}=O({\sqrt {p_{n}}}\log p_{n}),})$

큰 O 표기를 사용합니다.(사실 이 결과는 무한히 큰 지수를 견딜 수 있다면 더 약한 린델뢰프 가설만 필요하다.)^[33]나중에 그는 그 격차가 더 작다고 추측했다.대략적으로 말하면, 크라메르의 추측은 다음과 같다.

${\displaystyle g_{n}=O\!\left((\log p_{n})^{2}\오른쪽).}$

Firoozbakht의 추측에 따르면 ${\displaystyle p_{}^{}}$ ${\displaystyle {\mathrm{}}_{}^{}}$ 1$n ($${\displaystyle {여기}_{}}$서 p$$n {$displaystyle p_{n}$은 $$$n번째$ 소수)은 n의 엄밀한 감소 $함수$이다.

${\displaystyle p_{n+1}^1/(n+1)<p_{n}^1/n}{\text{모든}}n\geq 1.}$

이 추측이 참일 경우 $함수{\displaystyle {}_{}}$ ${\displaystyle g_{}}$ n ${\displaystyle {}_{}}$ ${\displaystyle {}_n}$ +${\displaystyle {}_{}{1}_{}}$ - ${\displaystyle p_{}}$ $n$ p_${n}$ = p_{$n+1}-p_{n}$ - p_${n$}은$$ n>에 n< ($log$ p )$2$ 을 합니다$.\{$ $text }$의 경우 { $display$ style $g_{n}$ - { n } - $log p_{$n}}지만 그랑빌과 Pintz[35][36][37]의g n을 제안하는 발견적 학습 법과 일치하지 않는 것 Cramér의 추측의 단단한 형태를 의미한다;2− ε eγ(로그 ⁡ pn)2{\displaystyle g_{n}>,{\frac{2-\varepsilon}{e^{\gamma}}}(\log p_{n})^{2}}무한히 종종ε 을에;0,{\displaystyle[34].\varepsilon>0,}이$§$ $(\displaystyle$ \gamma$)$는 오일러-마셰로니 상수를 나타냅니다.

한편, 오퍼만의 추측은 크라메르의 추측보다 약하다.오퍼만의 추측과의 예상 격차 크기는 대략 다음과 같다.

${\displaystyle g_{n}<\displayrt {p_{n}}}}.}$

그 결과 Oppermann의 추측에 따르면 모든 n> {\$displaystyle$ n > m {\displaystyle n > $m$}이( gn < n. {\$displaystyle$ $g_{n}$을(를) $충족하는$m {\$displaystyle$ m$$$= 30$이 $존재$합니다.$}$

오퍼만의 추측보다 더 약한 안드리카의 추측은 다음과^[38] 같이 말한다.

${\displaystyle g_{n}<2grt {p_{n}}+1.}$

이것은 연속되는 제곱수 사이에 항상 소수가 있다는 Legendre의 추측을 약간 강화한 것이다.

폴리냑의 추측에 따르면 모든 양의 짝수 k는 소수 간극으로 무한히 자주 발생한다.케이스 k = 2는 쌍둥이 소수 추측이다.이 추측은 k의 어떤 특정 값에 대해서도 아직 입증되거나 반증되지 않았지만, 장이탕의 결과는 70,000,000보다 작은 k의 적어도 하나(현재 알려지지 않은) 값에 대해 그것이 사실임을 증명한다. 위에서 논의한 바와 같이, 이 상한이 246으로 개선되었다.

산술 함수로서

n번째 소수와 (n + 1)번째 소수 사이의 간격_n g는 산술 함수의 예입니다.이 문맥에서는 보통 d로 표시되며_n 일차 ^[38]함수라고 불립니다.함수는 곱셈도 가법도 아닙니다.

「 」를 참조해 주세요.

• 본스 부등식
• 가우스 해자
• 트윈 프라임

레퍼런스

• Guy, Richard K. (2004). Unsolved problems in number theory (3rd ed.). Springer-Verlag. ISBN 978-0-387-20860-2. Zbl 1058.11001.

추가 정보

• Soundararajan, Kannan (2007). "Small gaps between prime numbers: the work of Goldston-Pintz-Yıldırım". Bull. Am. Math. Soc. New Series. 44 (1): 1–18. arXiv:math/0605696. doi:10.1090/s0273-0979-06-01142-6. S2CID 119611838. Zbl 1193.11086.
• Mihăilescu, Preda (June 2014). "On some conjectures in additive number theory" (PDF). Newsletter of the European Mathematical Society (92): 13–16. doi:10.4171/NEWS. hdl:2117/17085. ISSN 1027-488X.

외부 링크

• 토마스 R. 좋아요, 소수점에서의 컴퓨터 연구의 몇 가지 결과물 - 계산수 이론이 참조 웹 사이트에는 최초로 알려진 모든 주요 발생 간극 목록이 포함되어 있습니다.
• Weisstein, Eric W. "Prime Difference Function". MathWorld.
• "Prime Difference Function". PlanetMath.
• 베르트랑의 추측에 대한 체비셰프의 정리를 재확장하는 아르민 샴스는 다른 보고된 결과와 같이 '임의적으로 큰' 상수를 포함하지 않는다.
• Chris Caldwell, 소수점 사이의 간격, 기본 소개
• Andrew Granville, Intervals in Bounded Length; 2013년 11월 James Maynard의 연구를 포함하여 지금까지 얻은 결과의 개요.