다지관

이 문서에는 일반 참조 목록이 포함되어 있지만 해당 인라인 인용이 충분하지 않습니다. 좀 더 정확한 인용문을 소개하여 이 글을 개선할 수 있도록 도와주시기 바랍니다.(2021년 7월) (이 템플릿 메시지를 제거하는 방법 및 시기 알아보기)

수학에서 다양체는 각 점 근처의 유클리드 공간과 국소적으로 유사한 위상 공간입니다.더 정확하게 말하면$,$ {\$displaystyle$ n$}$ - 차원$$ 다양체, $또는{\displaystyle }$ 줄여서$$n {\$displaystyle$ n$}$ - 매니폴드는 각 점이 n$${\$displaystyle$ n$}$ - 차원$$ 유클리드 공간의 $열린{\displaystyle }$ 부분 집합과 동형인 속성을 가진 위상 공간입니다.

1차원 다양체는 선과 원을 포함하지만 렘니케이트는 포함하지 않습니다.2차원 다양체는 표면(surface)이라고도 합니다.그 예로는 평면, 구, 토러스, 그리고 클라인 병과 실제 투영 평면이 있습니다.

다양체의 개념은 복잡한 구조를 단순한 공간의 위상학적 특성의 관점에서 설명할 수 있기 때문에 기하학과 현대 수학 물리학의 많은 부분에서 중심적입니다.다양체는 자연스럽게 방정식 체계의 해집합과 함수의 그래프로 나타납니다.이 개념은 사진을 좌표(예: CT 스캔)와 연결해야 하는 필요성을 고려하여 컴퓨터 그래픽에 응용됩니다.

매니폴드에는 추가적인 구조물이 장착될 수 있습니다.다양체의 중요한 종류 중 하나는 미분 가능한 다양체입니다. 그것들의 미분 가능한 구조는 미적분학을 할 수 있게 해줍니다.다양체의 리만 메트릭은 거리와 각도를 측정할 수 있습니다.고전역학의 해밀토니안 형식주의에서 심플렉틱 다양체는 위상 공간의 역할을 하는 반면, 4차원 로렌츠 다양체는 일반 상대성 이론에서 시공간을 모델링합니다.

다양체에 대한 연구는 미적분학과 위상학에 대한 실무적인 지식을 필요로 합니다.

동기를 부여하는 예

원형

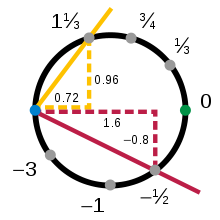
선 다음에는 원이 위상다양체의 가장 간단한 예입니다.위상은 굽힘을 무시하므로 원의 작은 조각은 선의 작은 조각과 동일하게 취급됩니다.예를 들어, y좌표가 양인 경우(그림 1의 노란색 호로 표시됨), 단위 원의 맨 위 부분인 x + y = 1을 고려합니다.이 호의 임의의 점은 x좌표에 의해 고유하게 설명될 수 있습니다.따라서 첫 번째 좌표에 투영하는 것은 위쪽 호에서 열린 간격(-1, 1)으로 연속적이고 가역적인 매핑입니다.

이와 같은 함수는 이들이 매핑하는 열린 영역과 함께 차트라고 합니다.마찬가지로 원의 아래쪽(빨간색), 왼쪽(파란색) 및 오른쪽(녹색) 부분에 대한 차트도 있습니다.

이 부분들은 함께 원 전체를 덮고, 네 개의 차트는 원에 대한 지도를 형성합니다.

$위{\displaystyle {}_{}}$ 차트와 오른쪽 차트인 ${\displaystyle {①\mathrm{}}_{}}$ 위 ${\$ \$chi _{\mathrm${top$}}}$와 ② ${\displaystyle {\mathrm{오른쪽}}_{}}$ 차트 ${\$ _${\mathrm {right}}}$는 각각 도메인에서 겹칩니다. 즉, 교차점은 x$${\$displaystyle$ x$}$ $및$ y$${\$displaystyle$ y$}$ 좌표가$$ $모두{\displaystyle }$ 양수인 원의 1/4에 위치합니다.이 부분을 구간${\displaystyle }$(${\displaystyle 0,}$ ${\displaystyle 1)}$ ${\displaystyle (0, 1$에 매핑합니다.따라서 ${\displaystyle {함수}_{}}$${\displaystyle }T$ :${\displaystyle }$( 0${\displaystyle ,1}$ ) → ( ${\displaystyle 0,1}$ ) = χ ${\displaystyle {\mathrm{right}}_{}}$ t ∘ ${\displaystyle {\mathrm{to}}_{}^{}}$ ${\displaystyle {\mathrm{top}}_{}^{}}$- 1$${\$displaystyle$ T : ($0,1)\rightarrow (0,1$) =\$chi$ _${\mathrm {right} }\circ$ \$chi _{\mathrm$ {top}$^{-1$}} 의 공 도메인에서 p ${\displaystyle \chi$ _${\mathrm {top}}$까지의 값을 역으로 사용하여 원으로 다시 가져오는 함수 T를 만들 수 있습니다.${\displaystyle {다음}_{}}$으로 χ ${\displaystyle {\mathrm{right}}_{}}$ ${\displaystyle \chi$ _${\mathrm {right}}}$이(가) 구간으로 돌아갑니다.a가 (${\displaystyle 0,}$ ${\displaystyle 1)}${\$displaystyle(0, 1$에${\displaystyle }$있는 숫자라면 다음과 같습니다.

이와 같은 함수를 전이 지도(transition Map.

위, 아래, 왼쪽 및 오른쪽 차트가 유일하게 가능한 아틀라스를 형성하지는 않습니다.차트가 기하학적 투영일 필요는 없으며, 차트의 수는 선택의 문제입니다.차트 고려

그리고.

여기서는 좌표 (x, y) 및 고정 피벗 지점 (-1, 0)의 점을 통과하는 선의 기울기입니다. 마찬가지로 t는 좌표 (x, y) 및 (+1, 0)의 점을 통과하는 선의 기울기와 반대입니다.s에서 (x, y)까지의 역맵핑은 다음과 같이 주어집니다.

s의 모든 값에 대하여 x + y = 1임을 확인할 수 있습니다.이 두 차트는 전이 지도와 함께 원에 대한 두 번째 아틀라스를 제공합니다.

(즉, s와 t가 모두 0이 아닌 모든 점에 대해 s와 t 사이에 이러한 관계가 있음).

각 관리도는 s 또는 t에 대한 (-1, 0) 점 중 하나를 생략하므로 두 관리도만으로는 전체 원을 포괄하기에 충분하지 않습니다.단일 차트로 전체 원을 커버할 수 없다는 것을 증명할 수 있습니다.예를 들어, 한 줄 간격으로 끝을 겹쳐서 "붙여" 원을 구성할 수는 있지만, 이렇게 하면 차트가 생성되지 않습니다. 원의 일부가 양쪽 끝에 한 번에 매핑되어 가역성이 손실됩니다.

구

구체는 표면의 한 예입니다.암시적 방정식의 단위 구

x + y + z – 1 = 0

평면 z = 0은 구를 두 개의 반구(z > 0 및 z < 0)로 나누고, 둘 다 xy 좌표 평면 상의 투영에 의해 디스크 x + y < 1에 매핑될 수 있습니다.그러면 두 개의 차트가 제공되고, 다른 네 개의 차트는 두 개의 다른 좌표 평면과 비슷한 구조로 제공됩니다.

원과 마찬가지로 하나의 점을 제외한 전체 구를 포함하는 하나의 차트를 정의할 수 있습니다.따라서 두 개의 차트로 충분하지만 구면은 단일 차트로 커버할 수 없습니다.

이 예는 용어에 동기를 부여했기 때문에 역사적으로 중요합니다. 지구 표면 전체가 단일 지도("차트"라고도 함)로 구성된 평면 표현을 가질 수 없음이 명백해졌기 때문에 지구 표면 전체를 덮기 위해 상자가 필요합니다.

기타곡선

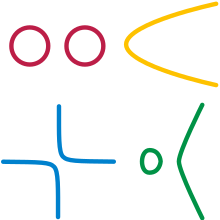
매니폴드를 연결할 필요는 없습니다(모두 "한 조각"으로 되어 있음). 예를 들어 한 쌍의 개별 원이 있습니다.

매니폴드는 닫힐 필요가 없으므로 끝점이 없는 선분은 매니폴드입니다.다양체의 차원이 0이 아닌 한 이들은 절대 셀 수 없습니다.이러한 자유를 종합하면, 다양체의 다른 예로는 포물선, 쌍곡선, 입방 곡선 y = x - x (닫힌 고리 조각과 열린 무한 조각)의 점들의 위치가 있습니다.

그러나 한 점을 공유하여 그림-8을 형성하는 두 개의 터치 원과 같은 예는 제외되며, 공유된 점에서는 만족스러운 차트를 생성할 수 없습니다.위상에 의해 허용되는 굽힘에도 불구하고, 공유된 점 근처는 선이 아닌 "+"처럼 보입니다."+"에서 중심점을 삭제하면 4개의 성분(즉, 조각)이 있는 공간이 제공되는 반면, 선분에서 점을 삭제하면 최대 2개의 조각이 있는 공간이 제공되므로, 위상 연산은 항상 조각 수를 유지합니다.

수학적 정의

비공식적으로 다양체는 유클리드 공간을 모델로 한 공간입니다.

다양한 종류의 다양체가 있습니다.기하학과 위상수학에서, 모든 다양체는 위상다양체이며, 아마도 추가적인 구조를 가질 것입니다.다양체는 좌표 차트의 집합, 즉 유클리드 공간에 대한 동형을 갖는 열린 집합에 의한 피복, 그리고 패치 함수를 제공함으로써 구성될 수 있다:서로 다른 두 좌표 차트에서 다양체의 동일한 부분에 해당하는 경우 유클리드 공간의 한 영역에서 다른 영역으로의 동형 사상.패치 함수가 연속성 이상의 공리를 만족하는 경우 매니폴드에 추가 구조가 부여될 수 있습니다.예를 들어, 미분 가능한 다양체는 중첩된 이웃이 서로 동형이므로, 다양체는 각 이웃에서 미분 가능하고, 따라서 다양체 전체에서 미분 가능한 잘 정의된 함수 집합을 갖습니다.

형식적으로, (위상학적) 다양체는 유클리드 공간과 국소적으로 동형인 두 번째 셀 수 있는 하우스도르프 공간입니다.

두 번째 계수와 하우스도르프는 점 집합 조건입니다. 두 번째 계수는 긴 선과 같이 어떤 의미에서 '너무 큰' 공간을 제외하는 반면 하우스도르프는 "두 개의 기원을 가진 선"과 같은 공간을 제외합니다(이러한 다양체의 일반화는 하우스도르프가 아닌 다양체에서 논의됨).

유클리드 공간에 국소적으로 동형인 것은 모든 점이 음이 아닌 정수 n에 $대한{\displaystyle {\mathbb{}}^{}}$ ${\displaystyle {}^{}}$ 공간$Rn$, ${\displaystyle \mathbb {R}^{$n}}의$$ 열린 부분 집합과 이웃 동형인 것을 의미합니다.

이는 점이 고립된 점이거나(${\displaystyle \mathrm{n}}$= 0 {\$displaystyle$ n =$$0}인 경우) 열린 공과 동형인 이웃이 있음을 의미합니다.

${\displaystyle {}^{}}$은 또한$Rn {\displaystyle$\mathbb {$R}^{$n$$}}이(가) 동형이기 때문에 $모든{\displaystyle {\mathbb{}}^{}}$ 점이 ${\displaystyle {}^{}}${\$displaystyle \mathbb {R$$}$^{n$$$}$와 동형이며, 심지어 그 안의 열린 공과 동형이기도 하다는 것을 의미합니다( {\$displaystyle$ n$>0}$의 경우).

앞의 정의에서 나타나는 것을 다양체의 국소 차원이라고 합니다.일반적으로 다양체는 일정한 국소 차원을 갖도록 하고, 국소 차원을 다양체 차원이라고 합니다.특히 매니폴드가 연결된 경우가 이에 해당합니다.그러나 일부 저자들은 연결되어 있지 않고 서로 다른 점들이 서로 다른 ^[1]차원을 가질 수 있는 다양체를 인정합니다.만약 다양체가 고정된 차원을 가지고 있다면, 이것은 순수 다양체라고 부르는 것으로 강조될 수 있습니다.예를 들어, (a) 구의 표면은 2의 상수 차원을 가지며 따라서 순수 다양체인 반면, 3차원 공간에서 구와 선의 분리 결합은 순수 다양체가 아닙니다.차원은 로컬 불변(즉, 각 점을 차트가 정의된 이웃의 차원으로 보내는 지도는 로컬 상수)이므로 연결된 각 구성 요소는 고정된 차원을 가집니다.

다양체 이론적으로, 다양체는 유클리드 공간의 연속적인(또는 미분 가능한, 또는 복소 해석적인 등의) 함수들의 집합과 국소적으로 동형인 국소적인 고리 공간입니다.이 정의는 대수기하학에서 해석 다양체를 논의할 때 주로 사용됩니다.

차트, 아틀라스 및 전환 맵

구면 지구는 지도나 도표를 사용하여 지도에 수집되어 탐색됩니다.마찬가지로, 다양체는 수학 지도에서 수집된 좌표 차트라고 불리는 수학 지도를 사용하여 설명될 수 있습니다.다양체의 전역적 구조가 단순한 차트의 구조와 다르기 때문에 하나의 차트만으로 다양체를 설명하는 것은 일반적으로 불가능합니다.예를 들어, 지도의 경계를 넘어 인접한 형상을 분리하거나 커버리지를 중복하지 않으면 단일 평면 지도가 지구 전체를 나타낼 수 없습니다.여러 개의 중첩된 차트에서 매니폴드를 구성할 때, 매니폴드가 중첩되는 영역은 전역 구조를 이해하는 데 필수적인 정보를 전달합니다.

차트

다양체의 좌표 맵(coordinate map), 또는 단순히 차트(chart)는 다양체의 부분집합과 단순 공간 사이의 가역적인 맵으로, 맵과 그 역이 모두 원하는 ^[2]구조를 유지합니다.위상 다양체의 경우, 단순 공간은 유클리드 $공간{\displaystyle {\mathbb{}}^{}}$ ${\displaystyle {}^{}}$ ${\$의 부분 집합이며, 관심은 위상 구조에 초점을 맞춥니다.이 구조는 양방향으로 연속되는 가역 맵인 동형화에 의해 보존됩니다.

미분 가능 다양체의 경우, 전이 함수(아래 참조)가 모두 미분 가능한 아틀라스라고 불리는 도표의 집합은 우리가 그 위에 미적분학을 할 수 있게 해줍니다.예를 들어 극좌표는 ${\displaystyle {}^{}}$의 x축과 원점을 뺀 평면 R2 {\$displaystyle$ \mathbb {R$}^{2}$에 대한 차트를 형성합니다$.$차트의 또 다른 예로는 위에서 언급한 지도 χ가 있는데, 원에 대한 차트입니다.

아틀라스

대부분의 매니폴드에 대한 설명에는 둘 이상의 차트가 필요합니다.다양체를 포함하는 특정한 차트 모음을 아틀라스라고 합니다.지도표는 모든 다양체를 여러 차트 조합을 사용하여 여러 가지 방법으로 덮을 수 있으므로 고유하지 않습니다.두 개의 아틀라스는 만약 그들의 조합이 아틀라스이기도 하다면 동등하다고 합니다.

주어진 아틀라스와 일치하는 모든 가능한 차트를 포함하는 아틀라스를 최대 아틀라스(즉, 주어진 아틀라스를 포함하는 등가 클래스)라고 합니다.일반적인 지도서와 달리, 주어진 다양체의 최대 지도서는 독특합니다.정의에는 유용하지만, 추상적인 객체이며 직접적으로 사용되지는 않습니다(예: 계산에서).

전이 지도

지도형의 차트는 중첩될 수 있으며 다양체의 단일 점이 여러 개의 차트로 표시될 수 있습니다.만일 두 개의 차트가 겹친다면, 유럽의 지도와 러시아의 지도가 모두 모스크바를 포함할 수 있는 것처럼, 그들의 일부는 다양체의 동일한 영역을 나타냅니다.두 개의 중첩된 차트가 주어지면 ${\displaystyle {}^{}}$ ${\$의 열린 $공$에서 매니폴드로 이동한 다음 ${\displaystyle {}^{}}$ ${\$의 다른(또는 동일한) 열린 공으로 다시 이동하는 전이 함수를 정의할 수 있습니다.결과 맵은 위의 원 예제의 맵 T와 마찬가지로 좌표 변경, 좌표 변환, 전이 함수 또는 전이 맵이라고 합니다.

부가구조

아틀라스를 사용하여 매니폴드에 추가 구조를 정의할 수도 있습니다.구조는 먼저 각 차트에서 개별적으로 정의됩니다.모든 전이 지도가 이 구조와 호환되면 구조가 매니폴드로 이동합니다.

이것이 미분 가능 다양체를 정의하는 표준 방법입니다.위상다양체에 대한 지도서의 전이함수가 ${\displaystyle {}^{}}$ ${\$즉, 미분동형인 경우)의 자연 미분 구조를 유지하면 미분 구조는 다양체로 이동하여 미분 다양체로 바뀝니다.복잡한 다양체는 아틀라스의 전이 함수가 동형 함수일 것을 요구함으로써 유사한 방식으로 도입됩니다.심플렉틱 다양체의 경우 전이 함수는 심플렉틱 동형이어야 합니다.

다양체의 구조는 아틀라스에 따라 다르지만 때로는 다른 아틀라스가 같은 구조를 만들어 낸다고 할 수 있습니다.이러한 병을 호환이라고 합니다.

이러한 개념들은 일반적으로 의사 집단을 사용함으로써 정확하게 만들어집니다.

경계가 있는 다양체

경계가 있는 다양체는 가장자리가 있는 다양체입니다.예를 들어, 종이 한 장은 1차원 경계가 있는 2-매니폴드입니다.$경계$가 있는 ${\displaystyle$ n$}$ - 매니폴드의$$ 경계는${\displaystyle }$(${\displaystyle n}$- ${\displaystyle 1)}${\$displaystyle (n-1)}$ - 매니폴드입니다$$.디스크(원+내부)는 경계가 있는 2-매니폴드입니다.그 경계는 원, 1-매니폴드입니다.내부가 있는 정사각형도 경계가 있는 2개의 다접이형입니다.공(구구+인테리어)은 경계가 있는 3개의 매니폴드입니다.경계는 구, 2-매니폴드입니다. (경계(위상)와 혼동하지 마십시오.)

기술 언어에서 경계를 갖는 다양체는 내부 점과 경계 점을 모두 포함하는 공간입니다.모든 내부 점은 열린 n {\displaystyle n} - 공 { ( x 1, x 2, …, x n ) Δ x i 2 < 1 } {\displaystyle \{(x_{1}, x_{2},\dots, x_{n})\vert \Sigma x_{i}^{2}<1\}. 모든 경계 점은 "하프" n {\displaystyle n} - 공 { ( x 1, x 2, …,x n ) σ x i 2 < 1 및 x 1 ≥ 0 }${\displaystyle \{(x_{1)}, x_{$2},\displaystyle \{$1}, x_{$2}\vert \$Sigma x_{i}^{2}<1{\text${ $and$}}}$x_{1}\geq$ 0 반구 사이의 동형 사상은 ${\displaystyle x_{}}$1 ${\displaystyle {}_{}}$ ${\displaystyle 0}$ ${\displaystyle x_$${$$1$}=$0$}인 점을 ${\displaystyle x_{}}$1 = ${\displaystyle 0}$ ${\displaystyle x_$${$$1$}=$0$인 점으로 보내야 합니다.이 불변성을 통해 경계점을 "정의"할 수 있습니다. 다음 단락을 참조하십시오.

경계 및 내부

$M$을$$경계가 $있는 다양체$ {\displaystyle$$ M$}$이라 하자.Int ⁡ ${\displaystyle M}$ ${\displaystyle$ M ${\displaystyle$M$\}$으로 ${\displaystyle \mathrm{표시}}$되는 M$${\displaystyle M$\}$의 내부는 ${\displaystyle {}^{}}$ ${\displaystyle \mathbb {R}^{n$의 열린 부분 집합과 동형인 M$${\$displaystyle$ M$}$의 점 집합입니다.∂${\displaystyle }$${\displaystyle M}$ {\$displaystyle$ $\backslash$partial M$}$으로 $표시$되는 M ${\displaystyle$M$}$의 $경계$는 M {\$displaystyle$ M$\}$에서 $Int$ ⁡ ${\displaystyle M}$ ${\displaystyle \operatorname {Int}$ M$}$의 ${\displaystyle \mathrm{보완}}$입니다.경계점은 일부 좌표 차트에서 R${\displaystyle {}_{}^{}}$+ ${\displaystyle {}_{}^{}}$ ${\displaystyle \mathbb {R}$ _${+}^{n}}$의 경계 초평면$({\displaystyle x_{}}$ n =${\displaystyle 0}$ )$${\$displaystyle (x_{n$}=$0)}$에 착지하는 점으로 특성화할 수 있습니다.

M {\displaystyle M}이(가) 차원 n {\displaystyle n}의 경계를 갖는 다양체라면, Int ⁡ M {\displaystyle \operatorname {Int} M은 차원 n {\displaystyle n}의 다양체(경계를 갖지 않는)이고, ∂ M {\displaystyle \partial M}은 차원 n - 1 {\displaystyle n-1}의 다양체(경계를 갖지 않는)이다.

시공

하나의 매니폴드는 다른 방식으로 구성될 수 있으며, 각 매니폴드의 다른 측면을 강조하여 약간 다른 관점으로 이어집니다.

차트

아마도 다양체를 구성하는 가장 간단한 방법은 원 위의 예제에서 사용되는 방법일 것입니다.먼저 ${\displaystyle {\mathrm{}}^{}}$ ${\$의 부분 집합을 식별한 후 이 부분 집합을 덮는 아틀라스를 구성합니다.다양체의 개념은 이와 같은 건축물로부터 역사적으로 발전했습니다.다음은 구의 건설에 이 방법을 적용하는 또 다른 예입니다.

차트가 있는 구

구체는 원과 거의 같은 방식으로 취급될 수 있습니다.수학에서 구(球, )는 R3 {\$displaystyle \mathbb {R}$^{$3$의 $부분{\displaystyle {\mathbb{}}^{}}$ 집합으로 정의할 수 있는 (고체 내부가 아닌) 표면입니다$.$

구면은 2차원이므로 각 차트는 구의 일부를 ${\displaystyle {\mathrm{}}^{}}${\$displaystyle \mathbb {R}^{2$의 열린 부분 집합에 매핑합니다. 양의 z 좌표를 가진 부분인 북반구를 생각해 보십시오(오른쪽 그림에서 빨간색으로 표시됨).에 의해 정의된 함수 χ

는 (x, y) 평면에 투영하여 북반구와 열린 단위 디스크를 매핑합니다.남반구에 대해서도 비슷한 도표가 있습니다.(x, z) 평면에 투영된 2개의 차트와 (y, z) 평면에 투영된 2개의 차트를 함께 사용하면 전체 구를 포함하는 6개의 차트 지도를 얻을 수 있습니다.

이는 고차원 구에 쉽게 일반화될 수 있습니다.

패치워크

다양체는 조각들을 일정한 방식으로 서로 붙여서 중첩된 차트로 만드는 방법으로 구성될 수 있습니다.이 구성은 모든 다양체에 대해 가능하므로, 특히 미분 가능한 다양체와 리만 다양체에 대해 종종 특성화로 사용됩니다.패치가 자연스럽게 차트를 제공하기 때문에 아틀라스에 초점을 맞추고 외부 공간이 없기 때문에 매니폴드의 고유한 뷰로 이어집니다.

다양체는 전이 지도에 의해 정의되는 아틀라스를 지정하여 구성됩니다.따라서 다양체의 점은 전이 지도에 의해 서로 매핑되는 점들의 동등성 클래스입니다.동등성 클래스를 단일 패치의 점에 매핑합니다.일반적으로 전이 지도의 일관성에 대한 강력한 요구가 있습니다.위상 다양체의 경우, 그들은 동형이어야 합니다. 만약 그들이 또한 동형이라면, 결과 다양체는 미분 가능 다양체입니다.

이는 원 예제의 후반부의 전이 지도 t = ⁄로 설명할 수 있습니다.행의 복사본 두 개부터 시작합니다.첫 번째 복사본에는 좌표를 사용하고 두 번째 복사본에는 t를 사용합니다.이제 두 번째 복사본의 점 t를 첫 번째 복사본의 점 s = ⁄로 식별하여 두 복사본을 모두 접착합니다(점 t = 0 및 s = 0은 첫 번째 복사본과 두 번째 복사본의 어떤 점으로도 식별되지 않음).이렇게 하면 원이 나옵니다.

내재적 관점과 외재적 관점

첫 번째 건축물과 이 건축물은 매우 유사하지만, 다소 다른 관점을 나타냅니다.첫 번째 구성에서 다양체는 유클리드 공간에 내장된 것으로 보입니다.이것이 외재적인 견해입니다.이와 같이 다양체를 볼 때, 유클리드 공간으로부터의 직관을 사용하여 추가적인 구조를 정의하기 쉽습니다.예를 들어, 유클리드 공간에서, 어떤 점의 벡터가 그 점을 통해 어떤 표면에 대해 접선인지 또는 정상인지는 항상 명확합니다.

패치워크 구조는 어떠한 임베딩도 사용하지 않고 단지 매니폴드 자체를 위상공간으로 보고 있습니다.이 추상적 관점을 내재적 관점이라고 합니다.접선 벡터가 무엇인지 상상하기 어려워질 수 있고, 정상 다발이라는 고유한 개념은 없고, 대신 고유한 안정 정상 다발이 있습니다.

n-Sphere as a patchwork

n-sphereⁿ S는 원(1-sphere)과 구(2-sphere)의 개념을 더 높은 차원으로 일반화한 것입니다.n-sphereⁿ S는 ${\displaystyle {}^{}}$ ${\$의 복사본 두 개를 붙여 구성할 수 있습니다.이들 사이의 전이 지도는 다음과 같이 정의되는 구의 반전입니다.

이 함수는 자체 역함수이므로 양방향으로 사용할 수 있습니다.전이 지도가 매끄러운 함수이므로 이 지도는 매끄러운 다양체를 정의합니다.n = 1인 경우 예제는 앞에서 주어진 원 예제로 단순화됩니다.

다지관의 식별

다양체의 여러 점을 동일하게 정의할 수 있습니다.이는 이러한 점들을 단일 점에서 서로 연결하여 몫 공간을 형성하는 것으로 시각화할 수 있습니다.그러나 그러한 몫의 공간이 다양체가 될 것이라고 기대할 이유는 없습니다.반드시 다양체가 아닌 가능한 몫 공간 중에서 orbifold와 CW 복합체는 비교적 잘 작동하는 것으로 간주됩니다.다양체인 다양체의 몫공간의 한 예는 대응하는 구의 몫공간으로 확인되는 실제 투영공간입니다.

점을 식별하는 한 가지 방법은 그룹의 오른쪽(또는 왼쪽) 작용을 통해 다양체에 작용합니다.어떤 그룹 요소에 의해 하나가 다른 하나로 이동되면 두 점이 식별됩니다.M이 다양체이고 G가 그룹인 경우, 결과적인 몫 공간은 M/G(또는 G \ M)로 표시됩니다.

점을 식별하여 구성할 수 있는 다양체에는 토리와 실제 투영 공간(평면과 구에서 각각 시작)이 포함됩니다.

경계를 따라 붙이기

경계가 있는 두 다양체는 경계를 따라 서로 접착될 수 있습니다.이것이 올바른 방식으로 수행된다면 결과도 다양체가 됩니다.마찬가지로, 단일 다양체의 두 경계는 서로 접착될 수 있습니다.

공식적으로, 접착제는 두 경계^{[dubious – discuss]} 사이의 편향(bijection)에 의해 정의됩니다.두 점은 서로 매핑될 때 식별됩니다.위상 다양체의 경우, 이 사영은 동형이어야 하며, 그렇지 않으면 결과는 위상 다양체가 되지 않습니다.마찬가지로, 미분 가능한 다양체의 경우, 그것은 미분 동형이어야 합니다.다른 매니폴드의 경우에는 다른 구조물을 보존해야 합니다.

유한 실린더는 스트립 [0,1] × [0,1]에서 시작하여 적합한 차분법에 의해 경계에 한 쌍의 반대쪽 가장자리를 접착함으로써 다양체로 구성될 수 있습니다.투영 평면은 구멍이 있는 구를 각각의 원형 경계를 따라 뫼비우스 띠에 붙임으로써 얻을 수 있습니다.

데카르트 제품

다양체의 데카르트 곱 또한 다양체입니다.

제품 다양체의 치수는 요인의 치수의 합입니다.위상은 제품 토폴로지이고 차트의 데카르트 곱은 제품 다양체에 대한 차트입니다.따라서 제품 다양체에 대한 아틀라스는 요인에 대한 아틀라스를 사용하여 구성할 수 있습니다.이러한 아틀라스가 요인에 대한 차동 구조를 정의하는 경우, 해당 아틀라스는 제품 매니폴드에 대한 차동 구조를 정의합니다.요인에 정의된 다른 구조에 대해서도 마찬가지입니다.요인 중 하나에 경계가 있으면 제품 다양체에도 경계가 있습니다.데카르트 곱은 예를 들어 S × S¹ 및 S × [0,1]과 같이¹¹ tori 및 유한 실린더를 구성하는 데 사용될 수 있습니다.

역사

다양체에 대한 연구는 수학의 많은 중요한 영역을 결합합니다: 그것은 선형 대수학과 위상학의 아이디어뿐만 아니라 곡선과 표면과 같은 개념을 일반화합니다.

초기발육

다양체의 현대적 개념 이전에는 몇 가지 중요한 결과가 있었습니다.

비유클리드 기하학은 유클리드의 평행 공준이 실패하는 공간을 고려합니다.사케리는 1733년에 처음으로 그러한 기하학을 연구했지만, 단지 그것들을 반증하려고 했습니다.가우스, 볼라이, 로바체프스키는 100년 후에 독립적으로 이들을 발견했습니다.그들의 연구는 고전적인 유클리드 공간의 기하학적 구조와 다른 두 종류의 공간을 발견했습니다; 이것들은 쌍곡 기하학과 타원 기하학을 낳았습니다.현대의 다양체 이론에서, 이러한 개념은 각각 일정한 음과 양의 곡률을 갖는 리만 다양체에 해당합니다.

칼 프리드리히 가우스는 추상적인 공간을 그 자체로 수학적인 대상으로 생각한 최초의 사람이었을지도 모릅니다.그의 이론은 표면이 놓여있는 주변 공간을 고려하지 않고 표면의 곡률을 계산하는 방법을 제공합니다.그러한 표면은 현대 용어로 다양체라고 불릴 것입니다. 그리고 현대 용어로 정리는 표면의 곡률이 고유한 성질이라는 것을 증명했습니다.다양체 이론은 주변 공간의 외재적 특성을 대체로 무시한 채 이러한 고유 특성(또는 불변량)에만 집중하게 되었습니다.

다양체의 고유 특성에 대한 또 다른 위상학적 예는 오일러 특성입니다.레온하르트 오일러는 V개의 꼭짓점(또는 모서리), E개의 모서리, F개의 면을 갖는 3차원 유클리드 공간의 볼록한 다면체에 대하여,

폴리토프의 꼭짓점과 모서리를 구면에 투영하여 V 꼭짓점, E 모서리, F 면으로 위상 지도를 생성하면 동일한 공식이 유지되며, 볼록 폴리토프에서 ^[3]발생하지 않더라도 실제로 구면 지도에 대해 참으로 유지됩니다.따라서 2는 오일러 특성이라 불리는 구의 위상 불변량입니다.반면에, 토러스는 V = 1 꼭짓점, E = 2 모서리, F = 1 면으로 지도를 만드는 '원형'과 '원형' 원에 의해 잘려질 수 있습니다.따라서 토러스의 오일러 특성은 1 - 2 + 1 = 0입니다.다른 표면의 오일러 특성은 유용한 위상 불변량이며, 이는 베티 수를 사용하여 더 높은 차원으로 확장될 수 있습니다.19세기 중반 가우스-보넷 정리는 오일러 특성을 가우스 곡률과 연결시켰습니다.

합성

19세기 전반에 닐스 헨리크 아벨과 칼 구스타프 야코비가 타원 적분을 반전시킨 연구는 그들이 현재 야코비안으로 알려진 특수한 유형의 복잡한 다양체를 고려하도록 이끌었습니다.베른하르트 리만은 복소 변수들의 함수들의 분석적 연속 과정의 기하학적 의미를 명확히 하면서 그들의 이론에 더 기여했습니다.

19세기 수학에서 다양체의 또 다른 중요한 원천은 시메온 포아송, 자코비, 윌리엄 로완 해밀턴에 의해 개발된 분석 역학이었습니다.기계 시스템의 가능한 상태는 라그랑지안과 고전 역학의 해밀턴 형식주의에서 추상적 공간, 위상 공간의 점으로 생각됩니다.이 공간은 사실상 고차원 다양체이며, 차원은 시스템의 자유도에 해당하고 점들이 일반화된 좌표에 의해 지정됩니다.자유 입자의 자유로운 움직임에 대해 다양체는 유클리드 공간과 동등하지만, 다양한 보존 법칙은 더 복잡한 형태, 예를 들어 리우빌 토리로 제한합니다.레온하르트 오일러와 조제프 루이 라그랑주에 의해 18세기에 개발된 회전하는 고체의 이론은 다양체가 사소하지 않은 또 다른 예를 제공합니다.위상수학의 창시자 중 한 명인 앙리 푸앵카레는 고전역학의 기하학적, 위상학적 측면을 강조했습니다.

리만은 표면의 아이디어를 더 높은 차원으로 일반화하는 광범위한 작업을 한 최초의 사람이었습니다.다양체라는 이름은 리만의 원래 독일어 용어인 Mannigfaltigkeit에서 비롯되었는데, William Kingdon Clifford는 이 용어를 "다양체"라고 번역했습니다.그의 괴팅겐 취임 강연에서, 리만은 특정한 제약 조건을 가진 변수의 모든 가능한 값의 집합을 Mannigfaltigkeit라고 묘사했는데, 그 이유는 변수가 많은 값을 가질 수 있기 때문입니다.그는 그 값이 연속적으로 변하는지 아닌지에 따라 스테티지 Mannigfaltigkeit와 원반형 Mannigfaltigkeit(연속 다양체와 불연속 다양체)를 구분합니다.연속적인 예로서, 리만은 공간에서 색상과 물체의 위치뿐만 아니라 공간 도형의 가능한 모양을 언급합니다.리만은 귀납법을 사용하여 n-1차원 다양성의 연속 스택으로 n-파카우젠트 만니그팔티게이트(n배 확장 다양성 또는 n차원 다양성)를 구성합니다.리만의 직관적인 Mannigfaltigkeit 개념은 오늘날 다양체로 공식화된 것으로 발전했습니다.리만 다양체와 리만 표면은 리만의 이름을 따서 지어졌습니다.

푸앵카레의 정의

앙리 푸앵카레(Henri Poincaré)는 그의 매우 영향력 있는 논문인 분석 시투스(Analysis Situs)^[4]에서 ^[5]다양체의 현대적 개념의 선구자 역할을 한 미분가능 다양체(variété)의 정의를 제시했습니다.

분석 시투스의 첫 번째 섹션에서, 푸앵카레는 다양체를 암시적 함수 정리의 비퇴행 가설을 만족하는 유클리드 공간 사이의 연속적으로 미분 가능한 함수의 수준 집합으로 정의합니다.세 번째 절에서 그는 연속적으로 미분 가능한 함수의 그래프가 후자의 의미에서 다양체임을 언급하는 것으로 시작합니다.그리고 나서 그는 '다양체의 사슬'(une chaîne des variétés)에 기초한 보다 일반적인 다양체의 새로운 정의를 제안합니다.

푸앵카레의 다양체 사슬 개념은 현대 아틀라스 개념의 선구자입니다.특히, 그는 함수 θ ( y) {\displaystyle \theta (y)} 와 θ' (y') {\displaystyle '\left(y'\right)} 의 그래프로 정의된 두 다양체를 고려한다. 만약 이 다양체가 겹친다면, 그는 좌표 y {\displaystyle y} 가 좌표 y' {\displaystyle y} 에 연속적으로 미분적으로 의존해야 한다$displaystyle$ y$'}$ 또는$$ 그 반대$('...lessy$ {\$displaystyle$ y$}$ sont$$ fonctions analytics $desy{\displaystyle {}^{}}$ $'$ {\displaystyle$$$$y'} et inverstation').이런 식으로 그는 차트와 전이 지도의 개념에 대한 선구자를 소개합니다.

예를 들어, 평면에서의 단위 원은 점 (1, 0)과 (-1, 0)을 제외한 모든 점의 이웃에서 함수 y = 1 - x 2 {\textstyle y={\sqrt {1-x^{2}}}의 그래프로 생각할 수 있으며, 그 외의 점들의 이웃에서는 다음과 같은 그래프로 생각할 수 있다,$각각$ x = $1\sqrt{}$- $\sqrt{y^{}}$ 2$${\$textstyle$ x = {\$sqrt {1-y^{2}}},$ x = - 1$\sqrt{}$- $\sqrt{{}^{}}$ $\sqrt{2^{}}${\$textstyle$ x = - {\$sqrt {1-y^{2$정의 $방정식$ ${\displaystyle x^{}}$2 + ${\displaystyle y^{}}$2 - ${\displaystyle 1}$ = ${\displaystyle 0}${\$displaystyle$ x$^{2}$ + $y^{2}$ - 1 =$0$의 왼쪽에는 원의 모든 점에서 0이 아닌 기울기가 있기 때문에 원은 모든 점의 이웃에 있는 그래프로 표시될 수 있습니다.암묵적 함수 정리에 의해, 유클리드 공간의 모든 하위 매니폴드는 국소적으로 함수의 그래프입니다.

헤르만 바일은 1911-1912년 리만 표면에 대한 강의 과정에서 미분 가능한 다양체에 대한 본질적인 정의를 내렸고, 곧이어 나온 위상 공간의 일반적인 개념으로 가는 길을 열었습니다.1930년대에 Hassler Whitney 등이 주제의 기초적인 측면을 명확히 하여 19세기 후반으로 거슬러 올라가는 직관들이 정밀해졌고, 미분기하학과 Lie 군 이론을 통해 발전했습니다.특히 휘트니 임베딩^[6] 정리는 차트 측면에서 본질적인 정의가 유클리드 공간의 부분 집합 측면에서 푸앵카레의 정의와 동일하다는 것을 보여주었습니다.

매니폴드의 토폴로지: 하이라이트

우리의 공통 3D 공간에 내장된 2차원 표면으로도 알려진 2차원 다양체는 리만 표면을 가장하여 리만에 의해 고려되었고, 20세기 초 폴 히가드와 막스 덴에 의해 엄격하게 분류되었습니다.푸앵카레는 3차원 다양체에 대한 연구를 개척했고 오늘날 푸앵카레 추측으로 알려진 그것들에 대한 근본적인 의문을 제기했습니다.그리고리 페렐만(Grigori Perelman)은 거의 1세기 후에 푸앵카레 추측을 증명했습니다(푸앵카레 추측의 해법 참조).1970년대 윌리엄 서스턴의 기하학 프로그램은 푸앵카레 추측을 일반적인 3차원 다양체로 확장시켰습니다.4차원 다양체는 1980년대 마이클 프리드먼에 의해 수학 연구의 선두에 섰고, 사이먼 도날드슨에 의해 다른 환경에서 이론 물리학(양-밀스 이론)의 최근 발전에 의해 동기를 부여 받아 일반적인 '평탄한' 시공간의 대체물 역할을 했습니다.Andrey Markov Jr.는 1960년에 4차원 다양체를 분류하는 알고리즘이 존재하지 않음을 보여주었습니다.푸앵카레 추측의 유사체를 포함한 고차원 다양체에 대한 중요한 연구는 르네 톰, 존 밀너, 스티븐 스몰, 세르게이 노비코프에 의해 일찍이 수행되었습니다.다양체의 위상에 대한 많은 연구의 기초가 되는 매우 광범위하고 유연한 기술은 모스 이론입니다.

부가구조

위상다양체

정의하기에 가장 간단한 종류의 다양체는 위상다양체인데, 이것은 국소적으로 어떤 "보통의" 유클리드 $공간{\displaystyle {\mathbb{}}^{}}$ ${\displaystyle {}^{}}${\$displaystyle \mathbb {R}^{n$처럼 보입니다. 정의에 의해, 모든 다양체는 위상다양체이므로, "위상다양체"라는 문구는 보통 다양체가 추가적인 구조를 결여하고 있다는 것을 강조하기 위해 사용됩니다.또는 위상학적 특성만을 고려하고 있는 경우.형식적으로 위상다양체는 유클리드 공간과 국소적으로 동형인 위상공간입니다.이것은 모든 점이 ${\displaystyle {}^{}}$ ${\$에 그 이웃을 매핑하는 동형 사상(역도 연속인 사영 연속 함수)이 존재하는 이웃을 가지고 있음을 의미합니다.이러한 동형은 다양체의 차트입니다.

위상다양체는 국소적으로 유클리드 공간처럼 다소 약한 방식으로 보입니다. 각 개별 차트에 대해 미분 가능한 함수를 구별하거나 거리와 각도를 측정하는 것은 가능하지만, 단지 위상다양체이기 때문에 공간은 그러한 ^[7]개념의 특별하고 일관된 선택을 가지고 있지 않습니다.다양체에 대한 이러한 성질을 논의하기 위해서는 추가적인 구조를 명시하고 아래에서 논의되는 미분 가능한 다양체와 리만 다양체를 고려해야 합니다.특히, 동일한 기본 위상 다양체는 서로 호환되지 않는 여러 종류의 미분 가능한 함수와 거리와 각도를 지정하는 무한한 방법을 가질 수 있습니다.

일반적으로 위상 공간에 대한 추가적인 기술적 가정은 병리학적 사례를 배제하기 위해 이루어집니다.공간을 하우스도르프와 두 번째 계산 가능한 공간으로 요구하는 것이 관례입니다.

특정 지점에서 다양체의 차원은 해당 지점의 차트가 매핑되는 유클리드 공간의 차원입니다(정의의 숫자 n).연결된 다양체의 모든 점은 동일한 차원을 갖습니다.일부 저자는 위상 다양체의 모든 차트를 동일한 차원의 유클리드 공간에 매핑할 것을 요구합니다.그 경우 모든 위상다양체는 위상 불변성, 그 차원을 갖습니다.

미분다양체

대부분의 응용 분야에서는 특수한 종류의 위상 다양체, 즉 미분 가능 다양체가 사용됩니다.매니폴드의 로컬 차트가 특정 의미에서 호환되는 경우 해당 매니폴드의 방향, 접선 공간 및 미분 가능한 함수를 정의할 수 있습니다.특히 미분 가능한 다양체에 미적분학을 사용하는 것이 가능합니다.n차원 미분 가능 다양체의 각 점에는 접선 공간이 있습니다.이것은 점을 통과하는 곡선의 접선 벡터로 구성된 n차원 유클리드 공간입니다.

미분 가능한 다양체의 두 가지 중요한 분류는 매끄럽고 분석적인 다양체입니다.매끄러운 다양체의 경우 전이 지도는 매끄럽습니다. 즉, 무한히 미분 가능합니다.해석 다양체는 매끄러운 다양체이며, 전이 지도가 해석적이라는 추가 조건을 갖습니다(이들은 멱급수로 표현될 수 있습니다).가장 익숙한 곡선과 표면처럼 구에 분석 구조를 부여할 수 있습니다.

정류 가능 집합은 부분적으로 매끄럽거나 정류 가능한 곡선의 개념을 더 높은 차원으로 일반화합니다. 그러나 정류 가능 집합은 일반적인 다양체에는 없습니다.

리만 다양체

매니폴드의 거리와 각도를 측정하려면 매니폴드가 리만식이어야 합니다.리만 다양체는 점마다 매끄럽게 변하는 방식으로 각 $접공간$에 내부곱 ⟨ ⋅ ⟩$$⋅ ⟩ \ { } display style in ⋅ l \ a \ with equipped an ot$$ \ ⟨ le cd each emann \ is ri in a which product space manifold manifold iable inner rang different smoothly is cd ian to tangent from ⋅ , a which두 접선 $벡터$ u$${\$displaystyle$u} $및$ v$${\$displaystyle$ v$\}$이(가) 주어졌을 때 내부 곱$$⟨ ${\displaystyle u}$, ${\displaystyle v}$ ⟩ {\$displaystyle \langle u,v\$rangle $}$은(는) 실수를 제공합니다.점(또는 스칼라) 제품은 내부 제품의 전형적인 예입니다.이를 통해 길이, 각도, 면적(또는 볼륨), 곡률 및 벡터 필드의 발산과 같은 다양한 개념을 정의할 수 있습니다.

(상수 차원의) 미분 가능한 모든 다양체는 리만 다양체의 구조가 주어질 수 있습니다.유클리드 공간 자체는 리만 다양체의 자연 구조를 가지고 있습니다(접선 공간은 유클리드 공간 자체와 자연스럽게 동일시되며 공간의 표준 스칼라 곱을 나릅니다).예를 들어 모든 n구를 포함한 많은 친숙한 곡선과 표면은 유클리드 공간의 하위 공간으로 지정되고 그 공간에 포함된 메트릭을 상속합니다.

핀러 다양체

핀슬러 다양체는 거리의 정의를 허용하지만 각도의 개념을 필요로 하지는 않습니다. 각 접선 공간에 점마다 매끄럽게 달라지는 방식으로 Δ${\displaystyle \cdot$인 법선이 장착된 해석 다양체입니다.이 표준은 곡선의 길이를 정의하는 메트릭으로 확장할 수 있지만 일반적으로 내부 곱을 정의하는 데 사용할 수는 없습니다.

임의의 리만 다양체는 핀슬러 다양체입니다.

거짓말군

소푸스 리의 이름을 딴 리 군은 군의 구조를 운반하는 미분 가능한 다양체로 군의 연산은 매끄러운 지도에 의해 정의됩니다.

벡터 덧셈의 그룹 연산이 있는 유클리드 벡터 공간은 비콤팩트 리 군의 한 예입니다.콤팩트한 Li 그룹의 간단한 예는 원입니다. 그룹 연산은 단순히 회전입니다.U ⁡ (${\displaystyle 1)}$ ${\displaystyle \operator$name {$U}$ ($1$로 $알려진$ 이 그룹은 또한 곱셈을 그룹 연산으로 하는 모듈러스 1의 복소수 그룹으로 나타낼 수 있습니다.

Lie 그룹의 다른 예로는 일반 선형 그룹의 모든 부분군인 특수 행렬 그룹, 0이 아닌 행렬식을 갖는${\displaystyle }$n × ${\displaystyle n}$ ${\displaystyle$ n$\times$ n$}$개$$ $행렬$의 그룹이 있습니다.행렬 항목이 실수인 경우 ${\displaystyle {2\mathrm{}}^{}}${\$displaystyle$ n$^{2}}$ -차원$$ 단절 다양체가 $됩니다{\displaystyle {}^{}}$.구와 초구의 대칭군인 직교군은 n${\displaystyle (n}$- ${\displaystyle 1)}$ / ${\displaystyle 2\mathrm{}}${\$displaystyle$ n$(n-1)/2}$차원$$ $다양체$이며, $여기$서${\displaystyle }$n - ${\displaystyle 1}${\$displaystyle n-1}$은 구의 차원입니다.추가적인 예는 Lie 그룹의 표에서 찾을 수 있습니다.

기타 유형의 매니폴드

• 복소다양체는 차트가 ${\displaystyle {}^{}}$ ${\$의 값을 취하고 중첩에서 전이 함수가 동형인 다양체입니다.이 다양체들은 복잡한 기하학에서 연구의 기본 대상입니다.일차원 다양체를 리만 표면이라고 합니다.$n개$의 {\$displaystyle$ n$}$차원$$ 복소 $다양체$는 실제 미분 가능한 다양체로서 $차원{\displaystyle \mathrm{}}$ $2n$ {\$displaystyle$ 2n$$$}$을 갖습니다.
• CR 다양체는 ${\displaystyle {}^{}}$ ${\$의 도메인 경계를 모델링한 다양체입니다.
• 무한 차원 다양체': 무한 차원을 허용하기 위해 바나흐 공간과 국소적으로 동형인 바나흐 다양체를 고려할 수 있습니다.마찬가지로, 프레셰 다양체는 프레셰 공간과 국소적으로 동형입니다.
• 심플렉틱 다양체는 고전역학에서 위상공간을 나타내기 위해 사용되는 다양체의 한 종류입니다.그들은 포아송 괄호를 정의하는 2-형태를 가지고 있습니다.접촉 매니폴드는 밀접하게 관련된 유형입니다.
• 조합 다양체는 다양체의 이산화인 다양체의 한 종류입니다.이것은 보통 단순한 복합체에 의해 만들어진 부분적인 선형 다양체를 의미합니다.
• 디지털 다양체는 디지털 공간에서 정의되는 조합 다양체의 특별한 종류입니다.디지털 토폴로지 참조.

분류 및 불변량

다양체의 다른 개념들은 분류와 불변의 다른 개념들을 가지고 있습니다. 이 절에서 우리는 매끄러운 닫힌 다양체에 초점을 것입니다.

매끄러운 닫힌 다양체의 분류는 원칙적으로 4차원을 제외하고 잘 이해됩니다. 낮은 차원(2, 3)에서는 균일화 정리와 푸앵카레 추측의 해를 통해 기하학적이고, 높은 차원(5 이상)에서는 수술 이론을 통해 대수적입니다.이것은 원칙적으로 분류입니다. 두 매끄러운 다양체가 미분동형인지에 대한 일반적인 질문은 일반적으로 계산할 수 없습니다.또한 특정 계산은 여전히 어렵고, 공개된 질문도 많습니다.

방향성이 있는 표면은 시각화할 수 있으며, 그들의 차분법 클래스는 속별로 열거됩니다.두 개의 배향 가능한 표면이 주어지면 각각의 속을 계산하고 비교함으로써 그들이 미분동형인지 여부를 결정할 수 있습니다. 속이 동일한 경우에만 미분동형이므로 속은 완전한 불변량 집합을 형성합니다.

이것은 고차원에서 훨씬 더 어렵습니다. 고차원 다양체는 (시각적 직관이 이해하는 데 유용하지만) 직접 시각화할 수도 없고, 그들의 차동형 클래스를 열거할 수도 없으며, 일반적으로 고차원 다양체에 대한 두 가지 다른 설명이 동일한 객체를 참조하는지 결정할 수도 없습니다.

그러나 두 다양체가 서로 구별되는 고유 특성이 있으면 서로 다른지 여부를 판단할 수 있습니다.그러한 기준은 일반적으로 불변량이라고 불리는데, 그 이유는 그것들이 일부 표현의 관점에서 정의될 수 있지만(삼각형의 관점에서 속과 같이), 그것들은 특정 다양체의 모든 가능한 설명에 대해 동일하기 때문입니다: 그것들은 다른 설명 아래에서 불변합니다.

순진하게도, 모든 다양체를 동형화까지 확정적으로 분류하는 불변의 기준의 무기고를 개발하기를 바랄 수 있습니다.안타깝게도 차원 4 이상의 다양체의 경우 두 다양체가 동형인지 여부를 결정할 수 있는 프로그램이 존재하지 않는 것으로 알려져 있습니다.

매끄러운 다양체는 점 집합 위상, 고전 대수 위상 및 기하 위상에서 오는 풍부한 불변량 집합을 가지고 있습니다.표면에 대해 보이는 가장 친숙한 불변량은 방향성(정상 불변량, 호몰로지에 의해 감지되기도 함)과 속(호몰로지 불변량)입니다.

매끄러운 닫힌 다양체에는 국소 불변량(차원 이외)이 없지만 기하학적 다양체에는 국소 불변량, 특히 리만 다양체의 곡률과 아핀 연결이 장착된 다양체의 비틀림이 있습니다.국소 불변량과 국소 불변량이 없는 것의 이러한 구분은 기하학과 위상을 구분하는 일반적인 방법입니다.매끄러운 닫힌 다양체의 모든 불변량은 따라서 전역적입니다.

대수적 위상학은 여러 중요한 전역 불변 특성의 원천입니다.일부 핵심 기준에는 단순히 연결된 속성과 방향성이 포함됩니다(아래 참조).실제로 다양체의 불변 특성을 연구하기 위해 호몰로지와 호모토피 이론과 특성 클래스 이론과 같은 수학의 여러 분야가 설립되었습니다.

표면

방향성

2차원 이상에서, 단순하지만 중요한 불변 기준은 다양체가 의미 있는 방향을 인정하느냐의 문제입니다.${\displaystyle {}^{}}$가$Rn {\displaystyle \mathbb {R} ^{$n$\}\}$에 매핑되는 위상 다양체를 생각해 보십시오. ${\displaystyle {}^{}}${\$displaystyle \mathbb {R}$^{$n$의 순서 기반이 주어졌을 때, 차트는 다양체의 조각 자체가 3차원에서 오른손 또는 왼손으로 볼 수 있는 순서 감각을 갖게 합니다.중첩된 차트는 순서도와 일치할 필요가 없으며, 이는 다양체에 중요한 자유를 줍니다.구와 같은 일부 다양체의 경우, 겹치는 영역이 "손잡이"와 일치하도록 차트를 선택할 수 있습니다.다른 사람들에게는 불가능한 일입니다.후자의 가능성은 간과하기 쉽습니다. 3차원 공간에 내장된(자기 교차 없이) 닫힌 표면은 방향을 잡을 수 있기 때문입니다.

방향을 잡을 수 없는 다양체의 몇 가지 예시적인 예로는 (1) 경계가 있는 다양체인 뫼비우스 띠, (2) 3-공간 표현에서 스스로 교차해야 하는 클라인 병, (3) 기하학에서 자연적으로 발생하는 실제 투영 평면 등이 있습니다.

뫼비우스 띠

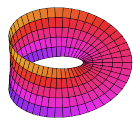
무한한 원기둥이 수직으로 서 있는 것부터 시작합니다. 경계가 없는 다양체입니다.높은 곳과 낮은 곳을 가로질러 잘라내어 두 개의 원형 경계와 그 사이의 원통형 띠를 만듭니다.이것은 경계가 있는 방향성 있는 다양체이며, 그 위에서 "수술"을 수행할 것입니다.스트립을 잘라내어 직사각형이 되도록 하되, 절단된 끝 부분을 잡고 있어야 합니다.한쪽 끝을 180° 비틀어 안쪽 표면이 바깥쪽을 향하도록 한 후 끝을 다시 매끄럽게 접착합니다.이로 인해 영구적인 반트위스트가 있는 스트립(Möbius strip)이 생성됩니다.그 경계는 더 이상 원의 쌍이 아니라 (위상적으로) 하나의 원입니다; 그리고 한 때 "안쪽"이었던 것이 그 "밖"과 합쳐져서, 지금은 한 면만 가지고 있습니다.아래의 클라인 보틀과 유사하게 이 2차원 표면은 2차원으로 교차해야 하지만 3차원 이상으로 쉽게 구성할 수 있습니다.

클라인병

두 개의 뫼비우스 스트립을 사용합니다. 각 스트립에는 경계로 하나의 루프가 있습니다.고리를 원 모양으로 곧게 펴서, 스트립이 십자 모양으로 변형되게 합니다.원들을 서로 붙이면 경계가 없는 닫힌 다양체인 클라인 병이 생성됩니다.표면을 닫는 것은 방향성의 부족을 개선하는 데 아무런 도움이 되지 않으며, 단지 경계를 제거할 뿐입니다.따라서 클라인 병은 내부와 외부의 구분이 없는 닫힌 표면입니다.3차원 공간에서 클라인 병의 표면은 그 자체를 통과해야만 합니다.자체 교차가 아닌 클라인 병을 만들기 위해서는 4차원 이상의 공간이 필요합니다.

실수투영면

원점을 중심으로 하는 구부터 시작합니다.원점을 통과하는 모든 선은 대극이라고 불리는 두 개의 반대 지점에서 구를 관통합니다.물리적으로 그렇게 할 수 있는 방법은 없지만, (할당량 공간을 고려하여) 각 반음극 쌍을 하나의 점으로 수학적으로 병합하는 것이 가능합니다.이렇게 만들어진 닫힌 표면은 실제 투영면이지만 방향을 잡을 수 없는 또 다른 표면입니다.이 경로는 동일한 설명과 구성을 여러 개 가지고 있지만, 이 경로는 이름을 설명합니다: 원점 프로젝트를 통해 주어진 선 상의 모든 점이 이 "평면"의 동일한 "점"으로 이동합니다.

속과 오일러 특성

2차원 다양체의 경우 핵심 불변 특성은 표면에 존재하는 "핸들의 수" 또는 속입니다.토러스는 손잡이가 하나 있는 구이고, 이중 토러스는 손잡이가 두 개 있는 구 등입니다.실제로, 속과 방향성에 기초하여 콤팩트한 2차원 다양체를 완전히 특성화하는 것이 가능합니다.고차원 다양체에서 속은 오일러 특성, 더 일반적으로 베티 수와 호몰로지 및 코호몰로지의 개념으로 대체됩니다.

다양체 지도

다양한 종류의 다양체가 있듯이 다양한 종류의 다양체 지도도 있습니다.일반적으로 연속 함수와 매끄러운 함수 외에도 특수한 성질을 가진 지도가 있습니다.기하학적 위상수학에서 기본적인 유형은 매듭 이론이 중심적인 예인 임베딩과 침지, 침수, 피복 공간, 라미네이팅 피복 공간과 같은 일반화입니다.기본적인 결과는 휘트니 임베딩 정리와 휘트니 몰입 정리를 포함합니다.

리만 기하학에서 등각 임베딩, 등각 몰입 및 리만 침수 개념으로 이어지는 리만 메트릭을 보존하기 위한 지도를 요청할 수 있습니다. 기본 결과는 내쉬 임베딩 정리입니다.

스칼라 값 함수

다양체 사이의 지도의 기본적인 예는 다양체 상의 스칼라 값 함수입니다.

아니면

때때로 대수기하학이나 선형대수학과 유추하여 정칙함수 또는 함수라고 불립니다.이것들은 그들 자신의 권리와 근본적인 다양성을 연구하는 데 모두 관심이 있습니다.

기하학적 위상수학에서 가장 일반적으로 연구되는 것은 모스 함수이며, 핸들 바디 분해를 산출하는 반면, 수학적 분석에서는 종종 편미분 방정식의 해를 연구하는데, 이 중 중요한 예는 조화 분석이며, 조화 함수를 연구하는 라플라스 연산자의 커널입니다.이것은 구면 조화와 같은 기능과 드럼의 모양과 아티야-싱어 지수 정리의 일부 증명을 듣는 것과 같은 다양체를 연구하는 커널 방법을 가열하는 것으로 이어집니다.

다양체의 일반화

무한 차원 다양체

다양체의 정의는 유한 차원성의 요구 사항을 삭제함으로써 일반화될 수 있습니다.따라서 무한 차원 다양체는 실제 위의 위상 벡터 공간과 국소적으로 동형인 위상 공간입니다.이는 점 집합 공리를 생략하여 더 높은 기수와 비 하우스도르프 다양체를 허용합니다. 그리고 유한 차원을 생략하여 힐베르트 다양체를 힐베르트 공간에서, 바나흐 다양체를 바나흐 공간에서, 프레셰 다양체를 프레셰 공간에서 모델링할 수 있습니다.일반적으로 하나는 하나 또는 다른 조건을 완화합니다. 점 집합 공리를 가진 다양체는 일반 토폴로지에서 연구되고, 무한 차원 다양체는 기능 분석에서 연구됩니다.

오비폴드

오비폴드는 위상수학에서 특정한 종류의 "특이점"을 허용하는 다양체의 일반화입니다.대략, 다양한 유한 그룹의 작용에 의해 국소적으로 어떤 단순한 공간(예: 유클리드 공간)의 몫처럼 보이는 공간입니다.특이점은 그룹 행동의 고정된 점에 해당하며, 행동은 특정한 의미에서 호환되어야 합니다.

대수적 다양성과 체계

실수 또는 복소수 위의 비단수 대수적 변이는 다양체입니다.하나는 첫 번째로 특이점을 허용함으로써, 두 번째로 다른 필드를 허용함으로써, 그리고 세 번째로 다양체의 패치 구조를 모방함으로써 이것을 일반화합니다: 다양체가 유클리드 공간의 열린 부분 집합으로부터 함께 접착되는 것처럼, 대수적 다양체는 아핀 대수적 다양체로부터 함께 접착됩니다.대수적으로 닫힌 필드 위에 0개의 다항식 집합인.체계들도 마찬가지로 대수적 다양성의 일반화인 아핀 체계들과 함께 붙어 있습니다.두 가지 모두 다 다양체와 관련이 있지만, 선형 구조 대신에 축을 사용하여 대수적으로 구성됩니다.

특이점 때문에, 다양체는 일반적으로 다양체가 아니지만, 언어학적으로는 프랑스의 다양체, 독일의 Mannigfaltigkeit, 영어의 다양체는 대부분 동의어입니다.프랑스어에서 대수적 다양성은 un variété algébrique (대수적 다양성), 매끄러운 다양체는 un variété differentielle (미분 다양성)이라고 불립니다.

성층 공간

"층화된 공간"은 각 지층이 다양한 형태로, 지층이 정해진 방식(공식적으로는 닫힌 부분집합에 의한 여과)으로 결합되어 조각("지층")으로 나눌 수 있는 공간입니다.다양한 기술적 정의가 있는데, 특히 매끄러운 다양체를 위한 휘트니 층화 공간(휘트니 조건 참조)과 위상 다양체를 위한 위상적 층화 공간이 있습니다.기본적인 예로는 경계가 있는 매니폴드(위 차원 매니폴드 및 코드 차원 1 경계)와 모서리가 있는 매니폴드(위 차원 매니폴드, 코드 차원 1 경계, 코드 차원 2 모서리)가 있습니다.휘트니 계층화 공간은 대수적 다양성, 분석적 다양성, 반대수적 집합 및 하위 분석 집합을 포함하는 넓은 계층의 공간입니다.

CW복합체

CW 콤플렉스는 차원이 다른 디스크들을 서로 붙여서 형성된 위상 공간입니다.일반적으로 결과 공간은 단수이므로 다양체가 아닙니다.그러나 이들은 대수적 위상, 특히 호모토피 이론에서 중심 관심사입니다.

상동성 다양체

호몰로지 다양체는 호몰로지 이론의 관점에서 다양체처럼 행동하는 공간입니다.이것들이 모두 다 다양체는 아니지만, (고차원적으로) 다양체와 유사하게 수술 이론에 의해 분석될 수 있으며, 다양체가 되지 못하는 것은 수술 ^[8]이론에서처럼 국소적인 장애입니다.

차분공간

M ${\displaystyle$ M$}$을(를) 비어 있지 않은 집합이라고 합니다.M ${\displaystyle$ M$}$의 일부 실제 함수 패밀리가 선택되었다고 가정합니다.C ⊆ ${\displaystyle {}^{}}$ ${\displaystyle$ C$\subseteq \mathbb {R}$^{$M$로 표시합니다. 점별 덧셈과 곱셈에 대한 대수입니다.M ${\displaystyle$ M$}$이(가$)$ C {\$displaystyle$ C$\}$에 의해 유도된 위상을 갖추었다고 $하자{\displaystyle }$. 또한 다음 조건들이 성립한다고 가정하자.첫째: 모든 H ∈ C ∞ ( R n ) {\displaystyle H\in C^{\infty }\left(\mathbb {R}^{n}\right)}에 대하여, n ∈ N {\displaystyle n\in \mathbb {N}}, 및 임의의 f 1, …, f n ∈ C {\displaystyle f_{1},\dots,f_{n}\in C}에 대하여, 조성 H ∘ (f 1, …, f n ) ∈ C {\displaystyle H\left(f_{1},\dots,f_{n}\right)\in C}. 둘째: 모든 함수, wM ${\displaystyle$ M$}$의 모든 점에서 C$${\$displaystyle$ C$\}$의 일부 함수와 국소적으로 일치하며, 또한 C$${\$displaystyle$ C$\}$에 속합니다. 위 조건이 성립하는${\displaystyle }$쌍 (${\displaystyle M,C}$)$${\$displaystyle (M, C)}$을 시코르스키 미분 ^[9]공간이라고 합니다.

참고 항목

• 지오데식 – 곡면 또는 리만 다양체 위의 직선 경로
• 방향성 통계 – 통계의 하위 분야 위키데이터 설명을 폴백(fallback)으로 표시하는 페이지:
• 다양체 목록
• 다양체 타임라인 – 수학 타임라인
• 일반상대성이론의 수학 – 일반상대성이론에서 사용되는 수학적 구조와 기술

차원별

• 3-매니폴드 – 수학적 공간
• 4-매니폴드 – 수학적 공간
• 5-매니폴드 – 치수 5의 매니폴드
• 다양한 매핑 – 매우 가벼운 완성도 조건을 만족하는 국소 볼록 벡터 공간 위키데이터 설명을 폴백으로 표시하는 페이지

메모들

참고문헌

• 프리드먼, 마이클 H. 및 퀸, 프랭크 (1990) 4-매니폴드의 위상프린스턴 대학 출판부.ISBN 0-691-08577-3.
• Guillemin, Victor and Pollack, Alan (1974) 미분 위상학프렌티스 홀.ISBN 0-13-212605-2.Milnor에게 영감을 받은 고급 학부/1학년 졸업 텍스트.
• 헴펠, 존 (1976) 3-매니폴드.프린스턴 대학 출판부.ISBN 0-8218-3695-1.
• Hirsch, Morris, (1997) 미분 위상학.스프링어 베를라그.ISBN 0-387-90148-5.역사적 통찰력과 훌륭하지만 어려운 문제가 있는 가장 완벽한 설명입니다.주제에 대한 깊은 이해를 원하는 사람들을 위한 표준 참고 자료.
• 커비, 로비온 C.와 시벤만, 로렌스 C. (1977) 위상다양체에 대한 기초 에세이. 평활화, 삼각 분할.프린스턴 대학 출판부.ISBN 0-691-08190-5.위상다양체 범주에 대한 상세한 연구.
• Lee, John M. (2000) 위상다양체 소개.스프링어-베를라그.ISBN 0-387-98759-2.상세하고 종합적인 1학년 졸업 텍스트
• Lee, John M. (2003) 매끄러운 다양체에 대한 소개.스프링어-베를라그.ISBN 0-387-95495-3.상세하고 포괄적인 1학년 대학원 교재; 위상다양체 소개의 속편.
• Massey, William S. (1977) 대수적 위상: 소개.스프링어-베를라그.ISBN 0-387-90271-6.
• Milnor, John (1997) 미분가능 관점에서의 위상프린스턴 대학 출판부.ISBN 0-691-04833-9.미분 토폴로지에 대한 고전적인 간략 소개.
• Munkres, James R. (1991) 다양체에 대한 분석Addison-Wesley (Westview Press 재인쇄) ISBN 0-201-51035-9${\displaystyle {}^{}}$ ${\$의 매니폴드를 처리하는 학부 텍스트입니다.
• 멍크레스, 제임스 R. (2000) 토폴로지.프렌티스 홀.ISBN 0-13-181629-2.
• 뉴워스, L. P., ed. (1975) 매듭, 그룹, 그리고 3-매니폴드. R. H. Fox의 기억을 위한 논문들 프린스턴 대학 출판부.ISBN 978-0-691-08710-0
• 리만, 베른하르트, 게삼멜테 수학자 베르켄드 비센샤프틀러 나클라스, 생디그 재인쇄.ISBN3-253-03059-8.
  • Grundlagen fürine allgemeineer Functionenerer veränderlichen complexen Grose.'매니폴드'(Manifold, Mannigfaltigkeit)가 처음 등장하는 1851년 박사학위 논문.
  • 우베르 다이 가설, 웰더 지오메트리 주 그룬데리겐.1854년 괴팅겐 첫 강의(하빌리츠 스크리프트).
• Spivak, Michael (1965) 다양체에 관한 미적분학: 고급 미적분학의 고전적 정리에 대한 현대적 접근W.A. Benjamin Inc. (애디슨-웨슬리 앤 웨스트뷰 프레스에서 재인쇄).ISBN 0-8053-9021-9.유명한 고급 학부/1학년 졸업 텍스트.
• Spivak, Michael (1999) 미분기하학에 대한 포괄적 소개 (제3판) 출판사 또는 Fly Inc.다양체 이론, 리만 기하학, 고전 미분 기하학 및 1학년과 2학년 졸업생 수준의 수많은 주제에 대한 체계적인 처리를 보여주는 백과사전적인 5권 시리즈.
• Tu, Loring W. (2011). An Introduction to Manifolds (2nd ed.). New York: Springer. ISBN 978-1-4419-7399-3.Tu, Loring W. (2011). An Introduction to Manifolds (2nd ed.). New York: Springer. ISBN 978-1-4419-7399-3.간결한 1학년 졸업문.

외부 링크

• "Manifold", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
• Dimensions-math.org (4차원까지 다양체를 설명하고 시각화한 영화.)
• 본의 막스플랑크 수학연구소의 다양체 지도 프로젝트