적분으로 정의된 특수 기능
적분 에서 타원 적분 은 특정 적분들의 값으로 정의되는 다수의 관련 함수들 중 하나이다. 원래 타원 의 호 길이 를 찾는 문제와 관련하여 생겨났으며, 줄리오 파냐노 와 레온하르트 오일러 (1750년 )c. 에 의해 처음 연구되었다. 현대 수학은 "엘리프틱 적분"을 어떤 형태로든 표현할 수 있는 함수 f
f ( x ) = ∫ c x R ( t , P ( t ) ) d t , {\displaystyle f(x)=\int _{c}^{x}R\left(t, {\sqrt {P(t)}}\,\mathrm {d} t,} 여기서 R 합리적 인 함수로서 P 다항식 이고, c
일반적으로, 이 형식의 통합은 기본적 인 기능 측면에서 표현될 수 없다. 이 일반적인 규칙의 예외는 P 또는 (x ,y ) 에 y 그러나 적절한 환원 공식 으로 모든 타원 적분은 합리적 기능과 세 가지 레전드르 표준형식에 대한 적분(즉, 제1종, 제2종, 제3종의 타원 적분)을 포함하는 형태로 가져올 수 있다.
아래에 주어진 레전드르 양식 외에 타원형 적분들도 칼슨 대칭 형태로 표현 될 수 있다. 타원 적분 이론에 대한 추가적인 통찰력은 슈바르츠-크리스토펠 매핑 연구를 통해 얻을 수 있다. 역사적으로 타원함수 는 타원형 적분들 의 역함수로 발견되었다.
인수 표기법 불완전한 타원형 통합은 두 개의 인수의 함수다; 완전 한 타원형 통합 은 단일 인수의 함수다. 이러한 주장은 다양하지만 동등한 방법으로 표현된다(동일한 타원 적분을 부여한다). 대부분의 텍스트는 다음과 같은 명명 규칙을 사용하여 표준 명명 체계를 준수한다.
하나의 주장을 표현하는 경우:
α 모듈 각도 k sin α 타원 계수 또는 편심률 m 2 sin2 α 파라미터 위의 세 가지 수량은 모두 다른 수량에 의해 완전히 결정된다(비음수임을 감안). 따라서, 그것들은 서로 교환해서 사용할 수 있다.
다른 주장은 마찬가지로 φ 진폭 또는 x u 여기 x = sin = = sn u sn 은 제이콥의 타원함수 중 하나이다.
이러한 수량 중 하나의 값을 지정하면 다른 수량이 결정된다. 너 또한 귀하
cas φ = cn u , 그리고 1 − m 죄를 짓다 2 φ = dn u . {\displaystyle \cos \varphi =\propertname {\textrm {and}\\sin ^{1-m\sin ^{2}\varphi }=\dn} u.} 후자는 델타 진폭이라고 도 하며 Δ(δ ) dn u 때때로 문헌은 보완적 매개변수 , 보완적 계수 또는 보완적 모듈 각도 를 언급하기도 한다. 이러한 사항 은 분기 기간 에 대한 기사에서 더 자세히 정의된다.
첫 번째 종류의 불완전한 타원 적분 첫 번째 종류 F 의 불완전한 타원 적분 은 다음과 같이 정의된다.
F ( φ , k ) = F ( φ ∣ k 2 ) = F ( 죄를 짓다 φ ; k ) = ∫ 0 φ d θ 1 − k 2 죄를 짓다 2 θ . {\displaystyle F(\varphi ,k)= F\왼쪽(\varphi \mid k^{2}\오른쪽)= F(\sin \varphi ;k)=\int _{0}^{\varphi }{\frac {\mathrm {d} \theta }{1-k^{2}\sin ^{2}\theta }}}. } 이것은 적분 삼각형 형식이다. t sin θ x sin φ
F ( x ; k ) = ∫ 0 x d t ( 1 − t 2 ) ( 1 − k 2 t 2 ) . {\displaystyle F(x;k)=\int _{0}^{x}{\frac {d}t}{\sqrt {\\d}t}{\좌(1-t^{2}\우)\좌(1-k^{2}t^{2}\우)}}}}}}}}}}. } 동등하게 진폭과 모듈 각도에 있어 다음과 같은 특징이 있다.
F ( φ ∖ α ) = F ( φ , 죄를 짓다 α ) = ∫ 0 φ d θ 1 − ( 죄를 짓다 θ 죄를 짓다 α ) 2 . {\displaystyle F(\varphi \setminus \alpha )=F(\varphi ,\sin \alpha )=\int _{0}^{0}{0}{\varphi }{\frac {d} \mathrmatrmetrt{1-(\sin \sin \sin \sin \sin \sin \alpha )^{}}). } 이 표기법에서 세로 막대를 구분 기호로 사용하는 것은 이를 따르는 인수가 "모수"(위에서 정의한 바와 같이)임을 나타내는 반면, 백슬래시는 모듈형 각임을 나타낸다. 세미콜론 사용은 세미콜론 앞에 있는 인수가 진폭의 사인임을 의미한다.
F ( φ , 죄를 짓다 α ) = F ( φ ∣ 죄를 짓다 2 α ) = F ( φ ∖ α ) = F ( 죄를 짓다 φ ; 죄를 짓다 α ) . {\displaystyle F(\varphi ,\sin \alpha )=F\left(\varphi \mid \sin ^{2}\alpha \right) =F(\varphi \setminus \alpha )=F(\sin \varphi ;\sin \alpha ) } 이렇게 서로 다른 주장 구분 기호를 혼동할 가능성이 있는 것은 타원형 통합으로 전통적이며 표기법 중 상당수는 아브라모위츠 와 스테건의 참고서에 사용된 것과 그라드쉬틴과 라이지크 의 통합 표에 사용된 것과 호환된다.
x sn(u , k )
F ( x ; k ) = u ; {\displaystyle F(x;k)=u;} 따라서, Jacobian 타원함수 는 타원형 적분과의 교차점이다.
제1종류의 불완전한 타원 적분에는 다음과 같은 추가 정리가 있다.
F [ 아크탄의 ( x ) , k ] + F [ 아크탄의 ( y ) , k ] = F [ 아크탄의 ( x k ′ 2 y 2 + 1 y 2 + 1 ) + 아크탄의 ( y k ′ 2 x 2 + 1 x 2 + 1 ) , k ] F[\arctan(x),k]+ F[\Arctan(y)]k]= F\left[\arctan \left({\frac {x{\sqrt {k'^{2}y^{2}+1}}}{\sqrt {y^{2}+1}}}\right)+\arctan \left({\frac {y{\sqrt {k'^{2}x^{2}+1}}}{\sqrt {x^{2}+1}}}\right),k\right]} 타원형 계수는 다음과 같이 변환할 수 있다.
F [ 아크신 ( x ) , k ] = 2 1 + 1 − k 2 F [ 아크신 [ ( 1 + 1 − k 2 ) x 1 + 1 − k 2 x 2 ] , 1 − 1 − k 2 1 + 1 − k 2 ] {\displaystyle F[\arcsin(x),k]={\frac {2}{1+{\sqrt {1-k^{2}}}}}F\left[\arcsin \left[{\frac {(1+{\sqrt {1-k^{2}}})x}{1+{\sqrt {1-k^{2}x^{2}}}}}\right],{\frac {1-{\sqrt {1-k^{2}}}}{1+{\sqrt {1-k^{2}}}}}\right]} 공칭 변형 문헌에 채택된 타원형 적분 표기법에는 여전히 다른 관습이 있다. 서로 교환된 인수인 F (k , 표기법은 흔히 접하게 되는데, 두 번째 종류의 적분인 경우 비슷하게 (k ,cs ) 도 접하게 된다. 아브라모위츠와 스테건 은 두 번째와 세 번째 종류의 통합에 대한 definition 의 정의에서 첫 번째 종류의 통합인 F (F , k , 이 주장이 뒤따르지 않는 한, 즉 E F ,k ) 의2 E(E 2 ). 더욱이 이들의 완전한 통합은 변수 k k 2 K (k 변수 k(k 2 ). 그리고 Gradshteyn과 Ryzhik 에 의해 정의된 제3종류의 적분인 π(φ ,n ,k )은 진폭 φ 을 "성격적" n 이 아닌 우선으로 한다.
따라서 다양한 평판이 좋은 참조와 소프트웨어 패키지는 타원 함수의 정의에서 서로 다른 규약을 사용하기 때문에 이러한 함수를 사용할 때는 표기법에 주의해야 한다. 예를 들어, 일부 참조와 울프램 의 매스매티카 소프트웨어와 울프램 알파 는 타원적 계수 k 대신 m
K ( m ) = ∫ 0 π 2 d θ 1 − m 죄를 짓다 2 θ {\displaystyle K(m)=\int _{0}^{\tfrac {\pi }{2}}:{\frac {\d}\mathrm {d}\theta }{1-m\sin ^{2}}}}}}}}}}} 두 번째 종류의 불완전한 타원 적분 삼각형 형태의 두 번째 종류 E 불완전한 타원 적분은
E ( φ , k ) = E ( φ k 2 ) = E ( 죄를 짓다 φ ; k ) = ∫ 0 φ 1 − k 2 죄를 짓다 2 θ d θ . {\displaystyle E(\varphi ,k)= E\왼쪽(\varphi \, \,k^{2}\오른쪽)= E(\sin \varphi ;k)=\int _{0}^{\varphi }{1-k^{2}\sin ^{2}\}\mathrm {d}\theta .} 대체 t sin θ x sin φ
E ( x ; k ) = ∫ 0 x 1 − k 2 t 2 1 − t 2 d t . {\displaystyle E(x;k)=\int _{0}^{x}{\frac {\sqrt{1-k^{2}t^{2}}:{\sqrt{1-t^{2}}:\,\mathrm{d} t.} 진폭과 모듈 각도에서 동등하게:
E ( φ ∖ α ) = E ( φ , 죄를 짓다 α ) = ∫ 0 φ 1 − ( 죄를 짓다 θ 죄를 짓다 α ) 2 d θ . {\displaystyle E(\varphi \setminus \alpha )=E(\varphi ,\sin \alpha )=\int _{0}^{0}{1-\varphi }{\sqrtea \sinalpha \right)^{2},\mathrmatrmatmetrmeta.} 자코비 타원함수 와의 관계에는 다음이 포함된다.
E ( 코를 풀다 ( u ; k ) ; k ) = ∫ 0 u dn 2 ( w ; k ) d w = u − k 2 ∫ 0 u 코를 풀다 2 ( w ; k ) d w = ( 1 − k 2 ) u + k 2 ∫ 0 u cn 2 ( w ; k ) d w . {\displaystyle E{\bigl (}\operatorname {sn} (u;k);k{\bigr )}=\int _{0}^{u}\operatorname {dn} ^{2}(w;k)\,\mathrm {d} w=u-k^{2}\int _{0}^{u}\operatorname {sn} ^{2}(w;k)\,\mathrm {d} w=\left(1-k^{2}\right)u+k^{2}\int _{0}^{u}\operatorname {cn} ^{2}(w;k)\,\mathrm {d} w.} 적도 에서 위도 φ 자오선호 길이는 E
m ( φ ) = a ( E ( φ , e ) + d 2 d φ 2 E ( φ , e ) ) , {\displaystyle m(\varphi )=a\left(E)(\varphi ,e)+{\frac {\mathrm {d}^{2}}:{varphi ^{2}}:E(\varphi ,e)\right),}} 여기서 a 반장축이고 , e 편심 이다.
제2종류의 불완전한 타원 적분에는 다음과 같은 추가 정리가 있다.
E [ 아크탄의 ( x ) , k ] + E [ 아크탄의 ( y ) , k ] = E [ 아크탄의 ( x k ′ 2 y 2 + 1 y 2 + 1 ) + 아크탄의 ( y k ′ 2 x 2 + 1 x 2 + 1 ) , k ] + k 2 x y k ′ 2 x 2 y 2 + x 2 + y 2 + 1 ( x k ′ 2 y 2 + 1 y 2 + 1 + y k ′ 2 x 2 + 1 x 2 + 1 ) [\displaystyle E[\arctan(x),k]+ E[\Arctan(y)]k]= E\left[\arctan \left({\frac {x{\sqrt {k'^{2}y^{2}+1}}}{\sqrt {y^{2}+1}}}\right)+\arctan \left({\frac {y{\sqrt {k'^{2}x^{2}+1}}}{\sqrt {x^{2}+1}}}\right),k\right]+{\frac {k^{2}xy}{k'^{2}x^{2}y^{2}+x^{2}+y^{2}+1}}\left({\frac {x{\sqrt {k'^{2}y^{2}+1}}}{\sqrt {y^{2}+1}}}+{\frac {y{\sqrt {k'^{2}x^{2}+1}}}{\sqrt {x^{2}+1}}}\right)} 타원형 계수는 다음과 같이 변환할 수 있다.
E [ 아크신 ( x ) , k ] = ( 1 + 1 − k 2 ) E [ 아크신 [ ( 1 + 1 − k 2 ) x 1 + 1 − k 2 x 2 ] , 1 − 1 − k 2 1 + 1 − k 2 ] − 1 − k 2 F [ 아크신 ( x ) , k ] + k 2 x 1 − x 2 1 + 1 − k 2 x 2 {\displaystyle E[\arcsin(x),k]=(1+{\sqrt{1-k^{2}} E\left[\arcsin \left[{\frac {(1+{\sqrt {1-k^{2}}})x}{1+{\sqrt {1-k^{2}x^{2}}}}}\right],{\frac {1-{\sqrt {1-k^{2}}}}{1+{\sqrt {1-k^{2}}}}}\right]-{\sqrt {1-k^{2}}}F[\arcsin(x),k]+{\frac {k^{2}x{\sqrt {1-x^{2}}}}{1+{\sqrt {1-k^{2}x^{2}}}}}} 3종류의 불완전한 타원 적분 제3종 π 의 불완전한 타원 적분은
Π ( n ; φ ∖ α ) = ∫ 0 φ 1 1 − n 죄를 짓다 2 θ d θ 1 − ( 죄를 짓다 θ 죄를 짓다 α ) 2 {\displaystyle \Pi (n;\varphi \setminus \alpha )=\int _{0}^{\varphi }{\frac {1}{1-n\sin ^{2}\theta }}{\frac {\mathrm {d} \theta }{\sqrt {1-\left(\sin \theta \sin \alpha \right)^{2}}}}} 또는
Π ( n ; φ m ) = ∫ 0 죄를 짓다 φ 1 1 − n t 2 d t ( 1 − m t 2 ) ( 1 − t 2 ) . {\displaystyle \Pi (n;\varphi \, \m)=\int _{0}^{0}{0}{\prac {1}{1-nt^{2}}:{\frac {d} t}{\matrixmatrm {d}{d}}{{{nt^}\오른쪽}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} } 숫자 특성 이라고 불리며, 다른 주장과 독립적으로 어떤 값도 떠맡을 수 있다. 참고지만 가치를 Π(1;.mw-parser-output .sfrac{white-space:nowrap}.mw-parser-output.sfrac.tion,.mw-parser-output.sfrac .tion{디스플레이:inline-block, vertical-align:-0.5em, font-size:85%;text-align:센터}.mw-parser-output.sfrac.num,.mw-parser-output.sfrac .den{디스플레이:블록, line-height:1em, 마진:00.1em}.mw-parser-output.sfrac .den{.Border-top:1px 고체}.mw-parser-output .sr-only{국경:0;클립:rect(0,0,0,0), 높이:1px, 마진:-1px, 오버 플로: 숨어 있었다. 패딩:0;위치:절대, 너비:1px}π/2 m), 어떤 m을 무한하다
Jacobian 타원함수와의 관계는
Π ( n ; am ( u ; k ) ; k ) = ∫ 0 u d w 1 − n 코를 풀다 2 ( w ; k ) . {\displaystyle \Pi {\bigl (}n;\\\operatorname {am}(u;k);\k{bigr )}=\int _{0}^{0}{0}^{{0}{{{1-n\,\mathrm {d} ^} ^{2}(w;k)}}). } 적도에서 위도 φ π 의 특수한 경우와 관련이 있다.
m ( φ ) = a ( 1 − e 2 ) Π ( e 2 ; φ e 2 ) . {\displaystyle m(\varphi )=a\왼쪽(1-e^{2}\오른쪽) \Pi \왼쪽(e^{2};\varphi \, \,e^{2}\오른쪽). } 제1종 완전 타원 적분 첫 번째 종류 K (k ) 타원형 적분율은 진폭 // 2 1일 때 '완전하다'고 한다. 따라서 첫 번째 종류 K 완전한 타원 적분 은 다음과 같이 정의될 수 있다.
K ( k ) = ∫ 0 π 2 d θ 1 − k 2 죄를 짓다 2 θ = ∫ 0 1 d t ( 1 − t 2 ) ( 1 − k 2 t 2 ) , {\displaystyle K(k)=\int _{0}^{\tfrac {\pi }{2}}{\frac {\mathrm {d} \theta }{\sqrt {1-k^{2}\sin ^{2}\theta }}}=\int _{0}^{1}{\frac {\mathrm {d} t}{\sqrt {\left(1-t^{2}\right)\left(1-k^{2}t^{2}\right)}}},} 또는 보다 간결하게 제1종류의 불완전한 적분이라는 관점에서.
K ( k ) = F ( π 2 , k ) = F ( π 2 k 2 ) = F ( 1 ; k ) . [\displaystyle K(k)=] F\왼쪽({\tfrac {\pi }{2}},k\오른쪽)= F\왼쪽({\tfrac {\pi }{2}}\, \, \,k^{2}\오른쪽) =F(1;k) } 파워 시리즈 로 표현할 수 있다.
K ( k ) = π 2 ∑ n = 0 ∞ ( ( 2 n ) ! 2 2 n ( n ! ) 2 ) 2 k 2 n = π 2 ∑ n = 0 ∞ ( P 2 n ( 0 ) ) 2 k 2 n , {\displaystyle K(k)={\frac {\pi }{2}}\sum _{n=0}^{\flac {(2n)! }{2^{2n}(n!) ^{2}}}\오른쪽)^{2}k^{2n}={\frac {\pi }}{2}}\sum _{n=0}^{\bigl (}{2n})({\bigr )}^{2}k^{2n}}}}}}}}} 여기서 P n Legendre 다항식 (Legendre polyomials)이며, 이는
K ( k ) = π 2 ( 1 + ( 1 2 ) 2 k 2 + ( 1 ⋅ 3 2 ⋅ 4 ) 2 k 4 + ⋯ + ( ( 2 n − 1 ) ! ! ( 2 n ) ! ! ) 2 k 2 n + ⋯ ) , {\displaystyle K(k)={\frac {\pi }{2}}\left(1+\left({\frac {1}{2}}\right)^{2}k^{2}+\left({\frac {1\cdot 3}{2\cdot 4}}\right)^{2}k^{4}+\cdots +\left({\frac {\left(2n-1\right)!! }}{\왼쪽(2n\오른쪽)!! }}\오른쪽)^{2}k^{2n}+\cdots \오른쪽),} where n !! 이중 요인 을 나타낸다. Gauss 초기하학 함수 의 관점에서, 제1종류의 완전한 타원 적분은 다음과 같이 표현할 수 있다.
K ( k ) = π 2 2 F 1 ( 1 2 , 1 2 ; 1 ; k 2 ) . {\displaystyle K(k)={\tfrac {\pi }{2}}\,{}_{2}F_{1}{1}{1}{1}:{\tfrac {1}{1}2}},{\tfrac {1}{1}{1};k^{2}\오른쪽). } 제1종류의 완전한 타원 적분을 쿼터 기간 이라고 부르기도 한다. 산술-기하 평균의 관점 에서 매우 효율적으로 계산할 수 있다.
K ( k ) = π 2 agm ( 1 , 1 − k 2 ) . {\displaystyle K(k)={\frac {\frac {\pi }{2}}:{{}{\opermname {agm} \left(1,{\sqrt{1-k^{2}}}\오른쪽)}}}}. } 자세한 내용은 칼슨(2010 , 19.8)을 참조하십시오.
따라서 계수는 다음과 같이 변형될 수 있다.
K ( k ) = π 2 agm ( 1 , 1 − k 2 ) = π 2 agm ( 1 / 2 + 1 − k 2 / 2 , 1 − k 2 4 ) = {\displaystyle K(k)={\frac {\pi }{2\operatorname {agm} (1,{\sqrt {1-k^{2}}})}}={\frac {\pi }{2\operatorname {agm} (1/2+{\sqrt {1-k^{2}}}/2,{\sqrt[{4}]{1-k^{2}}})}}=} = π ( 1 + 1 − k 2 ) agm [ 1 , 2 1 − k 2 4 / ( 1 + 1 − k 2 ) ] = 2 1 + 1 − k 2 K ( 1 − 1 − k 2 1 + 1 − k 2 ) {\displaystyle ={\frac {\pi }{(1+{\sqrt {1-k^{2}}})\operatorname {agm} [1,2{\sqrt[{4}]{1-k^{2}}}/(1+{\sqrt {1-k^{2}}})]}}={\frac {2}{1+{\sqrt {1-k^{2}}}}}K\left({\frac {1-{\sqrt {1-k^{2}}}}{1+{\sqrt {1-k^{2}}}}}\right)} 이 식은 모든 n n {\ displaystyle \mathb {N}
K ( k ) = n [ ∑ a = 1 n dn [ 2 a n K ( k ) ; k ] ] − 1 K [ k n ∏ a = 1 n 코를 풀다 [ 2 a − 1 n K ( k ) ; k ] 2 ] {\displaystyle K(k)=n\left[\sum _{a=1}^{n}\operatorname {dn} \left[{\frac {2a}{n}}K(k);k\right]\right]^{-1}K\left[k^{n}\prod _{a=1}^{n}\operatorname {sn} \left[{\frac {2a-1}{n}}K(k);k\right]^{2}\right]} 야코비 세타 함수와의 관계 자코비의 세타 함수 와의 관계는 다음과 같다.
K ( k ) = π 2 θ 3 2 ( q ) , {\displaystyle K(k)={\frac {\pi }{2}}\{3}^{2}(q),} nome q
q ( k ) = 생략하다 ( − π K ( 1 − k 2 ) K ( k ) ) . {\displaystyle q(k)=\exp \left(-\pi {\frac {K\left({1-k^{2}}\오른쪽)}{K(k)}}\오른쪽). } 점근식 K ( k ) ≈ π 2 + π 8 k 2 1 − k 2 − π 16 k 4 1 − k 2 {\displaystyle K\left(k\오른쪽)\cHBFF{}{2}}+{\frac {\pi }{8}{8}}{1-k^{2}}-{1-k^{2}}-{\frac {\pi }{16}}{1-k^{4}}}}}}{1-k^{2}}:}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} 이 1 2 3× 10 보다−4 나은 상대 정밀도를 가진다. k 1 2 [citation needed
미분방정식 제1종 타원 적분의 미분 방정식은
d d k ( k ( 1 − k 2 ) d K ( k ) d k ) = k K ( k ) {\displaystyle {\frac {\mathrm {d}{d}}{\mathrm {d}k}\왼쪽(1-k^{2}\오른쪽){\frac {\mathrm {d}{d}k}\right)=K(k)} 이 방정식의 두 번째 해법은 K(1 k 2 {\ displaystyle K\left({\sqrt{1-k^{2}}:}\오른쪽) . 이 용액은 관계를 만족한다.
d d k K ( k ) = E ( k ) k ( 1 − k 2 ) − K ( k ) k . {\displaystyle {\frac {\mathrm {d}{\mathrm {d}k(k)={\frac {E(k)}{k\왼쪽(1-k^{2}\오른쪽)}}}-{\frac {K(k)}{k}}}. } 연속분수 지속적인 분수 확장은 다음과 같다.[1]
K ( k ) 2 π = − 1 4 + ∑ n = 0 ∞ q n 1 + q 2 n = − 1 4 + 1 1 − q + ( 1 − q ) 2 1 − q 3 + q ( 1 − q 2 ) 2 1 − q 5 + q 2 ( 1 − q 3 ) 2 1 − q 7 + q 3 ( 1 − q 4 ) 2 1 − q 9 + … , {\displaystyle {\frac {K(k)}{2\pi }}=-{\frac {1}{4}}+\sum _{n=0}^{\infty }{\frac {q^{n}}{1+q^{2n}}}=-{\frac {1}{4}}+{\frac {1}{1-q+}}{\frac {(1-q)^{2}}{1-q^{3}+}}{\frac {q(1-q^{2})^{2}}{1-q^{5}+}}{\frac {q^{2}(1-q^{3})^{2}}{1-q^{7}+}}{\frac {q^{3}(1-q^{4})^{2}}{1-q^{9}+}}\ldots ,} 여기서 nome 은 q q (k .
두 번째 종류의 완전한 타원 적분 두 번째 종류 E( k {\displaystyle E(k)} 두 번째 종류 E 완전한 타원 적분 은 다음과 같이 정의된다.
E ( k ) = ∫ 0 π 2 1 − k 2 죄를 짓다 2 θ d θ = ∫ 0 1 1 − k 2 t 2 1 − t 2 d t , {\displaystyle E(k)=\int _{0}^{\tfrac {\pi }{2}}{\sqrt {1-k^{2}\sin ^{2}\theta }}\,\mathrm {d} \theta =\int _{0}^{1}{\frac {\sqrt {1-k^{2}t^{2}}}{\sqrt {1-t^{2}}}}\,\mathrm {d} t,} 또는 보다 콤팩트하게 제2종 E (제2종 ,k )
E ( k ) = E ( π 2 , k ) = E ( 1 ; k ) . [\displaystyle E(k)= E\왼쪽({\tfrac {\pi }{2}},k\오른쪽)=E(1;k) } 반주축 a b e √1 b 2 /a 2 있는 타원의 경우, 두 번째 종류 E (e )a c 원주 c의 1/4과 같다. 즉, 다음과 같다.
c = 4 a E ( e ) . [\displaystyle c=4aE(e)] } 두 번째 종류의 완전한 타원 적분은 파워 시리즈 로[citation needed 표현될 수 있다.
E ( k ) = π 2 ∑ n = 0 ∞ ( ( 2 n ) ! 2 2 n ( n ! ) 2 ) 2 k 2 n 1 − 2 n , {\displaystyle E(k)={\frac {\pi }{2}}\sum _{n=0}^{\flack({\frac {(2n)! }}{2^{2n}\왼쪽(n!\오른쪽)^{2}}\\오른쪽)^{2}{{\frac{k^{2n}},} 에 해당하는
E ( k ) = π 2 ( 1 − ( 1 2 ) 2 k 2 1 − ( 1 ⋅ 3 2 ⋅ 4 ) 2 k 4 3 − ⋯ − ( ( 2 n − 1 ) ! ! ( 2 n ) ! ! ) 2 k 2 n 2 n − 1 − ⋯ ) . {\displaystyle E(k)={\frac {\pi }{2}}\left(1-\left({\frac {1}{2}}\right)^{2}{\frac {k^{2}}{1}}-\left({\frac {1\cdot 3}{2\cdot 4}}\right)^{2}{\frac {k^{4}}{3}}-\cdots -\left({\frac {(2n-1)!! }{{(2n)!! }}}\오른쪽)^{2}{{\frac {k^{2n}{2n:1}}-\cdots \오른쪽). } Gauss 초기하학 함수 의 관점에서, 제2종류의 완전한 타원 적분은 다음과 같이 표현할 수 있다.
E ( k ) = π 2 2 F 1 ( 1 2 , − 1 2 ; 1 ; k 2 ) . {\displaystyle E(k)={\tfrac {}{2}}\,{}_{2}F_{1}{1}{1}{1}{1}{1},-{\tfrac {1}{1}{1},-{\tfrac {1}{1}{1};k^{2}\right). } 계수는 다음과 같이 변형될 수 있다.
E ( k ) = ( 1 + 1 − k 2 ) E ( 1 − 1 − k 2 1 + 1 − k 2 ) − 1 − k 2 K ( k ) {\displaystyle E(k)=(1+{\sqrt{1-k^{2}}} E\left({\frac{1-{\sqrt{1-k^{1-k^{2}}:}}{1+{1-k^{2}}}\오른쪽)-{\sqrt{1-k^{2}}K(k)}} 연산 제1종류의 적분처럼, 제2종류의 완전한 타원 적분은 산술-기하 평균 을 사용하여 매우 효율적으로 계산할 수 있다(Carlson 2010 , 19.8).
Define sequences a n {\displaystyle a_{n}} g n {\displaystyle g_{n}} a 0 = 1 {\displaystyle a_{0}=1} g 0 = 1 − k 2 = k ′ {\displaystyle g_{0}={\sqrt {1-k^{2}}}=k'} a n + 1 = a n + g n 2 {\displaystyle a_{n+1}={\frac {a_{n}+g_{n }{2}}: }}, g 1 n g displaystyle g_{n+1}={\sqrt{a_{n}g_{n}}}}}}}}} 또한 c n n 2 g 2 {\ displaystyle c_{n}={\sqrt{\n}^{n }-g_{n}^{2}\right }}} .
a ∞ = lim n → ∞ a n = lim n → ∞ g n = agm ( 1 , 1 − k 2 ) {\displaystyle a_{\infty }=\lim _{n\to \infty }a_{n}=\lim _{n\to \infty }g_{n}=\operatorname {agm} (1,{\sqrt {1-k^{2}}})} 또한 lim n ∞ c 0 {\displaystyle \lim _{n\to \infit }c_{n}=0} 그러면
E ( k ) = π 2 a ∞ ( 1 − ∑ n = 0 ∞ 2 n − 1 c n 2 ) . {\displaystyle E(k)={\frac {\pi }{2a_{\nflt }}}\좌측(1-\sum _{n=0}^{n=0}^{n-1}c_{n}^{n}^{2}\오른쪽). } 실제로 산술-기하계 평균은 단순히 어느 정도 한계까지 계산될 수 있다. 이 공식은 모든 k ≤ {\displaystyle \leq } . cn 1 a n 1 {\ displaysty c_{n+1}={\frac {c_{n}^{2}}:{4a_{n+ 사용할
파생식 및 미분방정식 d E ( k ) d k = E ( k ) − K ( k ) k {\displaystyle {\frac {\mathrm {d}E(k)}{\mathrm {d}k}={\frac {E(k)-K(k)}{k}}}}}} ( k 2 − 1 ) d d k ( k d E ( k ) d k ) = k E ( k ) {\displaystyle \left(k^{2}-1\right){\frac {d}{\mathrm {d}k}}{\frac {d}E(k){\mathrm {d}k}}}=kE(k)} 이 방정식의 두 번째 해법은 E ((1 k 2 (√1 - k 2 .
3종 완전 타원 적분 여러 displaystyle n} 종류 \( n k {\displaystyle \Pi(n,k)} 제3종 π 의 완전한 타원 적분 은 다음과 같이 정의할 수 있다.
Π ( n , k ) = ∫ 0 π 2 d θ ( 1 − n 죄를 짓다 2 θ ) 1 − k 2 죄를 짓다 2 θ . {\displaystyle \Pi(n,k)=\int _{0}^{\tfrac {\pi }{2}}:{\frac {\d} \theta }{{{{n\sin ^{2}\te \right){\sqrt{1-k^{2}}}}}}}}}}}}. } 때때로 세 번째 종류의 타원 적분은 특성 n
Π ′ ( n , k ) = ∫ 0 π 2 d θ ( 1 + n 죄를 짓다 2 θ ) 1 − k 2 죄를 짓다 2 θ . {\displaystyle \Pi '(n,k)=\int_{0}^{\tfrac {\pi }{2}}:{\frac {\d} \theetta }{{}}{\n\sin }{2}\sqrt{1-k^{2}}}}}}}}}}}. } 제1종과 제2종의 완전한 타원형 적분과 마찬가지로 제3종의 완전한 타원형 적분은 산술-기하 평균을 이용하여 매우 효율적으로 계산할 수 있다(Carlson 2010 , 19.8).
부분파생상품 ∂ Π ( n , k ) ∂ n = 1 2 ( k 2 − n ) ( n − 1 ) ( E ( k ) + 1 n ( k 2 − n ) K ( k ) + 1 n ( n 2 − k 2 ) Π ( n , k ) ) ∂ Π ( n , k ) ∂ k = k n − k 2 ( E ( k ) k 2 − 1 + Π ( n , k ) ) {\displaystyle {\begin{aligned}{\frac {\partial \Pi (n,k)}{\partial n}}&={\frac {1}{2\left(k^{2}-n\right)(n-1)}}\left(E(k)+{\frac {1}{n}}\left(k^{2}-n\right)K(k)+{\frac {1}{n}}\left(n^{2}-k^{2}\right)\Pi (n,k)\right) \\[10px]{\frac {\partial \Pi(n,k)}{\partial k}}{n-k^{2}}:}\좌측({\frac {E(k)}{k^-1}+\Pi(n,k)\end{aigned}}}}}}}}}}}} 기능적 관계 Legendre의 관계 :
K ( k ) E ( 1 − k 2 ) + E ( k ) K ( 1 − k 2 ) − K ( k ) K ( 1 − k 2 ) = π 2 . {\displaystyle K(k)E\left({\sqrt {1-k^{2}}}\right)+E(k)K\left({\sqrt {1-k^{2}}}\right)-K(k)K\left({\sqrt {1-k^{2}}}\right)={\frac {\pi }{2}}. } 참고 항목 참조 ^ 앤 바기스, 엘 글래서.(2015년)" 라마누잔의 지속적 분수에 대한 평가" 렌드 셈 매트 유니브 파도바, 133 페이지 1-10 Abramowitz, Milton ; Stegun, Irene Ann , eds. (1983) [June 1964]. "Chapter 17" . Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables 55 (Ninth reprint with additional corrections of tenth original printing with corrections (December 1972); first ed.). Washington D.C.; New York: United States Department of Commerce, National Bureau of Standards; Dover Publications. p. 587. ISBN 978-0-486-61272-0 LCCN 64-60036 . MR 0167642 . LCCN 65-12253 .Byrd, P. F.; Friedman, M.D. (1971). Handbook of Elliptic Integrals for Engineers and Scientists (2nd ed.). New York: Springer-Verlag. ISBN 0-387-05318-2 Carlson, B. C. (1995). "Numerical Computation of Real or Complex Elliptic Integrals". Numerical Algorithms . 10 (1): 13–26. arXiv :math/9409227 Bibcode :1995NuAlg..10...13C . doi :10.1007/BF02198293 . Carlson, B. C. (2010), "Elliptic integral" , in Olver, Frank W. J. ; Lozier, Daniel M.; Boisvert, Ronald F.; Clark, Charles W. (eds.), NIST Handbook of Mathematical Functions ISBN 978-0-521-19225-5 MR 2723248 Erdélyi, Arthur; Magnus, Wilhelm ; Oberhettinger, Fritz; Tricomi, Francesco G. (1953). Higher transcendental functions. Vol II (PDF) . McGraw-Hill Book Company, Inc., New York-Toronto-London. MR 0058756 . Gradshteyn, Izrail Solomonovich ; Ryzhik, Iosif Moiseevich ; Geronimus, Yuri Veniaminovich ; Tseytlin, Michail Yulyevich ; Jeffrey, Alan (2015) [October 2014]. "8.1.". In Zwillinger, Daniel; Moll, Victor Hugo (eds.). Table of Integrals, Series, and Products Academic Press, Inc. ISBN 978-0-12-384933-5 LCCN 2014010276 .Greenhill, Alfred George (1892). The applications of elliptic functions Hancock, Harris (1910). Lectures on the Theory of Elliptic Functions King, Louis V. (1924). On The Direct Numerical Calculation Of Elliptic Functions And Integrals Press, W. H.; Teukolsky, S. A.; Vetterling, W. T.; Flannery, B. P. (2007), "Section 6.12. Elliptic Integrals and Jacobian Elliptic Functions" , Numerical Recipes: The Art of Scientific Computing (3rd ed.), New York: Cambridge University Press, ISBN 978-0-521-88068-8 외부 링크
위키미디어 커먼즈에는 타원







![{\displaystyle F[\arctan(x),k]+F[\arctan(y),k]=F\left[\arctan \left({\frac {x{\sqrt {k'^{2}y^{2}+1}}}{\sqrt {y^{2}+1}}}\right)+\arctan \left({\frac {y{\sqrt {k'^{2}x^{2}+1}}}{\sqrt {x^{2}+1}}}\right),k\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dee3855e9b2ffc2f73fc5142aaead74e5bcc0238)
![{\displaystyle F[\arcsin(x),k]={\frac {2}{1+{\sqrt {1-k^{2}}}}}F\left[\arcsin \left[{\frac {(1+{\sqrt {1-k^{2}}})x}{1+{\sqrt {1-k^{2}x^{2}}}}}\right],{\frac {1-{\sqrt {1-k^{2}}}}{1+{\sqrt {1-k^{2}}}}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0ca0a87a094baa6bf1f142f99e81514692d2f872)






![{\displaystyle E[\arctan(x),k]+E[\arctan(y),k]=E\left[\arctan \left({\frac {x{\sqrt {k'^{2}y^{2}+1}}}{\sqrt {y^{2}+1}}}\right)+\arctan \left({\frac {y{\sqrt {k'^{2}x^{2}+1}}}{\sqrt {x^{2}+1}}}\right),k\right]+{\frac {k^{2}xy}{k'^{2}x^{2}y^{2}+x^{2}+y^{2}+1}}\left({\frac {x{\sqrt {k'^{2}y^{2}+1}}}{\sqrt {y^{2}+1}}}+{\frac {y{\sqrt {k'^{2}x^{2}+1}}}{\sqrt {x^{2}+1}}}\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/befdcddfc97edc9a6d0fe290118b77c2c509a14a)
![{\displaystyle E[\arcsin(x),k]=(1+{\sqrt {1-k^{2}}})E\left[\arcsin \left[{\frac {(1+{\sqrt {1-k^{2}}})x}{1+{\sqrt {1-k^{2}x^{2}}}}}\right],{\frac {1-{\sqrt {1-k^{2}}}}{1+{\sqrt {1-k^{2}}}}}\right]-{\sqrt {1-k^{2}}}F[\arcsin(x),k]+{\frac {k^{2}x{\sqrt {1-x^{2}}}}{1+{\sqrt {1-k^{2}x^{2}}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e914e94f842827749d5a08fad29969c7d2b55705)











![{\displaystyle K(k)={\frac {\pi }{2\operatorname {agm} (1,{\sqrt {1-k^{2}}})}}={\frac {\pi }{2\operatorname {agm} (1/2+{\sqrt {1-k^{2}}}/2,{\sqrt[{4}]{1-k^{2}}})}}=}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a45040eec194357241ff0f4562b5292bcba1cd83)
![{\displaystyle ={\frac {\pi }{(1+{\sqrt {1-k^{2}}})\operatorname {agm} [1,2{\sqrt[{4}]{1-k^{2}}}/(1+{\sqrt {1-k^{2}}})]}}={\frac {2}{1+{\sqrt {1-k^{2}}}}}K\left({\frac {1-{\sqrt {1-k^{2}}}}{1+{\sqrt {1-k^{2}}}}}\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/769c944f72cd0704d3ce2fb91c41dc92326e5277)

![{\displaystyle K(k)=n\left[\sum _{a=1}^{n}\operatorname {dn} \left[{\frac {2a}{n}}K(k);k\right]\right]^{-1}K\left[k^{n}\prod _{a=1}^{n}\operatorname {sn} \left[{\frac {2a-1}{n}}K(k);k\right]^{2}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0bf6877566831e9d7d844a24f5526cf77c811bc2)





























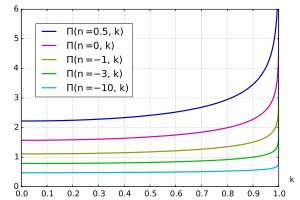
 세 번째
세 번째 

![{\displaystyle {\begin{aligned}{\frac {\partial \Pi (n,k)}{\partial n}}&={\frac {1}{2\left(k^{2}-n\right)(n-1)}}\left(E(k)+{\frac {1}{n}}\left(k^{2}-n\right)K(k)+{\frac {1}{n}}\left(n^{2}-k^{2}\right)\Pi (n,k)\right)\\[10px]{\frac {\partial \Pi (n,k)}{\partial k}}&={\frac {k}{n-k^{2}}}\left({\frac {E(k)}{k^{2}-1}}+\Pi (n,k)\right)\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dff1d0cac8f94db2e3e0b38cef7554432766f458)



