결합 상수

물리학에서 결합 상수 또는 게이지 결합 파라미터(또는 간단히 말하면 결합)는 상호작용에서 가해지는 힘의 강도를 결정하는 숫자입니다.원래 결합 상수는 두 정적인 물체 사이에 작용하는 힘(즉, 정전기 전하와 뉴턴의 중력에 대한 질량)을 물체 사이의 거리 $r^{2}$ r2 $(\$ r $r^{2}$ 2})로 나눈 것과 관련되었다. 따라서 F $F=GMm/r^{2}$ $F=GMm/r^{2}$ / $F=GMm/r^{2}$ 2의G \ $displaystyle$ G $}$ 는 $G$ 다음과 $같다$ . $F=GMm/r^{2}$ (Newton의 중력은 F $F=k_{\text{e}}q_{1}q_{2}/r^{2}$ $/r^{2}},$ 정전기는 F=k $k_{\text{e}}$ 1 q $F=k_{\text{e}}q_{1}q_{2}/r^{2}$ / $F=k_{\text{e}}q_{1}q_{2}/r^{2}$ 2 $({$ F $=k_{\text{e}q_{1}/r^{2})$ 의 $F=k_{\text{e}}q_{1}q_{2}/r^{2}$ k $(\$ $F=k_{\text{e}}q_{1}q_{2}/r^{2}$ ${\text{e}))$ 이다 $k_{\text{e}}$ .이 설명은 현대 물리학에서 정적 물체와 질량 없는 힘 운반체를 가진 선형 이론에서 유효하다.

현대적이고 일반적인 정의에서는 시스템의 $L($ 동등한 ${\mathcal {H}}$ H(\ $displaystyle\mathcal$ {H ${\mathcal {H}}$ 을 사용합니다.일반적으로 상호작용을 기술하는 시스템의 L $(\$ ${\mathcal {H}}$ H $(\displaystyle$ { $H$ 은 $운동부$ T(\ $displaystyle$ T $)$ 와 $T$ $상호작용부$ V(\ $displaystyle$ V $V$ : $=$ V $(\displaystyle$ {L $})$ 로 나눌 수 있다. $ystyle(\mathcal {H}}=T+V}).$ 필드 이론에서 V $(\displaystyle$ V $)$ 는 $V$ 항상 3개 이상의 필드 항을 포함하며, 예를 들어 초기 전자(필드 1)가 전자(필드 3)의 최종 상태를 생성하는 광자(필드 2)와 상호작용했음을 나타냅니다.이와는 대조적으로, 키네틱 $파트$ T(\ $style$ T $)$ 에는 $T$ 항상 두 개의 필드만 포함되어 있어 초기 입자(필드 1)가 이후 상태(필드 2)로 자유롭게 전파되는 것을 나타냅니다.결합 상수는V 부품( $또는$ 서로 다른 여러 필드가 존재하는 경우 상호 작용 부품의 두 섹터 간)에 대한 T $(\$ $displaystyle$ T $)$ $T$ 의 $T$ $V$ 크기를 결정합니다.예를 들어 입자의 전하는 두 개의 전하 전달장과 하나의 광자장과의 상호작용을 특징짓는 결합 상수입니다(따라서 두 개의 화살표와 하나의 파동선이 있는 일반적인 파인만 다이어그램).광자는 전자기력을 매개하기 때문에 이 결합은 전자가 얼마나 강하게 그러한 힘을 느끼는지 결정하며, 그 값은 실험에 의해 고정된다.QED 라그랑지안을 보면 실제로 커플링은 운동 $T={\bar {\psi }}(i\hbar c\gamma ^{\sigma }\partial _{\sigma }-mc^{2})\psi -{1 \over 4\mu _{0}}F_{\mu \nu }F^{\mu \nu }$ T $T={\bar {\psi }}(i\hbar c\gamma ^{\sigma }\partial _{\sigma }-mc^{2})\psi -{1 \over 4\mu _{0}}F_{\mu \nu }F^{\mu \nu }$ ( i $T={\bar {\psi }}(i\hbar c\gamma ^{\sigma }\partial _{\sigma }-mc^{2})\psi -{1 \over 4\mu _{0}}F_{\mu \nu }F^{\mu \nu }$ $T={\bar {\psi }}(i\hbar c\gamma ^{\sigma }\partial _{\sigma }-mc^{2})\psi -{1 \over 4\mu _{0}}F_{\mu \nu }F^{\mu \nu }$ - $T={\bar {\psi }}(i\hbar c\gamma ^{\sigma }\partial _{\sigma }-mc^{2})\psi -{1 \over 4\mu _{0}}F_{\mu \nu }F^{\mu \nu }$ c $T={\bar {\psi }}(i\hbar c\gamma ^{\sigma }\partial _{\sigma }-mc^{2})\psi -{1 \over 4\mu _{0}}F_{\mu \nu }F^{\mu \nu }$ ) $T={\bar {\psi }}(i\hbar c\gamma ^{\sigma }\partial _{\sigma }-mc^{2})\psi -{1 \over 4\mu _{0}}F_{\mu \nu }F^{\mu \nu }$ - $T={\bar {\psi }}(i\hbar c\gamma ^{\sigma }\partial _{\sigma }-mc^{2})\psi -{1 \over 4\mu _{0}}F_{\mu \nu }F^{\mu \nu }$ $T={\bar {\psi }}(i\hbar c\gamma ^{\sigma }\partial _{\sigma }-mc^{2})\psi -{1 \over 4\mu _{0}}F_{\mu \nu }F^{\mu \nu }$ $T={\bar {\psi }}(i\hbar c\gamma ^{\sigma }\partial _{\sigma }-mc^{2})\psi -{1 \over 4\mu _{0}}F_{\mu \nu }F^{\mu \nu }$ $T={\bar {\psi }}(i\hbar c\gamma ^{\sigma }\partial _{\sigma }-mc^{2})\psi -{1 \over 4\mu _{0}}F_{\mu \nu }F^{\mu \nu }$ $T={\bar {\psi }}(i\hbar c\gamma ^{\sigma }\partial _{\sigma }-mc^{2})\psi -{1 \over 4\mu _{0}}F_{\mu \nu }F^{\mu \nu }$ ( \ $displaystyle$ T = $far$ { $psi } μ$ $T={\bar {\psi }}(i\hbar c\gamma ^{\sigma }\partial _{\sigma }-mc^{2})\psi -{1 \over 4\mu _{0}}F_{\mu \nu }F^{\mu \nu }$ } ( \ $har$ )의 비례성을 설정하고 있음을 알 수 있다 $.$ $u}}$ $V=-e{\bar {\psi }}(\hbar c\gamma ^{\sigma }A_{\sigma })\psi$ $V=-e{\bar {\psi }}(\hbar c\gamma ^{\sigma }A_{\sigma })\psi$ 용어 V $V=-e{\bar {\psi }}(\hbar c\gamma ^{\sigma }A_{\sigma })\psi$ - $V=-e{\bar {\psi }}(\hbar c\gamma ^{\sigma }A_{\sigma })\psi$ $V=-e{\bar {\psi }}(\hbar c\gamma ^{\sigma }A_{\sigma })\psi$ （ $V=-e{\bar {\psi }}(\hbar c\gamma ^{\sigma }A_{\sigma })\psi$ c $V=-e{\bar {\psi }}(\hbar c\gamma ^{\sigma }A_{\sigma })\psi$ A $V=-e{\bar {\psi }}(\hbar c\gamma ^{\sigma }A_{\sigma })\psi$ $、$ { \ $bar$ { \ $psi$ } （ \ $displaystyle$ V = - $e {$ \ bar { \ psi } } （ \ $hbar$ c \ $sigma } ）$ $V=-e{\bar {\psi }}(\hbar c\gamma ^{\sigma }A_{\sigma })\psi$

커플링은 역학에서 중요한 역할을 합니다.예를 들어, 다양한 결합 상수의 중요도에 따라 근사 계층을 설정하는 경우가 많습니다.자화된 큰 철 덩어리의 운동에서는 결합 상수의 상대적 크기 때문에 중력보다 자기력이 더 중요할 수 있습니다.그러나 고전역학에서는 보통 힘을 비교함으로써 이러한 결정을 직접 내린다.결합 상수에 의해 수행되는 중심 역할의 또 다른 중요한 예는 그것들이 많은 물리학 분야에서의 주요 계산 방법인 섭동 이론에 기초한 제1원칙 계산을 위한 확장 매개변수라는 것입니다.

미세 구조 상수

결합은 양자장 이론에서 자연적으로 발생한다.상대론적 양자 이론에서 특별한 역할은 차원이 없는 커플링, 즉 순수한 숫자에 의해 이루어집니다.그러한 무차원 상수의 예는 미세 구조 상수이다.

({displaystyle \alpha = specfrac {e^{2}}}{4\pi \varepsilon _{0}\hbar c}})

$여기$ 서 e는 전자의 전하, $\varepsilon _{0}$ 0 $(\$ _ ${0})$ 은 $\varepsilon _{0}$ 자유 공간의 유전율, θ는 환원 플랑크 상수, $c$ 는 빛의 속도이다.이 상수는 전자장에 대한 전하의 결합 강도의 제곱에 비례합니다.

게이지 커플링

비 Abelian 게이지 이론에서 게이지 커플링 파라미터 $displaystyle$ g는 Lagrangian에 다음과 같이 표시됩니다.

{1}{4g^{2}}{\rm {Tr},G_{\mu \nu }G^{\mu \nu}

(여기서 G는 게이지 필드 텐서) 일부 규칙에서.또 다른 널리 사용되는 규약에서는 운동항 계수가 1/4이 되도록 G의 크기를 $g$ 하고 공변 도함수에 g ${\display style$ g $}$ 가 $g$ 나타나도록 한다.이는 다음과 같이 정의된 기본 전하의 무차원 버전과 유사한 것으로 이해해야 한다.

{frac {e} {\varepsilon _{0} \hbar c}} = scarrt {4\pi \alpha }} \ about 0.30282212 \ ~ .

약하고 강한 결합

결합 g를 갖는 양자장 이론에서 g가 1보다 훨씬 작을 경우, 그 이론은 약결합이라고 한다.이 경우, 그것은 섭동 이론이라고 불리는 g의 힘의 확장에 의해 잘 설명된다.결합정수가 1차 이상이면 이 이론은 강하게 결합되어 있다고 한다.후자의 예는 강한 상호작용의 강입자 이론입니다(그래서 처음부터 강입자 이론이라고 부릅니다).이러한 경우 이론을 조사하기 위해 비교란적 방법을 사용할 필요가 있다.

양자장 이론에서, 결합의 차원은 ^[1]이론의 재규격화 특성, 따라서 섭동 이론의 적용 가능성에서 중요한 역할을 한다.QED, QCD 및 Weak Force와 같이 자연 단위 시스템에서 커플링이 무차원인 경우( $c=1$ : c $c=1$ $\hbar =1$ { $displaystyle$ c $=1$ bar $\hbar =1$ $1$ { $displaystyle \hbar$ = 1) 이론은 정규화 가능하며 확장 시리즈의 모든 조건은 유한합니다(재규격화 후).결합이 중력 $[G_{N}]={\text{energy}}^{-2}$ $[G_{N}]={\text{energy}}^{-2}$ - $[G_{N}]={\text{energy}}^{-2}$ 2 $([G_{N$ ] $= energy}^{-2})$ 와 같이 차원적인 경우, 페르미 이론 $[G_{F}]={\text{energy}}^{-2}$ F $[G_{F}]={\text{energy}}^{-2}$ $[G_{F}]={\text{energy}}^{-2}$ - $[G_{F}]={\text{energy}}^{-2}$ 2([G F] $=$ energy - 2([ $G_$ } ] = $energy}^{-2})))$ 또는 강한 섭동 이론의 키랄성 이론 $rgy}}}})$ 의 경우, 이 이론은 통상 정규화할 수 없습니다.급수의 고차 항 대부분이 무한대이기 때문에 결합에서 섭동 확장은 제한 ^[2]^[3]범위 내이긴 하지만 여전히 실현 가능할 수 있다.

주행 커플링

그림 1 가상 입자는 커플링을 정규화한다.

사용된 탐침의 파장 또는 운동량 k를 변화시킴으로써 짧은 시간 또는 거리에서 양자장 이론을 탐사할 수 있다.고주파(즉, 짧은 시간) 프로브를 사용하면 모든 프로세스에 가상 입자가 관여하는 것을 볼 수 있습니다.에너지 보존에 대한 명백한 위반은 불확실성 관계를 조사함으로써 경험적으로 이해할 수 있다.

\displaystyle \Delta E\geq \frac \hbar }{2}

단시간에 위반할 수 있습니다.앞서 말한 언급은 양자장 이론의 일부 공식, 특히 상호작용 그림에서의 표준 양자화에만 적용된다.

다른 공식에서, 같은 사건은 질량 껍질에서 나오는 "가상" 입자에 의해 설명된다.이러한 과정은 커플링을 다시 정규화하고 커플링을 프로빙하는 에너지 스케일 μ에 의존하게 합니다.에너지 척도에 대한 커플링 g(μ)의 의존성을 "커플링의 실행"이라고 합니다.커플링 작동 이론은 재규격화 그룹에 의해 제시되지만, 재규격화 그룹은 물리적 시스템의 스케일 변동을 설명하는 보다 일반적인 개념이라는 점에 유의해야 합니다(자세한 내용은 전문 참조).

커플링 작동 현상학

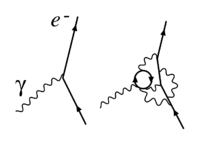
재규격화 그룹은 커플링의 실행을 유도하는 공식적인 방법을 제공하지만, 이러한 실행의 기초가 되는 현상학은 ^[4]직관적으로 이해할 수 있습니다.도입부에서 설명한 바와 같이 커플링 상수는 거리에 따라 작용하는 힘의 크기를 1 $1/r^{2}$ / $1/r^{2}$ 2 $({$ 1/ $r^{2$ 로 $1/r^{2}$ 합니다.1 $1/r^{2}$ 2 $({$ 1/ $r^{2}})$ $1/r^{2}$ 은 $1/r^{2}$ 힘 플럭스의 감소로 패러데이에 의해 처음 설명되었다. 힘을 생성하는 물체 A로부터 r $\style$ r만큼 $r$ $떨어진$ 지점 B에서, 이것은 선 AB에 수직인 기본 표면 S를 통과하는 계자 플럭스에 비례한다.플럭스는 공간 전체에 균일하게 퍼지기 때문에 표면 S를 지탱하는 고체 각도에 따라 감소한다.양자장 이론의 현대적 $1/r^{2}$ 에서 1/ $1/r^{2}$ 2 $(\displaystyle$ 1 $/r^{$ 2})는 $1/r^{2}$ 힘 캐리어의 전파자의 위치 공간 표현에서 유래합니다.일반적으로 전자기 또는 중력 또는 단거리 핵 상호작용에서와 같이 상대적으로 약한 상호작용 물체의 경우 단일 힘 운반체의 교환은 물체 간 상호작용의 좋은 첫 번째 근사치이며, 일반적으로 $1/r^{2}$ 은 $1/r^{2}$ 1/ $1/r^{2}$ 2 $(\$ 1/ $r^{2}})$ 법칙을 $1/r^{2}$ 준수한다.포스 캐리어가 큰 경우 r $\displaystyle$ r $\$ 의존성이 $r$ $r$ 된다는 점에 유의하십시오.상호작용이 더 강하거나(예: 전하 또는 질량이 더 $크거나$ r $\displaystyle$ r $r$ $\displaystyle$ r\ $displaystyle$ r\ $displaystyle$ r\ $r$ displaystyle $r\$ displaystyle r $\$ $displaystyle$ r $}),$ 더 많은 힘 캐리어가 관련되거나 입자 쌍이 생성되면 그림 1을 참조하여 1 $2가$ 분해됩니다 $.$ }의 $1/r^{2}$ 동작 $.$ 고전적인 등가물은 필드 플럭스가 더 이상 우주에서 자유롭게 전파되지 않지만, 예를 들어 추가 가상 입자의 전하 또는 이러한 가상 입자 간의 상호작용에서 스크리닝을 거친다. $1/r^{2}$ 1/ $1/r^{2}$ 과 이 $추가$ r $(displaystyle$ $r$ $)$ 의존성을 $1/r^{2}$ $r$ 분리하는 것이 편리합니다.이 결합은 결합에 포함되며, 결합은 1/r $\displaystyle$ 1/ $r-dependent$ (또는 동등한 μ-dependent)가 $1/r$ $1/r$ .단일력 캐리어 근사치를 넘는 추가 입자는 항상 가상이기 때문에, 즉 일시적인 양자장 변동이므로, 왜 커플링의 실행이 진정한 양자 및 상대론적 현상, 즉 힘의 강도에 대한 고차 파인만 다이어그램의 영향을 이해한다.

가동 커플링은 미시적 양자 효과를 효과적으로 설명하므로, 라그랑지안 또는 해밀턴에 존재하는 맨 커플링(상수)과는 대조적으로 종종 효과적인 커플링이라고 불립니다.

베타 함수

양자장론에서 베타함수 β(g)는 결합 파라미터 g의 실행을 부호화한다.이것은 다음 관계에 의해 정의됩니다.

{\displaystyle \displaystyle (g)=\mu {\displaystyle g}={\displaystyle \ln \mu},

여기서 μ는 주어진 물리적 과정의 에너지 척도입니다.양자장 이론의 베타 함수가 사라진다면, 그 이론은 규모 불변이다.

양자장 이론의 결합 매개변수는 대응하는 고전장 이론이 스케일 불변하더라도 흐를 수 있다.이 경우 0이 아닌 베타 함수는 고전적인 척도 불변성이 이상하다는 것을 알려줍니다.

QED와 란다우 극

베타 함수가 양수인 경우 해당 커플링은 에너지가 증가함에 따라 증가합니다.예를 들어 양자전기역학(QED)은 베타 함수가 양수라는 섭동 이론을 이용해 찾아낸다.특히 낮은 에너지에서는 α ≤ 1/137인 반면 Z 보손 척도에서는 약 90 GeV로 α ≤ 1/127을 측정한다.

또한 섭동 베타 함수는 결합이 계속 증가하고 QED가 높은 에너지에서 강하게 결합된다는 것을 알려준다.사실 어떤 유한 에너지에서 결합은 분명히 무한대가 된다.이 현상은 Lev Landau에 의해 처음 발견되었고, Landau 극이라고 불립니다.그러나 강한 결합에서 섭동 베타 함수가 정확한 결과를 줄 것으로 기대할 수 없기 때문에 란다우 극은 더 이상 유효하지 않은 상황에서 섭동 이론을 적용하는 인공물일 가능성이 높다.큰 에너지에서 $\alpha$ α(\ $displaystyle \alpha)$ 의 $\alpha$ 실제 스케일링 거동은 알려지지 않았다.

QCD 및 점근 자유도

비아벨 게이지 이론에서는 프랭크 윌체크, 데이비드 폴리처, 데이비드 그로스에 의해 처음 발견된 것과 같이 베타 함수가 음수일 수 있다.그 예로는 양자색역학(QCD)의 베타함수가 있으며, 그 결과 높은 에너지에서 ^[4]QCD 커플링이 감소한다.

게다가, 결합은 대수적으로 감소하는데, 이것은 점근 자유로 알려진 현상이다. (2004년에 노벨 물리학상을 받았다.)커플링은 대략 다음과 같이 감소합니다.

\displaystyle \alpha _{\text{s}(k^{2})\{stackrel {mathrm {def} {=}\{frac {g_{\text{s}}^2}(k^{2}){4\pi }}\approx {0}\ln left({k^{{2})

여기서₀ β는 Wilczek, Gross 및 Politzer에 의해 최초로 계산된 상수이다.

반대로 결합은 에너지 감소와 함께 증가합니다.이것은 낮은 에너지에서 결합이 커지며, 더 이상 섭동 이론에 의존할 수 없다는 것을 의미한다.

QCD 스케일

양자 색역학(QCD)에서 δ의 양을 QCD 척도라고 합니다.3가지 "활성" 쿼크 맛, 즉 프로세스에 관여하는 에너지 방출이 업, 다운 및 기묘한 쿼크만 발생시키는 경우 값은 δ $\Lambda _{\rm {MS}}=332\pm 17{\text{ MeV}}$ ^[4] M $\Lambda _{\rm {MS}}=332\pm 17{\text{ MeV}}$ $= 332$ $\Lambda _{\rm {MS}}=332\pm 17{\text{ MeV}}$ $MeV {\$ }}입니다 $.$ 이는 1.275GeV 미만의 에너지에 해당합니다.높은 에너지에서는 $\Lambda _{\rm {MS}}=210\pm 14$ $\Lambda _{\rm {MS}}=210\pm 14$ S $=$ $\Lambda _{\rm {MS}}=210\pm 14$ ± $\Lambda _{\rm {MS}}=210\pm 14$ {\ $display$ style \ $Lambda$ _ ${\rm {MS$ }}= $210\pm$ 14 $}$ MeV보다 $\Lambda _{\rm {MS}}=210\pm 14$ ^[5] 작습니다.최소 서브스펙션(MS) 체계 척도_MS δ의 의미는 치수 변환에 관한 기사에 제시되어 있다.

양성자 대 전자 질량비는 주로 QCD 척도에 의해 결정된다.

끈 이론

끈 이론에는 확장이 포함되기 때문에 현저하게 다른 상황이 존재한다.문자열 스펙트럼 분석 결과 이 필드는 슈퍼스트링의 보손 문자열 또는 NS-NS 섹터 중 하나에 존재해야 합니다.정점 연산자를 사용하면 이 필드를 자극하는 것은 스칼라 필드가 리치 스칼라에 결합하는 동작에 항을 추가하는 것과 같다는 것을 알 수 있습니다.따라서 이 필드는 결합 상수의 전체 함수 값입니다.이러한 결합 상수는 사전 결정, 조정 또는 범용 파라미터가 아니며 동적으로 결정되는 방식으로 공간과 시간에 따라 달라집니다.스트링 커플링을 고정된 것처럼 설명하는 선원은 일반적으로 진공 기대치를 참조합니다.이것은 초잠재력이 없는 보손 이론에서 어떤 가치도 가질 수 있다.

「」를 참조해 주세요.

레퍼런스

^ A. Zee. Quantum Field Theory in a Nutshell, Princeton University Press, ISBN 0691140340
^ Heinrich Leutwyler (2012), 키랄 섭동 이론, Scholarpedia, 7(10):8708.doi:10.4249/scholarpedia.8708
^ Donoghue, John F. (1995). "Introduction to the Effective Field Theory Description of Gravity". In Cornet, Fernando (ed.). Effective Theories: Proceedings of the Advanced School, Almunecar, Spain, 26 June–1 July 1995. Singapore: World Scientific. arXiv:gr-qc/9512024. Bibcode:1995gr.qc....12024D. ISBN 978-981-02-2908-5.
^ ^a ^b ^c QCD Running Coupling, A.듀르, S. J. Brodsky, G. F. de Teramond, Prog.파트, 누크물리 90 1 (2016)
^ C. Patrigani 등 (입자 데이터 그룹), Chin.Phys. C, 40, 100001 (2016)

외부 링크

2004년 노벨 물리학상 - 대중을 위한 정보
조지아 주립대학교 물리천문학부 - 기초력에 대한 결합 상수
검시관의 양자장 이론 소개.페스킨과 H.D.슈뢰더, ISBN 0-201-50397-2

[1] A. Zee. Quantum Field Theory in a Nutshell, Princeton University Press, ISBN 0691140340

[:0-2] Heinrich Leutwyler (2012), 키랄 섭동 이론, Scholarpedia, 7(10):8708.doi:10.4249/scholarpedia.8708

[:1-3] Donoghue, John F. (1995). "Introduction to the Effective Field Theory Description of Gravity". In Cornet, Fernando (ed.). Effective Theories: Proceedings of the Advanced School, Almunecar, Spain, 26 June–1 July 1995. Singapore: World Scientific. arXiv:gr-qc/9512024. Bibcode:1995gr.qc....12024D. ISBN 978-981-02-2908-5.

[PPNG_review_2016-4] QCD Running Coupling, A.듀르, S. J. Brodsky, G. F. de Teramond, Prog.파트, 누크물리 90 1 (2016)

[5] C. Patrigani 등 (입자 데이터 그룹), Chin.Phys. C, 40, 100001 (2016)

[1]

[2]

[3]

[4]

[5]

Search

결합 상수

네임스페이스

더

목차

미세 구조 상수

게이지 커플링

약하고 강한 결합