하이퍼플레인 분리 정리

하이퍼플레인 분리 정리 그림.

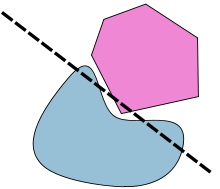
기하학에서 하이퍼플레인 분리 정리는 n차원 유클리드 공간에서 디스조인트 볼록 세트에 대한 정리다. 다소 비슷한 버전이 몇 가지 있다. 하나의 정리 버전에서, 이 두 세트가 모두 닫히고 적어도 한 세트가 콤팩트하다면, 그 사이에 하이퍼플레인이 있고 그 사이에 두 개의 평행 하이퍼플레인이 갭으로 분리되어 있다. 다른 버전에서, 두 개의 디스조인트 볼록 세트가 모두 열려 있다면, 그 사이에 하이퍼플레인이 존재하지만 반드시 어떤 틈새도 없다. 분리 하이퍼 평면에 직교하는 축은 분리 축이다. 왜냐하면 볼록한 신체의 축의 직교 투영은 분리되기 때문이다.

하이퍼플레인 분리정리는 헤르만 민코프스키 때문이다. 한-바나흐 분리정리는 위상학적 벡터공간에 대한 결과를 일반화한다.

관련 결과는 지원 하이퍼플레인 정리다.

서포트 벡터 기계의 맥락에서 최적으로 분리되는 하이퍼플레인 또는 최대 마진 하이퍼플레인(maximum-margin hyperplane)은 지점의 두 볼록한 선체를 분리하는 하이퍼플레인이며 두 지점과 동일하다.^[1]^[2]^[3]

진술 및 증거

하이퍼플레인 분리^[4] 정리 — A와 B를 R의ⁿ 두 개의 분리되지 않은 볼록 부분 집합으로 한다. 그러면 0이 아닌 벡터 v와 다음과 같은 실제 숫자 c가 존재한다.

\langle x,v\angle \geq c\,{\text{ 및 }\langle y,v\angle \leq c

A와 B의 y의 모든 x에 대해, 즉, 하이퍼플레인 $\langle \cdot ,v\rangle =c$ $\langle \cdot ,v\rangle =c$ $\langle \cdot ,v\rangle =c$ = $\langle \cdot ,v\rangle =c$ ${\displaystyle \langle$ \langle, $v\rangele$ = $c},$ v $정규$ 벡터는 $A$ 와 $\langle \cdot ,v\rangle =c$ B를 구분한다.

그 증거는 다음과 같은 보조정리법에 근거한다.

보조정리 — $K$ $K$ 을(를) R의ⁿ 비어 있지 않은 닫힌 볼록 부분 집합으로 한다 $K$ . $그리고$ K $K$ 에는 최소 규범(길이)의 $K$ 고유한 벡터가 존재한다.

보조정리 증명: Let $\delta =\inf\{ x :x\in K\}.$ Let $x_{j}$ be a sequence in $K$ such that $x_{j} \to \delta$ . Note that $(x_{i}+x_{j})/2$ is in ${\displa$ $K$ $K$ 이 $K$ (가) 볼록하고 $K$ $|x_{i}+x_{j}|^{2}\geq 4\delta ^{2}$ i $|x_{i}+x_{j}|^{2}\geq 4\delta ^{2}$ + $|x_{i}+x_{j}|^{2}\geq 4\delta ^{2}$ $|x_{i}+x_{j}|^{2}\geq 4\delta ^{2}$ $|x_{i}+x_{j}|^{2}\geq 4\delta ^{2}$ $|x_{i}+x_{j}|^{2}\geq 4\delta ^{2}$ ${\$ 4 $\delta ^{2$ 이후

x_{i}-x_{j} ^{2}=2 x_{i} ^{2}- x_{i}+x_{j} ^{2}- x_{i}-{2}\leq 2 x_{i} ^{2}+2 x_{j} ^{2}-4\reas{2}~{2}~{{2}~{2}~{no}\i}\i

as $i,j\to \infty$ , $x_{i}$ is a Cauchy sequence and so has limit x in $K$ . It is unique since if y is in $K$ and has norm δ, then ${\displaystyle x-y ^{2}\le$ $q$ 2 $|x-y|^{2}\leq 2|x|^{2}+2|y|^{2}-4\delta ^{2}=0$ x $^{2}+2$ y $^{2}-4\properties ^{2}=0}$ 및 $|x-y|^{2}\leq 2|x|^{2}+2|y|^{2}-4\delta ^{2}=0$ x = y. $\square$ $\square$

정리 증명: 주어진 분리되지 않은 볼록 집합 A, B, let

K=A+(-B)=\{x-y\mid x\in A,y\in B\}.

$-B$ $-B$ $-B$ 은 $-B$ (는) 볼록이고 볼록 집합의 합은 볼록하므로 $K$ $K$ 은 $K$ 볼록하다. 보조정리기로 볼록한 $K$ $K$ 의 ${\overline {K}}$ ${\overline {K}}$ K ${K$ 은(는) 최소규격의 $v$ 벡터 $v$ $v$ 을(를) 포함하고 있다. ${\overline {K}}$ 의 ${\$ 은(는) 볼록하므로 ${\overline {K}}$ , $K$ ${\displaystyle K$ 의 $n$ $n$ $n$ 에 대해 선 세그먼트

v+t(n-v),\,0\leq t\leq 1

${\overline {K}}$ 의 ${\$ {\ $overline{K$ }} 등에 ${\overline {K}}$ 놓여 있다.

v

|v|^{2}\leq |v+t(n-v)|^{2}=|v|^{2}+2t\langle v,n-v\rangle +t^{2}|n-v|^{2}

|v|^{2}\leq |v+t(n-v)|^{2}=|v|^{2}+2t\langle v,n-v\rangle +t^{2}|n-v|^{2}

v

|v|^{2}\leq |v+t(n-v)|^{2}=|v|^{2}+2t\langle v,n-v\rangle +t^{2}|n-v|^{2}

+ t

|v|^{2}\leq |v+t(n-v)|^{2}=|v|^{2}+2t\langle v,n-v\rangle +t^{2}|n-v|^{2}

(

|v|^{2}\leq |v+t(n-v)|^{2}=|v|^{2}+2t\langle v,n-v\rangle +t^{2}|n-v|^{2}

- v

|v|^{2}\leq |v+t(n-v)|^{2}=|v|^{2}+2t\langle v,n-v\rangle +t^{2}|n-v|^{2}

) 2

|v|^{2}\leq |v+t(n-v)|^{2}=|v|^{2}+2t\langle v,n-v\rangle +t^{2}|n-v|^{2}

= v

|v|^{2}\leq |v+t(n-v)|^{2}=|v|^{2}+2t\langle v,n-v\rangle +t^{2}|n-v|^{2}

+

|v|^{2}\leq |v+t(n-v)|^{2}=|v|^{2}+2t\langle v,n-v\rangle +t^{2}|n-v|^{2}

|v|^{2}\leq |v+t(n-v)|^{2}=|v|^{2}+2t\langle v,n-v\rangle +t^{2}|n-v|^{2}

|v|^{2}\leq |v+t(n-v)|^{2}=|v|^{2}+2t\langle v,n-v\rangle +t^{2}|n-v|^{2}

v

|v|^{2}\leq |v+t(n-v)|^{2}=|v|^{2}+2t\langle v,n-v\rangle +t^{2}|n-v|^{2}

n

|v|^{2}\leq |v+t(n-v)|^{2}=|v|^{2}+2t\langle v,n-v\rangle +t^{2}|n-v|^{2}

- v

|v|^{2}\leq |v+t(n-v)|^{2}=|v|^{2}+2t\langle v,n-v\rangle +t^{2}|n-v|^{2}

+

|v|^{2}\leq |v+t(n-v)|^{2}=|v|^{2}+2t\langle v,n-v\rangle +t^{2}|n-v|^{2}

|v|^{2}\leq |v+t(n-v)|^{2}=|v|^{2}+2t\langle v,n-v\rangle +t^{2}|n-v|^{2}

|v|^{2}\leq |v+t(n-v)|^{2}=|v|^{2}+2t\langle v,n-v\rangle +t^{2}|n-v|^{2}

- v -

|v|^{2}\leq |v+t(n-v)|^{2}=|v|^{2}+2t\langle v,n-v\rangle +t^{2}|n-v|^{2}

⟩ +

|v|^{2}\leq |v+t(n-v)|^{2}=|v|^{2}+2t\langle v,n-v\rangle +t^{2}|n-v|^{2}

n -

|v|^{2}\leq |v+t(n-v)|^{2}=|v|^{2}+2t\langle v,n-v\rangle +t^{2}|n-v|^{2}

2

{\

v

^{2}\leq

v

+t(n-v) ^{2}=

v

^{2}+2t\langle v,n-v\rangle +t^{2

}

|v|^{2}\leq |v+t(n-v)|^{2}=|v|^{2}+2t\langle v,n-v\rangle +t^{2}|n-v|^{2}

.

$0<t\leq 1$ < $0<t\leq 1$ $0<t\leq 1$ 1 ${\displaystyle 0<t\leq 1$ 에 대해 다음과 같은 내용을 제공한다.

0\leq 2\langle v,n\n\angle -2 v ^{2}+t n-v ^{2

and letting $t\to 0$ gives: $\langle n,v\rangle \geq v ^{2}$ . Hence, for any x in A and y in B, we have: $\langle x-y,v\rangle \geq v ^{2}$ . Thus, if v is nonzero, the proof is complete since

\inf _{x\in A}\langle x,v\rangle \geq v ^{2}+\sup_{y\in B}\langle y,v\rangle .

보다 일반적으로(사례 v = 0 포함) $K$ $K$ 의 내부가 비어 $K$ 있지 않을 때 먼저 사례를 들어 봅시다. The interior can be exhausted by a nested sequence of nonempty compact convex subsets $K_{1}\subset K_{2}\subset K_{3}\subset \cdots$ (namely, put ${\displaystyle K_{j}\equiv [-j,j]^{n}\cap \{x\$ ${\text{int}}(K):d(x,({\text{int})(K)^{c}\geq {\frac{1}{j}\}}}.$ Since 0 is not in $K$ , each $K_{n}$ contains a nonzero vector $v_{n}$ of minimum length and by the argument in the early part, we have: $\langle x,v_{n}\rangle \geq 0$ for any $x\in K_{n}$ . $v_{n}$ ${\$ 를 길이 1로 정상화시킬 수 있다 $v_{n}$ 그런 다음 $v_{n}$ $v_{n}$ ${\$ 시퀀스에는 한계 v(n-sphere가 좁기 때문에) 0이 아닌 수렴 하위 집합이 포함되어 $v_{n}$ 있다. $K$ ${\displaystyle$ K $} 내부$ 의 모든 x에 대해 $\langle x,v\rangle \geq 0$ $K$ $\langle x,v\rangle \geq 0$ v $displaystyle \langle x,v\rangele \geq$ 0 $}$ 이(가) 있으며 연속성에 의해 $K$ ${\\displaystyle$ K}의 모든 x에 대해 동일한 보류를 완료했다 $K$ 마지막으로 $K$ ${\displaystyle$ K $}$ 이(가) 비어 있는 내부를 가진 $K$ 경우, 그 내부가 확장되는 아핀 집합은 전체 공간의 그것보다 치수가 적다. 결과적으로 $K$ ${\$ $displaystyle K$ $}$ 은(는) 일부 하이퍼플레인 $\langle \cdot ,v\rangle =c$ $\langle \cdot ,v\rangle =c$ $\langle \cdot ,v\rangle =c$ = c ${\displaystyle \langle \cdot,v\rangle =c$ 에 포함되므로 $K$ , $\langle x,v\rangle \geq c$ x $\langle x,v\rangle \geq c$ v c $\langle x,v\rangle \geq c$ {\ $displaysty$ \ $langle$ x $,v\langele \geq c}$ 에 포함되며 $\langle x,v\rangle \geq c$ $K$ $,$ 전과 같이 증거를 마무리한다. $\square$

치수의 수는 한정되어야 한다. 무한 차원 공간에는 두 개의 닫힌 볼록한 분리형 세트의 예가 있는데, 이 세트는 불평등이 엄격하지 않은 약한 의미에서도 닫힌 하이퍼플레인(연속적인 선형 기능이 일정하게 같은 하이퍼플레인)으로 분리될 수 없다.^[5]

위의 증명은 또한 led에서 언급된 정리의 첫 번째 버전을 증명한다(이를 보기 위해, 증명에서 $K$ $K$ $K$ 는 아래의 정리의 가설에 따라 폐쇄된다는 점에 유의한다).

분리 정리 I — A와 B를 두 개의 분리 비빈 폐쇄 볼록 세트로 하고, 그 중 하나는 콤팩트하다. 그 다음 0이 아닌 벡터 v와 실수 c $c_{1}<c_{2}$ < $c_{1}<c_{2}$ $c_{1}<c_{2}$ ${\$ 2}}: 다음과 같은 $c_{1}<c_{2}$ 것이 존재한다.

\langle x,v\langle >c_{2}\,{\text{ 및 }\langle y,v\rangle <c_{1}}

모든 x in A와 y in B에 대해.

여기서 가설의 압축성은 완화할 수 없다. 다음 절의 예를 참조하라. 이 버전의 분리정리는 무한차원까지 일반화된다. 일반화는 한-바나흐 분리정리로 더 흔히 알려져 있다.

또한 다음과 같은 이점이 있다.

분리 정리 II — A와 B를 분리되지 않은 두 개의 볼록 세트로 한다. A가 열려 있으면 다음과 같은 $c$ 0이 아닌 벡터 v와 실제 번호 $c$ $c$ 이(가) 존재하게 된다.

\langle x,v\angle >c\,{\text{ 및 }\langle y,v\angle \leq c

모든 x in A와 y in B에 대해. 두 세트가 모두 열려 있으면 다음과 같은 $c$ 0이 아닌 벡터 v와 실제 번호 $c$ $c$ 이(가) 존재하게 된다.

\langle x,v\angle >c\,{\text{ 및 }\langle y,v\angle <c

모든 x in A와 y in B에 대해.

분리 하이퍼 평면이 볼록 세트 내부와 교차할 수 없기 때문에 표준 버전에서 이 값을 따른다.

컨버스 오브 정리

두 불평등이 엄격하지 않다는 약한 의미에서 두 볼록 세트만 "분리"하는 하이퍼플레인의 존재는 분명히 두 세트가 분리됨을 의미하지 않는다. 두 세트 모두 하이퍼플레인 위에 포인트가 있을 수 있다.

백범과 고유성

몸 중 하나가 볼록하지 않으면 정리가 적용되지 않는다.

만약 A나 B 중 하나가 볼록하지 않다면, 많은 가능한 백반증이 있다. 예를 들어, A와 B는 동심원일 수 있다. 보다 미묘한 currexample은 A와 B가 모두 닫혔지만 둘 중 어느 것도 압축되지 않은 것이다. 예를 들어, A가 닫힌 반쪽 평면이고 B가 하이퍼볼라의 한쪽 팔로 경계를 이루면 다음과 같이 엄격하게 분리되는 하이퍼플레인(hyperplane)은 없다.

A=\{(x,y):x\leq 0\

B=\{(x,y):x>0, y\geq 1/x\}.\

(하지만, 두 번째 정리의 한 예에 의해, 그들의 내부를 분리하는 하이퍼플레인(hyperplane이 있다. 다른 종류의 counterexample은 A 콤팩트와 B가 열려있다. 예를 들어 A는 닫힌 사각형이 될 수 있고 B는 A를 건드리는 열린 사각형이 될 수 있다.

정리의 첫 번째 버전에서 분명히 분리 하이퍼플레인(hyperplane)은 결코 독특하지 않다. 두 번째 버전에서는 독특할 수도 있고 아닐 수도 있다. 기술적으로 분리축은 번역될 수 있기 때문에 결코 독특하지 않다. 두 번째 정리 버전에서 분리축은 번역에 이르기까지 독특할 수 있다.

충돌 감지 시 사용

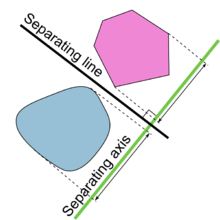
분리축 정리(SAT)는 다음과 같이 말하고 있다.

두 물체의 돌출부가 겹치지 않는 선(축이라고 함)이 존재한다면 두 볼록한 물체는 겹치지 않는다.

SAT는 두 볼록 고형물이 교차하는지 여부를 시험하기 위한 알고리즘을 제안한다.

차원성에 관계없이 분리축은 항상 선이다. 예를 들어 3D에서는 공간이 평면에 의해 분리되지만 분리 축은 분리 평면에 수직이다.

분리축 정리는 폴리곤 메쉬 간의 빠른 충돌 감지를 위해 적용할 수 있다. 각 면의 정상 또는 다른 형상 방향은 분리 축으로 사용된다. 이렇게 하면 선/플레인이 분리되지 않고 축이 분리될 수 있다는 점에 유의하십시오.

3D에서는 얼굴 표준만 사용해도 일부 최첨단 비충돌 사례를 분리할 수 없다. 각 물체에서 한 개씩 채취한 가장자리 쌍의 교차 생산물로 구성된 추가 축이 필요하다.^[6]

효율성 향상을 위해 병렬 축을 단일 축으로 계산할 수 있다.

참고 항목

메모들

^ Hastie, Trevor; Tibshirani, Robert; Friedman, Jerome (2008). The Elements of Statistical Learning : Data Mining, Inference, and Prediction (PDF) (Second ed.). New York: Springer. pp. 129–135.
^ Witten, Ian H.; Frank, Eibe; Hall, Mark A.; Pal, Christopher J. (2016). Data Mining: Practical Machine Learning Tools and Techniques (Fourth ed.). Morgan Kaufmann. pp. 253–254. ISBN 9780128043578.
^ Deisenroth, Marc Peter; Faisal, A. Aldo; Ong, Cheng Soon (2020). Mathematics for Machine Learning. Cambridge University Press. pp. 337–338. ISBN 978-1-108-45514-5.
^ 보이드 & 반덴버그 2004, 연습 2.22.
^ Hamm Brezis, Analysis ponpectionnelle : théory et applications, 1983, remarque 4, 페이지 7.
^ https://docs.godotengine.org/en/stable/tutorials/math/vectors_advanced.html#collision-detection-in-3d

참조

Boyd, Stephen P.; Vandenberghe, Lieven (2004). Convex Optimization (PDF). Cambridge University Press. ISBN 978-0-521-83378-3.
Golshtein, E. G.; Tretyakov, N.V. (1996). Modified Lagrangians and monotone maps in optimization. New York: Wiley. p. 6. ISBN 0-471-54821-9.
Shimizu, Kiyotaka; Ishizuka, Yo; Bard, Jonathan F. (1997). Nondifferentiable and two-level mathematical programming. Boston: Kluwer Academic Publishers. p. 19. ISBN 0-7923-9821-1.

외부 링크

충돌 감지 및 반응

[1] Hastie, Trevor; Tibshirani, Robert; Friedman, Jerome (2008). The Elements of Statistical Learning : Data Mining, Inference, and Prediction (PDF) (Second ed.). New York: Springer. pp. 129–135.

[2] Witten, Ian H.; Frank, Eibe; Hall, Mark A.; Pal, Christopher J. (2016). Data Mining: Practical Machine Learning Tools and Techniques (Fourth ed.). Morgan Kaufmann. pp. 253–254. ISBN 9780128043578.

[3] Deisenroth, Marc Peter; Faisal, A. Aldo; Ong, Cheng Soon (2020). Mathematics for Machine Learning. Cambridge University Press. pp. 337–338. ISBN 978-1-108-45514-5.

[4] 보이드 & 반덴버그 2004, 연습 2.22.

[5] Hamm Brezis, Analysis ponpectionnelle : théory et applications, 1983, remarque 4, 페이지 7.

[6] ttps://docs.godotengine.org/en/stable/tutorials/math/vectors_advanced.html#collision-detection-in-3d

[1]

[2]

[3]

[4]

[5]

[6]

v t 위상 벡터 공간(TV)
기본개념	바나흐 공간 연속 선형 연산자 함수 힐베르트 공간 선형 연산자 국소 볼록한 공간 동형성 위상 벡터 공간 벡터 공간
주요 결과	앤더슨-케이덱 정리 바나흐-알라오글루 정리 닫힌 그래프 정리 F. 리에스의 정리 한-바나흐(하이퍼플레인 분리) 벡터 값 한-바나흐) 개방형 매핑(Banach-Schauder)(경계 반전) 균일 경계(Banach-Steinhaus)
지도	거의 열려 있음 이린린(형식) 연산자) 및 Sesquilinar 형식 닫힌 콤팩트 연산자 연속 및 불연속 선형 지도 조밀하게 정의됨 동형성 함수 규범 연산자 세미놈 하위선형 전치하다
세트 종류	절대 볼록/디스크 흡수/방사선 아핀 균형/순환 디스크 배너치 경계점 경계 보완된 하위 공간 볼록스 볼록콘(하위 세트) 선형 원뿔(하위 세트) 극한점 사전 계산/완전 경계 퍼머드/샤이 방사상 방사형 볼록/별 모양 대칭
작업 설정	아핀 선체 (상대) 대수 내부(핵심) 볼록 선체 선형스팬 민코스키 덧셈 극지 (Quasi) 상대 인테리어
TV의 종류	아스플룬드 B-완전/P탁 바나흐 (카운트) 바렐라 (울트라-) 태생학 브레이너 완성하다 편리한 (DF)-공간 특출신 F-공간 프레셰트 (테메 프레셰트) 그로텐디크 힐베르트 엽기적인 보간공간 K-공간 LB-공간 LF-공간 국소 볼록한 공간 맥키 (사이비도)메트리저블 몬텔 콰시바라드 준완전 콰시노르메드 (폴리노멀리) 반)반사성 리에츠 슈워츠 반완전 스미스 고정관념 (B) 엄밀히 균일볼록스 (Quasi-) 초음파상 균일하게 매끈매끈함 웹베드 근사 특성 포함

Search