피타고라스 3중주

피타고라스의 삼중항은 a + b = c가 되도록 3개의 양의 정수 a, b, c로 구성됩니다. 이러한 세배는 일반적으로 (a, b, c) 쓰이며, 잘 알려진 예로는 (3, 4, 5)가 있습니다. 만약 (a, b, c)가 피타고라스의 3배라면, 임의의 양의 정수 k에 대하여 (ka, kb, kc)도 마찬가지입니다. 변들이 피타고라스의 세 개의 삼각형을 이루는 삼각형을 피타고라스 삼각형이라고 하며, 직각 삼각형입니다.

원시 피타고라스의 삼중항은 a, b, c가 코프프라임인 경우(즉, 1보다 큰 공약수가 없는 경우)입니다.^[1] 예를 들어, (3, 4, 5)는 원시적인 피타고라스의 삼중항인 반면 (6, 8, 10)은 그렇지 않습니다. 모든 피타고라스의 세 배는 (a, b, c)를 최대 공약수로 나눔으로써 고유한 원시 피타고라스의 세 배로 확장될 수 있습니다. 반대로, 모든 피타고라스 삼중은 원시 피타고라스 삼중의 원소에 양의 정수를 곱하여 얻을 수 있습니다 (세 원소도 마찬가지입니다).

이 이름은 모든 직각 삼각형이 $공식$ ${\displaystyle a^{}}$ 2${\displaystyle {}^{}}$+ ${\displaystyle b^{}}$ 2 = ${\displaystyle c^{}}$ 2 ${\displaystyle a^{2}$ + b$^{2$}를 만족하는 변의 길이를 갖는다는 피타고라스 정리에서 유래되었습니다.$}=c^{2$ 따라서 피타고라스 삼중항은 직각삼각형의 세 정수 변의 길이를 나타냅니다. 그러나 정수가 아닌 변을 가진 직각 삼각형은 피타고라스의 세 배를 형성하지 않습니다. 예를 들어, 변 ${\displaystyle a}$ = b = ${\displaystyle 1}$ ${\displaystyle$a = b = $1}$ 및 $c$ = ${\displaystyle 2}$ ${\displaystyle$c = {\$sqrt {2}}$은(는) 직각 삼각형이지만$,$ (${\displaystyle 1,}$ 1${\displaystyle ,}$ ${\displaystyle 2)}$ ${\$$displaystyle$($1,$ 1, {\$sqrt {2}}$은(는) 정수가 아니므로 피타고라스 삼중이 아닙니다. $또한{\displaystyle \mathrm{}}$ 1 ${\$$displaystyle$ $1}$ $및$ 2 ${\$ ${\sqrt {2}}$은$($는) 비합리적이기 때문에 정수 공용 배수를 갖지 않습니다$$.

피타고라스의 세쌍둥이는 예로부터 알려져 있습니다. 알려진 가장 오래된 기록은 60진법으로 쓰여진 기원전 1800년경의 바빌로니아 점토판인 플림톤 322에서 비롯됩니다. 1900년 직후 에드거 제임스 뱅크스가 발견했고 1922년 조지 아서 플림튼에게 10달러(현재 175달러에 해당)에 팔렸습니다.^[2][3]

정수해를 검색할 때 방정식 a + b = c는 디오판토스 방정식입니다. 따라서 피타고라스 삼중항은 비선형 디오판토스 방정식의 가장 오래된 알려진 해 중 하나입니다.

예

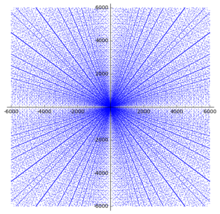
16개의 원시 피타고라스 수는 100개까지 존재합니다.

(3, 4, 5)	(5, 12, 13)	(8, 15, 17)	(7, 24, 25)
(20, 21, 29)	(12, 35, 37)	(9, 40, 41)	(28, 45, 53)
(11, 60, 61)	(16, 63, 65)	(33, 56, 65)	(48, 55, 73)
(13, 84, 85)	(36, 77, 85)	(39, 80, 89)	(65, 72, 97)

(6, 8, 10)과 같은 다른 작은 피타고라스의 세 배는 원시적이지 않기 때문에 나열되지 않습니다. 예를 들어 (6, 8, 10)은 (3, 4, 5)의 배수입니다.

각 점(배수 포함)은 오른쪽 산점도에 방사선을 형성합니다.

게다가, 이것들은 300까지의 수들 중에 남아있는 원시 피타고라스의 세 배입니다.

(20, 99, 101)	(60, 91, 109)	(15, 112, 113)	(44, 117, 125)
(88, 105, 137)	(17, 144, 145)	(24, 143, 145)	(51, 140, 149)
(85, 132, 157)	(119, 120, 169)	(52, 165, 173)	(19, 180, 181)
(57, 176, 185)	(104, 153, 185)	(95, 168, 193)	(28, 195, 197)
(84, 187, 205)	(133, 156, 205)	(21, 220, 221)	(140, 171, 221)
(60, 221, 229)	(105, 208, 233)	(120, 209, 241)	(32, 255, 257)
(23, 264, 265)	(96, 247, 265)	(69, 260, 269)	(115, 252, 277)
(160, 231, 281)	(161, 240, 289)	(68, 285, 293)

트리플 생성

유클리드의 공식은^[4] m > n > 0인 임의의 정수 쌍 m과 n이 주어지면 피타고라스 삼중항을 생성하는 기본 공식입니다. 공식에 따르면 정수는

${\displaystyle a=m^{2}-n^{2},\ \,b=2mn,\ \,c=m^{2}+n^{2}}$

피타고라스의 세쌍둥이를 이루다 예를 들어, 주어진

${\displaystyle m=2,\\,n=1}$

기본 트리플(3,4,5) 생성:

${\displaystyle a=2^{2}-1^{2}=3,\ \,b=2\times 2\times 1=4,\ \,c=2^{2}+1^{2}=5.}$

m과 n이 코프프라임이고 그 중 하나가 짝수인 경우에만 유클리드의 공식에 의해 생성된 삼중항은 원시적입니다. m과 n이 모두 홀수일 때, a, b, c는 짝수이고 삼중항은 원시적이지 않을 것이지만, a, b, c를 2로 나누면 m과 n이 코프프라임일 때 원시적인 삼중항이 생성됩니다.^[5]

모든 원시 삼중항은 고유한 코프프라임 수 m, n에서 발생하며, 그 중 하나는 짝수입니다. 따라서 원시 피타고라스의 세쌍둥이는 무한히 많습니다. 유클리드 공식의 a, b, c와 n의 관계는 이 글의 나머지 부분에서 참조됩니다.

모든 원시 삼중항을 생성함에도 불구하고 유클리드의 공식이 모든 삼중항을 생성하는 것은 아닙니다. 예를 들어 (9, 12, 15)는 정수 m과 n을 사용하여 생성할 수 없습니다. 수식에 추가 매개변수 k를 삽입하면 이 문제를 해결할 수 있습니다. 다음은 모든 피타고라스의 삼중항을 고유하게 생성합니다.

${\displaystyle a=k\cdot (m^{2}-n^{2}),\ \,b=k\cdot (2mn),\ \,c=k\cdot (m^{2}+n^{2})}$

여기서 m, n, k는 m > n인 양의 정수이고, m과 n의 코프프라임이며 둘 다 홀수가 아닙니다.

이 공식들이 피타고라스 삼중항을 생성한다는 것은 기본 대수를 사용하여 a² + b를² 확장하고 그 결과가 c와² 같음을 확인함으로써 확인할 수 있습니다. 모든 피타고라스의 세 배는 어떤 정수 k로 나누어져서 원시 세 배를 얻을 수 있기 때문에 모든 세 배는 m과 n이 있는 공식을 사용하여 원시 대응물을 생성한 다음 마지막 방정식과 같이 k를 곱하여 고유하게 생성될 수 있습니다.

특정 정수 시퀀스에서 m과 n을 선택하면 흥미로운 결과를 얻을 수 있습니다. 예를 들어, m과 n이 연속적인 Pell 수일 경우 a와 b는 1만큼 차이가 납니다.^[6]

유클리드 시대부터 특정한 성질을 가진 삼중항을 생성하는 많은 공식들이 개발되었습니다.

유클리드의 공식 증명

a, b, c에 의한 유클리드 공식의 만족도는 양의 정수 m과 n에 대하여 공식에 의하여 주어진 m > n, a, b, c가 모두 양의 정수라는 사실로부터, 그리고 다음과 같은 사실로부터 명백합니다.

${\displaystyle a^{2}+b^{2}=(m^{2}-n^{2})^{2}+(2mn)^{2}=(m^{2}+n^{2})^{2}=c^{2}.}$

a, b, c가 임의의 원시 피타고라스 삼중항에 대한 유클리드의 공식으로 표현될 필요성에 대한 증명은 다음과 같습니다.^[7] 모든 원시 삼중항은 (a, b, c)로 표기할 수 있으며, 여기서 a + b = c 및 a, b, c는 코프프라임입니다. 따라서 a, b, c는 쌍대 코프림(소수가 그들 중 두 개를 나눈다면 세 번째 코프림도 강제로 나눌 수 있습니다)을 돌봅니다. a와 b는 coprime이므로, 그들 중 적어도 하나는 이상합니다. 만약 a가 홀수라고 가정하면, b는 짝수이고 c는 홀수이다. (만약 b가 홀수이면 c는 짝수이고 c는² 4의 배수인 반면, a² + b는² 2 모듈로 4와 같으며, 홀수 제곱은 1 모듈로 4와 같음)

${\displaystyle a^{}}$ 2${\displaystyle {}^{}}$+ b ${\displaystyle 2^{}}$ = ${\displaystyle {}^{}}$ ${\displaystyle 2^{}}$ ${\displaystyle$ a$^{2}+b^{2$)부터$}=c^{2}}$는 a가 홀수라고 가정합니다. We obtain ${\displaystyle c^{2}-a^{2}=b^{2}}$ and hence ${\displaystyle (c-a)(c+a)=b^{2}}$. Then ${\displaystyle {\tfrac {(c+a)}{b}}={\tfrac {b}{(c-a)}}}$. $({\displaystyle \frac{c}{}}$+ a${\displaystyle \frac{)}{}}$ b ${\$ {$b}}$은(는) 합리적이므로 ${\displaystyle \frac{m}{}}$ ${\$과(는) 동일하게 설정합니다. 따라서 $({\displaystyle \frac{c}{}}$- a${\displaystyle \frac{)}{}}$ ${\displaystyle \frac{}{}}$ = n ${\displaystyle \frac{m}{}}$ ${\displaystyle {\tfrac {(c-a)}{b$}}={\$tfrac {n}{m}}}$의 역수이며$,$ (${\displaystyle \frac{c}{}}$+ ${\displaystyle \frac{a)}{}}$ b ${\displaystyle {\tfrac {(c+a)}{b}}$의 역수입니다$.$ 그런 다음 해결합니다.

${\displaystyle {\frac {c}{b}}+{\frac {a}{b}}={\frac {m}{n}},\quad \quad {\frac {c}{b}}-{\frac {a}{b}}={\frac {n}{m}}}$

${\displaystyle \frac{\mathrm{cb}}{}}$ ${\$ 및$$ ${\displaystyle \frac{b}{}}$ ${\$의 경우 다음과$$ 같습니다.

${\displaystyle {\frac {c}{b}}={\frac {1}{2}}\left({\frac {m}{n}}+{\frac {n}{m}}\right)={\frac {m^{2}+n^{2}}{2mn}},\quad \quad {\frac {a}{b}}={\frac {1}{2}}\left({\frac {m}{n}}-{\frac {n}{m}}\right)={\frac {m^{2}-n^{2}}{2mn}}.}$

${\displaystyle \frac{m}{}}$ ${\$이(가) 완전히 줄어들기 때문에 m과 n은 coprime이며 둘 다 균등할 수 없습니다. 둘 다 홀수인 경우 m ${\displaystyle \frac{{2\mathrm{}}^{}}{}}$- n ${\displaystyle \frac{{}^{}}{\mathrm{}}}$ ${\displaystyle \frac{\mathrm{mn}}{}}$ ${\$의 분자는 4의 배수이고$$ 분모 2mn은 4의 배수가 아닙니다. 4는 분자에서 가능한 최소 짝수 인자이고 2는 분모에서 가능한 최대 짝수 인자이므로 홀수로 정의하더라도 이는 a가 짝수임을 의미합니다. 따라서 m과 n 중 하나는 홀수이고 다른 하나는 짝수이며 분모가 2mn인 두 분수의 분자는 홀수입니다. 따라서 이 분수들은 완전히 감소합니다(이 분모를 나누는 홀수 소수는 m과 n 중 하나를 나누지만 다른² 하나는 나누지 않으므로 m ± n을² 나누지 않습니다). 따라서 분자는 분자와, 분모는 분모와 동일시하여 유클리드의 공식을 제공할 수 있습니다.

${\displaystyle }$a ${\displaystyle =}$ ${\displaystyle m^{}}$ 2${\displaystyle {}^{}}$- n ${\displaystyle 2^{},}$ b ${\displaystyle =}$ ${\displaystyle 2}$ ${\displaystyle \mathrm{m}}$ ${\displaystyle n,}$ ${\displaystyle c}$ = ${\displaystyle m^{}}$ 2${\displaystyle {}^{}}$+ ${\displaystyle n^{}}$ ${\displaystyle {}^{}}$ ${\displaystyl$ a =$m^{2}$ - n$^{2}},$=$2mn,\$ = $m^{2}$ + $n^{2}},$ m과 n의 코프프라임이 있고 패리티가 반대입니다.

Maor(2007)와 Sierpi ń스키(2003)에서 더 길지만 일반적인 증명이 제공됩니다. 또 다른 증거는 디오판토스 방정식 § 피타고라스 삼중의 예로, 차수 2의 모든 동질적 디오판토스 방정식에 적용되는 일반적인 방법의 예입니다.

유클리드 공식의 매개변수 해석

피타고라스 삼각형의 변의 길이가 m² - n², 2mn, m + n이라고²² 하고, 길이 m² - n의² 다리와 길이 m² + n의² 빗변 사이의 각도를 β로 나타낸다고 가정해 보겠습니다. 그러면 ${\displaystyle \frac{\tan }{}}$ ⁡ ${\displaystyle \frac{\beta }{}}$ 2 = n${\displaystyle \tan {\tfrac${\beta }{$2}}$=${\tfrac$ {n}{m}}이고 전각 삼각형${\displaystyle 값}$은 sin ⁡ ${\displaystyle \frac{{\beta }^{}}{}}$ = 2 m n m 2 + n 2${\displaystyle$ \$sin$ {\beta }={\tfrac {2mn}{m^{2}+n^{2}$}}}}$ ${\displaystyle cos}$ $⁡$ ${\displaystyle \frac{{}^{}}{}}$ $=$ m ${\displaystyle \frac{{}^{}}{}}$ -${\displaystyle \frac{n^{}}{}}$ ${\displaystyle \frac{{}^{}}{}}$ ${\displaystyle \frac{m^{}}{}}$ 2$$+ n 2${\displaystyle \cos$ {\$beta$} $=$ ${\tfrac {m^{2}-n^{2$}}} {m^{2} + n^{2}$}}}}$${\displaystyle 및}$$$${\displaystyle \tan }$ $⁡$ ${\displaystyle \frac{}{}}$ $=$ 2${\displaystyle \frac{{}^{}{}^{}}{}}$ ${\displaystyle \frac{m^{}}{}}$ 2$$- n 2${\displaystyle \tan$ {\$beta$} $=$ ${\tfrac {2mn}$ {m$^{$2$\}-$n^{2}}}}.

변종

다음과 같은 유클리드 공식의 변형은 때때로 m과 n에서 더 대칭적이기 때문에 더 편리합니다(m과 n에서 동일한 패리티 조건).

만약 m과 n이 m > n이 되는 두 개의 홀수 정수라면,

${\displaystyle a=mn,\quad b={\frac {m^{2}-n^{2}}{2}},\quad c={\frac {m^{2}+n^{2}}{2}}}$

는 피타고라스의 3중수를 이루는 세 개의 정수로, m과 n이 동족인 경우에만 원시적입니다. 반대로, 모든 원시 피타고라스 삼중항은 코프프라임 홀수의 고유 쌍 m > n > 0에서 발생합니다.

a와 b를 교환하지 않음

위의 발표에서 모든 피타고라스의 삼중항은 "a와 b의 교환 후, a가 짝수인 경우"라는 유클리드의 공식으로부터 유일하게 얻어진다고 합니다. 이 교환을 피하기 위해 유클리드의 공식과 위의 변형을 다음과 같이 병합하여 다음과 같은 결과를 얻을 수 있습니다.

모든 원시적인 피타고라스의 세가지는 독특하게 쓰여질 수 있습니다.

${\displaystyle a=2\varepsilon mn,\quad b=\varepsilon (m^{2}-n^{2}),\quad c=\varepsilon (m^{2}+n^{2}),}$

여기서 m과 n은 양의 코프림 정수이고, m과 n이 $모두$ 홀수인 경우 ε = $12 {\displaystyle$ \varepsilon =${\frac${1}{2}}이고, 그렇지 않은 경우 ε = 1 ${\displaystyle$ \$varepsilon$= 1}입니다. 마찬가지로 a가 $홀수$인 경우 ε $$= $12 {\displaystyle$ \varepsilon =${\frac${1}{2}}이고, a가 짝수인 경우 ε = 1 ${\displaystyle$ \$varepsilon$= 1}입니다.

원시 피타고라스 3쌍의 기본 성질

일반속성

(어떤 것이 짝수이고 어떤 것이 홀수인지를 지정하지 않고) < b < c를 갖는 원시 피타고라스 삼중주(a, b, c)의 속성은 다음과 같습니다.

• ${\displaystyle \frac{(}{}}$ ${\displaystyle \frac{c}{}}$- ${\displaystyle \frac{a}{}}$)${\displaystyle \frac{}{}}$( c${\displaystyle \frac{}{}}$- ${\displaystyle \frac{b}{}}$) 2 ${\$은(는) 항상 완벽한 정사각형입니다.^[11] 필요조건일 뿐 충분조건이 아니기 때문에 주어진 수의 3배가 피타고라스의 3배가 아닌지 확인하는 데 사용할 수 있습니다. 예를 들어, {6, 12, 18}과 {1, 8, 9}의 삼중항은 각각 (c - a)(c - b)/2가 완벽한 제곱이지만, 피타고라스 삼중항은 아닙니다.
• 수 a, b, c의 세 배가 원시 피타고라스의 세 배를 이룰 때 (c에서 짝수 다리를 뺀 값)와 (c에서 홀수 다리를 뺀 값)의 반은 모두 완전 제곱이지만, {1, 8, 9}라는 숫자는 완전 제곱 검정을 통과하지만 ≠ 9이기 때문에 피타고라스의 세 배는 아니기 때문에 이것은 충분 조건이 아닙니다.
• 기껏해야 a, b, c 중 하나는 정사각형입니다.^[12]
• 피타고라스 삼각형의 넓이는 정수의 제곱^{[13]: p. 17 [13]: p. 21} 또는 두 배일 수 없습니다.
• 정확히 a, b 중 하나는 2로 나뉠 수 있으며(짝수), 빗변 c는 항상 홀수입니다.^[14]
• 정확히 a 중 하나, b는 3으로 나눗셈되지만 c는 절대 아닙니다.^{[15][9]: 23–25}
• 정확히 a 중 하나인 b는 4로 나눗셈되지만 ^[9]c는 절대로 짝수가 아닙니다(c는 결코 짝수가 아니기 때문입니다).
• 정확히 a, b, c 중 하나는 5로 나뉠 수 있습니다.^[9]
• abc를 항상 나누는 가장 큰 수는 60입니다.^[16]
• 2m+1 형태의 임의의 홀수는, m은 정수이고 m>1인 원시 피타고라스 삼중의 홀수 다리가 될 수 있습니다. 아래의 원시 피타고라스 삼중항을 참조하십시오. 그러나 4로 나눌 수 있는 짝수만이 원시 피타고라스의 세쌍원소의 짝수 다리가 될 수 있습니다. 위에 주어진 짝수 다리에 대한 유클리드의 공식은 2mn이고 m 또는 m 중 하나는 짝수여야 하기 때문입니다.
• 빗변 c(항상 홀수임)는 두 제곱의 합입니다. 이를 위해서는 모든 주요 요인이 4n + 1 형태의 소수여야 합니다.^[17] 따라서 c는 4n + 1 형태입니다. 원시 피타고라스 삼중주에 대한 가능한 빗변 수열은 (OEIS의 A008846번 순서)에서 찾을 수 있습니다.
• 넓이(K = ab/2)는 6으로 나눌 수 있는 합동수입니다.
• 모든 피타고라스 삼각형에서 원의 반지름과 세 개의 원의 반지름은 양의 정수입니다. 구체적으로, 원시 삼중의 경우, 원의 반지름은 r = n(m - n)이고, 변 m - n, 2mn, 빗변 m + n은 각각 m(m - n), n(m + n), m(m + n)입니다.
• 어떤 직각삼각형에 대해서도 탈레스 정리의 반대는 원의 지름이 빗변과 같다고 말하고, 따라서 원시삼각형의 경우 원의 지름은 m² + n이고², 원의 반지름은 이것의 반이므로 유리수이지만 정수가 아닙니다(m과 n의 패리티가 반대이므로).
• 피타고라스 삼각형의 넓이에 원의 곡률과 3개의 원의 곡률을 곱하면 각각 4개의 양의 정수 w > x > y > z가 됩니다. 정수 -w, x, y, z는 데카르트의 원 방정식을 만족합니다.^[20] 마찬가지로, 임의의 직각 삼각형의 바깥쪽 소디 원의 반지름은 그 반지름과 같습니다. 외부 Soddy 중심은 D에 위치하며, 여기서 ACBD는 직사각형, ACB는 직각 삼각형, AB는 빗변입니다.^{[20]: p. 6}
• 원시 피타고라스 3중주는 유클리드의 원시 피타고라스 3중주 생성 공식에 의해 한쪽 다리가 합성이고 짝수여야 하기 때문에 원시 피타고라스 3중주의 두 면만 동시에 프라임이 될 수 있습니다.^[21] 하지만, 한 변만 완전 $거듭제곱$ $p$≥ 2 ${\displaystyle$$$p\geq 2}의 정수가 될 수 있습니다. 왜냐하면 두 변이$지수$가 동일한 완전 거듭제곱의 정수라면 디오판토스${\displaystyle {\mathrm{방정식}}^{}}$ ${\displaystyle {}^{}}$ 2 ${\displaystyle p^{}}$ ± y 2 ${\displaystyle p^{}}$ = z 2 {\$displaystyle$x^{2p}\pm에 대한 정수 해가 없다는 사실과 모순되기 때문입니다.$x$ ${\displaystyle$ $x$$\},$ $y$ ${\displaystyle$ y$}$ $및$ z ${\displaystyle z}$가 쌍별 코프림인$$y$^{2p}=z^{2}$입니다.
• 빗변과 한쪽 다리가 다른 피타고라스 삼각형의 다리인 피타고라스 삼각형은 존재하지 않습니다. 이것은 페르마의 직각삼각형 정리와 동등한 형태 중 하나입니다.^{[13]: p. 14}
• 각각의 원시 피타고라스 삼각형은 면적 K와 제곱 반지름 s의 비율을 가지며, 이는 그 자신에게 고유하며 다음과^[23] 같이 주어집니다.

${\displaystyle {\frac {K}{s^{2}}}={\frac {n(m-n)}{m(m+n)}}=1-{\frac {c}{s}}.}$

• 어떤 원시 피타고라스 삼각형도 빗변으로부터 정수 고도를 가지는 것은 없습니다. 즉, 모든 원시 피타고라스 삼각형은 분해할 수 없습니다.^[24]
• 모든 원시 피타고라스의 세쌍원소 집합은 자연적인 방법으로 뿌리를 내린 세쌍원소 나무를 형성합니다. 원시 피타고라스의 세쌍원소 나무를 참조하십시오.
• 피타고라스 삼각형의 예각 둘 다 유리수가 될 수 없습니다.^[25] (이는 니븐의 정리에서 따온 것입니다.)

특수한 경우

또한, 특정한 부가적인 특성을 가진 특별한 피타고라스의 삼중항이 존재한다는 것을 보장할 수 있습니다.

• 2보다 큰 모든 정수는 2 모드 4와 일치하지 않는 모든 정수(즉, 2보다 큰 모든 정수는 4k + 2의 형태가 아님)는 원시 피타고라스 삼중의 일부입니다. (만약 정수의 형태가 4k라면, 유클리드의 공식에서 n = 1과 m = 2k를 취할 수 있고, 2k + 1이라면, n = k와 m = k + 1을 취할 수 있습니다.)
• 2보다 큰 모든 정수는 원시적이거나 원시적이지 않은 피타고라스 삼중의 일부입니다. 예를 들어, 정수 6, 10, 14 및 18은 원시 삼중항의 일부가 아니라 원시 삼중항 (6, 8, 10), (14, 48, 50) 및 (18, 80, 82)의 일부입니다.
• 빗변과 가장 긴 다리가 정확히 1개 차이가 나는 피타고라스의 세쌍둥이는 무한히 많습니다. 이러한 삼중은 반드시 원시적이며 형태(2n + 1, 2n² + 2n, 2n² + 2n + 1)를 갖습니다. 이는 조건이 삼중항이 원시적이며 (m + n) - 2mn = 1을 확인해야 한다는 것을 의미한다고 언급함으로써 Euclid의 공식에서 비롯됩니다. 이는 (m – n) = 1을 의미하며, 따라서 m = n + 1을 의미합니다. 위와 같은 형태의 삼중항은 따라서 유클리드의 공식에서 m을 n+1로 치환하는 결과를 가져옵니다.
• 빗변과 가장 긴 다리가 정확히 두 개 차이가 나는 원시 피타고라스의 세쌍둥이는 무한히 많습니다. 이들은 모두 원시적인 것으로, 유클리드의 공식에 n=1을 넣으면 얻어집니다. 더 일반적으로, 모든 정수 k > 0에 대해, 빗변과 홀수 다리가 2k만큼² 다른 원시 피타고라스 3중주가 무한히 많이 존재합니다. 그것들은 유클리드의 공식에 n = k를 넣으면 얻어집니다.
• 두 다리가 정확히 하나씩 다른 피타고라스의 세쌍둥이는 무한히 많이 존재합니다. 예를 들어, 20 + 21 = 29입니다. 이들은 ${\displaystyle \frac{}{}}$- ${\displaystyle \frac{n}{}}$ ${\displaystyle {\tfrac {m-n}{n}}$이(가) $2$ ${\displaystyle {\sqrt {2}}$에 수렴할 때 Euclid의 공식에 의해 생성됩니다$.$
• 각각의 양의 정수 k에 대하여, 서로 다른 빗변과 같은 면적을 갖는 피타고라스 삼중항이 존재합니다.
• 각각의 양의 정수 k에 대해, a는 어떤 양의 정수(짝수 다리의 길이는 2mn이고, a = 4b와 같이 인수분해가 많은 a를 선택하기에 충분함)를 갖는 적어도 k개의 원시 피타고라스 삼중항이 존재합니다. 여기서 b는 k개의 서로 다른 홀수 소수들의 곱이며, 이는 적어도 2개의^k 서로 다른 원시 삼중항을 생성합니다).^{[9]: 30}
• 각각의 양의 정수 k에 대해, 같은 빗변을 갖는 적어도 k개의 서로 다른 피타고라스 삼중항이 존재합니다.^{[9]: 31}
• c = p가 소수일 경우, 소수 p가 4n + 1의 형태를 갖는 경우에만 원시 피타고라스 삼중 a + b = c가 존재하며, 이 삼중은 a와 b의 교환까지 유일합니다.
• 더 일반적으로 양의 정수 c는 c의 각 소인수가 1개의 모듈로 4에 일치하는 경우에만 원시 피타고라스 삼중의 빗변입니다. 즉, 각 소인수는 4n + 1의 형태를 갖습니다. 이 경우 b가 <인 원시 피타고라스의 삼중항(a, b, c)의 수는 2이고^k−1, 여기서 k는 c의 뚜렷한 소인수의 수이다.^[26]
• 빗변 c와 다리의 합 a + b 모두에 대해 제곱수를 갖는 피타고라스 3중주가 무한히 많이 존재합니다. 페르마에 따르면, 그러한 가장 작은 삼중항은 a = 4,565,486,027,761; b = 1,061,652,293,520; 및 c = 4,687,298,610,289를 갖습니다. Here a + b = 2,372,159² and c = 2,165,017². 이것은 매개변수 값 m = 2,150,905이고 n = 246,792인 Euclid의 공식에 의해 생성됩니다.
• 빗변에서 정수 고도를 갖는 원시가 아닌 피타고라스 삼각형이 존재합니다.^[28][29] 이러한 피타고라스 삼각형은 이 고도를 따라 분리되고 더 작은 두 개의 피타고라스 삼각형으로 분할될 수 있기 때문에 분해 가능하다고 알려져 있습니다.^[24]

유클리드 공식의 기하학

단위 원의 유리점

피타고라스 삼중항에 대한 유클리드의 공식

${\displaystyle a=m^{2}-n^{2},\quad b=2mn,\quad c=m^{2}+n^{2}}$

단위원 위의 유리점의 기하학적 측면에서 이해할 수 있습니다(Trautman 1998).

실제로 좌표가 (x, y)인 데카르트 평면의 한 점은 x + y = 1이면 단위 원에 속합니다. 만약 x와 y가 유리수라면 점은 유리수, 즉 다음과 같은 코프프라임 정수 a, b, c가 존재한다면

${\displaystyle {\biggl (}{\frac {a}{c}{\biggr}^{2}+{\biggl (}{\frac {b}{c}{\biggr)}^{2}=1.}$

두 구성원 모두에 c를² 곱하면 원 위의 유리점들이 원시 피타고라스의 세 쌍과 일대일 대응 관계에 있음을 알 수 있습니다.

단위 원은 매개 변수 방정식에 의해 정의될 수도 있습니다.

${\displaystyle x={\frac {1-t^{2}}{1+t^{2}}}\quad y={\frac {2t}{1+t^{2}}}.}$

피타고라스의 삼중항에 대한 유클리드의 공식과 역관계 t = y / (x + 1)은 (-1, 0)을 제외하고 원 위의 한 점 (x, y)이 유리수인 경우, 해당 t의 값이 유리수인 경우에만 유리수임을 의미합니다. t = y / (x + 1) = b / (a + c) = n / m은 길이 b의 삼각형 변에 반대되는 각도의 절반의 접선이기도 합니다.

입체적 접근

단위원 위의 점들과 유리좌표가 있는 원시 피타고라스의 세 배 사이에는 대응 관계가 있습니다. 이 시점에서 유클리드의 공식은 삼각법 또는 입체 투영법을 사용하여 동등하게 도출할 수 있습니다.

입체 접근법의 경우, P'가 유리 좌표를 갖는 x 축의 한 점이라고 가정합니다.

${\displaystyle P'=\left({\frac {m}{n}},0\right)}$

그러면, 점 P가 좌표를 갖는다는 것을 기본 대수로 나타낼 수 있습니다.

${\displaystyle P=\left({\frac {2\left({\frac {m}{n}}\right)}{\left({\frac {m}{n}}\right)^{2}+1}},{\frac {\left({\frac {m}{n}}\right)^{2}-1}{\left({\frac {m}{n}}\right)^{2}+1}}\right)=\left({\frac {2mn}{m^{2}+n^{2}}},{\frac {m^{2}-n^{2}}{m^{2}+n^{2}}}\right)}$

이것은 x축의 각 유리점이 단위원의 유리점으로 넘어간다는 것을 나타냅니다. 반대로, 단위 원의 모든 유리점은 x축의 그러한 점에서 온 것이며, 역 입체 사영을 적용하면 다음과 같습니다. P(x, y)가 x와 y의 유리수를 갖는 단위원의 한 점이라고 가정합니다. 그러면 x축에 입체 사영하여 얻은 점 P'는 좌표를 갖습니다.

${\displaystyle \left ({\frac {x}{1-y}},0\right)}$

합리적인 것입니다.

대수기하학의 관점에서, 단위원 위의 유리점들의 대수적 다양성은 유리수들 위의 아핀선에 대해 쌍대비례합니다. 따라서 단위원을 유리곡선이라고 하며, 이 사실은 유리함수를 통해 그 위의 (합리적인 수) 점들의 명시적인 매개변수화를 가능하게 합니다.

2차원 격자 내의 피타고라스 삼각형

2D 격자는 고립된 점들의 규칙적인 배열로, 어느 한 점을 데카르트 원점(0, 0)으로 선택하면 다른 모든 점들은 (x, y)에 있고, 여기서 x와 y는 모든 양과 음의 정수에 걸쳐 있습니다. 3중(a, b, c)인 모든 피타고라스 삼각형은 좌표 (0, 0), (a, 0) 및 (0, b)에 정점이 있는 2차원 격자 내에서 그릴 수 있습니다. 삼각형의 경계 내에 엄격하게 놓여 있는 격자점의 수는 (${\displaystyle \frac{\mathrm{a}}{}}$- 1${\displaystyle \frac{)}{}}$ (${\displaystyle \frac{\mathrm{b}}{}}$- 1${\displaystyle \frac{)}{}}$- ${\displaystyle \frac{gcd}{}}$(${\displaystyle \frac{a,}{}}$ b${\displaystyle \frac{)}{}}$+ ${\displaystyle \frac{\mathrm{}}{};}$ ${\displaystyle {\tfrac {(a-1)(b-1)-\gcd {(a,b)}$ + $1}$ {$2$}$}};}$원시 피타고라스 삼중의 $경우$^[30] 이 내부 격자 수는 (${\displaystyle \frac{a}{}}$- ${\displaystyle \frac{1)}{}}$ (${\displaystyle \frac{\mathrm{b}}{}}$- 1${\displaystyle \frac{)}{}}$ ${\displaystyle \frac{\mathrm{}}{}.}$ ${\displaystyle {\tfrac {(a-1)(b-1)}{2}}$입니다.$}$면적$$(Pick의 정리에 의해 내부 격자 수에 경계 격자 수의 절반을 더한 값)은 ${\displaystyle \frac{\mathrm{}}{}}$ ${\$와 같습니다.$$

같은 면적을 공유하는 두 원시 피타고라스의 세쌍원소의 첫 발생은 변(20, 21, 29), (12, 35, 37) 및 공통 면적 210(OEIS의 시퀀스 A093536)을 가진 삼각형에서 발생합니다. 동일한 내부 격자 수를 공유하는 두 원시 피타고라스 삼중항의 첫 번째 발생은 (18108, 252685, 25333), (28077, 162964, 165365) 및 내부 격자 수 2287674594(OEIS의 시퀀스 A225760)에서 발생합니다. (4485, 5852, 7373), (3059, 8580, 9109), (1380, 19019, 19069), (13123110), 같은 면적을 공유하는 원시 피타고라스의 세 쌍둥이가 발견되었습니다. 아직까지 동일한 내부 격자 수를 공유하는 원시 피타고라스의 세 쌍의 집합은 발견되지 않았습니다.

원시 피타고라스 3쌍의 수

By Euclid's formula all primitive Pythagorean triples can be generated from integers ${\displaystyle m}$ and ${\displaystyle n}$ with ${\displaystyle m>n>0}$, ${\displaystyle m+n}$ odd and ${\displaystyle \gcd(m,n)=1}$. $따라서{\displaystyle \frac{}{}}$ n m ${\$이 간격$({\displaystyle 0,}$ ${\displaystyle 1)}$ ${\displaystyle(0,$ 1$)}$이고 m${\displaystyle }$+ ${\displaystyle n}$ ${\displaystyle$ m$+n}$이 홀수인 원시 피타고라스 삼중에 대한 유리수의 1:1 매핑이 있습니다.

The reverse mapping from a primitive triple ${\displaystyle (a,b,c)}$ where ${\displaystyle c>b>a>0}$ to a rational ${\displaystyle {\tfrac {n}{m}}}$ is achieved by studying the two sums ${\displaystyle a+c}$ and ${\displaystyle b+c}$. 이 합 중 하나는${\displaystyle }$(${\displaystyle m}$+ ${\displaystyle n{}^{}}$ 2 ${\$+ $n)^{2}}$에 해당하는 정사각형이고, 다른 하나는 ${\displaystyle {2m\mathrm{}}^{}}$ 2 ${\$에 해당하는 정사각형의 두 배입니다$.$ 그런 다음 $유리$한 ${\displaystyle \frac{n}{}}$ m ${\$를 결정할 수 있습니다$.$

원시 피타고라스 3배를 열거하기 위해 유리수는 순서 쌍$({\displaystyle n,}$ ${\displaystyle m)}$ ${\displaystyle(n,m)}$으로 표현되고$$ 칸토어의 페어링 함수와 같은 페어링 함수를 사용하여 정수로 매핑될 수 있습니다. 예는 에서 확인할 수 있습니다(OEIS의 시퀀스 A277557). 시작합니다.

${\displaystyle 8,}$ ${\displaystyle 18,}$ ${\displaystyle 19,}$ ${\displaystyle 32,}$ ${\displaystyle 33,}$ ${\displaystyle 34,}$ … ${\displaystyle 8, 18, 19, 32, 33,$ }, 그리고 합리적 이유를 제시합니다.

${\displaystyle \frac{12}{},}$ ${\displaystyle \frac{23}{},}$ ${\displaystyle \frac{14}{},}$ ${\displaystyle \frac{34}{},}$ ${\displaystyle \frac{25}{},}$ ${\displaystyle \frac{16}{},}$… ${\displaystyle {\tfrac {1}{2$}}, ${\tfrac {2}{3$}, ${\tfrac {1}{4},$ {\$tfrac {3}{4},$ {\$tfrac {2}{5},$ {\$tfrac {1}{6},\tfrac$}, 이들은$$ 차례로 기본 트리플을 생성합니다.

${\displaystyle (3,4,5),(5,12,13),(8,15,17),(7,24,25),(20,21,29),(12,35,37),\dots }$

스피너 및 모듈 그룹

마찬가지로 피타고라스의 세쌍은 형태의 정사각형 행렬로 인코딩될 수 있습니다.

${\displaystyle X={\begin{bmatrix}c+b&a\\a&c-b\end{bmatrix}}.}$

이 형태의 행렬은 대칭입니다. 또한 X의 행렬식은

${\displaystyle \det X=c^{2}-a^{2}-b^{2}\,}$

정확히 (a,b,c)가 피타고라스의 3배일 때 0입니다. X가 피타고라스의 3배에 해당한다면 행렬로서 1순위를 가져야 합니다.

X는 대칭이므로 선형대수학에서의 결과로부터 외부곱이 되도록 열벡터 ξ = [m]가 존재함을 알 수 있습니다.

${\displaystyle X=2{\begin{bmatrix}m\n\end{bmatrix}}[m\ n]=2\xi \xi ^{T}\,}$

(1)

hold, 여기서 T는 행렬 전치를 나타냅니다. ξ와 -ξ는 동일한 피타고라스 삼중항을 생성하기 때문에 벡터 ξ는 스피너(로렌츠 그룹 SO(1, 2))로 간주될 수 있습니다. 추상적인 용어로 Euclid 공식은 (1)에서와 같이 각 원시 피타고라스 삼중항이 정수 입력을 가진 스피너의 자체를 갖는 외부 곱으로 작성될 수 있음을 의미합니다.

모듈러 그룹 γ는 정수 항목이 있는 2×2 행렬의 집합입니다.

${\displaystyle A={\begin{bmatrix}\alpha &\beta \\gamma &\delta \end{bmatrix}}$

행렬식이 1인 경우: α δ - β γ = 1. 이 집합은 γ에 있는 행렬의 역수가 다시 γ에 있으므로 γ에 있는 두 행렬의 곱과 마찬가지로 그룹을 형성합니다. 모듈식 그룹은 모든 정수 스피너의 수집에 작용합니다. 또한 그룹은 상대적으로 소수의 엔트리를 가진 정수 스피너 컬렉션에서 과도적입니다. [m]^T에 상대적으로 소수의 항목이 있는 경우,

${\displaystyle {\begin {bmatrix}m&-v\n&u\end{bmatrix}}{\begin{bmatrix}1\\0\end{bmatrix}}={\begin{bmatrix}m\\n\end{bmatrix}}$

여기서 u와 v는 (유클리드 알고리즘에 의해) mu + nv = 1이 되도록 선택됩니다.

(1)의 스피너 ξ에 작용함으로써, γ의 작용은 음의 성분을 가진 삼중항을 허용한다면 피타고라스 삼중항에 대한 작용으로 넘어갑니다. 따라서 A가 γ의 행렬이라면,

${\display style 2(A\xi )(A\xi )^{T}=AXA^{T}\,}$

(2)

(1)의 행렬 X에 대한 작업을 발생시킵니다. 원시 삼중항에서 원시 삼중항으로 이동하는 경우가 있기 때문에 원시 삼중항에 대해 잘 정의된 동작을 제공하지 않습니다. 이 시점에서 (Trautman 1998에 따라) c > 0이고 (a,b,c) 둘 중 하나가 상대적으로 소수이거나 (a/2,b/2,c/2)가 a/2 홀수로 상대적으로 소수인 경우 트리플 (a,b,c) 표준이라고 부르는 것이 편리합니다. 스피너 [m]^T에 상대적으로 소수의 엔트리가 있는 경우, (1)에 의해 결정되는 관련 트리플(a,b,c)은 표준 트리플입니다. 따라서 모듈 그룹의 동작은 표준 삼중 집합에 대해 과도적입니다.

또는 m이 홀수이고 n이 짝수인 m과 n의 값으로 주의를 제한합니다. γ의 부분군 γ(2)를 군 동형 사상의 커널이라고 하자.

${\displaystyle \Gamma =\mathrm {SL}(2,\mathbf {Z})\to \mathrm {SL}(2,\mathbf {Z} _{2})}$

여기서 SL(2,Z₂)은 정수 모듈로 2의 유한장 Z에₂ 대한 특수 선형 그룹입니다. 그런 다음 γ(2)는 각 항목의 패리티를 보존하는 단모듈 변환 그룹입니다. 따라서 ξ의 첫 번째 항목이 홀수이고 두 번째 항목이 짝수인 경우 모든 A ∈ γ(2)에 대한 A ξ도 마찬가지입니다. 실제로, (2) 작용 하에서, 그룹 γ(2)는 원시 피타고라스 세쌍의 수집에 대해 과도기적으로 작용합니다(Alper 2005).

그룹 γ(2)는 생성기가 행렬인 자유 그룹입니다.

${\displaystyle U={\begin{bmatrix}1&2\\0&1\end{bmatrix}},\qquad L={\begin{bmatrix}1&0\\2&1\end{bmatrix}}.}$

따라서 모든 원시 피타고라스 삼중항은 행렬 U와 L의 사본의 곱으로 독특한 방법으로 얻을 수 있습니다.

부모/자녀 관계

베르그렌(Berggren, 1934)의 결과로 모든 원시 피타고라스 삼중항은 아래의 세 선형 변환 T₁, T₂, T를₃ 사용하여 (3, 4, 5) 삼각형에서 생성될 수 있으며, 여기서 a, b, c는 삼중항의 변을 나타냅니다.

	신변	신변 b	신변 c
T1:	a − 2b + 2c	2a − b + 2c	2a − 2b + 3c
T2:	a + 2b + 2c	2a + b + 2c	2a + 2b + 3c
T3:	−a + 2b + 2c	−2a + b + 2c	−2a + 2b + 3c

다시 말해, 모든 원시 삼중은 세 개의 추가 원시 삼중에 대한 "부모"가 될 것입니다. 연산 T는 a = 3, b = 4, c = 5인 초기 노드에서 시작하여 새로운 트리플을 생성합니다.

(3 − (2×4) + (2×5), (2×3) − 4 + (2×5), (2×3) − (2×4) + (3×5)) = (5, 12, 13),

마찬가지로 T와₂ T는₃ 세 배(21, 20, 29)와 (15, 8, 17)를 생성합니다.

선형 변환 T₁, T₂ 및 T는₃ 이차 형식의 언어로 기하학적 해석을 갖습니다. 이러한 반사는 정수에 대해 x² + y² - z의² 직교 그룹을 생성하는 반사와 밀접한 관련이 있지만 동일하지는 않습니다.^[31]

가우스 정수와의 관계

또는 가우스 정수를 사용하여 유클리드의 공식을 분석하고 증명할 수 있습니다.^[32] 가우스 정수는 α = u + vi 형태의 복소수이며, 여기서 u와 v는 보통 정수이고 i는 음수의 제곱근입니다. 가우스 정수의 단위는 ±1과 ±i입니다. 보통의 정수들을 유리수라고 부르고 'Z'라고 표시합니다. 가우시안 정수는 Z[i]로 표시됩니다. 피타고라스 정리의 우변은 가우스 정수로 인수분해될 수 있습니다.

${\displaystyle c^{2}=a^{2}+b^{2}=(a+bi){\overline {(a+bi)}}=(a+bi)(a-bi).}$

원시 피타고라스의 삼중항은 a와 b가 코프프라임, 즉 정수에서 소인수를 공유하지 않는 삼중항입니다. 이러한 삼중의 경우 a 또는 b는 짝수이고, 다른 하나는 홀수이며, 이로부터 c도 홀수임을 알 수 있습니다.

원시 피타고라스의 두 인자 z := a + bi 와 z* := a - bi 는 각각 가우스 정수의 제곱과 같습니다. 이는 모든 가우시안 정수가 단위까지 가우시안 소수에 고유하게 인수분해될 수 있다는 속성을 사용하여 증명할 수 있습니다.^[33] (이 독특한 인수분해는 대략적으로 말하면 유클리드 알고리즘 버전을 정의할 수 있다는 사실에서 비롯됩니다.) 증명에는 세 단계가 있습니다. 먼저 a와 b가 정수에서 소인수를 공유하지 않으면 가우시안 정수에서도 소인수를 공유하지 않습니다. (단위가 아닌 가우시안 정수 g, u, v, g가 있는 a = gu 및 b = gv를 가정하자. 그러면 원점을 통해서 같은 선상에 누운다. 이러한 선 위의 모든 가우시안 정수는 어떤 가우시안 정수 h의 정수배입니다. 그러나 정수 gh ≠ ±1은 a와 b를 모두 나눕니다.) 둘째, z와 z*는 마찬가지로 가우시안 정수에서 소인수를 공유하지 않습니다. 만약 그렇다면, 그들의 공통 약수 δ은 z + z* = 2a 및 z - z* = 2ib로 나뉠 것입니다. a와 b는 코프라임이므로, 이는 δ가 2 = (1 + i) (1 - i) = i(1 - i)로 나눈다는 것을 의미합니다. 공식 c = zz*로부터, 그것은 차례로 c가 원시 피타고라스 3중주의 가설과 반대로 짝수라는 것을 의미합니다. 셋째, c는² 정사각형이기 때문에 인수분해의 모든 가우시안 프라임은 두 배, 즉 짝수 번 나타납니다. z와 z*는 소인수를 공유하지 않으므로 이 배가는 이들에게도 해당됩니다. 따라서 z와 z*는 사각형입니다.

따라서 첫 번째 요인을 작성할 수 있습니다.

${\displaystyle a+bi=\varepsilon \left(m+ni\right)^{2}},\quad \varepsilon \in \{\pm 1,\pm i\}$

이 방정식의 실수 부분과 허수 부분은 다음 두 가지 공식을 제공합니다.

${\displaystyle {\begin{case}\varepsilon =+1,&\quad a=+\left(m^{2}-n^{2}\right),\quad b=+2mn;\\\varepsilon =-1,&\quad a=-\left(m^{2}-n^{2}\right),\quad b=-2mn;\\\varepsilon =+i,&\quad a=-2mn,\quad b=+\left(m^{2}-n^{2}\right);\\\varepsilon =-i,&\quad a=+2mn,\quad b=-\left(m^{2}-n^{2}\right).\end{case}}$

어떤 원시 피타고라스 삼중항에 대해서도 이 두 방정식이 만족되도록 정수 m과 n이 있어야 합니다. 따라서 모든 피타고라스의 세 배는 이 정수들 중 어떤 선택으로부터 생성될 수 있습니다.

완전 제곱 가우스 정수

가우시안 정수의 제곱을 고려하면 유클리드 공식을 가우시안 정수의 완벽한 제곱을 나타내는 것으로 직접 해석할 수 있습니다.

${\displaystyle (m+ni)^{2}=(m^{2}-n^{2})+2mni.}$

가우시안 정수가 유클리드 영역이고 가우시안 정수 ${\displaystyle pp}$ ${\displaystyle {}^{}}$의 경우 ${\$ p$^{2}}$가 항상$$ 정사각형이라는 사실을 사용하면 빗변이 소수인 경우 피타고라스 삼중항이 소수 가우시안 정수의 제곱에 해당한다는 것을 보여줄 수 있습니다.

가우시안 정수가 소수가 아니면 p ${\displaystyle {}^{\mathrm{}}}$ ${\$p$^{2}}$ 및 ${\displaystyle {}^{\mathrm{}}}$ 2 ${\$q$^{2}}$ 정수를$$$$ 갖는 두 가우시안 정수 p 및 q의 곱입니다. 크기는 가우스 정수에서 곱하기 때문에 곱은 ${\displaystyle pq}$ $displaystyle pq}$이어야$$하며 제곱하면 피타고라스 삼중항이 합성되어야 합니다. 대조군이 증명을 완료합니다.

3배수 분포

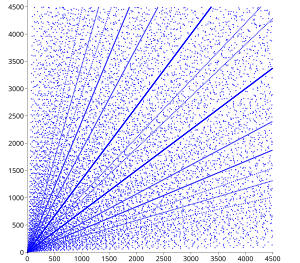
피타고라스의 세쌍원소 분포에 대해서는 여러 가지 결과가 있습니다. 산점도에는 이미 여러 가지 명백한 패턴이 표시되어 있습니다. 원시 삼중의 다리(a,b)가 그림에 나타날 때마다 (a,b)의 모든 정수 배수도 그림에 나타나야 하며, 이 속성을 사용하면 다이어그램에서 원점에서 방사되는 선이 나타납니다.

산란계 내에는 점의 밀도가 높고 원점에 초점이 있는 포물선 패턴 세트가 있으며, 네 방향 모두에서 열립니다. 서로 다른 포물선이 축에서 교차하며 입사각이 45도인 축에서 반사되는 것처럼 보이며 세 번째 포물선이 수직으로 들어갑니다. 이 사분면 내에서 원점을 중심으로 한 각 호는 포물선의 끝과 반라투스 직장과의 교차점 사이에 있는 부분을 보여줍니다.

이러한 패턴은 다음과 같이 설명할 수 있습니다. ${\displaystyle {2\mathrm{}}^{}\mathrm{4n}}$ ${\displaystyle$ a$^{2}/4n}$이 정수라면 (${\displaystyle a}$, n${\displaystyle }$- ${\displaystyle {}^{}}$ ${\displaystyle {2\mathrm{}}^{}\mathrm{4n}}$ $displaystyle n-a^{2}/4n$ n${\displaystyle }$+ ${\displaystyle {}^{}}$ ${\displaystyle {2\mathrm{}}^{}\mathrm{4n}}$ ${\displaystyle$ n$+a^{2}/4n$은 피타고라스의 삼중항입니다. (사실 모든 피타고라스의 삼중항 (a, b, c)은 정수 n을 사용하여 이러한 방식으로 작성할 수 있으며, 가능하면 a와 b를 교환한 후, ${\displaystyle n}$ =${\displaystyle }$(${\displaystyle b}$+ c${\displaystyle }$)${\displaystyle }$/ 2 ${\displaystyle$ n = ($b+c)/2}$ 및 a와 b는 모두 홀수일 수 없습니다.) 따라서 피타고라스의 삼중항은 $b$ = ${\displaystyle n}$- a ${\displaystyle 2^{}4}$ n $displaystyle$b = $n-a^{2}/4n$ 즉 a축에 반사된 포물선과 a와 b가 교환된 해당 곡선에 놓여 있습니다. 주어진 n(즉, 주어진 포물선에서)에 대해 a가 달라지면 n이 제곱 또는 제곱의 작은 배수인 경우 b의 정수 값이 비교적 자주 발생합니다. 만약 그러한 값들이 서로 가까이 놓여 있다면, 대응하는 포물선들은 대략 일치하고, 세 쌍은 좁은 포물선 띠 안에 모여 있습니다. 예를 들어, 38 = 1444, 2 × 27 = 1458, 3 × 22 = 1452, 5 × 17 = 1445 및 10 × 12 = 1440이며, n ≈ 1450 주위의 대응하는 포물선 스트립은 산점도에서 명확하게 볼 수 있습니다.

위에서 설명한 각 특성은 포물선의 함수 형태에서 바로 따릅니다. 포물선은 a = 2n의 a축에서 반사되며, 이 시점에서 a에 대한 b의 도함수는 –1이므로 입사각은 45°입니다. 클러스터는 모든 트리플과 마찬가지로 정수배로 반복되므로 값 2n도 클러스터에 해당합니다. 해당 포물선은 b = 2n에서 b 축과 직각으로 교차하므로 a와 b의 교환 시 반사는 a = 2n에서 a 축과 직각으로 교차하며, 여기서 정확히 n에 대한 포물선이 a 축에서 반사됩니다. (물론 a와 b를 교환한 경우에도 마찬가지입니다.)

Albert Fässler 등은 등각 매핑의 맥락에서 이러한 포물선의 중요성에 대한 통찰력을 제공합니다.^[34][35]

특수한 경우 및 관련 방정식

플라톤 수열

보다 일반적인 피타고라스 삼중항의 구성 중 case n = 1은 오래전부터 알려져 있습니다. 프로쿠스는 유클리드의 원소 제1서 제47차 명제에 대한 주석에서 다음과 같이 설명합니다.

이런 종류의 삼각형을 발견하는 특정한 방법들이 전해지는데, 하나는 플라톤을 지칭하고 다른 하나는 피타고라스를 지칭합니다. (후자는) 홀수에서 시작합니다. 그것은 홀수를 직각에 대한 변들 중 작은 것으로 만들고, 그 다음에 그것의 제곱을 취하고, 합을 빼고, 그 차이의 절반을 직각에 대한 변들 중 큰 것으로 만들고, 마지막으로 이것에 합을 더하고, 나머지 변인 빗변을 형성하기 때문입니다.
...플라톤의 방법은 짝수로부터 주장합니다. 주어진 짝수를 취하여 직각에 대한 변 중 하나로 만들고, 이 수를 2등분하여 반을 제곱한 다음 정사각형에 통일성을 더하여 빗변을 만들고, 정사각형에서 통일성을 빼서 직각에 대한 반대변을 만듭니다. ... 따라서 다른 방법으로 얻은 것과 동일한 삼각형을 형성했습니다.

등식 형태에서는 다음과 같습니다.

a는 홀수(Pythagoras, 기원전 540년경)입니다.

${\displaystyle {\text{side }}a:{\text{side }}b={a^{2}-1 \over 2}:{text{side }}c={a^{2}+1 \over 2}}}$

a is even (Plato, c. 기원전 380년):

${\displaystyle {\text{side}}a:{\text{side}}b=\left ({ a \over 2}\right)^{2}-1:{\text{side}c=\left ({ a \over 2}\right)^{2}+1}$

가 정수가 아닌 유리수 값을 취할 수 있도록 함으로써 기본 플라톤 수열(a, (a² - 1)/2 및 (a² + 1)/2)에서 모든 피타고라스 삼중항을 적절한 리스케일링으로 얻을 수 있음을 보여줄 수 있습니다. 시퀀스에서 a를 분수 m/n으로 대체하면 리스케일링 후 '표준' 트리플 제너레이터(2mn², m - n², m + n²²)와 동일한 결과가 됩니다. 따라서 모든 세 개의 세 개의 삼각형은 유사한 삼각형(세 개의 각도가 같고 원래와 같은 비율의 변이 있는 삼각형)을 생성하는 데 사용할 수 있는 상응하는 유리수 a 값을 가집니다. 예를 들어, (56, 33, 65)의 플라톤 당량은 (a, (a –1)/2, (a+1)/2) = (56/32, 33/32, 65/32) 로 = m/n = 7/4 로 생성됩니다. 플라톤 수열 자체는 디오판토스 II에 설명된 '사각형 분할' 단계를 따라 도출할^{[clarification needed]} 수 있습니다.VIII.

자코비-매든 방정식

그 방정식은.

${\displaystyle a^{4}+b^{4}+c^{4}+d^{4}=(a+b+c+d)^{4}}$

이것은 특별한 피타고라스의 세배에 해당합니다.

${\displaystyle (a^{2}+ab+b^{2})^{2}+(c^{2}+cd+d^{2})^{2}=((a+b)^{2}+(a+b)(c+d)+(c+d)^{2})^{2}}$

변수에 대한 풀이는 타원 곡선을 포함하기 때문에 이 방정식에는 무한히 많은 해가 있습니다. 작은 것들은.

${\displaystyle a,b,c,d=-2634,955,1770,5400}$

${\displaystyle a,b,c,d=-31764,7590,27385,48150}$

두 제곱의 같은 합

$a$ ${\displaystyle 2^{}}$+ b ${\displaystyle 2^{}}$ = ${\displaystyle {}^{}}$ ${\displaystyle 2^{}}$+ d ${\displaystyle 2^{}}$ ${\displaystyle$ a$^{2}$ + b$^{2$)에 대한 해를 생성하는 한 가지 방법$}=c^{2}+d^{2}}$는 a, b, c, d를 정수 m, n, p, q로 매개변수화하는 것입니다.

${\displaystyle (m^{2}+n^{2})(p^{2}+q^{2})=(mp-nq)^{2}+(np+mq)^{2}=(mp+nq)^{2}+(np-mq)^{2}.}$

네 번째 거듭제곱 두 개의 등합

피타고라스의 세쌍의 세쌍의 피타고라스의 세쌍이 주어졌을 때,

${\displaystyle (a^{2}-b^{2})^{2}+(2ab)^{2}=(a^{2}+b^{2})^{2}}$

${\displaystyle (c^{2}-d^{2})^{2}+(2cd)^{2}=(c^{2}+d^{2})^{2}}$

hypot 사용이 아닌 쪽과 사용이 적은 쪽의 동등한 제품을 찾는 문제,

${\displaystyle (a^{2}-b^{2})(a^{2}+b^{2})=(c^{2}-d^{2})(c^{2}+d^{2})}$

식과 동일한 것으로 쉽게 볼 수 있습니다.

${\displaystyle a^{4}-b^{4}=c^{4}-d^{4}}$

${\displaystyle \mathrm{그리고}}$ 오일러는 $처음$에 a${\displaystyle ,}$ b${\displaystyle ,}$ ${\displaystyle c,}$ ${\displaystyle d}$ = ${\displaystyle 133,}$ ${\displaystyle 59,}$ ${\displaystyle 158,}$ ${\displaystyle 134}$ ${\displaystyle$ a,$b, c,$ d = $133, 59, 158, 134}$로 해를 풀었습니다$.$ 그는 이것이 타원 곡선의 유리점이라는 것을 보여주었으므로, 해는 무한히 많습니다. 실제로 그는 7차 다항식 매개변수화도 발견했습니다.

데카르트의 원 정리

모든 변수가 제곱인 데카르트의 원 정리의 경우,

${\displaystyle 2(a^{4}+b^{4}+c^{4}+d^{4})=(a^{2}+b^{2}+c^{2}+d^{2})^{2}}$

오일러는 이것이 피타고라스의 세 번의 동시 삼중항과 동등하다는 것을 보여주었습니다.

${\displaystyle (2ab)^{2}+(2cd)^{2}=(a^{2}+b^{2}-c^{2}-d^{2})^{2}}$

${\displaystyle (2ac)^{2}+(2bd)^{2}=(a^{2}-b^{2}+c^{2}-d^{2})^{2}}$

${\displaystyle (2ad)^{2}+(2bc)^{2}=(a^{2}-b^{2}-c^{2}+d^{2})^{2}}$

또한 무한히 많은 해가 존재하며, 특수한 경우 $a{\displaystyle }$+ ${\displaystyle b}$ = c ${\displaystyle a+b$ = c$\}$인 경우 방정식은 다음과 같이 단순화됩니다.

${\displaystyle 4(a^{2}+ab+b^{2})=d^{2}}$

${\displaystyle \mathrm{작은}}$ 해를 $a{\displaystyle ,}$ b${\displaystyle ,}$ ${\displaystyle c,}$ ${\displaystyle d}$ = ${\displaystyle 3,}$ ${\displaystyle 5,}$ ${\displaystyle 8,}$ ${\displaystyle 14}$ ${\displaystyle$ a,$b,$ c,$$d = $3,$ 5,$8, 14}$로 하고 이진 이차 형식으로 풀 수 있습니다.

거의 이등변에 가까운 피타고라스의 세쌍둥이

피타고라스의 세 쌍은 이등변이 아닌데, 왜냐하면 다른 한 변에 대한 빗변의 비율은 √ 2이지만, √ 2는 2개의 정수의 비율로 표현될 수 없기 때문입니다.

그러나, 다음과 같이, 가설이 아닌 변의 길이가 1개씩 차이나는 변을 적분한 직각 삼각형이 있습니다.

${\displaystyle 3^{2}+4^{2}=5^{2}}$

${\displaystyle 20^{2}+21^{2}=29^{2}$

그리고 무한히 많은 사람들이 있습니다. 다음과 같이 완전히 매개변수화할 수 있습니다.

${\displaystyle \left ({\tfrac {x-1}{2}\right)^{2}+\left ({\tfrac {x+1}{2}}}\right)^{2}=y^{2}$

여기서 {x, y}는 Pell 방정식 ${\displaystyle x^{}}$ 2${\displaystyle {}^{}}$- ${\displaystyle 2}$ ${\displaystyle {}^{}}$ ${\displaystyle 2^{}}$ =${\displaystyle }$- 1 ${\displaystyle$ x$^{2}-2y^{2$}=-$1}$의 해입니다$.$

만약 a, b, c가 이러한 유형의 원시 피타고라스 3중 변이라면, 펠 방정식의 해는 재귀 공식에 의해 주어집니다.

${\displaystyle {}_{}{}_{}}$${\displaystyle 1_{}}$ $=$ ${\displaystyle 3}$ ${\display a$${\displaystyle {\_}_{}}$${1$}${\displaystyle {}_{}}$${\displaystyle {}_{}}$ $3$${\displaystyle {}_{}}$= ${\displaystyle 2_{}}$ = ${\displaystyle 20}$ ${\display a$${\displaystyle {\_}_{}}$${2$}$=$ ${\displaystyle 2_{}}$$0}$인 = ${\displaystyle {}_{}}$ $a$ -$$+${\display a$ = $20$

${\displaystyle {}_b}$ n $=$ ${\displaystyle {}_{}}$ ${\displaystyle b_{}}$- ${\displaystyle 1_{}}$- ${\displaystyle {}_{}}$ ${\displaystyle {\mathrm{n}}_{}}$- 2${\displaystyle {}_{}}$- ${\displaystyle 2}$ ${\displaystyle b$} ${\displaystyle {}_{}}$ ${\displaystyle 6}$ $b_{n-1}$ - $b_{n-2}-2}$$b$ ${\displaystyle 1_{}}$ ${\displaystyle {}_{}}$ 4 ${\displaystyle b$${\displaystyle {\_}_{}}$${1$} = 4$}$ 및${\displaystyle {}_{}}$${\displaystyle b_{}}$ 2 = ${\displaystyle 21}$ ${\displaystyle b$${\displaystyle {\_}_{}}$${2$} = $21}$

${\displaystyle {}_{cn}}$ $=$ ${\displaystyle 6}$ ${\displaystyle {\mathrm{cn}}_{}}$- 1${\displaystyle {}_{}}$- ${\displaystyle {cn}_{}}$- ${\displaystyle 2_{}}$ ${\displaystyle c$} ${\displaystyle {}_{}}$ $6c_{n-1}-c_{n-2}}$$c$ ${\displaystyle 1_{}}$ = ${\displaystyle 5}$ ${\displaystyle c$${\displaystyle {\_}_{}}$${1$} $=$ $5}$ 및${\displaystyle {}_{}}$$c$ ${\displaystyle 2_{}}$ = ${\displaystyle 29}$ ${\displaystyle c$${\displaystyle {\_}_{}}$${2$} = $29})$입니다$.$

원시 피타고라스 세쌍둥이의 이 순서는 원시 피타고라스 세쌍둥이의 뿌리가 있는 삼원수의 중심 줄기(줄기)를 형성합니다.

다음과 같이 하나씩 차이가 나는 것이 더 긴 비-효모 측면과 저-효모 측면일 때

${\displaystyle 5^{2}+12^{2}=13^{2}}$

${\displaystyle 7^{2}+24^{2}=25^{2}}$

그렇다면 원시 피타고라스 삼중 a, b, c에 대한 완전한 해는

${\displaystyle a=2m+1,\quad b=2m^{2}+2m,\quad c=2m^{2}+2m+1}$

그리고.

${\displaystyle (2m+1)^{2}+(2m^{2}+2m)^{2}=(2m^{2}+2m+1)^{2}}$

여기서 정수 > 0 ${\displaystyle m>$ 0$}$이(가) 생성 매개 변수입니다.

이는 모든 홀수(1보다 큰)가 거의 이등변 원시 피타고라스 3중주의 형태로 나타난다는 것을 보여줍니다. 원시 피타고라스 세쌍둥이의 이 순서는 원시 피타고라스 세쌍둥이의 뿌리가 박힌 삼원수의 오른쪽 바깥 줄기를 형성합니다.

거의 이등변에 가까운 원시 피타고라스 3중주의 또 다른 특징은 양변이 서로 관련이 있다는 것입니다.

${\displaystyle a^{b}+b^{a}=kc}$

어떤 정수 $K{\displaystyle }$ ${\displaystyle$ K$}$에 대하여$.$ 또는 ${\displaystyle b^{}}$+ b ${\displaystyle a^{}}$ ${\$ a$^{b}+b^{a}}$는 $다음$과 같이 c ${\displaystyle$ c$}$로 나뉠 수 있습니다.

${\displaystyle (}$ ${\displaystyle {}^{}}$ ${\displaystyle {12}^{}}$+ ${\displaystyle {125}^{}}$)${\displaystyle }$/${\displaystyle 13}$ $=$ ${\displaystyle 18799189}$ ${\displaystyle(5^{12}+12^{5}$18799189}

피타고라스의 세 배에 속하는 피보나치 수

5로 시작하는 매초 피보나치 수는 정수 변을 갖는 직각삼각형의 빗변의 길이, 즉 피타고라스 3중 가장 큰 수이다.

이 공식으로부터 얻어진 피타고라스 삼각형의 수열은 길이의 변을 갖습니다.

(3,4,5), (5,12,13), (16,30,34), (39,80,89), ...

각 삼각형의 가운데 변은 앞 삼각형의 세 변의 합입니다.^[39]

일반화

피타고라스의 세쌍원소 개념을 일반화하는 데에는 여러 가지 방법이 있습니다.

Pythagorean n-tuple

표정이.

${\displaystyle \left(m_{1}^{2}-m_{2}^{2}-\ldots -m_{n}^{2}\right)^{2}+\sum _{k=2}^{n}(2m_{1}m_{k})^{2}=\left(m_{1}^{2}+\ldots +m_{n}^{2}\right)^{2}}$

는²
₂ m²
₁ > m + ... + m인²
_n 양의 정수(m_1n, ..., m)의 임의의 튜플에 대한 피타고라스 n-튜플입니다. 피타고라스 n-튜플은 그 값들의 가장 큰 공약수로 나누어짐으로써 원시적인 것으로 만들 수 있습니다.

게다가, 어떤 원시 피타고라스 학파도²
₁ +...+ a = c는 이 접근법으로 구할 수 있습니다. (m, ..., m) = (c + a, a, ..., a)를 사용하여 위의 공식으로 피타고라스 n-tup를 구하고 2m = 2(c + a)인 가장 큰 공통 정수 약수로 나눕니다. 이들(m_1n, ..., m) 값을 가장 큰 공약수로 나누면 동일한 원시 피타고라스 n-튜플이 제공되며, m²
₁ > m²
₂ + ...을 만족하는 집합적인 코프프라임 양의 정수(m₁, ..., m_n)의 튜플 사이에는 일대일 대응 관계가 있습니다.+ m과²
_n 원시 피타고라스의 쌍쌍둥이.

설정된 코프림 값 $m$ → ${\displaystyle {\vec {m}}$과 원시 피타고라스 tup 레 사이의 관계의 예는 다음과 같습니다.

${\displaystyle {\begin{aligned}{\vec {m}}=(1)&\leftrightarrow 1^{2}=1^{2}\\{\vec {m}}=(2,1)&\leftrightarrow 3^{2}+4^{2}=5^{2}\\{\vec {m}}=(2,1,1)&\leftrightarrow 1^{2}+2^{2}+2^{2}=3^{2}\\{\vec {m}}=(3,1,1,1)&\leftrightarrow 1^{2}+1^{2}+1^{2}+1^{2}=2^{2}\\{\vec {m}}=(5,1,1,2,3)&\leftrightarrow 1^{2}+1^{2}+1^{2}+2^{2}+3^{2}=4^{2}\\{\vec {m}}=(4,1,1,1,1,2)&\leftrightarrow 1^{2}+1^{2}+1^{2}+1^{2}+1^{2}+2^{2}=3^{2}\\{\vec {m}}=(5,1,1,1,2,2,2)&\leftrightarrow 1^{2}+1^{2}+1^{2}+1^{2}+2^{2}+2^{2}+2^{2}=4^{2}\end{aligned}}}$

연속 사각형

m으로² 시작하는 k개의 연속 제곱의 합 F(k,m)는 공식에 의해 주어지므로,^[41]

${\displaystyle F(k,m)=km(k-1+m)+{\frac {k(k-1)(2k-1)}{6}}}$

F(k,m)가 정사각형이 되도록 하는 값(k,m)을 찾을 수 있는데, 예를 들어 Hirschhorn에 의해 항의 수가 그 자체가 정사각형인 경우,^[42]

${\displaystyle m={\tfrac {v^{4}-24v^{2}-25}{48}},\;k=v^{2},\;F(m,k)={\tfrac {v^{5}+47v}{48}}}$

그리고 v ≥ 5는 2 또는 3으로 나눌 수 없는 임의의 정수입니다. 가장 작은 경우 v = 5, 따라서 k = 25의 경우, 이는 잘 알려진 루카스의 대포알-stacking 문제를 산출합니다.

${\displaystyle 0^{2}+1^{2}+2^{2}+\dots +24^{2}=70^{2}}$

리치 격자와 연결된 사실

또한 피타고라스 n-튜플(n ≥ 4)에서 하나를 제외한 모든 덧셈이 연속적인 경우 방정식을 사용할 수 있습니다.

${\displaystyle F(k,m)+p^{2}=(p+1)^{2}}$

p의 두 번째 거듭제곱은 상쇄되므로, 이는 $p$ = F${\displaystyle \frac{}{}}$(${\displaystyle \frac{k,}{}}$ m${\displaystyle \frac{)}{}}$- ${\displaystyle \frac{}{}}$ ${\display$ style p={\$tfrac {F(k,m)-1}{2}}$를 사용하지만, p가 정수가 되도록 선택해야 하며, 작은 예는 k = 5, m = 1 양보,

${\displaystyle 1^{2}+2^{2}+3^{2}+4^{2}+5^{2}+27^{2}=28^{2}}$

따라서, 피타고라스 n-튜플을 생성하는 한 가지 방법은, 다양한 x에 대해,^[44]

${\displaystyle x^{2}+(x+1)^{2}+\cdots +(x+q)^{2}+p^{2}=(p+1)^{2},}$

여기서 q = n–2이고 여기서

${\displaystyle p={\frac {(q+1)x^{2}+q(q+1)x+{\frac {q(q+1)(2q+1)}{6}}-1}{2}}.}$

페르마의 마지막 정리

피타고라스의 삼중항 개념의 일반화는 엄밀하게 2보다 큰 n에 대해 a + b = c와 같은 양의 정수 a, b, c의 삼중항을 찾는 것입니다. 1637년 피에르 드 페르마는 그러한 삼중항이 존재하지 않는다고 주장했는데, 이 주장은 페르마가 증명하거나 반증하는 데 다른 어떤 추측보다 오랜 시간이 걸렸기 때문에 페르마의 마지막 정리로 알려지게 되었습니다. 첫번째 증거는 1994년 Andrew Wiles에 의해 주어졌습니다.

n - 1 또는 n차 전력 합 n차 전력

또 다른 일반화는 n + 1개의 양의 정수로 이루어진 수열을 찾는 것인데, 이 수열에서 마지막의 n번째 거듭제곱은 이전 항들의 n번째 거듭제곱의 합입니다. 알려진 n 값의 가장 작은 수열은 다음과 같습니다.

• n = 3: {3, 4, 5; 6}.
• n = 4: {30, 120, 272, 315; 353}
• n = 5: {19, 43, 46, 47, 67; 72}
• n = 7: {127, 258, 266, 413, 430, 439, 525; 568}
• n = 8: {90, 223, 478, 524, 748, 1088, 1190, 1324; 1409}

$x$ ${\displaystyle 3^{}}$+ y ${\displaystyle 3^{}}$+ ${\displaystyle {}^{}}$ ${\displaystyle 3^{}}$ = w ${\displaystyle 3^{}}$인 경우${\displaystyle {}^{}}$ ${\displaystyle$ x$^{3}$ + $y^{3}$ + z$^{3$페르마 입방체라고 불리는 $}=w^{3}},$ 모든 해를 주는 일반적인 공식이 존재합니다.

약간 다른 일반화를 사용하면 (k + 1)번째 거듭제곱의 합이 (n - k)번째 거듭제곱의 합과 같아집니다. 예:

• (n = 3): 1 + 12 = 9 + 10, 숫자 1729가 두 개의 다른 방식으로 정육면체의 합으로 표현될 수 있는 가장 작은 숫자라는 하디의 라마누잔과의 대화를 회상하면서 유명해졌습니다.

n의 거듭제곱이 n의 거듭제곱에 합하는 n - 1개의 양의 정수가 존재할 수도 있습니다(그러나 n = 3이 아닌 페르마의 마지막 정리에 의해). 이것들은 오일러의 거듭제곱 합 추측에 대한 반례입니다. 알려진 가장 작은 반례는 다음과^[45][46][16] 같습니다.

• n = 4: (95800, 217519, 414560; 422481)
• n = 5: (27, 84, 110, 133, 144)

헤로니안 삼각형 삼중항

헤로니안 삼각형은 일반적으로 넓이가 정수인 변을 가진 삼각형으로 정의됩니다. 이러한 삼각형의 변의 길이는 ≤ b ≤ c에 대하여 헤로니아 삼중항(a, b, c)을 형성합니다. 다리 중 적어도 하나인 a, b는 피타고라스 삼중항에 속해야 하므로, 면적 ab/2는 정수이기 때문에 모든 피타고라스 삼중항은 헤로니아 삼중항입니다. 그러나 영역 24가 있는 예(4, 13, 15)에서 알 수 있듯이 모든 헤로니아 트리플이 피타고라스 트리플인 것은 아닙니다.

만약 (a, b, c)가 헤로니아 삼중수라면, (ka, kb, kc)도 마찬가지이며, 여기서 k는 임의의 양의 정수이다. 그 넓이는 (a, b, c) 삼각형의 정수 넓이의² k 배인 정수가 될 것입니다. 헤로니안 삼중항(a, b, c)은 a, b, c가 집합적으로 coprime인 경우 원시적입니다. (원시적인 피타고라스의 경우에는 쌍대 코프프라임이라는 더 강한 진술이 적용되지만, 원시적인 헤로니안 삼각형의 경우에는 (7, 15, 20)과 같이 더 강한 진술이 항상 참인 것은 아닙니다.) 다음은 피타고라스의 세쌍둥이가 아닌 가장 단순한 원시 헤로니아의 세쌍둥이들입니다.

(4, 13, 15) 영역이 24인 경우

(3, 25, 26) 영역 36인 경우

(7, 15, 20) 영역 42인 경우

(6, 25, 29) 영역 60인 경우

(11, 13, 20) 영역 66인 경우

(13, 14, 15) 영역 84인 경우

(13, 20, 21) 영역 126인 경우

헤론의 공식에 의해, < b < c인 양의 정수 (a, b, c)의 3배가 헤론이 되는 추가 조건은 다음과 같습니다.

(a² + b² + c²)² − 2(a⁴ + b⁴ + c⁴)

또는 이와 동등하게

2(a²b² + a²c² + b²c²) − (a⁴ + b⁴ + c⁴)

16으로 나눌 수 있는 0이 아닌 완전 제곱수입니다.

암호학에 응용

원시 피타고라스 삼중항은 암호학에서 무작위 시퀀스로 사용되고 키를 생성하는 데 사용되었습니다.^[47]

참고 항목

메모들

참고문헌

• Alperin, Roger C. (2005), "The modular tree of Pythagoras" (PDF), American Mathematical Monthly, 112 (9): 807–816, CiteSeerX 10.1.1.112.3085, doi:10.2307/30037602, JSTOR 30037602, MR 2179860
• Berggren, B. (1934), "Pytagoreiska trianglar", Tidskrift för Elementär Matematik, Fysik och Kemi (in Swedish), 17: 129–139
• Barning, F.J.M. (1963), "Over pythagorese en bijna-pythagorese driehoeken en een generatieproces met behulp van unimodulaire matrices" (PDF), Math. Centrum Amsterdam Afd. Zuivere Wisk. (in Dutch), ZW-011: 37
• Eckert, Ernest (1992), "Primitive Pythagorean triples", The College Mathematics Journal, 23 (5): 413–417, doi:10.2307/2686417, JSTOR 2686417
• Elkies, Noam, Pythagorean triples and Hilbert's theorem 90 (PDF)
• Heath, Thomas (1956), The Thirteen Books of Euclid's Elements Vol. 1 (Books I and II) (2nd ed.), Dover Publications, ISBN 978-0-486-60088-8
• Long, Calvin T. (1972), Elementary Introduction to Number Theory (2nd ed.), Lexington: D. C. Heath and Company, LCCN 77171950
• Martin, Artemas (1875), "Rational right angled triangles nearly isosceles", The Analyst, 3 (2): 47–50, doi:10.2307/2635906, JSTOR 2635906
• McCullough, Darryl (2005), "Height and excess of Pythagorean triples" (PDF), Mathematics Magazine, 78 (1): 26–44, doi:10.1080/0025570X.2005.11953298, S2CID 1701449
• Romik, Dan (2008), "The dynamics of Pythagorean triples" (PDF), Trans. Amer. Math. Soc., 360 (11): 6045–6064, arXiv:math.DS/0406512, doi:10.1090/S0002-9947-08-04467-X, MR 2425702
• Teigen, M.G.; Hadwin, D.W. (1971), "On Generating Pythagorean Triples", The American Mathematical Monthly, 78 (4): 378–379, doi:10.2307/2316903, JSTOR 2316903
• Trautman, Andrzej (1998), "Pythagorean spinors and Penrose twistors", in S.A. Hugget; L.J. Mason; K.P. Tod; S.T. Tsou; N.M.J. Woodhouse (eds.), Geometric universe (Postscript)

외부 링크

• 클리포드 대수와 유클리드의 피타고라스 삼중항 매개변수화
• 복사되지 않은 이차원의 신기한 결과
• 피타고라스 삼중항의 성질, 상호작용 계산기, 퍼즐과 문제에 관한 논의
• 산술 진행을 이용한 피타고라스 삼중항 생성
• "Pythagorean numbers", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
• 피타고라스 삼중항에 대한 대화형 계산기
• 음의 펠 방정식과 피타고라스의 삼중항
• 다항식의 단일 삼중에 의한 피타고라스 삼중의 매개변수화
• Price, H. Lee (2008), The Pythagorean Tree: A New Species, arXiv:0809.4324
• 피타고라스의 세쌍둥이와 단위 원, 친구. Joseph H. Silverman, Third Ed., 2006, NJ, 어퍼 새들 리버, Pearson Prentice Hall, ISBN 0-13-186137-9
• 피타고라스 트리플에 대한 단위 원 관계를 보여주는 최첨단 인터랙티브 애플릿의 피타고라스 트리플
• 피타고라스 세쌍둥이
• 삼각형의 주목할 만한 원
• 피타고라스 삼중항과 관련된 2차 가환쌍의 해
• 피타고라스 세쌍원소의 이론적 특성과 기하학과의 연관성
• 원시 피타고라스의 세쌍을 이루는 세쌍나무
• Weisstein, Eric W., "Pythagorean Triple", MathWorld