진동

시리즈의 일부
고전 역학
$({displaystyle {textbf {F}}=squalfrac {d}{dt}})(m*textbf {v}})$ 운동 제2법칙
역사 타임라인 교재
나뭇가지 응용의 천상의 연속체 다이내믹스 운동학 동력학 스태틱스 통계
기초 액셀러레이션 각운동량 커플 달랑베르의 원리 에너지 동적인 잠재적인 힘. 기준범위 관성 기준 프레임 충동 관성/관성 모멘트 덩어리 기계력 기계 작업 순간. 모멘텀 공간 스피드 시간을 토크 속도 가상 작업
제제 뉴턴의 운동 법칙 해석역학 라그랑주 역학 해밀턴 역학 루시아 역학 해밀턴-야코비 방정식 아펠 운동 방정식 쿱만-본 노이만 역학
주요 토픽 감쇠비 변위 운동 방정식 오일러의 운동 법칙 가공의 힘 마찰 고조파 발진기 관성/비관성 기준 프레임 평면 입자 운동 역학 움직임(선형) 뉴턴의 만유인력의 법칙 뉴턴의 운동 법칙 상대 속도 강체 역학 오일러 방정식 단순 고조파 운동 진동
회전 원운동 회전 기준 프레임 구심력 원심력 반응성 코리올리 힘 진자 접선 속도 회전 속도 각도 가속도/변위/주파수/속도
과학자 케플러 갈릴레오 호이겐스 뉴턴 경이다. 호록스 핼리 모페르튀이 다니엘 베르누이 요한 베르누이 오일러 달랑베르 클라이어트 라그랑주 라플라스 해밀턴 포아송 코시 러스 리우빌 어필 깁스 쿠프만 폰 노이만
물리 포털 카테고리
v t

진동은 평형점 주변에서 진동이 일어나는 기계적 현상이다.이 단어는 라틴어의 진동(흔들림, 흔들림)에서 유래했습니다.진동은 진자의 움직임과 같은 주기적인 것일 수도 있고 자갈길에서 타이어의 움직임과 같은 무작위적일 수도 있다.

음차의 움직임, 목관악기나 하모니카의 리드, 휴대전화, 확성기의 콘 등의 진동이 바람직할 수 있다.

그러나 대부분의 경우 진동이 바람직하지 않아 에너지를 낭비하고 원치 않는 소리를 발생시킵니다.예를 들어 엔진, 전기 모터 또는 작동 중인 기계 장치의 진동 운동은 일반적으로 바람직하지 않습니다.이러한 진동은 회전 부품의 불균형, 불균일한 마찰 또는 기어 톱니의 맞물림에 의해 발생할 수 있습니다.신중한 설계는 보통 원치 않는 진동을 최소화합니다.

소리와 진동에 대한 연구는 밀접하게 관련되어 있다.소리 또는 압력파는 진동 구조물(예: 성대)에 의해 생성되며, 이러한 압력파는 구조물(예: 이어 드럼)의 진동을 유도할 수도 있습니다.따라서 소음을 줄이려는 시도는 종종 ^[1]진동 문제와 관련이 있다.

진동 종류

자유 진동은 기계 시스템이 초기 입력으로 작동하여 자유롭게 진동할 때 발생합니다.이런 종류의 진동은 그네를 타고 있는 아이를 뒤로 당기고 놓아주거나 음차를 쳐서 울리는 것을 예로 들 수 있다.기계 시스템은 고유 주파수 중 하나 이상에서 진동하며 움직임이 없을 때까지 감쇠합니다.

강제진동은 시간변동장애(하중, 변위, 속도 또는 가속도)가 기계 시스템에 적용되는 경우입니다.장애는 주기적 및 정상 상태 입력, 과도 입력 또는 랜덤 입력일 수 있습니다.주기적 입력은 고조파 또는 비 고조파 장애일 수 있습니다.이러한 유형의 진동에는 불균형에 의한 세탁기 흔들림, 엔진이나 울퉁불퉁한 노면에 의한 수송 진동, 지진 시 건물의 진동 등이 있습니다.선형 시스템의 경우, 주기적인 고조파 입력의 적용에 따른 정상 상태 진동 응답 주파수는 실제 기계 시스템에 따라 응답 크기가 달라지며, 가해진 힘 또는 운동의 주파수와 같다.

감쇠 진동:진동계의 에너지가 마찰 및 기타 저항에 의해 점차 소멸될 때 진동은 감쇠된다고 한다.진동은 주파수나 강도를 점차 감소시키거나 변화시키거나 멈추거나 시스템이 평형 위치에 머무릅니다.이러한 유형의 진동은 쇼크 업소버에 의해 감쇠된 차량 서스펜션을 예로 들 수 있습니다.

진동 시험

진동 테스트는 보통 일종의 진동기를 사용하여 구조물에 강제 기능을 도입함으로써 이루어집니다.또는 DUT(테스트 대상 장치)를 셰이커의 "테이블"에 부착합니다.진동 테스트는 정의된 진동 환경에 대한 테스트 대상 장치(DUT)의 응답을 검사하기 위해 수행됩니다.측정된 응답은 진동 환경, 피로 수명, 공진 주파수 또는 스퀵 앤 래틀 사운드 출력(NVH)에서 작동하는 능력일 수 있습니다.스퀵 및 래틀 테스트는 작동 중에 매우 낮은 소리 수준을 내는 특수 유형의 조용한 진동기를 사용하여 수행됩니다.

비교적 저주파 강제(일반적으로 100Hz 미만)의 경우 서보 유압(전기 유압) 셰이커가 사용됩니다.고주파수(일반적으로 5Hz~2000Hz)의 경우는, 전기 다이나믹 쉐이커가 사용됩니다.일반적으로 진동기구의 DUT 측에 위치한 하나 이상의 "입력" 또는 "제어" 지점은 지정된 ^[1]가속도로 유지됩니다.다른 "응답" 지점에서는 제어 지점보다 더 높은 진동 수준(공진) 또는 더 낮은 진동 수준(공진 방지 또는 댐핑)이 발생할 수 있습니다.시스템의 소음이 너무 심해지는 것을 방지하거나 특정 진동 ^[2]주파수에 의한 진동 모드에 의한 특정 부품의 부하를 줄이기 위해 공진 방지 효과를 달성하는 것이 바람직할 수 있습니다.

진동 테스트 연구소에서 실시하는 가장 일반적인 진동 테스트 서비스는 사인파 및 랜덤입니다.사인(한 번에 하나의 주파수) 테스트는 테스트 대상 장치(DUT)의 구조적 응답을 조사하기 위해 수행됩니다.진동 테스트의 초기 역사 동안 진동 기계 컨트롤러는 사인 모션 제어에만 국한되어 사인 테스트만 수행되었습니다.이후, 보다 정교한 아날로그 및 디지털 컨트롤러는 랜덤 제어를 제공할 수 있었습니다(모든 주파수를 한 번에).무작위(모든 주파수를 동시에) 테스트는 일반적으로 움직이는 자동차에 대한 도로 입력과 같은 실제 환경을 더 가깝게 복제하는 것으로 간주됩니다.

대부분의 실제 진동은 여러 축에서 동시에 발생하지만, 대부분의 진동 테스트는 한 번에 '단일 DUT 축'으로 수행됩니다.2008년 후반에 출시된 MIL-STD-810G 테스트 방법 527에서는 여러 개의 여기자 테스트가 필요합니다.진동 테스트 스펙트럼의 주파수 범위에 맞게 DUT를 진동자 테이블에 부착하는 데 사용되는 진동 테스트^[3] 고정장치를 설계해야 합니다.실제 사용 중인 마운팅의 동적 응답(기계적 ^[4]임피던스)을 복제하는 진동 테스트 픽스처를 설계하는 것은 어렵습니다.이러한 이유로 진동 시험 사이의 반복성을 보장하기 위해 진동 고정 장치는 시험 주파수 범위 내에서 공명이^[4] 발생하지 않도록 설계되었다.일반적으로 작은 고정장치와 낮은 주파수 범위의 경우 설계자는 테스트 주파수 범위에서 공진이 없는 고정장치 설계를 목표로 할 수 있습니다.이는 DUT가 커지고 테스트 빈도가 증가할수록 더욱 어려워집니다.이러한 경우 멀티포인트 제어 전략은^[5] 미래에 존재할 수 있는 공명 중 일부를 완화할 수 있습니다.

일부 진동시험방법은 진동시험기구가 표시할 수 있는 크로스톡(시험대상 축에 대하여 상호 수직방향의 응답점 이동)의 양을 제한한다.진동을 추적하거나 기록하도록 특별히 설계된 장치를 진동경이라고 합니다.

진동 분석

이 섹션은 어떠한 출처도 인용하지 않습니다. 신뢰할 수 있는 출처에 인용문을 추가하여 이 섹션의 개선에 도움을 주십시오. 조달되지 않은 자재는 제거될 수 있습니다.(2013년 7월) (이 템플릿메시지 삭제 방법 및 삭제 시기 확인)

산업용 또는 유지보수 환경에 적용되는 진동 분석(VA)은 장비 ^[6][7]고장을 감지하여 유지보수 비용과 장비 다운타임을 줄이는 것을 목적으로 합니다.VA는 상태 모니터링(CM) 프로그램의 핵심 구성 요소이며 종종 예측 유지보수(PdM)^[8]라고 합니다. 가장 일반적으로 VA는 불균형, 정렬 불량, 롤링 엘리먼트 베어링 결함 및 ^[9]공진 조건과 같은 회전 장비(팬, 모터, 펌프 및 기어박스 등)의 고장을 감지하는 데 사용됩니다.

VA는 시간 파형(TWF)으로 표시된 변위, 속도 및 가속 단위를 사용할 수 있지만, 가장 일반적으로 스펙트럼이 사용되며, 이는 TWF의 고속 푸리에 변환에서 파생됩니다.진동 스펙트럼은 고장 난 구성 요소를 정확히 파악할 수 있는 중요한 주파수 정보를 제공합니다.

진동 해석의 기초는 단순한 매스 스프링-댐퍼 모델을 연구함으로써 이해할 수 있다.실제로 자동차 본체와 같은 복잡한 구조도 단순한 질량-스프링-댐퍼 모델의 "합산"으로 모델링할 수 있습니다.질량-스프링-댐퍼 모델은 단순한 고조파 발진기의 예입니다.이 동작을 설명하는 데 사용되는 수학은 RLC 회로와 같은 다른 단순한 고조파 발진기와 동일합니다.

주의: 이 문서에서는 단계별 수학적 도출은 포함하지 않고 주요 진동 분석 방정식과 개념에 초점을 맞추고 있습니다.자세한 내용은 기사 말미에 있는 참고 자료를 참조하십시오.

댐핑 없는 자유 진동

질량-스프링-댐퍼에 대한 조사를 시작하려면 감쇠가 무시할만하고 질량에 가해지는 외부 힘(즉, 자유 진동)이 없다고 가정합니다.스프링에 의해 질량에 가해지는 힘은 스프링이 늘어나는 "x"의 양에 비례합니다(질량의 무게로 인해 스프링이 이미 압축되었다고 가정).비례 상수 k는 스프링의 강성이며 힘/거리 단위(예: lbf/in 또는 N/m)를 갖는다.음의 부호는 힘이 부착된 질량의 움직임에 항상 반대한다는 것을 나타냅니다.

$(\displaystyle F_{s}=-kx).\!}$

질량에 의해 생성되는 힘은 뉴턴의 두 번째 운동 법칙에 의해 주어진 질량의 가속도에 비례합니다.

$(\displaystyle\Sigma\F=ma{\ddot{x}=m440frac{d^{2}x}{dt^{2}}).}$

질량에 가해지는 힘의 합은 m x${\displaystyle \mu }$ + ${\displaystyle k}$ x $.\displaystyle \ mµdddot$ {x$}+kx=$${\displaystyle 0}$을 생성합니다.$}$

진동의 시작이 스프링을 A의 거리만큼 늘린 후 방출하는 것으로 시작된다고 가정할 때, 질량 운동을 설명하는 위의 방정식의 해는 다음과 같습니다.

${\displaystyle x(t)=A\cos(2\pi f_{n}t).\!}$

이 해는 진폭이 A이고 주파수가 f인_n 단순한 고조파 운동으로 진동할 것이라고 말한다.숫자_n f를 비감쇠 고유 주파수라고 합니다.단순 질량 스프링 시스템의 경우 f는_n 다음과 같이 정의된다.

${\displaystyle f_{n}={1 \over {2 \pi }}{\displayrt {k \over m}}.\!}$

참고: 초당 라디안의 단위를 갖는 각 주파수 θ(θ=2 µf)는 방정식을 단순화하기 때문에 방정식에 자주 사용되지만, 시스템의 주파수를 나타낼 때 일반적으로 일반 주파수(Hz 또는 동등한 초당 사이클)로 변환됩니다.시스템의 질량과 강성을 알고 있는 경우, 위의 공식에 따라 초기 교란으로 인해 시스템이 한번 작동하면 진동하는 주파수를 결정할 수 있습니다.모든 진동 시스템에는 한 번에 교란되는 고유 주파수가 하나 이상 있습니다.이 간단한 관계를 사용하여 질량이나 강성을 더하면 더 복잡한 시스템에 어떤 일이 일어나는지 일반적으로 이해할 수 있습니다.예를 들어, 위의 공식은 차량 또는 트럭에 가득 실렸을 때 서스펜션이 적재되지 않은 것보다 '느긋한' 느낌이 드는 이유를 설명합니다. 즉, 중량이 증가하여 시스템의 고유 주파수가 감소합니다.

시스템 진동을 일으키는 원인: 에너지 절약 관점에서 볼 때

진동 운동은 에너지 보존의 관점에서 이해될 수 있다.위의 예에서는 스프링이 x 값만큼 연장되어 있기 때문에 일부 위치 에너지$({$가 스프링에 저장됩니다.스프링은 일단 방출되면 늘어나지 않은 상태(최소 잠재 에너지 상태)로 되돌아가는 경향이 있으며 그 과정에서 질량이 가속됩니다.스프링이 늘어나지 않은 상태에 도달한 시점에서 스프링을 늘림으로써 공급되는 모든 잠재 에너지는 운동에너지로 $$되었습니다($v$ { $displaystyle${ 1$$}$mv^$ {2$}$） 。이제 스프링을 압축하고 운동 에너지를 다시 전위로 전달하는 과정에 있기 때문에 질량은 감속하기 시작합니다.따라서 스프링의 진동은 운동 에너지가 위치 에너지로 앞뒤로 이동하는 것과 같습니다.이 단순한 모델에서는 질량이 동일한 크기로 영원히 진동하지만, 실제 시스템에서는 댐핑이 항상 에너지를 소멸시켜 결국 스프링을 정지시킵니다.

댐핑 기능이 있는 자유 진동

모델에 "점점" 댐퍼가 추가되면 질량 속도에 비례하는 힘이 출력됩니다.감쇠는 물체 안에 있는 유체의 효과를 모델링하기 때문에 점성이라고 불립니다.비례 상수 c는 감쇠 계수라고 불리며 속도 대비 힘(lbfµs/in 또는 Nµs/m)의 단위를 가집니다.

$({displaystyle F_{\text{d}}=-cv=-c{\dot {x}}=-cccfrac{dt}{dt}}).}$

질량에 가해지는 힘을 합하면 다음과 같은 상미분 방정식이 됩니다.

${\displaystyle mbcdot {x}+cbcdot {x}}+kx=0.}$

이 방정식의 해법은 댐핑의 양에 따라 달라집니다.감쇠가 충분히 작아도 시스템은 계속 진동하지만 시간이 지남에 따라 진동이 멈춥니다.이러한 경우를 언더댐핑이라고 하는데, 이는 진동 분석에 중요합니다.시스템이 더 이상 진동하지 않을 정도로 댐핑이 증가하면 시스템이 심각한 댐핑에 도달한 것입니다.임계 댐핑을 지나 댐핑이 증가하면 시스템이 과다 감쇠됩니다.매스 스프링-댐퍼 모델에서 임계 댐핑을 위해 댐핑 계수가 도달해야 하는 값은 다음과 같습니다.

${\displaystyle c_{\text{c}}=220rt {text{km}}}.}$

시스템의 댐핑 양을 특성화하기 위해 댐핑 비율(댐핑 계수 및 % 임계 댐핑이라고도 함)이 사용됩니다.이 댐핑 비율은 임계 댐핑에 도달하는 데 필요한 댐핑 양에 대한 실제 댐핑의 비율에 불과합니다.매스 스프링 댐퍼 모델의 감쇠비( ( \$displaystyle \zeta$ $）$ 공식은 다음과 같습니다.

$({displaystyle \zeta = {c\over 2sqrt {text{km}}})}$

예를 들어, 금속 구조물 (예: 비행기 동체, 엔진 크랭크축)은 0.05 미만의 감쇠 계수를 가지며, 자동차 서스펜션은 0.2-0.3의 범위에 있습니다.매스 스프링-댐퍼 모델의 언더 댐프 시스템에 대한 솔루션은 다음과 같습니다.

${\displaystyle x(t)=Xe^{-\zeta \{n}t\cos \leftrt {1-\zeta ^{2}}\obmega _{n}t-\phi \right}, \qquad \ope \mega _{n}=2\pi f_{n}.}$

초기 크기인 X와 위상 $편이$인$,,$ \$displaystyle \phi$의 값은 스프링이 늘어나는 양에 따라 결정됩니다.이러한 값의 공식은 참조에서 확인할 수 있습니다.

감쇠 및 비감쇠 고유 주파수

솔루션에서 주목해야 할 주요 포인트는 지수 항과 코사인 함수입니다.지수 용어는 시스템의 "감쇠" 속도를 정의합니다. 감쇠비가 클수록 감쇠 속도가 0까지 빨라집니다.코사인 함수는 솔루션의 진동 부분이지만 진동 주파수는 비감쇠된 경우와 다릅니다.

이 경우의 주파수를 "${\displaystyle {감쇠}_{}}$ 고유 주파수", $f{\displaystyle {}_{}}$ d${\displaystyle {}_{}}$, ${\displaystyle f_{\text{d}}$라고 하며, 다음 공식에 따라 감쇠되지 않은 고유 주파수와 관련이 있습니다.

${\displaystyle f_{\text{d}}=f_{n}{\displayrt {1-\zeta ^{2}}}.}$

감쇠된 고유 주파수는 비감쇠된 고유 주파수보다 적지만, 많은 경우 감쇠비가 상대적으로 작기 때문에 그 차이는 무시할 수 있습니다.따라서 자연 주파수를 기술할 때 감쇠 및 비감쇠 설명은 종종 떨어집니다(예: 0.1 감쇠비의 경우 감쇠된 고유 주파수는 비감쇠 주파수보다 1%만 작습니다).

측면 그림은 0.1 및 0.3 댐핑 비율이 시간이 지남에 따라 시스템이 "링다운"되는 방식에 어떤 영향을 미치는지 보여줍니다.실제로 자주 행해지는 것은 충돌 후의 자유진동을 실험적으로 측정한 후(예를 들어 해머로), 붕괴율을 측정하여 진동수와 감쇠율을 측정하여 시스템의 고유진동을 결정하는 것입니다.고유 주파수와 감쇠비는 자유 진동에서 중요할 뿐만 아니라 시스템이 강제 진동 하에서 어떻게 동작하는지를 특징짓습니다.

^[10]

댐핑 시 강제 진동

스프링 질량 댐퍼 모델의 동작은 고조파 힘의 추가에 따라 달라집니다.예를 들어 이러한 유형의 힘은 회전 불균형에 의해 발생할 수 있습니다.

${\displaystyle F=F_{0}\sin(2\pi ft).\!}$

질량에 가해지는 힘을 합하면 다음과 같은 상미분 방정식이 됩니다.

${\displaystyle mµdot {x}+cµdot {x}}+kx=F_{0}\sin(2\pi ft).}$

이 문제의 정상 상태 해결 방법은 다음과 같이 기술할 수 있습니다.

$\displaystyle x(t)=X\sin(2\pi ft+\phi)\!}$

그 결과 매스는 가해진 힘의 동일한 주파수 f로 진동하지만 위상 $편이$가 θ$.$ {\$displaystyle$ \$phi}$임을 알 수 있습니다.

진동 "X"의 진폭은 다음 공식으로 정의됩니다.

${{displaystyle X={F_{0} \over k}{1 \over {1 - r^{2}^{2}+(2\zeta r)^{2}}}}.}$

여기서 "r"은 질량-스프링-댐퍼 모델의 비감쇠 고유 주파수에 대한 고조파 힘 주파수의 비율로 정의된다.

${\displaystyle r=syslogfrac {f}{f_{n}}}}.}$

$위상{\displaystyle }$ 편이 ${\displaystyle ,}$ ,$$\$displaystyle \phi ,$는 다음 공식으로 정의됩니다.

$(\displaystyle \phi =\arctan \leftfrac {-2\zeta r}{1-r^{2}}\right)}$

"시스템의 주파수 응답"이라고 불리는 이러한 기능의 플롯은 강제 진동에서 가장 중요한 특징 중 하나를 나타냅니다.약간 감쇠된 시스템에서는 강제 주파수가 고유 주파수(${\displaystyle 1}$1 \ $displaystyle$r \$$$about$1)에 가까워지면 진동의 진폭이 매우 커질 수 있습니다.이 현상을 공진이라고 합니다(따라서 시스템의 고유 주파수는 종종 공진 주파수라고 불립니다.로터 베어링 시스템에서는 공진 주파수를 들뜨게 하는 회전 속도를 임계 속도라고 합니다.

기계 시스템에서 공명이 발생할 경우 매우 해로울 수 있으며, 결과적으로 시스템 고장으로 이어질 수 있습니다.따라서 진동분석의 주요 이유 중 하나는 이러한 유형의 공명이 언제 발생할지 예측하고 그 발생을 방지하기 위해 어떤 조치를 취해야 하는지를 결정하는 것이다.진폭도에서 보듯이 댐핑을 추가하면 진동의 크기를 크게 줄일 수 있습니다.또, 시스템의 강성이나 질량을 변화시켜, 고유 주파수를 강제 주파수로부터 멀어질 수 있으면, 크기를 작게 할 수 있다.시스템을 변경할 수 없는 경우 강제 주파수를 변경할 수 있습니다(예를 들어 힘을 생성하는 기계의 속도 변경).

다음은 주파수 응답도에 표시된 강제 진동에 관한 몇 가지 다른 지점입니다.

• 주어진 주파수 비율에서 진동의 진폭 X는 $힘{\displaystyle {}_{}}$ ${\displaystyle {F\mathrm{}}_{}}$ 0$($$예$: 힘을 두 배로 하면 진동이 두 배로 증가함)의 진폭에 정비례합니다.
• 감쇠가 거의 또는 전혀 없는 경우 진동은 주파수 비 r < 1일 때 강제 주파수와 위상이 일치하며 주파수 비 r > 1일 때 위상이 180도 어긋납니다.
• r 1 1일 때 진폭은 정적 $힘{\displaystyle {}_{}}$ ${\displaystyle {F\mathrm{}}_{}}$0 .$${\$displaystyle F_${0$}$에서 스프링의 편향일 뿐입니다.$$ 이 처짐을 스태틱 ${\displaystyle {\mathrm{처짐}}_{}}$이라고 합니다$.\$ $displaystyle$\ $delta$_ { $st$} 。} 따라서$$ r 1 1일 때 댐퍼와 질량의 영향은 미미하다$.$
• r이 1일 때 진동의 진폭은 실제로 정적 ${\displaystyle {\mathrm{편향}}_{}}$보다 작습니다$.\$ $displaystyle \delta$_ { $st$} 。} 이$$ 영역에서는 질량에 의해 발생하는 힘(F = ma)이 지배적이다. 이는 질량에 의해 보이는 가속도가 주파수에 따라 증가하기 때문이다$.$이 영역에서는 스프링(X)에서 볼 수 있는 편향이 감소하므로 스프링(F = kx)에 의해 베이스로 전달되는 힘이 감소한다.따라서 질량-스프링-댐퍼 시스템은 진동 차단이라고 하는 고조파 힘을 장착 베이스로부터 격리합니다.더 많은 댐핑은 실제로 r ≤ 1일 때 진동 차단 효과를 감소시킵니다. 왜냐하면 댐핑 강도(F = cv)도 베이스로 전달되기 때문입니다.
• 댐핑이 무엇이든 주파수 비율 r = 1일 때 강제 주파수와 90도의 위상이 어긋나므로 시스템의 고유 주파수를 결정하는 데 매우 유용합니다.
• 댐핑이 무엇이든 r µ 1일 때 진동이 강제 주파수와 180도 어긋납니다.
• 댐핑이 무엇이든 r µ 1일 때 진동이 강제 주파수와 위상 일치합니다.

공명 원인

공명은 스프링과 질량이 운동 에너지를 저장하고 스프링이 위치 에너지를 저장하는 에너지 저장 요소로 간주되는 경우 이해하기 쉽습니다.앞에서 설명한 바와 같이 질량과 스프링에 작용하는 외부 힘이 없을 때 자연 주파수와 동일한 속도로 에너지를 앞뒤로 전달합니다.즉, 에너지를 질량과 스프링에 효율적으로 공급하려면 에너지원이 고유 주파수와 동일한 속도로 에너지를 공급해야 합니다.매스와 스프링에 힘을 가하는 것은 그네를 타고 있는 아이를 밀치는 것과 비슷하며, 그네를 점점 더 높게 만들기 위해서는 적절한 순간에 밀어주기가 필요합니다.스윙의 경우처럼 큰 움직임을 얻기 위해 가해지는 힘이 클 필요는 없고 시스템에 에너지를 더하기만 하면 된다.

댐퍼는 에너지를 저장하는 대신 에너지를 분산시킵니다.댐핑 세력은 속도에 비례하므로 움직임이 많을수록 댐퍼가 에너지를 더 많이 방출합니다.따라서 댐퍼에 의해 방산된 에너지가 힘에 의해 추가된 에너지와 동일한 지점이 있습니다.이 시점에서 시스템은 최대 진폭에 도달했으며 가해지는 힘이 변하지 않는 한 이 레벨에서 계속 진동합니다.댐핑이 존재하지 않으면 에너지를 소멸시킬 수 없으며 이론적으로 운동은 무한대로 계속 커집니다.

질량-스프링-댐퍼 모델에 "복잡한" 힘 적용

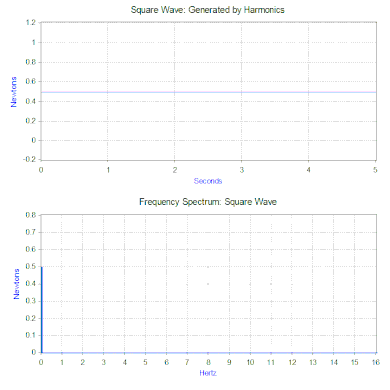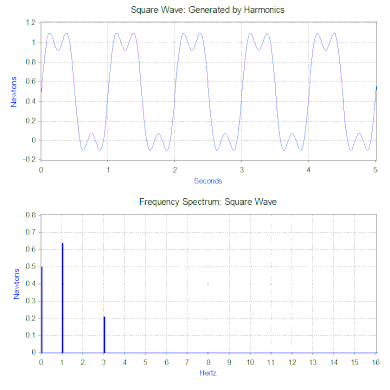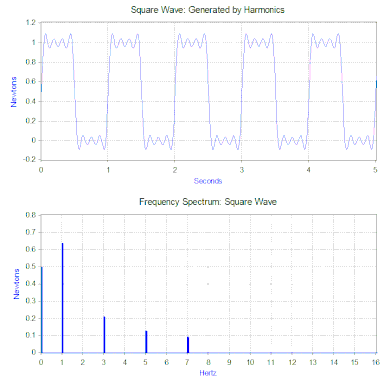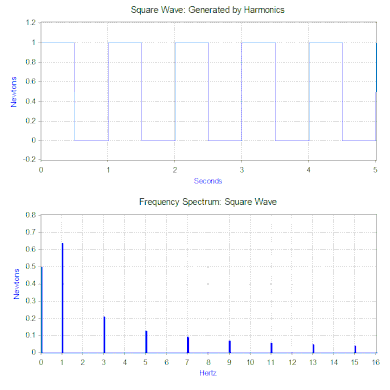
이전 섹션에서는 단순한 고조파 힘만 모델에 적용되었지만, 두 가지 강력한 수학적 도구를 사용하여 상당히 확장할 수 있습니다.첫 번째는 신호를 시간(시간 영역)의 함수로 받아들이고 이를 주파수(주파수 영역)의 함수로 조화 성분으로 분해하는 푸리에 변환입니다.예를 들어 질량-스프링-댐퍼 모델에 힘을 가하여 0.5초 동안 1뉴턴과 동일한 힘을 가한 다음 0.5초 동안 힘을 가하지 않는다.이런 종류의 힘은 1Hz 사각파 모양을 하고 있습니다.

사각파의 푸리에 변환은 사각파를 구성하는 고조파의 크기를 나타내는 주파수 스펙트럼을 생성합니다(위상도 생성되지만 일반적으로 덜 중요하므로 플롯되지 않는 경우가 많습니다).푸리에 변환은 과도기(예: 임펄스) 및 임의 함수와 같은 비주기적 함수를 분석하는 데도 사용할 수 있습니다.푸리에 변환은 거의 항상 창 함수와 함께 고속 푸리에 변환(FFT) 컴퓨터 알고리즘을 사용하여 계산됩니다.

사각파력의 경우 첫 번째 성분은 실제로는 0.5뉴턴의 일정한 힘이며 주파수 스펙트럼에서 0Hz의 값으로 나타납니다.다음 성분은 진폭 0.64의 1Hz 사인파입니다.이것은 1Hz의 라인으로 표시됩니다.나머지 구성요소는 홀수 주파수로 완벽한 사각파를 생성하는 데 무한대의 사인파가 필요합니다.따라서 푸리에 변환을 사용하면 힘을 더 "복잡한" 힘(예: 사각파) 대신 적용되는 사인파 힘의 합으로 해석할 수 있습니다.

이전 섹션에서는 단일 고조파에 대해 진동해를 제시했지만, 일반적으로 푸리에 변환은 여러 고조파에 대한 힘을 부여합니다.두 번째 수학적 도구인 중첩 원리는 시스템이 선형일 경우 여러 힘으로부터 해를 합산할 수 있게 합니다.스프링-질량-감쇠 모델의 경우 스프링력이 변위에 비례하고 댐핑이 관심의 이동 범위에 걸쳐 속도에 비례하는 경우 시스템은 선형이다.따라서 사각파 문제에 대한 해결책은 사각파의 주파수 스펙트럼에서 발견된 각 고조파 힘으로부터의 예측 진동을 합산하는 것이다.

주파수 응답 모델

진동 문제의 해결 방법은 입력/출력 관계(힘은 입력, 출력은 진동)로 볼 수 있습니다.주파수 영역(규모 및 위상)의 힘과 진동을 나타내면 다음과 같은 관계가 가능합니다.

${\displaystyle X(i\Omega)=H(i\Omega)\cdot F(i\Omega){\text{ 또는 }H(i\Omega)={X(i\Omega)\over F(i\Omega)}.}$

${\displaystyle }$H${\displaystyle (i}$ $))$ {$displaystyle$ H$(i\omega)}$는 주파수 응답 함수(전송 함수라고도 하지만 기술적으로 정확하지는 않음)라고 불리며, 크기와 위상 성분(복소수, 실제 및 가상의 성분으로 표현되는 경우)을 모두 가지고 있습니다.주파수 응답 함수(FRF)의 크기는 질량-스프링-댐퍼 시스템에 대해 앞서 제시되었습니다.

${\displaystyle H(i\obe) =\left {X(i\obe)} \over F(i\obe)} \right = {1 \over k} {1 \over {\verrt {(1-r^2}^2}^{2}}, {\text {\text {} r= frac {f} {f} {f} frac} {f}}$

FRF의 단계도 앞서 다음과 같이 제시되었다.

$(\displaystyle \angle H(i\Omega)=-\arctan \leftfrac {2\zeta r}{1-r^{2}}\오른쪽).}$

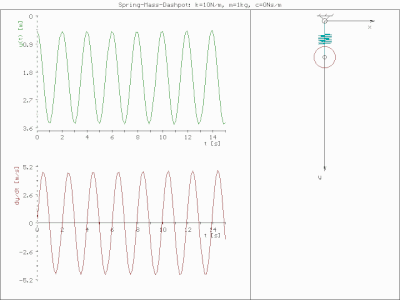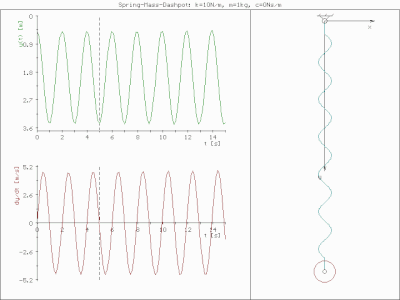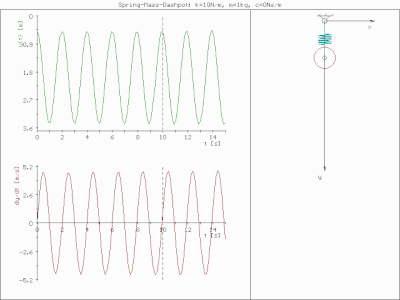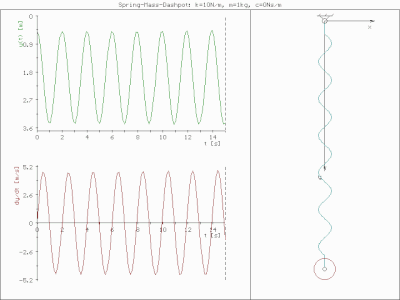
예를 들어 질량 1kg, 스프링 강성 1.93 N/mm, 감쇠비 0.1을 갖는 질량-스프링-댐퍼 시스템에 대한 FRF를 계산한다.스프링 및 질량 값은 이 특정 시스템에 대해 7Hz의 고유 주파수를 제공합니다.앞의 1Hz 사각파를 적용하면 매스의 예측 진동을 계산할 수 있습니다.그림은 그 결과 발생하는 진동을 나타내고 있습니다.이 예에서는 사각파의 네 번째 고조파가 7Hz로 떨어집니다.따라서 질량-스프링-댐퍼의 주파수 응답은 입력력이 상대적으로 낮은 7Hz 고조파를 가졌음에도 불구하고 높은 7Hz 진동을 출력합니다.이 예에서는 결과 진동이 강제 기능과 힘을 가하는 시스템 모두에 따라 결정된다는 점을 강조합니다.

그림에는 또한 결과 진동의 시간 영역 표현도 나와 있습니다.이는 주파수 영역 데이터를 시간 영역으로 변환하는 역 푸리에 변환을 수행하여 수행됩니다.실제로는 주파수 스펙트럼이 필요한 모든 정보를 제공하기 때문에 이 작업은 거의 수행되지 않습니다.

주파수 응답 함수(FRF)는 시스템의 질량, 댐핑 및 강성에 대한 지식에서 반드시 계산할 필요는 없지만 실험적으로 측정할 수 있습니다.예를 들어 주파수 범위에 걸쳐 알려진 힘이 가해지고 관련 진동이 측정되면 주파수 응답 함수를 계산할 수 있어 시스템의 특성을 파악할 수 있다.이 기술은 구조물의 진동 특성을 결정하기 위해 실험 모달 분석 분야에서 사용됩니다.

다중 자유도 시스템 및 모드 모양

단순한 질량-스프링-댐퍼 모델은 진동 분석의 기초가 되지만, 더 복잡한 시스템은 어떻습니까?위에서 설명한 질량-스프링-댐퍼 모델을 단일 자유도(SDOF) 모델이라고 하는데, 이는 질량이 위아래로만 움직인다고 가정하기 때문이다.보다 복잡한 시스템에서는 시스템을 여러 방향으로 이동하는 더 많은 질량으로 분리하여 자유도를 추가해야 합니다.다중자유도(MDOF)의 주요 개념은 그림과 같이 2자유도 모델을 보면 알 수 있습니다.

2DOF 시스템의 운동 방정식은 다음과 같습니다.

${\displaystyle m_{1}{\dot {x_{1}+c_{2}{\dot {x_{1}-{2}-c_{2}{\dot {x_{2}+(k_1}+k_{2})x_{1}-k_{2}=f1}_1}+dot$

$\displaystyle m_{2}{\dot {x_{2}-c_{2}{\dot {x_{1}+(c_{2}+c_{3}){\dot {x_{2}-k_{1}+(k_2}+k_{3})x_{2}=f2}.\!}$

이것은 매트릭스 형식으로 다시 쓸 수 있습니다.

${\displaystyle {bgin{bmatrix}m_{1}&0&m_{2}\end{bmatrix}{\begin{Bmatrix}{\ddot {x_{1}}\end{Bmatrix}}}+{\begin{c}-{c}}\end {bmatrix}{\begin {Bmatrix}{\dot {x_{2}}\\end {Bmatrix}}+{\begin {bmatrix}k_{1}+k_{2}&-k_{2}&k_{3}{\begin {x_{2}}\batrix}}\\\\\\\end {Bmatrix}}}}}}\end{bmatrix}{\begin{Bmatrix}x_{1}\\x_{2}\end{Bmatrix}={begin{Bmatrix}f_{1}\f_{2}\end{Bmatrix}}.}$

이 행렬 방정식의 보다 콤팩트한 형식은 다음과 같이 쓸 수 있습니다.

${\displaystyle {bmatrix} M\end {bmatrix} {\begin {Bmatrix} {\ddot {x} \end {Bmatrix} + {\begin {bmatrix} C \end {bmatrix} {\begin {bmatrix} + {\begin}$

여기서${\displaystyle }$[$],$ ${\displaystyle {bmatrix},$ {\$end{$$bmatrix$${\displaystyle }$ {$C },$ {\displaystyle {$bmatrix}$ 및$$${\displaystyle }$[$K$ {$displaystyle {bmatrix}$는 각각 질량, 강성 매트릭스라고 하는 대칭 $행렬이다.$행렬은 NxN 정사각형 행렬입니다. 여기서 N은 시스템의 자유도입니다.

다음 분석에는 댐핑이 없고 가해지는 힘이 없는 경우(즉, 자유 진동)가 포함됩니다.눈에 띄게 감쇠된 시스템의 해결책은 다소 ^[11]복잡하다.

$({displaystyle {bmatrix}M\end{bmatrix}{\begin{Bmatrix}}{\ddot {x}\end{Bmatrix}}+{\begin{bmatrix}K\end{Bmatrix}}{\begin{Bmatrix}}}=0).}$

이 미분방정식은 다음과 같은 유형의 해법을 가정하여 풀 수 있습니다.

$({displaystyle {bgin{Bmatrix}x\end{Bmatrix}={Bmatrix}X\end{Bmatrix}e^{i\mega t}).}$

${\displaystyle \begin{array}{c}주의\end{array}}$: { X ${\displaystyle \begin{array}{}\}\end{array}}$ ${\displaystyle e^{}}$ ${\displaystyle i^{}}$ ${\$ ${\displaystyle t^{}}$ \ $displaystyle$ {$begin$ { $Bmatrix }$ X \$end$ { Bmatrix$\}{\displaystyle }$ e$^${ i \ $obega$ t$$$}$의 지수해법은 선형미분방정식을 푸는 데 사용되는 수학적 기법입니다.오일러의 공식을 사용하고 솔루션의 실제 부분만 취하면 1 DOF 시스템에 대한 코사인 해와 동일합니다.지수 해법은 수학적으로 조작하기 쉽기 때문에만 사용됩니다.

그러면 방정식은 다음과 같이 됩니다.

$(\displaystyle {bmatrix}-\obega ^{2}M\end{bmatrix}}+{\begin{bmatrix}K\end{bmatrix}}{\begin{Bmatrix}X\end{Bmatrix}e^{i\obega}=0).}$

${\displaystyle e^{}}$ i ${\displaystyle t^{}}$ \$displaystyle$ e$^{i\obega$ t$}$는 0과 같을 수 $없으므로{\displaystyle {}^{}}$ 방정식은 다음과 같이 감소합니다.

${\displaystyle {\begin{bmatrix}K\end{bmatrix}-\obegin{bmatrix}M\end{bmatrix}{\begin{Bmatrix}X\end{Bmatrix}=0.}$

고유값 문제

이는 수학에서 고유값 문제를 말하며 방정식을 [$]$ - $({$로${\displaystyle {}^{}}$곱하면 표준 형식으로 만들 수 있다.

${\displaystyle {bmatrix}{\begin{bmatrix}{-1}{\begin{bmatrix}K\end{bmatrix}-\obegin{bmatrix}M\end{bmatrix}{-1}{\begin{bmatrix}}{\matrix}}{\end}$

또한${\displaystyle {}^{}}$[${\displaystyle {\begin{array}{c}M\end{array}]}^{}}$ - ${\displaystyle 1^{}}$[ ${\displaystyle \begin{array}{c}K\end{array}}$] ${\displaystyle =}$ [ $]{$ $displaystyle${ $begin${$bmatrix }{$ -$1$}{ \$begin${$bmatrix } = begin${ $bmatrix$}$A\end{bmatrix}}$ 및$$ $\lambda {\displaystyle }$ ${\displaystyle ={}^{}}{\displaystyle {2\mathrm{}}^{}}$ 2 { $displaystyle$\ $displayda$= \ $omega$^ {2} ,$$}

$\dis {bmatrix} {\displaystyle bmatrix}A\end {bmatrix}-\lambda {begin {bmatrix}I\end{bmatrix}\end{bmatrix}{\begin{Bmatrix}X\end{Bmatrix}}=0.}$

이 문제에 대한 해결책은 N개의 고유값(즉, ${\displaystyle {1\mathrm{}}_{}^{}}$ 1${\displaystyle {\mathrm{}}_{}^{}}$ 、${\displaystyle {\mathrm{}}_{}^{}}$ 2$$ N 2 \ $displaystyle$\ $obega _$ ${1}^{2}$ $\ obega _ {N}^2} \cdots$\{N}^2} )이 됩니다.$$$여기$서 N은 자유도에 해당합니다.고유값은 시스템의 고유 주파수를 제공합니다.이러한 고유값을 원래의 방정식 세트로 치환하면 각 고유값에 대응하는 {$}$ {\$displaystyle {Bmatrix}X\end {Bmatrix}}$의${\displaystyle }$값을 고유 벡터라고 합니다.이러한 고유 벡터는 시스템의 모드 모양을 나타냅니다.고유값 문제의 해결은 상당히 번거로울 수 있지만(특히 자유도가 많은 문제의 경우), 다행히 대부분의 수학 분석 프로그램에는 고유값 루틴이 있습니다.

고유값과 고유 벡터는 종종 다음과 같은 행렬 형식으로 작성되며 시스템의 모달 모형을 설명합니다.

${\displaystyle{\begin{bmatrix}^{\diagdown}\omega _{r\diagdown}^{2}\end{bmatrix}}={\begin{bmatrix}\omega _{1}^{2}&, \cdots, 0\\\vdots &, \ddots &, \vdots \\0&, \cdots & &, \omega _{N}^{2}\end{bmatrix}}{\text{과}}{\begin{bmatrix}\Psi \end{bmatrix}}={\begin{bmatrix}{\begin{Bmatrix}\psi _{1}\end{Bmatrix}}{\begin{Bmatrix}\psi _{2}\end{.Bmatrix}}\cdots{\begin{Bmatrix}\psi _{N}\end{Bmatrix}\end{bmatrix}}.}$

2개의 DOF 모델을 사용하는 간단한 예를 통해 개념을 설명할 수 있습니다.두 질량의 질량은 모두 1kg이고 세 개의 스프링의 강성은 모두 1000N/m와 동일하다고 가정한다.이 문제의 질량 및 강성 매트릭스는 다음과 같습니다.

[ $]$ { $displaystyle { bmatrix } M$ \$end$ { $bmatrix$ } = begin { $bmatrix$} $1$& $0$\ \ \ $0 & 1$ \ end${$ bmatrix}$=$[ $2000$- - 2000. { $displaystyle${ $begin${ $batrix$ } { $batrix$ }$}$

$그러면$[ [ - - 2000. { $displaystyle { bmatrix$}$A\end{bmatrix}=(begin{bmatrix}2000&-1000&2000\end{bmatrix})$$}$

고유값 루틴이 제공하는 이 문제의 고유값은 다음과 같습니다.

${\displaystyle {bmatrix}^{\diagdown}\omega _{r\diagdown}^{2}\end{bmatrix}=syslog {bmatrix}1000&0&3000\end{bmatrix}.}$

헤르츠 단위의 고유 주파수는 (기억 ${\displaystyle \mathrm{\omega }}$ ${\displaystyle =}$ 2$$ f { $displaystyle$ \scriptstyle $\obega$ $=$$2\pi$f$\}$ ) ${\displaystyle {f\mathrm{}}_{}}$ 1 ${\displaystyle {}_{}\mathrm{}}$5.${\displaystyle 033\mathrm{}}$ $(\$}=$5.033\mathrm {Hz})$ $및$ ${\displaystyle {f\mathrm{}}_{}}$ 2 $8$.$(\$style $f{2$ style f})입니다.$}$

각 고유 주파수에 대한 두 가지 모드 모양은 다음과 같습니다.

$(\displaystyle {bmatrix}\Psi \end {bmatrix}={\begin {Bmatrix}\psi _{1}\end {Bmatrix}\psi _{2}\end {Bmatrix}\end {Bmatrix}=begin{matrix}\batrix}\begin{batrix})}$

이 시스템은 2DOF 시스템이기 때문에 각각의 고유 주파수와 모양을 가진 두 가지 모드가 있습니다.모드 모양 벡터는 절대 운동이 아니라 자유도의 상대 운동을 나타냅니다.이 경우 첫 번째 모드의 형태 벡터는 질량들이 같은 값과 부호를 가지고 있기 때문에 위상적으로 함께 움직이고 있다고 말합니다.두 번째 모드 형상 벡터의 경우, 각 질량은 같은 속도로 반대 방향으로 이동하고 있습니다.

다중 DOF 문제 예시

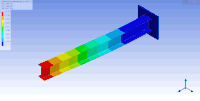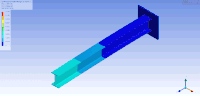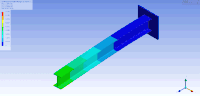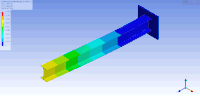
자유도가 많은 경우 모드 모양을 시각화하는 한 가지 방법은 ESI Group의 Femap, ANSYS 또는 VA One과 같은 구조 분석 소프트웨어를 사용하여 애니메이션화하는 것입니다.ANSYS의 모드 분석을 사용하여 시연된 캔틸레버 I 빔에 대한 애니메이션 모드 모양의 예는 아래 그림에 나와 있습니다.이 경우, 유한 요소 방법은 이산 고유값 문제를 해결하기 위해 관심 대상을 메쉬함으로써 질량과 강성 행렬의 근사치를 생성하기 위해 사용되었다.이 경우 유한요소법은 (무한 수의 진동 모드와 주파수가 존재하는) 메시 표면의 근사치를 제공한다.따라서 100도 이상의 자유도를 가진 이 비교적 단순한 모델은 많은 고유 주파수와 모드 모양을 통해 최초의 고유 주파수와 모드에^† 대한 근사치를 제공합니다.일반적으로 처음 몇 가지 모드만 실제 적용에 중요합니다.

이 표에서는 I빔의 제1 및 제2(상하 각각) 수평굴곡(좌측), 비틀림(중간) 및 수직굴곡(우측) 진동모드가 가시화된다.빔이 각각 높이, 폭 및 길이 방향으로 압축/연신되는 다른 종류의 진동 모드도 있습니다.
캔틸레버 I 빔의 모드 모양

^ 수학적 모델의 수치 근사치를 수행할 때 관심 매개변수의 수렴을 확인해야 합니다.

여러 DOF 문제가 단일 DOF 문제로 변환됨

고유 벡터는 직교성 속성이라고 하는 매우 중요한 속성을 가집니다.이러한 특성을 사용하여 다중 자유도 모델의 솔루션을 크게 단순화할 수 있습니다.고유 벡터는 다음과 같은 속성을 가지고 있음을 알 수 있습니다.

$(\displaystyle\begin{bmatrix\psi\end{bmatrix})^{T}{\begin{bmatrix}M\end{bmatrix}{\Begin{bmatrix}}={\diagdown}m_{r\diagdown}\end{bmatrix}},$

$(\displaystyle\begin{bmatrix\psi\end{bmatrix})^{T}{\begin{bmatrix}K\end{bmatrix}{\begin{bmatrix}}={\diagdown}k_{r\diagdown}\end{bmatrix}}.}$

${\displaystyle [\begin{array}{c}{}^{}{}_{}\end{array}}$ ${\displaystyle \begin{array}{c}{m}_{}\end{array}}$ r${\displaystyle \begin{array}{c}{}_{}\end{array}}$$]$$${{ $display style { bmatrix$} { \ $diagdown$} m$_$ {$r$ \ $diagdown$} \ m$$ _ { $r$ \ diagdown$$} 및 [${\displaystyle \begin{array}{c}{}^{}\end{array}}$ ${\displaystyle \begin{array}{c}{k}_{}\end{array}}$ r$]$ { $displaystyle$ {$bmatrix$}^{ \$diagdown$}는 강성 모달의 대각 행렬로서, 질량의 값을 포함한다.(주: 고유 벡터(모드 모양)는 임의로 스케일링할 수 있으므로, 각 모드의 모드 질량 값이 1이 되도록 종종 고유 벡터의 스케일링에 직교 특성을 사용합니다.따라서 모달 질량 행렬은 항등 행렬이다.)

이러한 특성은 다음과 같은 좌표 변환을 통해 다자유도 모델의 솔루션을 크게 단순화하는 데 사용할 수 있습니다.

${\displaystyle {bmatrix}x\end {Bmatrix}=(begin {bmatrix}\Psi \end {bmatrix}}{\begin {Bmatrix}q\end {Bmatrix}}}}.}$

원래의 자유 진동 미분 방정식에서 이 좌표 변환을 사용하면 다음과 같은 방정식을 얻을 수 있습니다.

${\displaystyle {bmatrix} M\end {bmatrix} {\begin {bmatrix} {\begin {bmatrix} {\ddot {q} {\end {Bmatrix} + {\begin {bmatrix} K\batrix} \psi {\begin {\matrix}}$

$[$og] T${\displaystyle {\begin{array}{}\end{array}}^{}}${ $style$\ $begin${$bmatrix$} \$Psi$ \$end$ { $bmatrix$}${\displaystyle {}^{}}$^{ 이 방정식을 사전 추출하여 직교 특성을 활용합니다.$T}}$

$(\displaystyle\begin{bmatrix\psi\end{bmatrix})^{T}{\begin{bmatrix}M\end{bmatrix}{\begin{bmatrix}}{\begin{bmatrix}}{\begin{bmatrix}}}+{\begin{bmatrix}}^{T}{\begin{bmatrix}K\end{bmatrix}{\begin{bmatrix}}{\begin{Bmatrix}}=0.}$

그런 다음 직교성 특성은 이 방정식을 다음과 같이 단순화합니다.

${\displaystyle {bmatrix}{\diagdown}m_{r\diagdown}{\begin{Bmatrix}{\dot {q}}\end {Bmatrix}+{\begin{bmatrix}{\diagdown}k_{r\diagdown}{batrix}{b}}}\batrix}}$

이 방정식은 다중 자유도 시스템에 대한 진동 분석의 기초가 됩니다.감쇠된 ^[11]시스템에 대해서도 유사한 유형의 결과를 도출할 수 있습니다.핵심은 모달 질량과 강성 행렬이 대각 행렬이기 때문에 방정식이 "분할"되었다는 것입니다.다시 말해, 이 문제는 다루기 어려운 다중 자유도 문제에서 위에서 설명한 것과 같은 방법을 사용하여 해결할 수 있는 많은 단일 자유도 문제로 변형되었다.

x에 대한 해법은 모달 좌표 또는 모달 참여 계수라고 하는 q에 대한 해법으로 대체됩니다.

{ ${\displaystyle \begin{array}{c}x\end{array}}$ ${\displaystyle \begin{array}{}\}\end{array}}$ ${\displaystyle =}$ [${\displaystyle \begin{array}{}\\ \psi \mathrm{}\end{array}}$ ] ${\displaystyle ]}$ { ${\displaystyle \begin{array}{c}q\end{array}}$ { $displaystyle${ \ $begin${ $Bmatrix$} $x \ end$ { $Bmatrix$ } =$be$ begin {$bmatrix$} \ Psi \$end$ { $bmatrix$} { \ $begin${ $bMatrix } q$ \ } { { as as as $as$ as as as as as as as as as as as as as as as as as as as as as as

${\displaystyle {Bmatrix}x_{n}\end {Bmatrix}=q_{1}{\begin {Bmatrix}_{1}+q_{2}{\begin {Bmatrix}\psi \end {Bmatrix}+q_{3}{begin}{Bmatrix}}$

이 형태로 작성하면 각 자유도에서의 진동이 모드 형상의 선형 합계에 불과함을 알 수 있습니다.또, 각 모드가 최종 진동에 「참가」하는 정도는, 그 모드 참가 계수인 q에 의해서 정의된다.

강체 모드

구속되지 않는 다자유도 시스템은 강체 변환 및/또는 회전과 진동을 모두 경험합니다.강체 모드가 있으면 자연 주파수가 0이 됩니다.대응하는 모드 모양을 강체 모드라고 합니다.

「 」를 참조해 주세요.

레퍼런스

추가 정보

외부 링크

• Excel 시트를 무료로 사용하여 모달 파라미터를 추정할 수 있습니다.
• 진동해석참고 자료 - Mobius Institude
• 상태 감시 및 기계 보호 - Siemens AG
• [3]