퇴화된 에너지 수준

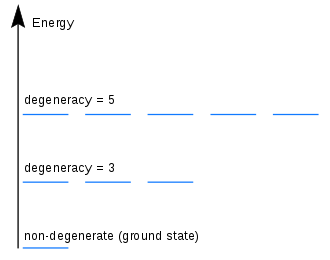
양자역학에서 에너지 수준은 양자 시스템의 둘 이상의 측정 가능한 상태에 해당하면 퇴화된다. 반대로 양자역학계의 둘 이상의 다른 상태는 측정 시 동일한 에너지 값을 부여하면 퇴보한다고 한다. 특정 에너지 수준에 해당하는 상이한 상태의 수를 그 수준의 퇴행 정도라고 한다. 동일한 에너지 고유값을 가진 둘 이상의 선형 독립 고유 상태를 가진 시스템에 대해 해밀턴식 시스템에 의해 수학적으로 표현된다.^{[1]: p. 48} 이럴 때 에너지만으로는 시스템이 어떤 상태에 있는지 특성화할 수 없고, 구분이 필요할 때 정확한 상태를 특성화할 수 있는 다른 양자수가 필요하다. 고전역학에서 이것은 동일한 에너지에 해당하는 다른 가능한 궤적 측면에서 이해할 수 있다.

타락은 양자 통계 역학에서 근본적인 역할을 한다. 3차원의 N-입자 시스템의 경우, 단일 에너지 레벨은 여러 가지 다른 파동 함수 또는 에너지 상태에 해당할 수 있다. 같은 수준의 이런 타락한 주들은 모두 똑같이 채워질 가능성이 있다. 그러한 상태의 수는 특정 에너지 수준의 퇴보성을 준다.

수학

양자 역학 시스템의 가능한 상태는 분리 가능하고 복잡한 힐버트 공간에서 추상 벡터로 수학적으로 다루어질 수 있는 반면, 관측 가능 여부는 그것들에 작용하는 선형 에르미트 연산자에 의해 표현될 수 있다. 적절한 기준을 선택함으로써, 이러한 벡터의 구성 요소와 그 기준의 운영자의 매트릭스 요소를 결정할 수 있다. 만약 A가 N × N 행렬, X가 0이 아닌 벡터, λ가 스칼라라면, A ${\displaystyle X}$= ${\displaystyle \lambda }$ X ${\displaystyle AX=\lambda X},$스칼라 X는 A의 고유값이고 벡터 X는 λ에 해당하는 고유값이라고 한다. 0 벡터와 함께 주어진 고유값 λ에 해당하는 모든 고유 벡터의 집합이 ℂ의ⁿ 아공간을 형성하는데, 이를 λ의 아공간이라고 한다. An eigenvalue λ which corresponds to two or more different linearly independent eigenvectors is said to be degenerate, i.e., ${\displaystyle AX_{1}=\lambda X_{1}}$ and ${\displaystyle AX_{2}=\lambda X_{2}}$, where ${\displaystyle X_{1}}$ and ${\displaystyle X_{2}}$ 선형 독립 고유 벡터. 그 고유값에 해당하는 아이겐스페이스의 치수는 유한하거나 무한할 수 있는 그 퇴화의 정도라고 알려져 있다. 고유값은 그 고유공간이 1차원이라면 비감소적이라고 한다.

양자역학에서 물리적 관측가능성을 나타내는 행렬의 고유값은 이러한 관측가능성의 측정가능한 값을 제공하는 반면, 이러한 고유값에 해당하는 고유값은 측정시 시스템이 발견될 수 있는 가능한 상태를 제공한다. 양자 시스템의 에너지의 측정 가능한 값은 해밀턴 연산자의 고유값에 의해 주어지는 반면, 그 고유성은 시스템의 가능한 에너지 상태를 제공한다. 에너지의 가치는 그것과 관련된 적어도 두 개의 선형 독립 에너지 상태가 존재하는 경우 퇴보한다고 한다. 더욱이 둘 이상의 퇴화된 고유성분의 어떤 선형 결합도 동일한 에너지 고유값에 해당하는 해밀턴 연산자의 고유상태다. 이는 에너지 값 고유값 λ의 eigenspace가 하위 공간(해밀턴의 낟알이 되어 정체성을 곱함)이기 때문에 선형 결합 하에서 닫힌다는 사실에서 분명히 나타난다.

위의 정리를 증명한다.[2]: p. 52

$H{\displaystyle \hat{}}$ ${\$이(가) 해밀턴 연산자를 나타내고 ${\displaystyle and{}_{}}$ 1${\displaystyle {}_{}{1\mathrm{}}_{}}$ ${\displaystyle \psi _${1$}\rangele }$ 및$$ ${\displaystyle {2\mathrm{}}_{}}$ 2${\displaystyle {}_{}}${$${\$displaystyle \psi \{2}\rangele}$이 동일한 고유값 E에 해당하는 두 개의 고유값인 경우 ${\displaystyle {\hat {H} \psi _{1}\rangele =E \psi _{1}\rangele }$ ${\displaystyle {\hat {H} \psi _{2}\rangele =E \psi _{2}\rangele }$ Let ${\displaystyle \psi \rangle =c_{1} \psi _{1}\rangle +c_{2} \psi _{2}\rangle }$, where ${\displaystyle c_{1}}$ and ${\displaystyle c_{2}}$ are complex(in general) constants, be any linear combination of ${\displaystyle \psi _{1}\rangle$$}$과 ${\displaystyle \psi {}_{}}$ ${\displaystyle {2\mathrm{}}_{}}$ ${\displaystyle {}_{}}$ ${\displaystyle \psi _{2}\rangele$$}.$ 그러면 ${\displaystyle {\begin{aigned}{\hat {H} \psi \angle &={{1} \psi _{1}\1}\{2} \{2} \{2} \{2} \{2} _{2} _{2} \c_{1}{H} \psi _{1}\{1}\{1}\{1}\1}\1}\1}\1}\1}\1}\1}\nangle +c_{c_{c_{c_{nangle +c_{{n1}}{\hat{H}} \psi _{2}\rangele \\\&=E(c_{1} \psi _{1}\{1} \psi _{1}\2}\{c_{2} \\&=E \psi \rangele \end{igned}}}}}}}}}}}}}}}}}}}}}}}$ ${\displaystyle which}$ ${\displaystyle \psi \rangele}$이(가) 동일한 고유값 E를 가진$$ $H{\displaystyle \stackrel{}{}}$^${\$ {$H}$의 고유 상태임을 나타낸다$$.

에너지 측정에 대한 퇴행의 영향

퇴행성이 없는 경우 양자체계의 측정된 에너지 값이 결정되면 각 에너지 고유값에 해당하는 고유상태는 단 한 개에 불과하므로 해당 시스템의 상태를 알 수 있다고 가정한다. 그러나 해밀턴 $H{\displaystyle \stackrel{}{}}$ ${\displaystyle \stackrel{}{^}}$ ${\$에 g의$$_n 퇴보 고유값 E ${\displaystyle n_{}}$ ${\$이 있는$$ 경우 이와 연관된 고유상태는 치수 g의_n 벡터 하위공간을 형성한다. 그러한 경우, 여러 최종 상태는 아마도 동일한 $결과{\displaystyle {}_{}}$ ${\displaystyle {En}_{}}${\$displaystyle E_{n}$과(와) 연관될 수 있으며$,$ 모두 g정형_n 고유 벡터 ${\displaystyle E{}_{}}$ ${\displaystyle {n,}_{}}$ ${\displaystyle i_{}}$⟩ ${\displaystyle E_{n,i}\rangele}$의 선형 결합이다$.$

이 경우 상태 ${{\displaystyle \psi \rangele}$에서 시스템에 대해 측정한 에너지 값이 값 ${\displaystyle {En}_{}}$ ${\$을 산출할$$ 확률은 이 기준에서 각 상태에서의 시스템 찾기 확률을 합한 값으로 주어진다$$.

${\displaystyle P(E_{n})=\sum _{i=1}^{g_{n} \langle E_{n,i} \psi \랑글 ^{2}}$

차원이 다른 퇴행성

이 절은 다른 차원으로 연구된 양자 시스템에서 퇴화된 에너지 수준의 존재를 설명하고자 한다. 1차원 시스템과 2차원 시스템에 대한 연구는 더 복잡한 시스템에 대한 개념적 이해를 돕는다.

일차원의 퇴행성

몇 가지 경우, 분석 결과는 1차원 시스템의 연구에서 더 쉽게 얻을 수 있다. 파동함수${\displaystyle \psi }$ ${\displaystyle \psi \rangele$}이$($가) 1차원 전위 $V{\displaystyle }$ ${\displaystyle (x}$ ${\displaystyle )}$ ${\displaystyle V(x)}$을(를) 사용하는$$ 양자 입자의 경우 시간 독립적인 슈뢰딩거 방정식을 다음과 같이 쓸 수 있다$.$

${\displaystyle -{\frac {\hbar ^{2}}:{2m}{\frac {d^{2}\psi }{dx^{2}}+V\psi =E\psi }}}$

이것은 일반적인 미분 방정식이기 때문에, 주어진 $에너지{\displaystyle }$ E ${\displaystyle E$}에 대해서는 기껏해야$$ 두 개의 독립적인 고유 기능이 있으므로, 퇴행의 정도가 두 개를 초과하지 않는다. 한 차원에서는 정상화할 수 있는 파동 기능에 대해 퇴행된 결합 상태가 없다는 것을 증명할 수 있다. 두 실수를 M, x0{\displaystyle M,x_{0}}M으로 ≠ 0과 같이 ∀)을{\displaystyle M\neq 0}의 낱낱으로 지속적인 잠재적인 V{V\displaystyle}과 에너지 E{E\displaystyle}에 관한 필요 충분 조건은 존재, x0{\displaystyle \forall x>, x_{0}}우리는 V())− E≥다. M 2${\displaystyle V(x)-E\geq M^{2$^[3] 특히 $이{\displaystyle }$ 기준에서$$V {\$displaystyle$ V}은(는$)$ 아래에 경계되어 있다$$.

위의 정리를 증명한다.

Considering a one-dimensional quantum system in a potential ${\displaystyle V(x)}$ with degenerate states ${\displaystyle \psi _{1}\rangle }$ and ${\displaystyle \psi _{2}\rangle }$ corresponding to the same energy eigenvalue ${\displaystyle E}$, writing the time-independent Schrödinger 시스템에 대한 방정식: ${\displaystyle -{\frac {\hbar ^{2}}:{2m}{\frac {d^{2}\psi _{1}{dx^{2}}+V\psi _{1}=E\psi _{1}:{1}}$ ${\displaystyle -{\frac {\hbar ^{2}}:{2m}{\frac {d^{2}\psi _{2}}:{dx^{2}}+V\psi _{2}=E\psi _{2}$ 첫 번째 방정식에 ${\displaystyle {\psi \mathrm{}}_{}}$ 2 ${\$을 곱하고 두 번째 방정식을 $\psi {\displaystyle {}_{}}$ ${\displaystyle {1\mathrm{}}_{}}$ ${\$을 곱하면 다음과 같은 결과를 얻을 수 있다. ${\displaystyle \prock \{d^{2}}:{dx^{2}}:}\properties _{2}-\properties _{dx^{2}}:{dx^}}\properties _{1}=0}$ 양측 통합 ${\displaystyle \cHB_{1}{\frac {d\properties_{2}}:{dx}-\properties_{1}{dx}={\mbox}}}}}}$ 잘 정의되고 정규화할 수 있는 파동 함수의 경우 위의 상수는 파동 함수가 최소 1포인트 이상 사라지며, 우리는 다음과 같은 것을 발견한다: ${\displaystyle {\psi \mathrm{}}_{}}$ 1${\displaystyle {}_{}}$( ${\displaystyle x}$)${\displaystyle }$= ${\displaystyle c}$ ${\displaystyle {\psi \mathrm{}}_{}}$ 2${\displaystyle {}_{}}$( ${\displaystyle x}$) ${\displaysty \psi _{1}(x)=c\psi _{2}(x)$ 여기서 $일반적$으로 c ${\displaysty$ c$}$는 복합$$ 상수이다. 바인딩 된 상태 eigenfunctions(즉 x → ∞{\displaystyle x\rightarrow \infty}을 0으로 내리는 경향이 있)것이라는 가정을 위해 V{V\displaystyle}, E{E\displaystyle}, 파동 함수가 접근이 제한치에 zero의 첫번째 파생)→ ∞{\displaystyle x\to \in이 될 수 있shown[3] 조건을 만족시켜 준다.피트$y }$, 그래서 위의 상수가 0이고 우리는 퇴보하지 않는다.

2차원 양자체계의 퇴행성

2차원 양자 시스템은 물질의 세 가지 상태 모두에서 존재하며, 3차원 물질에서 보이는 다양성의 많은 부분이 2차원에서 만들어질 수 있다. 진짜 2차원 물질은 고체 표면에 있는 단원자 층으로 만들어진다. 실험적으로 달성한 2차원 전자 시스템의 예로는 MOSFET, 헬륨, 네온, 아르곤, 제논 등의 2차원 슈퍼레이츠와 액체 헬륨의 표면이 있다. 퇴화된 에너지 수준의 존재는 상자 안의 입자와 2차원 고조파 오실레이터의 경우에 연구되며, 이는 여러 실제 세계 시스템에 유용한 수학 모델 역할을 한다.

직사각형 평면의 입자

치수 $L{\displaystyle {}_{}}$ ${\displaystyle x_{}}$ ${\$의 평면에 있는 자유 입자를, 관통할 수 없는 벽면에서는$$ ${\displaystyle L_{}}$ y ${\$ 파동함수 ${\displaystyle \psi }$ ${\displaystyle ⟩}${ {\$displaystyle \psi \rangele }$을(를) 가진 이 시스템에 대한 시간 독립적인 슈뢰딩거 방정식은 다음과 같이 쓸 수 있다$$.

${\displaystyle -{\frac {\hbar ^{2}}\{2m}\left\frac }{2}\flict x}^{2}}+{\fract ^{2}\frac }{{\flict y}}}}}}}\오른쪽)=E\psi }$

허용되는 에너지 값은 다음과 같다.

${\displaystyle E_{n_{x}},n_{y}}={\frac {\pi ^{2}\hbar ^{2}}:}{{\frac {n_{x}^{2}}:{L_{x}^}}}}}+{\frac {n_{y}^{2}}:{{{{{{{{}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}{{{{{{{{{{{}}}}}}}L_{y}^{2}}:}\오른쪽)}$

정규화된 파형 함수는

${\displaystyle \psi _{n_{x},n_{y}}(x,y)={\frac {2}{\sqrt {L_{x}L_{y}}}}\sin \left({\frac {n_{x}\pi x}{L_{x}}}\right)\sin \left({\frac {n_{y}\pi y}{L_{{y}}\오른쪽)}$

$여기$서 n ${\displaystyle x_{}}$ ${\displaystyle {}_{}}$ ${\displaystyle y_{}}$= ${\displaystyle 1}$,${\displaystyle 2}$,${\displaystyle \mathrm{3...}}$${\displaystyle n_{x},n_{y}=1,2,3...$$}$

따라서 에너지 고유값을 설명하기 위해 ${\displaystyle {양자수}_{}}$ n x ${\$ $및{\displaystyle {}_{}}$ n ${\displaystyle y_{}}${\$displaystyle n_{y}}$가 필요하며$$ 시스템의 가장 낮은 에너지는 다음과 같다.

${\displaystyle E_{1,1}=\pi ^{2}{\frac {\hbar ^{2}}:}\왼쪽({\frac {1}{L_{x}^{2}}}+{\frac {1}{1}{{L_{2}}}}}}}\오른쪽)}$

두$$ ${\displaystyle {길}_{}}$이 L x ${\$L_${x$} ${\displaystyle {및}_{}}$ L$$y {\$displaystyle$L_{$y}}$의 일부 일치 비율에 대해서는 특정 쌍의 상태가 퇴보된다$.$ If ${\displaystyle L_{x}/L_{y}=p/q}$, where p and q are integers, the states ${\displaystyle (n_{x},n_{y})}$ and ${\displaystyle (pn_{y}/q,qn_{x}/p)}$ have the same energy and so are degenerate to each other.

사각 상자 안의 입자

이 경우 상자 $L{\displaystyle {}_{}}$ ${\displaystyle x_{}}$= ${\displaystyle {}_{}}$ ${\displaystyle y{}_{}}$= L ${\displaystyle L_{x}=$$L_{y}=L}$ 및 에너지$$ 고유값은 다음과 같다.

${\displaystyle E_{n_{x},n_{y}={\frac {\pi ^{2}\hbar ^{2}}:{2mL^{2}}(n_{x}^{2}+n_{y)}^{2})}$

$n{\displaystyle {}_{}}$ ${\displaystyle x_{}}$ ${\$과 $n{\displaystyle {}_{}}$ $y{\displaystyle {}_{}}$ ${\$은(는) 에너지를 변경하지 않고 상호 교환할 수$$ 있으므로, 각 에너지 레벨은 ${\displaystyle n_{}}$ x ${\$와 ${\displaystyle n_{}}$ ${\$이 다를 때 최소 2의 변질성을 가진다. 퇴행상태는 다른 에너지 수준에 해당하는 양자수의 제곱합이 같은 경우에도 얻는다. 예를 들어, 세 상태(n_x = 7_y, n = 1) (n_xy = 1, n = 7), (n_xy = 5) 모두 $E{\displaystyle }$= ${\displaystyle 50}$ ${\displaystyle \frac{{\pi \mathrm{}}^{}}{}}$ 2 ${\displaystyle \frac{{}^{}{}^{}}{}}$ ${\displaystyle \frac{{2\mathrm{}}^{}}{}}$ ${\displaystyle \frac{{}^{}}{\mathrm{}}}$ ${\displaystyle \frac{m}{}}$ ${\displaystyle \frac{{}^{}}{}}$ ${\displaystyle \frac{{2\mathrm{}}^{}}{}}$ ${\$}}:00$}$를 구성한다$$.

사각형 상자 내 입자에 대한 다른 에너지 레벨의 퇴행도:

입방체 상자의 입자

이 경우 상자 L ${\displaystyle x_{}}$= ${\displaystyle {}_{}}$ ${\displaystyle y_{}}$= ${\displaystyle L_{}}$ ${\displaystyle {}_{}}$= ${\displaystyle L}$ ${\displaystyle L_{x}=$$L_{y}=L_{z}=L}$과 에너지 고유값은 세 개의 양자수에 따라 달라진다.

${\displaystyle E_{n_{x},n_{y},n_{z}}={\frac {\pi ^{2}\hbar ^{2}}(n_{x}^{2}}}^{2}+n_{y)}^{2}+n_{z}^{2}}}}$

$n{\displaystyle {}_{}}$ ${\displaystyle x_{}}$ ${\$ ${\displaystyle n_{}}$ y ${\$ $n$ ${\displaystyle z_{}}$ ${\$는 에너지를 변경하지 않고 상호 교환할 수 있으므로$$ 각 에너지 레벨은 세 개의 양자수가 모두 같지 않을 때 최소 3의 변질성을 가진다.

퇴화 시 고유 유전체 발견

If two operators ${\displaystyle {\hat {A}}}$ and ${\displaystyle {\hat {B}}}$ commute, i.e. ${\displaystyle [{\hat {A}},{\hat {B}}]=0}$, then for every eigenvector ${\displaystyle \psi \rangle }$ of ${\displaystyle {\hat {A}}}$, ${\displaystyle \hat{B}\psi }$$⟩{\displaystyle {\hat{B} \psi \rangele }$ 또한 동일한 고유값을 가진$$ $A{\displaystyle \stackrel{}{}}$ ${\displaystyle \stackrel{}{^}}${\$displaystyle {\hat {A}}$의 고유 벡터다$$. However, if this eigenvalue, say ${\displaystyle \lambda }$, is degenerate, it can be said that ${\displaystyle {\hat {B}} \psi \rangle }$ belongs to the eigenspace ${\displaystyle E_{\lambda }}$ of ${\displaystyle {\hat {A}}}$, which is said to be globally invariant under the action of ${\displaystyle \stackrel{}{B}}$ ${\displaystyle \stackrel{}{^}}$ ${\$

통근 관측용 A와 B 두 개의 경우, 두 운영자에게 공통적인 고유 벡터로 상태 공간의 정형화된 기초를 구성할 수 있다. However, ${\displaystyle \lambda }$ is a degenerate eigenvalue of ${\displaystyle {\hat {A}}}$, then it is an eigensubspace of ${\displaystyle {\hat {A}}}$ that is invariant under the action of ${\displaystyle {\hat {B}}}$, so the representation of ${\displaystyle {\hat {B}}}$$$ in the eigenbasis of ${\displaystyle {\hat {A}}}$ is not a diagonal but a block diagonal matrix, i.e. the degenerate eigenvectors of ${\displaystyle {\hat {A}}}$ are not, in general, eigenvectors of ${\displaystyle {\hat {B}}}$. However, it is always possible to choose, in every degenerate eigensubs$A{\displaystyle \stackrel{}{}}$ ${\displaystyle \stackrel{}{^}}$ ${\$$displaystyle {\$$hat {A$$}$과(와) $B{\displaystyle \stackrel{}{}}$ ${\displaystyle \stackrel{}{^}}$ {\$displaystyle {\a}$에 공통되는 고유 벡터의 기본인$$A ${\displaystyle \stackrel{}{^}}$ ${\$

통근 관찰 대상의 전체 세트 선택

만일 주어진 관측 가능한 A가 비감속형이라면, 그것의 고유 벡터에 의해 형성된 고유한 기초가 존재한다. 한편, $A{\displaystyle \stackrel{}{}}$ ${\displaystyle \stackrel{}{^}}$ ${\$의 하나 또는 여러 개의 고유값이 변질된 경우$$ 고유값을 지정하면 기준 벡터의 특성을 나타내기에는 충분하지 않다. If, by choosing an observable ${\displaystyle {\hat {B}}}$, which commutes with ${\displaystyle {\hat {A}}}$, it is possible to construct an orthonormal basis of eigenvectors common to ${\displaystyle {\hat {A}}}$ and ${\displaystyle {\hat {B}}}$, which is unique, for each of the poss고유값 {a,b} 다음에 $A{\displaystyle \stackrel{}{}}$ ${\displaystyle \stackrel{}{^}}$ ${\$ $B$ ${\displaystyle \stackrel{}{^}}$ ${\$의 ible 쌍이 통근 관측치의 완전한 집합을 형성한다고 한다$$. 그러나 고유 벡터 집합을 여전히 지정할 수 없는 경우, 적어도 고유값 쌍 중 하나에 대해 세 번째 관측 가능한 $C{\displaystyle \stackrel{}{}}$ ${\displaystyle \stackrel{}{^}}$ ${\$과($와{\displaystyle \stackrel{)}{}}$ B$$^ {\displaystyle {\b} 모두로 통용되는$$세 번째 관측 가능한 C ^ {\$displaystyle {\B}$이(가)가 완전한 s가 되도록 찾을 수 있다$$.출퇴근 관측 자료 등

공통의 에너지 값을 갖는 양자계의 해밀턴계의 고유 기능들은 해밀턴계와 통근하는 연산자를 선택함으로써 행할 수 있는 몇 가지 추가 정보를 줌으로써 라벨을 붙여야 한다. 이러한 추가 라벨은 고유 에너지 고유함수의 이름을 필요로 하며 일반적으로 시스템의 운동 상수와 관련이 있다.

퇴화된 에너지 고유상태 및 패리티 연산자

패리티 연산자는 ${\displaystyle r}$ ${\displaystyle ⟩}$ ${\displaystyle r\rangele }$의 동작으로 정의된다.

${\displaystyle \langle r P \psi \rangle =\psi(-r)}$

P의 고유값은${\displaystyle }$± 1 ${\displaystyle \pm 1$로 제한될 수 있으며, 이는 모두 무한 차원 상태 공간에서 퇴화된 고유값이다. 고유값 +1을 갖는 P의 고유 벡터는 짝수라고 하는 반면 고유값 -1을 갖는 것은 홀수라고 한다.

이제 짝수 연산자 $A{\displaystyle \stackrel{}{}}$ ${\displaystyle \stackrel{}{^}}$ ${\$이(가) 만족스러운 연산자지만$$

${\displaystyle {\tilde{A}=P{\hat{A}P}$

${\displaystyle [P,{\hat {A}]=0}$

반면 홀수 $연산자{\displaystyle \stackrel{}{}}$ B${\displaystyle \stackrel{}{}}$^$${\$displaystyle${\$hat {B}$은(는) 만족스러운 연산자임$$

${\displaystyle P{\hat {B}+{\hat {B}P=0}$

모멘텀 오퍼레이터 $P{\displaystyle {\stackrel{}{}}^{}}$^ ${\displaystyle 2^{\mathrm{}}}$ ${\$}}의 사각형이 짝수이므로$$ 잠재 V(r)가 짝수라면 해밀턴 $H{\displaystyle \stackrel{}{}}$ ${\displaystyle \stackrel{}{^}}$ ${\$ {$H}}}$은 짝수 오퍼레이터라고 한다$$. 이 경우 각각의 고유값이 비분해인 경우 각 고유벡터는 반드시 P의 고유상태로 되어 있으므로 짝수 상태와$$ 홀수 상태 중 $H{\displaystyle \hat{}}$ ${\$의 고유상태를 찾을 수 있다. 그러나 에너지 고유상태 중 하나에 확실한 패리티가 없는 경우에는 해당 고유값이 퇴보한다고 주장할 수 있으며, P ${\displaystyle p}$ {${\displaystyle \stackrel{}{}}${ ${\displaystyle$P$\$$psi \rangele$ $}}$은 $\}$ $displaystyle$ {\hat$${$H$$}}$의 고유값과 동일한$$ $고유벡터$다.

퇴행성과 대칭성

양자-기계적 시스템에서 퇴행성의 물리적 기원은 종종 시스템에 어떤 대칭성이 존재하는 것이다. 양자체계의 대칭성을 연구하는 것은 경우에 따라서는 슈뢰딩거 방정식을 풀지 않고도 에너지 수준과 퇴화를 찾아낼 수 있어 노력을 줄일 수 있다.

수학적으로 대칭성과 퇴행성의 관계를 다음과 같이 명확히 할 수 있다. 단일 연산자 S와 연관된 대칭 연산을 고려한다. 그러한 작업에서 새로운 해밀턴안은 $H{\displaystyle {}^{}}$ ${\displaystyle {\prime }^{}}$= ${\displaystyle S}$ ${\displaystyle H}$ ${\displaystyle {}^{}}$- ${\displaystyle 1^{}}$= S ${\displaystyle H}$ ${\displaystyle {}^{}}$ ${\displaystyle {†}^{}}$ ${\$와 같이 운용자 S에 의해 생성된 유사 변환에 의해 원래의 해밀턴인과 관련된다.$SHS^{-1}=$S는 단일하수체이기 때문에 $SHS^{\doger$ $\}\}.$ 해밀턴 인이 변환 작업 S에서 변하지 않는다면, 우리는

${\displaystyle SHS^{\daugger }=H}$

${\displaystyle SHS^{-1}=H}$

$HS=SH}$

${\displaystyle [S,H]=0}$

이제 ${\displaystyle \alpha }$α ${\displaystyle \alpha$\rangele$}$이(가) 에너지 고유 상태라면$$,

${\displaystyle H \alpha \rangele =E \alpha \rangele }$

여기서 E는 해당 에너지 고유값이다.

${\displaystyle HS \alpha \rangle =SH \alpha \rangle =SE \alpha \rangle =ES \alpha \rangle }$

$즉{\displaystyle }$, S ${\displaystyle \alpha }$ ${\displaystyle ⟩}$ ${\displaystyle$S$\alpha \rangele}$도 동일한 고유값 E를 가진 에너지 고유 상태라는$$ 것을 의미한다. 따라서$$ 두 상태 ${\displaystyle \alpha }$α α $\$ {\$displaystyle \alpha \rangele$}과 ${\displaystyle S}$ α α ${\displaystyle ⟩}$ ${\displaystyle$S$\alpha \rangele}$이(가) 선형적으로 독립되어 있으면(즉, 물리적으로 구별됨) 변질된다.

S가 연속 파라미터 $ϵ{\displaystyle }$ ${\displaystyle \epsilon }$으로 특징지어지는 경우$,$ $S{\displaystyle }$ (${\displaystyle \alpha }$) ${\displaystyle \alpha }$ ${\displaystyle ⟩}$ ${\displaystyle S(\epsilon$) $\alpha \rangle }$ 형식의 모든 상태는 동일한$$ 에너지 고유값을 갖는다.

해밀턴의 대칭군

양자계의 해밀턴계와 함께 통근하는 모든 연산자의 집합은 해밀턴계의 대칭 그룹을 형성한다고 한다. 이 집단의 발전기 정류자는 집단의 대수학을 결정한다. 대칭 그룹의 n차원 표현은 대칭 연산자의 곱셈표를 보존한다. 특정한 대칭 집단을 가진 해밀턴인의 가능한 퇴행성은 집단의 돌이킬 수 없는 표현들의 치수들에 의해 주어진다. n-폴드 퇴화 고유값에 해당하는 고유 특성은 해밀턴의 Symmetry 그룹의 n-차원 불가해한 표현을 위한 기초를 형성한다.

퇴행의 종류

양자체계의 타락은 본질적으로 체계적이거나 우연한 것일 수 있다.

체계적 또는 본질적 퇴보

이것을 기하학적 또는 정상적 퇴행이라고도 하며, 위에서 설명한 바와 같이 특정한 조작에 의한 해밀턴인의 불변, 즉 고려 중인 시스템에 어떤 종류의 대칭성이 존재하기 때문에 발생한다. 정상적인 퇴보에서 얻은 표현은 되돌릴 수 없으며 해당 고유 특성은 이 표현에 대한 기초를 형성한다.

우발적 퇴행

이는 시스템의 일부 특수 특성이나 고려 중인 잠재력의 기능적 형태에서 비롯되는 퇴행성의 한 유형이며, 시스템의 숨겨진 역동적 대칭성과 관련이 있을 수 있다.^[4] 그것은 또한 종종 식별이 쉽지 않은 보존된 수량을 낳는다. 우발적인 대칭은 불연속 에너지 스펙트럼에서 이러한 추가적인 퇴화를 초래한다. 우발적으로 퇴보하는 것은 해밀턴 일행이 완전하지 않기 때문일 수 있다. 이러한 퇴보들은 고전 물리학에서 경계 궤도의 존재와 연결된다.

예: 쿨롱과 하모니 오실레이터 전위

중심 1/r 전위의 입자의 경우, 라플라스-런지-렌츠 벡터는 회전 불변성으로 인한 각운동량의 보존 외에 우발적인 퇴화로 인한 보존량이다.

원뿔의 끝에서 중심되는 1/r과² r 전위의 영향으로 원뿔 위에서 움직이는 입자의 경우, 우발적인 대칭에 해당하는 보존 수량은 각운동량 벡터의 한 성분 외에 런지-렌츠 벡터와 동등한 두 가지 성분이 될 것이다. 이러한 양은 두 전위에 대해 모두 SU(2) 대칭을 생성한다.

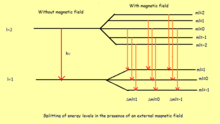
예: 일정한 자기장의 입자

일정한 자기장의 영향을 받아 움직이는 입자가 원형 궤도에서 사이클로트론 운동을 하는 것도 우연한 대칭의 중요한 예다. 이 경우 대칭 배수는 무한히 퇴보하는 랜도 레벨이다.

예

수소 원자

원자물리학에서, 수소 원자에 있는 전자의 경계 상태는 우리에게 퇴화의 유용한 예를 보여준다. 이 경우 해밀턴은 총 궤도 각도운동량 $L{\displaystyle \stackrel{}{{}^{}}}$ ${\displaystyle \stackrel{}{{2\mathrm{}}^{}}}$ ${\displaystyle \stackrel{}{{}^{}}}$ ${\$ 그 성분인 z 방향을 따라 L ${\displaystyle \stackrel{}{z_{}}}$ ${\displaystyle \stackrel{}{{}_{}}}$ ${\$ 총$$ 스핀 각도운동량 S ${\displaystyle \stackrel{}{{2\mathrm{}}^{}}}$ ${\displaystyle \stackrel{}{{}^{}}}$ ${\$ 그 $z-구성요소{\displaystyle \stackrel{}{{}_{}}}$ ${\displaystyle \stackrel{}{S_{}}}$ ^ ^${\displaystyle \stackrel{}{{}_{}}}$^.${\displaystyle {\hat {S_{z$ 이러한 연산자에 해당하는 양자 번호는 $각각{\displaystyle }$$$ l ${\displaystyle l$ ${\displaystyle m_{}}$ $l{\displaystyle {}_{}}$ ${\$ $s{\displaystyle }$ ${\displaystyle$ s$}($전자의 경우 항상 1/2), ${\displaystyle m_{}}$ s ${\$이다.

수소 원자의 에너지 수준은 주 양자수 n에만 의존한다. 주어진 n의 경우, ${\displaystyle l}$= ${\displaystyle 0}$,${\displaystyle }$…${\displaystyle }$, ${\displaystyle \mathrm{n}}$- 1 ${\displaystyle l=0,\ldots ,n-1}$에 해당하는 모든 상태는 동일한 에너지를 가지며$$ 퇴화된다. n과 l의 주어진 값과 마찬가지로${\displaystyle }$(${\displaystyle 2}$ ${\displaystyle l}$+ ${\displaystyle 1}$) ${\displaystyle (2l+1)}$ ,$$${\displaystyle m_{}}$=${\displaystyle }$- ${\displaystyle l}$,${\displaystyle }$…${\displaystyle }$, ${\displaystyle l}$ ${\displaystyle m_{l}=-l,\ldots ,l}$의 상태는 퇴보한다$$. 따라서 에너지 레벨 E의_n 퇴행도는 ${\displaystyle \underset{}{\overset{}{}}}$ ${\displaystyle \underset{}{\overset{}{l}}}$= ${\displaystyle \underset{}{\overset{}{}}}$ ${\displaystyle \underset{}{\overset{}{}}}$ ${\displaystyle \underset{}{\overset{}{\mathrm{n}}}}$- 1${\displaystyle \underset{}{\overset{}{}}}$( ${\displaystyle \underset{}{\overset{}{2}}}$ ${\displaystyle \mathrm{l}}$+ ${\displaystyle 1}$)${\displaystyle }$= n ${\displaystyle {}^{}}$ ${\$}}이며$,$ 스핀 퇴행성을 포함하면 2배가 된다.^{[1]: p. 267f}

$m{\displaystyle {}_{}}$ ${\displaystyle l_{}}$ ${\$에 대한 퇴행성은 중심 잠재력에 존재하는 본질적인 퇴행성으로$$, 선호하는 공간 방향이 없을 때 발생한다. $l{\displaystyle }$ ${\displaystyle l}$에 관한 퇴행성은 흔히 우발적인 퇴행으로 설명되지만$$, 쿨롱의 법칙에 의해 잠재적 에너지가 주어지는 수소 원자에만 유효한 슈뢰딩거 방정식의 특수한 대칭의 관점에서 설명할 수 있다.^{[1]: p. 267f}

등방성 3차원 고조파 오실레이터

그것은 3차원 공간에서 움직이는 질량 m의 스핀리스 입자로, 절대값이 힘의 중심으로부터 입자의 거리에 비례하는 중심력의 영향을 받는다.

$F=-kr}$

그것에 작용하는$$ 잠재적 $V{\displaystyle }$( ${\displaystyle r}$) ${\displaystyle V(r)}$이(가) 회전 불변성, 즉 : ${\displaystyle V}$( r${\displaystyle }$)${\displaystyle }$= ${\displaystyle 1}$/ ${\displaystyle 2\mathrm{}}$(${\displaystyle m}$ ${\displaystyle {}^{}}$ 2 ${\displaystyle {}^{}{}^{}}$ ${\displaystyle {2\mathrm{}}^{}}$)${\displaystyle V(r)=1/2(m\omega^{2}r^{2}}}})$이므로 등방성이라고 한다.

여기서 $\Omega {\displaystyle }$ ${\displaystyle \omega}$은(는) $k{\displaystyle \sqrt{}}$/ ${\displaystyle \sqrt{m}}$ ${\$이(가) 제공하는 각도 주파수 입니다$.$

그러한 입자의 상태공간은 개별적인 1차원 파동함수와 연관된 상태공간의 텐서적 산물이기 때문에, 그러한 시스템에 대한 시간독립적인 슈뢰딩거 방정식은 다음을 통해 주어진다.

${\displaystyle -{\frac {\hbar ^{2}}{2m}}\left({\frac {\partial ^{2}\psi }{\partial x^{2}}}+{\frac {\partial ^{2}\psi }{\partial y^{2}}}+{\frac {\partial ^{2}\psi }{\partial z^{2}}}\right)+(1/2){m\omega ^{2}(x^{2}+y^{2}+z^{2})\psi }=E\psi }$

따라서 에너지 고유값은 ${\displaystyle {En{}_{}}_{}}$ ${\displaystyle {x_{}}_{}}$, n ${\displaystyle {y_{}}_{}}$, n ${\displaystyle {z_{}}_{}}$= ${\displaystyle (n_{}}$ x${\displaystyle {}_{}}$+ ${\displaystyle n_{}}$ ${\displaystyle y_{}{}_{}}$+ ${\displaystyle {}_{}}$ z${\displaystyle {}_{}}$+ ${\displaystyle 3}$/${\displaystyle 2\mathrm{}}$) ${\displaystyle \hslash }$ ${\displaystyle \Omega }$ ${\displaystyle E_{n_{x},n_{y}},n_{z}}}}=(n_{x}+}+{z}/2)\hbar \omega$}

또는, ${\displaystyle {En}_{}}$=${\displaystyle }$(${\displaystyle n\mathrm{}}$+ 3${\displaystyle }$/ 2${\displaystyle }$) ${\displaystyle \Omega }$ ${\displaystyle E_{n}=(n+3/2)\hbar \omega }$

여기서 n은 음이 아닌 정수다. 따라서 에너지 레벨은 퇴보되고 퇴보의 정도는 $만족$스러운 n ${\displaystyle x_{}}$ ${\displaystyle {}_{}}$ ${\displaystyle y_{}}$ ${\displaystyle n_{}}$ z ${\$의 서로 다른 세트 수와 같다.

${\displaystyle n_{x}+n_{y}+n_{z}=n}$

$n{\displaystyle }$t ${\displaystyle {\mathrm{h}}^{}}$${\$$^{\mathrm{th$$}}}}}}$ 상태의$$$$ 변질성은 $n{\displaystyle {}_{}}$ ${\displaystyle x_{}}$ ${\$$x$$\},$ $n{\displaystyle {}_{}}$ ${\displaystyle y_{}}$ ${\$ $n$ ${\$$z}}}}$에 0이 ${\displaystyle {있으면}_{}}$ 알 수 있다.${\displaystyle }$${\displaystyle n_{}}$${\displaystyle }$+ ${\displaystyle 1}$ ${\$ 및$$ n ${\displaystyle z_{}}$ ${\$에 분포할 수 있는 $가능성$$.$ $n{\displaystyle {}_{}}$ ${\displaystyle x_{}}$ ${\$ $n_$${x}$에 1 퀀타를 가지면 ${\displaystyle n_{}}$ $y{\displaystyle {}_{}}$ ${\$${y$$}$ 및$$ n ${\displaystyle z_{}}$에 걸쳐서$$ ${\$ 가능성이 있다$$. 이는 n -${\displaystyle n_{}}$ ${\displaystyle {}_{}}$+ ${\displaystyle 1}$ ${\displaystyle n-n_{x}+1}$의 일반적인 결과로 이어지고, $모든$ n ${\displaystyle n}$을(를) 합치면 n ${\displaystyle {t\mathrm{}}^{}}$ ${\displaystyle {\mathrm{h}}^{}}$ ${\$ n$^{\mathrm{th}}}}}}$ 상태의$$ degernerability로 이어진다$$.

${\displaystyle \sum _{n_{x}=0}^{n}(n-n_{x}+1)=(n+1)(n+2)/2}$

${\displaystyle \mathrm{그림}}$과 같이 $n{\displaystyle }$= 0 ${\displaystyle n=0}$이(가) 비감소 상태인 접지 상태만($즉{\displaystyle \mathrm{}}$, degerancy가 1 ${\displaystyle 1}$임).

퇴보 제거

양자역학계에서의 퇴행성은 외부 섭동에 의해 기저 대칭이 깨지면 제거될 수 있다. 이것은 퇴화된 에너지 레벨에서 분열을 야기한다. 이것은 본질적으로 원래의 수정 불가능한 표현을 혼란스러운 시스템의 그러한 표현으로 나누는 것이다.

수학적으로 작은 섭동 전위의 적용으로 인한 분열은 시간 독립적인 퇴행 섭동 이론을 사용하여 계산할 수 있다. 이것은 양자계의 해밀턴₀ H에 대한 해밀턴 H에 대한 해밀턴 H에 대한 해밀턴 H에 대한 해답을 찾기 위해 적용할 수 있는 근사 방법이다. 그것은 섭동 시리즈에서 해밀턴 H의 고유값과 고유개열을 확장하는 것을 포함한다. 주어진 에너지 고유값을 가진 퇴행성 고유질소는 벡터 아공간을 형성하지만, 이 공간의 고유질체의 모든 기초가 섭동 이론의 좋은 출발점이 되는 것은 아니다. 왜냐하면 전형적으로 그들 근처에 변진계통의 고유질체는 존재하지 않을 것이기 때문이다. 올바른 선택 근거는 퇴화된 아공간 안에서 섭동 해밀턴을 대각선으로 만드는 것이다.

1차 퇴행성 섭동 이론에 의한 퇴행성의 과시.

동요하지 않는 해밀턴 $H{\displaystyle \stackrel{}{{}_{}}}$ ${\displaystyle \stackrel{}{{0\mathrm{}}_{}}}$ ${\displaystyle \stackrel{}{{}_{}}}$ ${\$과 동요 $V{\displaystyle \stackrel{}{}}$ ${\displaystyle \stackrel{}{^}}$ ${\$}}을(를) 고려해서 동요하지 않는 해밀턴식 H0 ^ {\dat ${V}$을(를) 고려하십시오$.$ ${\displaystyle {\hat{H}}={\hat {H_{0}}+{\hat {V}}}$ 변질된 고유국은 퇴보하지 않기 위해-에 의해 주어진다. ${\displaystyle \psi _{0}\rangele = n_{0}\rangele +\sum _{k\neq 0}V_{k0}/(E_{0}-E_{k}) n_{k}\k}\rangele }}$ E ${\displaystyle {0\mathrm{}}_{}}$= ${\displaystyle E_{}}$ k ${\$즉 에너지 수준의 퇴화가 있을 때 동요된 에너지 고유켓과 높은 순서의 에너지는 서로 다르다. $H{\displaystyle \stackrel{}{{}_{}}}$ ${\displaystyle \stackrel{}{{0\mathrm{}}_{}}}$ ${\displaystyle \stackrel{}{{}_{}}}$ ${\$이(가) 동일한 에너지 고유값 E와$$ 일반적으로 일부 비-degenerate eigenstatees ${\displaystyle m}$ ${\displaystyle ⟩}${\$displaystym m\rangele }$을(를) 소유하고$$ 있다고 가정한다. 동요하지 않는 고유상태 ${\displaystyle {\psi }_{}}$ j${\displaystyle {}_{}}$⟩ ${\displaystyle \psi _{j}\rangele }$은(는) 동요하지 않는 퇴행성 고유상태 linear의 선형 확장으로 쓸 수 있다$$. ${\displaystyle \c}\rangele =\sum _{i}m_{i}\langle m_{i}\langle m_{i}\nowle =\sum _{i}c_{i}m_{i}\rangele }}$ ${\displaystyle [{\hat {H_{0}}}+{\hat {V}}]\psi _{j}\rangle =[{\hat {H_{0}}}+{\hat {V}}]\sum _{i}c_{ji} m_{i}\rangle =E_{j}\sum _{i}c_{ji} m_{i}\rangle }$ 여기서 $E{\displaystyle {}_{}}$ ${\displaystyle j_{}}$ ${\$는 동요된 에너지 고유값을 가리킨다$$. $E{\displaystyle }$ ${\displaystyle E}$이(가) $H{\displaystyle \stackrel{}{{}_{}}}$ ${\displaystyle \stackrel{}{{0\mathrm{}}_{}}}$ ${\displaystyle \stackrel{}{{}_{}}}$ ${\$의 퇴행 고유값이기 때문에$,$ ${\displaystyle \sum \sum _{i}c_{ji}-E}\sum _{i_{ji}-e)\sum _{i}m_{i}\delta E_{j}\sum _{i}m_{i}\i}\rangele }}}}}}$ 방해받지 않는 또 다른 퇴화성 아이겐케트${\displaystyle k_{}}$ m${\displaystyle {}_{}}$k {\$displaystyle \langle m_{k}}$에 의한 전치화가 다음을$$ 제공한다. ${\displaystyle \sum \{i}c_{ji}[\langle m_{k}}{{V}} {\hat {V}\angle -\delta _{ik}(E_{j}-E)]=0}$ 이것은 고유값 문제인데, V ${\displaystyle i_{}}$ k${\displaystyle {}_{}}$= ${\displaystyle ⟨}$ ${\displaystyle {}_{}}$ ${\displaystyle i_{}}$ ${\displaystyle V{}_{}\stackrel{}{}}$ ${\displaystyle \stackrel{}{^}}$ ${\displaystyle m{}_{}}$ ${\displaystyle k_{}}$ ^ m k ${\displaystyle {}_{}}$ ${\displaystyle V_{i}=\langle m_{ni} {\hat{V}m_{k}\angle$ $\}\}\},$ 우리는... ${\displaystyle {\begin{vmatrix}V_{11}-\Delta E_{j}&V_{12}&\dots &V_{1}N}\\V_{21}&V_{22}-\Delta E_{j}&\dots &V_{2}N}\\\vdots &\vdots &\vdots &\\vdots \\\\\\\\V_{N1}&V_{N2}&\dots &V_{N}-\Delta E_{j}\end{vmatrix}.\,}$ 이 방정식을 풀어서 얻은 N 고유값은 적용된 섭동에 의한 퇴행 에너지 수준의 변화를 주는 반면, 고유 벡터는 동요하지 않는 퇴행성 기준 ${\displaystyle m}$ ${\displaystyle ⟩}$ ${\displaystyle m\rangele}$에 동요된 상태를 준다$.$ 처음부터 좋은 고유성을 선택하려면 연산자를 찾는 것이 유용하다.${\displaystyle \stackrel{}{\mathrm{원래}}}$ 해밀턴 H 0 ^ {\$displaystyle {\hat_{0}}}}$과(와) 통하고 동시에 고유성을 갖는 V ${\displaystyle \stackrel{}{^}}$ ${\$ ${\$$hat$ {$V$$}}.$

섭동에 의한 퇴행성 제거의 물리적 예

외부 섭동의 적용에 의해 양자 시스템의 퇴화된 에너지 수준이 분할되는 물리적 상황의 몇 가지 중요한 예는 다음과 같다.

2-레벨 시스템에서의 대칭 파괴

2단계 시스템은 기본적으로 에너지가 서로 가깝고 시스템의 다른 상태와 매우 다른 두 상태를 가진 물리적 시스템을 가리킨다. 그러한 시스템에 대한 모든 계산은 상태 공간의 2차원 하위 공간에서 수행된다.

물리적 시스템의 지상 상태가 2배 저하된 경우, 해당 두 상태 사이의 어떤 결합도 시스템의 지상 상태의 에너지를 낮추고, 이를 더욱 안정되게 한다.

If ${\displaystyle E_{1}}$ and ${\displaystyle E_{2}}$ are the energy levels of the system, such that ${\displaystyle E_{1}=E_{2}=E}$, and the perturbation ${\displaystyle W}$ is represented in the two-dimensional subspace as the following 2×2 matrix

${\displaystyle \mathbf {W} ={\begin{bmatrix}0&W_{12}\\W_{12}^{*}&0\end{bmatrix}}.}$

혼란에 빠진 에너지는

${\displaystyle E_{+}=E+ W_{12}}}$

${\displaystyle E_{-}=E- W_{12} }$

시스템의 고유 속성으로 인한 내부 상호작용에 의해 해밀턴식(Hamiltonian)에 비대각형 용어가 존재하여 에너지 상태의 퇴화가 깨지는 2개 상태 시스템의 예는 다음과 같다.

• 인접한 탄소 원자들 사이의 세 개의 이중 결합을 두 가지 가능성 있는 벤젠.
• 질소 원자가 세 개의 수소 원자에 의해 정의된 평면 위 또는 아래에 있을 수 있는 암모니아 분자.
• H⁺
  ₂ 분자, 두 개의 핵 중 하나를 중심으로 전자가 국부화 될 수 있다.

미세구조 분할

상대론적 움직임과 스핀-오비트 커플링으로 인해 수소 원자에서 전자와 양성자 사이의 쿨롱 상호작용에 대한 보정은 단일 주 양자수 n에 해당하는 l의 다른 값에 대한 에너지 수준의 저하를 깨게 된다.

상대론적 교정에 의한 섭동 해밀턴은 다음과 같이 주어진다.

${\displaystyle H_{r}=-p^{4}/8m^{3}c^{2}}$

$여기$서 $p{\displaystyle }$ ${\displaystyle p}$은 모멘텀 연산자, m ${\displaystyle$ m$}$은 $전자$의 질량이다. ${\displaystyle n}$ ${\displaystyle l}$ ${\displaystyle m}$ ${\displaystyle ⟩}$ ${\displaystyle nlm\rangele}$ 기반에서의$$ 1차 상대론적 에너지 보정은 다음과 같다.

${\displaystyle E_{r}=(-1/8m^{3}c^{2})\langle nlm p^{4}nlm\angle }$

이제 p ${\displaystyle {4\mathrm{}}^{}}$= ${\displaystyle {4m\mathrm{}}^{}}$ 2${\displaystyle {}^{}}$( ${\displaystyle {}^{}}$ ${\displaystyle {0\mathrm{}}^{}}$+ ${\displaystyle {e\mathrm{}}^{}}$ ${\displaystyle 2{}^{}}$/ r${\displaystyle {}^{}}$) ${\displaystyle {2\mathrm{}}^{}}$ ${\$}}

${\displaystyle {\reasoned}E_{r}&=(-1/2mc^{2})[E_{n}^{2}+2E_{n}e^{2}\langle 1/r\rangle +e^{4}\langle 1/r^{2}\langle ]\\&=(-1/2)mc^{2}\nmc^{4}\mc^{4}[-3/(4n^{4})+1/{n^{3}(l+1/2)}}]\end{aigned}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}"$

여기서 $\alpha {\displaystyle }$ ${\displaystyle \alpha }$은(는) 미세 구조 상수다.

스핀오빗 상호작용은 양성자와의 상대적인 움직임으로 인해 전자에 의해 경험되는 자기장과 전자의 내적인 자기 모멘트 사이의 상호작용을 말한다. 해밀턴의 상호작용은

${\displaystyle H_{so}=-(e/mc){{\vec {m}\cdot {\vec{{L}/r^{3}}}=[(e^{2}/(m^{2}c^{2}r^{3})]){\vec {S}\cdot {\vec {L}}$

라고 쓰여 있을 수 있는.

${\displaystyle H_{so}=(e^{2}/(4m^{2}c^{2}r^{3})[{\vec{J}}^{2}-{\vec{L}^{2}-{\vec{S}^{2}]}$

섭동 해밀턴이 대각선으로되어 있는 j, m, l, 1/2⟩{j,m,l,1/2\rangele\displaystyle}근위의 첫 번째 순서 에너지 보정은 다음과 같다.

${\displaystyle E_{so}=(\hbar^{2}e^{2})/(4m^{2}c^{2}][j(j+1)-l(l+1)-3/4]/(a_{0})^{3}n^{3}(l+1/2)(l+1)]}$

${\displaystyle {여기}_{}}$서 0 ${\$는 보어 반지름이다. 전체 미세 구조 에너지 시프트는 다음과 같다.

${\displaystyle E_{fs}=-(mc^{2}\alpha ^{4}/(2n^{3})[1/(j+1/2)-3/4n]}}$

$j{\displaystyle }$= ${\displaystyle \mathrm{l}}$± 1${\displaystyle }$/ ${\displaystyle 2\mathrm{}}$ ${\displaystyle j=l\pm$1$/2}$의 경우$.$

지만 효과

원자의$$ 자기모멘트 $m{\displaystyle \stackrel{}{}}$→ ${\$의 상호작용 때문에 외부 자기장에 놓였을 때 원자의 에너지 수준이 분할되는 것을 Zeman 효과라고 한다.

수소 원자 내 단일 전자의 궤도 및 회전 각도 모멘트 L→{\displaystyle{\vec{L}}S({\displaystyle{\vec{S}}을(를)고려하여,섭동 해밀턴은 다음과및같이 주어진다.

${\displaystyle {\v}=-({\vec {m_{l}}+{\vec {m_{s}}}}\cdot {\vec {B}}}}}$

${\displaystyle {여기}_{}}$서 $m{\displaystyle {}_{}}$=${\displaystyle }$- ${\displaystyle e}$ ${\displaystyle L\stackrel{}{}}$→${\displaystyle }$/ ${\displaystyle \mathrm{2m}}$ ${\displaystyle m_{l}=-e{\vec{L}/2m},$ ${\displaystyle m_{}}$ =${\displaystyle }$- ${\displaystyle e}$ ${\displaystyle S\stackrel{}{}}$→${\displaystyle }$/ ${\displaystyle m}$ ${\displaystyle m_{s}=-e{\vec}/m$ 그러므로,

${\displaystyle {\v}=e({\vec{L}+2{\vec {S})\cdot {\vec{B}/2m}$

이제 약한 필드 지만 효과의 경우, 적용된 필드가 내부 영역에 비해 약할 때 스핀-오비트 커플링이 지배하고 $L{\displaystyle \stackrel{}{}}$→ ${\$ S$$${\displaystyle \stackrel{}{}}$→ ${\$는 별도로 보존되지 않는다$$. 좋은 양자수는 n, l, j, m이며_j, 이 기초에서 첫 번째 순서 에너지 보정은 다음과 같이 주어지는 것으로 보여질 수 있다.

${\displaystyle E_{}}$ ${\displaystyle z_{}}$= -${\displaystyle {\mu }_{}}$ B ${\displaystyle {}_{}}$ B ${\displaystyle {}_{}}$ ${\displaystyle j_{}}$ ${\$ 여기서

${\displaystyle {\mu B}_{}}$= ${\displaystyle e}$ ${\displaystyle \hslash }$/ ${\displaystyle \mathrm{2m}}$ ${\displaystyle \mu _{B}={e\hbar }/2m}$을(를) 보어 마그넷온이라고 한다.따라서 m ${\displaystyle j_{}}$ ${\$의 값에 따라 각각 퇴화된 에너지 레벨이 여러 레벨로 분할된다$.$

강장 지만 효과의 경우, 적용된 필드가 충분히 강할 때, 궤도 및 회전 각도 모멘텀a 디커플링으로, 이제 좋은 양자수는 n, l, m_l, m이_s 된다. 여기 L과z S는z섭동 해밀턴은 있어서 보존되어...

${\displaystyle {\v}=eB(L_{z}+2S_{z}/2m}$

자기장이 z 방향을 따라 있다고 가정한다. 그렇게

${\displaystyle {\v}=eB(m_{l}+2m_{s})/2m}$

m의_l 각 값에는 m의_s 두 가지 가능한 값이 있는데$,{\displaystyle }$ ± ${\displaystyle 1}$/ ${\displaystyle 2\mathrm{}}$ ${\displaystyle \pm$1$/2}$이다$.$

스타크 효과

외부 전기장에 노출되었을 때 원자나 분자의 에너지 수준이 분할되는 것을 스타크 효과라고 한다.

수소 원자의 경우,섭동 해밀턴은

${\displaystyle {\hat{H}_{s}=- e Ez}$

z 방향을 따라 전장이 선택되는 경우.

적용된 필드로 인한 에너지 보정은 ${\displaystyle n}$ ${\displaystyle l}$ $⟩{\displaystyle{\$$hat{H$$}$$_{s$$}}$의 기대값으로 주어진다. It can be shown by the selection rules that ${\displaystyle \langle nlm_{l} z n_{1}l_{1}m_{l1}\rangle \neq 0}$ when ${\displaystyle l=l_{1}\pm 1}$ and ${\displaystyle m_{l}=m_{l1}}$.

그 퇴폐는 첫 순서로 선정 규칙을 준수하는 특정 주에 대해서만 해제된다. The first-order splitting in the energy levels for the degenerate states ${\displaystyle 2,0,0\rangle }$ and ${\displaystyle 2,1,0\rangle }$, both corresponding to n = 2, is given by ${\displaystyle \Delta E_{2,1,m_{l}}=\p$$m e(\hbar ^{2})/(m_{e}e^{2})$$E}$ $.$

참고 항목

• 상태 밀도

참조

추가 읽기

• Cohen-Tannoudji, Claude; Diu, Bernard & Laloë, Franck. Quantum Mechanics. 1. Hermann. ISBN 9782705683924.CS1 maint: 작성자 매개변수 사용(링크)^{[전체 인용 필요]}
• Shankar, Ramamurti (2013). Principles of Quantum Mechanics. Springer. ISBN 9781461576754.CS1 maint: 작성자 매개변수 사용(링크)^{[전체 인용 필요]}
• Larson, Ron; Falvo, David C. (30 March 2009). Elementary Linear Algebra, Enhanced Edition. Cengage Learning. pp. 8–. ISBN 978-1-305-17240-1.
• Hobson; Riley. Mathematical Methods For Physics And Engineering (Clpe) 2Ed. Cambridge University Press. ISBN 978-0-521-61296-8.
• Hemmer (2005). Kvantemekanikk: P.C. Hemmer. Tapir akademisk forlag. Tillegg 3: supplement to sections 3.1, 3.3, and 3.5. ISBN 978-82-519-2028-5.
• 2차원 시스템에서의 양자 퇴화, Debnarayan Jana, University of Science and Technology College 물리학과 학장
• Al-Hashimi, Munir (2008). Accidental Symmetry in Quantum Physics.