멀티스크롤 끌어당김기
Multiscroll attractor역동적인 시스템의 수학에서 더블스크롤 어트랙터(Chua의 어트랙터라고도 함)는 하나의 비선형 저항(Chua의 다이오드 참조)으로 물리적인 전자 혼돈 회로(일반적으로 Chua의 회로)에서 관찰되는 이상한 어트랙터다. 이중 스크롤 시스템은 흔히 3개의 비선형 일반 미분 방정식과 3-세그먼트 조각-선형 방정식으로 설명된다(추아 방정식 참조). 이것은 Chua의 회로의 단순한 설계로 인해 시스템을 수치적으로 쉽게 시뮬레이션하고 물리적으로 쉽게 나타낼 수 있게 한다.
Chua 회로를 사용하여 이 모양은 회로의 X, Y 및 Z 출력 신호를 사용하여 오실로스코프에서 볼 수 있다. 이 무질서한 끌어당기는 3차원 공간의 모양 때문에 이중 두루마리로 알려져 있는데, 이는 소용돌이 선으로 연결된 두 개의 토성 같은 고리와 비슷하다.
이 유인기는 처음에 시뮬레이션에서 관찰되었다가, 리온 추아가 추아의 회로로 알려진 자율적인 혼란 회로를 고안한 후에 물리적으로 실현되었다.[1] 추아 서킷의 더블스크롤 어트랙터는 3차원 주공간의 고유 벡터들의 구성방식으로 명백하게 도출한 어트랙터의 다수의 푸앵카레 리턴 맵을 통해 무질서하다는[2] 것이 엄밀하게 입증되었다.[3]
이중 스콜 끌림의 수치적 분석은 그것의 기하학적 구조가 무한한 수의 프랙탈과 같은 층으로 이루어져 있다는 것을 보여주었다. 각 단면은 모든 척도에서 프랙탈로 나타난다.[4] 최근에는 이중 두루마리 안에서 숨겨진 유인원이 발견됐다는 보도도 나오고 있다.[5]
1999년 관롱첸(關龍첸)과 우에타는 또 다른 이중 두루마기 무질서한 유인기를 제안하였는데, 이는 첸 계통 또는 첸 끌러라고 한다.[6][7]
첸 끌어당김기
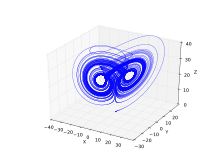
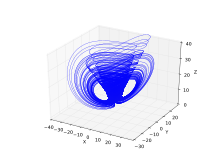
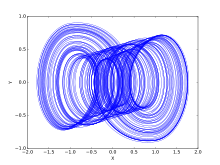
Chen 체계는 다음과[7] 같이 정의된다.
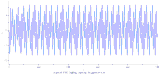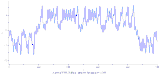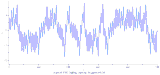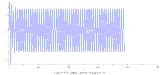
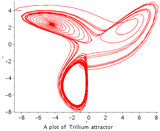
첸 유인기의 플롯은 룬게-쿠타 방법으로 얻을 수 있다.[8]
매개변수: a = 40, c = 28, b = 3
초기 조건: x(0) = -0.1, y(0) = 0.5, z(0) = -0.6
기타유인자
n스크롤 유치자로도 불리는 멀티스크롤 유치자에는 루첸 유치자, 변형된 천 혼돈 유치자, PWL 더핑 유치자, 라비노비치 파브리칸트 유치자, 변형된 츄아 혼돈 유치자, 즉 하나의 유치자에 여러 두루마기가 포함된다.[9]
루첸 끌어당김기
진후루(陳hu金)와 관롱첸이[9] 멀티스크롤을 가진 확장된 첸 시스템을 제안했다.
루첸계 방정식
매개변수:a = 36, c = 20, b = 3, u = -15.15
초기 조건:x(0) = .1, y(0) = .3, z(0) = -.6
수정루첸 끌어당김기
시스템 방정식:[9]
어느 곳에서
매개 변수 :=a = 35, c = 28, b = 3, d0 = 1, d1 = 1, d2 = -20.20, tau = .2
initv := x(0) = 1, y(0) = 1, z(0) = 14
변형 추아 무질서한 끌어당기기
2001년에 탕 외는 수정된 추아 혼란 시스템을[10] 제안했다.
어느 곳에서
매개 변수 :== 알파 = 10.82, 베타 = 14.286, a = 1.3, b = .11, c = 7, d = 0
initv := x(0) = 1, y(0) = 1, z(0) = 0
PWL 더핑 무질서한 끌어당기기
Aziz Alaoui는 2000년에 [11]PWL 더핑 방정식을 조사했다.
PWL 더핑 시스템:
파라 := e = .25, 감마 = .14+(1/20)i, m0 = -0.845e-1, m1 = .66, 오메가 = 1; c : (.14+(1/20)i)ii=-25...25;
initv := x(0) = 0, y(0) = 0;
수정된 로렌츠 혼돈 시스템
미란다 & 스톤은 다음과 같이 수정된 로렌츠 시스템을 제안했다.[12]
매개변수: a = 10, b = 8/3, c = 137/5;
초기 조건: x(0) = -8, y(0) = 4, z(0) = 10
갤러리
참조
- ^ Matsumoto, Takashi (December 1984). "A Chaotic Attractor from Chua's Circuit" (PDF). IEEE Transactions on Circuits and Systems. IEEE. CAS-31 (12): 1055–1058. doi:10.1109/TCS.1984.1085459.
- ^ Chua, Leon; Motomasa Komoru; Takashi Matsumoto (November 1986). "The Double-Scroll Family" (PDF). IEEE Transactions on Circuits and Systems. CAS-33 (11).
- ^ Chua, Leon (2007). "Chua circuits". Scholarpedia. 2 (10): 1488. Bibcode:2007SchpJ...2.1488C. doi:10.4249/scholarpedia.1488.
- ^ Chua, Leon (2007). "Fractal Geometry of the Double-Scroll Attractor". Scholarpedia. 2 (10): 1488. Bibcode:2007SchpJ...2.1488C. doi:10.4249/scholarpedia.1488.
- ^ Leonov G.A.; Vagaitsev V.I.; Kuznetsov N.V. (2011). "Localization of hidden Chua's attractors" (PDF). Physics Letters A. 375 (23): 2230–2233. Bibcode:2011PhLA..375.2230L. doi:10.1016/j.physleta.2011.04.037.
- ^ Chen G, Ueta T. 하지만 또 다른 혼란스러운 유혹자. 1999년 9시 1465분 분기와 혼돈의 저널.
- ^ a b CHEN, GUANRONG; UETA, TETSUSHI (July 1999). "Yet Another Chaotic Attractor". International Journal of Bifurcation and Chaos. 09 (7): 1465–1466. doi:10.1142/s0218127499001024. ISSN 0218-1274.
- ^ 阎振亚著 《复杂非线性波的构造性理论及其应用》第17页 SCIENCEP 2007年
- ^ a b c Chen, Guanrong; Jinhu Lu (2006). "Generating Multiscroll Chaotic Attractors: Theories, Methods and Applications" (PDF). International Journal of Bifurcation and Chaos. 16 (4): 775–858. Bibcode:2006IJBC...16..775L. doi:10.1142/s0218127406015179. Retrieved 2012-02-16.
- ^ Chen, Guanrong; Jinhu Lu (2006). "Generating Multiscroll Chaotic Attractors: Theories, Methods and Applications" (PDF). International Journal of Bifurcation and Chaos. 16 (4): 793–794. Bibcode:2006IJBC...16..775L. CiteSeerX 10.1.1.927.4478. doi:10.1142/s0218127406015179. Retrieved 2012-02-16.
- ^ J. Lu, G. Chen 페이지 837
- ^ J.Liu와 G Chen p834
외부 링크
- 더블스크롤 끌러와 츄아 회로
- Lozi, R.; Pchelintsev, A.N. (2015). "A new reliable numerical method for computing chaotic solutions of dynamical systems: the Chen attractor case". International Journal of Bifurcation and Chaos. 25 (13): 1550187. doi:10.1142/S0218127415501874.