텐트 지도

이 글은 검증을 위해 인용구가 추가로 필요하다. 신뢰할 수 있는 출처에 인용문을 추가하여 이 기사를 개선할 수 있도록 도와주십시오. 공급되지 않은 재료는 도전하여 제거할 수 있다. 출처 찾기: "텐트 맵" – 뉴스 · 신문 · 책 · 학자 · JSTOR(2009년 12월) (이 템플릿 메시지를 제거하는 방법과 시기 학습)

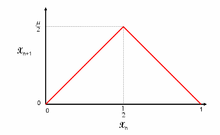
수학에서 매개변수 μ를 가진 텐트 맵은 f에 의해 정의되는 실제값 함수 f이다_μ.

${\displaystyle f_{\mu }=\mu \min\{x,\,1-x\}}$

그_μ 이름은 f의 그래프의 텐트 모양에서 기인한다. 0과 2 내의 파라미터 μ 값의 경우, f는_μ 단위 간격[0, 1]을 자체로 매핑하여, 그에 대한 이산 시간 동적 시스템(동등하게, 재발 관계)을 정의한다. 특히 [0, 1]에서 점 x를₀ 반복하면 시퀀스 ${\displaystyle x_{}}$ n ${\$$n}$ :

${\displaystyle x_{n+1}=f_{\mu }(x_{n})={\begin{cases}\mu x_{n}&\mathrm {for} ~~x_{n}<{\frac {1}{2}}\\\mu (1-x_{n})&\mathrm {for} ~~{\frac {1}{2}}\leq x_{n}\end{cases}}}$

여기서 μ는 양의 실제 상수다. 예를 들어, 파라미터 μ = 2를 선택하면_μ 함수 f의 효과는 장치 간격을 둘로 접은 다음, 결과 간격[0, 1/2]을 연장하여 간격을 다시 얻는 결과로 볼 수 있다[0, 1]. 절차를 반복하면서, 구간의 어떤 지점 x는₀ 위에서 설명한 대로 새로운 후속 위치를 가정하여 [0, 1]에서 시퀀스 x를_n 생성한다.

텐트 맵의 $\mu {\displaystyle }$= ${\displaystyle 2}$ ${\displaystyle \mu =$2$}$케이스는$$ 비트 시프트 맵과 로지스틱 맵의 r = 4 케이스의 비선형 변환이다.

행동

매개변수 μ = 2가 있는 텐트 맵과 매개변수 r = 4가 있는 로지스틱 맵은 위상학적으로 결합되며,^[1] 따라서 두 맵의 행동은 반복하에서도 이와 같은 의미에서 동일하다.

μ의 값에 따라 텐트 맵은 예측 가능한 것에서부터 혼란에 이르는 일련의 역동적인 행동을 보여준다.

• μ가 1보다 작을 경우 x = 0은 x의 모든 초기 값에 대해 시스템의 매력적인 고정점이다. 즉, 시스템은 x의 초기 값에서 x = 0으로 수렴한다.
• μ가 1이면 1/2 이하인 x 값은 모두 시스템의 고정점이다.
• μ가 1보다 크면 시스템에는 0에 1개, μ/(μ + 1)에 2개의 고정점이 있다. 두 고정점 모두 불안정하다. 즉, 어느 고정점이나 가까운 x의 값이 고정점으로부터 멀어지기보다는 고정점으로부터 멀어질 것이다. 예를 들어, μ가 1.5인 경우 x = 0.6(1.5(1 - 0.6) = 0.6)에 고정점이 있지만 x = 0.61에서 시작하면

${\displaystyle 0.61\to 0.585\to 0.56225\to 0.56625\to 0.155625\ldots}$

• μ가 1과 2의 제곱근 사이일 경우 시스템은 μ - μ²/2와 μ/2 사이의 간격을 자신에게 매핑한다. 이 간격의 집합은 지도의 줄리아 집합이다. 즉, 이 지도 아래의 실제 선 중에서 가장 작은 불변 부분집합이다. μ가 2의 제곱근보다 크면 이러한 구간이 병합되며, 줄리아 집합은 μ² - μ/2 ~ μ/2 사이의 전체 구간이다(분리기 도표 참조).
• μ가 1과 2 사이인 경우 [μ - μ²/2, μ/2] 간격은 모든 궤도가 불안정하지만 주기적인 점과 비주기적인 점을 모두 포함하고 있다(즉, 근처 지점이 궤도를 향하지 않고 궤도에서 멀어짐). 길이가 긴 궤도는 μ가 증가하면서 나타난다. 예를 들면 다음과 같다.

${\displaystyle {\frac {\mu}{2}+1}\mu ^{2}}:{\frac {\mu ^{2}+1}}\frac {\mu ^{2}+1}{\mbox{{}}}}이(가) }\mu =1}에 표시됨$

${\displaystyle {\frac {\mu }{\mu ^{3}+1}}\to {\frac {\mu ^{2}}{\mu ^{3}+1}}\to {\frac {\mu ^{3}}{\mu ^{3}+1}}\to {\frac {\mu }{\mu ^{3}+1}}{\mbox{ appears at }}\mu ={\frac {1+{\sqrt {5}}}{2}}}$

${\displaystyle {\frac {\mu }{\mu ^{4}+1}}\to {\frac {\mu ^{2}}{\mu ^{4}+1}}\to {\frac {\mu ^{3}}{\mu ^{4}+1}}\to {\frac {\mu ^{4}}{\mu ^{4}+1}}\to {\frac {\mu }{\mu ^{4}+1}}{\mbox{ appears at }}\mu \approx 1.8393}$

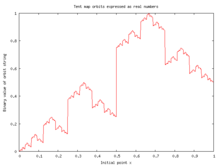
• μ가 2일 경우 시스템은 간격 [0, 1]을 자체로 매핑한다. 비주기적 점뿐만 아니라 이 간격 내에 모든 궤도 길이를 가진 주기적인 점들이 있다. [0, 1]에는 주기적인 지점이 밀집되어 있어 지도는 혼란스러워졌다. 실제로 $x{\displaystyle {}_{}}$ ${\displaystyle {0\mathrm{}}_{}}$ ${\$이(가) 비합리적인 경우에만 역학이 비주기적일 것이다. $이$는 x ${\displaystyle n_{}}$ ${\$이(가) 이진 표기법으로 표현되었을$$ 때 지도가 하는 행동을 주목함으로써 알 수 있다. 2진점을 오른쪽으로 한 자리 이동시킨 다음, 2진점의 왼쪽에 보이는 것이 "원"이면 모든 것을 0으로 바꾸고, 그 반대로 (한정 이진 확장의 경우 최종 비트 "원"을 제외하고) 비합리적인 숫자로부터 시작하여 이 과정은 반복되지 않고 영원히 계속된다. x에 대한 불변 측정치는 단위 간격에 걸친 균일한 밀도다.^[2] 충분히 긴 시퀀스 {${\displaystyle {xn}_{}}$ ${\$에 대한 자기 상관 함수는 0이 아닌 모든 시차에서 자기 상관을 0으로 표시한다.^[3] 따라서 $x{\displaystyle {}_{}}$ ${\displaystyle n_{}}$ ${\$는 자기 상관 함수를 사용하여 백색 노이즈와 구별할 수 없다$$. 유의할 점은 r = 로지스틱 지도의 경우 ${\displaystyle \mathrm{4개}}$와 텐트 지도의 $\mu {\displaystyle }$= 2 ${\displaystyle \mu =2}$케이스는$$ 서로 동형이다. 논리적으로 진화하는 변수를 ${\displaystyle y_{}}$ n ${\$로 나타내며$,$ 동형성은

${\displaystyle x_{n}={\tfrac {2}{\pi }}\sin ^{-1}(y_{n}^{1/2}).}$

• μ가 2보다 크면 지도 줄리아 집합은 연결이 끊기고, 간격 [0, 1] 내에 칸토어 집합으로 분할된다. 줄리아 집합은 여전히 비주기적 및 주기적 지점(궤도 길이에 대한 궤도를 포함)을 무한정 포함하고 있지만, [0, 1] 내의 거의 모든 지점은 결국 무한대로 갈릴 것이다. 표준 칸토어 세트(단위 라인의 하위 세트에서 중간 3분의 1을 연속적으로 삭제함으로써 파악됨)는 μ = 3을 위한 텐트 맵의 줄리아 세트다.

수치 오류

궤도 다이어그램 확대

• 궤도도를 자세히 보면 μ μ 1에 4개의 분리된 영역이 있음을 알 수 있다. 추가 확대를 위해 특정 μ(예: 1.10)에서 2개의 기준선(빨간색)을 팁에서 적절한 x까지 그린다.

• 해당 기준선으로부터 거리를 측정하면 지도 상부와 하부에 더 자세한 정보가 나타난다. (일부 μ에서 분리된 총 8개 지역)

비대칭 텐트 지도

비대칭 텐트 맵은 본질적으로 왜곡되었지만 여전히 조각처럼 선형으로, 텐트 맵의 $\mu {\displaystyle }$= ${\displaystyle 2}$ ${\displaystyle \mu =$2$}$케이스$$ 버전이다. 에 의해 정의된다.

${\displaystyle v_{n+1}={\displaysty}v_{n}/a&\mathrm {for}~v_{n}\in [0,a]\\(1-v_{n}/(1-a)&\matrmatrm {for}~v_{n}\in [a,1]\case}}}}}}}}}}}}}}}}}}}.$

매개 변수에 대해 한 ∈[0,1]{\displaystyle a\in[0,1]}. a=12{\displaystyle a={\tfrac{1}{2}의 텐트 지도의 μ x2{\displaystyle \mu =2}사건은 현재의 경우}}. 일련{vn{\displaystyle v_{n}}}이 같은 자기 상관 function[3] 것으로 데이터에서 first-order autoregres.sive 프로세스 $w{\displaystyle {}_{}}$ ${\displaystyle n_{}}$+ ${\displaystyle 1_{}}$=${\displaystyle }$( ${\displaystyle 2}$ a${\displaystyle }$- ${\displaystyle 1}$) w +${\displaystyle {}_{}{u}_{}}$ n${\displaystyle {}_{}}$+ ${\displaystyle 1_{}}$ w + 1 ${\$$n$+1}:{n$+1$}:{n$+$1}은(는$$) 독립적으로 분포하고 {${\displaystyle u_{}}$ n ${\$n$\}\}\}\}\}\}\}\}\}\}$은(으)은(으)은(으)로 동일하게 분포한다. 따라서 비대칭 텐트 맵의 데이터는 자기 상관 함수를 사용하여 1차 자동 회귀 프로세스에 의해 생성된 데이터와 구별할 수 없다.

참고 항목

• 시프트 스페이스
• 그레이 코드

참조

외부 링크

• ChaosBook.org