
= 4 및 =- 에 대한 가우스 맵의 거미줄 그림
=- 에 대한 가우스 맵의 거미줄 그림 이것은 8 사이클을 보여준다.
이것은 8 사이클을 보여준다. 수학에서 가우스 지도(Gaussian[1] map 또는 마우스 지도라고도 함)는 가우스 함수에 의해 주어지는 실제 간격의 실재에 대한 비선형 반복 지도다.

여기서 α와 β는 실제 매개변수다.
요한 칼 프리드리히 가우스(Johann Carl Friedrich Gauss)의 이름을 딴 이 함수는 로지스틱 지도와 유사한 종 모양의 가우스 함수를 지도화한다.
특성.
매개변수 실공간 {\은(는) 혼란스러울 수 있다 . 지도는 분기도가 마우스를 닮았기 때문에 마우스 지도라고도 불린다(그림 참조).
. 지도는 분기도가 마우스를 닮았기 때문에 마우스 지도라고도 불린다(그림 참조).
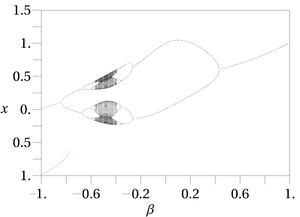 -1 ~ +1 범위에서 = 4 및 = 4 및 을(를) 사용한 가우스 맵의 분기 다이어그램. 이 그래프는 쥐를 닮았다. 을(를) 사용한 가우스 맵의 분기 다이어그램. 이 그래프는 쥐를 닮았다. | 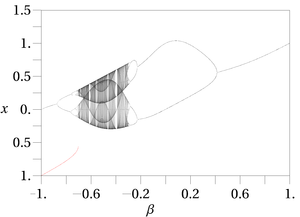 -1 ~ +1 범위에서 = 및 = 및 을(를) 사용한 가우스 맵의 분기 다이어그램. 을(를) 사용한 가우스 맵의 분기 다이어그램. |
참조
- ^ 혼돈과 비선형 역학: Robert C의 과학자와 엔지니어를 위한 소개. 힐본, 2부, 옥스퍼드, 유니브 2004년 뉴욕 언론.
|
|---|
| 개념 | | |
|---|
이론적
나뭇가지 | |
|---|
혼돈
지도(목록) | |
|---|
물리적인
시스템들 | |
|---|
혼돈
이론가들 | |
|---|
관련
기사들 | |
|---|













