로지스틱 지도

로지스틱 지도는 학위 2의 다항식 지도(동등하게, 반복적 관계)로, 매우 단순한 비선형 동적 방정식에서 얼마나 복잡하고 혼란스러운 행동이 발생할 수 있는지를 보여주는 원형적인 예로 자주 인용된다. 이 지도는 생물학자 로버트 메이(Robert May)에 의해 1976년 논문에서 대중화되었는데,^[1] 부분적으로 피에르 프랑수아 베르훌스트가 기록한 로지스틱 방정식과 유사한 이산 시간 인구학적 모델로서도 사용되었다.^[2] 수학적으로, 로지스틱 지도가 작성된다.

${\displaystyle x_{n+1}=rx_{n}\왼쪽(1-x_{n}\오른쪽)$

(1)

여기서 x는_n 0과 1 사이의 숫자로, 최대 가능한 모집단에 대한 기존 모집단의 비율을 나타낸다. 이 비선형 차이 방정식은 두 가지 효과를 포착하기 위한 것이다.

• 인구 규모가 작을 때 인구가 현재 모집단에 비례하여 증가하는 비율의 재생산
• 현재 모집단을 뺀 환경의 이론적 "기준 용량"을 취함으로써 얻어진 가치에 비례하여 성장률이 감소하는 기아(밀도-배출 사망률)

매개변수에 대한 일반적인 관심 값은 간격 [0, 4]에 있는 값들이므로, x는_n [0, 1]에 대한 경계를 유지한다. 로지스틱 맵의 r = 4 케이스는 비트 시프트 맵과 텐트 맵의 μ = 2 케이스의 비선형 변환이다. 만약 r > 4가 음의 모집단 크기로 이어진다면. (이 문제는 또한 혼란스러운 역학을 보여주는 구형 Ricker 모델에서는 나타나지 않는다.) 또한 [-2, 0] 구간에서 r 값을 고려할 수 있으므로, x가_n [-0.5, 1.5]^[3]에 대한 경계를 유지할 수 있다.

지도 특성

r에 의존하는 행동

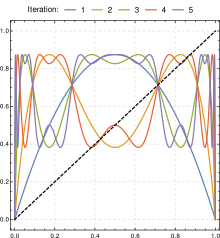
아래 이미지는 2 ~ 4 범위의 파라미터 값에 대해 반복하는 일부 로지스틱 맵의 진폭과 주파수 내용을 보여준다.

매개변수 r을 변경하여 다음과 같은 동작을 관찰한다.

• r이 0과 1 사이에 있으면, 인구는 결국 초기 인구와 무관하게 죽을 것이다.
• 1과 2사이의 r로, 인구는 빠르게 값 .mw-parser-output에 접근할 것이다 .sfrac{white-space:nowrap}.mw-parser-output.sfrac.tion,.mw-parser-output.sfrac .tion{디스플레이:inline-block, vertical-align:-0.5em, font-size:85%;text-align:센터}.mw-parser-output.sfrac .num,.mw-parser-output.sfrac .den{디스플레이:블록, line-height:1em, 마진:0. 0.1em}.mw-parser-output.sfrac .den{border-top:1px 고체}.mw-parser-output .sr-only{국경:0;클립:rect(0,0,0,0), 높이:1px, 마진:-1px, 오버 플로: 숨어 있었다. 패딩:0;위치:절대, 너비:1px}r − 1/r, 초기 인구의 독립.
• r이 2에서 3 사이일 경우, 모집단도 결국 같은 값 r - 1/r에 근접하게 되지만, 우선 그 값에서 얼마간 변동하게 된다. 수렴 속도는 r = 3을 제외하고, 극적으로 느릴 때 선형보다 작다(분리기억기 참조).
• r과 1 + √6 ≈ 3.44949 사이의 경우 모집단은 두 값 사이의 영구적 진동에 근접하게 된다. 이 두 값은 r에 따라 달라지며, $x{\displaystyle {}_{}}$±${\displaystyle {}_{}1\frac{\mathrm{}}{}}$ ${\displaystyle \frac{2}{}}$ ${\displaystyle \frac{r\mathrm{}}{}}$ ${\displaystyle \sqrt{r}}$+ ${\displaystyle 1}$± (${\displaystyle \sqrt{}}$r${\displaystyle \sqrt{}}$- ${\displaystyle \sqrt{3}}$)$$(${\displaystyle \sqrt{\mathrm{r}}}$+ ${\displaystyle \sqrt{1}}$) {\$displaystyle x_${\pm$}={\frac {1}{$1}{$2r}\pm(r+1})\\\sqrt {\$sqrt{($r-3)(r+1)}\rig)}$에 의해^[3] 주어진다$.$
• r이 3.44949와 3.54409(약) 사이일 때 거의 모든 초기 조건에서 모집단은 네 값 사이의 영구 진동으로 접근한다. 후자는 12도 다항식(OEIS에서 순서 A086181)의 루트다.
• r이 3.54409 이상으로 증가함에 따라, 거의 모든 초기 조건에서 모집단은 8개 값, 16개 값, 32개 값 사이의 진동으로 접근할 것이다. 주어진 길이의 진동을 생성하는 매개변수 간격의 길이는 빠르게 감소한다; 두 개의 연속적인 분기 간격의 길이 사이의 비율은 파이겐바움 상수 Δ 4.66920에 근접한다. 이 행동은 시대를 초월한 폭포의 한 예다.
• r ≈ 3.56995 (OEIS의 순서 A098587)에서는 혼란의 시작이며, 주기적인 폭포의 끝에서 혼란의 시작이다. 거의 모든 초기 조건에서 우리는 더 이상 유한한 기간의 진동을 볼 수 없다. 초기 인구의 약간의 차이는 시간이 지남에 따라 극적으로 다른 결과를 낳는데, 이것은 혼돈의 주요 특징이다.
• 3.56995 이상의 r 값은 대부분 무질서한 행동을 보이나, 비차오틱 행동을 보이는 특정한 r 범위가 여전히 존재한다. 이러한 값을 안정의 섬이라고 부르기도 한다. 예를 들어, 1 + 88^[4] (약 3.82843)에서 시작하여 3개의 값 사이에 진동을 보이는 매개변수 r의 범위가 있으며, 6개의 값 중 r 진동 값이 약간 높은 경우 12개 등이 있다.
• 매개변수 r이 약 3.56995에서 약 3.82843까지 변화함에 따라 로지스틱 시퀀스의 혼란스러운 동작의 발달은 때때로 Pofferau-Manneville 시나리오라고 불리며, 주기적(Linar) 위상이 aperiodic 동작의 버스트에 의해 중단되는 것이 특징이다. 그런 시나리오는 반도체 소자에 응용이 있다.^[5] 5개 값 사이에 진동을 생성하는 다른 범위가 있다. 모든 진동 주기는 r의 일부 값에 대해 발생한다. 매개변수 c가 있는 주기적 이중화 창은 하위 범위의 연속으로 구성된 r-값의 범위다. k번째 서브 레인지에는 기간 2c의^k 안정적 사이클(단위 측정의 초기 포인트 세트를 끌어들이는 사이클)이 있는 r의 값이 수록되어 있다. 이 하위 범위의 순서를 조화의 계단식이라고 한다.^[6] 주기 2c의^k* 안정적 주기가 있는 서브 레인지에서는 모든 k < k*에 대해 주기 2c의^k 불안정한 주기가 있다. 하위 범위의 무한 시퀀스 끝에 있는 r 값을 조화의 계단식 누적점이라고 한다. r이 상승함에 따라 c 값이 다른 새로운 창들이 연이어 생겨나고 있다. 첫 번째 창은 c = 1을 위한 것이다. 홀수 c를 포함하는 모든 후속 창은 임의적으로 큰 c로 시작하는 c의 감소 순서에서 발생한다.^[6][7]
• r = 4를 넘어서면, 거의 모든 초기 값은 결국 간격 [0,1]을 남기고 갈라진다.

r의 어떤 값에도 최대 한 번의 안정 사이클이 있다. 안정적 사이클이 존재한다면 거의 모든 포인트를 끌어모으는 등 세계적으로 안정적이다.^{[8]: 13} 일정 기간의 안정적 주기가 있는 r의 일부 값은 다양한 주기의 불안정 주기가 무한히 많다.

오른쪽의 분기 도표는 이것을 요약한다. 수평축은 매개변수 r의 가능한 값을 나타내고, 수직축은 해당 r 값을 가진 로지스틱 방정식의 반복에 의해 거의 모든 초기 조건에서 x 방문 값의 집합을 나타낸다.

분기 도표는 자가비슷한 것으로, 위에서 언급한 값 r ≈ 3.82843을 확대하여 세 개의 팔 중 한 개에 초점을 맞추면, 근처의 상황은 전체 도표의 축소되고 약간 왜곡된 형태로 보인다. 다른 모든 비차오틱 포인트도 마찬가지다. 이것은 혼돈과 프랙탈 사이의 깊고 보편적인 연결의 예다.

r:의 음수 값도 고려할 수 있다.

• r -2와 -1사이의 경우 로지스틱 시퀀스는 또한 혼란스러운 동작을 특징으로 한다.^[3]
• r -1과 1 - √6 사이의 경우, 그리고 1/r과 1-1/r 사이의 x의₀ 경우, 모집단은 3과 1 + √6 사이의 경우와 같이 동일한 공식으로 주어진 두 값 사이의 영구적 진동에 접근한다.^[3]

혼돈과 로지스틱 지도

로지스틱 지도의 상대적인 단순성은 혼돈의 개념에 대한 고려로 널리 사용되는 진입점을 만든다. 혼돈에 대한 대략적인 설명은 혼란스러운 시스템이 초기 조건에 대해 큰 민감도를 보인다는 것이다. 즉, 약 3.57과 4 사이의 r의 대부분의 값에 대한 로지스틱 지도의 속성이다(위에서 언급함).^[1] 초기 조건에 대한 그러한 민감성의 공통적인 원천은 지도가 정의된 공간의 반복적인 접기와 스트레칭을 나타낸다는 것이다. 로지스틱 지도의 경우 이를 설명하는 2차 차이 방정식은 구간(0,1)에 대한 스트레칭 및 접기 연산으로 생각할 수 있다.^[9]

다음 그림은 지도의 일련의 반복에 대한 스트레칭과 접기를 보여준다. 그림 (a) 왼쪽은 로지스틱 지도에서 r = 4에 대한 상태 공간의 2차원 푸앵카레 플롯을 보여주고, 차이 방정식(1)의 2차 곡선을 명확하게 보여준다. 그러나 우리는 지도의 더 깊은 구조를 조사하기 위해 3차원 상태 공간에 같은 순서를 삽입할 수 있다. 그림 (b), 오른쪽은 이것을 보여주며, 특히 그림의 더 가파른 부분에 해당하는_t x의 영역에서 근처의 점들이 어떻게 갈라지기 시작하는지를 보여준다.

이 스트레칭과 폴딩은 단순히 반복수의 순서가 점진적으로 차이 나는 것이 아니라 기하급수적인 차이(Lyapunov의 지수 참조)를 만들어 내는 것으로, 혼란스러운 로지스틱 지도의 복잡성과 예측 불가능성에 의해서도 증명된다. 사실, 이차의 기하급수적인 차이는 혼돈과 예측 불가능성의 연관성을 설명한다. 시스템의 초기 상태로 추정되는 작은 오류는 나중에 진화의 큰 오류에 대응하는 경향이 있다. 따라서, 미래 상태에 대한 예측은 초기 상태에 대한 우리의 지식에서 심지어 아주 작은 오류가 있을 때 점진적으로 더 나빠진다(사실, 기하급수적으로. 이러한 예측 불가능성과 명백한 무작위성의 품질은 로지스틱 지도 방정식을 초기 컴퓨터에서 의사 난수 생성기로 사용하게 했다.^[9]

지도는 실수선의 간격에 국한되므로 치수는 통일보다 작거나 같다. 수치적 추정치는 상관 치수가 0.500±0.005(그래스버거, 1983), 호스도프 치수는 약 0.538(그래스버거 1981), 정보 치수는 약 0.5170976(그래스버거 1983)이다(혼돈의 등). 참고: 상관 치수가 확실히 0.4926과 0.5024 사이임을 알 수 있다.

그러나 혼란스러운 시스템에서 미래 상태의 가능성에 대해 정확하고 정확한 진술을 하는 것은 종종 가능하다. 만일 (대단히 혼란스러운) 역동적인 시스템에 유인이 있다면, 유인의 다양한 지역에서 시스템에 의해 소비되는 시간의 장기적 비율을 주는 확률 측정치가 존재한다. 매개변수 r = 4이고 (0.1)의 초기 상태를 갖는 로지스틱 맵의 경우, 유인기는 구간(0,1)이기도 하며 확률 측정치는 매개변수 a = 0.5, b = 0.5를 갖는 베타 분포에 해당한다. 구체적으로는 불변적인 대책은 다음과 같다.^[10]

${\displaystyle {\frac {1}{\pi {\sqrt {x(1-x)}}}}$

예측 불가능한 것은 무작위가 아니지만, 어떤 상황에서는 그렇게 보인다. 따라서, 그리고 다행히도, 우리가 로지스틱 지도(또는 다른 어떤 혼란스러운 시스템)의 초기 상태에 대해 거의 알지 못한다 하더라도, 우리는 여전히 임의로 먼 미래까지 국가의 분포에 대해 뭐라고 말할 수 있으며, 이 지식을 이용하여 시스템의 상태에 근거한 결정을 알릴 수 있다.

지도에 대한 특별한 경우

0 ≤ r ≤ 1일 때 상한

재발 관계에 대한 정확한 해결책은 적은 수의 사례에서만 구할 수 있지만, 로지스틱 지도의 폐쇄형 상한이 0 ≤ r ≤ 1일 때 알려져 있다.^[11] 이 정권에서 상한이 포착해야 하는 로지스틱 지도의 행동에는 두 가지 측면이 있는데, 상수 r과 함께 점증하지 않는 기하학적 붕괴와 재발 관계에서 (1 - x_n) 용어에 의해 구동되는 x가₀ 1에 가까울 때의 빠른 초기 붕괴가 그것이다. 다음 바운드는 이러한 두 가지 효과를 모두 포착한다.

${\displaystyle \forall n\in \{0,1,\ldots \}\\datable\in[0,1]\r\in[0,1]\n}\frac{x_{0}}{r^{-n}+x_{0}n}n}}.}$

r = 4일 때 솔루션

r = 4의 특수한 경우는 r = 2의 경우와 마찬가지로 사실 정확하게 해결할 수 있지만,^[12] 일반적인 경우는 통계적으로만 예측할 수 있다.^[13] r = 4일 ^[12][14]때 해결책은

${\displaystyle x_{n}=\sin ^{2}\왼쪽(2^{n}\theta \pi \right),}$

여기서 초기 조건 매개변수 θ은 다음에 의해 주어진다.

${\displaystyle \theta ={\tfrac {1}{\pi }\sin ^{-1}\왼쪽 ^\sqrt {x_{0}}\오른쪽).}$

합리적인 θ의 경우, 한정된 반복 횟수가 지나면 주기적인 순서에 따라_n x 맵이 생성된다. 그러나 거의 모든 θ은 비이성적이며, 비이성 θ에게 x는_n 절대 반복되지 않는다 – 그것은 비주기적인 것이다. 이 솔루션 방정식은 스트레칭과 폴딩이라는 혼돈의 두 가지 주요 특징을 명확하게 보여준다: 인자 2는ⁿ 스트레칭의 지수 성장을 보여주며, 이는 초기 조건에 민감하게 의존하게 되는 반면, 제곱 사인 함수는 [0,1] 범위 내에서 X 접혀_n 있는 상태를 유지된다.

r = 4의 경우 삼각함수 대신 복잡한 숫자에 대한 등가 솔루션은^[15]

${\displaystyle x_{n}={\frac {-\fract ^{2^{n}-\properties ^{-2^{n}}}{4}}}}$

여기서 α는 복합수 중 하나이다.

${\displaystyle \pm =1-2x_{0}\pm {\sqrt}\\좌측(1-2x_{0}\우측)^{2}-1}}$

1과 같은 계수로 삼각법 용액의 제곱 사인 함수가 방문한 점 집합의 축소나 확장으로 이어지지 않는 것처럼, 후자의 용액에서 이 효과는 α의 단위 계수에 의해 달성된다.

대조적으로 r = 2일 때의 해법은^[15]

${\displaystyle x_{n}={\tfrac {1}{1}:{2}}-{1}{1}{1}:{2}}\좌측(1-2x_{0}\우측)^{2^{n}}}}$

x₀ ∈ [0,1)의 경우. (1 - 2x₀) ∈ (-1,1) x의₀ 값이 불안정한 고정점 0이 아닌 경우에는 (1 - 2x₀)²ⁿ가 0으로 가고 n이 무한대로 가므로 x는_n 안정된 고정점 1/2로 간다.

r = 4일 때 임의 길이의 사이클 찾기

r = 4의 경우, 거의 모든 초기 조건에서 반복 시퀀스는 혼란스럽다. 그럼에도 불구하고 사이클로 이어지는 초기 조건의 무한정 수가 존재하며, 실제로 모든 정수 k > 0에 길이 k의 사이클이 존재한다. 우리는 로지스틱 지도와 dynadic 변환(비트 시프트 맵이라고도 함)의 관계를 이용하여 어떤 길이의 사이클을 찾을 수 있다. x가 로지스틱 맵 x_{n + 1} = 4x_n(1 - x_n)를 따르고 y가 dynadic 변환을 따르는 경우

${\displaystyle y_{n+1}={\case}2y_{n}&#0\leq y_{n}<{\tfrac {1}{1}{2}}\\2y_{n}-1&{\tfrac {1}{1}{1}{1}:{n},\case}}}}}}}}}}}$

그러면 그 둘은 동족상동증에 의해 연관되어 있다.

${\displaystyle x_{n}=\sin ^{2}\왼쪽(2\pi y_{n}\오른쪽).}$

이음변형 변환을 비트-시프트 맵이라고도 하는 이유는 y를 이진 표기법으로 표기할 때 맵이 2진점을 오른쪽으로 한 자리 이동(그리고 2진점 왼쪽에 있는 비트가 "1"이 되면 이 "1"이 "0"으로 변경됨)하기 때문이다. 예를 들어, 길이 3의 주기는 반복이 이진 확장에 3비트 반복 시퀀스가 있는 경우(또한 1비트 반복 시퀀스가 아님): 001, 010, 100, 110, 101 또는 011. 001001001번 반복... 지도는 010010010... 100100100... 그리고 다시 원래의 001001001...; 이것은 비트 시프트 맵의 3주기 입니다. 그리고 나머지 3개의 바이너리 확장 반복 시퀀스는 3주기 110110... → 101101101... → 011011011... → 110110110.... 이러한 3주기 중 어느 하나를 분수 형태로 변환할 수 있다. 예를 들어, 처음 주어진 3주기에는 1/7 → 2/7 → 4/7 → 1/7로 쓸 수 있다. $비트{\displaystyle }$ 시프트 맵에서 r${\displaystyle }$= ${\displaystyle 4}$ ${\displaystyle r=4}$ 로지스틱$$ 맵으로의 위 번역을 사용하면 해당 로지스틱 사이클 0.611260467... → 0.950484434... → 0.188255099... → 0.611260467.... 유사한 방법으로 다른 비트 시프트 3 사이클을 해당 로지스틱 사이클로 변환할 수 있다. 마찬가지로 길이 k의 사이클은 비트-시프트 맵에서 찾아 해당 로지스틱 사이클로 변환할 수 있다.

그러나 [0,1)의 거의 모든 숫자가 비합리적이기 때문에 비트 시프트 맵의 거의 모든 초기 조건은 혼돈의 비주기성으로 이어진다. 이것은 로지스틱 r = 4 지도가 거의 모든 초기 조건에서 혼란스럽다는 것을 알 수 있는 한 가지 방법이다.

r = 4(μ = 2)를 갖는 로지스틱 지도에 대한 (최소) 길이 k = 1, 2, 3, 3의 사이클 수는 알려진 정수 순서(OEIS에서 순서 A001037)이다. 2, 1, 2, 9, 18, 30, 56, 99, 186, 335, 630, 1161.... 이는 r = 4가 있는 로지스틱 지도에는 2개의 고정점, 1개의 길이 2, 2개의 사이클의 길이 3 등이 있음을 말해준다. 이 순서는 prime k: 2 simple 2^{k − 1} - 1/k에 대해 특히 간단한 형태를 취한다. 예를 들어: 2 ⋅ 2^{13 − 1} - 1/13 = 630은 길이 13의 주기 수입니다. 이 로지스틱 지도의 경우는 거의 모든 초기 조건에 대해 혼란스럽기 때문에, 이러한 유한 길이 주기는 모두 불안정하다.

관련개념

1-D 지도 파이겐바움 보편성

파라볼릭 맥시마와 페이겐바움 상수 $\Delta {\displaystyle }$= ${\displaystyle 4.669201}$이 있는 1차원 맵의 보편성${\displaystyle \mathrm{...}}$$\displaystyle \cHB =4.669201...$$}$,${\displaystyle \alpha =\mathrm{2.502907...}}$$\displaystyle \cHB =2.502907...$}}은(는$)$ 이산 레이저 역학을 위한 완구 모델로 제안된 지도에서 잘 나타난다$$^[16][17]. x$$→ ${\displaystyle G}$ ${\displaystyle x}$( ${\displaystyle 1}$- ${\displaystyle \tanh }$h (${\displaystyle x}$ ) $displaystyle x\rightarrow Gx(1-$$\$$tanh(x$$)}$는 $전기장{\displaystyle }$ 진폭을 나타내며$$, $G{\displaystyle }$ ${\displaystystyle G}$은^[18] 분리 파라미터로 레이저 게인 것이다$.$

$[{\displaystyle 0}$,$$${\displaystyle \mathrm{\infty }}$ ){\$displaystyle$ [0$$$,\infit$에서 G {\$displaystyle$$G}$의 점진적인 증가는 로지스틱 지도와 질적으로 동일한 분기 도표를 사용하여 일반 도표에서 혼돈 도표로 역학을 변화시킨다$$.

참고 항목

• 로지스틱 함수, 로지스틱 맵의 연속 상대방식의 솔루션: 로지스틱 미분 방정식.
• Lyapunov 안정성# 이산 시간 시스템을 위한 정의
• 맬서스 성장 모델
• 복잡한 이차적 매핑의 주기적 지점, 그 중 로지스틱 지도가 실제 선에 국한된 특수한 경우
• 로지스틱 지도의 역 문제를 나타내는 방사형 기준 함수 네트워크.
• 슈뢰더 방정식
• 뻣뻣한 방정식

메모들

참조

• Grassberger, P.; Procaccia, I. (1983). "Measuring the strangeness of strange attractors". Physica D. 9 (1–2): 189–208. Bibcode:1983PhyD....9..189G. doi:10.1016/0167-2789(83)90298-1.
• Grassberger, P. (1981). "On the Hausdorff dimension of fractal attractors". Journal of Statistical Physics. 26 (1): 173–179. Bibcode:1981JSP....26..173G. doi:10.1007/BF01106792. S2CID 119833080.
• Sprott, Julien Clinton (2003). Chaos and Time-Series Analysis. Oxford University Press. ISBN 978-0-19-850840-3.
• Strogatz, Steven (2000). Nonlinear Dynamics and Chaos. Perseus Publishing. ISBN 978-0-7382-0453-6.
• Tufillaro, Nicholas; Abbott, Tyler; Reilly, Jeremiah (1992). An Experimental Approach to Nonlinear Dynamics and Chaos. Addison-Wesley New York. ISBN 978-0-201-55441-0.

외부 링크

위키북스에는 프랙탈/아이티페더레이션_of_real_number/r_iterations#Logistic_map이라는 주제로 책이 수록되어 있다.

• 혼돈 하이퍼텍스트 책이요 혼돈과 프랙탈에 대한 입문서.
• 로지스틱 지도를 주피터 노트북으로 대화형 시각화
• 엘머 G의 로지스틱 지도와 혼돈 와이엔스
• 로저 화이트의 복잡성 & 혼돈 (audiobook) 5장은 로지스틱 방정식을 다룬다.
• Stephen Wolfram이 쓴 새로운 종류의 과학에서 "반복된 지도들의 역사". 샴페인, 일리노이주: 울프램 미디어, 2002 페이지 918.
• P의 「기간 중의 보편성의 아주 짧은 역사」. 시비타노비치
• P의 「유니버설 함수의 짧은 역사」. 시비타노비치
• 필 람스든의 작업 후 마렉 보드나르의 이산 로지스틱 방정식, 울프램 시연 프로젝트
• C에 의한 2개의 로지스틱 맵의 곱하기 커플링. 펠리커-로스타오와 R. 로페즈-루이즈가 에드 페그 주니어의 작업 후 울프램 시연 프로젝트.
• SAGE를 사용하여 이산 로지스틱 방정식 조사