반복 함수

수학에서 반복되는 함수는 다른 함수를 자기 자신과 일정한 횟수만큼 구성하여 얻는 함수입니다. 같은 기능을 반복적으로 적용하는 과정을 반복이라고 합니다. 이 과정에서 어떤 초기 객체에서 시작하여 주어진 함수를 적용한 결과를 다시 입력으로 함수에 투입하고 이 과정을 반복합니다.

예를 들어 오른쪽 이미지에서:

${\displaystyle L=F(K),\M=F\circ F(K)=F^{2}(K)}$

반복 함수는 컴퓨터 과학, 프랙탈, 동적 시스템, 수학 및 재규격화 그룹 물리학에서 연구됩니다.

정의.

집합 X에 대한 반복 함수의 공식적인 정의는 다음과 같습니다.

X를 집합이라 하고 f를 X → X를 함수라 합니다.

f를 n번째 f의 비율(한스 하인리히 뷔르만과^{[citation needed]} 존 프레드릭 윌리엄 허셜이^[1][2][3][4] 도입한 표기법)로 정의하면, n은 음이 아닌 정수입니다.

그리고.

여기서 id는 X의 ID 함수이고 ($f$∘ {\$displaystyle \$circ } g)(x) = f(g(x))는 함수 구성을 나타냅니다.

표기법 f는 함수 f의 지수화를 위한 함수의 반복(구성)을 모두 참조할 수 있기 때문에( 후자는 삼각법에서 일반적으로 사용됨), 일부 수학자는 구성적 의미를 표시하기 위해 ∘를 사용하기로 선택하며, 예를 들어 f(f(f(f(x))를 의미하는 f(x)와 같이 함수 f(x)의 n번째 반복에 대해 f(x)를 씁니다. Benjamin Peirce는^{[5][4][nb 1]} 같은 목적으로 f(x)를 사용했지만 Alfred Pringsheim과 Jules Molk는 대신 f(x)를 제안했습니다.^{[6][4][nb 2]}

아벨 성질 및 반복 시퀀스

일반적으로 음이 아닌 모든 정수 m과 n에 대하여 다음 항등식이 성립합니다.

${\displaystyle f^{m}\circ f^{n}=f^{n}\circ f^{m}=f^{m+n}~.}$

이것은 aa = a인 지수의 성질과 구조적으로 같습니다.

일반적으로 임의의 일반(음, 비-정수 등) 지수 m과 n에 대하여 이 관계를 번역 함수식, cf라고 합니다. 슈뢰더 방정식과 아벨 방정식. 로그 척도에서 이는 T(x) = cos(narccos(x))이기 때문에 체비셰프 다항식의 둥지 속성인 T(T(x)) = T(x)로 감소합니다.

(f)(x) = (f)(x) = f(x) 관계는 (a) = (a) = a인 지수의 성질과 유사합니다.

함수 f의 수열은 샤를 에밀 피카르의 이름을 ^[7][8]따서 피카르 수열이라고 불립니다.

X의 주어진 x에 대하여, 값 fⁿ(x)의 순서를 x의 궤도라고 합니다.

어떤 정수 m > 0에 대해 f (x) = f (x)이면, 그 궤도를 주기 궤도라고 부릅니다. 주어진 x에 대한 m의 가장 작은 값을 궤도의 주기라고 합니다. 점 x 자체를 주기점이라고 합니다. 컴퓨터 과학에서 주기 검출 문제는 궤도에서 첫 번째 주기점을 찾는 알고리즘 문제, 그리고 궤도의 주기입니다.

고정점

X의 어떤 x에 대하여 x = f(x)이면(즉, x의 궤도 주기는 1), x를 반복되는 수열의 고정점이라고 합니다. 고정된 점들의 집합은 흔히 Fix(f)로 표시됩니다. 바나흐 고정점 정리, 브루어 고정점 정리 등 다양한 상황에서 고정점의 존재를 보장하는 다수의 고정점 정리가 존재합니다.

고정점 반복에 의해 생성된 시퀀스의 수렴 가속에 대한 몇 가지 기술이 있습니다.^[9] 예를 들어, 반복되는 고정점에 적용되는 Aitken 방법은 Steffensen의 방법으로 알려져 있으며, 2차 수렴을 생성합니다.

한계행동

반복해 보면, 한 점을 향해 수축하고 수렴하는 집합들이 있다는 것을 발견할 수 있습니다. 그런 경우 수렴되는 점을 매력적인 고정점이라고 합니다. 반대로, 반복은 점들이 한 점에서 멀어지는 것처럼 보일 수 있습니다. 이는 불안정한 고정점의 경우에 해당됩니다.^[10]

궤도의 점들이 하나 이상의 한계들로 수렴할 때, 궤도의 축적 점들의 집합은 한계 세트 또는 ω-한계 세트로 알려져 있습니다.

인력과 척력의 개념은 유사하게 일반화됩니다. 반복되는 작은 이웃의 행동에 따라 안정 집합과 불안정 집합으로 반복을 분류할 수 있습니다. 분석 함수의 무한한 구성도 확인할 수 있습니다.

다른 제한적인 동작도 가능합니다. 예를 들어, 방황하는 지점은 멀리 떨어져 있고, 시작한 지점 근처에도 다시 돌아오지 않는 지점입니다.

불변측량

개별 점 동역학이 아닌 밀도 분포의 진화를 고려할 경우, 한계 행동은 불변 측도에 의해 주어집니다. 반복적인 반복 하에서 포인트 클라우드 또는 먼지 클라우드의 동작으로 시각화할 수 있습니다. 불변 측도는 고유값 1에 해당하는 루엘-프로베니우스-페론 연산자 또는 전달 연산자의 고유 상태입니다. 더 작은 고유값은 불안정하고 붕괴하는 상태에 해당합니다.

일반적으로 반복적인 반복은 시프트, 전송 연산자 및 그 인접에 해당하므로, 쿠프만 연산자는 시프트 공간에 대한 시프트 연산자 동작으로 해석될 수 있습니다. 유한한 유형의 하위 이동 이론은 많은 반복되는 기능, 특히 혼돈으로 이어지는 기능에 대한 일반적인 통찰력을 제공합니다.

분수 반복 및 흐름, 음의 반복

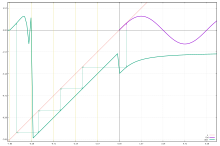
항등식의 함수근에 대한 배비지 방정식처럼 g(x) = f(x) 방정식이 여러 해를 가질 때 f 개념을 주의해서 사용해야 합니다. 예를 들어, n = 2이고 f(x) = 4x - 6인 경우, g(x) = 6 - 2x 및 g(x) = 2x - 2는 모두 해이므로, 수가 여러 대수적 근을 가지는 것처럼 f(x)라는 표현은 고유 함수를 의미하지 않습니다. 이 문제는 산술의 "0/0"이라는 표현과 상당히 유사합니다. f 의 도메인을 충분히 확장할 수 있다면 항상 사소한 루트 off를 얻을 수 있습니다. cf. picture. 선택한 뿌리는 일반적으로 연구 중인 궤도에 속하는 뿌리입니다.

함수의 부분 반복은 다음과 같이 정의할 수 있습니다: 예를 들어, 함수 f의 반 반복은 g(g(x)) = f(x)와 같은 함수 g입니다. 이 함수 g(x)는 f(x)와 같이 인덱스 표기법을 사용하여 쓸 수 있습니다. 마찬가지로 f(x)는 f(f(f(x)) = f(x)가 되도록 정의된 함수이며, f(x)는 f(f(x))와 같게 정의될 수 있으며, 이는 모두 앞에서 언급한 f ○ f = f 의 원리에 기초합니다. 이 아이디어는 반복 횟수 n이 연속 궤도의 일종의 연속 "시간"인 연속 파라미터가 되도록 일반화할 수 있습니다.^[12][13]

이러한 경우 시스템을 흐름(아래의 접합에 대한 cf. 섹션)이라고 합니다.

함수가 쌍방향인 경우(따라서 역함수를 소유함) 음의 반복률은 함수의 역수와 그 구성에 해당합니다. 예를 들어, f(x)는 f의 정규 역수이고, f(x)는 자신과 합성된 역수, 즉 f(x) = f(x)입니다. 분수 음의 반복률은 분수 양의 반복률과 유사하게 정의됩니다. 예를 들어, f(x)는 f(f(x) = f(x) 또는 동등하게 f(f(x) = x)와 같이 정의됩니다.

분수 반복에 대한 몇 가지 공식

고정점을 이용하여 분수 반복에 대한 급수 공식을 구하는 여러 방법 중 하나는 다음과 같습니다.^[14]

1. 먼저 f(a) = a와 같은 함수의 고정점을 정합니다.
2. 실수에 속하는 모든 n에 대하여 f (a) = a를 정의합니다. 이것은 어떤 면에서는 분수 반복에 적용하기에 가장 자연스러운 추가 조건입니다.
3. 고정점 a를 중심으로 fⁿ(x)를 테일러 급수로 전개하면,
   $${\displaystyle f^{n}(x)=f^{n}(a)+(x-a)\left.{\frac {d}{dx}}f^{n}(x)\right _{x=a}+{\frac {(x-a)^{2}}{2}}\left.{\frac {d^{2}}{dx^{2}}}f^{n}(x)\right _{x=a}+\cdots }$$

   
4. 펼침
   $${\displaystyle f^{n}(x)=f^{n}(a)+(x-a)f'(a)f'(f(a))f'(f^{2}(a))\cdots f'(f^{n-1}(a))+\cdots }$$

   
5. 임의의 k에 대하여 f(a) = a를 대입하면,
   $${\displaystyle f^{n}(x)=a+(x-a)f'(a)^{n}+{\frac {(x-a)^{2}}{2}}(f''(a)f'(a)^{n-1})\left(1+f'(a)+\cdots +f'(a)^{n-1}\right)+\cdots }$$

   
6. 기하학적 진행을 이용하여 용어를 단순화합니다.
   $${\displaystyle f^{n}(x)=a+(x-a)f'(a)^{n}+{\frac {(x-a)^{2}}{2}}(f''(a)f'(a)^{n-1}){\frac {f'(a)^{n}-1}{f'(a)-1}}+\cdots }$$

   
   f'(a) = 1일 때 특별한 경우가 있습니다.
   $${\displaystyle f^{n}(x)=x+{\frac {(x-a)^{2}}{2}}(nf''(a))+{\frac {(x-a)^{3}}{6}}\left({\frac {3}{2}}n(n-1)f''(a)^{2}+nf'''(a)\right)+\cdots }$$

   

이것은 비효율적이지만 후자의 용어가 점점 더 복잡해짐에 따라 무한정 계속될 수 있습니다. 좀 더 체계적인 절차는 Conjugacy에 대한 다음 섹션에서 설명합니다.

예1

예를 들어 f(x) = Cx + D를 설정하면 고정점 a = D/(1 - C)가 되므로 위 공식은 다음과 같이 종료됩니다.

확인하기에 사소한 것들입니다.

예2

22 ⋯ {\$displaystyle {\$sqrt {$2}}^{\sqrt {2}}^{\sqrt$ {$2}}^{\$cdots}}}의 값을 구합니다. 이 값은 n번 수행됩니다(아마도 n이 정수가 아닐 때 보간된 값일 것입니다). We have f(x) = √2^x. 고정점은 a = f(2) = 2 입니다.

따라서 고정점 값 2를 중심으로 확장된 집합 x = 1과 f (1)은 무한급수입니다.

n이 양수일 때 앞의 세 항만 취하면 소수점 첫째 자리까지 정확합니다. 테트레이션: f (1) = √2도 참조하십시오. 다른 고정점 a = f(4) = 4를 사용하면 급수가 발산됩니다.

n = -1인 경우, 급수는 역함수를 계산합니다. 2+ln x/ln 2.

예3

함수 f(x) = x를 사용하여 고정점 1을 중심으로 전개하여 급수를 구합니다.

그것은^{(bn )} 단순히 x의 테일러 급수가 약 1로 확장된 것입니다.

공액

만약 f와 g가 두 개의 반복되는 함수이고, g = h ○ f ○ h와 같은 동형 h가 존재한다면, f와 g는 위상적으로 켤레라고 합니다.

분명히 위상 접합은 g = h ○ f ○ h와 같이 반복 하에서 보존됩니다. 따라서, 하나의 반복되는 함수 체계에 대해 풀 수 있다면, 모든 위상 공액 체계에 대한 해도 있습니다. 예를 들어, 텐트 맵은 로지스틱 맵과 위상적으로 결합됩니다. 특별한 경우로, f(x) = x + 1을 취하면 다음과 같이 g(x) = h(h(x)) + 1의 반복을 갖습니다.

g(x) = h(h(x) + n), 임의의 함수 h에 대하여.

치환 x = h(y) = ϕ(y) 수율

g(ϕ(y)) = ϕ(y+1), 아벨 방정식으로 알려진 형태.

고정점 근처에서 x = 0, f(0) = 0이 되는 엄격한 동형이 없는 경우에도 종종 함수 ψ에 대한 슈뢰더의 방정식을 풀 수 있습니다. 이 방정식은 f(x)를 단순한 확장, g(x) = f '(0) x, 즉

f(x) = Ψ⁻¹(f '(0) Ψ(x)).

따라서, 그 반복 궤도 또는 흐름은 적절한 규정(예: f'(0) ≠ 1) 하에서, 단항의 궤도의 공액에 달합니다.

ψ(f'(0) ψ(x)),

이 식에서 n은 단순 지수의 역할을 합니다. 함수 반복이 곱셈으로 감소되었습니다! 그러나 여기서 지수 n은 더 이상 정수나 양일 필요가 없으며 전체 궤도에 대한 연속적인 "시간"입니다.^[16] 피카르 수열(cf. 변환 반군)의 모노이드는 전체 연속 그룹으로 일반화되었습니다.^[17]

이 방법(주 고유함수 ψ의 섭동 측정, cf. Carleman matrix)는 앞 절의 알고리즘과 동일하지만 실제로는 더 강력하고 체계적입니다.

마르코프 체인

함수가 선형이고 확률적 행렬, 즉 행 또는 열이 1로 합되는 행렬로 설명될 수 있는 경우 반복되는 시스템을 마르코프 체인이라고 합니다.

예

혼란스러운 지도들이 많이 있습니다. 잘 알려진 반복 함수로는 만델브로 집합과 반복 함수 시스템이 있습니다.

에른스트 슈뢰더는 1870년에 혼란스러운 경우 f(x) = 4x(1 - x)와 같은 로지스틱 맵의 특수한 경우를 계산하여 ψ √(x) = √x, 따라서 f(x) = sin(2 √x)를 계산했습니다.

또한 Schröder는 자신의 방법인 f(x) = 2x(1 - x)를 사용하여 설명했으며 ψ ψ(x) = -1/2 ln(1 - 2x)을 산출했으며 따라서 f(x) = -1/2((1 - 2x))를 산출했습니다.

f가 집합에 대한 그룹 요소의 작용이면 반복되는 함수는 자유 그룹에 해당합니다.

대부분의 함수에는 n번째 반복에 대한 명시적인 일반 폐쇄형 표현식이 없습니다. 아래 표는 몇 가지를^[19] 나열합니다. 이러한 모든 표현은 비-정수 n과 음의 정수 n뿐만 아니라 비-정수 n에도 유효합니다.

${\displaystyle f(x)}$	${\displaystyle f^{n}(x)}$
${\displaystyle x+b}$	${\displaystyle x+nb}$
${\displaystyle ax+b\ (a\n)eq 1)}$	${\displaystyle a^{n}x+{\frac {a^{n}-1}{a-1}}b}$
${\displaystyle ax^{b}\ (b\n)eq 1)}$	${\displaystyle a^{\frac {b^{n}-1}{b-1}}x^{b^{n}}}$
${\displaystyle {}^{}}$ ${\displaystyle {x\mathrm{}}^{}}$ 2${\displaystyle {}^{}}$+ ${\displaystyle b}$ ${\displaystyle x}$+ ${\displaystyle \frac{{b\mathrm{}}^{}}{}}$ ${\displaystyle 2\frac{{}^{}}{}}$- 2 ${\displaystyle \frac{b}{}}$ ${\displaystyle \frac{\mathrm{}}{}}$ a ${\$ $$(참고 참조)	${\displaystyle {\frac {2\alpha ^{2^{n}}-b}{2a}}$ 위치: ${\displaystyle \alpha = {\frac {2ax+b}{2}}}$
${\displaystyle {}^{}}$ x ${\displaystyle {2\mathrm{}}^{}}$+ b ${\displaystyle x}$+ ${\displaystyle \frac{{b\mathrm{}}^{}}{}}$ ${\displaystyle 2\frac{{}^{}}{}}$- 2 ${\displaystyle \frac{b}{}}$- ${\displaystyle \frac{\mathrm{}}{}}$ ${\displaystyle \frac{a}{}}$ ${\$ $$(참고 참조)	${\displaystyle {\frac {2\alpha ^{2^{n}}+2\alpha ^{-2^{n}}-b}{2a}}}$ 위치: ${\displaystyle \alpha ={\frac {2ax+b\pm {\sqrt {(2ax+b)^{2}-16}}}{4}}}$
${\displaystyle \frac{}{a}}$ ${\displaystyle \frac{x}{}}$+ b ${\displaystyle \frac{c}{}}$ x${\displaystyle \frac{}{}}$+ d ${\displaystyle {\frac {ax+b}{c$ (fract 선형 변환)	${\displaystyle {\frac {a}{c}}+{\frac {bc-ad}{c}}\left[{\frac {(cx-a+\alpha)\alpha ^{n-1}-(cx-a+\alpha)\beta ^{n-1}-{(cx-a+\beta)\alpha ^{n}-(cx-a+\beta )\beta^{n}\right]}$ 위치: ${\displaystyle \alpha ={\frac {a+d+{\sqrt {(a-d)^{2}+4bc}}}{2}}}$ ${\displaystyle \beta ={\frac {a+d-{\sqrt {(a-d)^{2}+4bc}}}{2}}$
${\displaystyle g^{-1}{\big(}h{\bigl(}g(x)){\bigr )}{\big( )}}$	${\displaystyle g^{-1}{\Bigl (}h^{n}{\bigl (}g(x){\bigr )}{\Bigr )}}$
${\displaystyle {\mathrm{g}}^{}}$- 1${\displaystyle {}^{}}$(${\displaystyle g}$(${\displaystyle x}$)${\displaystyle }$+ b${\displaystyle }$) ${\$ + $b{\bigr )}}$ $$(일반 아벨 방정식)	${\displaystyle g^{-1}{\bigl(}g(x))+nb{\bigr )}}$
${\displaystyle {\sqrt {x^{2}+b}}}$	${\displaystyle {\sqrt {x^{2}+bn}}}$
${\displaystyle g^{-1}{\Bigl(}a\g(x)+b{\Bigr )}\ (a\neq 1\vee b=0)}$	${\displaystyle g^{-1}{\Bigl (}a^{n}g(x)+{\frac {a^{n}-1}{a-1}}b{\Bigr )}}$
${\displaystyle {\sqrt {ax^{2}+b}}}$	${\displaystyle {\sqrt {a^{n}x^{2}+{\frac {a^{n}-1}{a-1}}b}}}$
${\displaystyle T_{m}x)}$ =${\displaystyle {}_{}\cos }$ $⁡$ ($르코스$ ⁡ x) {\displaystyle T_{m${\displaystyle {\}}_{}}$(x) =\cos(m\arcos x)} (정수 m에 대한 체비셰프 다항식)	${\displaystyle T_{mn}=\cos(m^{n}\arccos x)}$

참고: ax² + bx + c의 이 두 가지 특수한 경우는 닫힌 형태의 해를 갖는 유일한 경우입니다. b = 2 = –a 및 b = 4 = –a를 각각 선택하면 표 이전에 논의된 비혼란 및 혼돈 로지스틱 사례로 더 줄어듭니다.

이러한 예들 중 일부는 단순한 결합에 의해 서로 연관되어 있습니다.

학습수단

반복 함수는 Artin-Mazurzeta 함수와 전송 연산자를 사용하여 연구할 수 있습니다.

컴퓨터 과학에서

컴퓨터 과학에서 반복 함수는 재귀 함수의 특별한 경우로 발생하며, 이는 다시 람다 미적분학과 같은 광범위한 주제 또는 컴퓨터 프로그램의 지시 의미론과 같은 더 좁은 주제에 대한 연구를 고정시킵니다.

반복되는 함수에 대한 정의

반복되는 함수의 관점에서 두 가지 중요한 함수를 정의할 수 있습니다. 요약은 다음과 같습니다.

${\displaystyle \left\{b+1,\sum _{i=a}^{b}g(i)\right\}\equiv \left(\{i,x\}\rightarrow \{i+1,x+g(i)\}\right)^{b-a+1}\{a,0\}}$

그에 상응하는 제품:

${\displaystyle \left\{b+1,\prod _{i=a}^{b}g(i)\right\}\equiv \left(\{i,x\}\rightarrow \{i+1,xg(i)\}\right)^{b-a+1}\{a,1\}}$

함수 도함수

반복되는 함수의 함수 도함수는 다음과 같은 재귀적 공식으로 주어집니다.

${\displaystyle {\frac {\delta f^{N}(x)}{\delta f(y)}}=f'(f^{N-1}(x)){\frac {\delta f^{N-1}(x)}{\delta f(y)}}+\delta (f^{N-1}(x)-y)}$

Lie의 데이터 전송 방정식

g(f(x))와 같은 결합 함수의 직렬 확장에서 반복 함수가 생성됩니다.

반복 속도 또는 베타 함수(물리학)가 주어지면,

${\displaystyle v(x)=\left.{\frac {\partial f^{n}(x)}{\partial n}}\right _{n=0}}$

함수 f의 비율에^th 대해, 우리는^[21]

${\displaystyle g(f(x))=\exp \left[v(x){\frac {\partial }{\partial x}}\right]g(x)}$

예를 들어, 강직한 이류의 경우 f(x) = x + t이면 v(x) = t입니다. 결과적으로 g(x + t) = exp(t ∂/ ∂x) g(x)는 평시프트 연산자에 의한 작용입니다.

반대로 위에서 논의한 일반 아벨 방정식을 통해 임의의 v(x)가 주어지면 f(x)를 지정할 수 있습니다.

${\displaystyle f(x)=h^{-1}(h(x)+1),}$

어디에

${\displaystyle h(x)=\int {\frac {1}{v(x)}}\, dx.}$

이것은 다음과 같이 언급함으로써 명백합니다.

${\displaystyle f^{n}(x)=h^{-1}(h(x)+n)~.}$

연속 반복 지수 t의 경우, 이제 첨자로 쓰이게 되는데, 이것은 연속군에 대한 Lie의 유명한 지수적 실현에 해당합니다.

${\displaystyle e^{t~{\frac {\partial ~~}{\partial h(x)}}}g(x)=g(h^{-1}(h(x)+t))=g(f_{t}(x)).}$

초기 유속 v는 전체 흐름을 결정하기에 충분합니다. 이 지수적인 실현이 자동적으로 번역 함수식에 대한 일반적인 해를 제공한다면,^[22]

${\displaystyle f_{t}(f_{\tau }(x)=f_{t+\tau }(x)~.}$

참고 항목

메모들

참고문헌

외부 링크

• Gill, John (January 2017). "A Primer on the Elementary Theory of Infinite Compositions of Complex Functions". Colorado State University.