매듭 이론

작은 매듭(왼쪽 위)과 작은 매듭(아래)을 포함한 다양한 매듭의 예

가장 단순한 비사소한 매듭인 삼엽상 매듭의 매듭 다이어그램

위상수학에서 매듭이론은 수학적 매듭을 연구하는 학문이다.수학적인 매듭은 신발끈이나 밧줄의 매듭과 같이 일상생활에서 나타나는 매듭에서 영감을 얻었지만, 가장 단순한 매듭은 반지(또는 매듭 풀기)이다.수학 언어에서 매듭은 3차원 유클리드 $\mathbb {R} ^{3}$ , $\mathbb {R} ^{3}$ 3 $(\displaystyle \mathbb$ {R $} ^{3$ }) $\mathbb {R} ^{3}$ 에 원을 내장한 것입니다(위상학에서 원은 고전적인 기하학적 개념이 아니라 모든 동형사상에 구속됩니다).두 $\mathbb {R} ^{3}$ 의 수학적 매듭은 R $3($ 주변 등방성 등방성이라고 함 $)$ 의 $\mathbb {R} ^{3}$ 변형을 통해 다른 매듭으로 변환할 수 있는 경우 등가입니다. 이러한 변환은 절단을 수반하지 않거나 스스로 통과하지 않는 매듭 문자열의 조작에 해당합니다.

매듭은 다양한 방법으로 설명할 수 있습니다.다른 설명 방법을 사용하면 동일한 매듭에 대한 설명이 여러 개 있을 수 있습니다.예를 들어, 매듭을 기술하는 일반적인 방법은 매듭 다이어그램이라고 불리는 평면 다이어그램으로, 어떤 매듭도 다양한 방법으로 그릴 수 있습니다.그러므로 매듭 이론의 근본적인 문제는 두 서술이 언제 같은 매듭을 나타내는지 결정하는 것이다.

이 문제에 대한 완전한 알고리즘 솔루션이 존재하며, 복잡성은 알려지지 않았습니다.실제로, 매듭은 종종 매듭 불변량, 즉 매듭에 대한 다른 설명에서 계산했을 때 동일한 수량을 사용하여 구별된다.중요한 불변량에는 매듭 다항식, 매듭 군 및 쌍곡선 불변량이 포함됩니다.

매듭 이론의 창시자들에 대한 원래 동기는 매듭과 연결의 표를 만드는 것이었다. 이것은 서로 얽힌 여러 요소의 매듭이다.19세기 매듭 이론이 시작된 이래로 60억 개 이상의 매듭과 고리가 표로 작성되었습니다.

더 많은 통찰력을 얻기 위해 수학자들은 매듭 개념을 몇 가지 방법으로 일반화했다.매듭은 다른 3차원 공간에서 고려할 수 있으며 원 이외의 물체를 사용할 수 있습니다. 매듭(수학)을 참조하십시오.고차원 매듭은 (n+2)차원 유클리드 공간에 내장된 n차원 구이다.

역사

1200년 켈트어 책에 나오는 복잡한 켈트어 매듭 세공

고고학자들은 매듭 묶기가 선사시대로 거슬러 올라간다는 것을 발견했다.정보를 기록하고 사물을 묶는 것과 같은 용도 외에도, 매듭은 미학과 정신적 상징성 때문에 인간을 흥미롭게 했다.매듭은 기원전 수세기 전의 다양한 형태의 중국 미술품에 나타난다.끝없는 매듭은 티베트 불교에서 나타나는 반면, 보로미아 고리는 다른 문화에서 반복적으로 나타나며 종종 단결의 힘을 상징한다.켈트어 책을 만든 켈트어 수도승들은 복잡한 켈트어 매듭으로 페이지 전체를 장식했다.

첫 번째 매듭표 작성자 피터 거스리 타이트

매듭의 수학적 이론은 위치의 기하학과 관련된 매듭의 속성을 논할 때 위상 특성의 중요성을 명시적으로 지적한 알렉상드르-테오필 반데르몽드에 의해 1771년에 처음 개발되었다.매듭에 대한 수학 연구는 연결 적분을 정의한 칼 프리드리히 가우스와 함께 19세기에 시작되었습니다.1860년대에, 원자가 에테르에 매듭이 있다는 켈빈 경의 이론은 피터 거스리 테이트가 완전한 분류를 위한 최초의 매듭 표를 만들도록 이끌었다.1885년에 타이트는 최대 10개의 교차점이 있는 매듭 표를 발표했는데, 이것이 타이트 추측으로 알려지게 되었다.이 기록은 초기 매듭 이론가들에게 동기를 부여했지만, 매듭 이론은 결국 토폴로지의 떠오르는 과목의 일부가 되었다.

20세기 초의 위상학자 막스 덴, J. W. 알렉산더와 다른 사람들은 매듭군의 관점에서 매듭을 연구했고 알렉산더 다항식과 같은 호몰로지 이론의 불변성을 연구했다.이것은 일련의 돌파구가 주제를 바꾸기 전까지 매듭 이론의 주요 접근법이 될 것이다.

1970년대 후반, 윌리엄 서스턴은 쌍곡기하학을 쌍곡선 기하학을 쌍곡선화 정리와 함께 매듭 연구에 도입했다.많은 매듭이 쌍곡선 매듭인 것으로 나타나 새롭고 강력한 매듭 불변량을 정의할 때 기하학을 사용할 수 있게 되었습니다.1984년 Vaughan Jones에 의한 존스 다항식의 발견 (Sossinsky 2002, 페이지 71-89)과 에드워드 위튼, 막심 콘체비치 등의 후속 기여는 통계학 및 양자장 이론에서 매듭 이론과 수학적 방법 사이의 깊은 연관성을 드러냈다.그 이후로 수많은 매듭 불변성이 양자군이나 플로어 호몰로지와 같은 정교한 도구를 이용해 발명되었다.

20세기의 마지막 수십 년 동안, 과학자들은 DNA와 다른 고분자의 매듭 현상을 이해하기 위해 물리적 매듭을 연구하는 데 관심을 갖게 되었다.매듭 이론은 분자가 키랄인지 아닌지를 결정하기 위해 사용될 수 있다(Simon 1986).양끝이 제자리에 고정된 끈인 엉킴은 DNA에 대한 토포이소머라아제의 작용을 연구하는데 효과적으로 사용되어 왔다(Flapan 2000).매듭 이론은 위상 양자 계산 모델을 통해 양자 컴퓨터를 구성하는 데 매우 중요할 수 있다(Collins 2006).

매듭 등가

왼쪽에는 매듭을 풀고 그에 상응하는 매듭이 있습니다.오른쪽에 있는 매듭과 같은 복잡한 매듭이 매듭을 푸는 것과 동일한지 확인하는 것이 더 어려울 수 있습니다.

매듭은 1차원 선분부터 시작하여 임의로 주위를 감싸고 그 두 자유단을 융합하여 닫힌 루프를 형성함으로써 작성된다(Adams 2004). (Sossinsky 2002) $간단히$ 말해, 매듭K(\ $displaystyle$ K)는 $K$ "비활성"만을 갖는 "비활성" $K\colon [0,1]\to \mathbb {R} ^{3}$ 연속 함수 K: [ $K\colon [0,1]\to \mathbb {R} ^{3}$ 1 $K\colon [0,1]\to \mathbb {R} ^{3}$ $K\colon [0,1]\to \mathbb {R} ^{3}$ 3 $(\$ K $\colon [0,1]\to \mathBBR ^{3$ 이다. $K(0)=K(1)$ 위상학자들은 매듭이 다른 매듭과 일치하도록 교차하지 않고 부드럽게 밀 수 있다면 매듭과 고리나 땋기 같은 다른 얽힘이 동등하다고 생각한다.

매듭 등가성의 개념은 두 개의 매듭이 우주에서 상당히 다른 위치에 있더라도 언제 같은 것으로 간주되어야 하는지에 대한 정확한 정의를 제공하는 것입니다.공식 수학적 정의는 방향 보존 $h\colon \mathbb {R} ^{3}\to \mathbb {R} ^{3}$ h: $h\colon \mathbb {R} ^{3}\to \mathbb {R} ^{3}$ $h\colon \mathbb {R} ^{3}\to \mathbb {R} ^{3}$ $→$ R $h\colon \mathbb {R} ^{3}\to \mathbb {R} ^{3}$ \ $display h \ mathbb { R$ ^ { r } ^ { } \ $to$ \ $mathbb { R$ } ^ { 3 $h\colon \mathbb {R} ^{3}\to \mathbb {R} ^{3}$ $h(K_{1})=K_{2}$ $h(K_{1})=K_{2}$ = 2인 $h(K_{1})=K_{2}$ 의 $K_{1},K_{2}$ $K_{1},K_{2}$ $($ 스타일 $K_$ {1 $}, K_$ ${$ $2$ }})가 동일하다는 $K_{1},K_{2}$ 것입니다 $h\colon \mathbb {R} ^{3}\to \mathbb {R} ^{3}$ .

매듭 등가성을 정의하는 또 다른 방법은 $t_rightarrow \mathbb$ { $R$ \ $mathbb {$ R $} ^{$ 3} \mathbb { $R}$ \ $mathqle {\mathbb$ {R} \ $displaystyle {h_{t}$ \ $\{h_{t}:\mathbb {R} ^{3}\rightarrow \mathbb {R} ^{3}\ \mathrm {for} \ 0\leq t\leq 1\}$ { $\{h_{t}:\mathbb {R} ^{3}\rightarrow \mathbb {R} ^{3}\ \mathrm {for} \ 0\leq t\leq 1\}$ } \ $m}$ \ $m$ of $\{h_{t}:\mathbb {R} ^{3}\rightarrow \mathbb {R} ^{3}\ \mathrm {for} \ 0\leq t\leq 1\}$ 1 $\{h_{t}:\mathbb {R} ^{3}\rightarrow \mathbb {R} ^{3}\ \mathrm {for} \ 0\leq t\leq 1\}$ 2개의 동형상이 연속적으로 존재하는 경우 2개의 매듭 등가 동등하다는 것입니다.첫 번째 매듭을 두 번째 매듭으로 묶습니다(좀 더 형식적으로:두 개의 $K_{1}$ K $({$ 과 $K_{1}$ $K_{2}$ 2({ $displaystyle K_{2})$ 는 $K_{2}$ $H:\mathbb {R} ^{3}\times [0,1]\rightarrow \mathbb {R} ^{3}$ $다음$ 과 $H:\mathbb {R} ^{3}\times [0,1]\rightarrow \mathbb {R} ^{3}$ 같은 연속 $H:\mathbb {R} ^{3}\times [0,1]\rightarrow \mathbb {R} ^{3}$ H: $H:\mathbb {R} ^{3}\times [0,1]\rightarrow \mathbb {R} ^{3}$ × $H:\mathbb {R} ^{3}\times [0,1]\rightarrow \mathbb {R} ^{3}$ [ $H:\mathbb {R} ^{3}\times [0,1]\rightarrow \mathbb {R} ^{3}$ , 1 $H:\mathbb {R} ^{3}\times [0,1]\rightarrow \mathbb {R} ^{3}$ $H:\mathbb {R} ^{3}\times [0,1]\rightarrow \mathbb {R} ^{3}$ $H:\mathbb {R} ^{3}\times [0,1]\rightarrow \mathbb {R} ^{3}$ 3({ $displaystyle$ H:\ $mathbb$ {R $} ^{3}\times$ [ $0,$ 1 $]\rightarrow \mathbb {R})$ 이 있는 경우 등가 됩니다 $.$ $x\in \mathbb {R} ^{3}$ x $x\in \mathbb {R} ^{3}$ $x\in \mathbb {R} ^{3}$ 3 ( $H(x,t)\in \mathbb {R} ^{3}$ , $t$ ) $display$ R 3 ( $x$ , t $)\ display$ $style$ $x\in \mathbb {R} ^{3}$ H ( $x$ , $H(x,t)\in \mathbb {R} ^{3}$ )\ $in$ \ $mathbb { R$ ^ { $3}$ ） $H(x,t)\in \mathbb {R} ^{3}$ 、 R $\mathbb {R} ^{3}$ $H(x,t)\in \mathbb {R} ^{3}$ ( \ $displaystyle$ \ $mathbb { R }^$ { $3}$ $\mathbb {R} ^{3}$ display display $H(x,0)=x$ $H(x,t)\in \mathbb {R} ^{3}$ $=$ 0 $H(x,0)=x$ ) $H(x,t)\in \mathbb {R} ^{3}$ 。c) $H(K_{1},1)=K_{2}$ ( $H(K_{1},1)=K_{2}$ 1, $H(K_{1},1)=K_{2}$ ) $H(K_{1},1)=K_{2}$ $H(K_{1},1)=K_{2}$ 2 ( $H(K_{1},1)=K_{2}$ \ $displaystyle$ H ( $K _$ {1} ) = $K$ _ {2} $H(K_{1},1)=K_{2}$ ）. 이러한 $함수$ H ( \ $displaystyle$ H)를 $H$ 주변 아이소토피라고 합니다.)

이 두 개의 매듭 등가 개념은 어떤 매듭이 등가인지에 대해 정확히 일치합니다.방향 보존 동형사상 정의에서 등가하는 2개의 노트는 주변 아이소토피 정의에서도 동등하다. $\mathbb {R} ^{3}$ R $3$ 의 $\mathbb {R} ^{3}$ 보존 $동형사상$ 자체가 동일성에서 시작하는 $주변$ 아이소토피의 최종 단계이기 때문이다 $.$ 반대로, 주변 등위성의 t $= 1(최종$ ) $t=1$ $t=1$ 는 다른 매듭을 포함하는 방향 보존 동형이어야 하기 때문에 주변 등위성의 정의에서 2노트에 해당하는 2노트는 방향 보존 동형성 정의에서도 동일하다.

매듭 이론의 기본 문제인 인식 문제는 두 개의 매듭의 등가성을 결정하는 것입니다.이 문제를 해결하기 위한 알고리즘이 존재하며, 첫 번째 알고리즘은 1960년대 후반에 볼프강 하켄에 의해 제시되었다(Has 1998).그럼에도 불구하고 이러한 알고리즘은 매우 시간이 걸릴 수 있으며 이론의 주요 쟁점은 이 문제가 실제로 얼마나 어려운지를 이해하는 것입니다(Hass 1998).언노팅 문제라고 불리는 언노트를 인식하는 특별한 케이스가 특히 중요합니다(Hoste 2005).2021년 2월, Marc Lackenby는 준다항 ^[1]시간에 실행되는 새로운 언노 인식 알고리즘을 발표했습니다.

매듭도

매듭을 시각화하고 조작하는 유용한 방법은 매듭을 평면에 투영하는 것입니다. 매듭이 벽에 그림자를 드리우는 것을 생각해 보십시오.투영 방향을 조금만 바꾸면 매듭의 "그림자"가 한 번 가로로 교차하는 교차점이라고 불리는 이중점을 제외하고 1대 1이 됩니다(롤프슨 1976).각각의 교차로에서 원래의 매듭을 재현할 수 있도록 오버스트레인을 언더스트레인과 구별해야 합니다.이것은 종종 아래로 들어가는 가닥을 끊음으로써 이루어집니다.결과 다이어그램은 각 교차점에서 어느 가닥이 넘고 어느 가닥이 아래에 있는지 추가 데이터가 포함된 침지 평면 곡선입니다(이러한 다이어그램은 매듭을 나타낼 때 매듭 다이어그램, 링크 다이어그램을 나타낼 때 링크 다이어그램이라고 합니다).마찬가지로, 4공간에서 매듭된 표면은 3공간에서 침지된 표면과 관련될 수 있다.

축소도는 환원식 교차로(중간 또는 분리식 교차로도)가 없거나 환원식 교차로가 모두 ^[2]^[3]제거된 매듭 다이어그램입니다.꽃잎 돌기는 이중점을 형성하는 대신 매듭의 모든 가닥이 단일 교차점에서 만나며, 네스트되지 않은 "꽃잎"^[4]을 형성하는 루프로 연결된 돌기의 일종입니다.

리드마이스터 이동

1927년, J. W. Alexander와 Garland Baird Briggs, 그리고 독립적으로 Kurt Reidemister는 매듭의 이 도형 형태를 사용하여 동일한 매듭에 속하는 두 개의 매듭 도형이 아래 그림과 같이 세 가지 종류의 연속적인 움직임으로 연관될 수 있다는 것을 증명했다.현재 Reidemeister 움직임이라고 불리는 이러한 작전은 다음과 같습니다.

어느 방향으로든 비틀었다 폈다 하세요.
한 가닥을 다른 가닥 위로 완전히 옮깁니다.
교차로 위 또는 아래로 가닥을 완전히 이동합니다.

**리드마이스터 이동**
타입 I	타입 II


타입 III

동등한 매듭의 도표가 레이더미스터의 움직임에 의해 연결된다는 증거는 하나의 매듭을 다른 매듭으로 만드는 운동의 평면 투영 아래에서 일어나는 일에 대한 분석에 의존합니다.한 점에서 두 개 이상의 가닥이 교차하거나 한 점에서 여러 가닥이 접선하는 경우와 같이 "이벤트" 또는 "대격변"이 발생한 경우를 제외하고 거의 모든 시간이 매듭 다이어그램이 되도록 이동을 배열할 수 있습니다.면밀한 검사를 통해 복잡한 사건은 제거될 수 있으며, 가장 단순한 사건만 남습니다. (1) "꼬임" 형성 또는 펴짐, (2) 한 점에서 접선이 되어 통과하는 두 가닥, (3) 한 점에서 교차하는 세 가닥입니다.이것이 바로 Reidemeister의 움직임이다(Sossinsky 2002, ch. 3) (Likorish 1997, ch. 1)

매듭 불변량

그림 8매트의 보완을 나타내는 3D 프린팅
프랑수아 게리토, 사울 슐레이머, 앙리 세게르만의 작품

매듭 불변량은 동등한 매듭(Adams 2004)(1997년 Likorish)에 대해 동일한 수량(Rolfsen 1976)이다.예를 들어, 불변량이 매듭 다이어그램에서 계산되는 경우, 동등한 매듭을 나타내는 두 개의 매듭 다이어그램에 대해 동일한 값을 제공해야 합니다.불변량은 두 개의 다른 노트에서 동일한 값을 취할 수 있으므로, 그것만으로는 모든 노트를 구별할 수 없을 수 있습니다.기본 불변량은 삼색성이다.

"고전적" 매듭 불변량은 매듭 보체의 기본군인 매듭 군과 매듭 보체의 무한 순환 덮개로 구성된 모듈인 알렉산더 불변량에서 계산할 수 있는 알렉산더 다항식을 포함한다.20세기 후반에, "양자" 매듭 다항식, 바실리예프 불변량, 쌍곡 불변량과 같은 불변량이 발견되었다.앞서 언급한 불변량은 현대 매듭 이론의 빙산의 일각일 뿐이다.

매듭 다항식

매듭 다항식은 다항식인 매듭 불변량입니다.잘 알려진 예로는 존스와 알렉산더 다항식이 있다.알렉산더 다항식의 변형인 알렉산더-콘웨이 다항식은 정수 계수를 갖는 변수 z의 다항식이다.

알렉산더-콘웨이 다항식은 실제로는 서로 얽힌 하나 이상의 노트로 구성된 링크의 관점에서 정의됩니다.위에서 설명한 매듭에 대한 개념(예: 다이어그램 및 리드미스터 이동)도 링크에 적용됩니다.

방향성이 있는 링크 다이어그램, 즉 링크의 모든 구성요소가 화살표로 표시된 우선 방향을 갖는 링크 다이어그램에 대해 설명합니다.다이어그램의 특정 교차에 대해 $L_{+},L_{-},L_{0}$ L + $L_{+},L_{-},L_{0}$ , $L_{+},L_{-},L_{0}$ - , L $L_{+},L_{-},L_{0}$ { \ $displaystyle L_{$ + }, $L_{-}, L_{0}$ 을 $L_{+},L_{-},L_{0}$ 그림과 같이 다이어그램 변경에 따른 방향 링크 다이어그램으로 $L_{+},L_{-},L_{0}$ .

원래 다이어그램은 선택한 교차로 설정에 따라 $L_{+}$ L $L_{+}$ + {\ $displaystyle L_{+}}$ $L_{-}$ L $L_{-}$ - {\ $displaystyle L_$ 중 $L_{+}$ 입니다.그런 다음 규칙에 따라 Alexander-Conway 다항식 $C(z)$ ( $C(z)$ )\ $displaystyle$ C ( $z$ 가 재귀적으로 정의됩니다.

$C(O)=1$ ( $C(O)=1$ ) $=$ $C(O)=1$ {{ $displaystyle$ C $(O$ )=1 $}$ $C(O)=1$ ( $O$ 서O {\ $displaystyle$ O}는 $O$ 매듭을 푼 다이어그램입니다)
$C(L_{+})=C(L_{-})+zC(L_{0}).$

두 번째 규칙은 종종 스키인 관계라고 불리는 것입니다.이러한 규칙이 방향 링크의 불변성을 제공하는지 확인하려면, 다항식이 세 가지 리드미스터 이동 하에서 변하지 않음을 결정해야 한다.많은 중요한 매듭 다항식은 이러한 방식으로 정의할 수 있습니다.

다음은 스키인 관계를 사용한 일반적인 계산의 예입니다.그것은 삼각뿔 매듭의 알렉산더-콘웨이 다항식을 계산한다.노란색 패치는 관계가 적용되는 위치를 나타냅니다.

C()

= C()

+ z C()

는 unknot 및 Hopf 링크를 제공합니다.표시된 Hopf 링크에 관계를 적용합니다.

C()

= C()

+ z C()

는 0의 크로스(실제로 2개의 컴포넌트의 링크 해제)와 언노트로 변형 가능한 링크를 제공합니다.링크 해제에는 약간의 교묘함이 필요합니다.

C()

= C()

+ z C()

이는 처음 두 다항식이 매듭 해제이므로 C(두 성분의 연결 해제) = 0임을 의미합니다.

이 모든 것을 종합하면, 이하를 알 수 있습니다.

\displaystyle C(\mathrm {trfoil})=1+z(0+z)=1+z^{2}}

알렉산더-콘웨이 다항식이 매듭 불변량이기 때문에, 이것은 삼각형이 매듭 해제와 동일하지 않다는 것을 보여준다.그래서 트리포일은 정말 "코티드"입니다.

왼손 삼엽매듭이요.
오른손 삼엽매듭이요.

사실, 오른쪽과 왼쪽의 삼각뿔이라고 불리는 두 개의 삼각뿔 매듭이 있는데, 이것은 서로의 거울 이미지이다.이것들은 서로 같지 않다. 즉, 양성바이러스가 아니라는 뜻이다.이것은 매듭 다항식이 발명되기 전에 군 이론 방법을 사용하여 맥스 덴에 의해 증명되었다.그러나 각 종류의 삼엽충의 알렉산더-콘웨이 다항식은 거울 이미지로 위의 계산을 통해 볼 수 있듯이 같을 것입니다.존스 다항식은 사실 왼손과 오른손 삼엽 매듭을 구별할 수 있다(Lickorish 1997).

쌍곡선 불변량

윌리엄 서스턴은 많은 매듭이 쌍곡선 매듭이라는 것을 증명했는데, 이는 매듭이 보완된 것(즉, 매듭 위에 있지 않은 3-공백의 점 집합)이 특히 쌍곡선 기하학의 기하학적 구조를 허용한다는 것을 의미한다.쌍곡선 구조는 매듭에만 의존하므로 쌍곡선 구조에서 계산되는 모든 양은 매듭 불변량입니다(Adams 2004).

Borromean 링은 하나의 링을 제거하면 다른 링이 분리되는 속성을 가진 링크입니다.

SnapPea의 첨탑 뷰: Borromean 고리는 빨간색 구성요소 근처에 사는 거주자의 관점에서 보완합니다.

기하학은 기하학의 측지학을 따라 이동하는 광선을 상상함으로써 매듭이나 링크 보체의 내부를 시각화할 수 있게 합니다.예를 들면, 보롬환의 상보 화상에 의해서 제공된다.이 링크 보형의 거주자는 빨간색 컴포넌트 근처에서 공간을 보고 있습니다.사진 속 공은 링크의 호로볼 주변 풍경입니다.표준적인 방법으로 링크를 굵게 함으로써 링크 구성요소의 호로볼 근방을 얻을 수 있다.이웃의 경계는 토러스지만 링크 보체 안에서 보면 구체처럼 보인다.각 링크 컴포넌트는 옵서버에서 링크 컴포넌트로의 광선이 무한히 많으므로 (1가지 색상의) 무한히 많은 구를 표시합니다.기본 평행사변형(그림에 표시됨)은 수직 및 수평으로 타일링되며 구의 패턴을 무한히 확장하는 방법을 보여줍니다.

이 패턴, 호로볼 패턴은 그 자체로 유용한 불변량입니다.다른 쌍곡선 불변량에는 기본 평행 사변형의 모양, 최단 측지선의 길이, 부피가 포함됩니다.현대의 매듭과 링크 표 작성은 이러한 불변성을 효과적으로 활용했습니다.빠른 컴퓨터와 이러한 불변량을 얻는 현명한 방법은 실제로 이러한 불변량을 계산하는 작업을 단순하게 만듭니다(Adams, Hildebrand & Weeks 1991).

고차원

4차원 공간에 놓으면 3차원 매듭을 풀 수 있다.이는 교차로를 변경하여 이루어집니다.선택한 지점에서 볼 때 한 가닥이 다른 가닥 뒤에 있다고 가정합니다.장애물이 없도록 4차원으로 들어 올린 다음(전면 스트랜드에는 컴포넌트가 없습니다), 앞으로 슬라이드하여 앞으로 떨어뜨립니다.평면에 대한 유사점은 표면에서 끈을 들어 올리거나 원 안에서 점을 제거하는 것입니다.

사실 4차원에서 1차원 문자열의 비교차 폐쇄 루프는 매듭 해제와 동일합니다.먼저 루프를 3차원 서브스페이스로 "밀어넣기"합니다.이것은 항상 가능한 일이지만, 설명하기는 전문적입니다.

고차원의 매듭 구체

매듭은 위상적으로 1차원 구라고 간주할 수 있으므로 다음 일반화에서는 4차원 유클리드 공간( $\mathbb {R} ^{4}$ 4 $\mathbb {R} ^{4}$ \ $displaystyle \mathbb$ { $R$ $}$ ^{ $4})$ 에 포함된 2차원 구( $\mathbb {S} ^{2}$ 2 \ $displaystyle \mathbb {S}$ ^{2 $})$ 를 고려하는 것입니다.이러한 매립은 매립형 2-스피어를 표준 2-스피어의 "원형" 매립으로 가져가는 $\mathbb {R} ^{4}$ 4 $(\$ ^{ $4})$ 의 $\R^4$ 동형성이 없는 경우 매듭지어진다.현수 노트와 스핀 노트는 이러한 2-구면 노트의 두 가지 전형적인 계열입니다.

"일반 위치"라고 불리는 수학적 기법은 m차원 유클리드 공간에서 주어진 n-sphere에 대해 m이 충분히 크면(n에 따라 다름) 구에 매듭을 풀어야 한다는 것을 암시한다.일반적으로, 부분 선형 n-구체는 (n + 2)차원 공간(Zeeman 1963)에서만 매듭을 형성하지만, 이것은 더 이상 부드럽게 매듭진 구에 대한 요구사항이 아니다.실제로 6k $(4k-1)$ 차원 공간에는 매끄럽게 $(4k-1)$ $(4k-1)$ ({ $displaystyle(4k-1)})$ 구체가 $(4k-1)$ 있습니다. 예를 들어 R $({$ Haefliger 1962) (Levine 1965)에는 매끄럽게 매듭지어진 3구체가 있습니다.따라서 매끄러운 매듭의 코디멘션은 매듭된 구의 치수를 고정하지 않을 때 임의로 커질 수 있지만, $2n-3k-3>0$ - $2n-3k-3>0$ k - $2n-3k-3>0$ > $2n-3k-3>0$ {\ $displaystyle 2n-3k-3 >$ 0}인 $2n-3k-3>0$ R n $\mathbb {R} ^{n}$ {\ $displaystyle \mathbb {R} ^{n}}$ 에 $\mathbb {R} ^{n}$ 포함된 매끄러운 k-sphere는 분리되지 않습니다.매듭의 개념은 수학에서 더욱 일반화되었습니다. 매듭(수학), 임베딩의 등방성 분류를 참조하십시오.

$\mathbb {S} ^{n}$ $\mathbb {S} ^{n}$ n n \ $\mathbb {R} ^{n+1}$ $\mathbb {S}$ $\mathbb {R} ^{n+1}$ ^{ $n$ $\mathbb {R} ^{n+1}$ 의 $\mathbb{S}^n$ 각 매듭은 R n + $1(\$ +1})의 고립된 특이점을 갖는 실 대수 집합의 링크입니다(Akbulut & King 1981).

n-knot은 R $\mathbb {R} ^{m}$ {\ $displaystyle$ $\mathbb {S} ^{n}$ $\$ $mathbb {$ $S$ $}$ ^{ $n$ $}$ 에 $\mathbb{S}^n$ 포함된 $\mathbb {S} ^{n}$ S $\mathbb {S} ^{n}$ $\mathbb {S} ^{n}$ \displaystyle \mathbb $\mathbb {R} ^{m}$ ${$ R} ^{ $n$ $}$ $\mathbb {S} ^{n}$ 。n-link는 R $\mathbb {R} ^{m}$ ${\displaystyle$ \ $mathbb$ $\mathbb {S} ^{n}$ {S $} ^{$ n $\mathbb {S} ^{n}$ $\mathbb {R} ^{m}$ 의 $k-copies$ 로 구성됩니다. $m=n+2$ $m=n+2$ + $({displaystyle$ m $=n+2$ ) 및 $m=n+2$ m $m>n+2$ > $m>n+2$ + $m>n+2$ ({ $displaystyle$ m $>n+2})$ $m>n+2$ 는 $m>n+2$ 모두 잘 연구되어 있으며 $n>1$ $n>1$ $>$ ^[5]^[6]1({ $displaystyle n>$ 1 $n>1$ ) $n>1$ 도 잘 연구되어 있습니다.

매듭 추가

2노트의 추가

두 개의 매듭을 모두 자르고 한 쌍의 끝을 결합하면 두 개의 매듭을 추가할 수 있습니다.이 연산을 매듭합 또는 2개의 매듭의 연결합 또는 구성이라고 합니다.이것은 공식적으로 다음과 같이 정의할 수 있다(Adams 2004). 각 매듭의 평면 투영을 고려하고 이러한 투영들이 분리되었다고 가정한다.반대쪽 한 쌍이 각 매듭을 따라 호를 그리며 나머지 직사각형이 매듭에서 분리되는 평면에서 직사각형을 찾습니다.첫 번째 한 쌍의 반대쪽을 삭제하고 다른 한 쌍의 반대쪽을 나란히 하여 새로운 매듭을 만듭니다.결과 매듭은 원래 매듭의 합계입니다.이 조작 방법에 따라서는, 2개의 다른 매듭(단, 그 이상)이 생기는 일이 있습니다.합계의 이러한 모호성은 방향성이 있는 매듭에 관해 제거될 수 있다. 즉, 매듭을 따라 이동하는 바람직한 방향을 가지며, 합계의 매듭의 호는 직사각형의 방향 경계와 일관되게 방향성이 있어야 한다.

방향성 매듭의 매듭합은 가환성과 연관성이다.매듭은 사소하지 않은 경우 소수이며 사소하지 않은 두 개의 매듭 합으로 쓸 수 없습니다.합계로 쓸 수 있는 매듭은 합성이다.매듭에는 소수 및 합성수와 유사한 일차 분해가 있다(슈베르트 1949).방향성 매듭의 경우 이 분해도 독특합니다.고차원 매듭도 추가할 수 있지만 몇 가지 차이가 있습니다.2개의 사소한 매듭을 추가하여 3차원적으로 언노트를 형성할 수는 없지만 적어도 3차원 이상의 코디멘션의 스무스한 매듭을 고려할 때 더 높은 차원의 언노트를 형성할 수 있습니다.

표로 정리한 매듭

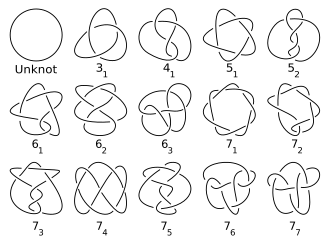
최대 7개의 교차로까지의 기본 매듭 표.매듭에는 알렉산더-브릭스 표기가 붙어 있습니다.

전통적으로 매듭은 교차 번호로 분류되어 왔다.일반적으로 매듭 테이블에는 주요 매듭만 포함되며 매듭과 거울 이미지(다르더라도)에 대한 엔트리는 1개뿐입니다(Hoste, Threstwaite & Weeks 1998).주어진 교차 번호의 중요하지 않은 매듭의 수는 빠르게 증가하여 표 계산을 어렵게 한다(Hoste 2005, 페이지 20).표 작업은 60억 개 이상의 노트와 링크를 열거하는 데 성공했다(Hoste 2005, 페이지 28).교차 번호 16까지 주어진 교차 번호의 소수 매듭의 순서는 0, 0, 1, 2, 3, 7, 21, 49, 165, 552, 2176, 9988, 46972, 253293, 1388705이다.(OEIS의 시퀀스 A002863).이 시퀀스의 지수 상한과 하한이 알려져 있지만, 이 시퀀스가 엄격하게 증가하고 있는 것은 증명되지 않았습니다(Adams 2004).

Tait, Little, Kirkman의 첫 번째 매듭 표는 매듭 도표를 사용했지만, Tait는 또한 Dowker 표기법의 전조를 사용했다.보다 효율적인 표기를 가능하게 하는 매듭에 대해 다양한 표기가 개발되었습니다(Hoste 2005).

초기 표에서는 최대 10개의 교차로의 모든 매듭과 11개의 교차로의 모든 교대로의 모든 매듭을 나열하려고 시도했다(Hoste, Thistlethwaite 및 Weeks 1998).알렉산더, 리데미스터, 세이퍼트 등에 의한 매듭 이론의 발전은 검증의 임무를 완화시켰고, 9개의 교차점을 포함한 매듭 표는 1920년대 말에 알렉산더-브리그스와 리데미스터에 의해 출판되었다.

이 작업의 첫 번째 주요 검증은 1960년대에 John Horton Conway에 의해 이루어졌다. 그는 새로운 표기법뿐만 아니라 알렉산더-콘웨이 다항식(Conway 1970)도 개발했다(Doll & Hoste 1991).이를 통해 최대 11개 교차로의 매듭 목록과 최대 10개 교차로의 새로운 링크 목록이 확인되었습니다.콘웨이는 Tait-Little 표에서 다수의 누락과 중복을 발견했지만, 그는 1974년에야 케네스 페르코(Perko 1974)에 의해 알아차린 페르코 쌍이라고 불리는 중복을 놓쳤다.이 유명한 오류는 데일 롤프슨이 콘웨이의 작품을 바탕으로 그의 영향력 있는 텍스트에 매듭표를 추가했을 때 확산되었다.Conway의 1970년 매듭 이론에 관한 논문도 11개의 교차 매듭 페이지에 인쇄상의 중복을 포함하고 있으며, 4개의 예시를 생략하고 있습니다(이전에는 D에 기재되어 있었습니다).롬바르데로의 1968년 프린스턴 시니어 논문과 알랭 카우드론에 의해 2개가 더 발견되었다.[Perko(1982), 특정 매듭의 원시성, 토폴로지 프로시딩 참조]10개의 교차 링크 테이블에 중복된 것은 별로 알려져 있지 않습니다.2.-20.20은 8*-20의 거울입니다.[Perko (2016), 비순환 매듭 이론의 역사적 하이라이트, J. Not Theory Ramifications 참조]

1990년대 후반에 Hoste, Thresthwaite 및 Weeks는 16개의 교차로를 통해 모든 매듭을 표로 만들었다(Hoste, Thresthwaite 및 Weeks 1998).2003년에 랭킨, 플린트, 셰르만은 22개의 교차로를 번갈아 가는 매듭을 표로 만들었다(호스트 2005).2020년에 버튼은 최대 19개의 교차로가 있는 모든 주요 매듭을 표로 작성했다(버튼 2020).

알렉산더-브릭스 표기법

이것은 1927년 제임스 W의 논문 때문에 가장 전통적인 표기법이다. 알렉산더와 갈랜드 B. 브릭스 그리고 나중에 데일 롤프슨이 그의 매듭 테이블에서 확장했습니다(위의 이미지와 주요 매듭 목록 참조).이 표기법은 단순히 교차 번호로 매듭을 정리합니다.교차 번호에 첨자를 붙여서 그 교차 번호와의 모든 매듭의 순서를 나타냅니다.이 순서는 임의이므로 특별한 의미가 없습니다(각 교차 수에서 트위스트 매듭은 토러스 매듭 뒤에 있습니다).링크는 컴포넌트 수를 나타내는 상위첨자 및 컴포넌트 수와 교차수가 동일한 링크 내의 순서를 나타내는 하위첨자를 사용하여 교차번호로 작성됩니다.따라서 trefoil not은 3으로 표기되며₁ Hopf 링크는 2가 됩니다²
₁.찰스 뉴턴 리틀의 최초 및 후속 매듭 표에서 페르코 쌍이 발견되었고,^[7] 이 지점 이후에 만들어진 매듭 표 및 기타 출판물에서 이 오류를 수정하기 위한 접근법의 차이 때문에 10에서₁₆₆ 10까지의 범위에₁₆₂ 있는 알렉산더-브릭스 이름은 모호하다.

다우커-시슬스웨이트 표기법

다우커 시퀀스에 대해 레이블이 지정된 교차점이 있는 매듭 다이어그램

다우커-다우커 표기법 또는 코드라고도 불리는 엉겅퀴 표기법은 짝수 정수의 유한 수열입니다.숫자는 매듭을 따라 교차점을 연속 정수로 표시하여 생성됩니다.각 교차점은 두 번 방문되므로 짝수 정수와 홀수 정수의 쌍이 생성됩니다.오버크로스 및 언더크로스를 나타내기 위해 적절한 부호가 주어집니다.예를 들어, 이 그림에서 매듭 다이어그램에는 (1,6)(3,-12)(5,2)(7,8)(9,-4) 및 (11,-10) 쌍으로 레이블이 지정된 교차점이 있습니다.다우커-이 라벨링의 엉겅퀴 표기법은 6, -12, 2, 8, -4, -10의 순서이다. 매듭 다이어그램에는 하나 이상의 다우커 표기법이 있으며 다우커에서 매듭을 재구성할 때 잘 알려진 모호성이 있다.엉겅퀴 표기법

콘웨이 표기법

매듭과 링크의 Conway 표기법은 John Horton Conway의 이름을 딴 것으로, 엉킴 이론(Conway 1970)에 근거하고 있습니다.이 표기법의 장점은 매듭 또는 링크의 일부 속성을 반영한다는 것입니다.

이 표기법은 링크의 특정 링크 다이어그램을 작성하는 방법을 설명합니다.기본 다면체, 디곤 영역이 없는 4가 연결 평면 그래프에서 시작합니다.이러한 다면체는 먼저 기본 다면체 목록에서 다면체의 위치를 결정하는 정점 수, 그리고 여러 개의 별표로 나타납니다.예를 들어, 10**는 Conway 목록에 있는 두 번째 10-vertex 다면체를 나타냅니다.

각 정점은 그 정점에 대입된 대수적 엉킴을 가진다(각 정점은 방향을 향하고 있기 때문에 치환에 있어서 임의의 선택은 없다).이러한 각 얽힘에는 숫자와 + 또는 - 기호로 구성된 기호가 있습니다.

예를 들어 1*2 - 3 2 입니다.1*은 유일한 1-vertex 기본 다면체를 나타냅니다.2-3 2는 유리 엉킴과 관련된 연속 분수를 나타내는 수열이다.기본 다면체 1*의 정점에 이 엉킴을 삽입합니다.

더 복잡한 예는 8*3.1.2 0.1.1.1입니다. 여기서도 8*은 8개의 정점이 있는 기본 다면체를 나타냅니다.마침표는 각 엉킴에 대한 표기법을 구분합니다.

어떤 링크라도 이러한 설명을 받아들일 수 있으며, 이는 매우 큰 교차 번호에도 매우 콤팩트한 표기법임이 분명합니다.일반적으로 사용되는 몇 가지 추가 줄임말이 있습니다.마지막 예시는 보통 8*3:2 0으로 쓰입니다.여기서 1은 생략하고 끝의 점을 제외한 점의 수를 유지합니다.첫 번째 예시와 같은 대수적 매듭의 경우 1*은 생략되는 경우가 많습니다.

이 주제에 관한 Conway의 선구적인 논문은 그가 링크를 표로 만드는 데 사용하는 10개의 기본 다면체를 열거하고 있으며, 이러한 다면체는 이러한 링크의 표준이 되었다.더 높은 정점 다면체의 추가 목록을 위해 사용할 수 있는 비표준 선택지가 있습니다.

가우스 코드

다우커와 유사한 가우스 코드-Thistlethwaite 표기법은 일련의 정수가 있는 매듭을 나타냅니다.그러나 모든 교차로가 두 개의 다른 번호로 표시되는 대신 교차로는 하나의 숫자로만 레이블이 지정됩니다.교차로가 오버크로스일 경우 양수가 나열됩니다.언더크로싱에서는 음수입니다.예를 들어 Gauss 코드의 trefoil note는 다음과 같이 지정할 수 있습니다.

가우스 코드는 매듭을 식별할 수 있는 능력이 제한되어 있습니다.이 문제는 확장 Gauss 코드로 부분적으로 해결됩니다.

회선 토폴로지

회로 토폴로지는 매듭 이론의 대안 프레임워크이며 매듭과 엉킴을 설명하고 분류할 수 있습니다.매듭이론은 얽힌 사슬을 기본 매듭의 연결된 합으로 간주한다.주요 매듭은 나눌 수 없고 분해할 수 없다.회선 토폴로지는, 차례로, 얽힌 체인(주요 매듭 포함)을 소프트 콘택트(s 콘택트)라고 불리는 기본적인 구조 단위로 분할해, s 콘택트를 조합하는 간단한 룰을 일람표시합니다.이러한 규칙은 s-contacts에 정의된 이진 연산으로 간주할 수 있습니다.직렬(S), 병렬(P) 또는 교차(X)에 두 개의 s-접촉을 배치하는 세 가지 주요 연산이 있으며, s-접촉을 일치(C)시키거나 첨자(Sub)를 추가하는 두 개의 보조 연산이 있습니다.회로 위상은 비다항식 접근법이지만 매듭 이론의 알렉산더 다항식과 일치할 수 있는 문자열 표기법과 함께 제공됩니다.

「」를 참조해 주세요.

레퍼런스

원천

Adams, Colin (2004), The Knot Book: An Elementary Introduction to the Mathematical Theory of Knots, American Mathematical Society, ISBN 978-0-8218-3678-1
Adams, Colin; Crawford, Thomas; DeMeo, Benjamin; Landry, Michael; Lin, Alex Tong; Montee, MurphyKate; Park, Seojung; Venkatesh, Saraswathi; Yhee, Farrah (2015), "Knot projections with a single multi-crossing", Journal of Knot Theory and Its Ramifications, 24 (3): 1550011, 30, arXiv:1208.5742, doi:10.1142/S021821651550011X, MR 3342136, S2CID 119320887
Adams, Colin; Hildebrand, Martin; Weeks, Jeffrey (1991), "Hyperbolic invariants of knots and links", Transactions of the American Mathematical Society, 326 (1): 1–56, doi:10.1090/s0002-9947-1991-0994161-2, JSTOR 2001854
Akbulut, Selman; King, Henry C. (1981), "All knots are algebraic", Comm. Math. Helv., 56 (3): 339–351, doi:10.1007/BF02566217, S2CID 120218312
Bar-Natan, Dror (1995), "On the Vassiliev knot invariants", Topology, 34 (2): 423–472, doi:10.1016/0040-9383(95)93237-2
Burton, Benjamin A. (2020). "The Next 350 Million Knots". 36th International Symposium on Computational Geometry (SoCG 2020). Leibniz Int. Proc. Inform. Vol. 164. Schloss Dagstuhl–Leibniz-Zentrum für Informatik. pp. 25:1–25:17. doi:10.4230/LIPIcs.SoCG.2020.25.
Collins, Graham (April 2006), "Computing with Quantum Knots", Scientific American, 294 (4): 56–63, Bibcode:2006SciAm.294d..56C, doi:10.1038/scientificamerican0406-56, PMID 16596880
Dehn, Max (1914), "Die beiden Kleeblattschlingen", Mathematische Annalen, 75 (3): 402–413, doi:10.1007/BF01563732, S2CID 120452571
Conway, John H. (1970), "An enumeration of knots and links, and some of their algebraic properties", Computational Problems in Abstract Algebra, Pergamon, pp. 329–358, doi:10.1016/B978-0-08-012975-4.50034-5, ISBN 978-0-08-012975-4
Doll, Helmut; Hoste, Jim (1991), "A tabulation of oriented links. With microfiche supplement", Math. Comp., 57 (196): 747–761, Bibcode:1991MaCom..57..747D, doi:10.1090/S0025-5718-1991-1094946-4
Flapan, Erica (2000), When topology meets chemistry: A topological look at molecular chirality, Outlook, Cambridge University Press, ISBN 978-0-521-66254-3
Haefliger, André (1962), "Knotted (4k − 1)-spheres in 6k-space", Annals of Mathematics, Second Series, 75 (3): 452–466, doi:10.2307/1970208, JSTOR 1970208
Hass, Joel (1998), "Algorithms for recognizing knots and 3-manifolds", Chaos, Solitons and Fractals, 9 (4–5): 569–581, arXiv:math/9712269, Bibcode:1998CSF.....9..569H, doi:10.1016/S0960-0779(97)00109-4, S2CID 7381505
Hoste, Jim; Thistlethwaite, Morwen; Weeks, Jeffrey (1998), "The First 1,701,935 Knots", Math. Intelligencer, 20 (4): 33–48, doi:10.1007/BF03025227, S2CID 18027155
Hoste, Jim (2005), "The enumeration and classification of knots and links", Handbook of Knot Theory (PDF), Amsterdam: Elsevier
Levine, Jerome (1965), "A classification of differentiable knots", Annals of Mathematics, Second Series, 1982 (1): 15–50, doi:10.2307/1970561, JSTOR 1970561
Kontsevich, Maxim (1993), "Vassiliev's knot invariants", I. M. Gelfand Seminar, Adv. Soviet Math., 2, Providence, RI: American Mathematical Society, 16: 137–150, doi:10.1090/advsov/016.2/04, ISBN 9780821841174
Lickorish, W. B. Raymond (1997), An Introduction to Knot Theory, Graduate Texts in Mathematics, vol. 175, Springer-Verlag, doi:10.1007/978-1-4612-0691-0, ISBN 978-0-387-98254-0, S2CID 122824389
Perko, Kenneth (1974), "On the classification of knots", Proceedings of the American Mathematical Society, 45 (2): 262–6, doi:10.2307/2040074, JSTOR 2040074
Rolfsen, Dale (1976), Knots and Links, Mathematics Lecture Series, vol. 7, Berkeley, California: Publish or Perish, ISBN 978-0-914098-16-4, MR 0515288
Schubert, Horst (1949), "Die eindeutige Zerlegbarkeit eines Knotens in Primknoten", Heidelberger Akad. Wiss. Math.-Nat. Kl. (3): 57–104
Silver, Dan (2006), "Knot theory's odd origins" (PDF), American Scientist, vol. 94, no. 2, pp. 158–165, doi:10.1511/2006.2.158
Simon, Jonathan (1986), "Topological chirality of certain molecules", Topology, 25 (2): 229–235, doi:10.1016/0040-9383(86)90041-8
Sossinsky, Alexei (2002), Knots, mathematics with a twist, Harvard University Press, ISBN 978-0-674-00944-8
Turaev, Vladimir G. (1994), "Quantum invariants of knots and 3-manifolds", De Gruyter Studies in Mathematics, Berlin: Walter de Gruyter & Co., 18, arXiv:hep-th/9409028, Bibcode:1994hep.th....9028T, ISBN 978-3-11-013704-0
Weisstein, Eric W. (2013). "Reduced Knot Diagram". MathWorld. Wolfram. Retrieved 8 May 2013.
Weisstein, Eric W. (2013a). "Reducible Crossing". MathWorld. Wolfram. Retrieved 8 May 2013.
Witten, Edward (1989), "Quantum field theory and the Jones polynomial", Comm. Math. Phys., 121 (3): 351–399, Bibcode:1989CMaPh.121..351W, doi:10.1007/BF01217730, S2CID 14951363
Zeeman, Erik C. (1963), "Unknotting combinatorial balls", Annals of Mathematics, Second Series, 78 (3): 501–526, doi:10.2307/1970538, JSTOR 1970538

각주

^ Marc Lackenby announces a new unknot recognition algorithm that runs in quasi-polynomial time, Mathematical Institute, University of Oxford, 2021-02-03, retrieved 2021-02-03
^ Weisstein 2013.
^ Weisstein 2013a.
^ 애덤스 외 2015년
^ Levine, J.; Orr, K (2000), "A survey of applications of surgery to knot and link theory", Surveys on Surgery Theory: Papers Dedicated to C.T.C. Wall, Annals of mathematics studies, vol. 1, Princeton University Press, CiteSeerX 10.1.1.64.4359, ISBN 978-0691049380 - 고급 독자를 위한 고차원 노트 및 링크 소개 기사
^ Ogasa, Eiji (2013), Introduction to high dimensional knots, arXiv:1304.6053, Bibcode:2013arXiv1304.6053O - 초보자용 고차원 매듭 및 링크 소개 기사
^ '퍼코 페어의 복수', RichardElwes.co.uk.2016년 2월에 접속.리처드 엘웨스는 페르코 쌍을 묘사할 때 흔히 볼 수 있는 실수를 지적한다.

추가 정보

입문 교재

매듭 이론에는 많은 서론이 있다.대학원생이나 상급 학부생을 위한 고전적인 소개는 다음과 같습니다(Rolfsen 1976).참고 자료에서 다른 좋은 텍스트는 (Adams 2004)와 (Likorish 1997)이다.Adams는 비공식적이고 대부분 고등학생들에게 접근하기 쉽다.Rickorish는 대학원생을 위한 엄밀한 소개로 고전과 현대 토픽이 혼합되어 있습니다. (Cromwell 2004)는 포인트 집합 토폴로지를 알고 있는 학부생에게 적합합니다.대수 토폴로지에 대한 지식은 필요하지 않습니다.

Burde, Gerhard; Zieschang, Heiner (1985), Knots, De Gruyter Studies in Mathematics, vol. 5, Walter de Gruyter, ISBN 978-3-11-008675-1
Crowell, Richard H.; Fox, Ralph (1977). Introduction to Knot Theory. ISBN 978-0-387-90272-2.
Kauffman, Louis H. (1987), On Knots, ISBN 978-0-691-08435-0
Kauffman, Louis H. (2013), Knots and Physics (4th ed.), World Scientific, ISBN 978-981-4383-00-4
Cromwell, Peter R. (2004), Knots and Links, Cambridge University Press, ISBN 978-0-521-54831-1

조사

Menasco, William W.; Thistlethwaite, Morwen, eds. (2005), Handbook of Knot Theory, Elsevier, ISBN 978-0-444-51452-3
- 메나스코와 테슬스웨이트의 핸드북은 고급 학부생들이 접근하기 쉽지만 전문 연구자들이 관심을 갖는 방식으로 현재의 연구 동향과 관련된 여러 주제를 조사한다.
Livio, Mario (2009), "Ch. 8: Unreasonable Effectiveness?", Is God a Mathematician?, Simon & Schuster, pp. 203–218, ISBN 978-0-7432-9405-8

외부 링크

수학과 매듭 1989년 왕립학회 '팝매스 로드쇼'를 위해 개발된 전시회의 온라인 버전입니다.그것의 목적은 일반 대중들에게 수학의 방법을 제시하기 위해 매듭을 사용하는 것이었다.

역사

Thomson, Sir William (1867), "On Vortex Atoms", Proceedings of the Royal Society of Edinburgh, VI: 94–105
Silliman, Robert H. (December 1963), "William Thomson: Smoke Rings and Nineteenth-Century Atomism", Isis, 54 (4): 461–474, doi:10.1086/349764, JSTOR 228151, S2CID 144988108
타이트의 스모크 링 실험을 현대적으로 재현한 영화
매듭 이론의 역사(Andrew Ranicki 홈페이지)

노트 테이블 및 소프트웨어

노트 정보:매듭 불변량 및 매듭 이론 리소스 표
노트 아틀라스 - 노트 테이블의 개별 노트에 대한 자세한 정보
Not Plot - 노트의 기하학적 특성을 조사하는 소프트웨어
노트스케이프 - 노트 이미지를 만드는 소프트웨어
Knoutilus - 온라인 데이터베이스 및 노트 이미지 생성기
NotData.html : 매듭을 조사하기 위한 Wolfram Mathematica 함수
레지나 - 노트와 링크를 네이티브하게 지원하는 저차원 토폴로지용 소프트웨어.최대 19개의 교차로가 있는 프라임 매듭 표

[1] Marc Lackenby announces a new unknot recognition algorithm that runs in quasi-polynomial time, Mathematical Institute, University of Oxford, 2021-02-03, retrieved 2021-02-03

[FOOTNOTEWeisstein2013-2] Weisstein 2013.

[FOOTNOTEWeisstein2013a-3] Weisstein 2013a.

[FOOTNOTEAdamsCrawfordDeMeoLandry2015-4] 애덤스 외 2015년

[5] Levine, J.; Orr, K (2000), "A survey of applications of surgery to knot and link theory", Surveys on Surgery Theory: Papers Dedicated to C.T.C. Wall, Annals of mathematics studies, vol. 1, Princeton University Press, CiteSeerX 10.1.1.64.4359, ISBN 978-0691049380 - 고급 독자를 위한 고차원 노트 및 링크 소개 기사

[6] Ogasa, Eiji (2013), Introduction to high dimensional knots, arXiv:1304.6053, Bibcode:2013arXiv1304.6053O - 초보자용 고차원 매듭 및 링크 소개 기사

[7] '퍼코 페어의 복수', RichardElwes.co.uk.2016년 2월에 접속.리처드 엘웨스는 페르코 쌍을 묘사할 때 흔히 볼 수 있는 실수를 지적한다.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

v t 매듭 이론(노트와 링크)
쌍곡선	그림 8(4₁) 3₂ 트위스트(5) 스테보도어₁(6) 6개₂ 6개₃ 엔드리스 (7₄) 캐릭₁₈ 매트(8) Perko 쌍(10₁₆₁) (-2,3,7) 프레첼 (12n242) 화이트헤드² ₁(5) 붕소환(6개³ ₂) L10a140
위성.	복합 매듭 할머니 광장 매듭합
토러스	매듭₁ 해제(0) 트리포일₁(3) 신퀘포일₁(5) Septafoil₁(7) 링크² ₁ 해제(0) 홉² ₁(2) 솔로몬의² ₁ (4)
불변량	교대로 Arf 불변량 브릿지 번호 2-브릿지 브루니안 키라리티 반전 가능 크로스 캡 번호 건널목 번호 유한형 불변량 쌍곡선 부피 호바노프 호몰로지 속 매듭군 링크 그룹 링크 번호 다항식 알렉산더 브래킷 홈플라이 존스 카우프만 프레첼 프라임 목록. 안 돼. 삼색성 노팅 해제 번호 및 문제
표기법 및 조작	알렉산더-브릭스 표기법 콘웨이 표기법 다우커 표기법 플라이페 돌연변이 리드마이스터 이동 스킨 관계 표
다른.	알렉산더의 정리 베르주 땋기 이론 콘웨이 구 보완하다 더블토러스 파이버 가공 매듭 매듭 및 링크 목록 리본 조각을 내라 합 타이트 추측 트위스트 야생의 비틀거리다 수술 이론
카테고리 공통

Search

매듭 이론

네임스페이스

더

목차

역사

매듭 등가