반대 광장

이 글은 검증을 위해 인용구가 추가로 필요하다. 신뢰할 수 있는 출처에 인용문을 추가하여 이 기사를 개선할 수 있도록 도와주십시오. 공급되지 않은 재료는 도전하여 제거할 수 있다. 출처 찾기: "반대 광장" – 뉴스 · 신문 · 책 · 학자 · JSTOR (2015년 2월) (이 템플릿 메시지를 제거하는 방법과 시기 알아보기)

용어 논리(철학적 논리의 한 분야)에서 반대 광장은 네 가지 기본적인 범주형 명제 사이의 관계를 나타내는 도표다. 광장의 기원은 아리스토텔레스가 모순과 반반성의 두 반대파 사이를 구별하는 것으로 거슬러 올라갈 수 있다. 그러나 아리스토텔레스는 어떤 도표도 그리지 않았다. 이것은 수세기 후에 아풀레이우스와 보에티우스에 의해 행해졌다.

요약

전통적인 논리학에서 명제(라틴어: propositio)는 언어와 논리의 현대철학에서와 같이 주장(oratio enunsativa)의 의미가 아닌 구어적 주장(oratio enunsativa)이다. 범주형 명제는 주어(S)와 술어(P)라는 두 가지 용어를 포함하는 간단한 명제로서, 술어가 주어에 대해 주장하거나 부인한다.

모든 범주형 명제는 라틴어 동의서(확언)에 근거한 A, E, I, O라는 네 가지 논리 형태 중 하나로 축소될 수 있으며, A와 I, 그리고 부정적인 명제 E와 O에 대해서는 Nego(난 부정한다)가 있다. 다음은 다음과 같다.

• 라틴어로 'omne S 에스트 P'가 되어 있는 'A' 명제인 보편적 긍정(Universalis appirmativa)은 보통 'every S is a P'로 번역된다.
• 'E' 명제, 보편적 부정(범용적 부정), 라틴어 형태 'nullum S 에스트 P'로 보통 'no S is P'로 번역된다.
• I' 명제, 특정 찬성(특정 찬성), 라틴어 '쿼드담 S 에스트 P'는 보통 'some S is P'로 번역된다.
• 'O' 명제, 특히 음(특정 음)인 라틴어 '쿼드담 S노엔 에스트 P'는 보통 'S는 P가 아니다'로 번역된다.

표 형식:

아리스토텔레스 4대 명제

이름	기호	라틴어	영어*	니모닉	모던[1] 폼
보편적 긍정	A	옴네 에스 에스트 P.	모든 S는 P(S는 항상 P)이다.	진술서 (확언한다)	${\displaystyle \ forall x(Sx\오른쪽 화살표 Px)}$
범용 네거티브	E	널름 S 에스트 P.	No S is P(S는 절대 P가 아니다)	네고 (거부한다)	${\displaystyle \forall x(Sx\오른쪽 화살표 \neg Px)}$
특별 긍정	I	Quoddam S 에스트 P.	일부 S는 P이다(S는 때때로 P이다)	진술서 (확언한다)	${\displaystyle \exists x(Sx\land Px)}$
특정부정	O	Quoddam Snnn 에스트 P.	일부 S는 P가 아니다(S는 항상 P가 아니다).	네고 (거부한다)	${\displaystyle \exists x(Sx\land \neg Px)}$

*제안 'A'는 "All S is P"로 명시할 수 있으나, "All S is P"로 상응하여 "All S is P"라고 기술할 경우, 제안 'E'는^[2] E 또는 O 명제일 수 있기 때문에 모호하며, 따라서 형식을 결정하는 맥락이 필요하며, "No S is P"는 명확하지 않기 때문에 선호된다. 명제 'O'는 또한 "때로는 S가 P가 아닐 때도 있다."와 "특정 S가 P가 아니다." (문법적으로 라틴어 'Quoddam Snn Est P.')의 형태를 취한다.

** ${\displaystyle \mathrm{현대적}}$ 형식의$$S x {\$displaystyle$ Sx$}$은(는) 문 $S{\displaystyle }$ ${\displaystyle$ $S$$}$이(가) $객체{\displaystyle }$ x ${\displaystyle$ x$}$에 적용됨을$$ 의미한다$.$ 많은 경우 단순히 "${\displaystyle }$ ${\displaystyle x}$은(는) S$${\$displaystyle$S$\}"$로 해석될 수 있다. ${\displaystyle S}$ ${\displaystyle x}$ ${\displaystyle Sx}$은(는) $S{\displaystyle }$( x${\displaystyle }$) ${\displaystyle S(x)}$로도 쓸 수 있다$$$.$

아리스토텔레스는 (페리 에르미네이아스의 6장과 7장에서, ερ μηεεαας, 라틴어 De 해석, 영어 'On 해석') 이 네 종류의 명제 사이에 일정한 논리적 관계가 있다고 명시하고 있다. 그는 모든 긍정에는 정확히 하나의 부정과 일치하며, 모든 긍정과 부정은 '반대'되기 때문에 그 중 하나는 항상 진실이어야 하고, 다른 하나는 거짓이어야 한다고 말한다. 한 쌍의 긍정적인 진술과 그 부정은 그가 '대조'라고 부르는 것이다. 모순의 예로는 '모든 사람은 백인이 아니다'와 '모든 사람이 백인이 아니다'(또한 '어떤 사람은 백인이 아니다')와 '어떤 사람은 백인이 아니다' 그리고 '어떤 사람은 백인이 된다'가 있다.

아래의 관계는, 반대로, 부차적, 부차적, 초대체적 관계로서, S(또는 현대 논리에서는 S를 충족하는 것)가 존재한다는 전통적인 논리 가정에 근거하여 유지된다. 만약 이 가정이 실행된다면, 이러한 관계는 유지되지 않는다.

'contractary'(중세: contractarae) 진술은 두 진술이 동시에 진실일 수 없는 진술이다. 이것들의 예로는 보편적 긍정 '모든 사람은 백인'과 보편적 부정 '아무도 백인'이 있다. 이것들은 동시에 사실일 수 없다. 그러나 두 가지 모두 거짓일 수 있기 때문에 이러한 것들은 모순이 아니다. 예를 들어 어떤 사람은 백인이 아니므로 모든 사람이 백인이라는 것은 거짓이다. 그러나 백인이 없는 것도 거짓이다. 백인이 몇 명 있기 때문이다.

모든 진술은 모순된 반대(부정)를 가지고 있기 때문에, 그리고 모순은 그 반대는 거짓일 때 사실이기 때문에, 그 반대는 (중대들이 하위 콘트라리아, 하위 콘트라리아라고 부르는) 반론의 대립은 둘 다 진실일 수 있지만 둘 다 거짓일 수는 없다. 하위내용은 보편적 진술의 부정이기 때문에 중세 논리학자들에 의해 '중요한' 진술이라고 불렸다.

이것에 의해 암시된 또 다른 논리적 관계는 아리스토텔레스에 의해 명시적으로 언급되지는 않았지만, '대체'(alternatio)로 구성되는 '대체'(alternatio)이다. 하위조항은 특별조항과 동일품질의 보편적 진술(확증적 또는 부정적) 사이의 관계로서, 초대체란 범주의 거짓(동등하게 보편적 부정)이 거짓에 의해 함축된 것과 같은 관계다. 특정(대부분 특정의 부정)^[3]의 (초대체는 하위 대체의 역방향이다.) 이러한 관계에서 특이점은 특정의 초신성인 보편의 하위신분이다. 예를 들어, '모든 사람은 백인'이 사실이라면, 그 반대인 '백인은 없다'는 것은 거짓이다. 그러므로 모순되는 '어떤 사람은 백인'은 사실이다. 마찬가지로 보편적인 '사람은 백인이 아니다'는 특정한 '모든 사람이 백인은 아니다'^[4][5]를 의미한다.

요약하면:

• 보편적인 진술은 반론이다: '모든 사람은 정의롭다'와 '아무도 정의롭지 않다'는 말은 비록 한 사람이 진실일 수도 있고 다른 한 사람이 거짓일 수도 있지만, 또한 둘 다 거짓일 수도 있다(최소한 한 사람이 정의롭고 한 사람이 정의롭지 않다면, 적어도 한 사람이 정의롭지 않다).
• 구체적인 진술은 부차적인 것이다. '어떤 사람은 정의롭다'와 '어떤 사람은 정의롭지 않다'가 함께 거짓일 수는 없다.
• 아리스토텔레스 의미론에서 '모든 A는 B'를 내포하고, 'NO는 B'는 'A는 B가 아니다'를 내포하고 있기 때문에, 한 품질의 특정 문장은 같은 품질의 보편적 문장의 하위 문장이며, 이는 아리스토텔레스에서 'A는 B가 아니다'를 내포하고 있기 때문이다. 영어 문장의 현대적 형식적 해석은 '모든 A는 B'를 '모든 x에 대해 x가 A라는 문장은 'x가 B라는 문구를 내포함'으로 해석하며, 이는 '일부 x는 A'를 의미하지 않는다는 점에 유의한다. 그러나 이것은 의미론적 해석의 문제일 뿐, 때로는 주장되듯이 아리스토텔레스 논리가 '잘못된' 것을 의미하는 것은 아니다.
• 보편적 긍정론(A)과 특정 부정론(O)은 모순이다. 일부 A가 B가 아니라면, 모든 A가 B는 아니다. 반대로 현대의 의미론에서는 그렇지 않지만, 모든 A가 B가 아니라면, 어떤 A는 B가 아니라고 생각되었다. 이러한 해석은 어려움을 야기시켰다(아래 참조). 아리스토텔레스의 그리스어는 특정한 음을 '일부 A는 B가 아니다'라고 표현하지는 않지만, '모든 A가 B는 아니다'라고 표현하고 있는 반면, 페리 헤르마네아스에 대한 그의 논평에 나오는 누군가는 특정 음을 '쿼담 A노엔 에스트 B', 문자 그대로 'A는 B가 아니다'라고 표현하며, 모든 논리에 관한 중세적에서는 특정한 음을 나타내는 것이 관습이다.이온을 이온으로 하다

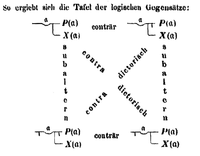
이러한 관계는 보에티우스에서 비롯되어 중세 논리학자들이 논리적 관계를 분류하는 데 사용한 도표의 기초가 되었다. 제안은 사각형의 네 모서리에 배치되어 있으며, 그 사이에 그려진 선으로 표현되는 관계는 '야당의 광장'이라는 이름을 붙인다. 따라서 다음과 같은 경우를 만들 수 있다.^[6]

1. A가 참이면 E가 거짓이면 나는 진실이고 O가 거짓이면 거짓이다.
2. E가 참이면 A가 거짓이고, 나는 거짓이고, O가 참이다.
3. 내가 사실이라면, E는 거짓이고, A와 O는 확실하지 않다.
4. O가 참이면 A가 거짓이고, E와 나는 불확실한 것이다.
5. A가 거짓이면 O가 참이고, E와 나는 불확실한 것이다.
6. E가 거짓이면 나는 진실이고, A와 O는 불확실한 것이다.
7. 내가 거짓이면, A는 거짓이고, E는 진실이고, O는 참이다.
8. O가 거짓이면 A가 진실이고 E가 거짓이면 나는 진실이다.

이들을 외우기 위해 메디컬들은 다음과 같은 라틴어 운율을 발명했다.^[7]

애드퍼마트, 네그랫 E, 진정 범용자 암바에,

나는 단호하고, 부정적이고, 선동적인 암바에.

A와 E는 위의 각각의 경우에서 모두 진실도 거짓도 아니라고 단언한다. I과 O도 마찬가지다. 처음 두 가지는 보편적인 진술이지만, 커플 I/O는 특정한 진술들을 가리킨다.

반대 광장은 그리스 철학자 아리스토텔레스가 설명한 단정적인 추론, 즉 변환, 전복, 대립에 이용되었다. 이 세 가지 유형의 범주형 추론은 각각 A, E, I, O의 네 가지 보에티안 논리 형식에 적용되었다.

실존적 수입의 문제

중세 논리학자들이 '쿼드담 A 에스트 B'(일부 특정 A는 B)와 '쿼담 A 비 에스트 B'(일부 특정 A는 B가 아님) 형태로 대표했던 하위 목록(I와 O)은 둘 다 거짓일 수 없는데, 이는 이들의 보편적인 모순된 진술(no A is B/모든 A는 B)이 될 수 없기 때문이다. 이것은 피터 아벨라르(1079년 – 1142년 4월 21일)에 의해 처음으로 식별된 난관으로 이어진다. '일부 A는 B'는 '무엇이 A'라는 뜻을 내포하고 있는 것 같은데, 다시 말해 A라는 것이 존재한다. 예를 들어 '어떤 사람은 백인이 된다'는 말은 적어도 존재하는 것이 한 사람, 즉 '어떤 사람은 백인이면 백인이어야 하는 사람'이라는 말이 사실임을 암시하는 것 같다. 그러나 '어떤 사람은 백인이 아니다'는 말은 '어떤 사람은 백인이 아니다'라는 말이 사실이라면, 인간으로서 존재하는 것, 즉 백인이 아닌 사람이 존재한다는 뜻도 내포하고 있다. 그러나 아리스토텔레스 논리학에서는 이러한 진술들 중 하나(더 일반적으로 '어떤 특정한 A는 B'이고 '어떤 특정한 A는 B가 아니다')가 반드시 사실임을 요구하고 있다. 즉, 둘 다 거짓일 수는 없다. 그러므로 두 진술 모두 적어도 한 가지 이상의 존재, 즉 한 사람의 존재를 암시하고 있기 때문에, 남자나 남자의 존재는 뒤따른다. 그러나, 아벨라르트가 방언시카에서 지적했듯이, 확실히 남자는 존재하지 않을지도 모른다.^[8]

사람이 전혀 존재하지 않는 상황에서 '모든 사람은 사람이다'라는 명제는 진실도 아니고 '어떤 사람은 사람이 아니다'라는 명제도 사실이 아니기 때문이다.^[9]

아벨라르트는 또한 '돌인 남자'와 같이 아무것도 나타내는 주어가 들어 있는 하위 콘텐트는 둘 다 거짓이라고 지적한다.

'모든 돌맨은 돌이다'가 사실이라면, 또한 억양당 변환도 사실이다('어떤 돌은 돌맨이다'). 그러나 어떤 돌도 돌맨이 아니다. 왜냐하면 이 사람이나 저 사람 등은 돌멩이도 아니기 때문이다. 그러나 또한 이 '어떤 돌맨은 돌이 아니다'는 것은 그것이 사실이라고 추측할 수 없기 때문에 필연적으로 거짓이다.^[10]

테렌스 파슨스(Terrence Parsons, 1939년 출생)는 고대 철학자들이 A(범용적 긍정)와 I(특히 긍정) 형식만이 실존적 수입만을 가지고 있었기 때문에 실존적 수입의 문제를 경험하지 않았다고 주장한다.(만약 진술서에 실존적 수입이라는 용어가 없는 경우, 즉 ex라는 용어와 관련된 어떤 것도 없다.ists, 그러면 그 진술은 그 용어와 관련하여 실존적 수입을 가지고 있다고 한다.)

긍정론에는 실존적 수입이 있고, 부정론에는 그렇지 않다. 따라서 옛사람들은 볼 만한 일관성이 없었기 때문에 아리스토텔레스가 공식화한 광장의 일관성을 보지 못했다.^[11]

그는 계속해서 중세 철학자 Moerbeke의 윌리엄(115–35–1286)을 인용한다.

긍정 제안에서 용어는 항상 어떤 것을 대신한다고 주장된다. 그러므로 만약 그것이 헛되이 보충된다면 그 명제는 잘못된 것이다. 그러나, 부정적인 명제에서 주장은 그 용어가 어떤 것에 대한 보충이 되지 않거나 또는 그 술어가 진정으로 거부되는 어떤 것에 대한 보충이다. 따라서 부정적인 명제는 두 가지 진리의 원인이 있다.^[12]

그리고 보에티우스가 아리스토텔레스의 작품을 번역한 것은 O형식이 실존적 수입을 가지고 있다는 그릇된 생각을 낳게 한 것이라고 지적한다.

그러나 보에티우스(477 – AD 524)가 이 글에 대해 언급할 때 그는 아리스토텔레스의 교리를 지금 유명한 도표로 설명하고 있으며, '어떤 사람은 그냥 있는 것이 아니다'라는 문구를 사용한다. 그래서 이것은 그에게 라틴어로 자연적으로 동등한 것으로 보였을 것이다. 영어로는 우리에게 이상하게 보이지만, 그는 그것에 개의치 않았다.^[13]

현대적 반대 광장

19세기에 조지 불(1815년 11월 8일 ~ 1864년 12월 8일)은 특정 청구권(I와 O)의 두 가지 조건에 모두 실존적 수입을 요구하지만, 보편적 청구권(A와 E)의 모든 조건은 실존적 수입이 부족하도록 허용한다고 주장했다. 이 결정은 특히 벤 도표를 용어 논리에 사용하기 쉽게 만들었다. 이 부울적인 가정 하에서 반대편의 광장은 종종 현대 반대파의 광장으로 불린다. 현대의 반대 광장에서, A와 O의 주장은 E와 I와 마찬가지로 모순이지만, 다른 모든 형태의 반대는 중단된다; 반론, 하위내용, 하위대립, 초대립이 없다. 그러므로 현대적인 관점에서 보면, 나이가 많은 논리학자들이 주장했듯이 주장에는 여러 가지 다른 대립적 요소가 있다고 주장하기보다는, 주장과 주장이 다른 '반대'에 대해 말하는 것이 이치에 맞는 경우가 종종 있다.

고틀로프 프레게(1848년 11월 8일 ~ 1925년 7월 26일)의 베그리프슈크리프트도 고전적 광장과 거의 동일한 방식으로 조직된 반대 정사각형을 제시하여 보편적 정량화, 부정, 함축으로 구성된 네 가지 공식 사이의 모순, 하위 대체 및 반론을 보여준다.

알기르다스 줄리앙 그레마스(1917년 3월 9일~1992년 2월 27일)의 기호 광장은 아리스토텔레스의 작품에서 유래되었다.

전통적인 반대 광장은 이제 종종 내적, 외적 부정에 기초한 광장과 비교된다.^[14]

논리 육각형 및 기타 단순형

반대는 6개 성명의 관계를 포함하는 논리적인 육각형까지 확대되었다. 아우구스틴 세스마트(Augustin Sesmat, 1885년 4월 7일 ~ 1957년 12월 12일)와 로버트 블랑케(1898–1975) 양쪽에 의해 독립적으로 발견되었다.^[15] '논리적 큐브'에 이은 사각형과 육각형 모두 '논리적 n차원 bi-simples of dimension n'이라는 규칙적인 n차원 객체에 속한다는 것이 증명되었다. 그 패턴은 또한 이것을 훨씬 뛰어넘는다.^[16]

반대(또는 논리 정사각형) 및 모달 논리

반대 정사각형 또는 아풀레이우스의 제곱이라고도 불리는 논리 정사각형은 삼단논법적 추론에 채용될 4개의 뚜렷한 문장에 기원을 두고 있다: "모든 사람은 나쁘다", 보편적 긍정 - 보편적 긍정성의 부정 "모든 사람이 나쁜 것은 아니다"(또는 "어떤 사람은 나쁜 것은 아니다") - "어떤 사람은 나쁜 것은 아니다" - "어떤 사람은 나쁜 것은 아니다" - 특히 긍정적이다. - 그리고 마지막으로, "아무도 나쁜 사람은 없다"라는 특정 긍정의 부정. 로버트 블랑케는 1966년 브린과 함께 그의 구조 지성인들과 함께 출판되었고 그 이후 많은 학자들은 4가지 가치를 나타내는 논리 정사각형이나 사각형의 반대는 6가지 가치를 나타내는 논리 정육각형으로 대체되어야 한다고 생각한다. 왜냐하면 그것은 논리학과 나투에 대해 더 많은 것을 설명할 수 있는 힘을 가지고 있기 때문이다.혀짤배기 같은 말씨

범주형 문장의 이론적 해석

현대 수학 논리학에서는 "all", "some", "no"라는 단어를 포함하는 문장이 집합 이론의 관점에서 명시될 수 있다. $모든{\displaystyle }$ A의 집합이 s${\displaystyle }$( ${\displaystyle A}$) ${\displaystyle$ s$(A)}$로, 모든 B의 $집합$이 s ${\displaystyle (B}$)$${\$displaystyle$ s$(B)}$로 라벨이 지정된 경우$:$

• "All A is B"(AaB)는 "${\displaystyle s}$( A${\displaystyle }$) ${\displaystyle$ s$(A)}$은(는) $s{\displaystyle }$( ${\displaystyle B)}$ ${\displaystyle s($${\displaystyle B}$$)}$ $$또는 $s{\displaystyle }$(${\displaystyle A)}$⊆ ${\displaystyle s(}$A${\displaystyle )}$ ${\displaystystyle s(A)\subseteq$ s$(B)}$의 하위 집합이다$.$
• "No A is B"(AeB)는 "${\displaystyle s}$( A${\displaystyle }$) ${\displaystyle s(A)}$과 $s{\displaystyle }$ ${\displaystyle (B)}$ ${\displaystyle$ s$(B)}$의 교차점이 비어 있음$$" 또는 $s{\displaystyle }$(${\displaystyle A)}$ ${\displaystyle \cap }$ s${\displaystyle (B)}$= ${\displaystyle \mathrm{\varnothing }}$ ${\displaystystyle s(A)=\empteset }$에 해당한다$.$
• "Some A is B" (AiB) is equivalent to "The intersection of ${\displaystyle s(A)}$ and ${\displaystyle s(B)}$ is not empty", or ${\displaystyle s(A)\cap s(B)\neq \emptyset }$.
• "일부 A는 B가 아니다"(AoB)는 "${\displaystyle }$ ( ${\displaystyle A}$${\displaystyle )}$와 동등하다$.$ s (${\displaystyle }A{\displaystyle }$$)$ ${\displaystyle s(B)}"$ 또는 s ($A$)${\displaystyle ⊈}$ ${\displaystyle s}$(${\displaystyle A)}$ ${\displaystyle s(A)\nsubseteq$ s$(B)$의 하위 집합이 아니다$.$

정의상 빈 집합$∅{\displaystyle \emptyset }$은(는) 모든 집합의 하위 집합이다$$. 이 사실로부터, 이 수학적 관례에 따르면, 만약 A가 없다면, "A는 모두 B"와 "No A는 B"라는 문장이 항상 진실인 반면, "Some A는 B"와 "Some A는 B가 아니다"라는 문장은 항상 거짓이다. 이는 또한 AaB가 AiB를 수반하지 않는다는 것을 의미하며, 위에서 언급한 일부 삼단논법들은 A의 (${\displaystyle }$(${\displaystyle A}$) = ${\displaystyle \mathrm{\varnothing }}$ ${\displaystyle$ s$(A)=\empteset }$이 없을 때 유효하지 않다.$$

참고 항목

• 볼의 삼단논법
• 자유 논리학

참조

외부 링크

위키미디어 커먼스는 반대 광장 관련 매체를 보유하고 있다.

• Parsons, Terence. "The Traditional Square of Opposition". In Zalta, Edward N. (ed.). Stanford Encyclopedia of Philosophy.
• 야권의 광장 국제회의
• 로지카 유니버설리스 특별호 2권 N. 1호(2008) 반대편 광장
• Catlogic: 범주적 명제와 삼단논법을 구성, 조사 및 계산하기 위해 루비로 작성된 오픈 소스 컴퓨터 스크립트