힐베르트 제도

이 글에는 여러 가지 문제가 있다. 이 문제를 개선하거나 대화 페이지에서 토의하십시오. (이러한 템플릿 메시지를 제거하는 방법 및 시기 알아보기) 이 글은 수학 전문가의 주의가 필요하다. 자세한 내용은 토크 페이지를 참조하십시오. 위키프로젝트 수학이 전문가 영입에 도움이 될 수도 있다(2011년 3월) 이 글은 일반적인 참고문헌 목록을 포함하고 있지만, 그에 상응하는 인라인 인용구가 충분하지 않기 때문에 대체로 검증되지 않은 상태로 남아 있다. 좀 더 정밀한 인용문을 도입하여 이 글을 개선할 수 있도록 도와주십시오. (2019년 10월) (이 템플릿 메시지를 제거하는 방법과 시기 알아보기) (이 템플릿 메시지를 제거하는 방법 및 시기 알아보기)

수학 물리학에서 힐버트 시스템은 C*-알지브라에 의해 기술된 물리적 시스템에 자주 사용되지 않는 용어다.

논리학, 특히 수학 논리학에서 힐버트 미적분학, 힐버트식 연역학 시스템 또는 힐버트-아커만 시스템이라고 불리는 힐버트 시스템은 고틀롭 프레게와^[1] 데이비드 힐버트에게 귀속된 형식적 추론의 한 유형이다. 이러한 연역적 시스템은 일차적 논리를 위해 가장 많이 연구되지만 다른 논리학에도 관심이 있다.

힐버트 시스템의 대부분의 변형들은 논리적 공리와 추론 규칙들 사이의 절충을 균형 있게 하는 방식으로 특징적인 방침을 취한다.^[1] 힐버트 시스템은 다수의 논리 공리와 소수의 추론 규칙의 선택에 의해 특징지어질 수 있다. 자연공제의 시스템은 많은 공제 규칙들을 포함하지만 공리적인 제도가 거의 없거나 전혀 없는 정반대의 방침을 취한다. 가장 일반적으로 연구되는 Hilbert 시스템은 단지 하나의 추론 규칙 - 명제 로직(proposal logics) - 또는 일반화(proposalization) - 술어 로직(presentic logic)을 처리하기 위한 두 가지 - 그리고 몇 가지 무한한 공리 체계를 가지고 있다. 힐버트-르위스 시스템이라고도 불리는 명제 모달 로직의 힐버트 시스템은 일반적으로 필수 규칙과 균일한 대체 규칙이라는 두 가지 추가 규칙으로 공리화된다.

힐버트 시스템의 많은 변종들의 특징적인 특징은 자연적 추론과 순열적 미적분학 둘 다 몇몇 문맥 변화 규칙을 포함하고 있는 반면에 문맥은 추론 규칙들 중 어떤 것에서도 변하지 않는다는 것이다. 그러므로 만약 어떤 사람이 가상적 판단이 아닌 tautology의 파생성에만 관심이 있다면, 그 추론의 규칙이 다소 단순한 형태의 판단만을 포함하는 방식으로 Hilbert 시스템을 공식화할 수 있다. 다른 두 가지 공제 시스템에서도 같은 것을 할 수 없다:^{[citation needed]} 일부 추론 규칙에서 맥락이 바뀌기 때문에 가상의 판단을 피할 수 있도록 공식화할 수 없다. 단지 우리가 그것들을 단지 tautology의 파생성을 증명하기 위해 사용하고 싶더라도 말이다.

형식공제

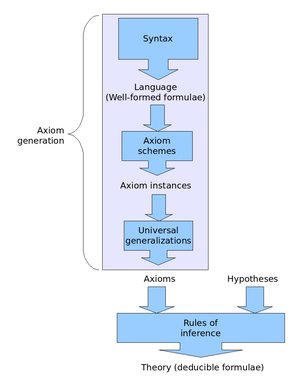
힐버트식 공제 시스템에서 형식 공제는 각 공식이 공리이거나 추론 규칙에 의해 이전 공식에서 얻은 공식의 유한한 순서다. 이러한 형식적 추론은 훨씬 더 상세하지만, 자연어 증거를 반영하기 위한 것이다.

$\gamma {\displaystyle \mathrm{}}$ ${\displaystyle \Gamma}$이(가) 가설로 간주되는 공식 집합이라고 가정해 보십시오. $예$를 들어 , ${\displaystyle \Gamma$}은$($는) 집단 이론이나 집합 이론의 공리 집합일 수 있다$$. The notation ${\displaystyle \Gamma \vdash \phi }$ means that there is a deduction that ends with ${\displaystyle \phi }$ using as axioms only logical axioms and elements of ${\displaystyle \Gamma }$. Thus, informally, ${\displaystyle \Gamma \vdash \phi }$ means that ${\displaystyle \phi }$ is provab$\gamma {\displaystyle \mathrm{}}$ ${\displaystyle \Gamma }$의 모든 공식을 가정한다$.$

힐버트식 공제 시스템은 논리적 공리의 수많은 체계를 사용하는 것이 특징이다. 공리 체계란 어떤 형태의 모든 공식을 특정 패턴으로 대체함으로써 얻은 공리의 무한 집합이다. 논리 공리 집합에는 이러한 패턴에서 생성된 공리뿐만 아니라 그러한 공리 중 하나를 일반화하는 것도 포함된다. 공식의 일반화는 ${\displaystyle \mathrm{공식}}$에 0개 이상의 범용 정량자를 접두사하여 얻는다. 예를 들어 ∀${\displaystyle \mathrm{}}$y (${\displaystyle \mathrm{\forall }}$ ${\displaystyle x}$ ${\displaystyle x}$ ${\displaystyle y}$→ ${\displaystyle P}$ ${\displaystyle t}$ )${\$$displaystyle$ \$forall$y$(\$$forall$ $xPxy$$\to Pty$$)}$는 $\forall {\displaystyle \mathrm{}}$ ${\displaystyle x}$ ${\displaystyle x}$ ${\displaystyle y}$→ $Py}$의 일반화다$.$

논리 공리

어떤 논리든 그 논리를 특징짓는 공리와 규칙을 선택할 자유가 있기 때문에 술어 논리의 몇 가지 변형된 공리주의가 있다. 우리는 여기에 9개의 공리와 단지 규칙모드만 있는 힐버트 시스템을 기술하는데, 이것을 우리는 하나의 규칙 공리화라고 부르고 고전적인 등가 논리를 기술한다. 공식에서 connectives $\neg {\displaystyle \mathrm{}}$ ${\displaystyle \lnot }$ 및$$${\displaystyle }$→ ${\displaystyle \to }$만 사용하고$$ 계량자 $\forall {\displaystyle \mathrm{}}$ ${\displaystyle$ $\$$ally$}. 나중에$.$${\displaysty$ \$land}$과 같은 추가적인$$ 논리적 connectives를 포함하도록 시스템을 확장하는 방법을 보여 준다. ${\displaystyle }$해석 가능한 공식의 클래스를 확대하지 않고 ${\displaystyle \vee }$ ${\displaystyle \lor$

최초의 네 가지 논리 공리 체계는 (모더스 폰과 함께) 논리 연결 장치의 조작을 허용한다.

P1. $\varphi {\displaystyle }$→ ${\displaystyle \varphi }$ ${\displaystyle \pi \to \phi }$

P2. $\varphi {\displaystyle }$→ (${\displaystyle \psi }$ →${\displaystyle \varphi }$) ${\$

P3. ${\displaystyle \left(\phi \to \left(\psi \rightarrow \xi \right)\right)\to \left(\left(\phi \to \psi \right)\to \left(\phi \to \xi \right)\right)}$

${\displaystyle \mathrm{P4}}$. (${\displaystyle \neg \mathrm{}}$→ → ${\displaystyle \mathrm{\neg }}$\ →${\displaystyle }$) ) → ( → → )$$ ) {\$displaystyle \left(\lnot \pi \to \lnot \psi \right)\to \lt(\$psi $\pi \rig)}$

공리 P1은 P3, P2 및 모드 폰(증거 참조)에서 따르기 때문에 중복된다. 이 공리들은 고전적인 명제적 논리를 묘사한다; 공리 P4가 없으면 우리는 긍정적인 관계적 논리를 얻는다. 최소 논리는 공리 P4m를 대신 추가하거나$,{\displaystyle \mathrm{}}$ ¬ ${\displaystyle \varphi }$ { ${\displaystyle \lnot \pi }$을(를) $\varphi {\displaystyle }$→ $⊥$ {\$displaystyle \pi \to \bot }$로 정의함으로써 달성된다$.$

P4m.${\displaystyle }$( ${\displaystyle \varphi }$→ ${\displaystyle \psi }$)${\displaystyle }$→${\displaystyle }$(${\displaystyle }$(${\displaystyle }$→ ${\displaystyle \mathrm{\neg }\psi }$ ) →${\displaystyle \mathrm{\neg }\varphi }$ ) ${\$

직감적 논리는 긍정적인 관계적 논리에 공리 P4i와 P5i를 더하거나 최소한의 논리에 공리 P5i를 더함으로써 달성된다. P4i와 P5i 모두 고전적인 명제 논리의 이론이다.

P4i. (${\displaystyle \varphi }$→ ${\displaystyle \mathrm{\neg }}$ ${\displaystyle \varphi }$)${\displaystyle }$→ ${\displaystyle \mathrm{\neg }}$ ${\displaystyle$ {\$phi \left(\phi \to$ \$lnot$\phi $\right)\lnot \phi$\}

P5i. $\neg {\displaystyle \mathrm{}}$ ${\displaystyle \varphi }$→ (${\displaystyle \varphi }$→ ${\displaystyle \psi }$) ${\$\lnot \$pi \to \psi \right}$

이것들은 공리의 많은 구체적인 예를 나타내는 공리 체계라는 점에 유의한다. 예를 들어 P1은 특정 공리 인스턴스 $p{\displaystyle }$→ p → ${\displaystyle p}$ →$$p {\$displaystyle p\to$p$}$을${\displaystyle (}$를$){\displaystyle }$ 나타내거나${\displaystyle }$(${\displaystyle p}$ →${\displaystyle q}$ )$${\$displaystyle \p\to q\right}을($를) 나타낼 수 있다:$$$\varphi {\displaystyle }$ ${\displaystystylement \pi$}은$$ 공식을 배치할 수 있는 곳이다. 이와 같은 변수를 공식에 걸쳐서 '스케줄 변수'라고 한다.

획일적인 대체(미국)의 두 번째 규칙으로 우리는 이러한 각각의 공리 체계들을 하나의 공리로 바꿀 수 있고, 우리가 말하는 대체 공리화라고 하는 것을 얻기 위해 어떤 공리론에서 언급되지 않은 어떤 명제적 변수로 각 개략적 변수를 대체할 수 있다. 두 공식 모두 변수가 있지만, 일률 공리화에는 논리의 언어 밖에 있는 개략적 변수가 있는 경우, 대체 공리화에는 대체 공리화를 사용하는 규칙으로 공식에 걸친 변수의 개념을 표현함으로써 동일한 작업을 수행하는 명제적 변수를 사용한다.

US. ${\displaystyle \varphi }$( p${\displaystyle }$) ${\displaystyle \pi (p)}$을(를) 하나 이상의 제안 변수 $p{\displaystyle }$ ${\$displaystyle p$\}$의 인스턴스를 $포함$하는 공식으로 하고, be$$ ${\displaysty \psi}$을(를) 다른 공식으로$$ 한다. 그런 다음 $\varphi {\displaystyle }$( ${\displaystyle p}$) ${\displaystyle \pi (p)}$에서$$$\varphi {\displaystyle }$ (${\displaystyle \psi )}$ ${\displaystyle \pi$(\$psi )}$을(를) 추론하십시오$.$^{[dubious – discuss]}

다음 세 가지 논리 공리 체계는 범용 정량자를 추가, 조작 및 제거하는 방법을 제공한다.

Q5. $\forall {\displaystyle \mathrm{}}$ ${\displaystyle x}$ (${\displaystyle )}$) → ${\displaystyle [}$ [ ${\displaystyle x}$:= ${\displaystyle t}$]$${\$displaystyle \forall$ x$\left(\phi \right)\\pi[x:=t]}$로, 여기서$$ t는 ${\displaystyle \varphi }$ ${\displaysty \,\\pi }$에서 x를 대체할 수 있다.

${\displaystyle \mathrm{Q6}}$. $∀$ x (${\displaystyle \varphi }$→ $ψ$ )${\displaystyle }$→${\displaystyle \forall \mathrm{}}$ x (${\displaystyle }$(${\displaystyle }$)${\displaystyle \to }$ ${\displaystyle \mathrm{\forall }}$ ${\displaystyle x}$ ${\displaystyle (\psi }$ )${\$ x$\좌$)(\$phi \rift(\$phi $\rig)\우)}$

Q7. $\varphi {\displaystyle }$→ ${\displaystyle \mathrm{\forall }}$ x (${\displaystyle \varphi }$ ) ${\$여기서 x는 $\varphi {\displaystyle }$ ${\displaystyle \pi }$에서 사용할 수 없음$.$

이 세 가지 추가 규칙은 명제 체계를 고전적 술어 논리학으로 확장시킨다. 마찬가지로 이 세 가지 규칙은 직관적 명제 논리(P1-3, P4i, P5i)에 대한 시스템을 직관적 술어 논리까지 확장시킨다.

범용 계량화는 흔히 일반화의 추가 규칙(메타테오렘의 섹션 참조)을 이용한 대체 공리화가 주어지는데, 이 경우 규칙 Q6와 Q7은 중복된다.^{[dubious – discuss]}

동일성 기호를 포함하는 공식으로 작업하려면 최종 공리계획이 필요하다.

$모든{\displaystyle }$ 변수 x에 대해$$ ${\displaystyle \mathrm{I8}}$. x${\displaystyle }$= x ${\displaystyle$ x$=x}$

${\displaystyle I9}$.${\displaystyle }$( x${\displaystyle }$= ${\displaystyle y}$)${\displaystyle }$→ (${\displaystyle \varphi }$ [ ${\displaystyle z}$:= ${\displaystyle x}$ ${\displaystyle ]}$→ ${\displaystyle \varphi }$[ ${\displaystyle z}$ ${\displaystyle :=}$ y${\displaystyle ]}$ ${\$

보수연장

힐버트식 공제 시스템에는 함축과 부정의 공리만을 포함하는 것이 일반적이다. 이러한 공리들을 감안할 때, 추가 접속사 사용을 허용하는 공제 정리의 보수적인 확장을 형성할 수 있다. 이러한 확장을 보수적인 것으로 부르는 이유는 새로운 결합체를 포함하는 공식 φ이 부정, 함축, 보편적 정량화만을 포함하는 논리적으로 동등한 공식 θ으로 다시 쓰여진다면 φ은 원래 시스템에서 θ이 파생될 수 있는 경우에만 확장된 시스템에서 파생될 수 있기 때문이다. 완전히 확장되면 힐버트식 시스템은 자연 공제의 시스템과 더 밀접하게 유사할 것이다.

실존적 정량화

• 소개

${\displaystyle \forall x(\phi \to \phi [x:=y])}$

• 제거

${\displaystyle \mathrm{\forall }}$ ${\displaystyle x}$ (${\displaystyle \varphi }$ →${\displaystyle \psi }$ )${\displaystyle }$→ ${\displaystyle \mathrm{\exists }}$ x${\displaystyle }$(${\displaystyle \varphi }$ ${\displaystyle )}$→ → (ϕ ) → $ψ (\phi \to$\ \ $)\to$\ \ x$(\phi )\to$ \$phote$ \to \phy \$to$ \to$$\} }} }의 $자유$ 변수가 아닌$$ $경우$ x$$${\displaystaystystypaystypecon$

접속과 분리

• 결합소개 및 제거

소개: $\alpha {\displaystyle }$→ ${\displaystyle \beta }$→ ${\displaystyle \alpha }$ ${\displaystyle \to$\to \$to$ \$to$\to \to \to \to \to $\land \$

제거 왼쪽: $\alpha {\displaystyle }$ ${\displaystyle \wedge }$ ${\displaystyle \beta }$ →${\displaystyle \alpha }$ ${\displaystyle \alpha \wedge \beta$ \beta $\to \alpha}$

제거권: $\alpha {\displaystyle }$ ${\displaystyle \wedge }$ ${\displaystyle \beta }$→ ${\displaystyle \beta }$ ${\displaystyle \alpha \wedge \beta$ \beta $\to \beta }$

• 분리 소개 및 제거

소개 왼쪽: $\alpha {\displaystyle }$→${\displaystyle \alpha }$ α ${\displaystyle \beta }$ ${\displaystyle \to \to$ \$to$ \$ve$\cHBE$\cHB$}

소개권: $\beta {\displaystyle }$→${\displaystyle \alpha }$ β$$ {\$displaystyle$\to $\to$ \$to$ \$ve$\ve $\cHB }$

제거:${\displaystyle }$(${\displaystyle \alpha }$→ ${\displaystyle \gamma }$)${\displaystyle }$→${\displaystyle }$(${\displaystyle \beta }$ →${\displaystyle \gamma }$)${\displaystyle }$→ ${\displaystyle \alpha }$ ${\displaystyle \vee }$ ${\displaystyle \beta }$ → $γ${ β β${\displaystyle }$β β { { { { { {$\to \to \to$\to \to \to \to \to \to \$ve \to$ \$to$\}

메타테오렘스

힐버트식 시스템은 공제 규정이 거의 없기 때문에, 새로운 공제 규칙을 사용한 공제는 원래 공제 규칙만을 사용하여 공제로 전환될 수 있다는 점에서 추가 공제 규칙이 연역력을 추가하지 않는다는 것을 보여주는 메타테옴을 증명하는 것이 일반적이다.

이러한 형태의 일반적인 전이법은 다음과 같다.

• 공제 정리: $\gamma {\displaystyle \mathrm{};}$ ${\displaystyle \varphi }$ ${\displaystyle ⊢}$ { {$${ {\$displaystyle \Gamma ;\pi \vdash \psi }$ $만약$ 그렇다면 → →${\displaystyle \to }$ → ${\displaystyle \psi }$ { $\displaystyle \Gamma \vdash \phi$ \$to \psi$
• ${\displaystyle \Gamma \vdash \phi \leftrightarrow \psi }$ if and only if ${\displaystyle \Gamma \vdash \phi \to \psi }$ and ${\displaystyle \Gamma \vdash \psi \to \phi }$.
• 대조: $만약$ ${\displaystyle ;}$ ;${\displaystyle }$; { { { \ \$$\$displaystyle \Gamma ;\phi$ \$vdash \psi }$ } ¬${\displaystyle \mathrm{\neg }}$ ${\displaystyle \{}$ { { {\$displaystyle \lnot \psi \vdash$ \$lnot \pi$
• 일반화: $\gamma {\displaystyle \mathrm{}}$ ${\displaystyle ⊢}$ ${\displaystyle$ \$Gamma \vdash \phi$ $}$과$($와) x가$$$display$ {\displaystyle $\$${\displaystyle \mathrm{Gamma}}$ \$vdash \fr$ for all $x\phi$의 어떤 공식에서도 무료로 발생하지 않으면$$ $\gamma {\displaystyle \mathrm{}}$ γ \ \ ${\displaystyle \backslash }$ ${\displaystyle \mathrm{\backslash }}$ \ \ \ \ \ \ \ \ \ \ \ \${\displaystyle v}$ \\$displaystal$ \dma \$vdma$\display \vdma.

몇 가지 유용한 이론과 그 증거들

다음은 명제논리의 몇 가지 이론과 그 증명(또는 다른 기사의 이 증명들에 대한 링크)이다. (P1) 자체는 다른 공리를 사용하여 증명될 수 있으므로, 사실 (P2)와 (P3) 그리고 (P4)는 이러한 모든 이론들을 증명하는 것으로 충분하다는 점에 유의한다.

(HS1)${\displaystyle }$(${\displaystyle q}$→ r${\displaystyle }$)${\displaystyle }$→${\displaystyle (}$p${\displaystyle }$→ ${\displaystyle q}$ ${\displaystyle )}$→ (p → q ) → ${\displaystyle (p}$→ ${\displaystyle r}$)${\displaystyle (q\to r)\to (p\to r)}}$ $$- 가설적 삼단논법, 증거 참조.

(L1) $p{\displaystyle }$→${\displaystyle }$(${\displaystyle p}$→ ${\displaystyle q}$ ${\displaystyle )}$→ ${\displaystyle q}$) ${\displaystyle p\to ((p\to q)\to q)}$ -$$ 증명:

(1)${\displaystyle }$(${\displaystyle }$( p${\displaystyle }$→$$)${\displaystyle }$→${\displaystyle }$( ${\displaystyle p}$→ ${\displaystyle q}$ ${\displaystyle )}$→${\displaystyle }$(${\displaystyle }$(${\displaystyle p}$ →${\displaystyle }$q${\displaystyle }$) →${\displaystyle p}$ ) → (${\displaystyle }$p → q${\displaystyle }$)${\displaystyle }$→ (${\displaystyle p}$ →${\displaystyle }$q ${\displaystyle )}$ → ($p$→ $)}$ {\$displaystyle$(($p\to q)\to(p\to q)\to$ ($p3)}}}$의 (P3)의 인스턴스)

(2)${\displaystyle }$( ${\displaystyle p}$→ ${\displaystyle q}$)${\displaystyle }$→${\displaystyle }$( p${\displaystyle }$→ ${\displaystyle q}$) ${\displaystyle (p\to q)\to (p\to q)}($p\to q)}($$의 경우)

(3)${\displaystyle }$(${\displaystyle }$(${\displaystyle p}$→ ${\displaystyle q}$ ${\displaystyle )}$→ ${\displaystyle p}$)${\displaystyle }$→${\displaystyle (p}$→ ${\displaystyle q}$)${\displaystyle }$→ (p → ${\displaystyle q}$ )$()\displaystyle ($ $(p\to q)\to p)}}$ $$(($2),$ (1) modus ponens)

(4) ${\displaystyle (((p\to q)\to p)\to ((p\to q)\to q))\to ((p\to ((p\to q)\to p))\to (p\to ((p\to q)\to q)))}$ (instance of (HS1))

(5)${\displaystyle }$( ${\displaystyle p}$→${\displaystyle q}$)${\displaystyle }$→ ( ${\displaystyle p}$ →${\displaystyle q}$ ${\displaystyle )}$→${\displaystyle }$(${\displaystyle }$p${\displaystyle }$→ ${\displaystyle q}$) ${\displaystyle \to }$ ( ${\displaystyle p}$ →${\displaystyle q}$ ${\displaystyle )\}}$ ${\displaystyle (p\to$(p$\to q)\to$ (p$\to q)}}($$3$)부터 (4) 모듀스폰으로)

(6) $p{\displaystyle }$→${\displaystyle }$(${\displaystyle }$( p${\displaystyle }$→${\displaystyle q}$) →${\displaystyle p}$ ) ${\displaystyle p\to ((p\to q)\to$ p$)}($ (P2)의 인스턴스)

(7) $p{\displaystyle }$→${\displaystyle }$(${\displaystyle p}$→ ${\displaystyle q}$ ${\displaystyle )}$→ ${\displaystyle q}$ ${\displaystyle )}$ ${\displaystyle p\to ((p\to q)\to q)}(($6)부터, (5) modus ponens까지)

다음의 두 가지 이론은 함께 이중 부정이라고 알려져 있다.

(DN1) ${\displaystyle \mathrm{}}$ ${\displaystyle \mathrm{\neg }}$ ${\displaystyle p}$→ ${\displaystyle p}$ ${\displaystyle \neg \neg p\to p}$

(DN2) $p{\displaystyle }$→ ${\displaystyle \mathrm{\neg }}$ ${\displaystyle p}$ ${\displaystyle p\to \neg \neg p}$

증거를 보다.

(L2)${\displaystyle }$(${\displaystyle p}$→${\displaystyle }$(${\displaystyle q}$→ ${\displaystyle r}$)${\displaystyle }$→${\displaystyle }$(${\displaystyle q}$ ${\displaystyle \to }$ r ) → (${\displaystyle }$q → ( ${\displaystyle p}$→ r${\displaystyle }$) )$}$ {\$displaystyle (p\to$r)\$to (q\$to r$)\to ($p$\to$ r$)}$ $$- 이 증빙을 위해 우리는 가상의 삼단법의 방법을 다음과 같은 몇 가지 증명 단계를 위한 속기로 사용한다.

(1)${\displaystyle }$(${\displaystyle p}$→ (${\displaystyle q}$ →${\displaystyle r}$) →${\displaystyle }$(${\displaystyle p}$→ ${\displaystyle q}$)${\displaystyle }$→ ( p → q ) →${\displaystyle }$( ${\displaystyle p}$→ ${\displaystyle r)\}}$ ${\displaystyle (p\to r)\to (p\to r$)\$to (p\to$ r$)}}($P3)의 경우)$$

(2)${\displaystyle }$(${\displaystyle }$( ${\displaystyle p}$→ ${\displaystyle q}$)${\displaystyle }$→${\displaystyle }$( p${\displaystyle }$→ ${\displaystyle r}$)${\displaystyle }$→${\displaystyle }$(${\displaystyle q}$→${\displaystyle }$( p${\displaystyle }$→ ${\displaystyle q}$) → (${\displaystyle q}$ →${\displaystyle q}$ )${\displaystyle }$→${\displaystyle }$( ${\displaystyle p}$ r${\displaystyle }$)${\displaystyle }$) $()\displaystyle$ ( $((p\to q)\to (p\to$ r$))\to ())}}}$ (HS1)의 인스턴스)$$

(3)${\displaystyle }$( ${\displaystyle p}$→ (${\displaystyle q}$ →${\displaystyle r}$)${\displaystyle }$→${\displaystyle }$(${\displaystyle q}$→ (${\displaystyle p}$ →${\displaystyle q}$) → ( ${\displaystyle p}$ → q )${\displaystyle }$→ (${\displaystyle p}$→ ${\displaystyle r}$)${\displaystyle }$) $()\displaystyle (p\to r)\to (p\to q)\to (p\to$)\to$)}}}}$ (1)부터 (2)까지 가상의 삼단계를 사용한다.

(4) ${\displaystyle ((p\to (q\to r))\to ((q\to (p\to q))\to (q\to (p\to r))))\to (((p\to (q\to r))\to (q\to (p\to q)))\to ((p\to (q\to r))\to (q\to (p\to r))))}$ (instance of (P3))

(5) ${\displaystyle ((p\to (q\to r))\to (q\to (p\to q)))\to ((p\to (q\to r))\to (q\to (p\to r)))}$ (from (3) and (4) using modus ponens)

(6) $q{\displaystyle }$→${\displaystyle }$(${\displaystyle p}$→ ${\displaystyle q}$) ${\displaystyle q\to (p\to q)}($p2의 인스턴스)

(7) (${\displaystyle q}$→${\displaystyle }$( ${\displaystyle p}$→ ${\displaystyle q}$)${\displaystyle \to }$(${\displaystyle p}$→${\displaystyle q}$→ ${\displaystyle r}$)${\displaystyle }$→${\displaystyle }$($$ ${\displaystyle \to }$ q →${\displaystyle }$q ) → ( p →${\displaystyle (q\to q)\to (p\to q)}}}$ (P2)의 인스턴스)

(8)${\displaystyle }$( ${\displaystyle p}$→ (${\displaystyle q}$ →${\displaystyle }$r${\displaystyle }$) →${\displaystyle }$(${\displaystyle q}$ ${\displaystyle \to q}$ →${\displaystyle }$q )${\displaystyle }$() ) ${\displaystyle (p\to (q\to$ r$)\to (p\to q)}$ $$(6)부터 (7)까지 모더스 포넨스를 사용하여)

(9) $({\displaystyle p}$→ ${\displaystyle (q}$→ ${\displaystyle r}$)${\displaystyle }$→${\displaystyle }$(${\displaystyle q}$ → r ) → (${\displaystyle q}$→${\displaystyle r}$)${\displaystyle }$) ${\displaystyle (p\to (q\to$ r$)\to (p\to r)}$ $$(8)부터 (5)까지 모더스 포넨스를 사용하여)

(HS2) ( ${\displaystyle p}$→ ${\displaystyle q}$ ${\displaystyle )}$→${\displaystyle }$(${\displaystyle q}$ → ${\displaystyle r}$) →${\displaystyle }$( ${\displaystyle p}$→ r${\displaystyle }$)${\displaystyle }$) ${\displaystyle (p\to q)\to (q\to$ r)\$to (p\to r)}}$ - 가설적 삼단논법의 대안 형식이다.$$ 증명:

(1) (${\displaystyle q}$→${\displaystyle r}$ )${\displaystyle }$→${\displaystyle }$(${\displaystyle }$p${\displaystyle }$→ ${\displaystyle q}$)${\displaystyle }$→${\displaystyle }$( ${\displaystyle p}$ → ${\displaystyle q}$ ) → ( ${\displaystyle p}$→ r${\displaystyle }$)${\displaystyle }$) ${\displaystyle (q\to r)\to (p\to r)}}($HS1)의 경우)

(2) ${\displaystyle ((q\to r)\to ((p\to q)\to (p\to r)))\to ((p\to q)\to ((q\to r)\to (p\to r)))}$ (instance of (L2))

(3) (${\displaystyle p}$→ ${\displaystyle q}$ ${\displaystyle )}$→${\displaystyle }$(${\displaystyle q}$→ ${\displaystyle r}$)${\displaystyle }$→${\displaystyle }$( ${\displaystyle p}$→ r${\displaystyle }$) )${\displaystyle }$) ${\displaystyle (p\to q)\to ((q\to$ r$)\to (p\to$ r$)}}}(($1) 및 (2) by modus ponens)

(TR1)${\displaystyle }$(${\displaystyle p}$→ ${\displaystyle q}$)${\displaystyle }$→ (${\displaystyle \mathrm{\neg }}$ ${\displaystyle q}$→ ${\displaystyle \mathrm{\neg }}$ ${\displaystyle p}$) ${\displaystyle (p\to q)\to (\neg q\to \neg p)}$ $$- Transplosition (\neg q\to \neg p)} - Transplosition (다른 방향은 (P4)을 참조한다.

(TR2) (${\displaystyle \mathrm{\neg }}$ ${\displaystyle p}$→ ${\displaystyle q}$)${\displaystyle }$→ (${\displaystyle \mathrm{\neg }q}$ → ${\displaystyle p}$) ${\displaystyle (\neg$ p$\to q)\to (\neg q\to p)}$ $$- 다른 형태의 전이; 증거:

(1) (${\displaystyle \mathrm{\neg }}$ ${\displaystyle p}$→ ${\displaystyle q}$)${\displaystyle }$→ (${\displaystyle \mathrm{\neg }}$ ${\displaystyle q}$→ ${\displaystyle \mathrm{\neg }}$ ${\displaystyle p}$ p${\displaystyle }$)$${\$displaystyle (\neg p\to$q)\$to (\neg \to$ \to \to)(\$neg \to$ \$neg p)}$ $$(TR1)의 인스턴스)

(2) $\neg {\displaystyle \mathrm{}}$ ${\displaystyle \mathrm{\neg }}$ ${\displaystyle p}$→ ${\displaystyle p}$ ${\displaystyle \neg \neg p\to p}$ $$(DN1)의 인스턴스)

(3) ($$${\displaystyle \mathrm{\neg }}$ $p p$→${\displaystyle }$p )${\displaystyle }$→${\displaystyle }$(${\displaystyle \mathrm{}q}$q${\displaystyle \mathrm{}}$→ ${\displaystyle \mathrm{\neg }}$ q ${\displaystyle q}$ p ) → ($q$q →$q$ q$q$ →${\displaystyle }$q q q q q q q q q q $q$ $q$ $q q$ q q $q q$ q q q q q q q q p q q q p p q q p p p p p p p ${\displaystyle p}$ p$→$ → p p p p p p p p

(4) (${\displaystyle \mathrm{\neg }}$ ${\displaystyle q}$ →${\displaystyle \mathrm{\neg }}$ ¬ ${\displaystyle p}$)${\displaystyle }$→ (${\displaystyle \mathrm{}q}$ q ${\displaystyle \to }$ ${\displaystyle p}$)$${\$displaystyle (\neg \to \neg$\neg \$p)\to (\neg q\to p)}$ $$(2), (3) by modus ponens)

(5) (${\displaystyle \mathrm{\neg }}$ p${\displaystyle }$→ ${\displaystyle q}$)${\displaystyle }$→ (${\displaystyle \mathrm{\neg }}$ ${\displaystyle q}$ ${\displaystyle \to }$ ${\displaystyle p}$) ${\displaystyle (\neg p\to q)\to (\neg q\to$ p$)}$ $$(1), (4)에서 가상의 삼단논법 메타테오렘을 사용)

(${\displaystyle \mathrm{L3}}$) (${\displaystyle \mathrm{\neg }}$ ${\displaystyle p}$→ p${\displaystyle }$)${\displaystyle }$→ ${\displaystyle p}$ ${\displaystyle (\neg p\to$ p$)\to p}$ -$$ 증명:

(1) $\neg {\displaystyle \mathrm{}}$ ${\displaystyle p}$→ (${\displaystyle \mathrm{\neg }}$ ${\displaystyle \mathrm{\neg }}$ (${\displaystyle q}$ →${\displaystyle q}$) →${\displaystyle \mathrm{}p}$p )$${\$displaystyle \neg$p\$to (\neg \to q)\to \ng$ p$)}($의 경우)

(2) (${\displaystyle \mathrm{\neg }}$ ${\displaystyle \mathrm{\neg }}$ ${\displaystyle (q}$→ ${\displaystyle q}$)${\displaystyle }$→ ${\displaystyle \mathrm{\neg }}$ p${\displaystyle }$)${\displaystyle }$→${\displaystyle }$( p${\displaystyle }$→ ${\displaystyle \mathrm{\neg }}$(${\displaystyle q}$→ ${\displaystyle q}$ )${\displaystyle \}}$ ${\displaystyle (\neg \to$ q$)\to \to (p\to q)}}($P4)의 경우)

(3) $\neg {\displaystyle \mathrm{}}$ ${\displaystyle p}$→${\displaystyle }$( p${\displaystyle }$→${\displaystyle \mathrm{}q}$→${\displaystyle q}$ )${\displaystyle \neg p\to (p\to q)}}($1) $$및 (2)에서 가상의 삼단논법 메타테오렘을 사용)

(4) ${\displaystyle (\neg p\to (p\to \neg (q\to q)))\to ((\neg p\to p)\to (\neg p\to \neg (q\to q)))}$ (instance of (P3))

(5) (${\displaystyle \mathrm{\neg }}$ ${\displaystyle p}$→ p${\displaystyle }$)${\displaystyle }$→ (${\displaystyle \mathrm{\neg }}$ ${\displaystyle p}$→ ${\displaystyle \mathrm{\neg }}$ (${\displaystyle q}$ →${\displaystyle q}$)${\displaystyle (\neg p\to$ p$)\to (\neg p\to q)}}$ $$(3)부터 (4) 모드 포넨을 사용하여)

(6) (${\displaystyle \mathrm{\neg }}$ ${\displaystyle p}$→${\displaystyle q}$→${\displaystyle q}$ )${\displaystyle }$→${\displaystyle }$(${\displaystyle q}$→${\displaystyle q}$ )${\displaystyle }$→ p${\displaystyle }$) ${\displaystyle (\neg p\to \neg (q\to q)\to$ p$)}}$ $$($p4$)의 경우)

(7) (${\displaystyle \mathrm{\neg }}$ ${\displaystyle p}$→ ${\displaystyle p}$)${\displaystyle }$→${\displaystyle }$(${\displaystyle q}$→${\displaystyle q}$ )${\displaystyle }$→ p${\displaystyle }$) ${\displaystyle (\neg p\to$ p$)\to ((q\to q)\to p)}$ $$(5)부터 (6)까지 가상의 삼단논법을 사용하여)

(8) $q{\displaystyle }$→ ${\displaystyle q}$ ${\displaystyle q\to q}($ (P1) 인스턴스)

(9) (${\displaystyle q}$→${\displaystyle q}$ )${\displaystyle }$→${\displaystyle }$( ${\displaystyle (q}$→${\displaystyle q}$ ) ${\displaystyle \to }$ p${\displaystyle }$)$$→ ${\displaystyle p}$) {\$displaystyle (q\to q$)\to $(((q\to q)\to$ p$)}}$ $$(L1)의 인스턴스)

(10)${\displaystyle }$( (${\displaystyle q}$→ ${\displaystyle q}$ ${\displaystyle )}$→ ${\displaystyle p}$)${\displaystyle }$→ p ${\displaystyle ((q\to q)\to p)\to p}$ $$(8)부터 (9)까지 (모드 폰 사용)

(11)${\displaystyle }$( ${\displaystyle \mathrm{\neg }}$ ${\displaystyle p}$→ p${\displaystyle }$)${\displaystyle }$→ ${\displaystyle p}$ ${\displaystyle (\neg p\to$ p$)\to p}$ $$(7) 및 (10)에서 가상의 삼단논법 메타테오렘을 사용하여)

대체 공리화

위의 공리 3은 우카시오비츠에게 인정된다.^[2] Frege에 의한 원래의 시스템은 공리 P2와 P3를 가지고 있었지만, 공리 P4 대신에 다른 4개의 공리를 가지고 있었다(Frege의 명제 미적분학 참조). 러셀과 화이트헤드도 5개의 명제 공리를 가진 시스템을 제안했다.

추가 연결

공리 P1, P2 및 P3은 공제 규칙모드(형식화된 직관적 명제 논리)를 가진 것으로서, 응용 프로그램 운영자와의 결합 논리 기반 결합기 I, K, S에 해당한다. 힐버트 시스템의 증거는 전투적 논리에서의 결합자 용어에 해당한다. Curry-Howard 서신을 참조하십시오.

참고 항목

• 힐베르트 시스템 목록
• 자연공제

메모들

참조

• Curry, Haskell B.; Robert Feys (1958). Combinatory Logic Vol. I. Vol. 1. Amsterdam: North Holland.
• Monk, J. Donald (1976). Mathematical Logic. Graduate Texts in Mathematics. Berlin, New York: Springer-Verlag. ISBN 978-0-387-90170-1.{{cite book}}: CS1 maint : 포스트스크립트(링크)
• Ruzsa, Imre; Máté, András (1997). Bevezetés a modern logikába (in Hungarian). Budapest: Osiris Kiadó.
• Tarski, Alfred (1990). Bizonyítás és igazság (in Hungarian). Budapest: Gondolat. 알프레드 타르스키가 선정한 진리의 의미론 논문을 헝가리어로 번역한 것이다.
• 데이비드 힐버트(1927년) "수학의 기초"는 스테판 바우어 멩글러버그와 다그핀 뢰엘레스달(pp. 464–479)이 번역한 것이다.
  • van Heijenoort, Jean (1967). From Frege to Gödel: A Source Book in Mathematical Logic, 1879–1931 (3rd printing 1976 ed.). Cambridge MA: Harvard University Press. ISBN 0-674-32449-8.
  • 힐베르트의 1927년, 이는 앞서 1925년"재단"강의(를 대신하여 서명함. 367–392)에 기초하여, 및에 대해 공리, 그리고 V#5-10, 부정#11-12의 공리, 그의 논리 정연한 ε-axiom#13, 평등을 공리계#에서는, 부품 번호 공리#16일-17일--그의Formalist"입증 이론"의 다른 필요한 요소로--e.가 17공리, 함축#1에서 4공리 선물.g. 유도 공리, 재귀 공리 등. L.E.J. 브루워의 직관주의에 대항하는 활발한 방어도 제공한다. 또한 헤르만 베일의 논평과 반박 (pp. 480–484)과 힐버트의 강의에 대한 폴 버네이(1927), 그리고 루이스젠 에그베르투스 얀 브루워의 응답 (pp. 490–495)도 볼 수 있다.
• Kleene, Stephen Cole (1952). Introduction to Metamathematics (10th impression with 1971 corrections ed.). Amsterdam NY: North Holland Publishing Company. ISBN 0-7204-2103-9.
  • 특히 IV 형식 시스템(pp. 69–85)에서 클렌은 §16 형식 기호, §17 형성 규칙, §18 자유 및 바인딩 변수(대체 포함), §19 변환 규칙(예: 모드스 포넨)을 제시하고, 이 중에서 21개의 "직접" -- 18개의 공리와 3개의 "즉각-일치" 관계를 다음과 같이 나누었다. 예언 미적분 #1-8에 대한 가정, 술어 미적분 #9-12에 대한 추가 가정, 숫자 이론 #13-21에 대한 추가 가정.

외부 링크

• Gaifman, Haim. "A Hilbert Type Deductive System for Sentential Logic, Completeness and Compactness" (pdf).
• Farmer, W. M. "Propositional logic" (pdf). 그것은 (다른 것 중) 힐버트식 공제 시스템의 일부(명제 미적분학에 제한됨)를 설명한다.