교대방향 암묵적 방법
Alternating-direction implicit method수치 선형대수학에서 교대방향 암묵적(ADI) 방법은 실베스터 행렬 방정식을 푸는 데 사용되는 반복적 방법이다.시스템 이론과 제어에서 발생하는 큰 행렬 방정식을 해결하기 위한 인기 있는 방법이며,[1] 메모리 효율적이고 팩터링된 형태로 솔루션을 구성하도록 공식화할 수 있다.[2][3]포물선과 타원형 부분 미분방정식을 수치적으로 푸는 데도 사용되며, 열전도를 모델링하고 확산방정식을 2차원 이상에서 푸는 데 사용되는 고전적인 방법이다.[4]연산자 분할 방식의 예다.[5]
행렬 방정식의 ADI
방법
ADI 방법은 X- = C 에 대략적인 용액의 열과 행 공간을 교대로 업데이트하는 2단계 반복 과정이다 하나의 ADI 반복은 다음과 같은 단계로 구성된다.[6]
. X + 1/ X2 여기서 - + 1 ) X( j+ / )= X() - j+ 1 )+
2. Solve for , where .
숫자 + , + ) 을 시프트 파라미터라고 하며, 이러한 파라미터의 선택에 따라 수렴이 강하게 좌우된다.[7][8]ADI의 번 반복을 수행하려면 초기 X ( X뿐만 아니라 시프트 파라미터 {( , ) = {\alpha }},\veta _{j},\ _{j},\beta 가 필요하다.
ADI 사용 시기
If and , then can be solved directly in using the Bartels-Stewart method.[9] A B 을(를) 포함하는 매트릭스 벡터 곱셈과 선형 해결책이 저렴하게 적용될 수 있을 때만 ADI를 사용하는 것이 유익하다.
만일 σ(A)∩ σ(B))M{M\displaystyle}의σ(M){\displaystyle \sigma(M)}스펙트럼 .[1]∅{\displaystyle \sigma(A)\cap \sigma(B)=\emptyset},σ(A) 하지만, 유해 물질 1일 허용량 검사 방법은 특히는 잘 돌아간다{\와 같이 그 방정식 한 X− XB=C{AX-XB=C\displaystyle}고유한 솔루션을 가지고 있다.경멸하다 \와 ( 은(는) 잘 분리되어 있으며, 와 B B}은는) 인 행렬이다.를 들어, A 이(가) 양수일 때 랴푸노프 X+ A = C 에 의해 이러한 가정이 충족된다.이러한 가정 하에서, 거의 최적인 이동 는 A 및 {\B}의 여러 선택 항목에 대해 알려져 있다[7][8] 또한 선행 오류 한계를 계산할 수 있으므로 구현 시 잔류 오류를 모니터링할 필요가 없다.
위의 가정이 충족되지 않는 경우에도 ADI 방법을 적용할 수 있다.차최적 이동 매개변수의 사용은 수렴에 부정적인 영향을 미칠 수 있으며 [1]수렴 또한 B 의 비정규성에 의해 영향을 받는다(때로는 유리한 경우도 있음).[10]Rational Krylov Subspace Method와 같은 [11]Krylov 아공간 방법은 일반적으로 이 설정에서 ADI보다 더 빠르게 수렴되는 것이 관찰되며,[1][3] 이것이 하이브리드 ADI-투영 방법의 개발로 이어졌다.[3]
Shift-parameter 선택 및 ADI 오류 방정식
좋은 시프트 매개변수를 찾는 문제는 비견적이다.이 문제는 ADI 오류 방정식을 조사하면 알 수 있다. 을(를) 반복한 후 오류는
( )= 을 선택하면 상대 오류에 대해 다음과 같은 바인딩이 발생한다.
여기서 \2}}은규범이다.이상적인 시프트 매개변수 집합{ j , ) = defines a rational function that minimizes the quantity . If and are normal matrices and have eigendecompositions = B V 그 다음
.
최적에 가까운 시프트 매개변수
Near-optimal 변화 매개 변수 할 때와 같이 Λ에[a, b]{\displaystyle[a,b]}과[c, d]{\displaystyle[c,d]}은 차갑간격 A⊂[a, b]{\displaystyle \Lambda_{A}\subset[a,b]}과Λ B⊂[c, d]{\displaystyle \Lambda_{B}\subset[c,d]}, 진짜 라인으로 어떤 경우에 알려져 있다.[7][8]예를 들어 Lyapunov 방정식 X+ = C 는 A 이(가) 양수일 때 이러한 가정을 만족한다이 경우 시프트 매개변수는 타원형 적분법을 사용하여 폐쇄형으로 표현할 수 있으며, 쉽게 숫자로 계산할 수 있다.
More generally, if closed, disjoint sets and , where and , are known, the optimal shift parameter selection problem is approximately solved by finding an extremal rational function 가치를 획득하는
.[8]이 근사 문제 잠재적인 theory,[12][13]에서 여러가지 결과와 관련된가 어디에 하한 정도의{\displaystyle(K,K)}(K, K)모든 합리적인 기능을 둘러싸고 Zolotarev에 의해 1877년에 E{E\displaystyle})[a, b]과 F에 해결되었다)− E.{\displaystyle F=-E.}이다[14]그 해결책 또한 wh 알려져 있다.시스템 E{\di과( F {\ F}[15]은(는 복합 평면에서 분리형 디스크다.
휴리스틱 시프트-매개 변수 전략
( ) 및 ( 에 대해 덜 알려진 경우 A B 이(가 비정규 행렬인 경우)인 경우 최적인 변속 매개 변수를 찾을 수 없을 수 있다.이 설정에서는 양호한 변속 매개변수를 생성하기 위한 다양한 전략을 사용할 수 있다.이 전략 점근 결과에 잠재적인 theory,[16]에 기반을 두고 동일한 작은 컬렉션 o.는 한 욕심 많은 approach,[17]과 순환 방법을 명확히 표현하는 것은 매트릭스의 리츠 값 A{A\displaystyle}, A− 1{\displaystyle A^{)}}, B{B\displaystyle}이며, B− 1{\displaystyle B^{)}}사용이 포함되fshift 매개변수는 수렴 공차가 충족될 때까지 재사용된다.[17][10]반복마다 동일한 시프트 파라미터를 사용할 때 ADI는 스미스의 방법이라는 알고리즘과 동일하다.[18]
인수 ADI
In many applications, and are very large, sparse matrices, and can be factored as , where = ,2 [1] 이러한 설정에서는 잠재적으로 밀도가 높은 행렬 X을(를) 명시적으로 저장하는 것이 불가능할 수 있다.A variant of ADI, called factored ADI,[3][2] can be used to compute , where . The effectiveness of factored ADI depends on whether is well-approximated by a low rank matrix.는 A 및 에 대한 다양한 가정 하에서 사실로 알려져 있다[10][8]
포물선 방정식의 ADI
역사적으로 ADI 방식은 한정된 차이를 이용해 사각지대에 놓인 2D 확산 방정식을 해결하기 위해 개발됐다.[4]매트릭스 방정식의 ADI와 달리 포물선 방정식의 ADI는 각 반복에 나타나는 이동이 시간 스텝, 확산 계수, 격자 간격과 같은 매개변수에 의해 결정되기 때문에 이동 매개변수의 선택이 필요하지 않다.매트릭스 방정식의 ADI 연결은 시스템에 대한 ADI 반복의 작용을 정상 상태에서 고려할 때 관찰할 수 있다.
예제: 2D 확산 방정식
열전도 방정식을 숫자로 푸는 전통적인 방법은 크랭크-니콜슨 방법이다.이 방법은 다차원 방정식의 매우 복잡한 집합으로 귀결되는데, 이것은 해결하는데 비용이 많이 든다.ADI 방식의 장점은 각 단계에서 풀어야 할 방정식은 구조가 단순하고 3각 행렬 알고리즘으로 효율적으로 풀 수 있다는 점이다.
선형 확산 방정식을 2차원으로 고려한다.
암묵적 크랭크-니콜슨 방법은 다음과 같은 유한 차이 방정식을 생성한다.
여기서:
및 2}}은 p-th 좌표에 대한 중앙 두 번째 차이 연산자임
= 또는 및 은 격자점, j) 의 속기어).
안정성 분석을 수행한 후 이 방법은 모든 t{\ t에 대해 안정적이라는 것을 알 수 있다
크랭크-니콜슨 방법의 단점은 위 방정식의 매트릭스가 일반적으로 상당히 큰 밴드 너비로 밴딩된다는 것이다.이는 선형 방정식 시스템의 직접적인 해답을 상당히 비싸게 만든다(예를 들어, 불완전한 숄스키 인수화로 전제된 결합 구배법의 사용과 같은 효율적인 근사 해법이 존재함).
ADI 방법의 이면에 있는 아이디어는 유한 차이 방정식을 둘로 나누는 것이다. 하나는 암시적으로 취한 x-분열이고 다른 하나는 암시적으로 취한 y-분열이다.
관련 방정식의 체계는 대칭과 삼지각형(대역 3)이며, 일반적으로 삼지각 행렬 알고리즘을 사용하여 해결된다.
이 방법은 시공간적으로 무조건 안정적이고 제2의 순서임을 알 수 있다.[19]더글러스 방법이나 [20]3차원 이상에 사용할 수 있는 f-인자 방법[21] 등 보다 정교한 ADI 방법이 있다.
일반화
운영자 분할 체계로서의 ADI 방법의 사용은 일반화될 수 있다.즉, 우리는 일반적인 진화 방정식을 고려할 수 있다.
여기서 및 }}는 Banach 공간에 정의된 (비선형 비선형)[22][23] 연산자다.위의 확산 예에서 1= 2 2}} 및 = 2 {\2} y
기본 ADI(FADI)
ADI와 FADI 간 단순화
기존 ADI 방식을 왼쪽에만 유사 운영자를 두고 오른쪽에는 운영자가 없는 기본 ADI 방식으로 단순화할 수 있다.이것은 일반적으로 방정식의 양쪽에 있는 연산자로 구성되는 대부분의 전통적인 암묵적 방법과 달리 우측에 더 이상 연산자(축소될)가 없는 [24][25]ADI 방법의 근본적(기본적) 체계로 간주될 수 있다.FADI 방법은 기존 ADI 방법의 정확성을 저하시키지 않고 보다 단순하고 간결하며 효율적인 업데이트 방정식으로 이어진다.
다른 암묵적 방법에 대한 관계
피스맨-래크포드, 더글라스-건, 디야코노프, 빔-와밍, 크랭크-니콜슨 등에 의한 많은 고전적 암묵적 방법들은 운영자가 없는 우측을 가진 기본적인 암묵적 방법으로 단순화할 수 있다.[25]그 기본 형태에서 2차 시간 정확도의 FADI 방법은 3차원의 맥스웰 방정식과 같이 2차원의 시간 정확도로 업그레이드할 수 있는 기본적인 국소 1차원(FLOD) 방법과 밀접하게 관련될 수 있다.2차원 및 3차원 열전도 및 확산 방정식의 경우 FADI 및 FLOD 방법 모두 기존 방법에 비해 단순하고 효율적이며 안정적인 방법으로 구현할 수 있다.[28][29]
참조
- ^ a b c d e Simoncini, V. (2016). "Computational Methods for Linear Matrix Equations". SIAM Review. 58 (3): 377–441. doi:10.1137/130912839. hdl:11585/586011. ISSN 0036-1445. S2CID 17271167.
- ^ a b Li, Jing-Rebecca; White, Jacob (2002). "Low Rank Solution of Lyapunov Equations". SIAM Journal on Matrix Analysis and Applications. 24 (1): 260–280. doi:10.1137/s0895479801384937. ISSN 0895-4798.
- ^ a b c d Benner, Peter; Li, Ren-Cang; Truhar, Ninoslav (2009). "On the ADI method for Sylvester equations". Journal of Computational and Applied Mathematics. 233 (4): 1035–1045. Bibcode:2009JCoAM.233.1035B. doi:10.1016/j.cam.2009.08.108. ISSN 0377-0427.
- ^ a b Peaceman, D. W.; Rachford Jr., H. H. (1955), "The numerical solution of parabolic and elliptic differential equations", Journal of the Society for Industrial and Applied Mathematics, 3 (1): 28–41, doi:10.1137/0103003, hdl:10338.dmlcz/135399, MR 0071874.
- ^ *Press, W. H.; Teukolsky, S. A.; Vetterling, W. T.; Flannery, B. P. (2007). "Section 20.3.3. Operator Splitting Methods Generally". Numerical Recipes: The Art of Scientific Computing (3rd ed.). New York: Cambridge University Press. ISBN 978-0-521-88068-8.
- ^ Wachspress, Eugene L. (2008). "Trail to a Lyapunov equation solver". Computers & Mathematics with Applications. 55 (8): 1653–1659. doi:10.1016/j.camwa.2007.04.048. ISSN 0898-1221.
- ^ a b c Lu, An; Wachspress, E.L. (1991). "Solution of Lyapunov equations by alternating direction implicit iteration". Computers & Mathematics with Applications. 21 (9): 43–58. doi:10.1016/0898-1221(91)90124-m. ISSN 0898-1221.
- ^ a b c d e Beckermann, Bernhard; Townsend, Alex (2017). "On the Singular Values of Matrices with Displacement Structure". SIAM Journal on Matrix Analysis and Applications. 38 (4): 1227–1248. arXiv:1609.09494. doi:10.1137/16m1096426. ISSN 0895-4798. S2CID 3828461.
- ^ Golub, G.; Van Loan, C (1989). Matrix computations (Fourth ed.). Baltimore: Johns Hopkins University. ISBN 1421407949. OCLC 824733531.
- ^ a b c Sabino, J (2007). Solution of large-scale Lyapunov equations via the block modified Smith method. PhD Diss., Rice Univ. (Thesis). hdl:1911/20641.
- ^ Druskin, V.; Simoncini, V. (2011). "Adaptive rational Krylov subspaces for large-scale dynamical systems". Systems & Control Letters. 60 (8): 546–560. doi:10.1016/j.sysconle.2011.04.013. ISSN 0167-6911.
- ^ Saff, E.B.; Totik, V. (2013-11-11). Logarithmic potentials with external fields. Berlin. ISBN 9783662033296. OCLC 883382758.
- ^ Gonchar, A.A. (1969). "Zolotarev problems connected with rational functions". Mathematics of the USSR-Sbornik. 7 (4): 623–635. Bibcode:1969SbMat...7..623G. doi:10.1070/SM1969v007n04ABEH001107.
- ^ Zolotarev, D.I. (1877). "Application of elliptic functions to questions of functions deviating least and most from zero". Zap. Imp. Akad. Nauk. St. Petersburg. 30: 1–59.
- ^ Starke, Gerhard (July 1992). "Near-circularity for the rational Zolotarev problem in the complex plane". Journal of Approximation Theory. 70 (1): 115–130. doi:10.1016/0021-9045(92)90059-w. ISSN 0021-9045.
- ^ Starke, Gerhard (June 1993). "Fejér-Walsh points for rational functions and their use in the ADI iterative method". Journal of Computational and Applied Mathematics. 46 (1–2): 129–141. doi:10.1016/0377-0427(93)90291-i. ISSN 0377-0427.
- ^ a b Penzl, Thilo (January 1999). "A Cyclic Low-Rank Smith Method for Large Sparse Lyapunov Equations". SIAM Journal on Scientific Computing. 21 (4): 1401–1418. doi:10.1137/s1064827598347666. ISSN 1064-8275.
- ^ Smith, R. A. (January 1968). "Matrix Equation XA + BX = C". SIAM Journal on Applied Mathematics. 16 (1): 198–201. doi:10.1137/0116017. ISSN 0036-1399.
- ^ Douglas, Jr., J. (1955), "On the numerical integration of uxx+ uyy= ut by implicit methods", Journal of the Society for Industrial and Applied Mathematics, 3: 42–65, MR 0071875.
- ^ Douglas Jr., Jim (1962), "Alternating direction methods for three space variables", Numerische Mathematik, 4 (1): 41–63, doi:10.1007/BF01386295, ISSN 0029-599X, S2CID 121455963.
- ^ Chang, M. J.; Chow, L. C.; Chang, W. S. (1991), "Improved alternating-direction implicit method for solving transient three-dimensional heat diffusion problems", Numerical Heat Transfer, Part B: Fundamentals, 19 (1): 69–84, Bibcode:1991NHTB...19...69C, doi:10.1080/10407799108944957, ISSN 1040-7790.
- ^ Hundsdorfer, Willem; Verwer, Jan (2003). Numerical Solution of Time-Dependent Advection-Diffusion-Reaction Equations. Berlin, Heidelberg: Springer Berlin Heidelberg. ISBN 978-3-662-09017-6.
- ^ Lions, P. L.; Mercier, B. (December 1979). "Splitting Algorithms for the Sum of Two Nonlinear Operators". SIAM Journal on Numerical Analysis. 16 (6): 964–979. Bibcode:1979SJNA...16..964L. doi:10.1137/0716071.
- ^ Tan, E. L. (2007). "Efficient Algorithm for the Unconditionally Stable 3-D ADI-FDTD Method" (PDF). IEEE Microwave and Wireless Components Letters. 17 (1): 7–9. doi:10.1109/LMWC.2006.887239. S2CID 29025478.
- ^ a b Tan, E. L. (2008). "Fundamental Schemes for Efficient Unconditionally Stable Implicit Finite-Difference Time-Domain Methods" (PDF). IEEE Transactions on Antennas and Propagation. 56 (1): 170–177. arXiv:2011.14043. Bibcode:2008ITAP...56..170T. doi:10.1109/TAP.2007.913089. S2CID 37135325.
- ^ Tan, E. L. (2007). "Unconditionally Stable LOD-FDTD Method for 3-D Maxwell's Equations" (PDF). IEEE Microwave and Wireless Components Letters. 17 (2): 85–87. doi:10.1109/LMWC.2006.890166. S2CID 22940993.
- ^ Gan, T. H.; Tan, E. L. (2013). "Unconditionally Stable Fundamental LOD-FDTD Method with Second-Order Temporal Accuracy and Complying Divergence" (PDF). IEEE Transactions on Antennas and Propagation. 61 (5): 2630–2638. Bibcode:2013ITAP...61.2630G. doi:10.1109/TAP.2013.2242036. S2CID 7578037.
- ^ Tay, W. C.; Tan, E. L.; Heh, D. Y. (2014). "Fundamental Locally One-Dimensional Method for 3-D Thermal Simulation". IEICE Transactions on Electronics. E-97-C (7): 636–644. Bibcode:2014IEITE..97..636T. doi:10.1587/transele.E97.C.636.
- ^ Heh, D. Y.; Tan, E. L.; Tay, W. C. (2016). "Fast Alternating Direction Implicit Method for Efficient Transient Thermal Simulation of Integrated Circuits". International Journal of Numerical Modelling: Electronic Networks, Devices and Fields. 29 (1): 93–108. doi:10.1002/jnm.2049.





 시프트 파라미터라고 하며, 이러한 파라미터의 선택에 따라 수렴이 강하게 좌우된다.
시프트 파라미터라고 하며, 이러한 파라미터의 선택에 따라 수렴이 강하게 좌우된다.
 필요하다.
필요하다.











 .이상적인 시프트 매개변수 집합
.이상적인 시프트 매개변수 집합
















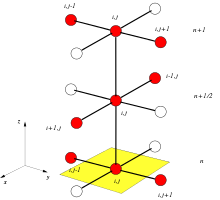









 격자점
격자점









