역학 시스템 이론
Dynamical systems theory역학 시스템 이론은 복잡한 역학 시스템의 행동을 기술하는데 사용되는 수학 영역으로, 보통 미분 방정식이나 차이 방정식을 채택함으로써 사용된다. 미분방정식을 채용하면 그 이론을 연속동력계라고 한다. 물리적 관점에서 연속 동적 시스템은 고전 역학의 일반화로서 운동 방정식이 직접 가정되고 최소 작용 원리의 오일러-라그랑주 방정식이 되도록 제약되지 않는 일반화다. 차이 방정식이 채택되면 이 이론은 이산 다이나믹 시스템이라고 불린다. 시간 변수가 일정 간격에 걸쳐 불연속적이고 다른 간격에 걸쳐 연속되는 집합에 걸쳐 실행되거나 캔터 집합과 같은 임의의 시간 집합인 경우, 시간 척도에 동적 방정식을 얻는다. 일부 상황은 미분차 방정식과 같이 혼합 연산자에 의해 모델링될 수도 있다.
이 이론은 동적 시스템의 장기적 질적 행동을 다루며, 행성의 궤도와 전자 회로의 거동 등 본질적으로 주로 기계적이거나 그 밖의 물리적인 시스템의 운동 방정식 및 생물학에서 발생하는 시스템의 특성 및 가능한 경우 그 해결책을 연구한다.로지, 경제, 그리고 다른 곳들. 현대 연구의 많은 부분이 혼란스러운 시스템 연구에 집중되어 있다.
이 연구 분야는 또한 단지 역동적인 시스템, 수학적인 역동적인 시스템 이론 또는 역동적인 시스템의 수학적 이론이라고도 불린다.
개요
역동적인 시스템 이론과 혼돈 이론은 역동적인 시스템의 장기적인 질적 행동을 다룬다이나믹 시스템 이론과 혼돈 이론은 역동적인 시스템의 장기적인 질적 행동을 다룬다. 여기서 초점은 역동적인 시스템을 정의하는 방정식에 대한 정확한 해법(흔히 절망적인 경우가 많다)을 찾는 것이 아니라, 오히려 "시스템이 장기적으로 안정된 상태로 정착할 것인가, 그렇다면 가능한 안정 상태는 무엇인가?" 또는 "시스템의 장기적 동작이 초기 콘돔에 따라 달라지는가"와 같은 질문에 대답하는 것이다.이션?"
중요한 목표는 주어진 역동적인 시스템의 고정점 또는 안정된 상태를 설명하는 것이다. 이것들은 시간이 지남에 따라 변하지 않는 변수의 값이다. 이러한 고정점 중 일부는 매력적인데, 즉 시스템이 가까운 상태에서 시작되면 고정점을 향해 수렴한다는 것을 의미한다.
마찬가지로, 사람들은 주기적인 점, 즉 몇 번의 시간 단계 후에 반복되는 시스템의 상태에 관심이 있다. 주기적인 포인트도 매력적일 수 있다. 샤르코프스키의 정리는 1차원 이산 동적 시스템의 주기적 지점 수에 관한 흥미로운 진술이다.
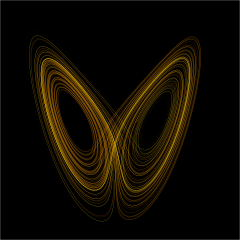
단순한 비선형 동적 시스템도 흔히 혼돈이라고 불린 겉보기에는 무작위적인 행동을 보인다.[1] 혼돈의 깨끗한 정의와 조사를 다루는 역동적 시스템의 분기를 혼돈 이론이라고 한다.
역사
역동적인 시스템 이론의 개념은 뉴턴 역학에 기원을 두고 있다. 그곳에서 다른 자연과학과 공학 분야와 마찬가지로 역동적인 시스템의 진화 법칙은 시스템의 상태를 미래에 단 짧은 시간만 주는 관계에 의해 암묵적으로 주어진다.
고속 컴퓨팅 기계가 등장하기 전에, 역동적인 시스템을 푸는 것은 정교한 수학 기법을 필요로 했고, 소수의 역동적인 시스템에 대해서만 성취될 수 있었다.
수학적 동적 시스템 이론의 훌륭한 발표로는 벨트라미(1990) 1990 루엔베르거(1979), 파둘로 & Arbib(1974), 스트로가츠(1994) 등이 있다.[2]
개념
다이너믹 시스템
동적 시스템 개념은 주변 공간에서 점 위치의 시간 의존성을 설명하는 고정된 "규칙"에 대한 수학적 공식화다. 예를 들어 시계추의 흔들림, 파이프 안의 물의 흐름, 그리고 호수에서 봄마다 물고기의 수를 설명하는 수학적 모델들이 있다.
동적 시스템은 실수의 집합에 의해 또는 보다 일반적으로 적절한 상태 공간의 점 집합에 의해 결정되는 상태를 가진다. 시스템 상태의 작은 변화는 숫자의 작은 변화에 해당한다. 이 숫자들은 기하학적 공간인 다지관의 좌표이기도 하다. 역동계의 진화 법칙은 미래의 상태가 현재 상태에서 따르는 것을 설명하는 고정 규칙이다. 규칙은 결정론적(특정 시간 간격의 경우 현재 상태에 따라 하나의 미래 상태를 정확하게 예측할 수 있음) 또는 확률론적(국가 진화는 특정 확률로만 예측할 수 있음)일 수 있다.
다이나믹리즘
인지과학이나 동적인식에서 동적 가설 또는 동적 가설이라고도 하는 동적주의는 철학자 팀 반 겔더의 업적으로 예증된 인지과학의 새로운 접근법이다. 그것은 미분 방정식이 전통적인 컴퓨터 모델보다 인지 모델링에 더 적합하다고 주장한다.
비선형 시스템
수학에서 비선형 시스템은 선형적이지 않은 시스템, 즉 중첩 원리를 만족시키지 못하는 시스템이다. 덜 기술적으로, 비선형 시스템은 해결할 변수를 독립 요소의 선형 합으로 작성할 수 없는 어떤 문제라도 된다. 독립변수의 함수의 존재와는 직선적으로 떨어져 있는 비동종계통은 엄격한 정의에 따라 비선형이지만, 그러한 시스템은 특정 해법이 알려진 한 선형계통으로 변환될 수 있기 때문에 대개 선형계통과 나란히 연구된다.
관련분야
산술역학
- 산술역학은 1990년대에 등장한 분야로 수학, 역동 시스템, 숫자 이론의 두 분야를 융합한 분야다. 고전적으로 이산 역학이란 복잡한 평면이나 실제 선의 자기맵의 반복에 관한 연구를 말한다. 산술 역학은 다항식 또는 이성 함수의 반복적 적용에 따른 정수, 이성, -adic 및/또는 대수 점의 수 이론적 특성에 대한 연구다.
혼돈 이론
- 혼돈 이론은 초기 조건에 매우 민감한 (대중적으로 나비효과라고 불리는) 역동성을 나타낼 수 있는 특정 역동적 시스템, 즉 시간이 흐름에 따라 진화하는 시스템들의 행동을 설명한다. 초기 조건에서 섭동의 기하급수적인 성장으로 나타나는 이 민감성의 결과로서, 무질서한 시스템의 동작은 무작위로 나타난다. 이러한 시스템들이 결정론적임에도 불구하고, 이는 미래의 역학이 무작위 요소 없이 초기 조건에 의해 완전히 정의된다는 것을 의미한다. 이 행동은 결정론적 혼란, 즉 단순히 혼란이라고 알려져 있다.
복잡한 시스템
- 복합체계는 자연, 사회, 과학에서 복합체로 간주되는 시스템의 공통적인 특성을 연구하는 과학 분야다. 그것은 또한 복잡한 시스템 이론, 복잡성 과학, 복잡한 시스템에 대한 연구 및/또는 복잡성의 과학이라고도 불린다. 그러한 시스템의 주요 문제점은 공식적인 모델링과 시뮬레이션의 어려움이다. 그러한 관점에서, 서로 다른 연구 맥락에서 복잡한 시스템들은 그들의 다른 속성의 기초 위에 정의된다.
- 복잡한 시스템에 대한 연구는 보다 전형적인 환원주의적 전략이 부족한 과학의 많은 분야에 새로운 활력을 불어넣고 있다. 그러므로 복잡한 시스템은 신경과학, 사회과학, 기상학, 화학, 물리학, 컴퓨터과학, 심리학, 인공생명, 진화 연산, 경제학, 지진예측, 분자생물학 및 t에 대한 문의를 포함한 많은 다양한 분야의 문제에 대한 연구접근법을 포괄하는 넓은 용어로 자주 사용된다.살아있는 세포 자체의 특성.
제어 이론
에고다이즘
기능분석
- 기능분석(functional analysis)은 수학, 특히 분석의 한 분야로, 벡터 공간과 이에 작용하는 연산자의 연구와 관련이 있다. 그것은 기능 공간, 특히 푸리에 변환과 같은 기능의 변환과 미분방정식과 적분방정식의 연구에 역사적 뿌리를 두고 있다. 함수라는 단어의 이 용법은 변동의 미적분학으로 거슬러 올라가며, 그 주장이 함수인 함수를 암시한다. 일반적으로 그것의 용도는 수학자 및 물리학자 비토 볼테라(Vito Volterra)에 기인하고 있으며, 그것의 창시지는 수학자 스테판 바나흐(Stefan Banach)에 기인하는 것이 크다.
그래프 역학 시스템
- GDS(Graph Dynamic System)의 개념은 그래프나 네트워크에서 일어나는 광범위한 프로세스를 포착하는 데 사용될 수 있다. 그래프 동적 시스템의 수학적 및 계산적 분석에서 주요 주제는 구조 특성(예: 네트워크 연결)과 그로 인해 발생하는 글로벌 역학을 연관시키는 것이다.
예상 동력학 시스템
- 투영된 동적 시스템은 솔루션이 제약조건 집합으로 제한되는 동적 시스템의 동작을 연구하는 수학 이론이다. 이 부문은 최적화 및 평형 문제의 정적 세계와 일반 미분 방정식의 역동적 세계와의 연결을 공유한다. 투영된 동적 시스템은 투영된 미분 방정식에 대한 흐름에 의해 주어진다.
상징역학
- 심볼 역학이란 시프트 운영자가 제공하는 역학(진화)으로 시스템 상태에 해당하는 추상 기호들의 무한 시퀀스로 구성된 이산 공간에 의해 위상학적이거나 매끄러운 역학 시스템을 모델링하는 실천이다.
시스템 역학
- 시스템 역학은 시간의 경과에 따른 시스템의 행동을 이해하는 접근법이다. 그것은 전체 시스템의 행동과 상태에 영향을 미치는 내부 피드백 루프와 시간 지연을 다룬다.[3] 시스템 역학을 다른 연구 시스템 접근방식과 다르게 만드는 것은 피드백 루프와 주식 및 흐름의 사용이다. 이러한 요소들은 겉보기에는 단순한 시스템조차 어떻게 비선형성을 당황하게 하는지 설명하는 데 도움이 된다.
위상역학
- 위상역학(topological dynamics)은 다이너믹 시스템의 질적, 무증상적 특성을 일반 위상의 관점에서 연구한 동적 시스템 이론의 한 분야다.
적용들
생체역학에서
스포츠 생체역학에서 역동적인 시스템 이론은 운동 과학에서 운동 경기와 효율을 모델링하는 실행 가능한 프레임워크로 등장했다. 역동적인 시스템 관점에서 볼 때, 인간 이동 시스템은 다수의 상호작용 요소(예: 혈액 세포, 산소 분자, 근육 조직, 대사 효소, 결합 조직, 보)로 구성된 공동의존적인 하위 시스템(호흡기, 순환기, 신경, 편심, 지각)의 매우 복잡한 네트워크다.ne). 역동적 시스템 이론에서 이동 패턴은 물리적 및 생물학적 시스템에서 발견되는 자기 조직의 일반적인 과정을 통해 나타난다.[4] 이 프레임워크의 개념적 적용과 관련된 청구에 대한 연구 검증은 없다.
인지과학에서
신경과학과 인지발달 분야, 특히 인지발달의 신피아제트 이론에 역동적인 시스템 이론이 적용되어 왔다. 구문이나 AI에 기반한 이론보다는 물리적 이론으로 가장 잘 대변되는 것이 인지 발달이라는 믿음이다. 또한 미분방정식이 인간의 행동을 모델링하는 데 가장 적절한 도구라고 믿었다. 이 방정식들은 주 공간을 통과하는 주체의 인지 궤적을 나타내는 것으로 해석된다. 즉, 동적주의자들은 심리학이 특정한 환경적, 내부적 압력 하에서 작용자의 인식과 행동에 대한 설명이어야 한다고 주장한다. 혼돈 이론의 언어 또한 자주 채택된다.
그 속에서 학습자의 마음은 오래된 패턴이 허물어진 불안정한 상태에 도달한다. 이것이 인지 발달의 단계적 전환이다. 활동 수준이 서로 연결되면서 자기 조직화(일관적인 형태의 자발적인 생성)가 시작된다. 새로 형성된 거시적이고 미시적인 구조물이 서로를 지지하며 속도를 낸다. 이러한 연결고리는 가리비(복잡한 수행의 반복적인 구축과 붕괴)라는 과정을 통해 마음속의 새로운 질서의 구조를 형성한다. 이 새롭고 새로운 상태는 진보적이고 이산적이며 특이하며 예측할 수 없다.[5]
동적 시스템 이론은 최근에 A-not-B 오류로 언급되는 아동 발달에서 오래 전부터 알고 있던 문제를 설명하기 위해 사용되었다.[6]
제2언어발달에서
제2언어 습득을 연구하기 위한 동적 시스템 이론의 적용은 1997년 다이앤 라슨 프리먼이 제2언어 습득을 언어 습득뿐만 아니라 언어 소모도 포함하는 발달 과정으로 보아야 한다고 주장한 기사를 게재한 데 기인한다.[7] 그녀는 기사에서 언어는 역동적이고, 복잡하고, 비선형적이며, 무질서하고, 예측 불가능하며, 초기 조건에 민감하고, 개방적이고, 자기 조직적이며, 피드백에 민감하고, 적응적인 동적 시스템으로 보아야 한다고 주장했다.
참고 항목
- 관련 과목
- 관련 과학자
메모들
- ^ Grebogi, C.; Ott, E.; Yorke, J. (1987). "Chaos, Strange Attractors, and Fractal Basin Boundaries in Nonlinear Dynamics". Science. 238 (4827): 632–638. Bibcode:1987Sci...238..632G. doi:10.1126/science.238.4827.632. JSTOR 1700479. PMID 17816542. S2CID 1586349.
- ^ 제롬 R. Busemeyer(2008), "다이내믹 시스템". 등장인물: 맥밀란 인지과학 백과사전 2008년 5월 8일 검색됨 2008년 6월 13일 웨이백 머신에 보관
- ^ MIT SDEP(System Dynamics in Education Project) 2008-05-09 Wayback Machine에 보관
- ^ Paul S Glazier, Keith Davids, Roger M Bartlett(2003). "다이나믹 시스템 이론: 성능 지향 스포츠 생체역학 연구를 위한 관련 프레임워크" in: Sportscience 7. 2008-05-08에 접속했다.
- ^ Lewis, Mark D. (2000-02-25). "The Promise of Dynamic Systems Approaches for an Integrated Account of Human Development" (PDF). Child Development. 71 (1): 36–43. CiteSeerX 10.1.1.72.3668. doi:10.1111/1467-8624.00116. PMID 10836556. Retrieved 2008-04-04.
- ^ Smith, Linda B.; Esther Thelen (2003-07-30). "Development as a dynamic system" (PDF). Trends in Cognitive Sciences. 7 (8): 343–8. CiteSeerX 10.1.1.294.2037. doi:10.1016/S1364-6613(03)00156-6. PMID 12907229. S2CID 5712760. Retrieved 2008-04-04.
- ^ "Chaos/Complexity Science and Second Language Acquisition". Applied Linguistics. 1997.
추가 읽기
- Abraham, Frederick D.; Abraham, Ralph; Shaw, Christopher D. (1990). A Visual Introduction to Dynamical Systems Theory for Psychology. Aerial Press. ISBN 978-0-942344-09-7. OCLC 24345312.
- Beltrami, Edward J. (1998). Mathematics for Dynamic Modeling (2nd ed.). Academic Press. ISBN 978-0-12-085566-7. OCLC 36713294.
- Hájek, Otomar (1968). Dynamical systems in the plane. Academic Press. OCLC 343328.
- Luenberger, David G. (1979). Introduction to dynamic systems: theory, models, and applications. Wiley. ISBN 978-0-471-02594-8. OCLC 4195122.
- Michel, Anthony; Kaining Wang; Bo Hu (2001). Qualitative Theory of Dynamical Systems. Taylor & Francis. ISBN 978-0-8247-0526-8. OCLC 45873628.
- Padulo, Louis; Arbib, Michael A. (1974). System theory: a unified state-space approach to continuous and discrete systems. Saunders. ISBN 9780721670355. OCLC 947600.
- Strogatz, Steven H. (1994). Nonlinear Dynamics and Chaos: With Applications to Physics, Biology, Chemistry, and Engineering. Addison Wesley. ISBN 978-0-7382-0453-6. OCLC 49839504.