위상 공간

미분 방정식
Navier – 장애물 주위의 공기 흐름을 시뮬레이션하는 데 사용되는 Stokes 미분 방정식
범위
필드 자연과학 공학 기술 천문학 물리 화학 생물학 지질학 응용 수학 연속체 역학 카오스 이론 동적 시스템 사회과학 경제학 모집단 역학
분류
종류들 보통의 부분적 미분 대수 적분 미분 프랙셔널 선형 비선형 변수 유형별 종속 및 독립 변수 오토노마스 결합/분리 정확한 동종/비동종 특징들 주문 교환입니다. 표기법
프로세스와의 관계 차이(이산 아날로그) 확률적 확률적 부분 지연
솔루션
존재와 고유성 피카르-린델뢰프 정리 페아노 존재 정리 카라테오도리의 존재 정리 코시-코왈레프스키 정리
일반적인 토픽 브롱스키안 위상 세로 위상 공간 랴푸노프 / 점근 / 지수 안정성 수렴 속도 시리즈 / 통합 솔루션 수치 적분 디랙 델타 함수
해결 방법 감사 특징의 방법 오일러 지수 반응 공식 유한차이 (크랭크-니콜슨) 유한 요소 무한 요소 유한 부피 갤러킨 페트로프갈레르킨 적분 계수 통합 변환 섭동 이론 룽게쿠타 변수 분리 미결정 계수 파라미터의 변동
사람
목록. 아이작 뉴턴 조제프 푸리에 고트프리드 라이프니츠 레온하르트 오일러 에밀 피카르 유제프 마리아 호엔 브론스키 에른스트 린델뢰프 루돌프 립시츠 오귀스틴 루이 코시 존 크랭크 필리스 니콜슨 칼 다비드 톨메 룽지 마르틴 쿠타
v t

동적 시스템 이론에서 위상공간은 시스템의 모든 가능한 상태가 표현되는 공간이며, 각각의 가능한 상태는 위상공간 내의 하나의 고유한 점에 대응한다.기계 시스템의 경우 위상 공간은 일반적으로 위치 및 운동량 변수의 가능한 모든 값으로 구성됩니다.그것은 직접 공간과 상호 공간의 외적 산물이다.위상 공간의 개념은 19세기 말에 루드비히 볼츠만, 앙리 푸앵카레, 조시아 윌라드 ^[1]깁스에 의해 개발되었다.

서론

위상공간에서 시스템의 모든 자유도 또는 매개변수는 다차원 공간의 축으로 표현됩니다. 1차원 시스템은 위상선이라고 불리며, 2차원 시스템은 위상 평면이라고 불립니다.시스템의 가능한 모든 상태 또는 시스템 파라미터 값의 허용된 조합에 대해 점이 다차원 공간에 포함됩니다.시간이 지남에 따라 진화하는 시스템의 상태는 고차원 공간을 통과하는 경로(시스템에 대한 위상 공간 궤적)를 추적합니다.위상 공간 궤적은 초기 조건부터 시작하는 것과 호환되는 상태 집합을 나타내며, 초기 조건부터 시작하는 것과 호환되는 상태 집합을 나타내는 전체 위상 공간에 위치합니다.전체적으로 위상도는 시스템의 모든 기능을 나타내며, 그 모양은 시스템의 특성을 쉽게 설명할 수 있습니다.위상 공간에는 다수의 차원이 포함될 수 있습니다.예를 들어, 많은 분자를 포함하는 가스는 각 입자의 x, y 및 z 위치와 모멘타(이상화된 단원자 가스의 경우 6차원)에 대해 별도의 치수를 필요로 할 수 있으며, 보다 복잡한 분자 시스템의 경우 분자 결합의 진동 모드를 기술하기 위해 3개의 축을 중심으로 회전하기 위해 추가 치수가 필요하다.위상 공간은 로봇 팔의 움직임 범위를 분석하거나 특정 위치/운동 결과를 달성하기 위한 최적의 경로를 결정하는 것과 같이 다양한 회전 축 또는 변환 축을 따라 이동하도록 제한된 기계 시스템의 동작을 분석할 때 더 쉽게 사용할 수 있다.

켤레 모멘타

고전역학에서 위치(즉 구성공간상의 좌표)에 대한 일반화 좌표_i q의 선택은 위상공간상의 좌표를 함께 정의하는 켤레 일반화 모멘타_i p를 정의한다.보다 추상적으로 말하면, 고전역학 위상공간은 구성공간의 코탄젠트다발이며, 이 해석에서는 위의 절차가 구성공간의 로컬 좌표를 선택하면 코탄젠트 공간상의 표준 심플렉틱 구조에 대해 자연스러운 로컬 다르부 좌표를 선택할 수 있음을 나타냅니다.

위상 공간의 통계 앙상블

이 공간에서의 시스템 앙상블의 움직임은 고전 통계역학에 의해 연구된다.이러한 시스템에서 점의 국소 밀도는 Liouville의 정리에 따르며, 따라서 일정하게 받아들여질 수 있다.고전 역학에서 모델 시스템의 컨텍스트 내에서, 주어진 시간에 시스템의 위상 공간 좌표는 시스템의 모든 동적 변수로 구성됩니다.이 때문에 해밀턴이나 라그랑주 운동방정식의 적분을 통해 미래 또는 과거의 주어진 시간에 시스템의 상태를 계산할 수 있다.

예

저차원

단순한 시스템의 경우 자유도는 1~2도 정도밖에 되지 않을 수 있습니다.자유도는 단일 변수 $d{\displaystyle y}$ / ${\displaystyle d}$ t ${\displaystyle =f}$ (${\displaystyle y}$)$$, {$displaystyle$ dy$/dt=f(y)}$에 자율 상미분방정식을 가지며 결과적으로 생성되는 1차원 시스템을 위상선이라고 하며 시스템의 정성적 거동을 위상선에서 즉시 볼 수 있는 경우에 발생합니다.가장 단순하지 않은 예로는 지수 성장 모델/감소(불안한/안정적인 평형)와 로지스틱 성장 모델(평형 2개, 안정적/불안한 1개)이 있습니다.

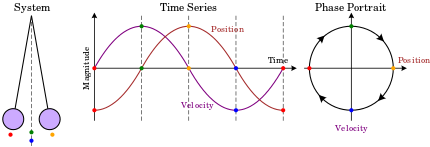
2차원 시스템의 위상 공간은 위상 평면이라고 불리며, 고전 역학에서 하나의 입자가 1차원으로 움직이며 두 변수가 위치와 속도입니다.이 경우 위상 초상화의 스케치는 다이어그램에 표시된 반데르폴 발진기의 한계 사이클과 같은 시스템의 역학에 대한 정성적 정보를 제공할 수 있습니다.

여기서 수평축은 위치와 수직축에 속도를 부여한다.시스템이 진화함에 따라 그 상태는 위상 다이어그램의 라인(트래저리) 중 하나를 따릅니다.

카오스 이론

카오스 이론의 위상 다이어그램의 고전적인 예는 다음과 같습니다.

• 로렌츠 어트랙터
• 인구 증가(예: 로지스틱 지도)
• Mandelbrot 집합이 있는 복잡한 2차 다항식의 매개변수 평면.

위상도

시간 함수로서의 위치 및 운동량 변수의 플롯은 위상도 또는 위상도라고 불리기도 합니다.그러나 후자의 표현인 "위상도"는 일반적으로 압력, 온도 및 조성으로 구성된 화학 시스템의 열역학 상의 다양한 안정성 영역을 보여주는 도표에 대해 보류되어 있다.

양자역학

양자역학에서 위상공간의 좌표 p와 q는 보통 힐베르트 공간에서 에르미트 연산자가 된다.

그러나 그것들의 함수가 (그로네월드의 1946년 별곱을 통해) 새로운 대수적 방법으로 구성된다면, 그들은 그들의 고전적 해석을 유지할 수 있다.이것은 양자역학의 불확도 원리와 일치한다.관측 가능한 모든 양자역학은 헤르만 바일(1927년)에 의해 지정되고 존 폰 노이만(1931년), 유진 위그너(1932년)에 의해 보충된 것과 같이 위상공간의 고유한 함수 또는 분포에 대응하며, 대합성에서는 HJ 그로네월드(1946년)에 의해 보충된다.J E Moyal(1949년)과 함께, 이것들은 양자 역학의 위상 공간 공식화, 완전하고 논리적으로 자율적인 양자 ^[2]역학의 재구성의 기초를 완성했다.(현대 추상화에는 변형 양자화와 기하 양자화가 포함됩니다.)

위상공간 양자화에서의 기대치는 힐버트 공간에서의 밀도 매트릭스를 갖는 트레이스 연산자 관측치와 동형상으로 구해진다.이러한 기대치는 위그너 준확률 분포가 효과적으로 척도가 되는 관측치의 위상공간 적분에 의해 구해진다.

따라서, (고전 역학과 같은 야망) 위상 공간에서의 양자 역학을 표현함으로써, 바일 맵은 변형 파라미터 δ/S를 사용하여 양자 역학을 고전 역학의 변형(일반화)으로 인식하기 쉽게 한다. 여기서 S는 관련 과정의 작용이다. (물리학의 다른 익숙한 변형은 디폴러를 포함한다.)변형 매개 변수 v/^{[citation needed][citation needed]}c를 사용하여 고전 뉴턴의 상대론적 역학을 결합하거나 변형 매개 변수 슈바르츠실트 반지름/특성-차원을 사용하여 일반 상대성 이론으로 뉴턴 중력을 변형합니다.)

고전식, 관측 가능 및 연산(포아송 괄호 등)은 고전 역학에 적용되는 기존의 교환 곱셈이 양자 역학을 특징짓고 불확실성 원리의 기초가 되는 비교환적 별 곱셈으로 일반화됨에 따라 γ 의존적 양자 보정에 의해 수정된다.

열역학 및 통계역학

열역학 및 통계역학에서 위상공간이라는 용어는 두 가지 의미를 가집니다. 하나는 고전역학에서와 같은 의미로 사용됩니다.열역학 시스템이 N개의 입자로 구성되어 있는 경우, 6N차원 위상 공간의 한 점은 각 입자가 3개의 위치 변수와 3개의 운동량 변수와 연관되어 있기 때문에 해당 시스템의 모든 입자의 동적 상태를 나타냅니다.이러한 의미에서 입자가 구별 가능한 한 위상공간의 한 점은 시스템의 마이크로스테이트라고 한다(구분이 불가능한 입자의 경우 마이크로스테이트는 N개의 모든 가능한 교환에 대응하는 일련의 N!포인트로 구성된다).N은 전형적으로 아보가드로의 숫자에 가깝기 때문에 미시적인 수준에서 시스템을 설명하는 것은 종종 비현실적이다.이로 인해 위상 공간이 다른 의미로 사용됩니다.

위상 공간은 압력, 온도 등 시스템의 거시적 상태에 의해 파라미터화된 공간도 참조할 수 있습니다.예를 들어 압력-체적도 또는 엔트로피 온도도를 이 위상공간의 일부로 볼 수 있다.이 위상공간의 점을 매크로스테이트라고 한다.같은 매크로 스테이트를 가지는 복수의 마이크로 스테이트가 존재할 가능성이 있습니다.예를 들어, 일정한 온도의 경우, 시스템은 미시적인 수준에서 많은 동적 구성을 가질 수 있습니다.이러한 의미에서 위상은 예를 들어 액상 또는 고체상 등과 같이 해당 시스템이 있는 위상 공간의 영역입니다.

매크로 상태보다 더 많은 미소 상태가 존재하기 때문에, 첫 번째 의미에서의 위상 공간은 보통 두 번째 의미에서의 것보다 훨씬 더 큰 차원의 다양체입니다.시스템의 모든 세부 사항을 분자 또는 원자 눈금으로 등록하려면 단순히 시스템의 온도 또는 압력을 지정하는 것보다 훨씬 더 많은 매개변수가 필요합니다.

광학

위상 공간은 조명에 전념하는 광학 분야인 비이미징 ^[3]광학에서 광범위하게 사용됩니다.그것은 또한 해밀턴 광학에서 중요한 개념이다.

위상 적분

고전적인 통계역학(연속 에너지)에서 위상 공간의 개념은 위상 ^[4]적분으로 알려진 분할 함수(sum over state)와 고전적인 유사성을 제공합니다.볼츠만 인자를 (각 자유도에 대해 적절한 정수 양자수로 정의됨) 이산적 간격의 에너지 상태에 합하는 대신 연속 위상 공간에 통합할 수 있다.이러한 통합은 기본적으로 모든 자유도의 운동량 성분(모멘텀 공간) 통합과 모든 자유도의 위치 성분(구성 공간) 통합의 두 부분으로 구성됩니다.일단 위상 적분이 알려지면 단위 위상 공간당 양자 에너지 상태의 수를 나타내는 정규화 상수의 곱에 의해 고전적인 분할 함수와 관련될 수 있다.이 정규화 상수는 ^[5]플랑크의 상수가 계의 자유도와 같은 거듭제곱으로 상승하는 역수입니다.

「 」를 참조해 주세요.

레퍼런스

추가 정보

• Nolte, D. D. (2015). Introduction to Modern Dynamics: Chaos, Networks, Space and Time. Oxford University Press. ISBN 978-0-19-965703-2.
• Nolte, D. D. (2018). Galileo Unbound: A Path Across Life, the Universe and Everything. Oxford University Press. ISBN 978-0-19-880584-7.

외부 링크

• "Phase space", Encyclopedia of Mathematics, EMS Press, 2001 [1994]