미국의 수학교육

Mathematics education in the United States
한 학생이 그래핑 계산기로 몇몇 수학 문제를 풀었습니다 (2010)
이 기사는 다음에 대한 시리즈의 일부입니다.
교육은 다음과 같다.
미국
요약
문제들
교육수준
icon 교육포털
flag 미국 포털

미국의 수학 교육은 한 주마다, 심지어 한 주 안에서도 상당한 차이가 있습니다. 그러나 2010년부터 대부분의 주와 컬럼비아 특별구에서 공통 핵심 표준이 채택되면서 전국의 수학 내용은 학년별로 더욱 밀접한 합의를 이루게 되었습니다. 평준화 대학입시인 수능이 공통 핵심의 내용을 더 잘 반영할 수 있도록 개편되었습니다.[1] 그러나 많은 학생들이 가속 트랙을 포함한 전통적인 경로에 대한 대안을 취합니다. 2023년 현재, 27개 주에서 고등학교 졸업 전에 3개의 수학 과목(일반적으로 14세에서 18세 학생의 경우 9학년에서 12학년)을 통과하도록 요구하고 있으며, 17개 주와 컬럼비아 특별구는 4개의 수학 과목을 통과하도록 요구하고 있습니다.[2] 중등학교(6학년~12학년) 수학 과목의 전형적인 순서는 사전 대수학(7학년 또는 8학년), 대수학 I, 기하학, 대수학 II, 사전 미적분학 또는 통계학입니다. 그러나, 많은 학생들이 미적분학이나 통계학을 통과하지 않고 고등학교를 졸업하는 반면, 일부 학생들은 통합 프로그램에[3] 등록합니다.[4][5] 반면, 경쟁력 있는 공립 또는 사립 고등학교의 상담원들은 보통 재능 있고 야망 있는 학생들이 명문 대학에[6] 입학할 가능성을 높이고 그들의 부모님들이 그들을 수학의 풍부한 프로그램에 등록시키기 위해 미래의 계획과 상관없이 미적분학을 수강하도록 권장합니다.[7]

중등학교 대수학은 많은 학생들이 극복하기 위해 고군분투하는 어려움의 전환점임이 증명되었고,[8][9][10][11] 이와 같이, 많은 학생들은 과학, 기술, 공학, 수학([10][11][12]STEM)의 대학 프로그램이나 미래의 고숙련 직업에 대한 준비가 부족합니다.[13][14] 미국 교육부의 1997년 보고서에 따르면, 엄격한 고등학교 수학 과목을 통과하는 것은 전공이나 가정 수입에 상관없이 대학 프로그램의 성공적인 마무리를 예측하고 있다고 합니다.[15][16] 한편, 대수Ⅰ에 등록된 8학년 학생의 수는 2010년대 초반에서 2020년대 초반 사이에 감소했습니다.[17] 미국 전역에서 자격을 갖춘 수학 강사가 부족합니다.[18][19] 최선의 의도에도 불구하고, 부모들은 자신의 수학적 불안감을 자녀들에게 전달할 수도 있고,[20][21] 자녀들의 수학적 능력을 과대평가하는 학교 선생님도 있을 수 있습니다.[22] 미국 성인 다섯 명 중 한 명은 기능적으로 숫자가 많지 않습니다.[18] 압도적인 다수가 수학이 중요하다는 것에 동의하는 반면, 많은 사람들, 특히 젊은 사람들은 자신의 수학적 능력에 대해 확신하지 못합니다.[18][23] 반면에, 성과가 높은 학교들은 학생들에게 ( 미적분학 이후 대학 과정을 수강할 수 있는 가능성을 포함하여)[24] 가속 트랙을 제공하고 수학 대회를 위해 영양을 공급할 수 있습니다.[25][26] 3차 수준에서는 STEM에 대한 학생들의 관심이 상당히 높아졌습니다.[27] 하지만, 많은 학생들이 고등학교 수학[28][29] 보충 과정을 수강해야 하고, 많은 학생들이 수학 능력 부족으로 STEM 프로그램을 중퇴해야 한다는 것을 알게 되었습니다.[12][7]

경제협력개발기구(OECD)의 다른 선진국들과 비교해 볼 때, 미국 학생들의 수학적 소양의 평균 수준은 보통 수준입니다.[8][30][31][32][33] 하지만, 아시아계와 유럽계 미국인 학생들은 OECD 평균 이상입니다.[34] 다른 많은 나라들과 마찬가지로, COVID-19 팬데믹 동안 수학 점수가 떨어졌습니다.[35]

교과내용 및 기준

2016년 기준으로 공통 핵심 국가 표준을 채택했거나 채택하지 않았거나 부분적으로 채택했거나 폐지한 미국의 주들을 보여주는 지도입니다.
표준을 채택한 주
표준을 부분적으로 채택한 주들
표준을 채택했다가 나중에 폐지한 주들
표준을 채택한 적이 없는 주

미국의 각 주에서는 자체적으로 교육과정 기준을 정하고 있으며, 세부적인 사항은 보통 각 지역 교육구에서 정해집니다. 연방 표준은 없지만, 2015년 이후 대부분의 주에서는 수학 공통 핵심 주 표준에 기반을 두고 교육 과정을 운영하고 있습니다. Common Core Mathematics 표준의 명시된 목표는 교육과정에서 더 높은 집중력과 일관성을 달성하는 것입니다.[36] 이는 대체로 미국의 수학 교육과정이 "폭이 1마일이고 깊이가 1인치"라는 비판에 대한 응답입니다.[37][38] 전국수학교사협의회는 1989년과 2000년에 수학교육에 대한 교육 권고안을 발표하였는데, 유치원부터 고등학교까지 수학적 지식과 기술, 교육학적 강조점을 기술하고 있습니다. 2006학년도 NCTM 교육과정 초점은 8학년까지 학년별로 가장 중요한 수학적 주제를 추천하는 데에도 영향을 미쳤습니다. 그러나 일부 주에서는 Common Core 표준을 포기하거나 채택한 적이 없으며 대신 자체적으로 제도화했습니다. (주별 Common Core 구현 참조) 실제로 국가적인 기준이 아예 있어야 하는가의 문제를 포함하여 수학 교수의 스타일과 내용에 대해서는 상당한 이견이 있어 왔습니다.[4][39][38]

미국에서는 초등학교와 중학교의 수학 교과과정이 통합되어 있는 반면, 고등학교에서는 전통적으로 주제별로 분리되어 있으며, 각 주제는 보통 학년 전체 동안 지속됩니다. 그러나 일부 지역에서는 통합 교육과정을 실시하거나 공통 핵심이 채택된 후 통합 교육과정을 시도하기로 결정했습니다.[3][40] 1950년대 스푸트니크 시대 이후 중등학교 수학 과목의 순서는 변하지 않았습니다: 사전 대수학, 대수학 I, 기하학, 대수학 II, 사전 미적분학. 삼각법은 일반적으로 다른 과정에 통합됩니다. 미적분학은 일부 소수만 수강합니다.[4][41] 어떤 학교들은 기하학보다 대수학을 먼저 가르칩니다.[41] 중학교 수학 과목의 성공은 1학년 시작까지 수에 대한 이해와 관련이 있습니다.[42] 이 전통적인 순서는 학생들이 대학에서 STEM 프로그램을 추구할 것이라고 가정하지만, 실제로는 소수만이 이 옵션을 기꺼이 선택할 수 있습니다.[4] 통계학 과정도 종종 제공됩니다.[18]

대부분의 학교 선생님들은 수업을 핵심 커리큘럼에 기반을 두고 있지만, 그들은 반드시 편지에 따라 수업을 하는 것은 아닙니다. 많은 사람들은 또한 자신의 학군에서 제공하지 않는 추가 자원을 활용합니다.[43]

초등학교

숫자 선에서 확장되는 것으로 보이는 곱셈

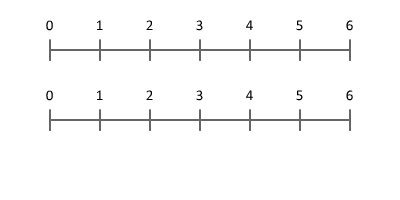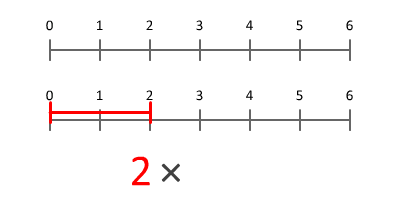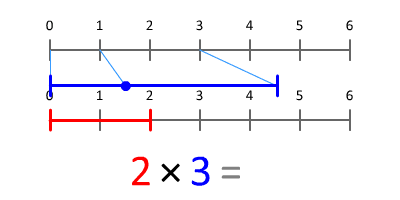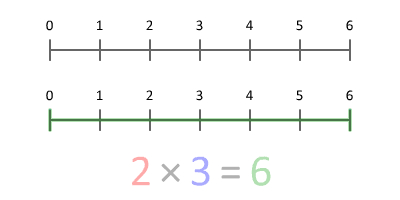
초등학교 아이들은 계산, 연산, 기하학, 측정, 통계 및 확률의 계산, 산술 및 속성을 배웁니다. 그들은 일반적으로 3학년 때 분수를 공부하기 시작합니다.

중등 학교.

제임스 가필드의 피타고라스 정리 증명.

사전 대수학은 중학교에서 7학년이나 8학년이 수강할 수 있습니다. 학생들은 일반적으로 실수와 기본적인 수론(소수, 소인수분해, 산술의 기본 정리, 비율, 백분율), 대수학( 거듭제곱, 근, 그래핑, 연산의 순서, 변수, 식, 과학적 표기법), 기하학(4차, 다각형, 평면 도형의 넓이, 피타고라스 정리, 거리 공식, 선의 방정식, 단순한 고체, 표면적, 부피, 그리고 때로는 도입 삼각법(삼각함수의 정의). 그런 과정은 일반적으로 단순한 선형 방정식과 부등식의 해법과 함께 간단한 대수학으로 들어갑니다.

대수학 I은 학생들이 대수학에서 가장 먼저 수강하는 과목입니다. 비록 일부 학생들은 8학년 때 이 수업을 듣지만,[44] 이 수업은 학생들이 대뇌 이전 수업을 들은 후인 9학년이나 10학년 때 가장 흔하게 듣습니다. 학생들은 실수와 연산의 순서(PEMDAS), 함수, 일차방정식, 그래프, 다항식, 인수정리, 라디칼, 이차방정식(팩터링, 제곱완료, 이차식), 멱함수에 대해 배웁니다.

이 과정은 8학년 때 대수Ⅰ을 수강하면 결국 고등학교를 졸업하기 전에 미적분을 수강할 수 있기 때문에[11] STEM을 추구하는 사람들에게 문지기로 여겨집니다.[45] 이처럼 학생들을 적성에 따라 추적하고 언제 대수학을 들어야 할지 결정하는 것이[46] 캘리포니아와 메사추세츠에서 논란의 대상이 되었습니다.[47] 성적이 좋은 학생들의 부모님들은 중학교에서 대수학 I을 수강하는 것을 단념시키는 정책에 대해 가장 목소리를 높이는 비평가들 중 한 명입니다.[46][47]

보통 9학년이나 10학년에 수강하는 기하학은 주로 유클리드 기하학의 몇 가지 기본 개념을 통해 학생들에게 수학의 엄격함이라는 개념을 소개합니다. 학생들은 명제 논리의 기초, 증명 방법(직접 및 모순에 의한), 평행선, 삼각형(수렴 및 유사성), 원(분음, 접선, 화음, 중심각, 내접각), 피타고라스 정리, 기초 삼각법(상승 및 함몰의 각도, 사인의 법칙), 기본 해석기하학(선, 점-slope 및 기울기-intercept 형태, 수직선 및 벡터의 equations) 및 기하학적 확률. 학생들은 전통적으로 2열 증명을 사용하여 간단한 기하학 정리를 보여주도록 배우는데, 이 방법은 미국에서 20세기 초에 특별히 이 과정을 위해 개발된 방법이지만 다른 방법도 사용될 수 있습니다.[49][50] 예를 들어 소진법과 카발리에리의 원리를 도입하는 등 교육과정과 교수자에 따라 미적분학에 대한 방향성을 얻을 수 있습니다.[48]

사인에 대한 이중각 항등식의 시각적 증명

대수 Ⅱ는 대수 Ⅰ을 필수조건으로 하며 전통적으로 고등학교 수준의 과정입니다. 과정 내용에는 부등식, 함수 표기, 2차 방정식, 멱함수, 지수 함수, 로그, 선형 방정식 시스템, 행렬(행렬 곱셈, 2 × 2 2 행렬 행렬식, Cramer's rule, 2× 2 의 역수 포함), 라디안 측도, 삼각함수의 그래프, 삼각형 항등식 (피타고라스 항등식, 합과 차, 이중각, 반각 공식, 사인과 코사인의 법칙), 원뿔 절 등.[51] 대수학 II는 AP 컴퓨터 과학 A와 AP 컴퓨터 과학 원리의 전제 조건입니다.

고등학교 졸업을 위해 대수학 II를 요구하는 것은 2010년대 초에 미국 전역에서 주목을 받았습니다.[52] 공통 핵심 수학 표준은 고등학교 수학을 가르치는 데 순차적 접근과 통합적 접근을 모두 인정하고 있어 고등학교 통합 수학 프로그램의 채택이 증가했습니다. 이에 따라 중등 교육 후 교육을 제공하는 기관은 등록 요구 사항을 업데이트했습니다. 예를 들어, 캘리포니아 대학교(UC) 시스템은 "초등 및 고급 대수학과 2차원 및 3차원 기하학에서 다루는 주제를 포함하는 대학 준비 수학"[53]을 3년 동안 인정하도록 요구합니다. 캘리포니아 교육부가 공통 코어를 채택한 후, UC 시스템은 "승인된 통합 수학 과정을 사용하여 이 입학 요건의 일부 또는 전부를 충족시킬 수 있다"[53]고 명확히 했습니다. 한편, 논란이 된 결정에서 텍사스 교육 위원회는 고등학교 졸업 필수 과정으로 대수학 Ⅱ를 삭제하기로 의결했습니다.[54]

캘리포니아에서, 대수학 II가 데이터 사이언스 (대수학, 통계학, 컴퓨터 과학의 조합)에 유리하도록 강조를 완화해야 한다는 제안들은 그러한 경로가 학생들이 대학 교육을 위한 준비를 제대로 하지 못하게 할 것이라는 우려 때문에 심각한 비판에 직면했습니다. 2023년 캘리포니아 대학교 시스템의 교수진은 대수학 II 대신 데이터 사이언스를 받아들이는 입학 정책을 종료하기로 투표했습니다.[46]

파스칼의 산술 삼각형은 대수학뿐만 아니라 조합론에서도 이항 정리를 통해 등장합니다.

프리칼큘러스는 위에서 본 것을 따르며, 일반적으로 대학에 진학한 학생들이 수강합니다. 사전 계산은 대수학, 분석 기하학, 삼각법, 분석 삼각법을 결합합니다. 대수학의 주제에는 이항 정리, 복소수, 대수학의 기본 정리, 근 추출, 다항식 장분법, 부분 분수 분해, 행렬 연산 등이 있습니다. 해석기하학에 관한 장에서 학생들은 극좌표를 배우고 원뿔 단면에 대한 지식을 심화시킵니다. 삼각법의 구성 요소에서 학생들은 삼각 함수의 그래프, 단위 원 위의 삼각 함수, 점 곱, 한 벡터를 다른 벡터로 투영하는 방법, 벡터를 분해하는 방법을 배웁니다. 시간과 적성이 허락한다면, 학생들은 Heron의 공식, Sarrus의 규칙을 통해 × 3 3 행렬의 행렬식을 계산하는 방법, 그리고 벡터 교차 곱을 배울 수 있습니다. 학생들은 그래핑 계산기를 사용하여 방정식의 도표를 시각화하고 유리근 정리나 데카르트 부호 규칙과 같은 다항식의 근을 찾는 전통적인 기술을 보완하는 방법을 배우게 됩니다. 프리칼큘러스는 함수의 극한에 대한 소개로 끝납니다. 일부 강사는 이 과정에서 수학적 귀납법과 조합론에 대한 강의를 할 수 있습니다.[55][56][57] Precalculus는 AP Physics 1과 AP Physics 2(이전의 AP Physics B)의 필수 조건입니다.

AP Precalculus는 3개의 필수 챕터만 있습니다. 다항 함수와 유리 함수, 지수 함수와 로그 함수, 삼각 함수와 극곡선. 선택적 재료에는 매개변수 방정식, 암시적 함수, 원뿔 섹션, 벡터 및 행렬 대수(× 2 행렬 반전, × 2 행렬식 및 선형 변환)[58]가 포함됩니다.

학구에 따라 순차적으로 또는 동시에 학습하는 한 학년 내에 여러 과정이 압축 및 결합될 수 있습니다. 예를 들어, 캘리포니아에서는 대수 Ⅱ와 프리칼큘러스를 하나의 압축 코스로 수강할 수 있습니다.[45] 이러한 가속도가 없다면 고등학교에서 미적분학과 같은 고급 수업을 듣는 것은 불가능할 수도 있습니다.

오리건 주에서는 고등학교 3학년과 3학년 학생들이 관심사에 따라 세 개의 트랙 중 하나를 선택할 수 있습니다. 수학, 물리학, 공학 분야에서 경력을 목표로 하는 사람들은 대수학 II와 프리칼큘러스를 수강하며 전통적인 길을 추구할 수 있습니다. 생명과학, 사회과학 또는 비즈니스 분야에서 경력을 쌓고 싶은 사람은 통계학 및 수학 모델링을 수강할 수 있습니다. 기술 교육을 받는 학생들은 응용수학과 수학 모델링을 수강할 수 있습니다.[59] 고등학교에서도 수학적 논리와 집합론에 대한 수업을 다양한 학년 단위로 받을 수 있는데, 2020년 새로운 개혁안에 따라 플로리다에서 그러합니다.[60] 새로운 플로리다 표준은 또한 금융 이해력을 증진시키고 학년별로 다른 수학 주제들이 어떻게 연결되는지를 강조합니다.[61] 유타주에서는 고등학교의 최종 필수 수학 과목에 대수 Ⅱ, 삼각법, 프리칼큘러스, 데이터 사이언스의 요소가 포함되어 있습니다. 그러나 2023년 현재 학생들은 학부모님의 서명이 있는 편지로 이 수업을 중단할 수 있으며, 절반 정도가 이 수업을 중단할 수 있습니다.[62]

대학 대수학은 미적분학 이전에 과정을 통과하지 못한 학생들을 위한 보충 과정으로 많은 지역 대학에서 제공됩니다.[63] 4년제 대학에서 수학 및 관련 분야(컴퓨터 과학 등)를 전공하는 학생들이 수강하는 추상대수 및 선형대수와 혼동해서는 안 됩니다.

함수의 극한에 대한 엡실론-델타 정의의 그림

미적분은 보통 고등학교 3학년이나 대학교 1학년이 수강하지만, 빠르면 10학년부터 수강할 수 있습니다. STEM 진로를 목표로 하거나 고급 수학이 미적분학을 공부할 수 있는 궤도에 오른 프랑스에서 이스라엘, 싱가포르에 이르기까지 많은 다른 나라들과 달리, 미국은 일반적으로 미적분학을 대학수학으로 취급합니다. 고급 배치 프로그램(AP 미적분 AB 및 AP 미적분 BC)을 통해 제공되는 것처럼 성공적으로 이수된 대학 수준의 미적분 과정은 편입 수준의 과정으로, 즉 대학에서 졸업 요건에 대한 학점으로 인정받을 수 있습니다. 명문 대학들은 입학을 위해 AP 미적분학을 포함한 AP 과정을 성공적으로 마쳐야 한다고 여겨집니다.[64][65] 미적분학은 AP 물리학 C: 역학과 AP 물리학 C: 전기와 자기를 위한 필수조건 또는 필수조건입니다. 1990년대부터 고등학교 교육과정에서 미적분학의 역할은 논란의 대상이 되었습니다.[4]

이 수업에서 학생들은 극한과 연속성(중간값 정리와 평균값 정리), 미분(곱, 몫, 사슬 규칙)과 그 응용에 대해 배웁니다(묵시 미분, 대수 미분, 관련 비율, 최적화, 오목성, 뉴턴 방법, L'Hotpital's rules). 적분과 미적분학의 기본 정리, 적분의 기법(u-치환, 부분에 의한 삼각법과 쌍곡 치환, 부분 분수 분해), 적분의 추가적인 적용(누적 변화 계산, 과학과 공학의 다양한 문제 계산, 분리 가능한 상미분 방정식, 곡선의 호 길이, 곡선 사이의 면적, 부피 및 회전 고체의 표면적), 부적절한 적분, 수치 적분(중간점 규칙, 사다리꼴 규칙, 심슨의 규칙), 무한수열과 급수 그리고 이들의 수렴(n차, 비교, 비율, 근, 적분), p계열 및 교대계열 검정), 테일러 정리(라그랑주 나머지 포함), 뉴턴의 일반화된 이항 정리, 오일러의 복소 항등식, 복소수의 극 표현, 모수 방정식 및 극좌표의 곡선.[66][67][68][69]

과정과 강사에 따라 미적분학 입문의 특별한 주제에는 곡선의 고전적 미분기하학(호 길이 매개변수화, 곡률, 비틀림 및 프레네-세레트 공식), 극한의 엡실론-델타 정의, 1차 선형 보통 미분 방정식, 베르누이 미분 방정식이 포함될 수 있습니다.[66][68] 오늘날 일부 미국 고등학교에서는 다변수 미적분학[24](편미분, 다변수 연쇄법칙과 Clairault 정리, 제한적 최적화, 라그랑주 승수와 헤센, 다차원 적분, 푸비니 정리, 변수의 변화, 자코비안 행렬식, 그래디언트, 방향 도함수, 발산, 컬, 그래디언트의 기본 정리, 그린의 정리, 스톡스의 정리, 가우스의 정리).[66][68][69]

통계학(AP Statistics 포함)이나 비즈니스 수학과 같은 다른 선택 수학 과정이 제공될 수 있습니다. 학생들은 그래픽 및 수치 기법을 사용하여 데이터의 분포(일변량, 이변량 및 범주형 데이터 포함), 다양한 데이터 수집 방법 및 이로부터 도출할 수 있는 결론의 종류, 확률 및 통계적 추론(점 추정, 신뢰 구간 및 유의성 검정)을 분석하는 방법을 배웁니다.

뛰어난 능력을 가진 [70][25]고등학생들은 미국 수학 올림피아드나 국제 수학 올림피아드와 같은 대회에 참가하도록 선발될 수 있습니다.[26][71]

고등학교

벡터 미적분학에서 스톡스 정리의 예시

STEM의 모든 학생들, 특히 수학, 물리학, 화학, 컴퓨터 과학, 공학은 고급 배치 학점(또는 IB Math HL과 같은 동등한 것)을 가지고 있지 않은 한, 단일 변수 미적분학을 수강해야 합니다. Students majoring in mathematics, the physical sciences,[72][73] and engineering[74] then take multivariable calculus,[66][68][69] linear algebra,[75][76][77] complex variables,[78][79][80] ordinary differential equations,[81][82][83] and partial differential equations.[84][85][86] 학생들에게 현대 수학 개념에 대한 엄격한 소개를 제공하는 과정이 있을 수 있습니다.[87][88][89] In addition, mathematics students study abstract algebra,[90][91][92] number theory,[93][94][95] real analysis,[96][97][98][99] advanced calculus,[100][101][102] complex analysis,[103][104][105][106] probability theory,[107][108] statistics,[109][110] and advanced topics, such as set theory and mathematical logic,[111][112][113][114] stochastic processes,[115] integration and measure theory,[116][117][118][119] Fourier analysis,[120][121] functional analysis,[122] differential geometry,[123][124][125] 그리고 토폴로지.[126][127] 그들은 수학 모델링, 수치 분석,[128] 게임 이론 [129][130][131]또는 수학 최적화와 같은 응용 수학 과정을 추가로 선택할 수 있습니다. The calculus of variations,[132][133][134] the history of mathematics,[135][136][137][138] and topics in theoretical or mathematical physics (such as classical mechanics,[139][133][140][141] electrodynamics,[142][143] nonlinear dynamics,[144] fluid mechanics,[145][146] quantum mechanics,[147][148][149] or general relativity[150][151][152][153]) may be taken as electives. 컴퓨터 과학 전공자들은 이산 수학[154][155](조합론, 그래프 이론 등), 정보 이론,[156] 계산 이론,[157][158] 암호학 등의 과목을 수강해야 합니다. 생물 의학과 사회 과학을 공부하는 사람들은 기초 확률과[159] 통계를 공부해야 합니다.[160] 컴퓨터 과학과 경제학을 전공하는 학생들은 알고리즘 게임 이론을 수강할 수 있습니다.[161] 물리학 및 공학 분야의 학생들은 실험실 세션과 과정에 대한 오류 분석을 이해해야 합니다.[162][163] 고급 대학원생들과 물리학과 초급 대학원생들은 물리학의 고급 수학 방법에 대한 강의를 들을 수 있습니다.[164][165][166][167][168][169] 정확한 요구 사항과 이용 가능한 과정은 해당 기관에 따라 다릅니다.

많은 대학들에서, 자신감 있는 학생들은 통합 대회에서 경쟁할지도 모릅니다.[170][171][172][173] 우수한 학부생들은 매년 열리는 William Lowell Putnam 수학 대회에 참가할 수 있습니다.[174][175] 많은 성공적인 경쟁자들은 수학 분야에서 성과 있는 연구 경력을 쌓았습니다. 퍼트넘을 잘 하는 것이 수학자가 되기 위한 요건은 아니지만, 그것은 학생들이 성공적인 연구자가 되도록 도울 수 있는 기술을 개발하고 직관을 연마하도록 장려합니다.[174][176] 상금 외에도 수상자들은 명문 대학원에 사실상 합격이 보장됩니다.[177] 이러한 대회는 수학적 재능이 돋보일 수 있는 하나의 방법입니다.[178]

출석률 및 이수율

대수학 I의 완성에는 상당한 인종이나 성별 차이가 존재합니다.[179]

많은 학생들에게 대수학을 통과하는 것은 종종 매우 어려운 도전이기 때문에 많은 학생들이 그것 때문에 고등학교를 중퇴했습니다.[8][10][11][8] 대수학을 잘 하는 데 가장 큰 장애물은 분수의 유창성인데, 많은 미국인들은 이것을 가지고 있지 않습니다.[9] 고등학교 대수학인 대수학 I과 II를 숙달하지 않으면 학생들은 대학 STEM 과정을 추구할 수 없을 것입니다.[11][10][179] 사실 STEM의 소모율이 높은 이유는 수학에서 적절한 준비가 부족하기 때문입니다.[12] 1986년부터 2012년까지, 더 많은 학생들이 대수학 II를 이수하고 있었지만, 그들의 평균 성적은 하락했습니다. 실제로 "명예" 과목을 포함하여 고등학교 과정을 통과한 학생들은 대학 배치 시험에 여전히 실패할 수 있고 보충 과목을 들어야 했습니다.[28] 대수Ⅰ의 경우, 2012년 34%였던 13세 학생 수가 2023년에는 24%로 떨어졌습니다.[17]

종단 분석 결과, AP 과목을 포함한 미적분학과 통계학 고등학교 과정을 이수하는 학생 수는 2019년 이전에 감소한 것으로 나타났습니다.[5][180] 2000년대 후반부터 2010년대 중반까지 학생들의 성적서( = {\displaystyle N = 15,188})에서 수집한 데이터에 따르면 대다수의 학생들이 대수Ⅰ(96%), 기하학(76%), 대수Ⅱ(62%)를 이수한 것으로 나타났습니다. 그러나 프리칼큘러스(34%), 삼각법(16%), 미적분학(19%) 또는 통계학(11%)을 수강한 사람은 그리 많지 않았고, 통합수학(7%)을 수강한 절대 소수에 불과했습니다. 전체적으로 여학생이 통계학과 미적분학을 제외한 모든 수학 과목을 이수할 확률이 높았습니다. 아시아계 미국인은 프리칼큘러스(55%), 통계학(22%), 미적분학(47%)을, 아프리카계 미국인은 미적분학(8%)을 이수할 가능성이 낮았지만 고등학교 때 통합수학(10%)을 이수할 가능성이 가장 높았습니다.[181] PSAT에 의해 수학에 능숙하다고 확인된 학생들 중 아시아인들은 흑인들보다 수학의 우등생이나 고급 배치 과정에 참석할 가능성이 훨씬 더 높습니다.[182] 또한 아시아인들은 AP 미적분학 시험에서 최소 3점 이상을 받았을 가능성이 가장 높습니다.[64] 사회경제적 지위가 낮은 학생들은 프리칼큘러스, 미적분학, 통계학에 합격할 가능성이 낮았습니다.[181] 남학생과 여학생이 동일하게 AP 통계학과 AP 미적분학 AB를 수강할 가능성이 높은 반면, 남학생은 AP 미적분학 BC (59%)에서 다수를 차지하고 있으며, AP 컴퓨터 과학 A (80%), AP 물리학 C: 역학 (74%), AP 물리학 C: 전기 및 자기 (77%)와 같은 다른 수학 과목들도 있습니다.[183] 학부생 남녀가 평균적으로 미적분 I(대학)에서 같은 점수를 받지만, 수학적 불안감 때문에 여성이 남성보다 중도 탈락할 가능성이 높습니다.[184] 여자 아이들이 남자 아이들보다 수학 능력이 부족하다는 인식과 고정관념은 빠르면 2학년부터 시작되고, 그것들은 여자 아이들이 실제로 수업시간이나 국제 수학 올림피아드와 같은 대회에서 어떻게 성적을 내는지에 영향을 미칩니다.[185] 미적분학을 수강한 대학생들 사이에서는 공학 분야가 남성들 사이에서, 생물학 분야는 여성들 사이에서 가장 인기가 많습니다.[64]

1970년대와 1980년대에 대학에서 보충 과목을 수강하는 학생들의 수는 상당히 증가했는데, 이는 부분적으로 고등학교에서 미적분학이 강조되지 않았기 때문이며, 이로 인해 미적분학 이전 주제에 대한 노출이 줄었습니다.[4] 21세기 미국 커뮤니티 칼리지는 프로그램에 따라 학생의 60%가 수학 과목을 적어도 한 과목은 통과해야 합니다.[29] 그러나 약 80%는 이 요구 사항을 충족하지 못하고 [29]60%는 치료 과정이 필요합니다.[10] 이 학교들의 많은 학생들은 대수학 II와 같은 보충 과정에서도 실패한 후 자퇴합니다.[186] 반면, 4년제 기관들은 수학과 통계를 포함한 STEM 프로그램에 대한 학생들의 관심이 증가했습니다.[27]

수학과 통계를 포함한 의료와 STEM 과목의 인기가 높아졌고 인문사회, 특히 역사는 시장의 힘으로 인해 하락했습니다.[27][187]

논란과 쟁점

시애틀의 한 남학생 (1961). 수학 교육의 내용은 수십 년 동안 논쟁의 대상이 되어 왔습니다.

수학 교육은 학계, 학부모는 물론 교육자들 사이에서 논쟁의 대상이 되어 왔습니다.[4][9][188][38] 수학이 중요하다는 것에 대다수의 의견이 일치하지만, 어떤 수학을 가르쳐야 하는지, '현실 세계'와의 관련성이나 엄밀성을 강조해야 하는지에 대해서는 의견이 분분했습니다.[45][13] 또 다른 논쟁의 원인은 이탈리아와 같은 다른 나라의 경험에서 볼 수 있는 그러한 프로그램의 이점에도 불구하고 전국적으로 시행되는 표준 교육과정을 도입하는 것을 어렵게 하는 미국 교육의 분산된 특성입니다.[189] 2020년대 초, 일부 교육자들이 인종과 섹슈얼리티의 주제를 수학 교육과정에 포함시키기로 결정한 것도 강한 저항에 부딪혔습니다.[190]

진보교육

20세기 전반 동안, 미국의 공교육을 보다 "진보적인" 근거를 따라 체계적으로 개혁하려는 움직임이 있었습니다. 진보적인 교육의 가장 목소리가 큰 지지자 중 한 명인 윌리엄 허드 킬패트릭은 대수학, 기하학, 삼각법과 같은 지적인 "명품"의 강조를 완화할 것을 주장하며, 그것들을 "일반적인 생활에 필요한 사고의 종류에 도움이 되기 보다는 해롭다"고 말했습니다. 그는 수학에서 더 발전된 주제는 선택된 소수에게만 가르쳐야 한다고 권장했습니다. 사실, 2차 세계대전 이전에, 교육학자들은 다수의 고등학생들이 고등교육을 향한 길을 걷지 못하고 대신에, 고등교육을 향한 길을 걷게 된다고 가정하면서, 학문적인 과목들의 교육에 반대하고 "집, 가게, 가게, 시민권, 그리고 건강"이라는 더 실용적인 관심사에 찬성하는 것이 일반적이었습니다. 숙련되지 않은 노동자나 그들의 아내가 될 운명입니다.[4]

그러나 1940년대에 이르러 군 신병들의 수학 능력 부족은 세간의 스캔들이 되었습니다. 체스터 니미츠 제독 자신은 훈련 중인 장교들과 자원봉사자들 사이에서 공립학교에서 가르쳐야 할 기술의 부족에 대해 불평했습니다. 이 문제를 해결하기 위해 군은 부기나 총기를 위한 산술과 같은 기초 기술을 가르치는 과정을 개설해야 했습니다.[4]

실제로 많은 학부모들이 내용이 부족하다고 비판하며 진보적 개혁에 반대했습니다. 21세기 중반까지 레이더, 원자력, 제트 엔진과 같은 기술적인 경이로움은 진보적인 교육을 유지할 수 없게 만들었습니다.[4]

새로운 수학

나바호 학생들은 산술을 배웁니다 (c. 1940). 1950년대 후반까지 수학 교육은 더욱 엄격해졌습니다.

1957년 소련 위성 스푸트니크의 성공적인 발사 이후 만들어진 '새로운 수학' 구상에 따라 계산이 아닌 개념적 추상화가 수학 교육의 중심 역할을 하게 되었습니다.[39] 교육 현상은 국가적 망신을 주는 요인으로 맹비난을 받았고 개혁이 요구되어 의회는 1958년 국방 교육법을 도입하게 되었습니다.[4] 드와이트 D 대통령이 이끄는 미국 연방정부. 아이젠하워는 이념적 라이벌인 소련의 힘에 걸맞게 수천 명의 과학자와 기술자가 필요하다는 것을 깨닫고 교육뿐만 아니라 연구와 개발에 막대한 자금을 쏟아 붓기 시작했습니다.[191][192] 진보적인[4] 교육의 내용에 대한 강조가 부족하고 제2차 세계 대전의 기술 발전에 대응하여 고안된 [193]뉴 수학은 프랑스의 니콜라스 부르바키 학교의 영향을 받은 국제 운동의 일부였으며 학교에서 가르치는 수학을 수학자들이 실제로 사용하는 연구에 더 가깝게 만들려고 시도했습니다. 학생들은 수학자들이 실수의 집합을 구성하기 위해 실제로 사용하는 집합론에서 수업을 받았고, 일반적으로 실해석학에서 고급 학부생들에게 가르쳤습니다(데데킨드 컷과 코시 시퀀스 참조). 10이 아닌 다른 기수를 가진 산술도 가르쳤습니다(이진 산술 및 모듈식 산술 참조).[194] 다른 주제로는 정수론, 확률론, 해석기하학 등이 있었습니다.[193]

하지만, 이 교육 계획은 곧 새로운 자료를 가르치기는커녕 이해하기 위해 고군분투하는 선생님들뿐만 아니라, 아이들의 숙제를 돕는 데 문제가 있는 부모님들로부터도 강력한 반대에 부딪혔습니다.[39] 전문가들로부터도 비판을 받았습니다. 물리학자 Richard Feynman은 1965년 수필에서 "첫 번째는 생각의 자유가 있어야 한다; 둘째는 우리는 단지 단어만을 가르치고 싶지 않다; 그리고 셋째는 목적이나 이유를 설명하지 않고 또는 자료가 흥미로운 것을 발견하는데 실제로 사용될 수 있는 방법을 제공하지 않고 주제를 소개해서는 안 됩니다"라고 주장했습니다. 그런 내용을 가르칠 가치가 없다고 생각합니다."[195] 수학자이자 수학 역사학자인 모리스 클라인은 1973년 저서 "왜 조니는 더하지 못하나: 새로운 수학의 실패"에서 새로운 수학적 창조물을 배우는 것은 오래된 것들을 먼저 이해하지 않고는 "실질적으로 불가능하다"며 "추상은 수학적 발전에서 첫 번째 단계가 아니라 마지막 단계"라고 관찰했습니다."[196]클라인은[196] '새로운 수학' 교과서의 저자들이 수학적인 능력이 아니라 수학에 대한 접근이 협소하고 교육학과 교육심리학에 대한 이해가 제한적이라고 비판했습니다.[197] 수학자 조지 F. 시몬스는 자신의 저서 '전두엽 수학'(Precalculus Mathematics in a Nutshell, 1981)의 대수학 부문에서 뉴매쓰는 "교환 법칙은 들어봤지만 곱셈표는 알지 못한" 학생들을 배출했다고 썼습니다.[198]

1970년대 초까지 이 운동은 패배했습니다. 그럼에도 불구하고, 그것이 홍보한 몇몇 아이디어들은 여전히 살아있었습니다. 뉴 수학 계획의 주요 기여 중 하나는 고등학교에서 미적분학을 가르친 것입니다.[4]

표준에 기초한 개혁과 NCTM

주요 기사: 수학전쟁과 NCTM

20세기 후반부터 21세기 초반까지 수학을 어떻게 가르쳐야 하는지에 대한 치열한 논쟁이 있었습니다. 한편으로, 어떤 사람들은 알고리즘과 약간의 암기를 특징으로 하는 보다 전통적인 교사 주도 교육 과정을 캠페인합니다. 반면에, 어떤 사람들은 문제 해결과 숫자에 대한 감각에 초점을 둔 개념적 접근을 선호합니다.[199] 그러나 수학자 우흥시가 설명한 바와 같이, 기본적인 기술과 수학적 개념의 이해 사이의 명백한 이분법은 망상입니다.[200]

1989년 전국수학교사협의회(NCTM)는 학교수학 교육과정과 평가기준을 만들었습니다. 새로운 표준을 널리 채택했음에도 불구하고, 교육학적 관행은 1990년대 미국에서 거의 변하지 않았습니다.[201] 사실 수학교육은 1990년대와 2000년대 초반에 뜨거운 논쟁거리가 되었습니다. 이 토론은 수학자들(UC버클리 수학자 우훙-쉬시와 같은)과 부모들을 가르쳤으며, 그들 중 많은 이들이 수학에 대해 상당한 지식을 가지고 있습니다(물리학자 치아라 R 연구소와 같은). 이른바 '개념 이해'를 강조하려는 교육 전문가들에 대한 NCTM의 개혁에 반대했던 Nappi). 그러나 많은 경우 교육 전문가들은 비평가들뿐만 아니라 수학을 이해하지 못했습니다. 이것은 리핑 마에 의해 초등 수학을 알고 가르치고(1999)라는 책이 출판되면서 명백해졌습니다. 저자는 대부분의 중국 교사들이 정규 교육을 받은 지 11년 또는 12년밖에 되지 않았지만, 그들 중 많은 사람들이 석사 과정을 밟고 있는 미국 교사들보다 기초 수학을 더 잘 이해한다는 증거를 제시했습니다.[4]

1989년에는 더 급진적인 NCTM 개혁이 사라졌습니다. 대신 실질적인 수학에 더 큰 비중을 두었습니다.[4] 일부 대규모 학군에서는 대학생과 가장 고급인 중학생만을 추적하여 대수학을 수강하는 전통에 비해, 이것은 9학년까지 모든 학생의 대수학을 어느 정도 요구하게 되었습니다. 교육과정 및 평가 기준을 구현하는 데 있어 어려움은 당시 기준의 취지에 맞게 설계된 교육 자료가 없다는 것이었습니다. 1990년대에 국립과학재단은 코어 플러스 수학 프로젝트와 같은 교육과정 개발에 자금을 지원했습니다. 1990년대 후반과 2000년대 초반, 이른바 수학 전쟁이 수학 수업의 일부 더 급진적인 변화에 반대하는 지역 사회에서 일어났습니다. 일부 학생들은 그들의 새로운 수학 과목이 그들을 대학에서 보충 수학에 빠지게 했다고 불평했습니다.[202] 그러나 미시건 대학 등록관이 동시에 제공한 자료에 따르면 미시건 대학의 대학수학 과정에서 코어플러스 졸업생들은 전통적인 수학 교과과정 졸업생들과 같거나 더 잘했다고 합니다. 그리고 전통적인 과정을 수강하는 학생들도 보충 수학 과정에 배치되었습니다.[203] 수학 강사인 하이메 에스칼란테는 NCTM 기준을 체육 선생님이 쓴 것이라고 일축했습니다.[4]

2001년과 2009년에 NCTM은 이전 표준 문서의 작업을 확장한 PSSM(Principles and Standards for School Mathematics)과 커리큘럼 포커스 포인트(Curriculum Focal Points)를 발표했습니다. 특히 PSSM은 1989년의 기준을 보다 균형 있게 재반복하였지만, Focus Points는 각 학년별로 3가지 중점 분야를 제시하였습니다. NCTM은 이전의 기준을 부인하고 있다는 보도와[204] 사설을 반박하면서 포커스 포인트가 학생들의 수학적 이해를 심화시키고 기술을 개발하는 수업의 필요성을 크게 다시 강조하고 있다고 주장했습니다. 이 문서들은 제2차, 제3차 국제 수학 및 과학 연구의 결과를 통해 미국의 수학 교육과정이 대부분의 다른 나라의 수학과 비교할 때 "마일 폭과 깊이가 1인치"라는 비판을 반복했습니다.

통합수학

일부 기하학적 곡선은 극좌표에서 대수적으로 표현됩니다.

앞에서 언급한 바와 같이, 미국 아이들은 보통 중등학교(6학년에서 12학년)에서 한 번에 한 과목씩 배우는 독특한 일련의 수학 과정을 따릅니다. 그들은 기하학의 1년으로 끝나는 대수학의 2년이 걸립니다. 지금까지 대학 과정이었던 기하학은 19세기에 고등학교에 도입되었습니다. 유럽에서 학교들은 기하학을 다른 수학 과목들과 통합해야 한다는 펠릭스 클라인의 요구를 따랐습니다. 1892년 미국 10인 위원회는 미국에 같은 전략을 권고했지만, 미국 교사들은 이미 기하학을 가르치는 습관을 길러내고 있었습니다. 결국 1912년에 미국 고등학교 기하학 교육과정이 성문화되었고, 그러한 과정에 대한 독특한 미국식 기하학적 증명법인 "두 개의 열" 증명법을 개발했습니다.[49] 이것은 증명 기반 고등학교 수학 수업으로서 기하학과 함께 오늘날에도 대체로 사실로 남아 있습니다. 한편, 이스라엘에서 이탈리아에 이르기까지 세계의 많은 나라들은 미국인들이 말하는 통합 교육과정에 따라 수학을 가르치며 중등학교 내내 미적분학의 다양한 측면과 필수조건을 학생들에게 친숙하게 합니다.[64][65] 실제로 미국인들이 고등학교에서 주로 배우는 대수학과 기하학의 많은 주제들은 유럽의 중학교에서 가르치고 [189]있어 유럽 국가들이 고등학교에서 미적분학을 요구하고 가르치는 것이 가능합니다. 프랑스와 독일에서는 각각 앙리 푸앵카레와 펠릭스 클라인과 같은 유명한 수학자들의 옹호 덕분에 미적분학이 중등학교 교육과정에 도입되었습니다.[64][65] 그러나 싱가포르의 사례가 보여주듯이 미적분학의 개념을 일찍 접하는 것이 반드시 고등학생들의 실제 이해로 이어지는 것은 아닙니다.[205][65] 미국에서, 이것은 많은 대학 교수들이 제기한 우려에 반영되어 있는데, 그들의 학생들은 미적분학 이전의 수학에 대한 충분한 준비가 부족하다고 합니다.[64] 통합 교육과정을 가르치는 것을 지지하는 사람들은 학생들이 수학의 다른 분야들 사이의 연결을 더 잘 이해할 것이라고 믿습니다. 반면에, 학부모와 선생님을 포함한 비평가들은 전통적인 미국식 접근법에 익숙하기 때문에 그리고 특정한 주요 주제들이 생략되어 학생이 대학에 갈 준비가 불충분할 수 있다는 우려 때문에 모두 전통적인 미국식 접근법을 선호합니다.[3] 위에서 언급한 바와 같이 미국 고등학생의 7%만이 통합수학을 수강하고 있습니다.[181]

대학입학준비

2011년부터 대부분의 주에서는 NCTM의 이전 작업에 일부 기반을 둔 수학 공통 핵심 표준을 채택했습니다. 커먼코어 기준이 학생들의 대학 진학을 충분히 준비하지 못한다는 지적과 일부 학부모들의 자녀들이 배우는 수학을 이해하지 못한다는 불만이 이어지면서 여전히 논란이 계속되고 있습니다. 실제로, 비록 그들이 고등학교에서 과학, 기술, 공학, 수학 (STEM)을 추구하는 것에 관심을 표현했을지 모르지만, 많은 대학생들은 수학에 대한 불충분한 준비 때문에 엄격한 STEM 교육을 받을 자격이 부족하다는 것을 알게 됩니다.[12][7] 한편, 중국, 인도, 싱가포르 학생들은 어린 나이에 높은 수준의 수학과 과학에 노출되어 있습니다.[12] 2003년과 2009년 사이에 미국의 STEM 학생의 절반 가량이 프로그램을 중단했습니다.[7] 게다가, 많은 수학 학교 선생님들은 그들의 과목에 대해 그들만큼 잘 알지 못했고, 수학 자체에 대해 불편할 수도 있습니다.[20][7][206] 속도와 암기력을 강조하는 것은 5세 이상의 학생들에게 3분의 1이나 수학적 불안감을 줍니다.[32]

학부모와 고등학교 상담교사들은 학생들이 경쟁력 있는 대학에 입학하기 위해서는 미적분학에 합격하는 것이 중요하다고 생각합니다. 사립학교 상담원들은 특히 이 추천을 할 가능성이 높은 반면, 입학사정관들은 일반적으로 이 추천을 필수조건으로 여기는 경향이 덜합니다.[45] 게다가, 대학에서 STEM 과목을 전공하지 않을 계획인 사람들을 위해 통계학과 데이터 과학을 선호하는 고등학교에서 미적분학을 마지막 수학 수업으로 하는 전통적인 길을 탈강조화하려는 움직임이 있었습니다.[6] 그럼에도 불구하고, 미적분학은 야망 있는 학생들에게 가장 권장되는 과정으로 남아 있습니다.[6] 그러나 유타주의 경우, 2023년 현재 학생들은 고등학교 졸업을 위한 최종 필수 과정인 대수학 II, 삼각법, 프리칼큘러스 및 통계학 요소를 결합한 과정을 생략할 수 있습니다. 이 결정이 대학 입학 기회를 위태롭게 할 수 있음을 인정하는 부모의 서명이 담긴 편지를 제출하면 말입니다.[62]

2010년대 중반까지 미국 고등학교 3학년 학생의 4분의 1만이 학년 수준의 수학을 할 수 있지만,[207] 절반 정도는 A 학생으로 고등학교를 졸업하기 때문에 학년 인플레이션이 우려되고 있습니다.[208] 대수학 I, 기하학, 대수학 II의 강력한 성적은 고등학교에서 미적분학을 듣는 것보다 대학 수준의 미적분학에서 좋은 성적을 예측합니다.[44]

수학 교육의 또 다른 쟁점은 과학 교육과의 통합입니다. 공립학교는 과학과 수학을 독립적으로 가르치기 때문에 이것은 어렵습니다. 통합의 가치는 과학이 가르치는 수학 개념에 대한 진정한 맥락을 제공할 수 있다는 것이고, 더 나아가 수학이 과학과 동시에 가르치는 경우 학생들은 이 상관관계로부터 이익을 얻을 수 있다는 것입니다.[209]

농축 프로그램 및 가속 트랙

텍사스의 한 예비학교 수학동아리 (2018)

부유한 백인과 아시아계 가정을 걱정하는 학교 관계자들과 마찰을 빚으며 학부모들이 학원이나 수학계를 선택하도록 유도하는 학부모들이 늘고 있습니다. 저소득층 지역에 봉사하는 몇몇 공립학교들은 수학적으로 재능이 있는 학생들의 존재를 부인하기도 했습니다.[7] 사실, 미국의 교육자들은 아시아의 교육자들과 달리 상위권에 있는 학생들보다 성적이 좋지 않은 학생들에게 초점을 맞추는 경향이 있습니다.[210] 자녀를 위한 가속 트랙을 제안하는 학부모의 제안은 종종 학교 관리자들에 의해 적대감에 부딪힙니다.[211] 반대로, 대수학 I과 같은 특정한 핵심 과목들을 강조를 완화하는 것을 목표로 한 계획들은 학부모들과 대학 교직원들로부터 강한 반발을 불러 일으켰습니다.[46][47] 수학 조숙 청소년 연구에 의해 SAT의 수학(그리고 나중에는 언어) 영역에서 최고 점수를 받은 학생들은 종종 그들의 분야에서 매우 성공적이었습니다.[212] 2010년대 중반까지 일부 공립학교는 학생들에게 풍부한 프로그램을 제공하기 시작했습니다.[7]

마찬가지로, 일부 학구들은 그들이 같은 수준으로 고등학교를 시작하는 것을 보장하기 위해 수학적 능력에 의해 학생들을 분리하는 것을 중단할 것을 제안했지만, 재능 있는 아이들의 부모들은 그들의 아이들의 미래의 대학 입학 전망을 위태롭게 할 것을 우려하여 이 계획에 반대해 왔습니다. 특히 STEM 분야에서.[45][6] 예를 들어 샌프란시스코에서는 결과가 엇갈리고 여론의 반발이 겹쳐 이런 계획이 무산됐습니다.[45]

강사부족

자격을 갖춘 수학 학교 선생님들의 부족은 수년 동안 미국에서 심각한 문제였습니다.[18][19] 이러한 문제점을 시정하기 위해 초등교사 양성을 목적으로 하는 학부 프로그램에서 수학 내용을 전담하는 수업 시수를 늘렸습니다.[213] 교사는 자신도 모르게 학생들에게 수학에 대한 자신의 부정적인 태도를 전달하여 수업의 질을 해치는 경우가 많습니다.[206]

표준화시험

  • PISA average mathematics scores (2018)
    PISA 평균 수학 점수 (2018)
  • TIMSS 4th grade average mathematics scores (2019)
    TIMSS 4학년 평균 수학 점수 (2019)

국제 학생 평가 프로그램(PISA)은 전 세계 15세 학생들을 대상으로 3년마다 열립니다. 2012년에 미국은 과학과 독서에서 평균 점수를 얻었습니다. 65개 국가 중 36위를 차지하며 다른 진보적인 국가들보다 수학 성적이 뛰어났습니다. PISA 평가는 학생들의 수학에 대한 이해와 이 주제에 대한 접근 방법 및 응답을 분석하였습니다. 이것은 학습에 대한 세 가지 접근 방식을 나타냅니다. 일부 학생들은 주로 암기에 의존했습니다. 다른 사람들은 더 새로운 개념에 대해 더 많이 반성했습니다. 또 다른 그룹은 아직 공부하지 않은 원리에 더 집중했습니다. 미국은 다른 선진국에 비해 암기식의 비중이 높았습니다.[32] 2015년 테스트에서 미국은 수학을 포함한 모든 항목에서 상위 10위 안에 들지 못했습니다. 72개국에서 온 540,000명 이상의 십대들이 시험을 봤습니다. 미국 학생들의 수학 평균 점수는 이전 시험에 비해 11점 하락했습니다.[31] 2022년 PISA 시험은 수학의 미국 국가 평균이 다른 선진국들보다 뒤쳐지고 OECD 평균보다 낮은 것으로 나타났습니다.[215] 게다가, 미국 학생들의 3분의 1은 수학 기초 능력에 대한 요구를 충족시키지 못했습니다.[216]

하지만, 유럽계, 특히 아시아계 미국인 학생들은 OECD 평균 이상의 성적을 기록하고 있습니다. 아래 도표 참조.[34]

미국 국립과학재단(NSF)의 2021년 보고서에 따르면, 미국 학생들의 수학적 소양은 경제협력개발기구(OECD) 37개국 중 25위를 차지했습니다.[217]

2000년대와 2010년대에, 점점 더 많은 대학생들이 SAT를 치르면서, 점수는 하락했습니다 [218][33][30](아래 도표 참조). 이는 일부 주에서 대학 진학 여부와 상관없이 모든 고등학생에게 SAT 시험을 치르도록 요구했기 때문입니다.[218]

역사적 평균 SAT 수학 점수는 1980년에 최하점에 도달했고, 2005년과 2016년 사이에 하락했고, 2016년 재척도화 이후 하락했습니다.

2015년, Duke 대학교의 교육심리학자 Jonathan Wai는 1946년 육군 일반분류시험(10,000명), 1952년 선택복무대학 자격시험(38,420명), 1970년대 초 프로젝트 인재(40만명), 2002년과 2005년 사이 대학원 기록시험(120만명 이상)의 평균 시험 점수를 분석했습니다. 그리고 2014년 SAT 수학과 언어(160만). Wai는 한 가지 일관된 패턴을 발견했습니다: 가장 높은 시험 점수를 받은 학생들은 수학과 통계학, 자연과학과 사회과학, 공학을 전공으로 선택하는 경향이 있었고, 가장 낮은 학생들은 의료, 교육, 농업을 선택할 가능성이 더 높았습니다. (아래 두 차트를 참조하십시오.)[219][220]

NAEP (National Assessment of Education Progress) 시험의 결과는 수학 점수가 2010년대에 평준화되고 있지만, 상위권 학생들과 하위권 학생들 사이의 격차가 증가하고 있다는 것을 보여줍니다. 학교를 강제로 폐쇄하고 온라인으로 수업을 받게 한 COVID-19 대유행은 최고의 학생들이 최악의 학생들에 비해 실점이 적어 더 빠르게 따라잡을 수 있기 때문에 격차를 더욱 벌렸습니다.[35] 모든 과목에서 학생들의 점수가 하락한 반면 수학은 8점이 [221]하락해 50년 만에 가장 가파른 하락세를 보였습니다.[17] 소수의 예외를 제외하고 모든 인종, 성별, 사회경제적 계층, 학교의 유형, 주의 학생들의 점수가 떨어졌습니다.[222][223] 수학 교육이 독서보다 교실 경험에 더 의존하기 때문일 수도 있는데,[223] 대면 수업으로 복귀한 학생들은 대체로 독서보다 수학을 더 잘했기 때문입니다.[224] 그러나 통계와 확률이라는 주제에서 학생들의 성적은 팬데믹 이전에 이미 하락했습니다.[14] 결과적으로 2022-23학년도 대학생 코호트 전체는 평균 성적과 수학 수준이 더 낮습니다.[225]

2023년 부모들의 견해와 표준화된 시험 점수를 비교한 결과, 대부분의 부모들은 자녀들의 학업 적성을 과대평가했습니다. 수학은 90%의 학부모가 자녀가 성적 기준에 적합하다고 생각했음에도 불구하고 26%만이 능숙했습니다.[22] 8학년 때 NAEP 수학 점수가 더 높은 것은 높은 학업 수준, 높은 수입, 낮은 청소년 부모 형성 비율 및 낮은 범죄 가능성과 관련이 있습니다.[226]

고급 배치 수학

1950년대 초 AP(Advanced Placement) 수학 과목이 처음 제안되었을 때 미적분을 포함해야 하는지에 대한 논의가 상당했습니다. AP Mathematics는 물리학자들과 공학자들 덕분에 AP 미적분학으로 발전했습니다. 그들은 대학 프로그램 초기에 이러한 과목의 학생들을 미적분학에 노출시킬 필요가 있다는 것을 수학자들에게 설득시킨 덕분입니다.[24]

21세기 초, AP 다변수 미적분학의 개발에 대한 요구가 있었고, 실제로 많은 미국 고등학교들이 이 수업을 제공하기 시작하여, 대학들이 신입생을 배치하는 데 어려움을 겪고 있습니다.[24]

2021년 현재 AP Precalculus는 대학 위원회에 의해 개발 중이었지만, 학생들이 입학 전에 이 자료를 알고 있어야 한다는 점을 고려할 때 대학과 대학이 그러한 과정에 학점을 부여하지 않을 것이라는 우려가 있었습니다.[24] AP 프리칼큘러스는 2023년 가을에 출시되었습니다.[227]

컨퍼런스

수학교육 연구 및 실천가 회의는 NCTM의 지역회의 및 박람회와 연례회의 및 박람회를 포함합니다. 수학교육의 심리학 북미장 연례회의, 그리고 수많은 소규모 지역회의.

참고 항목

참고문헌

  1. ^ Lewin, Tamar (March 5, 2014). "A New SAT Aims to Realign With Schoolwork". The New York Times. Archived from the original on May 13, 2014. Retrieved May 14, 2014. He said he also wanted to make the test reflect more closely what students did in high school and, perhaps most important, rein in the intense coaching and tutoring on how to take the test that often gave affluent students an advantage.
  2. ^ Schwartz, Sarah (January 17, 2023). "Do Students Need Four Years of High School Math?". Education Week. Archived from the original on January 26, 2023. Retrieved January 26, 2023.
  3. ^ a b c Will, Madeline (November 10, 2014). "In Transition to Common Core, Some High Schools Turn to 'Integrated' Math". Education Week. Archived from the original on August 31, 2022. Retrieved August 31, 2022.
  4. ^ a b c d e f g h i j k l m n o p Klein, David (2003). "A Brief History of American K-12 Mathematics Education in the 20th Century". California State University, Northridge. Retrieved March 16, 2023.
  5. ^ a b Bressoud, David (September 1, 2022). "The Decline of High School Calculus". Math Values. Mathematical Association of America. Retrieved March 18, 2023.
  6. ^ a b c d Schwartz, Sarah (September 7, 2022). "Why Elite College Admissions May Play an Outsized Role in K-12 Math Programs". Education Week. Archived from the original on September 10, 2022.
  7. ^ a b c d e f g Tyre, Peg (February 8, 2016). "The Math Revolution". The Atlantic. Archived from the original on June 28, 2020. Retrieved February 4, 2021.
  8. ^ a b c d Hacker, Andrew (July 28, 2012). "Is Algebra Necessary?". The New York Times. Archived from the original on July 6, 2021. Retrieved April 24, 2023.
  9. ^ a b c Lewin, Tamar (March 14, 2008). "Report Urges Changes in Teaching Math". The New York Times. Archived from the original on April 24, 2023. Retrieved April 24, 2023.
  10. ^ a b c d e Hanford, Emily (February 3, 2017). "Trying to Solve a Bigger Math Problem". The New York Times. Retrieved April 9, 2023.
  11. ^ a b c d e Schwartz, Sarah (June 22, 2021). "Algebra 1 Is a Turning Point. Here's How to Help Incoming Students". Education Week. Archived from the original on March 24, 2023. Retrieved March 24, 2023.
  12. ^ a b c d e Drew, Christopher (November 4, 2011). "Why Science Majors Change Their Minds (It's Just So Darn Hard)". Education Life. The New York Times. Archived from the original on 2011-11-04. Retrieved October 28, 2019.
  13. ^ a b Cavanagh, Sean (June 7, 2007). "What Kind of Math Matters?". Education Week. Archived from the original on October 18, 2022. Retrieved April 17, 2023.
  14. ^ a b Schwartz, Sarah (February 24, 2023). "Students' Data Literacy Is Slipping, Even as Jobs Demand the Skill". Education Week. Archived from the original on April 25, 2023. Retrieved April 25, 2023.
  15. ^ U.S. Department of Education. "Mathematics Equals Opportunity" (PDF).
  16. ^ Pickover, Clifford A. (2009). The Math Book: From Pythagoras to the 57th Dimension, 250 Milestones in the History of Mathematics. New York: Sterling. p. 10. ISBN 978-1-4027-5796-9.
  17. ^ a b c Rubin, April (June 21, 2023). "Middle schoolers' reading and math scores plummet". Axios. Retrieved August 7, 2023.
  18. ^ a b c d e The Editorial Board (December 7, 2013). "Who Says Math Has to be Boring?". The New York Times. Archived from the original on April 30, 2023. Retrieved April 29, 2023.
  19. ^ a b Sparks, Sarah D. (September 7, 2022). "What School Staffing Shortages Look Like Now". Education Week. Archived from the original on April 25, 2023. Retrieved April 25, 2023.
  20. ^ a b Sparks, Sarah D. (May 16, 2011). "Researchers probe causes of math anxiety". Education Week. Archived from the original on May 3, 2023. Retrieved May 3, 2023.
  21. ^ Hoffman, Jan (August 24, 2015). "Square Root of Kids' Math Anxiety: Their Parents' Help". The New York Times. Archived from the original on August 25, 2015. Retrieved April 25, 2023.
  22. ^ a b Nawaz, Amna; Cuevas, Karina (April 6, 2023). "Study shows parents overestimate their student's academic progress". PBS Newshour. Retrieved April 9, 2023.
  23. ^ "In a New Survey, Americans say, "We're Not Good At Math"". Change the Equation. Archived from the original on March 2, 2012. Retrieved April 29, 2023.
  24. ^ a b c d e Bressoud, David (July 1, 2022). "Thoughts on Advanced Placement Precalculus". MAA Blog. Retrieved September 13, 2022.
  25. ^ a b Greitzer, S. (March 1973). "The First U.S.A. Mathematical Olympiad". American Mathematical Monthly. 80 (3): 276–281. doi:10.2307/2318449. JSTOR 2318449.
  26. ^ a b Miller, Michael E. (July 18, 2015). "Winning formula: USA tops International Math Olympiad for first time in 21 years". The Washington Post. Archived from the original on April 23, 2023. Retrieved April 27, 2023.
  27. ^ a b c Dutt-Ballerstadt, Reshmi (March 1, 2019). "Academic Prioritization or Killing the Liberal Arts?". Inside Higher Ed. Retrieved March 1, 2021.
  28. ^ a b Robelen, Erik W. (September 4, 2013). "Algebra 2: Not the Same Credential It Used to Be?". Education Week. Archived from the original on May 7, 2023. Retrieved May 6, 2023.
  29. ^ a b c Lattimore, Kayla; Depenbrock, Julie (July 19, 2017). "Say Goodbye To X+Y: Should Community Colleges Abolish Algebra?". NPR. Retrieved April 9, 2023.
  30. ^ a b Anderson, Nick (September 3, 2015). "SAT scores at lowest level in 10 years, fueling worries about high schools". The Washington Post. Retrieved September 17, 2020.
  31. ^ a b Jackson, Abby; Kiersz, Andy (December 6, 2016). "The latest ranking of top countries in math, reading, and science is out — and the US didn't crack the top 10". Business Insider. Retrieved July 25, 2016.
  32. ^ a b c Boaler, Jo; Zoido, Pablo (2016-10-13). "Why Math Education in the U.S. Doesn't Add Up". Scientific American Mind. 27 (6): 18–19. doi:10.1038/scientificamericanmind1116-18. ISSN 1555-2284. Archived from the original on August 23, 2022.
  33. ^ a b Hobbs, Tawnell D. (September 24, 2019). "SAT Scores Fall as More Students Take the Test". The Wall Street Journal. Archived from the original on November 28, 2020. Retrieved February 2, 2021.
  34. ^ a b "Highlights of U.S. PISA 2018 Results Web Report" (PDF).
  35. ^ a b Mervosh, Sarah (September 1, 2022). "The Pandemic Erased Two Decades of Progress in Math and Reading". The New York Times. Archived from the original on September 1, 2022. Retrieved September 1, 2022.
  36. ^ "Common Core State Standards for Mathematics" (PDF). Common Core State Standards Initiative. p. 3. Retrieved February 11, 2014.
  37. ^ "Mathematics". Common Core State Standards Initiative. Retrieved January 8, 2014.
  38. ^ a b c Schmidt, William H. (January 5, 2013). "The Common Core State Standards in Mathematics". Huffington Post. Retrieved March 17, 2023.
  39. ^ a b c Knudson, Kevin (2015). "The Common Core is today's New Math – which is actually a good thing". The Conversation. Retrieved September 9, 2015.
  40. ^ Fensterwald, John. "Districts confirm they're moving ahead with Common Core". EdSource. Retrieved 18 November 2013.
  41. ^ a b Sarikas, Christine (May 17, 2019). "The High School Math Courses You Should Take". PrepScholar. Retrieved August 18, 2023.
  42. ^ Geary, David; Hoard, Mary; Nugent, Lara; Bailey, Drew H. (January 30, 2013). "Adolescents' Functional Numeracy Is Predicted by Their School Entry Number System Knowledge". PLOS ONE. 8 (1): e54651. doi:10.1371/journal.pone.0054651. PMC 3559782. PMID 23382934.
  43. ^ Schwartz, Sarah (May 18, 2023). "What Does Math Teaching Look Like in U.S. Schools? 5 Charts Tell the Story". Education Week. Archived from the original on May 19, 2023. Retrieved May 25, 2023.
  44. ^ a b Sparks, Sarah D. (June 28, 2021). "Doubling Down on Algebra Can Pay Off in College, But Who Your Peers Are Matters, Too". Education Week. Archived from the original on April 25, 2023. Retrieved April 25, 2023.
  45. ^ a b c d e f Schwartz, Sarah (March 21, 2023). "San Francisco Insisted on Algebra in 9th Grade. Did It Improve Equity?". Education Week. Archived from the original on March 22, 2023. Retrieved March 23, 2023.
  46. ^ a b c d Schwartz, Sarah (July 12, 2023). "California Adopts Controversial New Math Framework. Here's What's In It". Education Week. Archived from the original on July 14, 2023. Retrieved July 21, 2023.
  47. ^ a b c Huffaker, Christopher (July 14, 2023). "Cambridge schools are divided over middle school algebra". Boston Globe. Archived from the original on July 14, 2023. Retrieved July 21, 2023.
  48. ^ a b Geometry. Prentice Hall. 2008. ISBN 978-0-133-65948-1.
  49. ^ a b National Council of Teachers of Mathematics (NCTM) (1912). "Final Report of the National Committee of Fifteen on Geometry Syllabus". The Mathematics Teacher. 5 (2): 46–131. JSTOR 27949764.
  50. ^ Herbst, Patricio G. (March 2002). "Establishing a custom of proving in American school geometry: evolution of the two-column proof in the early twentieth century". Educational Studies in Mathematics. 49: 283–312.
  51. ^ Algebra 2. Prentice Hall. 2008. ISBN 978-0-133-19759-4.
  52. ^ Whoriskey, Peter (April 3, 2011). "Requiring Algebra II in high school gains momentum nationwide". The Washington Post. Archived from the original on May 7, 2023. Retrieved May 6, 2023.
  53. ^ a b "University of California admission subject requirements". Retrieved 2018-08-24.
  54. ^ Loewus, Liana (January 31, 2014). "Texas Officially Drops Algebra 2 Requirement for Graduation". Education Week. Archived from the original on May 7, 2023. Retrieved May 6, 2023.
  55. ^ Demana, Franklin D.; Waits, Bert K.; Foley, Gregory D.; Kennedy, Daniel (2000). Precalculus: Graphical, Numerical, Algebraic (7th ed.). Addison-Wesley. ISBN 978-0-321-35693-2.
  56. ^ Simmons, George (2003). Precalculus Mathematics in a Nutshell: Geometry, Algebra, Trigonometry (Illustrated ed.). Wipf & Stock Publishers. ISBN 978-1-592-44130-3.
  57. ^ Stewart, James; Redlin, Lothar; Watson, Saleem (2006). Algebra and Trigonometry (2nd ed.). Cengage Learning. ISBN 978-0-495-01357-0.
  58. ^ "AP Precalculus Course Framework (Preview)" (PDF). AP Central. College Board. November 2022.
  59. ^ Gewertz, Catherine (November 13, 2019). "Should High Schools Rethink How They Sequence Math Courses?". Education Week. Archived from the original on May 7, 2023. Retrieved May 6, 2023.
  60. ^ "Florida B.E.S.T Standards: Mathematics" (PDF). Florida Department of Education. 2020.
  61. ^ "Florida's B.E.S.T.: Here's what's next for the state's new educational standard". February 12, 2020.
  62. ^ a b Sparks, Sarah D. (July 31, 2023). "Are Students Getting All the Math They Need to Succeed?". Education Week. Archived from the original on July 31, 2023. Retrieved January 5, 2024.
  63. ^ Bailey, Thomas; Dong Wook Jeong; Sung-Woo Cho (Spring 2010). "Referral, enrollment and completion in developmental education sequences in community colleges". Economics of Education Review. 29 (2): 255–270. doi:10.1016/j.econedurev.2009.09.002.
  64. ^ a b c d e f Bressoud, David M. (2021). "The Strange Role of Calculus in the United States". ZDM – Mathematics Education. 53 (3): 521–533. doi:10.1007/s11858-020-01188-0. S2CID 225295970.
  65. ^ a b c d Bressoud, David (August 1, 2021). "Calculus Around the World". Math Values. Mathematical Association of America. Retrieved March 18, 2023.
  66. ^ a b c d Thomas, George B.; Weir, Maurice D.; Hass, Joel (2010). Thomas's Calculus: Early Transcendentals (12th ed.). Addison-Wesley. ISBN 978-0-321-58876-0.
  67. ^ Finney, Ross L.; Demana, Franklin D.; Waits, Bert K.; Kennedy, Daniel (2012). Calculus: Graphical, Numerical, Algebraic (4th ed.). Prentice Hall. ISBN 978-0-133-17857-9.
  68. ^ a b c d Stewart, James (2012). Calculus: Early Transcendentals (7th ed.). Brooks/Cole Cengage Learning. ISBN 978-0-538-49790-9.
  69. ^ a b c Adams, Robert; Essex, Christopher (2021). Calculus: A Complete Course (10th ed.). Pearson. ISBN 978-0-135-73258-8.
  70. ^ "United States of America Mathematical Olympiad - USAMO". The Mathematical Association of America. 2006. Archived from the original on November 6, 2006. Retrieved 2006-11-29.
  71. ^ Levy, Max G. (February 16, 2021). "The Coach Who Led the U.S. Math Team Back to the Top". Quanta Magazine. Retrieved April 27, 2023.
  72. ^ Boas, Mary (2005). Mathematical Methods in the Physical Sciences (3rd ed.). Wiley. ISBN 978-0-471-19826-0.
  73. ^ Hassani, Sadri (2008). Mathematical Methods: For Students of Physics and Related Fields (2nd ed.). Spring. ISBN 978-0-387-09503-5.
  74. ^ Riley, K.F.; Hobson, Michael P.; Bence, S.J. (2006). Mathematical Methods for Physics and Engineering. Cambridge University Press. ISBN 978-0-521-67971-8.
  75. ^ Strang, Gilbert (2016). Introduction to Linear Algebra (5th ed.). Wellesley-Cambridge Press. ISBN 978-0-980-23277-6.
  76. ^ Axler, Sheldon (2014). Linear Algebra Done Right. Springer. ISBN 978-3-319-11079-0.
  77. ^ Halmos, Paul (2017). Finite-Dimensional Vector Spaces (2nd ed.). Dover Publications. ISBN 978-0-486-81486-5.
  78. ^ Spiegel, Murray R.; Lipschutz, Seymour; Schiller, John J.; Spellman, Dennis (2009). Schaum's Outline of Complex Variables (2nd ed.). McGraw-Hill Companies. ISBN 978-0-071-61569-3.
  79. ^ Kwok, Yue Kuen (2010). Applied Complex Variables for Scientists and Engineers (2nd ed.). Cambridge University Press. ISBN 978-0-521-70138-9.
  80. ^ Krantz, Steven G. (2008). A Guide to Complex Variables. Mathematical Association of America. ISBN 978-0-883-85338-2.
  81. ^ Zill, Dennis G.; Wright, Warren S. (2013). Differential Equations with Boundary-Value Problems (8th ed.). Brooks/Cole Cengage Learning. ISBN 978-1-111-82706-9.
  82. ^ Boyce, William E.; DiPrima, Richard C. (2012). Elementary Differential Equations and Boundary Value Problems (10th ed.). Wiley. ISBN 978-0-470-45831-0.
  83. ^ Arnold, Vladimir (1978). Ordinary Differential Equations. Translated by Silverman, Richard. The MIT Press. ISBN 978-0-262-51018-9.
  84. ^ Bleecker, David D.; Csordas, George (1997). Basic Partial Differential Equations. International Press of Boston. ISBN 978-1-571-46036-3.
  85. ^ Asmar, Nakhlé H. (2016). Partial Differential Equations with Fourier Series and Boundary Value Problems (3rd ed.). Dover Publications. ISBN 978-0-486-80737-9.
  86. ^ Strauss, Walter A. (2007). Partial Differential Equations: An Introduction. Wiley. ISBN 978-0-470-05456-7.
  87. ^ Eccles, Peter J. (1998). An Introduction to Mathematical Reasoning: Numbers, Sets and Functions. Cambridge University Press. ISBN 978-0-521-59718-0.
  88. ^ Hammack, Richard (2013). Book of Proof (2nd ed.). Lightning Source Inc. ISBN 978-0-989-47210-4.
  89. ^ Hamkins, Joel David (2020). Proof and the Art of Mathematics. MIT Press. ISBN 978-0-262-53979-1.
  90. ^ Artin, Michael (2017). Algebra (2nd ed.). Pearson. ISBN 978-0-134-68960-9.
  91. ^ Dummit, David S.; Foote, Richard M. (2003). Abstract Algebra (3rd ed.). Wiley. ISBN 978-0-471-43334-7.
  92. ^ Pinter, Charles C. (2010). A Book of Abstract Algebra (2nd ed.). Dover Publications. ISBN 978-0-486-47417-5.
  93. ^ Scharlau, Winfried; Opolka, Hans (2010). From Fermat to Minkowski: Lectures on the Theory of Numbers and Its Historical Development. Springer-Verlag. ISBN 978-1-441-92821-4.
  94. ^ Granville, Andrew (2019). Number Theory Revealed: A Masterclass. Rhode Island: American Mathematical Society. ISBN 978-1-4704-6370-0.
  95. ^ Dudley, Underwood (2008). Elementary Number Theory (2nd ed.). Dover Publications. ISBN 978-0-486-46931-7.
  96. ^ Mattuck, Arthur (2013). Introduction to Analysis. CreateSpace Independent Publishing Platform. ISBN 978-1-484-81411-6.
  97. ^ Bartle, Robert G.; Sherbert, Donald R. (2011). Introduction to Real Analysis (4th ed.). John Wiley & Sons, Inc. ISBN 978-0-471-43331-6.
  98. ^ Abbott, Stephen (2016). Understanding Analysis (2nd ed.). Springer. ISBN 978-1-493-92711-1.
  99. ^ Rudin, Walter (1976). Principles of Mathematical Analysis (3rd ed.). McGraw Hill. ISBN 978-0-070-54235-8.
  100. ^ Spivak, Michael (1965). Calculus on Manifolds: A Modern Approach to Classical Theorems of Advanced Calculus. CRC Press. ISBN 978-0-367-09190-3.
  101. ^ Loomis, Lynn Harold; Sternberg, Shlomo Zvi (2014). Advanced Calculus (revised ed.). World Scientific. ISBN 978-9-814-58393-0.
  102. ^ Marsden, Jerrold E.; Tromba, Anthony J. (2011). Vector Calculus (6th ed.). W. H. Freeman. ISBN 978-1-429-21508-4.
  103. ^ Ahlfors, Lars Valerian (1978). Complex Analysis: An Introduction to the Theory of Analytic Functions of One Complex Variable. McGraw-Hill Higher Education. ISBN 978-0-070-00657-7.
  104. ^ Gamelin, Theodore W. (2001). Complex Analysis. Springer. ISBN 978-0-387-95069-3.
  105. ^ Stein, Elias M.; Shakarchi, Rami (2003). Complex Analysis. Princeton University Press. ISBN 978-0-691-11385-2.
  106. ^ Bak, Joseph; Newman, Donald J. (2010). Complex Analysis (3rd ed.). New York: Springer. ISBN 978-1-441-97287-3.
  107. ^ Anderson, David F.; Seppalainen, Timo; Valko, Benedek (2017). Introduction to Probability. Cambridge University Press. ISBN 978-1-108-41585-9.
  108. ^ Billingsley, Patrick (2012). Probability and Measure (Anniversary ed.). Wiley. ISBN 978-1-118-12237-2.
  109. ^ Wackerly, Dennis D.; Mendenhall, William; Scheaffer, Richard L. (2008). Mathematical Statistics with Applications (7th ed.). Thomson Brooks/Cole. ISBN 978-0-495-11081-1.
  110. ^ Wasserman, Larry (2003). All of Statistics: A Concise Course in Statistical Inference. Springer. ISBN 978-0-387-40272-7.
  111. ^ Lipschutz, Seymour (1998). Schaum's Outline of Set Theory and Related Topics. McGraw-Hill Companies. ISBN 978-0-070-38159-9.
  112. ^ Stoll, Robert Roth (1979). Set Theory and Logic. Dover Publications. ISBN 978-0-486-63829-4.
  113. ^ Halmos, Paul R. (1968). Naive Set Theory. Springer. ISBN 978-0-387-90092-6.
  114. ^ Rautenberg, Wolfgang (2006). A Concise Introduction to Mathematical Logic. Springer. ISBN 978-0-387-30294-2.
  115. ^ Dobrow, Robert P. (2016). Introduction to Stochastic Processes with R. Wiley. ISBN 978-1-118-74065-1.
  116. ^ Bartle, Robert G. (2001). A Modern Theory of Integration. American Mathematical Society. ISBN 978-0-821-80845-0.
  117. ^ Stein, Elias M.; Shakarchi, Rami (2005). Real Analysis: Measure Theory, Integration, and Hilbert Spaces. Princeton University Press. ISBN 978-0-691-11386-9.
  118. ^ Folland, Gerald B. (2007). Real Analysis: Modern Techniques and Their Applications (2nd ed.). Wiley. ISBN 978-0-471-31716-6.
  119. ^ Cohn, Donald L. (2015). Measure Theory (2nd ed.). Birkhäuser. ISBN 978-1-489-99762-3.
  120. ^ Stein, Elias M.; Shakarchi, Rami (2003). Fourier Analysis: An Introduction. Princeton University Press. ISBN 978-0-691-11384-5.
  121. ^ Lighthill, M.J. (1958). An Introduction to Fourier Analysis and Generalised Functions. Cambridge University Press. ISBN 978-0-521-09128-2.
  122. ^ Stein, Elias M.; Shakarchi, Rami (2009). Functional Analysis: Introduction to Further Topics in Analysis. Princeton University Press. ISBN 978-0-691-11387-6.
  123. ^ Sochi, Taha (2017). Introduction to Differential Geometry of Space Curves and Surfaces. CreateSpace. ISBN 978-1-546-68183-0.
  124. ^ Do Carmo, Manfredo P. (2016). Differential Geometry of Curves and Surfaces. Dover Publications. ISBN 978-0-486-80699-0.
  125. ^ Pressley, Andrew (2010). Elementary Differential Geometry (2nd ed.). Springer. ISBN 978-1-848-82890-2.
  126. ^ Munkres, James R. (2000). Topology (2nd ed.). Pearson. ISBN 978-0-131-81629-9.
  127. ^ Mendelson, Bert (1990). Introduction to Topology (3rd ed.). Dover Publications. ISBN 978-0-486-66352-4.
  128. ^ Süli, Endre; Mayers, David (2003). An Introduction to Numerical Analysis. Cambridge University Press. ISBN 978-0-521-00794-8.
  129. ^ Osborne, Michael J.; Rubinstein, Ariel (1994). A Course in Game Theory. MIT Press. ISBN 978-0-262-65040-3.
  130. ^ Tadelis, Steven (2013). Game Theory: An Introduction. Princeton University Press. ISBN 978-0-691-12908-2.
  131. ^ Gibbons, Robert (1992). Game Theory for Applied Economists. Princeton University Press. ISBN 978-0-691-00395-5.
  132. ^ Kot, Mark (2014). A First Course on the Calculus of Variations. American Mathematical Society. ISBN 978-1-4704-1495-5.
  133. ^ a b Lanczos, Cornelius (1986). The Variational Principles of Mechanics (4th ed.). Dover Publications. ISBN 978-0-486-65067-8.
  134. ^ Gelfand, Israel M.; Fomin, S.V. (2000). Calculus of Variations. Translated by Silverman, Richard. Dover Publications. ISBN 978-0-486-41448-5.
  135. ^ Stillwell, John (2010). Mathematics and Its History (3rd ed.). Springer. ISBN 978-1-441-96052-8.
  136. ^ Katz, Victor (2008). A History of Mathematics: An Introduction (3rd ed.). Addison Wesley Longman. ISBN 978-0-321-38700-4.
  137. ^ Boyer, Carl B.; Merzbach, Uta C. (1991). A History of Mathematics. Wiley. ISBN 978-0-471-54397-8.
  138. ^ Kline, Morris (1972). Mathematical Thought from Ancient to Modern Times. New York: Oxford University Press. ISBN 978-0-195-01496-9.
  139. ^ Taylor, John R. (2005). Classical Mechanics. University Science Books. ISBN 978-1-891-38922-1.
  140. ^ Goldstein, Herbert; Poole, Charles; Safko, John (2001). Classical Mechanics (3rd ed.). Pearson. ISBN 978-0-201-65702-9.
  141. ^ Arnold, Vladimir (1978). Mathematical Methods of Classical Mechanics. Springer-Verlag. ISBN 978-0-387-90314-9.
  142. ^ Purcell, Edward M.; Morin, David J. (2013). Electricity and Magnetism (3rd ed.). Cambridge University Press. ISBN 978-1-107-01402-2.
  143. ^ Griffiths, David J. (2017). Introduction to Electrodynamics (4th ed.). Cambridge University Press. ISBN 978-1-108-42041-9.
  144. ^ Strogatz, Steven H. (1994). Nonlinear Dynamics and Chaos: With Applications to Physics, Biology, Chemistry, and Engineering. CRC Press. ISBN 978-0-367-09206-1.
  145. ^ Batchelor, G. K. (2000). An Introduction to Fluid Dynamics. Cambridge University Press. ISBN 978-0-521-66396-0.
  146. ^ Landau, Lev D.; Lifshitz, Evgeny (1987). Fluid Mechanics (2nd ed.). Butterworth-Heinemann. ISBN 978-0-750-62767-2.
  147. ^ Townsend, John S. (2012). A Modern Approach to Quantum Mechanics (2nd ed.). University Science Books. ISBN 978-1-891-38978-8.
  148. ^ Shankar, Ramamurti (2012). Principles of Quantum Mechanics (2nd ed.). Springer-Verlag. ISBN 978-1-475-70578-2.
  149. ^ Sakurai, J. J.; Napolitano, Jim (2020). Modern Quantum Mechanics (3rd ed.). Cambridge University Press. ISBN 978-1-108-47322-4.
  150. ^ Hartle, James B. (2002). Gravity: An Introduction to Einstein's General Relativity. Pearson. ISBN 978-0-805-38662-2.
  151. ^ Carroll, Sean (2019). Spacetime and Geometry: An Introduction to General Relativity. Cambridge University Press. ISBN 978-1-108-48839-6.
  152. ^ Misner, Charles; Thorne, Kip; Wheeler, John (2017). Gravitation. Princeton University Press. ISBN 978-0-691-17779-3.
  153. ^ Wald, Robert (1984). General Relativity. The University of Chicago Press. ISBN 978-0-226-87033-5.
  154. ^ Graham, Ronald L.; Knuth, Donald; Patashnik, Oren (1994). Concrete Mathematics: A Foundation for Computer Science (2nd ed.). Addison-Wesley Professional. ISBN 978-0-201-55802-9.
  155. ^ Rosen, Kenneth H. (2018). Discrete Mathematics and Its Applications (8th ed.). McGraw-Hill. ISBN 978-1-259-67651-2.
  156. ^ Cover, Thomas M.; Thomas, Joy A. (2006). Elements of Information Theory (2nd ed.). Wiley-Interscience. ISBN 978-0-471-24195-9.
  157. ^ Sipser, Michael (1996). Introduction to the Theory of Computation (3rd ed.). Cengage Learning. ISBN 978-1-133-18779-0.
  158. ^ Cormen, Thomas H.; Leiserson, Charles E.; Rivest, Ronald L.; Stein, Clifford (2009). Introduction to Algorithms (3rd ed.). The MIT Press. ISBN 978-0-262-03384-8.
  159. ^ Gross, Benedict; Harris, Joseph; Riehl, Emily (2019). Fat Chance: Probability from 0 to 1. Cambridge University Press. ISBN 978-1-108-72818-8.
  160. ^ Johnson, Robert; Kuby, Patricia (2003). Just the Essentials of Elementary Statistics (3rd ed.). Thomson Brooks/Cole. ISBN 0-534-38472-2.
  161. ^ Roughgarden, Tim (2016). Twenty Lectures on Algorithmic Game Theory. Cambridge University Press. ISBN 978-1-107-17266-1.
  162. ^ Taylor, John R. (1996). Introduction to Error Analysis: The Study of Uncertainties in Physical Measurements (2nd ed.). University Science Books. ISBN 978-0-93570-275-0.
  163. ^ Hughes, Ifan G.; Hase, Thomas P. A. (2013). Measurements and their Uncertainties: A Practical Guide to Modern Error Analysis. Oxford: Oxford University Press. ISBN 978-0-19-956633-4.
  164. ^ Weber, Hans J.; Harris, Frank E.; Arfken, George B. (2012). Mathematical Methods for Physicists (7th ed.). Elsevier Science & Technology. ISBN 978-9-381-26955-8.
  165. ^ Hassani, Sadri (2013). Mathematical Physics: A Modern Introduction to Its Foundations (2nd ed.). Springer. ISBN 978-3-319-01194-3.
  166. ^ Neuenschwander, Dwight E. (2014). Tensor Calculus for Physics: A Concise Guide. Johns Hopkins University Press. ISBN 978-1-421-41565-9.
  167. ^ Jeevanjee, Nadir (2015). An Introduction to Tensors and Group Theory for Physicists (2nd ed.). Boston: Birkhäuser. ISBN 978-3-319-14793-2.
  168. ^ Zee, Anthony (2016). Group Theory in a Nutshell for Physicists (Illustrated ed.). Princeton University Press. ISBN 978-0-691-16269-0.
  169. ^ Bender, Carl; Orszag, Steven A. (2010). Advanced Mathematical Methods for Scientists and Engineers I: Asymptotic Methods and Perturbation Theory. Springer. ISBN 978-1-441-93187-0.
  170. ^ Baker, Billy (January 20, 2012). "An integral part of MIT life". Boston Globe. Retrieved February 6, 2021.
  171. ^ "Integration Bee". AMS Student Chapter, University of Connecticut. 2018. Retrieved February 6, 2021.
  172. ^ "WVU Integration Bee Competition". School of Mathematical and Data Sciences, West Virginia University. 2023. Retrieved May 4, 2023.
  173. ^ "Integration Bee". Berekley SPS. University of California, Berkeley. Retrieved February 6, 2021.
  174. ^ a b Miller, Sandi (March 3, 2020). "MIT students dominate annual Putnam Mathematical Competition". MIT News. Retrieved April 27, 2023.
  175. ^ Jiang, Georgia (February 27, 2023). "UMD Students Win Fourth Place in Putnam Mathematical Competition". Maryland Today. University of Maryland. Retrieved April 27, 2023.
  176. ^ Shelton, Jim (March 29, 2023). "Yale team excels at Putnam student mathematics competition". Yale Daily News. Retrieved May 7, 2023.
  177. ^ Nasar, Sylvia (1998). "2: Carnegie Institute of Technology". A Beautiful Mind. New York: Simon & Shuster. pp. 43–44. ISBN 0-7432-2457-4.
  178. ^ Miller, Sandi (March 27, 2019). "Solving for fun (and sometimes prizes)". MIT News. Retrieved May 6, 2023.
  179. ^ a b "A Leak in the STEM Pipeline: Taking Algebra Early". U.S. Department of Education. November 2018. Retrieved May 13, 2023.
  180. ^ "AP Exam Volume Change (2009-2019)" (PDF). AP Data Archive. College Board. 2019.
  181. ^ a b c Champion, Joe; Mesa, Vilma (2017). "Factors Affecting Calculus Completion among U.S. High School Students". In Bressoud, David (ed.). The Role of Calculus in the Transition from High School to College Mathematics (PDF). Washington, D.C.: MAA and NCTM. pp. 9–25.
  182. ^ Quinton, Sophie (December 11, 2014). "The Race Gap in High School Honors Classes". The Atlantic. Archived from the original on April 2, 2021. Retrieved May 17, 2023.
  183. ^ Robelen, Erik W. (February 15, 2012). "Girls Like Biology, Boys Like Physics? AP Data Hint at Preferences". Education Week. Archived from the original on April 30, 2023. Retrieved April 30, 2023.
  184. ^ Loewus, Liana (August 3, 2016). "What's Keeping Women Out of Science, Math Careers? Calculus and Confidence". Education Week. Archived from the original on April 30, 2023. Retrieved April 30, 2023.
  185. ^ Whitney, A.K. (April 18, 2016). "Math for Girls, Math for Boys". The Atlantic. Archived from the original on April 4, 2021. Retrieved May 2, 2023.
  186. ^ Quinton, Sophie (October 29, 2013). "Algebra Doesn't Have to Be Scary". The Atlantic. Archived from the original on July 8, 2022. Retrieved May 2, 2023.
  187. ^ "Was your degree really worth it?". The Economist. April 3, 2023. Archived from the original on April 8, 2023. Retrieved April 14, 2023.
  188. ^ Stephanie Banchero (May 8, 2012). "School-standards pushback". The Wall Street Journal. Retrieved March 23, 2013.
  189. ^ a b Nappi, Chiara (May 1990). "On Mathematics and Science Education in the US and Europe". Physics Today. 43 (5): 77. Bibcode:1990PhT....43e..77N. doi:10.1063/1.2810564.
  190. ^ Blad, Evie (April 17, 2023). "Parents, Teachers Agree: Math Matters, But Schools Must Make It Relevant". Education Week. Archived from the original on April 17, 2023. Retrieved April 17, 2023.
  191. ^ Garraty, John A. (1991). "Chapter XXXII Society in Flux, 1945-1980. Rethinking Public Education". The American Nation: A History of the United States. United States of America: Harper Collins. pp. 896–7. ISBN 978-0-06-042312-4.
  192. ^ Farmelo, Graham (2009). "Twenty-six: 1958-1962". The Strangest Man: the Hidden Life of Paul Dirac, Mystic of the Atom. Basic Books. p. 363. ISBN 978-0-465-02210-6.
  193. ^ a b Gandel, Stephen (May 30, 2015). "This 1958 Fortune article introduced the world to John Nash and his math". Fortune. Retrieved March 16, 2023.
  194. ^ Gispert, Hélène. "L'enseignement des mathématiques au XXe siècle dans le contexte français". CultureMATH (in French). Archived from the original on July 15, 2017. Retrieved November 4, 2020.
  195. ^ Feynman, Richard P. (1965). "New Textbooks for the 'New' Mathematics" (PDF). Engineering and Science. XXVIII (6): 9–15. ISSN 0013-7812.
  196. ^ Kline, Morris (1973). Why Johnny Can't Add: The Failure of the New Math. New York: St. Martin's Press. pp. 17, 98. ISBN 0-394-71981-6.
  197. ^ Gillman, Leonard (May 1974). "Review of Why Johnny Can't Add". American Mathematical Monthly. 81 (5): 531–2. JSTOR 2318615.
  198. ^ Simmons, George F. (2003). "Algebra – Introduction". Precalculus Mathematics in a Nutshell: Geometry, Algebra, Trigonometry: Geometry, Algebra, Trigonometry. Wipf and Stock Publishers. p. 33. ISBN 9781592441303.
  199. ^ "America's Maths Wars". The Economist. November 6, 2021. Archived from the original on November 4, 2021. Retrieved August 23, 2022.
  200. ^ Wu, Hung-Hsi (Fall 1999). "Basic Skills Versus Conceptual Understanding: A Bogus Dichotomy in Mathematics Education" (PDF). American Educator. American Federation of Teachers.
  201. ^ Hiebert, James; Stigler, James W. (September 2000). "A proposal for improving classroom teaching: Lessons from the TIMSS video study". The Elementary School Journal. 101 (1): 3–20. doi:10.1086/499656. S2CID 144020162.
  202. ^ Wayback Machine에 보관된 Christian Science Monitor 2008-05-09
  203. ^ "Frequently Asked Questions About the Core-Plus Mathematics Project". Archived from the original on 2010-08-21. Retrieved 2009-10-26.
  204. ^ 월스트리트저널, 뉴욕타임스, 시카고선타임스
  205. ^ Toh, Tin Lam (2021). "School calculus curriculum and the Singapore mathematics curriculum framework". ZDM – Mathematics Education. 53 (3): 535–547. doi:10.1007/s11858-021-01225-6. S2CID 233904989.
  206. ^ a b Sparks, Sarah D. (January 7, 2020). "The Myth Fueling Math Anxiety". Education Week. Archived from the original on August 31, 2022. Retrieved August 31, 2022.
  207. ^ Gonser, Sarah (April 12, 2018). "Students are being prepared for jobs that no longer exist. Here's how that could change". Culture Matters. NBC News. Retrieved October 25, 2019.
  208. ^ Wang, Amy X. (July 19, 2017). "No wonder young Americans feel so important, when half of them finish high school as A students". Quartz. Archived from the original on June 19, 2021.
  209. ^ Furner, Joseph M. and Kumar, David D. [1], "수학과 과학 통합 논쟁: 교사 교육을 위한 입장", 유라시아 수학, 과학 및 기술 교육 저널, Vol. 3, Num. 3, 2007년 8월 15일 접속
  210. ^ Clynes, Tom (September 7, 2016). "How to raise a genius: lessons from a 45-year study of super-smart children". Nature. 537 (7619): 152–155. Bibcode:2016Natur.537..152C. doi:10.1038/537152a. PMID 27604932. S2CID 4459557.
  211. ^ Matthews, Jay (September 10, 2022). "Middle schools shun challenges, such as teaching your kid algebra". The Washington Post. Archived from the original on September 12, 2022. Retrieved April 29, 2023.
  212. ^ Clynes, Tom (January 2017). "Nurturing Genius". Scientific American. Archived from the original on December 23, 2016.
  213. ^ Will, Madaline (May 18, 2022). "Are Aspiring Elementary Teachers Learning Enough Math?". Education Week. Archived from the original on August 31, 2022. Retrieved May 10, 2023.
  214. ^ "What the world can learn from the latest PISA test results". The Economist. Retrieved 2018-07-25.
  215. ^ Saric, Ivana (December 5, 2023). "U.S. students' math scores plunge in global education assessment". Axios. Retrieved January 7, 2024.
  216. ^ Mervosh, Sarah (December 5, 2023). "Math Scores Dropped Globally, but the U.S. Still Trails Other Countries". The New York Times. Archived from the original on December 5, 2023. Retrieved January 7, 2024.
  217. ^ Rotermund, Susan; Burke, Amy (July 8, 2021). "Elementary and Secondary STEM Education - Executive Summary". National Science Foundation. Retrieved January 27, 2023.
  218. ^ a b Finder, Alan (August 28, 2007). "Math and Reading SAT Scores Drop". The New York Times. Archived from the original on April 24, 2023. Retrieved April 24, 2023.
  219. ^ Wai, Jonathan (February 3, 2015). "Your college major is a pretty good indication of how smart you are". Quartz. Archived from the original on January 16, 2020. Retrieved January 30, 2021.
  220. ^ Crew, Bec (February 16, 2015). "Your College Major Can Be a Pretty Good Indication of How Smart You Are". Humans. Science Magazine. Retrieved January 30, 2021.
  221. ^ Binkey, Collin (October 24, 2022). "Test scores show how COVID set kids back across the U.S." PBS Newshour. Retrieved December 31, 2022.
  222. ^ Sparks, Sarah D. (October 24, 2022). "Explaining That Steep Drop in Math Scores on NAEP: 5 Takeaways". Education Week. Archived from the original on March 20, 2023. Retrieved April 25, 2023.
  223. ^ a b Chapman, Ben (October 24, 2022). "Math Scores Dropped in Every State During Pandemic, Report Card Shows". The Wall Street Journal. Archived from the original on October 24, 2022. Retrieved May 18, 2023.
  224. ^ Lasarte, Diego (May 3, 2023). "US eighth graders' history test scores hit lowest levels on record". Quartz. Archived from the original on May 19, 2023. Retrieved May 18, 2023.
  225. ^ Fawcett, Eliza (November 1, 2022). "The Pandemic Generation Goes to College. It Has Not Been Easy". The New York Times. Archived from the original on November 1, 2022. Retrieved May 25, 2023.
  226. ^ Doty, Elena; Kane, Thomas J.; Patterson, Tyler; Staiger, Douglas O. (December 2022). "What Do Changes in State Test Scores Imply for Later Life Outcomes?". NBER Working Papers. Working Paper Series. National Bureau of Economic Research. doi:10.3386/w30701.
  227. ^ Najarro, Ileana (May 19, 2022). "A New AP Precalculus Course Aims to Diversify the Math Pipeline". Education Week. Archived from the original on March 24, 2023.

더보기

  • Garelick, Barry; Wilson, JR (2022). Traditional Math: An effective strategy that teachers feel guilty using. John Catt Educational. ISBN 978-1-91526-154-0.

외부 링크