컨볼루션

수학(특히 함수해석학)에서 컨볼루션(convolution)은 두 함수(f와 g)에 대한 수학적 연산으로, 하나의 모양이 다른 함수에 의해 어떻게 수정되는지를 나타내는 세 번째 함수(${\displaystyle g}$g \ $displaystyle$ f$*g$를 생성한다.컨볼루션이란 결과함수와 그 계산과정 모두를 말합니다.이는 한 함수가 반전 및 이동된 후 두 함수의 곱의 적분으로 정의됩니다.적분은 모든 시프트 값에 대해 평가되어 컨볼루션 함수를 생성합니다.

연속형 또는 이산형 변수의 실제값 함수의 경우 f(x) 또는 g(x) 중 하나가 y축에 대해 반영된다는 점에서만 f($x$) ${\displaystyle }$ f(x)와 f(x)의 상호상관 또는 f(x)의 상호상관이라는 점에서 cross-correlation (f${\displaystyle g}$ g\$style$ f$\styleg$과 유사합니다.복소수 함수의 경우 교차 상관 연산자는 컨볼루션 연산자의 인접입니다.

Convolution은 확률, 통계, 음향, 분광학, 신호 처리 및 이미지 처리, 지구물리학, 공학, 물리, 컴퓨터 비전 및 미분 ^[1]방정식을 포함하는 응용 프로그램이 있습니다.

컨볼루션은 유클리드 공간과 다른 그룹의 ^{[citation needed]}함수에 대해 정의될 수 있다.예를 들어 이산시간 푸리에 변환과 같은 주기함수는 원상에서 정의되어 주기적 컨볼루션에 의해 수렴될 수 있다.(DTFT의 18행 속성 참조).정수 집합의 함수에 대해 이산 컨볼루션을 정의할 수 있습니다.

컨볼루션의 일반화는 수치해석 및 수치선형대수 분야 및 신호처리에서의 ^{[citation needed]}유한임펄스 응답 필터의 설계 및 구현에 응용된다.

컨볼루션 연산의 역연산을 디콘볼루션이라고 합니다.

정의.

f와 g의 convolution은 fµg로 표기되며, 기호가 ^[B]θ인 연산자를 나타낸다.이는 한 함수가 반전 및 이동된 후 두 함수의 곱의 적분으로 정의됩니다.이와 같이, 이것은 특정 종류의 적분 변환입니다.

${\displaystyle (f*g)(t):=\int _{-\infty }^{\infty}f(\infty)g(t-\interface),d\interface.}$

동등한 정의는 다음과 같습니다(환산성 참조).

${\displaystyle (f*g)(t):=\int _{-\infty }^{\infty }f(t-\infty)g(\interface ), d\interf .}$

기호 t는 위에서 사용되지만 시간 영역을 나타낼 필요는 없습니다.단, 이 문맥에서 컨볼루션 공식은 함수 g(-θ)에 의해 무게 부여되는 함수 f(θ) 아래의 면적 t로 기술할 수 있다.t의 변화에 따라 가중치 함수 g(t - θ)는 입력 함수 f(θ)의 다른 부분을 강조한다.

함수 f, g가 [0, θ]에서만 지원되는 경우(즉, 마이너스 인수의 경우 0), 적분 한계는 잘려 다음과 같은 결과를 얻을 수 있습니다.

$\displaystyle (f*g)(t)=\int _{0}^{t}f(\displays)g(\displays)\d\displays \text{\infty}f,g:[0,\infty}\mathbbb {R}로 이동합니다.$

컨볼루션의 다차원 공식은 정의 영역(아래)을 참조하십시오.

표기법

일반적인 엔지니어링 표기 규칙은 다음과 같습니다.^[2]

${\displaystyle f(t)*g(t)\mathrel {:=} \underbrace {int _{-\infty }^{\infty }f(\display)g(t-\display ), d\display }_{(f*g)(t)},$

혼동을 피하기 위해 신중하게 해석해야 합니다.예를 들어 f(t)gg(t - t₀)는 (fgg)(t - t₀)에 상당하지만 f(t₀ - t)(g(t₀ - t)는 (f)g)(t₀ - ^[3]2t)에 상당한다.

파생

양쪽 라플라스 변환으로 f$t)$ {$displaystyle$ f$(t)}$ $및$ g$)$ {$displaystyle$ g$(t)}$의 두 가지 $함수$가 지정됩니다.

${\displaystyle F(s)=\int_{-\infty}^{\infty}e^{-su}\f(u)\{text{d}u}$

그리고.

$\displaystyle G(s)=\int _{-\infty}^{\infty}e^{-infty}\g(v)\{text{d}v}$

각각 컨볼루션 $연산{\displaystyle }$f (${\displaystyle t}$ )${\displaystyle }$g${\displaystyle g}$ ( ${\displaystyle t}$ $){$ $displaystyle$ f$(t)*g(t)}$는 F${\displaystyle }$(${\displaystyle s}$ $){$ $displaystyle$ F$(s)}$와${\displaystyle }$G ( $){$ $displaystyle$ G$(s$^[4][5]의 곱의 역라플라스 변환이라고 정의할 수 있습니다. 보다 정확하게는,

${\displaystyle {begin{aligned}F&=\int _{-\infty}^{\infty}e^{-su}\f(u)\cdot \int _{-\infty}^{-\infty}e^{-su}{-int}{-\infty}{\d}{\text}$

v ${\displaystyle =}$ ${\displaystyle t}$-$$ (\$style$ v$=t-u)$로 $하면{\displaystyle }$ 다음과 같이 됩니다.

$d{정렬}}}$

$F{\displaystyle }$(${\displaystyle s}$ )${\displaystyle g}$G ( s$){$ $displaystyle$F ($s$ )\$cdot$G ($s$ )는 f${\displaystyle }$(${\displaystyle t}$ )${\displaystyle }$( ${\displaystyle g}$ ($$t${\displaystyle }$){ $displaystyle f$ ( $t)*g$( t$)\}$의 쌍방향 라플라스 변환입니다.동일한 파생은 일방 라플라스 변환을 사용하여 실행할 수 있습니다.

또한 컨볼루션 연산은 LTI(Linear Time-Invariant)로 알려진 중요한 연산 클래스의 출력(입력 측면에서)을 설명합니다.LTI 제약의 결과로 인한 회전의 파생은 LTI 시스템 이론을 참조하십시오.LTI 연산의 입출력의 푸리에 변환에 관해서는 새로운 주파수 성분이 생성되지 않는다.기존의 것은 변경되었을 뿐입니다(진폭 및/또는 위상).즉, 출력 변환은 세 번째 변환(전송 함수라고 함)을 사용하는 입력 변환의 포인트별 곱입니다.컨볼루션의 특성 유도에 대해서는 컨볼루션 정리를 참조한다.반대로, 컨볼루션은 2개의 푸리에 변환의 포인트별 곱의 역 푸리에 변환으로 도출할 수 있다.

시각적 설명

각 함수를 더미 변수 ${\displaystyle .}$로 표현합니다$.\$ $displaystyle$\$tau$. } ${\displaystyle g}$($$ ) \ $displaystyle$ g ( \$displaystyle$ g ( \ ${\displaystyle \mathrm{displaystyle}}$ ) →$$${\displaystyle }g{\displaystyle }$( - ${\displaystyle )}$)$$. \ $displaystyle$ g $\tautautau$tautautautautautau 。$}$ g ( ${\displaystyle t}$-${\displaystyle }$,$$) { $displaystyle$g ( $t$- $tau$) $}$이${\displaystyle (}$가) \$displaystyle \tau$} 축을$$ 따라 미끄러질 수 $있는{\displaystyle }$ 타임오프셋 t를 추가합니다. t를 -θ에서 시작하여 +θ까지 슬라이드시킵니다.두 기능이 교차하는 모든 위치에서 해당 제품의 적분을 찾습니다.즉, 시각 t에서는 가중치 $함수{\displaystyle }$ g${\displaystyle (t}$- ${\displaystyle )}$)에 의해 가중치${\displaystyle }$부여되는 ${\displaystyle \mathrm{함수}}$ f($the$$$){ $displaystyle$ f$(\tau$ $).\displaystyle$ g$(t-\tau)$의 면적을 계산합니다.$}$ 결과 파형(여기에는 표시되지 않음)은 함수 f와 g의 합성입니다. f(t)가 단위 임펄스일 경우 이 프로세스의 결과는 단순히 g(t)입니다.형식: $\displaystyle \int _{-\infty}^{\infty}\displays (\display)g(t-\displays ), d\displays = g(t)}$
이 예에서는 빨간색으로 표시된 "${\displaystyle g}$${\displaystyle "}$ ( ${\displaystyle )}$)$$, {\$displaystyle \ g$ (${\displaystyle }$\${\displaystyle }$displaystyle \ $g$${\displaystyle }$( \${\displaystyle \mathrm{displaystyle}}$ ) = g ($g$ )$$、 \ $displaystyle$ ( \$displaystyle$ ) $= g$( \ displaystyle ) \ g ( \ displaystyle )\ displaystyle )\ g$$ ( \ scraps )\ r )\$$ $)\$ }는${\displaystyle }$짝수 함수이므로, connel ( \ g ( \ scruptions )이 "$displaystyle$$"$의 스냅샷은 $\theta {\displaystyle }$ ${\displaystyle =}$ ${\displaystyle 0}$(\$displaystyle$ \$displaystyle = 0)$ 축에서$$ 빨간색 펄스의 중심까지의 거리로 임의 정의되는 $파라미터{\displaystyle }$t의$$ 일부 값에 대한 $함수{\displaystyle }$ g$t$ -$)$ ) $및$ f${\displaystyle (}$$$ $)(파란색)$를 보여줍니다.노란색의 양은 convolution/cdot g(${\displaystyle \mathrm{t-tau}}$)로 계산되는 $제품{\displaystyle }$ f${\displaystyle (}$ ${\displaystyle )}$ ) ${\displaystyle (}$ ${\displaystyle g(t}$ - ${\displaystyle )}$)$$、 \ $displaystyle$ f$(\tau$)\$cdot$ g$(t-\tau )$의 면적입니다.무비는 t$\displaystyle$t를$$ 지속적으로 $변경$하고 적분을 재계산하여 작성됩니다.결과(검은색 표시)는 t$$, {$displaystyle$ t$,}$의 함수이지만 $편$의 및 비교를 위해 ${\displaystyle ,}$, {\$displaystyle \tau}$와 같은 축에 표시됩니다.
$이{\displaystyle }$ 그림에서 f${\displaystyle (}$ ${\displaystyle )}$ )$${$displaystyle$ f$(\displaystyle$ f(\displaystyle$)$ $=$ $0 .$${\displaystyle \}}$${\displaystyle \mathrm{즉}}$$(=)$ $δ$(\$displaystyle g$(\displaystyle) =\$display(\$display$)$의 ${\displaystyle \mathrm{결과}}$는${\displaystyle }convolution$입니다$.$} 단$$, ${\displaystyle g}$ ( $)$ ) { $displaystyle$g ( \$tau$ ) }가 넓은 펄스(빨간색)일${\displaystyle }경우{\displaystyle }$ ${\displaystyle \mathrm{응답}}$은 f${\displaystyle }$($$t ) .${\displaystyle }${ $displaystyle f($t)의 "스멀" $버전$입니다$.$} $t$를$=$ 0({$displaystyle$ \displaystyle$$$= 0$$)$ 축에서 와이드 펄스 중심(선단 가장자리의 중심)까지의 거리로$정의$했기 때문에 t${\displaystyle =}$ - ${\displaystyle 0}$.5${\displaystyle ,}$ {$displaystyle$ t$$$=-0$.5$$$}$에서 $시작$합니다$.$

역사적 발전

콘볼루션 ^[6]적분의 가장 초기 사용 중 하나는 달랑베르가 1754년에 출판한 Recherches surce different points importants du systéme du monde에서 Taylor's 정리의 파생에서 나타났다.

또한 다음 유형의 표현식:

$\displaystyle \int f(u)\cdot g(x-u),du}$

는 실베스트르 프랑수아 라크루아가 백과사전 시리즈 3권 중 마지막 권인 '차이점과 시리즈에 관한 논문' 505페이지에서 사용하고 있습니다.Chez Coursier, 파리, 1797–1800,^[7] Atribute du calculate differentiel et du calculate intergral.곧이어 피에르 시몬 라플라스, 장 밥티스트 조제프 푸리에, 시메온 데니스 푸아송 등의 작품에서 컨볼루션 연산이 등장한다.그 용어 자체는 1950년대나 60년대에 이르러서야 널리 쓰이게 되었다.그 이전에는 Faltung(독일어로 접는다는 뜻), 구성 산물, 중첩 적분 및 Carson's ^[8]적분으로 알려져 있었습니다.그러나 1903년경에 그 정의가 오래된 ^[9][10]용법에서는 다소 생소하지만, 그것은 일찍부터 나타난다.

조작:

$\displaystyle \int _{0}^{t}\varphi(s)\psi(t-s),ds,\display 0\leq t <\infty ,}$

1913년 ^[11]이탈리아 수학자 비토 볼테라에 의해 고려된 구성 산물의 특별한 경우이다.

원형 회전

함수_T g가 주기 T로 주기적인 경우 f µ_T g가 존재하는 함수 f에 대해서도 주기적이고 다음과 같다.

${\displaystyle (f*g_{T})(t)\equiv \int _{t_{0}^{0}+T}\left[\sum_{k=-\infty}{\infty}f(\sum +kT)\right]g_{T}(t-\tau)\d,\lefty,\lefty,\lefti}$

여기서₀ t는 임의의 선택입니다.합계를 함수 f의 주기적 합이라고 합니다.

g가 다른 함수 g의 주기적 합일 때_T f δ_T g는 f와 g의 원형 또는 순환적 합으로 알려져 있다.

그리고 위의 주기 합계를 f로_T 바꾸면 연산을 f와_T g의 주기_T 합이라고 합니다.

이산 컨볼루션

정수의 집합 Z에 정의된 복소수 함수 f, g의 경우 f와 g의 이산 제곱은 다음과 같이 ^[12]구한다.

${{displaystyle (f*g)[n]=\sum _{m=-\infty}^{\infty}f[m]g[n-m],}$

또는 동등하게(정류성 참조):

${\displaystyle (f*g)[n]=\sum _{m=-\infty}^{\infty}f[n-m]g[m]g[m]}$

두 유한 시퀀스의 컨볼루션은 시퀀스를 정수 집합에서 완전히 지원되는 함수로 확장함으로써 정의됩니다.시퀀스가 두 다항식의 계수일 때, 두 다항식의 일반 곱의 계수는 원래 두 시퀀스의 제곱입니다.이를 시퀀스 계수의 코시 곱이라고 합니다.

따라서 g가 세트${\displaystyle }${ -${\displaystyle M}$ ${\displaystyle \}}$ ,${\displaystyle }$- ${\displaystyle \mathrm{M}}$ +${\displaystyle }$1 , ${\displaystyle ...}$ ,${\displaystyle M}$ -${\displaystyle 1}$ , ${\displaystyle M}$ $}$ { $displaystyle$ \ { - $M$, -$M$ +$1$, \$dots$ , $M-1$ , M \$$} (예를 들어 유한 임펄스 응답을 나타냄)에서 유한 합계를 사용할 ^[13]수 있습니다.

${\displaystyle (f*g)[n]=\sum _{m=-M}^{M}f[n-m]g[m]}$

원형 이산 회전

함수_N g가 주기 N으로 주기적인 경우 fµg가_N 존재하는 함수 f에 대해서도 주기적이고 다음과 같다.

${\displaystyle (f*g_{N}[n]\equiv \sum _{m=0}^{N-1}\left(\sum _{k=-\infty}^{f}[m+kN]\right)g_{N}[n-m]}$

k의 합을 함수 f의 주기적 합이라고 합니다.

g가_N 다른 함수 g의 주기적 합이라면 f∗g는_N f와 g의 원환승으로 알려져 있다.

f와 g의 비제로 지속 시간이 간격 [0, N - 1]로 제한되면 fµg는_N 다음과 같은 일반적인 형태로 감소합니다.

${\displaystyle {begin {aligned}\left(f*g_{N}\right)[n]&=\sum _{m=0}^{N-1}f[m]g_{N}[n-m]\\&=\sum _{m=0}^{n}f[m]g[n-m]+\sum _{m=n+1}^{N-1}f[m]g[N+n-m]\\[2pt]&={m=0}^{N-1}f[m]g[(n-m)_{\bmod {N}}\[2pt]&\triangleq \left(f*_{N}g\right)[n]\end{aligned}}}$

(제1호)

순환 순환의 표기법(f _Ng g)은 정수 모듈로 N의 순환 그룹에 대한 순환을 나타낸다.

원형 컨볼루션은 고속 푸리에 변환(FFT) 알고리즘을 사용한 고속 컨볼루션의 맥락에서 발생합니다.

고속 컨볼루션 알고리즘

많은 상황에서 이산 컨볼루션을 원형 컨볼루션으로 변환할 수 있으므로 컨볼루션 특성을 가진 고속 변환을 사용하여 계산을 구현할 수 있습니다.예를 들어, 디지트 시퀀스의 컨볼루션이란, 복수의 디지트 번호의 곱셈에 있어서의 커널 연산이며, 따라서 변환 기술에 의해서 효율적으로 실장할 수 있다(Knuth 1997, § 4.3.3).C; von zur Gathen & Gerhard 2003, § 8.2).

eq.1에서는 출력 값당 N개의 산술 연산과² N개의 출력에 N개의 연산이 필요합니다.이것은, 몇개의 고속 알고리즘으로 큰폭으로 삭감할 수 있습니다.디지털 신호 처리 및 기타 애플리케이션은 일반적으로 고속 컨볼루션 알고리즘을 사용하여 O(N log N) 복잡도로 컨볼루션 비용을 줄입니다.

가장 일반적인 고속 컨볼루션 알고리즘은 원형 컨볼루션 정리를 통해 고속 푸리에 변환(FFT) 알고리즘을 사용합니다.구체적으로는 각 시퀀스의 FFT를 취하여 포인트 단위로 곱한 후 역FFT를 실행함으로써 2개의 유한길이 시퀀스의 원형회전을 구한다.그 후, 상기 타입의 컨볼루션은, 출력의 제로 확장 및/또는 폐기 부분과 함께, 그 기술을 사용해 효율적으로 실장된다.Schönhage-Strassen 알고리즘이나 메르센 ^[14]변환과 같은 다른 고속 컨볼루션 알고리즘은 다른 링에서 고속 푸리에 변환을 사용합니다.

한 시퀀스가 다른 시퀀스보다 훨씬 긴 경우, 짧은 시퀀스와 빠른 원형 회전의 제로 익스텐션은 ^[15]사용 가능한 가장 효율적인 계산 방법이 아닙니다.대신 긴 시퀀스를 블록으로 분해하고 각 블록을 분해하면 오버랩-저장 방법 ^[16]및 오버랩-추가 방법과 같은 더 빠른 알고리즘이 가능합니다.블록 알고리즘과 FIR 알고리즘을 조합한 하이브리드 컨볼루션 방식은 실시간 컨볼루션 ^[17]계산에 유용한 입출력 레이텐시를 0으로 만들 수 있습니다.

정의 영역

R 위의^d 2개의 복소수 함수의 컨볼루션 자체는 R 위의^d 복소수 함수이며, 다음과 같이 정의됩니다.

${\displaystyle (f*g)=\int _{\mathbf {R}^{d}f(y)g(x-y),dy=\int _{\mathbf {R}^{d}f(x-y)g(y),dy,}$

f와 g가 적분이 존재하기 위해 무한대에서 충분히 빠르게 붕괴하는 경우에만 잘 정의된다.무한대에서의 g에서의 팽창은 f에서의 충분히 빠른 붕괴에 의해 쉽게 상쇄될 수 있기 때문에 컨볼루션의 존재 조건은 까다로울 수 있다.따라서 존재의 문제는 f와 g에 대해 다른 조건을 수반할 수 있다.

콤팩트하게 지원되는 기능

f와 g가 콤팩트하게 지지된 연속함수인 경우, 그 회전수는 존재하며 콤팩트하게 지지되고 연속함수이다(Hörmander 1983, 제1장).보다 일반적으로 어느 하나의 함수(예를 들어 f)가 콤팩트하게 지원되고 다른 함수(예를 들어 f)가 국소적으로 적분 가능한 경우, convolution fµg는 잘 정의되고 연속적입니다.

f와 g의 컨볼루션은 두 함수가 R에서 국소적으로 제곱 적분 가능하며 형식 [a, +θ](또는 [-θ, a]에서 둘 다 지원됨)의 간격으로 지원되는 경우에도 잘 정의된다.

통합 가능한 기능

f와 g가 L(R^d)에서¹ 모두 르베그 적분 가능한 함수인 경우 f와 g의 제곱이 존재하며, 이 경우 f isg도 적분 가능하다(Stein & Weiss 1971, 정리 1.3).이것은 토넬리 정리의 결과이다.이것은 또한 L의¹ 함수, 이산 컨볼루션, 또는 더 일반적으로 모든 그룹의 컨볼루션에도 해당된다.

마찬가지로 f l¹ L(R^d) 및 g l^p L(R^d)이 1 p p ≤ L(R)이면 f g^p L(R^d)이 됩니다.

$\ displaystyle \ { f } * g \ _ { p } \ leq \ f \ _ {1} \ g \ { p } 。}$

특정한 경우 p = 1에서, 이것은 L이 컨볼루션 하의 바나흐 대수임을 보여준다¹(그리고 f와 g가 거의 모든 곳에서 음이 아닌 경우 양쪽의 동등성이 유지된다).

보다 일반적으로, 영의 부등식은 컨볼루션(convolution)이 적절한^p L 공간 사이의 연속 쌍선형 맵임을 암시한다.구체적으로는 1 'p, q, r '가 다음을 만족하는 경우:

${{displaystyle {1}{p}}+{\frac {1}{q}}=black {1}{r}+1,}$

그리고나서

$\displaystyle \left\Vert f*g\right\Vert f\right\Vert g\right\Vert _{p},\quad f\in {L}{p},\g\g\in {mathcal {L}{q},\g\r}\vert f\vert$

따라서 컨볼루션은 L^q×L에서^pr L로의 연속 쌍선형 매핑이 되도록 한다.컨볼루션의 젊은 부등식은 다른 맥락(원 그룹, Z의 컨볼루션)에서도 마찬가지입니다.앞의 부등식은 실선상에서 뚜렷하지 않다.1 < p, q, r < , 에서는 다음과 같은 상수_p,q B < 1이 존재한다.

$\displaystyle \left \Vert f*g \right \Vert B_{p,q} \leq \좌측 \Vert f\right \Vert _{p} \좌측 \좌측 \right \Vert _{q},\quad f\in \mathcal {L},\g.}$

B의_p,q 최적값은 1975년에^[18] 발견되었고 ^[19]1976년에 독립적으로 브라스캠프-립 부등식을 참조한다.

1 < p, q, r < : :

$\ displaystyle \ f*g \ _ { r } \ leq C _ { p , q } \ f \ { p } \ g \ _ { q , w }$

여기서${\displaystyle }$"${\displaystyle g{}_q}$ ,$$ \ $style \ g$ \ $_ {$q$$,$w}$는 약한^q L 노름입니다.컨볼루션은 또한 약한 ^[20]부등식으로 인해 1< , , r , r$∞$ 1 \ $displaystyle$ 1 $< p$ ,$r$ , $r$, \ $infty$ 에 대해 쌍선형 연속 $맵{\displaystyle {}^{}}$ ${\displaystyle L^{}}$p ,${\displaystyle {}^{}{}^{}}$ × ${\displaystyle L^{}}$ , $w$ ${\displaystyle {}^r}$ ,$w$ \ $times$ L^ {$q$ , w } 를 정의합니다.

$\ displaystyle \ f * g \ _ { r , w } \leq C _ { p , q } \ f \ { p , w } \ { r , w } 。}$

급속한 붕괴의 함수

콤팩트하게 지원되는 함수 및 적분 가능한 함수 외에 무한대에서 충분히 빠른 감쇠가 있는 함수도 컨볼루션할 수 있다.convolution의 중요한 특징은 f와 g가 모두 빠르게 붕괴하면 fµg도 빠르게 붕괴한다는 것입니다.특히 f와 g가 함수를 급격히 감소시키는 경우, convolution fµg도 감소한다.컨볼루션과 미분이 일치한다는 사실과 결합하면(#속성 참조), 슈워츠 함수의 클래스는 컨볼루션 하에서 닫힙니다(Stein & Weiss 1971, Oremory 3.3).

배포

경우에 따라서는 분포 또는 두 분포의 함수곱을 정의할 수 있습니다.f가 콤팩트하게 지지된 함수이고 g가 분포인 경우, f isg는 다음과 같은 분포 공식에 의해 정의된 매끄러운 함수이다.

$\displaystyle \int _{\mathbf {R}^{d}}{f}(y)g(x-y),dy}$

보다 일반적으로, 협정의 정의를 독특한 방법으로 확장할 수 있으며, 그래서 연합법은 다음과 같이 할 수 있다.

$\displaystyle f*(g*\varphi)=(f*g)*\varphi }$

f가 분포이고 g가 콤팩트하게 지원되는 분포(Hörmander 1983, § 4.2)인 경우 유효하다.

방안

2개의 보렐 측정값 μ 및 δ의 유계 변동의 제곱은 (Rudin 1962)에 의해 정의된 $측정값{\displaystyle }$ ${\displaystyle \mu }$ ${\displaystyle \ast }$∗ （ \ $displaystyle \mu$* \$nu ）$이다.

$\displaystyle \int _{\mathbf {R} ^{d} f(x),d(\mu *\nu)(x)(x)=\int _{\mathbf {R} ^{d}} f(x+y),d\nu(y)}$

특히,

$\displaystyle (\mu *\nu)(A)=\int _{\mathbf {R}^{d}\times \mathbf {R}^{d}1_{A}(x+y),d(\mu \times \nu)(x,y),$

${\displaystyle {}^{}}$서 A${\displaystyle }$urable R d$$\ $display style$A \$subset$ \ $mathbf${ $R$} ^ { $d$}는$$ 측정 가능한 $집합$이고 1$$(\ $displaystyle 1_{A})$는 A$(\$ $displaystyle$ A$)$의 표시기 함수입니다.

이는 위에서 정의한 μ와 δ가 분포로 간주될 때와 μ와 δ가 르베게 측정치에 대해 절대적으로 연속적일 때 L 함수의¹ Convolution과 일치한다.

조치의 합의는 또한 영의 불평등의 다음 버전을 충족시킨다.

$\displaystyle \\mu *\nu \leq \mu \\nu \ }$

여기서 노름은 측정값의 총 변동입니다.유계 변동의 측정 공간은 바나흐 공간이기 때문에, 측정의 계산은 분포의 계산에는 적용되지 않을 수 있는 표준 함수 분석 방법으로 처리할 수 있다.

특성.

대수적 성질

컨볼루션은 적분 가능한 함수의 선형 공간에 대한 곱을 정의합니다.이 곱은 다음과 같은 대수적 특성을 만족하며, 이는 공식적으로 컨볼루션에 의해 주어진 곱과 적분 가능한 함수의 공간이 항등식 없는 교환 연상 대수임을 의미한다(Strichartz 1994, § 3.3).콤팩트 서포트의 연속함수의 공간과 같은 함수의 다른 선형공간은 컨볼루션에 의해 닫히고, 따라서 가환연관대수를 형성한다.

정류성

$${\displaystyle f*g=g*f}$$

실증: 정의별:

$${\displaystyle (f*g)(t)=\int _{-\infty }^{\infty}f(\display)g(t-\displays ),d\displays }$$

통합 변수를 ${\displaystyle u}$ ${\displaystyle =}$ t${\displaystyle }$-$$ { $displaystyle$ u =$t-\display }$로 $변경$하면 다음과 같은 결과가 나옵니다.

연관성

$${\displaystyle f*(g*h)=(f*g)*h}$$

증명: 이것은 Fubini의 정리를 사용한 결과이다(즉, 이중 적분은 어느 순서로든 반복 적분으로 평가할 수 있다).

유통성

$${\displaystyle f*(g+h)=(f*g)+(f*h)}$$

증명: 이는 적분의 선형성에서 비롯됩니다.

스칼라 곱셈과의 연관성

$${\displaystyle a(f*g)=(af)*g}$$

$실제$또는 복합$)$ $a$에 대해 설명합니다.

곱셈 항등식

어떤 함수의 대수학도 컨볼루션의 항등식을 가지고 있지 않다.컨볼루션이 실행되는 함수의 대부분의 집합은 델타 분포(제로를 중심으로 한 단일 임펄스)로 컨볼루전하거나 최소한(L의¹ 경우처럼) 아이덴티티에 대한 근사치를 인정할 수 있기 때문에 일반적으로 식별성의 결여는 큰 불편이 되지 않습니다.그러나 콤팩트하게 지원되는 분포의 선형 공간은 이 방정식에서 동일성을 인정합니다.구체적으로는

$${\displaystyle f*\displays = f}$$

여기서 is 、 델타 분포입니다.

역원소

일부 분포 S는 다음 조건을 만족시켜야 하는 합성곱에 대한 역원소⁻¹ S를 가진다.

$${\displaystyle S^{-1}*S=\delta}$$

여기서 S에⁻¹ 대한 명시적 공식을 얻을 수 있다.

가역 분포의 집합은 그 방정식에서 아벨 군을 형성한다.

복소 활용

${\displaystyle {f*g}}=오버라인 {f}*{\overline {g}}$

차별화와의 관계

$${\displaystyle (f*g)'=f'*g=f*g'}$$

실증:

$${\displaystyle {displaystyle}(f*g)`&=syslogfrac {d}{\infty}f(\infty})g(\infty}f(\infty)g(\displaystyle \[4pt]&=int _{-infty }{\infty }f(\displaysty)\end { aligned}}$$

통합과의 관계

$F$($t$ ) $=$ ${\int }_{}^{}$ -${\mathrm{}}_{}^{}t$ ${}_{}^{}$f ( $)$ ) $d$、$${ \ $textstyle$F ( t ) = \$int$ _ { - \ $int$ _ { - \ $infty$} $f$ ( \$int$) $d$\ $\mathrm{t<img\; alt="\{\backslash textstyle\; F(t)=\backslash int\; \_\{-\backslash infty\; \}^\{t\}f(\backslash tau\; )d\backslash tau\; ,\}"\; aria-hidden="true"\; class="mwe-math-fallback-image-inline"\; src="https://wikimedia.org/api/rest\_v1/media/math/render/svg/2ac0792eba9d5398066050439c3b9d396a1e5729"\; style="vertical-align:\; -1.171ex;\; width:19.481ex;\; height:3.676ex;">}$$$}$=$ - ${\mathrm{\infty }}_{}^{}$ t${}_{}^{}$ ( $)$ ) $d$、 { $txtextstyle$G ( $t$ } \ t$$} \ t } 、 { $t$}

$${\displaystyle (F*g)(t)=(f*G)(t)=\int _{-\infty }^{t}(f*g)(\displaystyle ),d\display .}$$

통합

f와 g가 적분 가능한 함수일 경우, 전체 공간에서의 이들 합의 적분은 단순히 적분의 ^[21]곱으로 구한다.

$\displaystyle \int _{\mathbf {R} ^{d}(f*g)(x) ^{\left(\int _{\mathbf {R} ^{d}f(x)\right)\left(\int _{\mathbf {R} ^{d}g(x)\right)\light).}$

이것은 Fubini의 정리에 따른 것이다.토넬리의 정리에 의해 f와 g가 음이 아닌 측정 가능한 함수라고 가정할 경우에도 같은 결과가 유지된다.

차별화

단변수의 경우,

${\displaystyle\frac {d}{f*g}=black {df}{f*g}=f*{\frac {dg}{flac}}$

여기서 d/model은 도함수입니다.보다 일반적으로, 여러 변수의 함수의 경우, 유사한 공식이 편도함수에 적용된다.

${\displaystyle {\frac x_{i}}(f*g)=param frac {\frac x_i}*g=f*{\frac x_i}}.}$

이것의 특별한 결과는 컨볼루션(convolution)이 "평활화" 연산으로 간주될 수 있다는 것입니다. 즉, f와 g의 컨볼루션(convolution)은 f와 g의 합계 수만큼 미분할 수 있습니다.

이러한 동일성은 영의 회전 부등식의 결과로 f와 g가 절대적으로 적분 가능하고 적어도 하나는 절대적으로 적분 가능한 (L¹) 약한 도함수를 갖는 정확한 조건 하에 유지된다.예를 들어, f가 콤팩트 서포트로 연속적으로 미분 가능하며 g가 임의의 로컬 적분 가능 함수일 경우,

${\displaystyle\frac {d}{df}(f*g)=flac {df}{df}*g.}$

f 또는 g 중 하나가 급속하게 감소하는 강화 분포, 콤팩트하게 지원되는 강화 분포 또는 Schwartz 함수이고 다른 하나가 강화 분포인 경우 이러한 식별성은 강화 분포의 의미에서도 훨씬 더 광범위하게 유지됩니다.반면, 두 개의 양의 적분 가능 함수와 무한히 구별 가능한 함수는 어디에도 연속적인 컨볼루션(convolution)이 없을 수 있습니다.

이산적인 경우, 차분 연산자 D f(n) = f(n + 1) - f(n)는 다음과 같은 유사한 관계를 만족합니다.

$\displaystyle D(f*g)=(Df)*g=f*(Dg)}$

컨볼루션 정리

컨볼루션 정리는 다음과 같이 기술한다.

${\displaystyle {F}\{f*g\}=k\cdot {f\}\cdot {f\}\cdot {F}\cdot {mathcal {F}\g\}$

$여기$서${\displaystyle }$F { ${\displaystyle f}$ $}$ {{$displaystyle {F}}$ \{$f\}}$는 f$${$displaystyle$ f$\}$의 푸리에 변환을 $나타내고{\displaystyle }$k {$displaystyle$ k$}$는 푸리에 변환의 특정 정규화에 따라 달라지는 상수입니다.이 정리 버전은 라플라스 변환, 양면 라플라스 변환, Z 변환 및 멜린 변환에도 적용됩니다.

한편$,$ W$(\style$ {\$mathcal${$W}})$가 푸리에 변환 행렬이라면,

${\displaystyle \mathcal{W}}$( ${\displaystyle C{}^{}}$( ${\displaystyle 1^{}}$)$2$C (${\displaystyle {}^{}}$2 )${\displaystyle {}^{}=}$ ( ${\displaystyle W{}^{}{}^{}C}$ (${\displaystyle {}^{}{1}^{}}$)${\displaystyle {}^{}}$( W ${\displaystyle {\mathrm{C}}^{}}$(${\displaystyle {}^{}}$2 ${\displaystyle ))}$ ${\displaystyle =}$ ${\displaystyle W\mathcal{}{}^{}C{}^{}}$ ( ${\displaystyle 1^{}}$)${\displaystyle x\mathcal{}}$ W C${\displaystyle {}^{}}$($2$ )$($\ $displaystyle${ $W$} \$left$ ( $C${ 1 $)$x \ Ast C ( 2 )$}$

여기서 ${\$ { $displaystyle$\ $bullet }$는 페이스 분할 제품,^{[22][23][24][25][26]} ${\$ { $displaystyle \otimes }$는 Kronecker 제품, ${\$ { \ $displaystyle \circ }$은 Hadamard 제품(이 결과는 카운트^[27] 스케치 속성에서 진화한 것입니다)을 나타냅니다.

번역 등변수

이 컨벤션에는 번역이 포함되어 있습니다.즉,

$\displaystyle _{x}(f*g)=(\display_{x}f)*g=f*(\display_{x}g)}$

여기서 θf는_x f에 x를 곱한 함수의 변환입니다.

$\displaystyle (\displaystyle _{x}f)(y)=f(y-x)}$

f가 Schwartz 함수일 경우, f는_x 변환된 Dirac 델타 함수 f_x = f ∗ δ_x a a a a a a a a a a a so so so so so so so so so so so so so so so so so so so so so so so so so so if if if if the so if if if if if if if if if the the the the if if if

또한 특정 조건 하에서 컨볼루션은 가장 일반적인 번역 불변 연산이다.비공식적으로 말하면 다음과 같다

S가 모든 x에 대해 S(θf_x) = θ_x(Sf)와 같은 변환과 일치하는 함수에 작용하는 유계 선형 연산자라고 가정합니다.그런 다음 S는 함수(또는 분포) g_S, 즉 Sf = g_S µ f와 함께 컨볼루션으로 주어진다.

따라서 일부 변환 불변 연산은 컨볼루션으로 표현될 수 있습니다.컨볼루션은 시간 불변 시스템, 특히 LTI 시스템 이론 연구에 중요한 역할을 합니다.표현함수_S g는 변환 S의 임펄스 응답이다.

위에서 인용한 정리의 보다 정밀한 버전은 정리가 정의되는 함수의 클래스를 명시할 필요가 있으며, 또한 S가 적절한 위상에 관해 연속 선형 연산자여야 한다고 가정할 필요가 있다.예를 들어, L 위의 모든¹ 연속 변환 불변 연속 선형 연산자는 유한 보렐 측정값을 갖는 컨볼루션인 것으로 알려져 있습니다.보다 일반적으로, L 위의^p 모든 연속 변환 불변 연속 선형 연산자는 푸리에 변환이 유계된 강화 분포를 갖는 컨볼루션이다.위트로는, 그것들은 모두 유계 푸리에 승수에 의해 주어집니다.

그룹에서의 컨볼루션

만약 G가 측도 θ를 부여받은 적절한 군이고, f와 g가 G에 대한 실제 또는 복잡한 가치의 적분함수라면, 우리는 그들의 분해능을 다음과 같이 정의할 수 있다.

${\displaystyle (f*g)(x)=\int _{G}f(y)g\left(y^{-1}x\right),d\lambda(y).}$

그것은 일반적으로 가환적이지 않다.일반적인 경우 G는 국소적으로 콤팩트한 하우스도르프 토폴로지 그룹이고 θ는 (좌측) Haar 측정값이다.이 경우 G가 단모듈형이 아닌 한 이 방법으로 정의된 회전수는$\theta$f ( $x{}^{}$ -${}^{}{1}^{}$)$g$ ($y$ ) $d\delta$ ($y$ $)\textstyle \int$ f$\left (xy^{-1}\right) g(y),$ d$\lambda (y$와 같지 않습니다.한쪽이 다른 쪽보다 우선되어 고정 함수 g를 갖는 변환이 그룹 내 왼쪽 변환과 일치하도록 합니다.

${\displaystyle L_{h}(f*g)=(L_{h}f)*g.}$

또한, 이 협약은 아래에 제시된 조치의 협약의 정의와 일관성을 유지하기 위해서는 협약이 필요하다.그러나 왼쪽 Haar 측정 대신 오른쪽을 사용하는 경우 후자의 적분이 전자보다 선호됩니다.

국소 콤팩트 아벨 군에서, 컨볼루션 정리의 버전은 유지된다: 컨볼루션의 푸리에 변환은 푸리에 변환의 점곱이다.르베그 측정값이 있는 원 군 T가 바로 그 예입니다.L(T)의¹ 고정 g의 경우, 힐베르트 공간² L(T)에 다음과 같은 익숙한 연산자가 작용한다.

${\displaystyle T{f}(x)=blac {1}{2\pi }}\int _{\mathbf {T}}{f}(y)g(x-y),dy}$

연산자 T는 콤팩트합니다.직접 계산 결과, 인접 T*는 다음과 같이 변환됩니다.

${\displaystyle {g}}(-y).}$

위에서 언급한 정류성 특성에 따르면 T는 정규값이다.T* T = TT*. 또한 T는 변환 연산자와 통신합니다.이러한 모든 합성곱과 변환 연산자로 구성된 연산자 계열 S에 대해 생각해 보십시오.그러면 S는 일반 작업자의 통근 가족입니다.스펙트럼 이론에 따르면, 동시에 S를 대각선으로 하는 직교 정규 기저 {h}이_k 존재한다.이것은 원의 곡선을 특징짓습니다.구체적으로는

$\displaystyle h_{k}(x)=e^{ikx},\display k\in \mathbb {Z},\;}$

정확히 T의 캐릭터입니다.각 회전수는 이 기준에서 콤팩트 곱셈 연산자입니다.이것은 위에서 논의한 컨볼루션 정리의 한 버전이라고 볼 수 있다.

이산적인 예는 순서 n의 유한 순환군이다.여기서 컨볼루션 연산자는 순환행렬로 나타내며 이산 푸리에 변환으로 대각화할 수 있다.

콤팩트 그룹(반드시 아벨은 아니다)에 대해서도 같은 결과가 나타난다.유한 차원 유니터리 표현의 행렬 계수는 피터-바일 정리에 의해 L에서² 직교 정규 기저를 형성하고, 푸리에 변환에 의존하는 고조파 해석의 많은 다른 측면과 함께 컨볼루션 정리의 아날로그는 계속 유지된다.

조치의 정리

G를 (곱셈으로 쓴) 토폴로지 그룹이라고 하자.μ와 μ가 G에 대한 유한한 보렐 측정치인 경우, 이들의 컨볼루션 μμθ는 군 작용의 푸시포워드 측정치로서 정의되며 다음과 같이 쓸 수 있다.

$\displaystyle (\mu *\nu)(E)=\iint 1_{E}(xy),d\mu(x),d\nu(y)}$

측정 가능한 G의 각 부분 집합 E에 대해.또한 총 변동은 다음을 만족하는 유한 측도이다.

$\displaystyle \mu *\nu \leq \left \mu \right \nu \right \ .}$

G가 국소적으로 (좌)Haar 측정θ로 콤팩트하고, μ 및 μ가 θ에 대해 절대 연속이며, 각각 밀도함수를 갖는 경우, μθ도 절대 연속이며, 그 밀도함수는 2개의 다른 밀도함수의 회전함수이다.

μ와 μ가 위상군(R,+)에 대한 확률 측도일 경우, μθ는 각각 μ와 μ인 2개의 독립 랜덤 변수 X와 Y의 합 X + Y의 확률 분포이다.

바이알게브라

(X, δ, ,, ,, ), ))를 공복수 ,, 곱셈 ,, 단위 , 및 counit ε의 바이얼 대수로 한다.컨볼루션은 다음과 같이 내형 대수 End(X)에서 정의된 곱이다.예를 들어, θ, θ, θ: X → X는 X의 모든 대수적 구조를 존중하는 함수이며, θ는 구성으로서 정의된다.

$(*displaystyle X\rightarrow\Delta}) X\mathrel X\mathrel X\mathrel X\mathrel X\mathrel X\rightarrow {nabla})$

이 법칙은 홉프 대수의 정의에 특히 나타난다(카셀 1995, §III.3).바이알대수는 대척점이 있는 경우에만 Hopf 대수이다: 다음과 같은 내형성 S.

${\displaystyle S*\operatorname {id}_{X}=\operatorname {id}_{X}*S=\eta \varepsilon .}$

적용들

컨볼루션 및 관련 연산은 과학, 공학 및 수학의 많은 응용 분야에서 찾아볼 수 있습니다.

• 이미지 처리 중

  디지털 이미지 처리에서 컨볼루션 필터링은 에지 검출 및 관련 프로세스에서 많은 중요한 알고리즘에 중요한 역할을 합니다.'커널'(이미지 처리) 참조

  광학에서 초점이 맞지 않는 사진은 렌즈 기능을 가진 선명한 이미지를 합성한 것이다.이것을 나타내는 사진용어는 bokeh이다.

  이미지 처리 어플리케이션에서는 흐림 추가 등입니다.

• 디지털 데이터 처리 중

  분석 화학에서 Savitzky-Golay 스무딩 필터는 분광 데이터 분석에 사용된다.스펙트럼 왜곡을 최소화하여 신호 대 잡음 비를 개선할 수 있습니다.

  통계학에서 가중 이동 평균은 컨볼루션입니다.

• 음향학에서 반향은 음원을 둘러싼 물체로부터의 에코와 원음을 합성한 것입니다.

  디지털 신호 처리에서 컨볼루션(convolution)은 실제 룸의 임펄스 응답을 디지털 오디오 신호에 매핑하기 위해 사용된다.

  일렉트로닉 음악에서 컨볼루션(convolution)은 음에 스펙트럼 또는 리듬 구조를 부여하는 것이다.종종 이 봉투나 구조물은 다른 소리에서 가져온다.2개의 신호의 변환은 1개의 신호를 다른 ^[28]신호로 필터링하는 것입니다.

• 전기공학에서 하나의 함수(입력신호)와 두 번째 함수(임펄스 응답)의 컨볼루션은 선형시간불변시스템(LTI)의 출력을 제공한다.어느 순간이라도 출력은 입력 함수의 모든 이전 값의 누적 효과이며, 일반적으로 가장 최근의 값이 가장 큰 영향을 미칩니다(승수로 표현됨).임펄스 응답 함수는 각 입력 값이 발생한 이후 경과된 시간의 함수로 이 계수를 제공합니다.
• 물리학에서, "중첩 원리"를 가진 선형 계가 있는 곳이라면, 회전 연산이 나타난다.예를 들어 분광학에서 도플러 효과에 의한 선확대 자체는 가우시안 스펙트럼 선형을, 충돌확대만으로는 로렌츠 선형을 나타낸다.두 효과가 모두 작동하면 선 모양은 Voigt 함수인 가우스 및 로렌츠 함수의 합성곱이 됩니다.

  시간분해형광분광학에서는 들뜸신호를 델타펄스의 연쇄로서 취급할 수 있으며, 측정된 형광은 각 델타펄스로부터의 지수분해합이다.

  계산유체역학에서 대형와일시뮬레이션(LES) 난류모델은 계산에서 필요한 길이 스케일 범위를 낮추기 위해 컨볼루션 연산을 사용한다.

• 확률론에서, 두 독립 랜덤 변수의 합계의 확률 분포는 개별 분포의 제곱이다.

  커널 밀도 추정에서는 등방성 ^[29]가우스 등의 커널과의 컨볼루션에 의해 샘플 포인트로부터 분포를 추정한다.

• 방사선 치료 계획 시스템에서 모든 최신 계산 코드의 대부분은 컨볼루션 중첩 ^{[clarification needed]}알고리즘을 적용한다.
• 구조신뢰성에서는 컨볼루션 정리에 근거해 신뢰성 지수를 정의할 수 있다.

  비정규 분포를 갖는 한계 상태 함수에 대한 신뢰성 지수의 정의는 공동 분포 함수에 대응하여 확립될 수 있다.실제로 결합분포함수는 컨볼루션 ^[30]이론을 이용하여 얻을 수 있다.

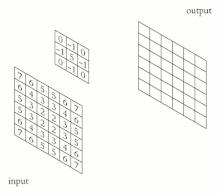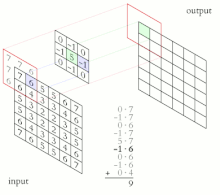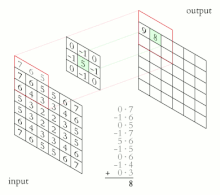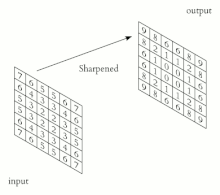
• 컨볼루션 뉴럴 네트워크는 다중 캐스케이드 컨볼루션 커널을 기계 비전과 ^[31][32]인공지능의 애플리케이션과 함께 적용합니다.그러나 대부분의 ^[33]경우 이러한 것들은 사실 conversion이라기 보다는 cross-correlations입니다.
• 평활입자 유체역학에서 유체역학 시뮬레이션은 각각 주변 입자를 사용하여 계산됩니다.특정 $입자{\displaystyle }$i(\$displaystyle$ i$)$에 대해 일부 ${\displaystyle {물리량}_{}}$Ai(\$displaystyle A_{$i$$})는 가중치 함수를 ${\displaystyle {가진}_{}}$A j(\$displaystyle A_{$j$$})의 제곱으로 계산됩니다. $여기$서$$j(\$displaystyle$j)는 입자$$i(\$displaystyle$i$)$의 이웃을 나타냅니다.. 이 값은 각 ^[34]네이버에 대한 합계로 근사됩니다.

「 」를 참조해 주세요.

메모들

레퍼런스

추가 정보

• 를 클릭합니다Bracewell, R. (1986), The Fourier Transform and Its Applications (2nd ed.), McGraw–Hill, ISBN 0-07-116043-4.
• Damelin, S.; Miller, W. (2011), The Mathematics of Signal Processing, Cambridge University Press, ISBN 978-1107601048
• Diggle, P. J. (1985), "A kernel method for smoothing point process data", Journal of the Royal Statistical Society, Series C, 34 (2): 138–147, doi:10.2307/2347366, JSTOR 2347366, S2CID 116746157
• 도밍게즈토레스, 알레한드로(2010년 11월 2일)."콘볼루션의 기원과 역사" 41파운드http://www.slideshare.net/Alexdfar/origin-adn-history-of-convolution 를 참조해 주세요.크랜필드, 베드포드 MK43 OAL, 영국2013년 3월 13일 취득.
• Ghasemi, S. Hooman; Nowak, Andrzej S. (2017), "Reliability Index for Non-normal Distributions of Limit State Functions", Structural Engineering and Mechanics, 62 (3): 365–372, doi:10.12989/sem.2017.62.3.365
• Grinshpan, A. Z. (2017), "An inequality for multiple convolutions with respect to Dirichlet probability measure", Advances in Applied Mathematics, 82 (1): 102–119, doi:10.1016/j.aam.2016.08.001
• 를 클릭합니다Hewitt, Edwin; Ross, Kenneth A. (1979), Abstract harmonic analysis. Vol. I, Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences], vol. 115 (2nd ed.), Berlin, New York: Springer-Verlag, ISBN 978-3-540-09434-0, MR 0551496.
• 를 클릭합니다Hewitt, Edwin; Ross, Kenneth A. (1970), Abstract harmonic analysis. Vol. II: Structure and analysis for compact groups. Analysis on locally compact Abelian groups, Die Grundlehren der mathematischen Wissenschaften, Band 152, Berlin, New York: Springer-Verlag, MR 0262773.
• 를 클릭합니다Hörmander, L. (1983), The analysis of linear partial differential operators I, Grundl. Math. Wissenschaft., vol. 256, Springer, doi:10.1007/978-3-642-96750-4, ISBN 3-540-12104-8, MR 0717035.
• 를 클릭합니다Kassel, Christian (1995), Quantum groups, Graduate Texts in Mathematics, vol. 155, Berlin, New York: Springer-Verlag, doi:10.1007/978-1-4612-0783-2, ISBN 978-0-387-94370-1, MR 1321145.
• 를 클릭합니다Knuth, Donald (1997), Seminumerical Algorithms (3rd. ed.), Reading, Massachusetts: Addison–Wesley, ISBN 0-201-89684-2.
• Narici, Lawrence; Beckenstein, Edward (2011). Topological Vector Spaces. Pure and applied mathematics (Second ed.). Boca Raton, FL: CRC Press. ISBN 978-1584888666. OCLC 144216834.
• Reed, Michael; Simon, Barry (1975), Methods of modern mathematical physics. II. Fourier analysis, self-adjointness, New York-London: Academic Press Harcourt Brace Jovanovich, Publishers, pp. xv+361, ISBN 0-12-585002-6, MR 0493420
• 를 클릭합니다Rudin, Walter (1962), Fourier analysis on groups, Interscience Tracts in Pure and Applied Mathematics, vol. 12, New York–London: Interscience Publishers, ISBN 0-471-52364-X, MR 0152834.
• Schaefer, Helmut H.; Wolff, Manfred P. (1999). Topological Vector Spaces. GTM. Vol. 8 (Second ed.). New York, NY: Springer New York Imprint Springer. ISBN 978-1-4612-7155-0. OCLC 840278135.
• 를 클릭합니다Stein, Elias; Weiss, Guido (1971), Introduction to Fourier Analysis on Euclidean Spaces, Princeton University Press, ISBN 0-691-08078-X.
• 를 클릭합니다Sobolev, V.I. (2001) [1994], "Convolution of functions", Encyclopedia of Mathematics, EMS Press.
• 를 클릭합니다Strichartz, R. (1994), A Guide to Distribution Theory and Fourier Transforms, CRC Press, ISBN 0-8493-8273-4.
• 를 클릭합니다Titchmarsh, E (1948), Introduction to the theory of Fourier integrals (2nd ed.), New York, N.Y.: Chelsea Pub. Co. (published 1986), ISBN 978-0-8284-0324-5.
• Trèves, François (2006) [1967]. Topological Vector Spaces, Distributions and Kernels. Mineola, N.Y.: Dover Publications. ISBN 978-0-486-45352-1. OCLC 853623322.
• Uludag, A. M. (1998), "On possible deterioration of smoothness under the operation of convolution", J. Math. Anal. Appl., 227 (2): 335–358, doi:10.1006/jmaa.1998.6091
• 를 클릭합니다von zur Gathen, J.; Gerhard, J . (2003), Modern Computer Algebra, Cambridge University Press, ISBN 0-521-82646-2.

외부 링크

• 초기 사용:컨벤션 항목에는 몇 가지 역사적 정보가 포함되어 있습니다.
• Configuration, 데이터 분석 개요 책
• http://www.jhu.edu/~visual/convolve/index.visual convolution
• http://www.jhu.edu/~syslog/syslogconv2/index.syslog 이산 시간 함수용 비주얼 컨볼루션 Java 애플릿
• https://get-the-solution.net/projects/discret-convolution discret-convolution 온라인 계산기
• https://lpsa.swarthmore.edu/Convolution/CI.html javascript에서의 컨볼루션 데모 및 시각화
• https://phiresky.github.io/convolution-demo/ javascript의 또 다른 컨볼루션 데모
• 이미지 처리 강의: Vanderbilt University의 pdf 형식의 18개 강의 모음입니다. 강의 7은 Alan Peters의 2-D 컨볼루션에 관한 것입니다.
• * https://archive.org/details/Lectures_on_Image_Processing
• 컨볼루션 커널 마스크 작동 대화형 튜토리얼
• MathWorld에서의 컨볼루션
• Freeverb3 임펄스 응답 프로세서:VST 플러그인을 사용하여 제로 레이텐시 임펄스 응답 프로세서를 오픈합니다.
• Stanford University CS 178 인터랙티브 플래시 데모: 공간 컨볼루션의 구조를 보여줍니다.
• Salman Khan의 컨벤션 주제에 대한 비디오 강의
• 패턴 인식을 위한 FFT 컨볼루션의 예(이미지 처리)
• 직관적인 컨버전스 가이드 직관적인 컨버전스 해석에 관한 블로그 포스트.