균일 폴리토프

이 글은 독자들에게 혼란스럽거나 불명확할 수 있다. 기사에 대해 명확하게 설명할 수 있도록 도와주십시오. 토크 페이지에서 이에 대한 논의가 있을 수 있다. (2008년 9월) (이 템플릿 메시지를 제거하는 방법과 시기 알아보기)

볼록 균일 폴리토페스

2D	3D
Coxeter 다이어그램과 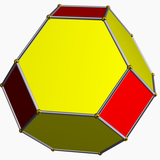함께 잘린 삼각형 또는 균일한 육각형.	잘린 팔면체,
4D	5D
잘린 16셀,	잘린 5정맥,

치수 3 이상의 균일한 폴리토프는 균일한 면에 의해 경계된 정점 변환 폴리토프다. 2차원의 균일한 폴리토프는 일반 폴리곤(두 개의 서로 다른 길이의 가장자리를 교대하는 정점 변환 짝수 다각형을 제외하기 위해 2차원의 정의가 다르다)이다.

이것은 반정형 폴리토페스(semiiregular polytopes)의 구 범주를 일반화한 것이지만, 일반 폴리토페스도 포함한다.polytopes)도 포함한다. 또한 항성 정규면 및 꼭지점 형상(별 폴리곤)이 허용되어 가능한 해결책이 크게 확대된다. 엄격한 정의는 균일한 폴리토프를 유한하게 하고, 보다 광범위한 정의는 유클리드 및 쌍곡선 공간의 균일한 허니콤(2차원 기울기와 고차원 허니콤)도 폴리토프로 간주할 수 있도록 한다.

운영

거의 모든 균일한 폴리토프는 와이토프 건설에 의해 생성될 수 있으며, 콕시터 다이어그램으로 표현된다. 주목할 만한 예외는 3차원의 대 디롱비코시도데카헤드론, 4차원의 대반민주의 등이다. 균일 다면체, 균일 4폴리토프, 균일 5폴리토프, 균일 6폴리토프, 균일 타일링, 볼록 균일 벌집 기사에 사용되는 볼록 균일 다면체의 용어는 노먼 존슨이 만들었다.^{[citation needed]}

마찬가지로 와이토피안 폴리토페스는 그 차원의 일반 폴리토페스에 기본 연산을 적용함으로써 생성될 수 있다. 이 접근법은 요하네스 케플러에 의해 처음 사용되었으며, 콘웨이 다면체 표기법의 기초가 된다.

정류 연산자

일반 n폴리토프는 정류 순서가 n개다. 제로트 수정이 원래 형태다. (n-1)-th 정류는 이중이다. 정류하면 가장자리가 정점으로 감소하고, 양방향은 정점으로 감소하며, 삼방향정은 세포를 정점으로 감소시키며, 정사각형은 정점으로 4단계 감소하고, 5단계 방향은 정점으로 감소한다.

확장된 Schléfli 기호는 하나의 첨자로 수정 양식을 나타내기 위해 사용할 수 있다.

• k-th 정류 = t_k{p₁₂, p, ..., p_n-1} = kr.

잘라내기 연산자

임의의 조합에서 일반 n-폴리토피에 적용할 수 있는 잘라내기 작업. 결과 Coxeter 다이어그램에는 두 개의 링이 있는 노드가 있으며, 그 사이의 거리에 따라 연산이 명명된다. 잘리면 정점이 잘리고, 통조림이 가장자리가 잘리고, 운행이 면이 잘리고, 멸균 절단 세포가 잘린다. 각각의 높은 동작은 낮은 동작도 잘라내므로, 운율 또한 정점을 잘라낸다.

1. t_0,1 또는 t: 절단 - 다각형 이상에 적용됨 잘리면 정점이 제거되고, 이전 정점 대신 새 정점이 삽입된다. 얼굴이 잘려서 가장자리가 두 배가 된다. (케플러(Kepler)가 만든 이 용어는 '잘라서' 라틴어 트렁크에서 유래한다.)

   

   • 또한 비트런테이션 t_1,2 또는 2t, 삼중수소런테이션 t_2,3 또는 3t, 쿼드런테이션 t_3,4 또는 4t, 5분위 t 또는_4,5 5t 등이 있다.
2. t_0,2 또는 rr: Cantellation - 다면체 이상에 적용된다. 그것은 그것의 정정을 바로잡는 것으로 보여질 수 있다. 표시는 정점과 가장자리를 모두 잘라내고 그것들을 새로운 면으로 대체한다. 세포는 위상학적으로 확장된 자기들의 복사본으로 대체된다. (존슨이 만든 이 용어는 베벨과 같이 비스듬한 얼굴로 자른다는 뜻의 동사 캔트에서 유래되었다.)

   

   • 또한 더 높은 수치로도 볼 수 있다: 쌍곡선 t_1,3 또는 r2r, 삼곡선 t_2,4 또는 r3r, 사방곡선_3,5 t 또는 r4r 등.
   • t_0,1,2 또는 tr: Cantitruncation - 다면체 이상에 적용된다. 그것은 그것의 정정을 잘라내는 것으로 보여질 수 있다. 캔티트런케이션은 정점과 가장자리를 모두 잘라내고 그것들을 새로운 면으로 대체한다. 세포는 위상학적으로 확장된 자기들의 복사본으로 대체된다. (합성 용어는 통풍과 잘림을 결합함)
     • 또한 더 높은 수치로도 볼 수 있다: 쌍동 구획 t 또는_1,2,3 t2r, 삼동 구획 t_2,3,4 또는 t3r, 사분 구획 구획 t 또는_3,4,5 t4r.
3. t_0,3: 런케인팅 - 균일 4폴리토프 이상에 적용. 런케이트는 꼭지점, 가장자리, 면들을 잘라내고 각각을 새로운 면으로 대체한다. 4-패스는 토폴로지적으로 확장된 그들 자신의 복사본으로 대체된다. (존슨이 만든 이 용어는 라틴어 런시나 '카펜터의 비행기'에서 유래되었다.)
   • 또한 분만 t_1,4, 삼분해 t 등이_2,5 더 많이 있다.
4. t_0,4 또는 2r2r: 스테로케이션 - 균일 5폴리탑 이상에 적용. 그것은 그것의 양방향화를 간접적으로 하는 것으로 볼 수 있다. 정점, 가장자리, 면, 셀을 잘라내고 각각을 새로운 면으로 대체한다. 5-패스는 위상학적으로 확장된 그들 자신의 복사본으로 대체된다. (존슨이 만든 이 용어는 그리스 스테레오 '솔리드'에서 유래되었다.)
   • 또한 이염 t 또는_1,5 2r3r, 삼염 t 또는_2,6 2r4r 등 높은 장력이 있다.
   • t_0,2,4 또는 2t2r: Stericantellation - 균일 5폴리탑 이상에 적용. 그것은 그것의 양방향성을 비트는 것으로 볼 수 있다.
     • 또한 높은 강직물도 있다: 이스테리칸텔레이션 t_1,3,5 또는 2t3r, 삼스테리칸텔레이션 t 또는_2,4,6 2t4r 등.
5. t_0,5: Pentellation - Uniform 6-polytopes 이상에 적용. 펜텔레이션은 꼭지점, 가장자리, 면, 셀, 4-페이스를 잘라내어 각각 새로운 면으로 대체한다. 6-페이스를 위상학적으로 확장된 자신의 복사본으로 대체한다. (펜텔레이션은 그리스 펜테 '5'에서 유래한다.)
   • 또한 높은 펜텔링(bipentellation t_1,6, tripentellation t 등_2,7)이 있다.
6. t_0,6 또는 3r3r: Hexcication - 균일 7 폴리탑 이상에 적용. 3보정이라고 볼 수 있다. 육각은 정점, 가장자리, 면, 셀, 4-패스, 5-패스를 잘라내며 각각을 새로운 면으로 대체한다. 7-패스는 위상학적으로 확장된 자신의 사본으로 대체된다. (헥사케이션은 그리스 육각형 '6'에서 유래한다.)
   • 또한 더 높은난독도 있다:생물학:t1,7 또는 3r4r, 3학:t또는2,8 3r5r 등.
   • t_0,3,6 또는 3t3r: 헥시룬케이트 - 균일 7 폴리토프 이상에 적용. 그것은 삼중수소가 3정정을 하는 것으로 볼 수 있다.
     • 또한_2,5,8 16진법이 더 높다: bihexiruncited: t_1,4,7 또는 3t4r, t 또는 3t5r 등.
7. t_0,7: 헵텔레이션 - 균일 8폴리탑 이상에 적용. 헵텔레이션은 꼭지점, 가장자리, 면, 셀, 4-패스, 5-패스, 6-패스를 잘라내며 각각을 새로운 면으로 대체한다. 8-132는 토폴로지적으로 확장된 자신의 복사본으로 대체된다. (헥텔레이션은 그리스 헵타 '7'에서 유래한다.)
   • 또한 더 높은 헵틱이 있다: 생물 헵틱 t_1,8, 3 헵틱 t 등_2,9.
8. t_0,8 또는 4r4r: 옥텔레이션 - 균일 9 폴리탑 이상에 적용.
9. t_0,9: 활성화 - 균일 10 폴리토피 이상에 적용.

또한 새로운 균일한 폴리토프를 생성하는 잘라내기 조합도 수행할 수 있다. 예를 들어, 런시민화는 함께 적용되는 런닝과 잘림이다.

모든 절개를 한 번에 적용하면 일반적으로 수술을 잡동사니라고 할 수 있다.

교대

교대라고 불리는 하나의 특별한 수술은 짝수 면만 있는 폴리토프에서 정점을 제거한다. 대체된 다종류는 스너브라고 불린다.

결과적인 폴리토페스는 항상 구성될 수 있고, 일반적으로 반사되지 않으며, 일반적으로 균일한 폴리토페 용액을 가지고 있지 않다.

하이퍼큐브를 교대로 형성하는 다면체 세트는 데미큐브라고 알려져 있다. 이것은 3차원에서 사면체를 생성하며, 4차원에서 이것은 16세포 또는 탈원형을 생성한다.

정점수

균일한 폴리탑은 정점, 각 정점 주위의 가장자리, 면, 셀 등의 배열로 구성될 수 있다. Coxeter 다이어그램으로 대표되는 균일한 폴리토프는 링으로 활성 거울을 표시하고 반사 대칭을 가지며, 정점 형상의 반복반사로 간단하게 구성할 수 있다.

더 적은 수의 비반사성 균일 폴리탑은 하나의 꼭지점을 가지지만 단순한 반사에 의해 반복되지 않는다. 이 중 대부분은 다른 균일한 폴리토페의 교대 같은 조작으로 나타낼 수 있다.

단일 링 Coxeter 다이어그램의 꼭지점 수치는 링 노드를 제거하고 인접 노드를 링잉하여 다이어그램에서 구성할 수 있다. 그러한 꼭지점 수치는 그 자체로 정점 변환이다.

다선형 폴리탑은 조금 더 복잡한 시공 공정에 의해 시공될 수 있으며, 그 위상은 균일한 폴리토프가 아니다. 예를 들어 잘린 일반 폴리토프(고리가 2개 있는 경우)의 꼭지점은 피라미드다. 모든 노드가 울린 다원형(모든 노드가 울림)은 항상 그 꼭지점 모양으로 불규칙한 심플렉스(simplex)를 갖는다.

할레라디우스

균일한 폴리토페스는 가장자리 길이가 같고, 모든 꼭지점은 중심으로부터 같은 거리로, 회음부라고 불린다.

균일 폴리토페스(called polytopes)는 균일 벌집(honeycomb)의 꼭지점 수치로 사용할 수 있다. 예를 들어, 정육각형은 6개의 정삼각형으로 나뉘며 정삼각형의 정점이다. 또한 큐옥타헤드론은 8개의 정사각형 피라미드와 6개의 정사각형 피라미드(반팔면체)로 나뉘며, 대체 입방형 벌집모양의 꼭지점이다.

치수별 균일한 폴리토피

균일한 폴리토페스를 치수별로 분류하는 것이 유용하다. 이는 Coxeter 다이어그램의 노드 수 또는 Wythoffian 구성의 하이퍼플레인의 수와 동일하다. (n+1)차원 폴리토페스는 n차원 구형 공간의 틸팅이기 때문에 n차원 유클리드 및 쌍곡선 공간의 틸팅도 (n+1)차원으로 간주된다. 따라서 2차원 공간의 기울기는 3차원 고형물과 그룹화된다.

원차원

유일한 1차원 폴리토프는 선분할이다. 콕시터 가문 A에₁ 해당한다.

2차원

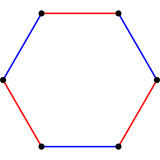
2차원으로 볼록한 균일한 폴리토프의 무한 계열, 즉 규칙적인 폴리곤이 있으며, 가장 단순한 것이 정삼각형이다. 잘린 일반 폴리곤은 기하학적으로 2개의 면, t{p}={2p}. 처음 몇 개의 일반 다각형(및 Quasiregular 형식)은 아래에 표시된다.

이름	삼각형 (2-510x)	사각형 (2정형) (2개)	펜타곤	육각형	헵타곤	팔각형	에네아곤	데카곤	헨데카곤
슐레플리	{3}	{4} t{2}	{5}	{6} t{3}	{7}	{8} t{4}	{9}	{10} t{5}	{11}
콕시터 도표를 만들다
이미지
이름	도데카곤	삼각형	테트라데카곤	펜타데카곤	육각형	헵타데카곤	팔각형	에네아데카곤	이코사곤
슐레플리	{12} t{6}	{13}	{14} t{7}	{15}	{16} t{8}	{17}	{18} t{9}	{19}	{20} t{10}
콕시터 도표를 만들다
이미지

또한 항성 다각형의 무한 집합(합리적 수 2보다 큰 각 숫자에 하나씩)이 있지만, 이것들은 비콘벡스다. 가장 간단한 예는 합리적인 숫자 5/2에 해당하는 펜타그램이다. 일반 항성 다각형, {p/q}은(는) 반정형 항성 다각형으로 자를 수 있지만 t{p/q}=t{2p/q}}이(가) 짝수이면 이중 덮개가 된다. 역방향 다각형 t{p/(p-q)}={2p/(p-q)}={2p/(p-q)}}을(를) 사용하여 잘라낼 수도 있다(예: t{5/3}={10/3}).

이름	펜타그램	헵타그램		옥타그램	엔네아그램		디카그램	...n-agrams
슐레플리	{5/2}	{7/2}	{7/3}	{8/3} t{4/3}	{9/2}	{9/4}	{10/3} t{5/3}	{p/q}
콕시터 도표를 만들다
이미지

p-곤의 경우 Schléfli 기호 {p}로 표시되는 일반 다각형. 일반 폴리곤은 자가이중이기 때문에 정류하면 동일한 폴리곤이 생성된다. 균일 절단 작업은 측면을 {2p}(으)로 두 배로 늘린다. 스너브 작업은 잘라내기 작업을 번갈아 수행하면 원래 폴리곤 {p}을(를) 복원한다. 따라서 모든 균일한 다각형도 규칙적이다. 일반 다각형에 대해 다음과 같은 연산을 수행하여 균일한 다각형을 도출할 수 있으며, 이 또한 일반 다각형이다.

작전	확장됨 슐레플리 기호		정규 결과	콕시터 도표를 만들다	포지션		대칭
					(1)	(0)
부모	{p}	t0{p}	{p}		{}	--	[p] (주문 2p)
수정됨 (이중)	r{p}	t1{p}	{p}		--	{}	[p] (주문 2p)
잘림	t{p}	t0,1{p}	{2p}		{}	{}	[[p] = [2p] (주문 4p)
절반	h{2p}		{p}		--	--	[1+,2p]=[p] (주문 2p)
스너브	s{p}		{p}		--	--	[[p]=[+p] (주문 2p)

삼차원

3차원으로 보면 상황이 더 흥미로워진다. 플라토닉 고형물로 알려진 5개의 볼록한 일반 다면체가 있다.

이름	슐레플리 {p,q}	도표	이미지 (iii)	이미지 (솔리드)	이미지 (Sphere)	얼굴 {p}	가장자리	정점 {q}	대칭	이중
사면체 (3-630x) (피라미드)	{3,3}					4 {3}	6	4 {3}	Td	(셀프)
큐브 (3개) (헥사헤드론)	{4,3}					6 {4}	12	8 {3}	Oh	팔면체
팔면체 (3정맥)	{3,4}					8 {3}	12	6 {4}	Oh	큐브
도데카헤드론	{5,3}					12 {5}	30	20 {3}2	Ih	이코사헤드론
이코사헤드론	{3,5}					20 {3}	30	12 {5}	Ih	도데카헤드론

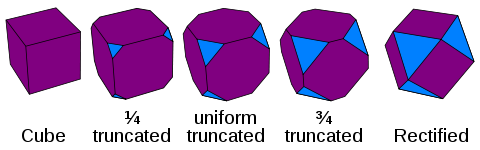
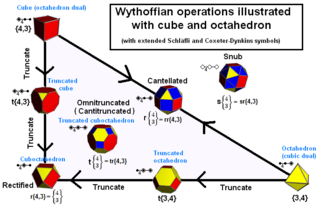
이들 외에도 13개의 반정형 다면체 또는 아르키메데스 고형물도 있는데, 이 고형물은 와이토프 시공을 통해 얻거나 플라토닉 고형물에서 잘라내는 등의 작업을 수행함으로써 얻을 수 있다.

	부모	잘림	수정됨	비트런어드 (트론 듀얼)	양방향으로 (iii)	알 수 있는	옴니트런어드 (칸티트런치)	스너브
사면체 3-3-2	{3,3}	(3.6.6)	(3.3.3.3)	(3.6.6)	{3,3}	(3.4.3.4)	(4.6.6)	(3.3.3.3.3)
팔면체 4-3-2	{4,3}	(3.8.8)	(3.4.3.4)	(4.6.6)	{3,4}	(3.4.4.4)	(4.6.8)	(3.3.3.3.4)
이코사헤드랄 5-3-2	{5,3}	(3.10.10)	(3.5.3.5)	(5.6.6)	{3,5}	(3.4.5.4)	(4.6.10)	(3.3.3.3.5)

또한 프리즘의 무한 집합이 있으며, 각 정규 다각형마다 하나씩 있으며, 그에 상응하는 일련의 반격도 있다.

#	이름	사진	타일링	꼭지점 형상을 나타내다	도표 그리고 슐레플리 기호
P2p	프리즘				tr{2,p}
A을p	항정신병				sr{2,p}

균일한 항성 다면체에는 추가로 4개의 일반 별 다면체, 케플러-푸인소트 다면체, 53개의 반정형 별 다면체가 있다. 또한 항성 프리즘(별 폴리곤별 1개)과 항성 항성(합리적 수별 3/2보다 큰 각 1개)의 두 가지 무한 집합이 있다.

시공

와이토프 유니폼 다면체 및 틸팅은 물체의 기본 영역을 지정하는 와이토프 기호로 정의할 수 있다. Coxeter에 의해서도 사용되는 Schléfli 표기법의 확장은 모든 차원에 적용되며, 문자 't'로 구성되며, Coxeter 도표의 링 노드에 해당하는 일련의 첨자 번호와 일반 종자 폴리토프의 Schléfli 기호로 구성된다. 예를 들어 잘린 옥타헤드론은 t_0,1{3,4}라는 표기법으로 표현된다.

작전	슐레플리 기호			콕시터 도표를 만들다		와이토프 심볼	위치:
부모	${\displaystyle {\begin{Bmatrix}p,q\end{Bmatrix}}$	{p,q}	t0{p,q}			q2 p	{p}	{ }	--	--	--	{ }
양방향으로 (또는 이중)	${\displaystyle {\begin{Bmatrix}q,p\end{Bmatrix}}$	{q,p}	t2{p,q}			p 2 q	--	{ }	{q}	{ }	--	--
잘림	${\displaystyle t{\begin{Bmatrix}p,q\end{Bmatrix}}$	t{p,q}	t0,1{p,q}			2시 15분	{2p}	{ }	{q}	--	{ }	{ }
비트런어드 (또는 잘린 이중)	${\displaystyle t{\begin{Bmatrix}q,p\end{Bmatrix}}}$	t{q,p}	t1,2{p,q}			2p q	{p}	{ }	{2q}	{ }	{ }	--
수정됨	${\displaystyle {\begin{Bmatrix}p\\q\end{Bmatrix}}$	r{p,q}	t1{p,q}			2p q	{p}	--	{q}	--	{ }	--
알 수 있는 (또는 확장)	${\displaystyle r{\begin{Bmatrix}p\\q\end{Bmatrix}}}$	rr{p,q}	t0,2{p,q}			p Q 2	{p}	{ }×{ }	{q}	{ }	--	{ }
캔트런커트 (또는 옴니트런)	${\displaystyle t{\begin{Bmatrix}p\\q\end{Bmatrix}}$	tr{p,q}	t0,1,2{p,q}			2p q	{2p}	{ }×{}	{2q}	{ }	{ }	{ }

작전	슐레플리 기호			콕시터 도표를 만들다		와이토프 심볼	위치:
스너브 수정	${\displaystyle s{\begin{Bmatrix}p\\q\end{Bmatrix}}$	sr{p,q}				2p q	{p}	{3} {3}	{q}	--	--	--
스너브	${\displaystyle s{\begin{Bmatrix}p,q\end{Bmatrix}}$	s{p,2q}	ht0,1{p,q}				s{2p}	{3}	{q}	--	{3}

삼각형 생성 중

4차원

4차원으로 볼록 정규 4폴리토프 6개, 플라토닉과 아르키메데스 고형물(이미 테세락트로 계산된 큐브프리즘 제외)에 17개의 프리즘이 있고, 볼록 대척점에 있는 프리즘, 두 개의 무한세트인 2개가 있다. 또한 41개의 볼록 반월형 4폴리토프가 있는데, 여기에는 비위토피아 대항정신병, 스너브 24셀 등이 포함된다. 이 특별한 4-폴리토프는 600-셀의 정점의 부분군으로 구성되어 있다.

4차원 균일한 별 폴리토페스가 모두 열거된 것은 아니다. 획일적인 항성 폴리헤드라에 있는 10개의 정규성(슐라펠리-헤스) 4폴리토페스와 57개의 프리즘을 포함한 세 개의 무한가족, 즉 항성항쟁의 프리즘, 두 개의 항성폴리곤에 곱하여 형성된 듀오프라임, 그리고 일반적인 폴리곤에 별폴리곤을 곱하여 형성된 듀오프라임 등이 있다. 위의 범주에 들어맞지 않는 4폴리토프의 수는 알 수 없다. 지금까지 1,000개 이상이 발견되었다.

모든 규칙적인 폴리토프는 소수의 거울 속에 있는 기본 영역의 이미지로 볼 수 있다. 4차원 폴리토프(또는 3차원 입방형 벌집형)에서 기본 영역은 4개의 거울로 경계를 이룬다. 4-공간의 거울은 3차원 하이퍼플레인이지만, 우리 목적상 하이퍼피어의 3차원 표면과의 2차원 교차점만을 고려하는 것이 더 편리하여 거울은 불규칙한 사면체를 형성한다.

16개의 정규 4폴리탑 각각은 다음과 같이 4개의 대칭군 중 하나에 의해 생성된다.

• 그룹 [3,3,3]: 자가 분해된 5-셀 {3,3,3};
• 그룹 [3,4]: 16-셀 {3,3,4} 및 이중 테서락트 {4,3,3};
• 그룹 [3,4,3]: 24-셀 {3,4,3}, 자가 측정;
• 그룹 [3,5,5]: 600-셀 {3,3,5}, 이중 120-셀 {5,3,3}, 그리고 그들의 10개의 정규 스텔링.
• 그룹 [3^1,1,1]: [3,3,4] 계열의 반복 멤버만 포함한다.

(이 그룹들은 Coxeter 표기법으로 이름 지어진다.)

유클리드 3공간에 있는 볼록한 균일 벌집 중 8개는 와이토피안 균일 4폴리토페스를 생성하기 위해 사용한 동일한 연산을 적용하여 입방 벌집 {4,3,4}에서 유사하게 생성된다.

주어진 대칭 심플렉스에는 정점 4개, 가장자리 6개, 면 4개 또는 내부 볼륨 중 하나에 생성점을 배치할 수 있다. 이 15개 요소 각각에는 네 개의 거울에 비친 이미지가 균일한 4폴리토프의 정점인 점이 있다.

확장된 Schléfli 기호는 t에 의해 만들어지고 첨자 0,1,2,3을 1~4개 포함시킨다. 첨자가 하나라면 발생 지점은 기본 영역의 한 모퉁이, 즉 거울 세 개가 만나는 지점이다. 이 모퉁이는 로 표기되어 있다.

• 0: 상위 4-제곱의 꼭지점(듀얼 셀의 중심)
• 1: 부모 가장자리 중앙(듀얼 얼굴 중앙)
• 2: 부모 얼굴 중앙(듀얼 가장자리 중앙)
• 3: 부모 세포의 중심(듀얼의 제곱)

(두 개의 자체 이중 4 폴리탑에 대해 "듀얼"은 이중 위치에서 유사한 4 폴리탑을 의미한다.) 첨자가 두 개 이상이면 생성점이 표시된 모서리 사이에 있음을 의미한다.

건설적 요약

가족에 의한 15가지 건설적인 형태는 아래에 요약되어 있다. 자체 이중 패밀리는 한 열에 나열되며, 다른 패밀리는 대칭 Coxeter 다이어그램에 공유 항목이 있는 두 개의 열로 나열된다. 마지막 10번째 줄에는 스너브 24 셀 구조물이 나열되어 있다. 여기에는 콕시터 가문이 없는 비위토피아 대항쟁을 제외한 모든 비프리즘적 제복 4폴리토페가 포함된다.

A을4	기원전4		D4	F4	H4
[3,3,3]	[4,3,3]		[3,31,1]	[3,4,3]	[5,3,3]
5세포 {3,3,3}	16 셀 {3,3,4}	큐테릭트 {4,3,3}	반신반의하다 {3,31,1}	24셀 {3,4,3}	600셀 {3,3,5}	120 셀 {5,3,3}
교정된 5세포 r{3,3,3}	교정된 16세포 r{3,3,4}	수정 큐테락트 r{4,3,3}	정정된 신분 증명서. r{3,31,1}	정류 24세포 r{3,4,3}	정류 600셀 r{3,3,5}	정류된 120 셀 r{5,3,3}
잘린 5세포 t{3,3,3}	잘린 16셀 t{3,3,4}	잘린 테세락트 t{4,3,3}	잘린 소수점. t{3,31,1}	잘린 24셀 t{3,4,3}	잘린 600셀 t{3,3,5}	잘린 120셀 t{5,3,3}
알 수 있는 5세포 rr{3,3}	알 수 있는 16세포 rr{3,4}	알 수 있는 테서락트 rr{4,3,3}	알 수 있는 반신불수. 2r{3,31,1}	24세포로 알 수 있는 rr{3,4,3}	알 수 있는 600셀 rr{3,5}	알 수 있는 120 셀 rr{5,3,3}
윤이 나는 5세포 t0,3{3,3,3}	룬케이트 16셀 t0,3{3,3,4}	윤활제 테세락트 t0,3{4,3,3}		윤택 24셀 t0,3{3,4,3}	윤활유 600셀 재질의 120셀 t0,3{3,3,5}
박리된 5세포 t1,2{3,3,3}	박리 16셀 2t{3,4}	가늘게 말린 큐브락트 2t{4,3,3}	캔트런드 demitesseract. 2t{3,31,1}	24구경. 2t{3,4,3}	600셀의 박리. 120셀의 박리. 2t{3,5}
캔트런으로 된 5셀 tr{3,3}	캔트런으로 된 16셀 tr{3,4}	캔트런 경량형 tr{4,3,3}	종합격리제. tr{3,31,1}	캔트런 24셀 tr{3,4,3}	캔트런 600셀 tr{3,5}	120셀의 캔트런을 가진 tr{5,3,3}
구획 5셀 t0,1,3{3,3,3}	구획 16셀 t0,1,3{3,3,4}	시금치를 넣은 테서락트. t0,1,3{4,3,3}	시금석 같은 반감제 rr{3,31,1}	24구경. t0,1,3{3,4,3}	6백 셀을 달리다. t0,1,3{3,3,5}	120셀의 경사로를 달리다. t0,1,3{5,3,3}
잡동사니 5세포 t0,1,2,3{3,3,3}	전지형 16셀 t0,1,2,3{3,3,4}	잡탕의 정방체 t0,1,2,3{3,3,4}		전지 24셀 t0,1,2,3{3,4,3}	다량의 120셀 다량의 600셀 t0,1,2,3{5,3,3}
	교번식 캔트런 16 셀 sr{3,4}		반신반의하다. sr{3,31,1}	교번 절단 24-셀 s{3,4,3}

잘린 양식

다음 표는 15가지 양식을 모두 정의한다. 각 트루션 형태는 위에서 정의한 위치 0,1,2,3에 위치한 1개에서 4개까지의 셀 유형을 가질 수 있다. 그 세포들은 다면 절단 표기법으로 라벨이 붙어 있다.

• n-곤알 프리즘은 {n}×{ }로 표현된다.
• 녹색 배경은 부모 또는 이중과 동등한 양식에 표시된다.
• 빨간색 배경은 부모의 잘라낸 부분을 나타내고, 파란색은 이중의 잘라낸 부분을 나타낸다.

작전	슐레플리 기호		콕시터 도표를 만들다	위치별 셀:
				(3)	(2)	(1)	(0)
부모	{p,q,r}	t0{p,q,r}		{p,q}	--	--	--
수정됨	r{p,q,r}	t1{p,q,r}		r{p,q}	--	--	{q,r}
양방향으로 (또는 수리된 이중)	2r{p,q,r} = r{r,q,p}	t2{p,q,r}		{q,p}	--	--	r{q,r}
삼보정 (또는 이중)	3r{p,q,r} = {r,q,p}	t3{p,q,r}		--	--	--	{r,q}
잘림	t{p,q,r}	t0,1{p,q,r}		t{p,q}	--	--	{q,r}
비트런어드	2t{p,q,r}	2t{p,q,r}		t{q,p}	--	--	t{q,r}
삼중수소경사 (또는 잘린 이중)	3t{p,q,r} = t{r,q,p}	t2,3{p,q,r}		{q,p}	--	--	t{r,q}
알 수 있는	rr{p,q,r}	t0,2{p,q,r}		rr{p,q}	--	{ }×{r}	r{q,r}
바이칸텔레이트 (또는 알 수 있는 이중)	r2r{p,q,r} = rr{r,q,p}	t1,3{p,q,r}		r{p,q}	{p}×{ }	--	rr{q,r}
런케이티드 (또는 확장)	e{p,q,r}	t0,3{p,q,r}		{p,q}	{p}×{ }	{ }×{r}	{r,q}
캔트런커트	tr{p,q,r}	tr{p,q,r}		tr{p,q}	--	{ }×{r}	t{q,r}
바이칸티트룬말림 (또는 캔트런치 듀얼)	t2r{p,q,r} = tr{r,q,p}	t1,2,3{p,q,r}		t{q,p}	{p}×{ }	--	tr{q,r}
런시트랄드	et{p,q,r}	t0,1,3{p,q,r}		t{p,q}	{2p}×{ }	{ }×{r}	rr{q,r}
룬시칸텔레이트 (또는 런커런트 듀얼)	e3t{p,q,r} = et{r,q,p}	t0,2,3{p,q,r}		tr{p,q}	{p}×{ }	{ }×{2r}	t{r,q}
런시칸티트런치드 (혹은 전지형)	o{p,q,r}	t0,1,2,3{p,q,r}		tr{p,q}	{2p}×{ }	{ }×{2r}	tr{q,r}

하프 폼

절반의 구조물은 링이 달린 노드보다는 구멍이 있는 상태로 존재한다. 인접한 구멍과 비활성 노드는 짝수여야 한다. 절반의 건설은 동일한 고리 구조의 정점을 가지고 있다.

작전	슐레플리 기호		콕시터 도표를 만들다	위치별 셀:
				(3)	(2)	(1)	(0)
절반 교대형	h{p,2q,r}	ht0{p,2q,r}		h{p,2q}	--	--	--
교대로 수리됨	hr{2p,2q,r}	ht1{2p,2q,r}		hr{2p,2q}	--	--	h{2q,r}
스너브 교번 절단	s{p,2q,r}	ht0,1{p,2q,r}		s{p,2q}	--	--	h{2q,r}
비스눕 대체 비트런지	2s{2p,q,2r}	ht1,2{2p,q,2r}		s{q,2p}	--	--	s{q,2r}
스너브 수정 교대로 잘린 부분이 수리됨	sr{p,q,2r}	ht0,1,2{p,q,2r}		sr{p,q}	--	s{2,2r}	s{q,2r}
옴니스누브 교대형 잡식성	os{p,q,r}	ht0,1,2,3{p,q,r}		sr{p,q}	{p}×{ }	{ }×{r}	sr{q,r}

5차원 이상

5개 이상의 차원에는 하이퍼큐브, 심플렉스, 크로스폴리토프 등 3개의 일반 폴리토페가 있다. 그것들은 각각 3차원 입방체, 4면체, 8면체의 일반화다. 이 치수에는 일반 항성 폴리토페스가 없다. 대부분의 균일한 고차원 폴리토페스는 일반 폴리토페스를 수정하거나 더 낮은 치수의 폴리토페스의 카르테시안 제품을 취함으로써 얻는다.

6, 7, 8차원에서는 예외적으로 단순한 거짓말 그룹인 E₆, E, E가₇₈ 작용한다. 0이 아닌 수의 Coxeter 다이어그램 노드에 링을 배치하면 63개의 새로운 6폴리토페, 127개의 새로운 7폴리토페, 255개의 새로운 8폴리토페를 얻을 수 있다. 주목할 만한 예가 4개의₂₁ 폴리토프다.

균일 벌집

유한 균일 폴리토페스의 대상과 관련하여 유클리드 공간과 쌍곡선 공간에는 균일한 꿀콤이 있다. 유클리드 균일 벌꿀컴은 아핀 콕시터 그룹에 의해 생성되고 쌍곡 벌꿀컴은 쌍곡선 콕시터 그룹에 의해 생성된다. 두 개의 아핀 콕시터 그룹을 함께 곱할 수 있다.

쌍곡선 Coxeter 그룹에는 콤팩트 그룹과 파라콤팩트 그룹이라는 두 가지 등급이 있다. 콤팩트 그룹에 의해 생성되는 균일한 벌집들은 유한한 면과 정점 수치를 가지며, 2~4차원으로 존재한다. 파라콤팩트 그룹은 아핀 또는 쌍곡선 서브그래프, 무한 면 또는 정점 형상을 가지며 2~10차원으로 존재한다.

참고 항목

• 슐레플리 기호

참조

• Coxeter 기하학의 아름다움: 1999년 12편의 에세이 도버 출판사 ISBN978-0-486-40919-1 (제3장: 균일 폴리토페스를 위한 와이토프의 건설)
• Norman JohnsonUniform Polytopes, 원고(1991)
  • N.W. 존슨: 균일다각체와 허니컴의 이론, 박사학위. 1966년 토론토 대학교의 논문
• A. Boole Stott: 일반 폴리토페와 공간충전에서 반정형의 기하학적 차감, 코닌클리케 아카데미 판 웨텐샤펜 폭 단위 암스테르담, 에르스테 챕티 11,1, 암스테르담, 1910
• H.S.M. Coxeter:
  • H.S.M. Coxeter, M. Longuet-Higgins, J.C.P. Miller: 1954년 런던 왕립학회의 철학적 거래, 통일 폴리헤드라
  • H.S.M. Coxeter, 일반 폴리토페스, 제3판 도버 뉴욕, 1973년
• 케일리디스코어: H.S.M. Coxeter의 선별된 글, F가 편집한 글. 아서 셔크, 피터 맥멀런, 앤서니 C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN978-0-471-01003-6
  • (용지 22) H.S.M. Coxeter, 정규 및 반정규 폴리토페스 I, [산술] Zeit. 46 (1940) 380-407, MR 2,10]
  • (용지 23) H.S.M. Coxeter, 정규 및 반정규 폴리토페스 II, [수학] Zeit. 188 (1985) 559-591]
  • (용지 24) H.S.M. Coxeter, 정규 및 반정규 폴리토페스 III, [산술] Zeit. 200 (1988) 3-45]
• 콕시터, 롱구엣-하이긴스, 밀러, 제복 다면체, 필 Trans. 1954, 246 A, 401-50. (확장된 Schléfli 표기법 사용)
• 마르코 뮐러, 비에르디멘탈레 아르키메디스체 폴리토페, 논문, 함부르크 유니버시아드, 함부르크(2004) (독일어

외부 링크

• Olshevsky, George. "Uniform polytope". Glossary for Hyperspace. Archived from the original on 4 February 2007.
• 4차원의 균일하고 볼록한 폴리탑:, 마르코 뮐러(독일어)

v t 치수 2-10의 기본 볼록형 일반 및 균일한 폴리토프
가족	A을n	Bn	I2(p) / Dn	E6 / E7 / E8 / F4 / G2	Hn
정규 다각형	삼각형	사각형	p-곤	육각형	펜타곤
균일다면체	사면체	옥타헤드론 • 큐브	데미큐브		도데카헤드론 • 이코사헤드론
균일 폴리초론	펜타코론	16-셀 • 테세락트	데미테세락트	24셀	120 셀 • 600 셀
제복5폴리토프	5와섹스	5정형 • 5정형	5데미큐브
제복6폴리토프	6-630x	6-정통 • 6-118	6데미큐브	122 • 221
제복7폴리토프	7시 15분	7정맥 • 7정맥	7데미큐브	132 • 231 • 321
제복8폴리토프	8시 15분	8정형 • 8정형	8데미큐브	142 • 241 • 421
제복9폴리토프	9시 15분	9-정통 • 9-11	9데미큐브
균일 10폴리토프	10센트짜리	10정형 • 10정형	10데미큐브
균일 n폴리토프	n-제곱스	n-직관 • n-직관	n-데미큐브	1k2 • 2k1 • k21	n-자갈 폴리토프
주제: 폴리토페 패밀리 • 일반 폴리토페 • 일반 폴리토페 및 화합물 목록