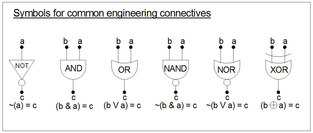
제안식
Propositional formula명제적 논리학에서 명제적 공식은 잘 형성되고 진리가치를 갖는 통사적 공식의 한 유형이다. 명제 공식에 있는 모든 변수의 값이 주어지면, 그것은 고유한 진리 값을 결정한다. 명제 공식은 명제적 표현, 문장 또는 전위적 공식이라고도 할 수 있다.
명제 공식은 "5가 3보다 크다"와 같은 간단한 명제나 p와 q와 같은 명제 변수로 구성되며, NOT, AND, OR 또는 INMAS와 같은 연결고리나 논리 연산자를 사용한다. 예를 들어 다음과 같다.
- (p AND NOT q) 함축적 (p OR q)
수학에서 명제 공식은 흔히 '제안'이라고 더 간단히 언급되지만, 더 정확히 말하면 명제 공식은 명제가 아니라 형식적인 표현으로, 마치 "x + y"와 같은 표현이 가치가 아니라 가치를 나타내는 것처럼, 논의 중인 형식적인 대상을 가리킨다. 어떤 맥락에서, 구별을 유지하는 것이 중요할 수도 있다.
제안
명제 미적분학의 목적상 명제(언어, 문장, 주장)는 단순하거나 복합적인 것으로 간주된다.[1] 복합 명제는 보초적 연결 장치에 의해 연계되는 것으로 간주되며, 그 중 가장 일반적인 것은 "AND", "OR", "IF ..."이다. 그렇다면...", "아니오... NOR...", "..." IS EQUILT TO..." . 연결 세미콜론 ";"와 연결형 "BUT"는 "AND"의 표현으로 간주된다. 이산형 문장의 순서는 "AND"에 의해 연계되는 것으로 간주되며, 형식 분석은 간단한 명제의 순서와 관련하여 반복적인 "부모법 규칙"을 적용한다(아래 잘 구성된 공식에 대한 자세한 내용 참조).
- 예를 들면 다음과 같다. 그 주장은 "이 소는 파랗다. 저 말은 오렌지색인데 여기 이 말은 보라색이다."는 사실 "AND"s와 연관된 복합 명제다. ("이 소는 파랗고" "저 말은 오렌지색") 그리고 "여기 이 말은 보라색이다" 입니다.
간단한 명제는 자연에서 선언적인 것으로서, 즉 그들은 "이 소는 파랗다", "코요테가 있다!"와 같은 특정한 감각 대상의 조건이나 성질에 대해 주장을 한다.[2] 따라서 단순한 "원초적" 주장은 특정한 사물이나 특정한 정신 상태에 관한 것이어야 한다. 각자는 적어도 하나의 주제(생각이나 관찰의 직접적인 대상), 동사(활성 음성 및 현재 시제 선호), 그리고 아마도 형용사나 부사를 가지고 있어야 한다. "개!"는 아마도 "개가 보인다"는 의미를 내포하고 있지만, 너무 모호하다고 거부되어야 한다.
- 예: "저 보라색 개가 달리고 있다", "이 소는 파란색이다", "스위치 M31이 닫혔다", "이 모자는 꺼졌다", "내일은 금요일이다."
명제 미적분학의 목적상 복합 명제는 보통 일련의 간단한 문장으로 다시 쓰여질 수 있지만, 결과는 아마도 지루하게 들릴 것이다.
명제 공식과 술어 공식 사이의 관계
그 서술은 미적분학을 한 걸음 더 그 명제 계산보다 그것은 두 부분(나는) 담화의 지배(개체를(또는의 단수 복수))에 술어(동사나 혹은 가능하면 그 verb-clause(s 개체의 품질이나 특성을 주장하고)(ii)단순한 문장 파괴되는"명제의 내부 구조의 분석"[3]에 간다.cm이다. 그런 다음 미적분학은 "주체 술어" 형태(여기서 기호들의 결합(끈으로 묶음)를 상징함)를 다음과 같은 빈-주체 구조 "__ 술어"를 가진 형태로 일반화하고, 술어는 그 성질을 가진 모든 사물에 일반화한다.
- 예: "이 푸른 돼지는 날개가 있다"는 명제 미적분학에서 내부 구조를 고려하지 않은 "이 돼지는 날개가 있다"와 "이 돼지는 파란색이다"라는 두 문장이 된다. 이와는 대조적으로, 술어 미적분학에서는 첫 번째 문장이 주어로 "이 돼지"로, 술어로는 "날개가 있다"로 나뉜다. 따라서 그것은 "이 돼지"라는 물체가 "날개 있는 것"의 클래스(세트, 수집)의 일원이라고 주장한다. 두 번째 문장은 "이 돼지"라는 물체는 "파란색" 속성이므로 "파란색"의 등급에 속한다고 주장한다. AND와 연결된 두 문장을 다음과 같이 쓰도록 선택할 수 있다.
- p W AND P B
'이 돼지'를 '날개 있는 것'과 '푸른 것' 두 계급의 (잠재적인) 멤버에게 일반화한다는 것은 이 두 계급 모두와 진실 관계를 맺고 있다는 것을 의미한다. 즉, 담론의 영역인 "날개 있는 것"에 따라 p는 이 영역의 구성원으로 밝혀지거나 그렇지 않은 것으로 밝혀진다. 따라서 p(pig)와 {T, F }, {T, F }, W(p)는 {T, F }(으)로 평가하며, 여기서 {T, F }은 부울 값 "true"와 "false"의 집합이다. B(블루어티)와 p(pig)와 {T, F }: B(p)는 {T, F }(으)로 평가한다. 따라서 이제 하나의 연결된 주장 "B(p) AND W(p)"를 분석하여 전체적인 진리 가치를 얻을 수 있다. 즉, 다음과 같다.
- (B(p) 및 W(p) )는 { T, F }에 대해 평가한다.
특히 논리 정량자라 불리는 "전부", "일부", "소수", "일부" 등의 개념을 채용한 간단한 문장들은 술어 미적분학에 의해 처리된다. 새로운 함수 상징 "F(x)"와 함께 ∀ (모두에게)와 ∃ (존재하는 ..., 적어도 ...중 하나 이상의 새로운 기호가 도입된다. 존재 등). 명제 미적분은 아니지만 술어 미적분은 다음 문장의 형식적 타당성을 확립할 수 있다.
- "모든 푸른 돼지는 날개가 있지만 어떤 돼지는 날개가 없기 때문에 어떤 돼지는 파란색이 아니다."
아이덴티티
타르스키는 (논리적 동등성과 구별되는) IDENTITY의 개념은 명제적 미적분학 밖에 있다고 주장하지만, 논리가 수학과 과학에 사용되려면 IDENT의 "이론"을 포함해야 한다고 그는 지적한다.[4] 일부 저자는 이 연장을 강조하기 위해 "정체성을 가진 논리를 강조한다"고 언급한다. 자세한 내용은 아래를 참조하십시오.
명제 대수학, 명제 미적분학
이 섹션은 위키백과 편집자의 개인적인 감정을 진술하거나 주제에 대한 원론적인 주장을 제시하는 개인적인 성찰, 개인적인 에세이 또는 논쟁적인 에세이처럼 쓰여진다. (2021년 6월)(이과 시기 |
대수학(그리고 많은 다른 것이 있다)은 느슨하게 정의되어 있는 것으로서 괄호 (, )와 같은 일부 다른 기호들과 함께 변수라고 불리는 기호들의 집합과 *, +, ~, &, ∨, =, ≡, ∧, ¬ 등의 일부 하위 집합이 규칙의 체계 안에서 조작되는 방법이다. 이 기호들, 그리고 그것들의 잘 형성된 문자열들은 물체를 나타낸다고 하지만, 특정한 대수학 체계에서는 이 물체들은 의미를 가지고 있지 않다. 따라서 대수 내부의 일은 기호의 의미론(의미)보다는 대수구문(기호형식)의 특정 법칙(규칙)을 준수하는 연습이 된다. 그 의미는 대수학 밖에서 발견된다.
대수에서 잘 형성된 기호 순서(공식)의 경우, 대수 외부에 유용성을 가지기 위해 기호는 의미가 할당되고 결국 변수에는 값이 할당된다. 그런 다음 일련의 규칙에 의해 공식을 평가한다.
그 값이 단 두 개로 제한되고 명제에 의해 연결된 단순한 문장(예: 구어발언 또는 서면주장)의 개념에 적용될 때, 이 전체 대수 체계인 기호 및 규칙과 평가 방법들을 보통 명제 미적분학 또는 송신 미적분학이라고 부른다.
산술대수의 익숙한 규칙 중 일부는 명제의 대수학(예: AND와 OR에 대한 정류법 및 연관법)에서 계속 유지되지만, 그렇지 않은 규칙(예: AND, OR 및 NOT에 대한 분배법)은 계속 유지되지 않는다.
명제 공식의 유용성
분석: 연역적 추론에서 철학자와 수사학자, 수학자는 주장을 공식으로 줄인 다음 정확성(건전성)을 위해 (대개 진리표를 사용하여) 연구한다. 예를 들면 다음과 같다. 다음과 같은 주장이 들리는가?
엔지니어는 합성 기법을 이용해 설계한 논리회로를 분석한 뒤 다양한 축소·최소화 기법을 적용해 설계를 단순화한다.
합성: 특히 엔지니어들은 진리표에서 명제 공식(결국 기호의 회로로 끝나는)을 합성한다. 예를 들어 변수 "b"와 "a"와 "carry_in" "ci"가 추가되고 "carry_out" "co"와 "sum" results이 추가되는 경우, 이진 추가가 어떻게 동작해야 하는지에 대한 진실 표를 작성할 수 있다.
- 예: 5행에서 (b+a) + ci ) = (1+0) + 1 = 이진수로 작성된 숫자 "2"는 10이며2 여기서 "co"=1 및 and=0은 맨 오른쪽 열에 표시된 것과 같다.
| 배를 젓다 | b | a | ci | (b+a)+ci | 공동의 | Σ | |
|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 1 | 0 | 0 | 1 | 1 | 0 | 1 | |
| 2 | 0 | 1 | 0 | 1 | 0 | 1 | |
| 3 | 0 | 1 | 1 | 2 | 1 | 0 | |
| 4 | 1 | 0 | 0 | 1 | 0 | 1 | |
| 5 | 1 | 0 | 1 | 2 | 1 | 0 | |
| 6 | 1 | 1 | 0 | 2 | 1 | 0 | |
| 7 | 1 | 1 | 1 | 3 | 1 | 1 |
제안 변수
가장 간단한 유형의 명제 공식은 명제 변수다. 단순(원자적), 상징적 표현인 명제는 흔히 p, q 또는 P, Q 등의 이름으로 명명된 변수에 의해 표시된다. 명제 변수는 "토요일이다" = p (여기서 기호 = " ...는 "..."라는 변수가 할당됨) 또는 "나는 월요일에만 영화를 보러 간다" = q)와 같은 원자 명제(주장)를 나타내려고 한다.
진실 가치 할당, 공식 평가
명제 공식의 평가는 각 변수에 대한 진실 값의 할당에서 시작된다. 각 변수는 단순한 문장을 나타내기 때문에 이러한 단순한 문장의 "진실성" 또는 "신실성"에 진리 값이 적용되고 있다.
수사학, 철학, 수학의 진실 가치: 진리 값은 두 가지에 불과하다: {TRUE "T", PHANISITY "F". 경험론자는 모든 명제를 분석적(예: tautology)과 합성적(synthetic)이라는 두 가지 광범위한 분류로 분류한다. 경험에서 파생되어 제3자에 의한 확인(의식 검증 이론)에 영향을 받기 쉽다.[5] 경험론자들은 일반적으로 합성 명제의 진리 가치에 도달하기 위해서는 의미(패턴 매칭 템플릿)가 단어들에 먼저 적용되어야 하며, 그 다음에 이러한 의미-템플릿이 주장되고 있는 어떤 의미-템플릿과 비교되어야 한다고 주장한다. 예를 들어, "저 소는 파랗다!"라고 말하는 내 말이 그렇다. 이 진술이 진실인가? 정말로 나는 말했다. 그리고 어쩌면 나는 파란 소를 보고 있을지도 모른다. 내가 거짓말을 하고 있지 않는 한, 내 진술이 내 (아마도 결함이 있는) 인식의 대상과 관련된 진실이다. 하지만 그 파란 소는 "정말 거기"일까? 같은 창밖을 내다보면 무엇이 보이나? 검증을 진행하기 위해서는 "cow"와 "blue"의 사전 개념(템플릿)과 감각의 대상(실제로 템플릿이 있는 경우)과 템플릿을 매치할 수 있는 능력이 필요하다.[citation needed]
공학에서의 진실 가치: 공학자들은 철학자들을 괴롭히는 진실과 거짓의 개념을 피하려고 노력하지만, 최종 분석에서 공학자들은 그들의 측정기를 신뢰해야 한다. 강건성을 추구하면서, 기술자들은 작은 도서관, 즉 큰 조합에서도 잘 정의되고 예측 가능한 행동을 하는 사물에서 알려진 물체를 끌어내는 것을 선호한다(명제 미적분학: "합성 논리"를 위해 그들의 이름을 정함). 단일 물체의 가장 적은 동작은 두 가지(예: { OFF, ON }, {open, shut }, { UP, DOWN } 등)이며, 이러한 동작은 {0, 1 }과(와) 일치한다. 그러한 요소를 디지털이라고 하며, 동작의 연속적인 범위를 가지는 것을 아날로그라고 한다. 아날로그 시스템에서 결정을 내려야 할 때마다 엔지니어는 비교기를 사용하여 아날로그 동작(도어가 45.32146% UP)을 디지털 동작(예: DOWN=0 )으로 변환하는 경우가 꽤 많다.[6]
따라서 변수와 두 개의 값 상징 { 0, 1 }의 의미 할당은 (일반적으로) 복합 개체의 동작을 나타내는 공식을 "외부"에서 비롯된다. 예를 들어 UP 라벨 SW_U와 DOW 라벨이 부착된 SW_D, 그리고 도어 회로에 있는 다른 모든 것과 같은 두 개의 "제한 스위치"가 있는 차고 문이 있다. 회로 검사(도표 또는 실제 물체 자체—도어, 스위치, 와이어, 회로기판 등)를 보면 회로 기판에서 "노드 22"는 스위치 "SW_D"의 접점이 기계적으로 접촉("폐쇄")되고 도어가 "하강" 위치(95% 다운")에 있고 "노드 29"는 +0볼트로 가는 것이 밝혀질 수 있다.n 도어가 95% UP이고 스위치 SW_U의 접점이 기계적 접촉("닫힘")[7]에 있다. 엔지니어는 이러한 전압의 의미와 "나쁜" 것을 포함한 가능한 모든 조합(예: 0V에서 22와 29 노드, 문이 동시에 열리고 닫힌다는 의미)을 정의해야 한다. 회로는 TRUE 또는 FALSE, RIGHT 또는 ROWN, SAFE 또는 DEAND를 전혀 인식하지 않고 어떤 전압이든 부주의하게 반응한다.[citation needed]
프로포지셔널 코넥티브
임의의 명제 공식은 명제적 변수 및 명제적 결합체를 사용하는 다른 명제적 공식으로부터 만들어진다. 커넥티브의 예는 다음과 같다.
- 단항 부정 연결성. 이 공식이라면α {\은 공식이다.
- 고전적인 이항 연결은 →→, →↔, ↔, {, ↔, ↔, ↔, \ 따라서 \
- NAND, NOR 및 XOR와 같은 기타 이진 연결 장치
- 3차 결합형 IF... 그럼... 그렇지 않은 경우...
- 상수 0-ari connectives ⊤ 및 ⊥ (대체로 상수 {T, F }, { 1, 0 } 등)
- "이론적 확장 \좌우 이동 화살표} (대체로, IDENTITY 또는 기호 " = "는 "논리적 결합형" {\\좌우 화살표
수사학, 철학, 수학의 연결고리
다음은 미사여구, 철학, 수학에 공통적인 연결고리와 그 진리표를 합친 것이다. 사용되는 상징은 작가마다 그리고 노력의 분야마다 다를 것이다. 일반적으로 "T"와 "F"는 명제 공식의 변수에 적용되는 평가 RURISS와 FRSITY를 나타낸다(예: "저 소는 파랗다"는 주장)는 경우에 따라 진실 가치 "T" 또는 거짓 가치 "F"가 있을 것이다.
연결 장치는 여러 가지 다른 용어로 통한다. 예를 들어, "A INMISS b"는 또한 "라고 한다.만약 A가 B"라면. 이것들 중 일부는 표에 나와 있다.
| b 만약 a가 있다면 | |||||||||||
| b는 a에 충분하다. | b 정확히 언제 | ||||||||||
| a b에 필요한 IS FOR B. | b if 및 a일 경우에만, b ifF a | ||||||||||
| 포함 OR | IF b THE A | b는 a에 필요하고 충분하다. | |||||||||
| 부정 | 부정 | 접속사 | 분리 | 함축 | 양면성의 | ||||||
| 변수들 | NOT b | NOT a | b와 a | b OR a | b는 a를 암시한다. | b 논리적으로 동일한 IS *** | f IS A tautology | A와 B 둘 다 아니다. | b 스트로크 a | 독점적 수술실 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| b | a | ¬(b) | ¬(a) | (b ∧ a) | (b ∨ a) | (b → a) | (b 파운드 a) | (f = 공식) | (a NOR b) | (b a) | 여러 가지 |
| F | F | T | T | F | F | T | T | T | T | T | F |
| F | T | T | F | F | T | T | F | T | F | T | T |
| T | F | F | T | F | T | F | F | T | F | T | T |
| T | T | F | F | T | T | T | T | T | F | F | F |
엔지니어링 연결 장치
일반적으로 공학적 결합체는 "1" = "T" 및 "0" = "F"로 평가하는 경향이 있다는 점을 제외하면 수학 결합체와 동일하다. 이것은 minterms와 Karnaugh maps(아래 참조)의 개념을 이용하여 분석/minimization 및 공식 합성을 목적으로 한다. 엔지니어들은 또한 Boole의 개념(a*a = a)에서 논리 산출물이라는 단어를 사용하고 Jevons의 개념(a+a = a)에서 논리합계를 사용한다.[8]
| 논리적 산물 | 논리적 합계 | 반접착(반입) | |||||||
|---|---|---|---|---|---|---|---|---|---|
| 독점적 수술실 | |||||||||
| 행 번호 | 변수들 | NOT | NOT | AND | OR | 낸드 | NOR | XOR | |
| b*21+a*20 | b | a | ~(b) | ~(a) | (b & a) | (b ∨ a) | ~(b&a) | ~(b ∨ a) | ⊕ |
| 0 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 1 |
| 2 | 1 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 1 |
| 3 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 |
사례 연결: IF... 그럼... 그렇지 않은 경우...
IF... 그럼... EASTER ... connective는 재귀 이론과 계산 이론의 가장 단순한 CASE 연산자의 형태로 나타나며 조건부 goto(점프, 분기)를 담당하는 connective이다. 이 한 개의 결합체로부터 다른 모든 결합체를 구성할 수 있다(아래 참조). "IF C DEN B "는 가장 축소된 형태로, 결정을 내리고 결과로서 제공하는 스위치는 두 가지 대안인 "a" 또는 "b"(C 프로그래밍 언어로 이름 스위치 문을 정의함) 중 하나만 암시하는 것처럼 들린다.[9]
다음 세 가지 명제는 동등하다(논리적 동등성 부호 ≡ ≡ by로 표시됨).
- ('카운터가 0'인 경우 '지시 b '기타 '지시 a'로 이동) ≡
- (c → b) & (~c → a) ) ≡ (IF 'counter is 0') ≡ (IF 'counter is 0') then (IF 'counter is 0') ' (IF 'Counter is not that case is that that is not the case is not the case is no)' instruction) ≡?
- (c&b) ∨ (~c&a) ) ≡ " (counter is zero) AND '지시 b ) OR ('counter is zero') AR ('counter is zero') AND '지시 a'로 가는 것은 아니다'
따라서 IF... 그럼... ELASS(의미)와 달리 첫 번째 명제가 거짓일 경우(c → b) 모호한 "TRUTH"로 평가하지 않는다. 예를 들어, 대부분의 사람들은 두 번째 문장이 첫 번째 문장과 의미상 연결되지 않기 때문에 다음의 복합 명제를 터무니없는 비순서로서 거부할 것이다.[10]
- 예: '윈스턴 처칠은 중국인이었다면 '동쪽에서 태양이 떠오른다'는 명제는 '윈스턴 처칠은 중국인이었고' '동쪽에서 태양이 떠오른다'는 명제는 '진리'로 평가한다.
이 문제를 인식하여 명제 미적분학에서 형식적인 함축의 부호 → 그것을 일상적이고 직관적인 함축과 구별하기 위한 물질적 함축이라고 한다.[11]
IF의 사용... 그럼... EAST 구조는 명시된 두 가지 대안 사이에서 완전히 결정론적인 선택을 제공하므로 논란을 피할 수 있다. 즉, 두 가지 대안(두 가지 대안 b와 a)을 제공하고, 그 중 하나를 철저히 그리고 모호하지 않게 선택한다.[12] 아래의 진실 표에서 d1은 (IF c THEN b) AND (IF NOT-c THEN a)의 공식이다. 그것의 완전히 축소된 형태 d2는 공식이다: (C AND b) OR (NOT-c AND a) 두 공식은 "=d1"과 "=d2" 열에 표시된 것과 같다. 전기 공학자들은 완전히 줄어든 공식을 AND-OR-SELECT 연산자라고 부른다. CASE (또는 SWITCH) 운영자는 같은 아이디어를 가능한 n가지로 확장하지만 상호 배타적인 결과물이다. 전기 기술자들은 CASE 운영자를 멀티플렉서라고 부른다.
| d1 | d2 | ||||||||||||||||||||||||||||||||||||||
| 배를 젓다 | c | b | a | ( | ( | c | → | b | ) | & | ( | ~ | ( | c | ) | → | a | ) | ) | =d1 | ( | ( | c | & | b | ) | ∨ | ( | ~ | ( | c | ) | & | a | ) | ) | =d2 | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | ||||||||||||||||||
| 1 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | ||||||||||||||||||
| 2 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | ||||||||||||||||||
| 3 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | ||||||||||||||||||
| 4 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | ||||||||||||||||||
| 5 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | ||||||||||||||||||
| 6 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 0 | 1 | ||||||||||||||||||
| 7 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 1 |
IDENTITY 및 평가
이 절의 첫 번째 표에는 "논리적 동등성"이 "아이덴티티"와 같지 않다는 사실에 주목하기 위한 항목 논리적 동등성 ***이 표시된다. 예를 들어, 대부분의 사람들은 "저 소는 파란색"이라는 주장이 "저 소는 파란색"이라는 주장과 동일하다는 데 동의할 것이다. 반면에, 논리적으로 동등하다는 것은 이 예에서와 같이 때때로 언어에서 나타난다: '태양은 빛나고 있다'는 말은 '나는 자전거를 탄다'라는 뜻이다. 명제적인 공식으로 번역된다:'태양이 비치고 있다'고 하면 '자전거를 타고 있다'고 하면 '태양이 비치고 있다'고 하면:[13]
- "IF 's'를 'b'로, IF 'b'를 'b'로, 또는 (s → b) & (b → s)로, 또는 (s → s)로 축약하여 's b'로 표기한다. 가장 오른쪽의 기호 문자열은 왼쪽의 기호와 관련하여 새로운 기호에 대한 정의이므로 IDENTITY 기호 =의 사용이 적절하다.
- (s → b) & (b → s) = (s £ b)
작가마다 논리적 등가성에 대해 £(예: Suppes, Goodstein, Hamilton), ≡(예: Robbin), ender(예: Bender, Williamson) 등의 다른 부호를 사용한다. 전형적으로 아이덴티티는 등호=로 표기된다. 이 규칙의 한 가지 예외는 프린세스 매티카에서 찾을 수 있다. IDENTITY 개념의 철학에 대한 자세한 내용은 라이프니츠의 법칙을 참조하십시오.
위에서 언급한 바와 같이 타르스키는 IDENTY를 명제 미적분학 밖에 있다고 생각하지만, 개념 없이는 수학이나 연역학에는 "논리학"이 불충분하다고 단언한다. 사실 그 부호는 공식을 평가할 때 명제 미적분학으로 들어온다.[14]
일부 시스템에는 진실 표가 없고 형식적인 공리(예: 집합 { ~, →, (, ), 변수1 p, p, p23, p, ... } 및 수식 분석 규칙(대체 및 모드스 폰 등의 사용으로 이전 문자열에서 더 많은 기호 문자열을 만드는 방법에 대한 설명). 그러한 미적분학의 결과는 다른 공식(즉, 잘 형성된 기호 문자열)이 될 것이다. 그러나 결국 미적분학을 사용하여 타당성과 진리의 개념을 연구하려면 다른 기호에 비해 "진리값" {T, F}(또는 {1, 0} 등)이라는 기호의 행동을 정의하는 공리를 추가해야 한다.
그가 너가 제대로 구성된 공식에 대한 평가'v'의 개념을 정의합니다 예를 들어, 해밀턴 두개의 기호, ≠를 사용하여(wffs)A와 B에 그의"공식 성명은 미적분학"L.A평가 v는 함수에서 wffs 시스템을 L범위(출력){T, F}, 고려한다면, 각 변수 p1, p2, p3에서 wff은 할당된 임의의 진리 값{T,. F}.
- v(A) ≠ v(~A)
(i)
- v(A → B) = v(A) = T 및 v(B) = F인 경우에만 F
(ii)
(i)와 (ii) 두 정의는 그의 시스템의 ~ (NOT) 및 → (IMPplication) 연결기에 대한 진실 표와 동등한 것을 정의한다. 첫 번째 것은 F ≠ T와 T ≠ F를 파생한 것으로, 즉 "v(A)는 v(~A)를 의미하지 않는다"는 뜻이다. 정의 (ii)는 진리 테이블에서 세 번째 행을 지정하고, 나머지 세 행은 정의 (i)의 적용에서 나온다. 특히 (ii)는 F 값(또는 "F"의 의미)을 전체 식에 할당한다. 정의는 또한 공식으로 이전에 도출된 값을 대체할 수 있는 형성 규칙의 역할을 한다.
| v(A→B) | ||||
| ( | v(A) | → | v(B) | ) |
| F | T | F | ||
| F | T | T | ||
| T | F | F | ||
| T | T | T |
일부 공식적인 시스템은 처음부터 이러한 가치평가 공리를 모순의 법칙이나 정체성과 무효의 법칙과 같은 특정한 공식의 형태로 명시한다. 공리 집합이 완성되는 한(즉, 시스템에서 생성되는 공식을 형성하고 평가할 수 있을 만큼 충분히) 어떤 공리들을 사용할 것인지의 선택은 시스템 설계자에게 달려 있다.
더 복잡한 공식
위와 같이, CASE (IF C THE B 기타 a ) connective는 2-cources connectives IF ...로 구성된다. 그럼... 그리고... 그리고 OR과 AND로부터 그리고 1-의론은 그렇지 않다. n-argument AND(a & b & c & ...&n), OR(a b b ∨ c ∨ … ∨ n)과 같은 connectives는 2-argument AND와 OR의 문자열로 구성되며 괄호 없이 축약된 형태로 작성된다. 이들, 그리고 다른 커넥티브 역시 아직 추가 커넥티브를 위한 빌딩 블록으로 사용될 수 있다. 수사학자, 철학자, 수학자들은 진리표와 다양한 이론들을 사용하여 그 공식들을 분석하고 단순화한다.
전기공학은 그려진 기호를 사용하여 대체와 대체의 수학적 행위를 나타내는 선과 연결한다. 그런 다음 진실 표로 도면을 검증하고 카노 지도의 사용이나 정리 등을 통해 아래와 같은 표현을 단순화한다. 이러한 방식으로 엔지니어들은 "디코더", "엔코더", "오작동 게이트", "주요 논리", "이중 추가자", "산술 논리 단위" 등과 같은 다수의 "결합 논리"(즉, 피드백이 없는 연결자)를 만들어냈다.
정의들
정의는 종종 약어의 목적을 위해 새로운 기호와 그 행동을 만든다. 일단 정의가 제시되면, 등가 기호나 공식의 어느 한 형태를 사용할 수 있다. 다음과 같은 상징성=Df라이첸바흐의 관례를 따르고 있다.[15] 기호 집합 { ~, &, (, ) } 및 변수에서 도출된 편리한 정의의 몇 가지 예. 각 정의는 대체 또는 대체에 사용될 수 있는 논리적으로 동등한 공식을 생산하고 있다.
- 새 변수 정의: (c&d) Df= s
- OR: ~(~a & ~b) =Df (a ∨ b)
- 시사: (~a ∨ b) Df= (a → b)
- XOR: (~a & b) ∨ (a & b) Df= (a ⊕ b)
- 논리적 동등성: (a → b) & (b → a) Df= ( ≡ b )
공리 및 정의 스키마
OR, INCREMENT, XOR 및 논리적 동등성에 대한 위의 정의는 실제 스키마(또는 "스케마타"), 즉 일반 공식 형식에는 모델(시뮬레이션, 예제)이지만 변수에 대해서는 특정 문자 a, b, c가 표시되며, 반면에 모든 변수 문자는 레테만 있으면 제자리에 들어갈 수 있다.r 교체는 아래 대체 규칙을 따른다.
- 예: 정의(~a ∨ b) Df= (a → b)에서 "SW2" 및 "CON1"과 같은 다른 변수 기호를 사용할 수 있다. 즉, 공식적으로:
- a Df= SW2, b Df= CON1이므로 정의 스키마(~SW2 ∨ CON1) Df= (SW2 → CON1)의 인스턴스로서 존재하게 된다.
대체 대 교체
대체: 다른 변수, 상수 또는 보조 공식을 대체할 변수 또는 보조 공식을 전체 공식에서 모든 경우에 교체해야 한다.
- 예: (c&d) ∨ (p & ~ (c & ~d)) 그러나 (q1 & ~q2) occurs d. 이제 변수 "d"가 발생하는 곳이면 모두 대체(q1 & ~q2):
- (c & (q1 & ~q2) ∨ (p & ~ (c & (q1 & ~q2))))
대체: (i) 대체될 공식은 (i) tautology, 즉 교체 공식을 대체하는 공식과 논리적으로 동등해야 한다(≡ 또는 £로 연결됨). 그리고 (ii) 대체 공식이 한 곳에서만(즉, 하나의 공식에 대해) 가능한 것과 달리.
- 예: 다음 수식 스키마/등가 집합 사용:
- ( ∨ 0) ≡ a )
- (a & ~a) ≡ 0 ).
- (~a ∨ b) Df= (a → b) )
- ( ~ (~a) ≡ a )
- "a"로 시작하다
- 1을 사용하여 "a"를 (a ∨ 0)로 교체하십시오. (a replace 0)
- "schema"라는 개념을 사용하여 2: ( (a & ~a) ) 0 )의 a로 b를 대체한다.
- 2를 사용하여 0을 (b & ~b): ( ∨ (b & ~b))로 교체하십시오.
- ("a b"을 (b & ~b) 위에 배포하는 방법은 아래를 참조하십시오)
귀납적 정의
명제논리의 고전적 표현(Enderton 2002 참조)은 connectives ∧, →{\,\to를 사용한다 주어진 명제 변수 집합에 대한 공식 집합은 귀납적으로 다음과 같은 최소 표현 집합으로 정의된다.
- 세트의 각 명제 변수는 공식이고
- () {\(\은(는) α{\일 때마다 공식이며,
- is a formula whenever and are formulas and is one of the binary connectives .
이 귀납적 정의는 쉽게 확장되어 추가 커넥티브를 포함할 수 있다.
귀납적 정의는 폐쇄 작동 측면에서도 다시 인용될 수 있다(Enderton 2002). V는 명제 변수 집합을 나타내며V X는 V의 기호, 왼쪽 및 오른쪽 괄호, 고려 중인 모든 논리 연결부를 포함한 알파벳 문자열을 나타내도록 한다. 각 논리 결합은 공식 건물 연산에 해당하며, XX에서V XX까지의V 함수:
- 문자열 가 지정되면 ( z) 작업에서 ) 을(를) 반환한다
- y와 z 문자열이 주어지면 , z) 이(가) 반환된다 z) z 바이너리 커넥션에 해당하는 {→ 등이 있다.
V에 대한 공식 집합은 V를 포함하는 XX의V 가장 작은 부분 집합으로 정의되며 모든 공식 구성 작업에서 닫힌다.
수식 구문 분석
명제 미적분학의 다음의 "법칙"은 복잡한 공식들을 "축소"하기 위해 사용된다. "법률"은 진실 표로 쉽게 검증될 수 있다. 각 법에서 주(가장 먼) 결합은 논리 등가성 ≡ 또는 정체성 =과 연관된다. n개의 고유 변수에 대한n 두 가지 진리 값의 조합 모두를 완전하게 분석하면 이 결합체 아래에 1의 열(T)이 생성될 것이다. 이 발견은 정의상 각각의 법칙을 상호작용으로 만든다. 그리고, 주어진 법칙의 경우, 왼쪽과 오른쪽의 공식은 동등하기 때문에(또는 동일하기 때문에) 서로 대체할 수 있다.
- 예: 다음 진리표는 OR을 넘어서는 안 되는 행동에 대한 드 모건의 법칙이다: ~ (a b b) ≡ (~a & ~b) 주결합식 ≡("taut"으로 표시된 노란색 기둥)의 왼쪽에서 ~(b ∨ a)는 라벨 "P" 아래에 있는 (1, 0, 0, 0)으로 평가한다. "taut"의 오른쪽에서 공식 (~(b) ∨ ~(a)도 라벨 "Q" 아래의 (1, 0, 0, 0)으로 평가한다. 두 열은 등가 평가를 하기 때문에 "완전" 하의 논리적 동등성 ≡은 (1, 1, 1, 1) 즉, P q Q로 평가한다. 따라서 두 공식 중 하나가 더 큰 공식으로 나타날 경우 다른 공식으로 대체될 수 있다.
| P | 팽팽한 | Q | ||||||||||||||||||||
| b | a | ( | ~ | ( | b | V | a | ) | ≡ | ( | ~ | ( | b | ) | & | ~ | ( | a | ) | ) | ) | |
| 0 | 0 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 1 | 1 | 0 | |||||||||||
| 0 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | |||||||||||
| 1 | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | |||||||||||
| 1 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 0 | 1 |
Enterprising 독자들 자체가 상징들이 형성 규칙 위는 법 아래 나열된 가능한 몇 안 되며, 그 이론은 다른 사람들뿐만 아니라 ∨, 및에 대한truth-table 평가로 유도하다 지정된{∨,&,~,(,), variables a, b, c}를 사용하는"공리 체제"를 발명하고 싶고,~. 하나로 귀속을 세웠다에 도전할 수 있다. Huntington (1904) (공급:204)은 아래에 정의된 법률 중 8개를 사용한다.
자명제에서 사용할 경우 기호 1과 0(또는 T와 F)은 잘 형성된 공식으로 간주되어 변수와 동일한 규칙을 모두 준수한다. 따라서 아래에 열거된 법칙은 실제로 공리 스키마, 즉 무한한 수의 예시를 대신하여 서 있다. 따라서 ( x ∨ y ) ≡ ( y ∨ x )은 한 예에, ( p 0 0 ) ( ( 0 p p ) ≡ ( 1 ∨ q ) ≡ ( q 1 ) 등에 사용될 수 있다.
연공서열(기호순위)
일반적으로 명제 공식의 분석과 평가 중 혼동을 피하기 위해 괄호를 자유롭게 사용한다. 하지만, 꽤 자주 작가들은 그것들을 제외한다. 복잡한 공식을 구문 분석하려면 먼저 각 결합체(* 제외)가 다른 결합체 위에 가지고 있는 연공서열 또는 순위를 알아야 한다. 수식을 "정확히 형성"하려면, 가장 높은 순위를 가진 결합체부터 시작하여 구성요소 주위에 괄호를 추가한 다음, 순위 아래로 이동하십시오(연결체가 작동하는 범위에 주의). 가장 나이가 적은 사람부터 성인까지, 술어 부호 ∃x와 ∃x로, IDENTY =와 산술 부호는 완전성을 위해 다음과 같이 추가되었다.[16]
- ≡
- (논리적 동등성)
- →
- (IMPplication)
- &
- (AND)
- ∨
- (OR)
- ~
- (NOT)
- ∀x
- (모든 x에 대해)
- ∃x
- (x가 존재함)
- =
- (IDENTITY)
- +
- (초과 합계)
- *
- (수치 곱하기)
- '
- (s, 산술 후계자).
따라서 공식은 구문 분석할 수 있지만 NOT는 분배 법칙을 따르지 않기 때문에 내부 공식(~c&d) 주위의 괄호(~c&d)는 필수 사항이다.
- 예: " d&c ∨ w " 다시 쓴 것은 (d&c) w w )
- 예: " a & a → b ≡ a & ~a " b " 다시 쓴 (강력하게)는
- ≡에는 연공서열이 있다: ( a & a → b ) ≡ ( a & ~a ∨ b )
- → 연공서열 : ( a & (a → b) ) ≡ ( a & ~a ∨ b ) )
- &는 양쪽 다 연공서열이 있다: ( (a) & (a → b) ) ≡ (a) & (~a b b )
- ~는 연공서열: ( (a) & (a → b) ) ≡ (a) & (~(a) ∨ b) ) )
- 체크 9 ( -parentex and 9 ) -parentex: ( (a) & (a → b) ) ≡ (a) & (a) ∨ b) )
- 예:
- d&c p& ~(c & ~d) ≡ c&d p&c & p&c & p&d p&d 다시 쓴 것은 (d&c) ∨ (p&d) ∨ (p&d) ) ≡ (c&d) ) (c&d) ) (p&d) )
상호 및 연관법
- OR에 대한 역법: ( ∨ b ) ≡ (b ∨ a )
- AND에 대한 역법: ( a & b ) ≡ (b & a )
- OR에 대한 연관법칙: ( ( ∨ b ) ∨ c ) ≡ (b ∨ c )
- AND에 대한 연관법칙: ( ( a & b ) & c ) ≡ ( a & (b & c) )
AND 및 OR 문자열에서 괄호 생략: 커넥티브는 단항(예: NOT)과 이항(예: 2변수 AND, OR, IRAMES)으로 간주된다. 예를 들면 다음과 같다.
- (c&d) ∨ (p&c) ∨ (p&d) ∨ (p&d) ∨ (p&c) ∨ (p&d) ∨ (p&c) ∨ (p&c) ) (p&d) ) 또는 (c&d) ) (p&d) ) (p&(d) )로 표기해야 한다.
그러나 진위표 시연은 추가 괄호가 없는 형식이 완벽하게 적합하다는 것을 보여준다.
단일 변수에 관한 괄호 생략 NOT: a가 단일 변수인 ~(a)는 완벽하게 명확하지만 ~a는 적절하고 이 문자 그대로 나타나는 일반적인 방법이다. NOT가 둘 이상의 기호가 있는 공식을 초과하는 경우, 괄호는 필수 사항(예: ~ (a ∨ b))이다.
분배법
또는 AR은 AND로 배포되고 OR로 배포되지 않는다. AR은 AND 또는 OR로 배포되지 않는다. De Morgan의 법칙에 대해 아래를 참조하십시오.
- OR에 대한 분배 법칙: (c ∨ ( a & b) ) ≡ (c ∨ a) & (c ∨ b) )
- AND에 대한 분배 법칙: (c & ( ∨ b) ) ≡ (c & a) ∨ (c & b) )
드 모건의 법칙
OR 또는 AND에 분산되어 있을 때 다음과 같은 특이한 작업을 수행하지 않는다(또한, 이는 진실 표로 검증할 수 있음:
- OR에 대한 De Morgan의 법칙: ¬ (a ∨ b) ≡ (¬a ^ ¬b)
- AND에 대한 De Morgan의 법칙: :(a ^ b) ≡ (≡a ∨ ∨b)
흡수 법칙
특히 첫 번째 흡수는 논리의 "법칙"이 산술의 "법칙"과 다르도록 한다.
- OR에 대한 흡수(유전성) : (a ∨ a) ≡ a
- AND에 대한 흡수(유전성): (a & a) ≡ a
평가의 법칙: 신원, 무효 및 보완
부호 " = " (논리적 등가성 ≡, ↔ 또는 ↔과 구별됨)는 가치나 의미의 배정을 상징한다. 따라서 문자열(a & ~ (a)은 "0"을 상징한다. 즉, 기호 "0"과 같은 것을 의미한다. 일부 "시스템"에서는 (a & ~ (a) Df= 0 )으로 표시되는 공리(정의)가 될 수 있으며, 다른 시스템에서는 아래의 진실 표에서 도출될 수 있다.
| c | 팽팽한 | c | |||||||||||
| a | ( | ( | a | & | ~ | ( | a | ) | ) | ≡ | 0 | ) | |
| 0 | 0 | 0 | 1 | 0 | 1 | 0 | |||||||
| 1 | 1 | 0 | 0 | 1 | 1 | 0 |
- 평등의 정류: (a = b) ≡ (b = a)
- OR에 대한 ID: (a ∨ 0) = a 또는 (a ∨ F) = a
- AND에 대한 ID: (a & 1) = a 또는 (a & T) = a
- OR에 대한 무효: (a ∨ 1) = 1 또는 (a ∨ T) = T
- AND에 대한 무효: (a & 0) = 0 또는 (a & F) = F
- OR에 대한 보완책: (a ∨ ~a) = 1 또는 (a ∨ ~a) = T, 제외된 중간 법칙
- AND에 대한 보완책: (a & ~a) = 0 또는 (a & ~a) = F, 모순의 법칙
이중 음극(점화)
- ¬(¬a) a a
올바른 형식의 공식(wffs)
공식의 주요 속성은 제안적 변수 및 논리적 연결에 있어 공식의 구조를 결정하기 위해 고유하게 구문 분석할 수 있다는 것이다. 위와 같이 공식을 infix 표기법으로 작성할 때, 공식의 정의에서 괄호의 적절한 사용을 통해 고유한 가독성이 확보된다. 또는 폴란드어 표기법이나 역 폴란드어 표기법으로 공식을 쓸 수 있어 괄호 전체를 따로 쓸 필요가 없다.
앞 절의 infix 공식에 대한 귀납적 정의는 Backus-Naur 형식으로 형식 문법으로 변환할 수 있다.
<<formula> ::=<proposition>< variable>> (<formula>>) (<formula>><>><formula><formula>< →>< →>< →>< →>< →>< →>< ↔>< ↔>>< →>< ↔>< ↔>< ↔>< ↔>< ↔>< ↔>< )>< )>< )>>< ). 문법과 일치하는 어떤 표현도 좌우 괄호 수가 균형 잡힌 것을 보여줄 수 있고, 공식이 비어 있지 않은 초기 부분은 오른쪽 괄호보다 왼쪽이 더 많다는 것을 알 수 있다.[17] 이 사실은 공식을 구문 분석하는 알고리즘을 제공하는 데 사용될 수 있다. 예를 들어, 식 x가 ( 두 번째 기호 다음에 시작하여 균형 괄호가 있는 x의 가장 짧은 하위 표현 y와 일치한다고 가정합시다. x가 공식이라면 이 표현식 뒤에 정확히 하나의 기호가 남고, 이 기호는 닫는 괄호, y 자체는 공식이다. 이 아이디어는 공식에 대한 재귀적 하강 파서를 생성하는 데 사용될 수 있다.
괄호 계산 예제:
이 방법은 가장 바깥쪽 괄호(흔히 생략된)에 대해 공식의 전체 평가가 발생하는 결합체인 주 결합체로 위치한다.[18] 또한 "레벨 6"에서와 같이 진실 표를 사용하지 않고 공식의 평가를 시작할 수 있는 가장 안쪽의 결합체를 찾는다.
| 출발하다 | ( | ( | ( | c | & | d | ) | V | ( | p | & | ~ | ( | ( | c | & | ~ | ( | d | ) | ) | ) | ) | ) | = | ( | ( | ( | c | & | d | ) | V | ( | p | & | d | ) | ) | V | ( | p | & | ~ | ( | c | ) | ) | ) | ) | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 수를 세다 | 0 | 1 | 2 | 3 | 3 | 3 | 3 | 2 | 2 | 3 | 3 | 3 | 3 | 4 | 5 | 5 | 5 | 5 | 6 | 6 | 5 | 4 | 3 | 3 | 1 | 1 | 2 | 3 | 4 | 4 | 4 | 4 | 3 | 3 | 4 | 4 | 4 | 4 | 3 | 2 | 2 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 2 | 1 | 0 |
올바른 공식 대 유효한 공식 추론
유효한 논쟁의 개념은 보통 논쟁에서 추론에 적용되지만, 논쟁은 명제 공식으로 축소되고 다른 명제 공식과 동일하게 평가될 수 있다. 여기서 유효한 추론은 다음과 같다: "추론을 나타내는 공식은 그 변수에 어떤 진실 값이 할당되든 간에 주요 결합체 아래에 있는 "진실"로 평가한다." 즉, 그 공식은 자동학이다.[19] 공식이 잘 형성되겠지만 유효하지는 않을 것이다. 또 다른 표현방식은 "형성이 잘 되는 것은 공식이 유효하기 위해서는 필요하지만 충분하지 않다"는 것이다. 올바른 형태와 유효성을 모두 확인할 수 있는 유일한 방법은 진실 표와 함께 검증에 제출하거나 "법령"을 사용하여 제출하는 방법:
- 예 1: 다음과 같은 이해하기 어려운 주장에 대해 어떻게 생각하는가? 유효한가? "햇볕이 들지만 개구리가 삐걱거리면 햇볕이 안 쨍쨍한데 개구리가 삐걱거리지 않는다는 말과 똑같아." 이를 다음과 같이 명제 공식으로 변환하십시오.
- "IF (A AND (IF B THEN NOT-a) THE NO-a" 여기서 ""는 "햇볕"을 나타내고 "b"는 "개구리가 울고 있다"를 나타낸다.
- ( (a) & (b) → ~ (a) ) ≡ ~ (b) )
- 이것은 모양은 좋은데, 과연 유효한가? 즉, 이것을 평가할 때 논리 등가 기호 ≡ 아래의 tautology(모든 T)를 산출할 것인가? 대답은 NO, 유효하지 않다. 그러나 함축적으로 재구성되면 그 주장은 유효하다.
- "날씨가 맑다고 하지만, 개구리가 지저귀고 있다면 해가 나지 않는다는 것은 개구리가 우는 것이 아니라는 것을 의미한다."
- 다른 환경은 개구리가 우는 것을 막는 것일지도 모른다: 아마도 학이 개구리를 잡아먹었을 것이다.
- 예 2(Bertrand Russell을 통해 Reichenbach):
- "돼지에 날개가 있다면 어떤 날개는 먹기에 좋다. 날개가 달린 동물도 먹기에 좋으니 돼지는 날개가 있다고 말했다.
- ((a) → (b) & (b) → (a) )은 잘 형성되어 있으나, 주요 함축에 따른 적색평가에 나타난 바와 같이 유효하지 않은 주장은 다음과 같다.
| W | G | 아그 | |||||||||||||
| a | b | ( | ( | ( | a | -> | b | ) | & | b | ) | -> | a | ) | |
| 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | |||||||
| 0 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | |||||||
| 1 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | |||||||
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
커넥티브 세트 감소
모든 명제 공식이 그 집합에 있는 결합체만 있는 공식과 자동적으로 동등하다면 논리 결합체 집합은 완전체라고 불린다. There are many complete sets of connectives, including , , and . There are two binary connectives that are complete on their own, corresponding to NAND and NOR, respectively.[20] 일부 쌍은 완전하지 않다. 예를 들어 {
스트로크(NAND)
NAND에 해당하는 이진 결합체를 쉐퍼 스트로크라고 하며, 세로 막대 또는 세로 화살표 ↑으로 표기한다. 이 결합의 완전성은 프린세스 매티카(1927:xvii)에서 언급되었다. 단독으로 완성되기 때문에 다른 모든 커넥티브는 스트로크만으로 표현할 수 있다. 예를 들어 기호 "≡"가 논리적 동등성을 나타내는 경우:
- ~p ≡ p
- p → q q p ~q
- p q q ≡ ~p ~q
- p&q ≡ ~(p q)
특히 0-arlive connectives }(진실을 나타냄) 및 }(가짜를 나타냄)은 스트로크를 사용하여 표현할 수 있다.
만약... 그렇다면... 기타
{0, 1 }(또는 {F, T } 또는 { }})과 함께 이 결합체는 완전한 집합을 형성한다. 다음의 IF에서는...THE...ELSE 관계(c, b, a) = d는 (c → b) ∨ (~c → a) ≡ (c & b) ∨ (~c & a) = d를 나타낸다.
- (c, b, a):
- (c, 0, 1) ≡ ~c
- (c, b, 1) ≡ (c → b)
- (c, c, a) ≡ (c ∨ a)
- (c, b, c) ≡ (c & b)
예: 다음은 "(c, b, 1) ≡ (c → b)"의 정리 기반 증거가 어떻게 진행될지 보여주는데, 그 증거 아래는 진실-표적 검증이다. (주: (c → b)는 (~c ∨ b) ) 로 정의된다.
- 축소된 형태부터 시작: (c&b) ∨ (~c&a) )
- a: (c&b) ∨ (~c&1)를 "1"로 대체한다.
- 아이덴티티(~c & 1) = ~c: (c&b) ∨ (~c) )
- V: (~c) ∨ (c&b)의 감응법칙
- ~c V를 (c&b) 위에 배포한다: ( (~c) ) c ) & (~c) ∨ b )
- 제외중간의 법칙 ((~c) ∨ c ) = 1 ) : (1) & (~c) ∨ b ) )
- (~c) ∨ b에 (~c) &"를 배부한다: ( (1) & (~c) ∨ ( (1) & b ) )
- 동일률과 동일성 (1 & ~c) = (~c & 1) = ~c, (1 & b) ≡ (b & 1) ≡ b: ( ~c ∨ b )
- ( ~c ∨ b )는 c → b Q. E. D로 정의된다.
다음 진리표에서 tautology에 대해 "taut"으로 표시된 열은 d로 표시된 두 열 사이의 논리적 동등성(여기서 ≡로 ≡로 표기됨)을 평가한다. "tut" 아래의 네 행은 모두 1의 행이기 때문에 등가성은 실제로 tutology를 나타낸다.
| d | 팽팽한 | d | |||||||||||||||||||||||||||||
| 노를 젓다 | c | b | a | ( | ( | ( | c | & | b | ) | V | ( | ~ | ( | c | ) | & | a | ) | ) | ≡ | ( | ~ | ( | c | ) | V | b | ) | ) | |
| 0,1 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | |||||||||||||||
| 2,3 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | |||||||||||||||
| 4,5 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 1 | 0 | 0 | |||||||||||||||
| 6,7 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 1 |
정상형식
임의의 명제 공식은 매우 복잡한 구조를 가질 수 있다. 보통 형태라고 알려진 단순한 형태를 갖는 공식으로 작업하는 것이 종종 편리하다. 일반적인 정상 형태로는 결합 정상 형태와 분리 정상 형태를 들 수 있다. 어떤 명제 공식도 그 결합형 또는 분리형 정상형식으로 축소될 수 있다.
정상형태로감소
공식에 대한 진리표가 준비되면 정상 형태로의 감소는 비교적 간단하다. 그러나 리터럴 수를 최소화하기 위한 추가 시도(아래 참조)에는 몇 가지 도구가 필요하다: 드 모건의 법칙과 진리표에 의한 축소는 다루기 어려울 수 있지만, 카노 지도는 소수의 변수(5개 이하)에 매우 적합하다. 다중 출력이 있는 보다 복잡한 회로에 대해서는 일부 정교한 표 형식의 방법이 존재하지만, 이는 본 문서의 범위를 벗어난 것이다. 자세한 내용은 Quine-McCluskey 알고리즘을 참조하십시오.
리터럴, 용어, 연어
전기공학에서 변수 x 또는 그 부정이 ~(x)는 리터럴이라고 하는 하나의 개념으로 뭉쳐진다. AND에 의해 연결된 일련의 리터럴을 용어라고 부른다. OR에 의해 연결된 일련의 리터럴을 연어라고 부른다. 일반적으로 리터럴 ~(x)는 ~x로 축약된다. 때때로 &-심볼은 대수 곱셈의 방법으로 모두 생략된다.
- 예
- a, b, c, d는 변수다. (( a & ~ (b)) & ~ (c) & d)는 용어다. 이것은 (a & ~b & ~c&d) 또는 a~b~cd로 축약할 수 있다.
- p, q, r, s는 변수다.((p & ~ (q)&r) & r & (s) )는 연어다. 이것은 (p ∨ ~q ∨ r ∨ ~s)로 축약할 수 있다.
민테름
2행n 진리표에서 변수의 가능한 2개n 값에 대한 명제 공식의 평가를 표시하는 것과 마찬가지로, n 변수는 2-제곱n Karnaugh 지도를 생성한다(전차원 실현에서는 그릴 수 없음에도 불구하고). 예를 들어, 3개의 변수는 23 = 8행과 8 Karnaugh 제곱을 생성하며, 4개의 변수는 16개의 진리표 행과 16개의 정사각형을 생성하므로 16분의 1을 생성한다. 각 Karnaugh 지도 사각형과 그에 상응하는 진리표 평가는 1분기를 나타낸다.
모든 제안 공식은 활성(예: "1"- 또는 "T" 값) 문자의 "논리적 합계" (OR)로 축소될 수 있다. 이 형태에서 공식은 분리 정규 형태라고 한다. 그러나 이런 형태라고 하더라도 항수나 리터럴 수에 관해서 반드시 최소화되는 것은 아니다.
다음 표에서 (0, 1, 3, 2, 6, 7, 5, 4, 0) 행의 고유 번호 지정을 준수하십시오. 첫 번째 열은 숫자 "cba"에 해당하는 이진수 등가 십진수, 즉 다음과 같다.
- 예
- cba2 = c*22 + b*21 + a*20:
- cba = (c=1, b=0, a=0) = 1012 = 1*22 + 0*21 + 1*20 = 510
이 번호 매기는 한 번에 한 변수만 테이블에서 행으로 이동할 때 값이 바뀌기 때문에 발생한다. 회색 코드는 이 개념에서 파생된 것이다. 이 개념은 각 모서리의 변수가 큐브의 가장자리를 한 바퀴 돌면서 한 번에 하나씩만 변하는 하세 다이어그램이라고 불리는 3차원 및 4차원 하이퍼큐브까지 확장될 수 있다. 2차원으로 편평하게 된 하세 다이어그램(하이퍼큐브)은 Veitch 다이어그램이나 Karnaugh 지도(이 지도들은 사실상 동일한 것이다).
Karnaugh 지도로 작업할 때는 항상 상단 가장자리가 하단 가장자리로 "바퀴 돌기"하고 왼쪽 가장자리가 오른쪽 가장자리로 감는다는 것을 명심해야 한다. Karnaugh 다이어그램은 정말로 3차원 또는 4차원 또는 n차원 평평한 물체다.
| (c, b, a)의 십진수 등가 | c | b | a | 민기의 |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | (~c&~b&a) |
| 1 | 0 | 0 | 1 | (~c&~b&a) |
| 3 | 0 | 1 | 1 | (~c&b&a) |
| 2 | 0 | 1 | 0 | (~c&b&a) |
| 6 | 1 | 1 | 0 | (c & b & ~a) |
| 7 | 1 | 1 | 1 | (c&b&a) |
| 5 | 1 | 0 | 1 | (c & ~b & a) |
| 4 | 1 | 0 | 0 | (c & ~b & ~a) |
| 0 | 0 | 0 | 0 | (~a & ~b & ~c) |
지도법을 이용한 감소 (Vitch, Karnaugh)
Veitch는 원을 교대 사각형으로 변환하여 Venn 다이어그램의 개념을 개선하였고, Karnaugh는 문자 형태(예: ~abc~d)로 쓰여진 minterms를 숫자로 변환하여 Veitch 다이어그램을 단순화하였다.[21] 방법은 다음과 같이 진행된다.
공식의 진실 표 생성
공식의 진실 표 생성 n 변수에 대해 변수의 이항 등가(일반적으로 순차적으로 0~n-1)를 사용하여 행의 번호를 매긴다.
- 기술적으로 명제 함수는 (비민원화) 결합 정상 형태로 축소되었다. 각 행에는 미니어처 표현이 있으며, 이는 (비민원화) 결합 정상 형태로 공식을 생산하기 위한 OR'd가 될 수 있다.
예: (c&d) ∨ (p & ~ (c & (~d))) = q in 결벽 정상 형태:
- (~p&d&c ) ∨ (p&d&c) ∨ (p&d & ~c) ( (p&d & ~c) = q
단, 이 공식은 항 수(4개에서 3개까지)와 리터럴 총계(12개에서 6개까지)에서 모두 감소한다.
| 배를 젓다 | 민테름 | p | d | c | ( | ( | c | & | d | ) | ∨ | ( | p | & | ~ | ( | ( | c | & | ~ | ( | d | ) | ) | ) | ) | ) | 활성 minterms | 결막정상형식 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | ( ~p & ~d & ~c ) | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | ||||||||||||||
| 1 | ( ~p & ~d&c) | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | ||||||||||||||
| 2 | ( ~p&d&c ) | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | ||||||||||||||
| 3 | ( ~p&d&c ) | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | (~p&d&c) | |||||||||||||
| 4 | (p & ~d & ~c ) | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 0 | (~p&d&c) | |||||||||||||
| 5 | (p & ~d & c ) | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 1 | 1 | 0 | ||||||||||||||
| 6 | (p&d & ~c ) | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | (p&d & ~c) | |||||||||||||
| 7 | (p&d&c ) | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | (p&d&c ) | |||||||||||||
| q | = (~p&d&c) ∨ (~p&d&c) ∨ (p&d&c) ∨ (p&d&c ) |
공식의 Karnaugh 지도 만들기
진리 테이블 방법에 의해 발견된 공식 값(예: "p")을 사용하여 각(관련된) Karnaugh 제곱(이 값은 그레이 코드 규칙에 따라 번호가 부여됨)에 넣으십시오. "상관없음"에 대한 "d" 값이 표에 나타나면, 이것은 감소 단계 동안에 유연성을 더한다.
최소 단위 수 감소
인접한(오퍼팅) 1-제곱(T-제곱)의 최소값은 리터럴 수에 따라 줄일 수 있으며, 그 과정에서 숫자 용어 또한 줄어들 것이다. 교대 사각형 2개(수평 2 x 1 또는 수직 1 x 2, 가장자리조차 교대 사각형을 나타냄)는 문자 1개를 잃고, 4 x 1 사각형(수평 또는 수직) 또는 2 x 2 사각형(수평 또는 4 모서리가 교대 사각형을 나타냄)은 2 리터럴, 직사각형 8개의 사각형은 3리터를 잃음 등(가장 큰 사각형을 추구함). 또는 직사각형 안에 완전히 포함된 작은 사각형이나 직사각형을 무시하고 무시한다.) 이 과정은 모든 교대 사각형이 설명될 때까지 계속되며, 이때 명제 공식은 최소화된다.
예를 들어, 정사각형 #3과 #7 abut. 이 두 개의 교대 제곱은 하나의 문자 그대로를 잃을 수 있다(예: 정사각형 #3과 #7의 "p"), 직사각형 또는 정사각형의 네 칸은 2 리터럴을 잃을 수 있고, 직사각형의 여덟 칸은 3 리터럴을 잃을 수 있다(한 칸은 가장 큰 칸이나 직사각형을 찾는다). 이 과정은 모든 교대 정사각형이 설명될 때까지 계속되며, 이때 제안 공식은 최소화된다고 한다.
예: 지도 방법은 보통 검사에 의해 이루어진다. 다음 예는 카노 지도에 용어 조합 뒤의 "트릭"을 나타내기 위해 대수법을 확장한다.
- 민테름 #3과 #7 어부트, #7 어부트, #6 어부트, #4 어부트, #6 어부트(테이블의 가장자리가 휘감기 때문에). 그래서 이 쌍들은 각각 줄어들 수 있다.
Idempotency 법칙(A ∨ A) = A에 의해 더 많은 용어를 만들 수 있음을 관찰하십시오. 그런 다음 연관성과 분배법에 의해 사라질 변수를 쌍으로 만든 다음 모순의 법칙(x & ~x)=0과 함께 " 소멸"할 수 있다. 다음은 괄호 [와 ]만을 사용하여 항을 추적한다. 그것들은 특별한 의미가 없다.
- 공식을 축소할 공식을 결합 정규 형태로 넣으십시오.
- q = (~p&d&c ) ∨ (p&d&c) ∨ (p&d & ~c) ∨ (p&d & ~c) ∨ ( #3 ∨ #7 ∨ #6 ∨ #4 )
- 공차(흡수) [ A ∨ A) = A:
- ( #3 ∨ [ #7 ∨ #7 ] ∨ [ #6 ∨ #6 ] ∨ #4 )
- 연관법(x ∨ (y ∨ z) = (x ∨ y) ∨ z )
- ( [ #3 ∨ #7 ] ∨ [ #7 ∨ #6 ] ∨ [ #6 ∨ #4] )
- [ (~p&d&c ) ] 【(p&d&c)】 [(p&d&c)】 [(p&d&c) 【(p&d&c)】 [(p&d&c)】 [p&d&c] 【(p&d&c)】.
- 분배법(x & (y ∨ z) ) = (x & y) ∨ (x & z) :
- ( (d&c) ∨ (~p&p) ] ] [ (p&d) ∨ (~c&c) ] ∨ [ (p&c) ]
- 상보법칙 및 모순법칙(x & ~x) = (~x & x) = 0:
- ( (d&c) ∨ (0) ] ∨ [ (p&d) ∨ (0) ] ( [ (p& ~c) 0 (0) ]
- 정체성의 법칙(x ∨ 0 ) = 공식의 축소된 형태로 이어지는 x:
- q = (d&c) ∨ (p&d) ∨ (p&c) )
진실 표로 감소 확인
| 배를 젓다 | 민테름 | p | d | c | ( | ( | d | & | c | ) | ∨ | ( | p | & | d | ) | ∨ | ( | p | & | ~ | ( | c | ) | ) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | ( ~p & ~d & ~c ) | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | |||||||||
| 1 | ( ~p & ~d&c) | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | |||||||||
| 2 | ( ~p&d&c ) | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | |||||||||
| 3 | ( ~p&d&c ) | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | |||||||||
| 4 | (p & ~d & ~c ) | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | |||||||||
| 5 | (p & ~d & c ) | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | |||||||||
| 6 | (p&d & ~c ) | 1 | 1 | 0 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | |||||||||
| 7 | (p&d&c ) | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | |||||||||
| q |
충동적 명제
다음과 같은 정의의 예를 들어 볼 때, 그 이후의 추론은 어떻게 되는가?
- (1) "이 문장은 간단하다." (2) "이 문장은 복잡하고, AND가 결합한다."
그런 다음 변수의 "s"를 가장 왼쪽 문장 "이 문장은 간단하다"에 할당하십시오. compound c = "not simple" ~s를 정의하고 c = ~s를 "이 문장은 복합이다"에 할당하고, "j"를 "It [이 문장]은 AND에 의해 결합된다"에 할당한다. 두 번째 문장은 다음과 같이 표현할 수 있다.
- ( NOT(s) AND j )
만약 진실 값이 c = ~s와 j 문장에 배치된다면, 모든 것은 명백하게 WISLS이다: 예: "이 문장은 복잡하다"는 것은 FALSE이다(정의상 단순하다). 그래서 그들의 접속사(AND) 그러나 조립된 형태로 취했을 때, 문장은 TRUE이다.
이것은 귀납적 정의에서 비롯되는 역설의 예로서, 즉 객체 m이 속성 P를 가지고 있지만 객체 m이 속성 P의 관점에서 정의되는 경우다.[22] 수사학자나 연역 분석에 관여하는 사람에게 가장 좋은 조언은 충동적인 정의를 피하는 동시에 그들이 정말로 역설을 만들 수 있기 때문에 그들을 경계하는 것이다. 반면에 기술자들은 그것들을 피드백과 함께 명제 공식의 형태로 작업하도록 했다.
"피드백"을 사용한 제안 공식
명제 공식이 자체 변수의 하나로 나타난다는 개념은 그 공식을 변수에 할당할 수 있는 형성 규칙을 필요로 한다. 일반적으로 이런 일이 일어나는 것을 금하는 규정(자명하거나 사물과 관계의 진실된 표제)은 없다.[23]
가장 간단한 경우는 OR 공식이 자체 입력물이 될 때 발생한다. 예를 들어, p = q. (p s s) = q로 시작하고, p = q. q의 "정의"가 "q"뿐만 아니라 "s"와 OR connective"에도 의존한다는 것을 관찰하라. q의 정의는 따라서 귀납적이다. 두 가지 조건 중 하나가 발생할 수 있다:[24] 진동 또는 메모리.
공식을 블랙박스로 생각하면 도움이 된다. 외부에서 "내부" 공식을 "내부"하지 않으면 출력이 더 이상 입력의 함수가 아닌 것처럼 보일 것이다. 즉, 때로는 q를 보고 0을 보고 다른 때는 1을 보는 것이다. 이 문제를 피하려면 상자 안에 있는 "숨겨진" 변수 p의 상태(조건)를 알아야 한다(즉, q를 피드백하여 p에 할당하는 값). 이것이 알려지면 명백한 모순은 사라진다.
피드백이 있는 공식의 [예측] 동작을 이해하려면 순차 회로에 대한 보다 정교한 분석이 필요하다. 피드백 리드가 있는 제안 공식은, 가장 간단한 형태로, 기계를 명시한다. 또한 그것들은 튜링 테이프와 카운터 머신 카운터 형태의 기억으로 이어진다. 이러한 요소들의 조합으로부터 모든 종류의 경계 계산 모델(예: 튜링 머신, 카운터 머신, 레지스터 머신, 매킨토시 컴퓨터 등)을 구축할 수 있다.
진동
추상적(이상적) 사례에서 가장 단순한 진동 공식은 그 자체로 공급되지 않는 것이다: ~(~(p=q) = q. 진실 표에 있는 추상적(이상적) 명제 공식의 분석은 p=1과 p=0 사례 모두에 대한 불일치를 나타낸다. p=1, q=0일 때 p=0과 q=1일 때 p=q; ditto일 수 없다.
| q | |||||||
|---|---|---|---|---|---|---|---|
| p | ~ | ( | p | ) | = q | ||
| 0 | 1 | 0 | 1 | q&p 불일치 | |||
| 1 | 0 | 1 | 0 | q&p 불일치 |
지연이 있는 진동: p와 q 사이의 추상 공식에 지연[25](이상 또는 비이상)이 삽입되면 p는 1과 0 사이에 진동한다: 10101010...101...101... 애드 인피니텀 지연과 NOT 중 하나가 추상적이지 않은 경우(즉, 이상적이지 않은 경우), 사용할 분석 유형은 발진기를 구성하는 물체의 정확한 특성에 따라 달라진다. 그러한 것들은 수학 바깥에 있고 공학에 속한다.
분석을 위해서는 지연을 삽입한 다음 지연과 입력 "p" 사이의 루프를 절단해야 한다. 지연은 "qd"(q-delayed)를 "qd"(q-delayed)를 입력으로 출력하는 일종의 제안으로 보아야 한다. 이 새로운 명제는 진실 표에 또 다른 칼럼을 추가한다. 이 불일치는 이제 빨간색으로 표시된 "qd"와 "p" 사이에 있다. 그 결과 다음과 같은 두 가지 안정적 상태가 발생한다.
| q | ||||||||
|---|---|---|---|---|---|---|---|---|
| qd | p | ( | ~ | ( | p | ) | = q | |
| 0 | 0 | 1 | 0 | 1 | 주 1 | |||
| 0 | 1 | 0 | 1 | 0 | qd&p 불일치 | |||
| 1 | 0 | 1 | 0 | 1 | qd&p 불일치 | |||
| 1 | 1 | 0 | 1 | 0 | state 0 |
기억력

지체 없이 불일치는 진실 테이블 분석에서 제거되어야 한다. "지연"이라는 개념에서, 이 조건은 Fed-back 출력 변수 q와 p = qdelayed 사이의 순간적인 불일치로 그 자체를 나타낸다.
진실 표는 입력에서 p = q와delayed 출력에서 q 사이에 불일치가 발생하는 행을 나타낸다. 피드백을 "파쇄"한 후, 진실 테이블 구축은 전통적인 방식으로 진행된다.[26] 그러나 이후 모든 행에서 출력 q는 현재 독립적인 입력 p와 비교되고 p와 q 사이의 불일치가 기록된다(즉, p=0과 q=1 또는 p=1과 q=0이 함께 기록됨). "라인"이 "제거"되면 모순의 법칙 ~(p & ~p)에 의해 둘 다 불가능하게 된다. 불일치를 나타내는 행은 과도상태로 간주되거나 일관성이 없는 행으로 제거되어 "불가능"하게 된다.
원스 플립 메모리
OR의 출력이 입력 중 하나에 다시 공급될 때 가장 간단한 메모리 결과, 이 경우 출력 "q"는 다시 "p"로 공급된다. 공식을 p=0 & q=0으로 먼저 평가(초기화)한다는 점을 감안하면 s=1로 "설정"하면 한 번 "깜빡"하게 된다. 이후 출력 "q"는 "fliped" 조건(state q=1)에서 "q"를 유지할 것이다. 이제 시간에 의존하는 이러한 행동은 한때 플립의 오른쪽에 있는 상태 다이어그램으로 나타난다.
| q | ||||||||
|---|---|---|---|---|---|---|---|---|
| p | s | ( | s | ∨ | p | ) | = q | |
| 0 | 0 | 0 | 0 | 0 | 0 | 상태 0, s=0 | ||
| 0 | 1 | 1 | 1 | 0 | q&p 불일치 | |||
| 1 | 0 | 0 | 1 | 1 | 1 | 상태 1(s = 0) | ||
| 1 | 1 | 1 | 1 | 1 | 1 | 상태 1(s = 1) |
플립플롭 메모리
다음으로 간단한 경우는 한 번 플립 아래에 표시된 "set-reset" 플립플롭이다. 처음부터 r=0 & s=0과 q=0을 고려하면, 한 번 플립과 유사한 방식으로 "set"(s=1)이다. 그러나 "r"=1일 경우 q=0을 "재설정"할 수 있는 조항이 있다. 그리고 set=1과 reset=1 둘 다 set=1이면 추가적인 합병증이 발생한다. 이 공식에서, set=1은 출력 q=1을 강제하므로 (s=0 & r=1) 언제 그리고 만일 (s=0 & r=1) 플립 플롭이 재설정된다. 또는 (s=1 & r=0)인 경우 플립플롭이 설정된다. s=1 ⇒ s=0 & r=1 ⇒ r=0 ⇒ ide r=0이 동시에 나타나는 추상적(이상적) 예에서는 공식 q가 불확정(결정할 수 없음)된다. "실제" OR의 지연으로 인해, AND와 NOT의 결과는 처음부터 알 수 없을 것이지만, 그 이후로는 알 수 없을 것이다.
| q | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| p | s | r | ( | s | ∨ | ( | p | & | ~ | ( | r | ) | ) | ) | = q | |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 상태 0(s=0 & r=0 ) | ||||||
| 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 상태 0(s=0 & r=1) | ||||||
| 0 | 1 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | q&p 불일치 | |||||||
| 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | q&p 불일치 | |||||||
| 1 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 1 | 상태 1 (s=0 & r=0 ) | ||||||
| 1 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | q&p 불일치 | |||||||
| 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 상태 1 (s=1 & r=0 ) | ||||||
| 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 상태 1(s&r)과 동시에 1 |
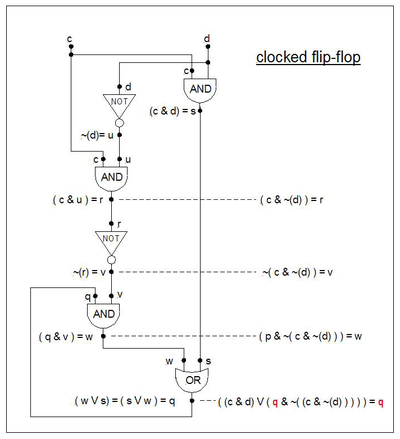
클럭 처리된 플립 플롭
"클록 플립 플롭" 메모리("c"는 "클록"이고 "d"는 "데이터")로 알려진 공식은 다음과 같다. 다음과 같이 작동한다. c = 0인 경우 데이터 d(0 또는 1)는 출력 q에 영향을 주기 위해 "통과"할 수 없다. c = 1일 때 d 데이터는 "통과"하고 출력 q는 d의 값을 "추월"한다. c가 1에서 0으로 넘어가면 데이터의 마지막 값은 출력 "q"에서 "포장" 상태로 유지된다. c=0인 한 d는 q의 변화를 유발하지 않고 값을 변경할 수 있다.
- 예
- ( (c & d ) ∨ ( p & ( ~ ( c & ~ ( d ) ) ) ) = q, 그러나 이제 p = q:
- ( ( ( c & d ) ( ( ~ ( c & ~ ( d ) ) )) = q
상태 다이어그램은 플립플롭의 상태 다이어그램과 모양은 유사하지만 전환에 다른 라벨이 표시된다.
| s | q | w | v | r | u | |||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 배를 젓다 | q | d | c | ( | ( | c | & | d | ) | ∨ | ( | q | & | ~ | ( | ( | c | & | ~ | ( | d | ) | ) | ) | ) | ) | = q | 설명 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 상태 0(s=0 & r=0 ), 0이(가) | ||||||||||||
| 1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 상태 0(d=0 & c=1 ): q=0이 d=0 다음에 온다. | ||||||||||||
| 2 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 상태 0(d=1 & r=0 ), 0이 갇힘 | ||||||||||||
| 3 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | q&p 불일치 | |||||||||||||
| 4 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 0 | 1 | 상태 1(d =0 & c=0 ), 1이 갇힘 | ||||||||||||
| 5 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 1 | 1 | 0 | q&p 불일치 | |||||||||||||
| 6 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 상태 1(d =1 & c=0 ), 1이 갇힘 | ||||||||||||
| 7 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 상태 1(d=1 & c=1 ): q=1은 d=1을 따르고 있다. |
역사적 발전
베르트랑 러셀(1912:74)은 아리스토텔레스로부터 파생된 세 가지 사상 법칙을 열거한다. (1) 정체성의 법칙: "무엇이든, 있는 것은.", (2) 모순의 법칙: "아무것도 있을 수 없고, 없을 수도 없다.", (3) 배제된 중간 법칙: "모든 것은 반드시 있거나 아니면 안 될 것이다."
- 예: 여기서 O는 개체의 BEE 또는 Quality에 대한 표현이다.
- 정체성의 법칙: O = O
- 모순의 법칙: ~(O & ~ (O))
- 제외중간의 법칙 : (O ∨ ~ (O))
배제된 중간 법칙에서 "모든 것"이라는 단어를 사용하는 것은 러셀이 이 법칙을 표현하는 것을 논쟁의 여지가 있게 한다. 한정된 개체 집합(한정된 "담론의 단일한 우주")을 기준으로 BEE 또는 Quality에 대한 표현으로 제한되는 경우(주장의 유무에 대해 구성원들을 차례로 조사할 수 있음) 법률은 직관적으로 적절한 것으로 간주된다. 따라서 "이 물체는 반드시 BE 또는 NOT BE (수집 중)" 또는 "이 물체는 이 품질 또는 NOT 이 품질(수집 내 물체와 상대적)을 가져야 한다"와 같은 주장이 허용된다. 자세한 내용은 벤 다이어그램에서 확인하십시오.
명제 미적분은 아리스토텔레스에서 비롯되었지만 명제에 적용되는 대수학의 개념은 19세기 초까지 기다려야 했다. 2000년 아리스토텔레스의 삼단논법의 전통에 대한 (반대) 반응에서 인간 이해에 관한 존 로크의 에세이는 기호학(기호의 사용 이론)이라는 단어를 사용했다. 1826년까지 리처드 휘틀리는 로크의 기호학에 대한 동정심으로 삼단논리를 비판적으로 분석하였다. 조지 벤담의 작품(1827년)은 '술어의 수량화'(1827년)라는 개념(요즘은 adays ≡ "모든 것을 위해"로 상징된다. 윌리엄 해밀턴이 아우구스투스 드 모건과의 우선권 분쟁을 놓고 선동한 "행"은 "조지 불에게 논리에 관한 자신의 생각을 적어 1847년 MAL [논리의 수학적 분석]으로 발표하도록 부추겼다"(Grattin-Guinness and Bornet 1997:xxviiiii)고 했다.
그의 기여에 대해 Grattin-Guinness와 Bornet은 다음과 같이 말했다.
- "부울의 주된 단일 혁신은 논리에 대해 [법]법칙 [xn = x ]이었다: 재산 x를 선택하고 x를 반복해서 선택하는 정신적 행위는 x를 한 번 선택하는 것과 같다고 기술했다... 그 결과 그는 x•(1-x)=0과 x+(1-x)=1 등식을 만들었고, 이 등식은 그를 위해 각각 모순의 법칙과 배제된 중간(p. xxviff)의 법칙을 표현했다. Boole "1"은 담론의 우주였고 "0"은 아무것도 아니었기 때문이다.
Gottlob Frege의 대규모 사업(1879)은 공식적인 명제 미적분학을 초래했지만 그의 상징성은 너무 위압적이어서 한 사람을 제외하고는 거의 영향을 받지 않았다. 버트랜드 러셀 알프레드 노스 화이트헤드의 제자였던 그는 프레지의 작품을 처음으로 연구했고, 프레지의 치료법에서 발견한 항모술의 문제(cf 러셀의 역설)에 대해 (유명하고 악명 높은) 에 대해 (1904) 에 대해 에미네이션을 제안했다. 러셀의 연구는 1912년에 제1권인 프린시비아 매스매티카(PM)를 제작한 화이트헤드와의 공동작업으로 이어졌다. 우리가 "현대적" 명제논리가 처음 등장한 것은 바로 여기에 있다. 특히 PM은 NOT와 OR, 주장 기호 ⊦을 원시성으로 소개한다. 이러한 개념의 관점에서 그들은 시사 → (def)를 정의한다. *1.01: ~p ∨ q), 그 다음 AND(def. *3.01: ~(~p ~ ~q)), 그 다음 동등성 p →→ q(*4.01: (p → q) & (q → )).
- 헨리 M. 셰퍼(1921년)와 장 니코드는 단 하나의 결합체, 즉 "스트로크"가 모든 명제적 공식들을 표현하기에 충분하다는 것을 증명한다.
- 에밀 포스트(1921년)는 자신의 '초급 명제 일반론 소개'에서 진리표 분석 방법을 개발한다. 그는 니코드의 뇌졸중을 주목한다.
- 화이트헤드와 러셀은 1927년 PM의 재공개에 대한 소개를 덧붙이며, 부분적으로는 스트로크에 대한 호의적인 대우가 더해졌다.
계산 및 전환 논리:
- 윌리엄 에클레스와 F. W. 조던(1919년)은 진공 튜브로 만든 "트리거 릴레이"를 설명한다.
- 조지 스티비츠(1937년)는 기계식 계전기(mechanical relay)를 이용해 바이너리 Adder를 발동한다. 그는 이것을 부엌 식탁 위에 쌓는다.
- 예: 이진 비트 a와i b 및i 이월 비트(c_ini)를 고려할 때, 이들의 합계 σ과i 이월(c_outi)은 다음과 같다.
- ( ( XORi bi ) XOR c_ini )= σi
- ( ai & bi ) ∨ c_ini ) = c_outi;
- 앨런 튜링은 계전기(1937–1938)를 사용하여 승수를 쌓는다. 그는 이것을 하기 위해 자신의 릴레이 코일을 손으로 감아야 한다.
- "스위치 회로"에 관한 교과서는 1950년대 초에 나온다.
- 윌러드 퀴네 1952년과 1955년, E. W. 비치 1952년, M. 카노(1953)는 제안적 기능을 단순화하기 위한 지도 방법을 개발한다.
- George H. Maly(1955)와 Edward F. 무어(1956)는 순차적(즉, 개폐회로) "기계"의 이론을 설명한다.
- E. J. McCluskey와 H. Shorr은 제안형(스위치형) 회로를 단순화하는 방법을 개발한다(1962년).
각주
- ^ 해밀턴 1978:1
- ^ 프린세스 매티매티카 (PM) 페이지 91은 명확한 "감각의 대상"이 필요하기 때문에 "the"를 지지한다; 그들은 "this"의 사용을 규정한다.
- ^ (이탈리아 추가) 레이헨바흐[clarification needed] p.80.
- ^ 타르스키 페이지 54-68. Suppes는 IDENTITY를 "추론의 더 많은 규칙"이라고 부르며 그 주변에서 간략하게 발전하고 있다; Robbin, Bender, Williamson, Goodstein은 아무런 언급이나 설명 없이 이 표지와 그 용법을 소개한다. 해밀턴 페이지 37은 공식 미적분학에서 공식의 평가와 관련하여 two과 = 두 개의 부호를 사용한다. 클린 페이지 70과 해밀턴 페이지 52는 특히 자연수의 산술에 관하여 그것을 술어 미적분학에 배치한다.
- ^ 경험론자들은 선험적인 지식의 개념을 지지한다. 존 로크, 데이비드 흄과 같은 "급진적 환원론자들"은 1996년 발행된 갈랜드 출판사의 논리 엠프리즘의 출현에서 인용한 "논리적 엠프리즘의 출현"에서 "모든 아이디어는 감각적 경험에서 직접 유래하거나 또는 이와 같이 유래된 아이디어로 복합되어야 한다"고 주장했다. http://www.marxists.org/reference/subject/philosophy/works/us/quine.htm
- ^ 신경망 모델링은 다음과 같은 대조군에 좋은 수학적 모델을 제공한다:신호 S와 임계값 "thr"을 주어진다면, S에서 "thr"를 빼고 이 차이 d를 S자형 함수에 대체한다. 큰 "게인" k의 경우, 예: k=100, 1/(1 + e ) = 1/(1 + e−k*d ) = { {0, ≃1−k*(S-thr) }.[clarification needed] 예를 들어, "도어가 올라오는 길의 50% 미만"을 의미한다면, 0.5*5.0 = +2.50V에 해당하는 임계값 sr=0.5를 완전히 닫았을 때 출력이 0V이고 완전히 열렸을 때 +5.0V인 "선형" 측정 장치에 적용할 수 있다.
- ^ 실제로 디지털 1과 0은 오버랩되지 않는 범위(예: { "1" = +5/+0.2/-1.0V, 0 = +0.5/-0.2V })[clarification needed]에 걸쳐 정의된다. 값이 정의된 범위를 벗어나면 값이 "u"가 되고 -- 알 수 없음; 예: +2.3은 "u"가 된다.
- ^ 논리 산출물의 개념은 그렇게 특이하지는 않지만(예: 0*0=0, 0*1=0, 1*0=0, 1*0=0, 1*0=0, 1*1=1)의 개념은 특이하다. 사실 (+) b = (+) = (b - a*b) 여기서 "+"는 "논리적 합계"이지만 +와 - -는 진정한 산술상이다. 때때로 모든 네개의 개념 공식으로:존 Wakerly 1978년 A및 B=1(A에 B를 더하는 것은 마이너스(XORB)-RSB-(비교하라 우편 146, 오류 Detecting 코드 Self-Checking 회선과 응용, North-Holland, 뉴욕,.mw-parser-output cite.citation{font-style:상속을 하다;word-wrap:break-word}.mw-parser-output .citation q{인용:")"""\"""'""'"}.mw-p 나타나는 데.Arser-output .citation:target{background-color:rgba(0,127,255,0.133)}.mw-parser-output.id-lock-freea,.mw-parser-output .citation.cs1-lock-free a{배경:linear-gradient(transparent,transparent),url("//upload.wikimedia.org/wikipedia/commons/6/65/Lock-green.svg")right 0.1emcenter/9pxno-repeat}.mw-parser-output .id-lock-limited a,.mw-parser-ou.Tput .id-lock-registration a,.mw-parser-output .citation .cs1-lock-limiteda,.mw-parser-output .citation .cs1-lock-registration a{배경:linear-gradient(transparent,transparent),url("//upload.wikimedia.org/wikipedia/commons/d/d6/Lock-gray-alt-2.svg")right 0.1emcenter/9pxno-repeat}.mw-parser-output .id-lock-subscription a,.mw-parser-output .ci.Tation .cs1-lock-subscription a{배경:linear-gradient(transparent,transparent),url("//upload.wikimedia.org/wikipedia/commons/a/aa/Lock-red-alt-2.svg")right 0.1emcenter/9pxno-repeat}.mw-parser-output .cs1-ws-icon{배경:linear-gradient(transparent,transparent),url("//upload.wikimedia.org/wikipedia/commons/4/4c/Wikisource-logo.svg")right.0.1em center/12pxno-repeat}.mw-parser-output .cs1-code{색:상속을 하다;배경:상속을 하다;국경 아무 것도 없고 패딩: 물려받다}.mw-parser-output .cs1-hidden-error{디스플레이:아무도, 색:#d33}.mw-parser-output .cs1-visible-error{색:#d33}.mw-parser-output .cs1-maint{디스플레이:아무도, 색:#3a3, margin-left:0.3em}.mw-parser-output .cs1-format{.Font-size:95%}.mw-parser-output .cs1-kern-left{padding-left:0.2em}.mw-parser-output .cs1-kern-right{padding-right:0.2em}.mw-parser-output .citation 0-444-00259-6 pbk .mw-selflink{font-weight:상속}ISBN.).
- ^ Karnaugh 지도를 자세히 보면 IF가...그러면...ELSE는 또한 (b AND (c XOR a) OR (a AND (c XOR b) ) = d라는 두 가지 배타적 OR의 관점에서 다소 동그라미처럼 표현될 수 있다.
- ^ 로빈 페이지 3
- ^ 로젠블룸 페이지 30과 페이지 54ff는 이 함축적 문제에 대해 어느 정도 길게 논한다. 대부분의 철학자와 수학자들은 위에 주어진 물질적 정의를 받아들인다. 그러나 몇몇은 직감주의자들을 포함해서 그렇지 않다; 그들은 그것을 배제된 중간이 잘못 적용되는 법칙의 한 형태라고 생각한다.
- ^ 실제로, 클레인이 CASE 운영자에게 제공한다는 정의에 의해 대안들 사이의 철저한 선택 - 상호 배제 -이 요구되고 있다(Kleene 1952229).
- ^ 표현 주위에 인용 부호를 사용하는 것은 우연이 아니다. 타르스키는 자신의 '18'에서 인용문 사용에 대해 언급했다. 사물의 정체성과 그 지정의 정체성; 인용 부호 사용" 페이지 58ffff.
- ^ 해밀턴 페이지 37. 벤더와 윌리엄슨 p. 29 주(州)는 "그 뒤에 오는 것은 "평등"을 보통 논리에 사용되는 기호 "⇔" (평등)으로 대체한다. 의미와 가치를 부여하기 위해 더 친숙한 " = "를 사용한다.
- ^ 라이헨바흐 페이지 20-22에 그리고 PM의 규약을 따른다. 기호 ==Df는 금속어구에 있으며, "기호 's에 의한 '는 공식 '(c&d)'와 같은 의미를 갖는다는 의미를 가진 형식적인 기호가 아니다.
- ^ 로젠블룸 1950:32. 클레인 1952:73-74는 11개의 상징을 모두 순위를 매긴다.
- ^ cf 민스키 1967:75, 섹션 4.2.3 " 괄호 계산 방법" 민스키는 그 일을 할 국가 기계를 제시하고, 유도(재발적 정의)를 이용하여 민스키는 '방법'을 증명하고 그 결과로서 정리를 제시한다. 완전하게 일반화된 "보완문법"은 계산을 하기 위해 무한 상태 기계(예: 튜링 기계)를 필요로 한다.
- ^ 로빈 페이지 7
- ^ cf 라이헨바흐 p. 68 (cf Reichenbach p. 68) : "추론이 타당하고 전제(presidential)가 사실이라면 추론을 확정(frinal)이라고 한다.
- ^ 처음 세 개뿐 아니라 해밀턴 pp.19-22는 오직 (NAND), ↓ (NOR)에서만 구축된 논리학에 대해 논한다.
- ^ 위크스 1967:36ff. Wickes는 2 x 4(3변수 지도) 중 8개, 4 x 4(4변수 지도) 중 16개의 좋은 예를 제공한다. 임의의 3변수 맵은 28=256 2x4 지도 중 하나를 나타낼 수 있고 임의의 4변수 맵은 216 = 65,536 다른 공식 평가 중 하나를 나타낼 수 있으므로, 모든 것을 기록할 수 없다.
- ^ 이 정의는 Stephen Kleene에 의해 주어진다. 커트 괴델과 클레네 둘 다 고전적 역설들이 한결같이 이런 종류의 정의의 예라고 믿었다. 그러나 클레네는 계속해서 그 문제가 만족스럽게 해결되지 않았으며, 충동적인 정의는 분석에서 찾을 수 있다고 주장했다. 그는 예를 들어 M의 최소 상한(l.u.b) u의 정의를 제시한다. 숫자 라인 C의 데데킨드 컷과 숫자 라인이 절단되는 두 부분, 즉 M과 (C - M), l.u.b = u는 개념 M의 관점에서 정의되는 반면, M은 C의 관점에서 정의된다. 따라서 C의 요소인 u의 정의는 전체성 C의 관점에서 정의되며 이는 그것의 정의를 충동적으로 만든다. Kleene은 이것을 멀리 주장하려는 시도가 역설의 충동적인 정의를 지지하는 데 사용될 수 있다고 주장한다.(Kleene 1952:43)
- ^ McCluskey는 "출력이 입력의 이전 값과 동일하다"는 단어 문구를 얻지 못했기 때문에 분석이 여전히 불완전하다고 주장할 수 있다. 그는 계속해서 "영어는 수학적 의미에서는 정식 언어가 아니며, 형식적인 프로슈즈를 갖는 것이 실제로 가능하지 않다"고 우려한다.단어 진술서"를 얻기 위해 노력하다. (185 페이지)
- ^ 더 정확히 말하면, 충분한 "루프 이득"이 주어진다면 진동이나 메모리가 발생할 것이다(cf McCluskey 페이지 191-2). 추상적(이상화된) 수학 시스템에서는 적절한 루프 획득은 문제가 되지 않는다.
- ^ 궁극적으로 빛의 속도에 의해 야기되는 지연의 개념과 국부적 인과관계의 원리는 J. 바와이즈, H. J. Keisler, K의 "교회의 논문과 메커니즘에 대한 원리" 로빈 간디(1980)에 나타난다. 쿠넨, 에드스 North-Holland 출판사 클레인 심포지엄(1980) 123-148. 간디는 이것을 그의 원칙 중 가장 중요한 것으로 여겼다: "비례 물리학은 거리에서의 즉각적인 행동의 가능성을 거부한다." (p. 135 페이지. 간디는 앨런 튜링의 학생이자 친한 친구였다.
- ^ 맥클루스키 p. 194-5는 "고리를 깨는 것"에 대해 논하고 이를 위해 "암페어"를 삽입하고, 위크스(p. 118-121)는 삽입 지연에 대해 논한다. McCluskey 페이지 195ff는 지연에 의해 야기된 "레이스"의 문제를 논한다.
참조
- 벤더, 에드워드 A.와 윌리엄슨, S. 길, 2005년, 미놀라 NY, 도버 출판사, ISBN0-486-43946-1. 이 텍스트는 UC 샌디에이고의 "하급 2/4[컴퓨터 과학] 과정"에서 사용된다.
- Enderton, H. B., 2002, 수학 논리 입문. 하코트/학술신문사. ISBN 0-12-238452-0
- Goodstein, R. L, (Pergamon Press 1963), 1966, (Dover Edition 2007), 부울 대수, Dover Publications, Inc. 뉴욕 미놀라, ISBN 0-486-45894-6 ∩, ∪, ', '(NOT), pl(IMPLIs)과 같은 세트의 이데아 기호를 가진 "계급의 알브라"의 개념을 강조한다. 후에 골드스타인은 "Sentence Logic" 페이지 76–93에 대한 그의 치료에서 이것들을 &, ,, ¬, ¬, → (존중하게)로 대체한다.
- Ivor Gratan-Guinness and Gérard Bornet 1997, George Boole: 논리학과 철학에 관한 선별된 원고, Birkhauser Verlag, Basil, ISBN 978-0-8176-5456-6 (보스턴)
- A. G. 해밀턴 1978, 수학자를 위한 논리, 영국 캠브리지 대학 출판부, ISBN 0-521-21838-1.
- E. J. McCluskey 1965, McGraw-Hill Book Company, McGraw-Hill Book Company, 개폐회로 이론 소개 ISBN 없음. 의회 도서관 카탈로그 카드 번호 65-17394. McCluskey는 Willard Quine의 학생이었고 Quine과 스스로 몇 가지 주목할 만한 이론들을 개발했다. 역사에 관심이 있는 사람들을 위해 이 책에는 많은 참고 문헌이 수록되어 있다.
- 마빈 L. 민스키 1967, 연산: 유한 및 무한 기계, 프렌티스 홀, Inc., Englewood Cliffs, N.J. ISBN 없음. 의회 도서관 카탈로그 카드 번호 67-12342. 특히 계산성과 우수한 출처에 유용하다.
- 폴 C. 로젠블룸 1950, 도버판 2005, The Elements of Matheical Logic, Dover Publishments, Inc., Minola, New York, ISBN 0-48617-4.
- 조엘 W. Robbin 1969, 1997, Mathematical Logic: A First Course, Dover Publications, Inc., Minola, New York, ISBN 0-486-45018-X (pbk.
- Patrick Suppes 1957 (1999년 도버판), 뉴욕주 Minola, Dover Publications, Inc.의 Logic 소개. ISBN 0-486-40687-3(PBK). 이 책은 인쇄되어 있어서 쉽게 구할 수 있다.
- 각주의 204페이지에서 그는 자신의 공리 세트를 E. V.에 언급한다. 헌팅턴, "논리의 대수학을 위한 독립적 체계의 집합", 미국수학협회의 거래, 제5권 91904) 페이지 288-309.
- 알프레드 타르스키 1941 (1995년 도버판), 뉴욕주 마이놀라, 도버 출판사, 도버 출판사, 로직과 연역 과학의 방법론 소개. ISBN 0-486-28462-X(PBK). 이 책은 인쇄되어 있어서 쉽게 구할 수 있다.
- 장 반 헤이제노르트 1967, 1976년 에멘데이션과 함께 세 번째 인쇄, From Frege to Gödel: A Source Book in Mathematical Logic, 1879-1931, Harvard University Press, Cambridge, Massachusettscheds. ISBN 0-674-32449-8(pbk). 프레지의 번역/재인쇄(1879년), 프레즈가 프레지에게 보낸 편지(1902년), 프레지가 러셀에게 보낸 편지(1902년), 리차드의 역설(1905년), 포스트(1921년) 등을 여기서 찾아볼 수 있다.
- Alfred North Whitehead와 Bertrand Russell 1927 2판, *53 1962년까지의 페이퍼백판, Principia Mathematica, Cambridge University Press, ISBN 없음. 1912년 초판과 1927년 2판 사이의 해 동안, H. M. 셰퍼 1921과 M. 진 니코드(무년 인용)는 러셀과 화이트헤드의 주의를 끌게 했는데, 그들이 그들의 원시적인 명제(연결)를 고려했던 것이 오늘날 "스트로크"나 NAND(NOT-AND, NOR...)로 알려진 단일으로 줄어들 수 있다는 것이었다. 러셀-화이트헤드는 그들의 "제2판 소개"에서 이것을 논의하고 위에서 논의한 대로 정의를 내린다.
- 윌리엄 E. Wickes 1968, 집적회로를 이용한 로직 디자인, 뉴욕주 John Wiley & Sons, Inc. ISBN 없음. 의회 도서관 카탈로그 카드 번호: 68-21185. 엔지니어링 분석 및 합성 방법에 대한 엄격한 프레젠테이션은 McCluskey 1965를 참조한다. 수페스와 달리 위크스의 "부울 대수학"에 대한 발표는 진실-테이블 성질의 일련의 가정으로부터 시작되어 그들에 대한 관습적인 이론들을 도출한다(18fp).
외부 링크
 Wikimedia Commons의 Proposal 공식과
Wikimedia Commons의 Proposal 공식과