일반화 스톡스 정리

벡터 미적분학과 미분 기하학에서 일반화된 스톡스 정리(Stokes-Cartan 정리로서 아포스트로피 또는 스톡스의 정리로서 아포스트로피를 사용하기도 함)는,^[1] 스톡스-카르탄 정리라고도 불리는 다지관에서의 미분형 통합에 관한 진술로, 벡터 미적분학으로부터 여러 가지 정리를 단순화하고 일반화한다.2차원 선 통합과 3차원 표면 통합과 관련 있는 아이작 뉴턴의 미적분학의 기본 정리를 일반화한 것이다.^[2]null

스톡스의 정리는 어떤 방향성 매니폴드 $Ω$ 의 경계 위에 있는 차동 형태 $Ω$ 의 적분은 $Ω$ 의 전체, 즉 Ω의 외부 파생상품 $Ω$ 의 적분과 동일하다고 말한다.

\int _{\partial \Oomega }\omega =\int _{\Oomega }d\omega \,

스톡스의 정리는 비토 볼테라, 에두아르 구르사트, 앙리 푸앵카레 등의 벡터 미적분학의 정리 일반화에 관한 앞선 저작에 이어 1945년 에일리 카르탄에 의해 현대적인 형태로 공식화되었다.^[3]^[4]^[5]null

이 현대적인 형태의 스톡스의 정리는 켈빈 경이 1850년 7월 2일의 편지에서 조지 스톡스에게 전한 고전적 결과의 광대한 일반화다.^[6]^[7]^[8]스톡스는 이 정리를 1854년 스미스상 시험의 문제점으로 설정했고, 그로 인해 그의 이름이 적힌 결과가 나왔다.1861년 헤르만 행클에 의해 처음 출판되었다.^[8]^[9]이 고전적인 경우는 유클리드 3공간에 있는 표면 위에 있는 $벡터장$ F의 컬(즉, 컬 $F$ 의 플럭스)의 표면 적분을 표면 경계 위에 있는 벡터장 적분선(루프 적분이라고도 함)과 연관시킨다.null

간단한 고전적 벡터 분석 예제

Let $γ :$ [ $a,$ $b]$ → $R$ 은² 조각처럼 매끄러운 요르단 평면 곡선이 된다.요르단 곡선 정리는 $R$ 을² 콤팩트한 성분과 비콤팩트한 성분으로 나누는 것을 의미한다. $D$ 는 $γ$ 으로 경계된 콤팩트한 부분을 나타내며, $S$ $:=$ $ψ (D$ )로 $ψ :$ $D$ → $R$ 이³ 매끄러워졌다고 가정한다 $.$ $γ$ 이 $γ(t) [note 1]$ = $ψ (γ)$ 에 의해 정의된 공간 곡선이고 $F$ 가 $R$ 에³ 대한 부드러운 벡터 필드인 경우:^[10]^[11]^[12]

\point _{\Gammatbf {F} \,\cdot \,d\cdot \d},\cdot \,d\mathb {S}}},\mathb \s}}},\mathb \s}},\time \mathb

이 고전적 진술은 1-형식의 벡터장과 2-형식의 컬을 통해 식별한 후 위에 기술된 일반적인 공식화의 특별한 경우다.

{\begin{pmatrix}F_{x}\\F_{y}\\F_{z}\\end{pmatrix}\cdot d\Gamma \to F_{x}\,dx+F_{y}\,dy+F_{z}\,dz

\nabla \times {\begin{pmatrix}F_{x}\\F_{y}\\F_{z}\end{pmatrix}}\cdot d\mathbf {S} ={\begin{pmatrix}\partial _{y}F_-\partial _{z}F_{y}\\partial _{x}-\partial _{x}-\partial _{x}-{y}-\partial _{x_{x}\end{pmatrix}\cdot d\mathb {S}\s}\to

d(F_{x}\,dx+F_{y}\,dz)=(\partial _{y_{z}\,dz)=(partial _{y}F_-\partial _{z})F_{y}\,dy\wedge dz+(\partial _{z}-{x}-\partial _{x}-{x}-\partial _{x}-{x}-\partial _{x}-{y}-}-partial _{y}\dx\wedge dy.}}

그 밖에 미적분학의 기본정리에 대한 고전적 일반화, 그린의 정리 등은 미분형(고전적 이론 각각에 따라 다른)으로 벡터장을 표준적으로 식별한 후 위에 기술한 일반적 제형의 특수한 경우다.null

소개

미적분학의 기본 정리는[ $a,$ $b]$ 간격에 걸친 함수 $f$ 의 적분은 $f$ 의 반변성 $F$ 를 찾아 계산할 수 있다고 명시한다.

\int _{a}^{b(x)\,dx=F(b)-F(a)\,

스톡스의 정리란 다음과 같은 의미에서 이 정리를 광대한 일반화한 것이다.null

F의 선택으로,.mw-parser-output .sfrac{white-space:nowrap}.mw-parser-output.sfrac.tion,.mw-parser-output.sfrac .tion{디스플레이:inline-block, vertical-align:-0.5em, font-size:85%;text-align:센터}.mw-parser-output.sfrac.num,.mw-parser-output.sfrac .den{디스플레이:블록, line-height:1em, 마진:00.1em}.mw-parser-output.sfrac .den{border-top:1px. }고체.mw-parser-output .sr-only{국경:0;클립:rect(0,0,0,0), 높이:1px, 마진:-1px, 오버 플로: 숨어 있었다. 패딩:0;위치:절대, 너비:1px}dF/dx)f()).미분형식의 비유에서 $f (x) dx$ 는 0형식, 즉 함수 F: $즉$ $dF$ = $fdx$ 의 외부 파생형이라고 하는 것이다.일반 스톡스 정리는 $F$ 와 같은 0형식만이 아닌 $Ω$ 의 상위 차등형식에 적용된다.
닫힌 간격 $[a,$ $b]$ 은 경계가 있는 1차원 다지관의 간단한 예다.그것의 경계는 $a$ 와 b $두$ 점으로 구성된 세트다.그 간격에 걸쳐 $f$ 를 통합하는 것은 더 높은 차원 다지관의 형태를 통합하는 것으로 일반화될 수 있다.두 가지 기술적 조건이 필요하다: 다지관은 방향을 잡을 수 있어야 하고, 형태는 잘 정의된 적분을 주기 위해 압축적으로 지지되어야 한다.
두 점 $a$ 와 $b$ 는 닫힌 구간의 경계를 형성한다.보다 일반적으로 스톡스의 정리는 경계가 있는 방향 다지관 $M$ 에 적용된다. $M$ 의 경계 $\partial M$ 은 그 자체로 다지관이며 $M$ 의 경계로부터 자연적인 방향을 계승한다.예를 들어, 구간의 자연 방향은 두 경계점에 대한 방향을 제공한다.직관적으로 $a$ 는 구간의 반대쪽 끝에 있기 때문에 반대 방향을 $b$ 로 상속한다.따라서, 두 경계점 $a$ 에 대해 $F$ 를 "통합"하고, $b$ 는 $F (b)$ - $F (a$ )의 차이를 취하고 있다 $.$

더 간단한 용어로 점을 곡선 경계, 즉 1차원 다지관의 0차원 경계로 간주할 수 있다.So, just as one can find the value of an integral ( $f dx = dF$ ) over a 1-dimensional manifold ( $[a, b]$ ) by considering the anti-derivative ( $F$ ) at the 0-dimensional boundaries ( ${a, b}$ ), one can generalize the fundamental theorem of calculus, with a few additional caveats, to deal with the value of integrals ( $dω$ ) over $n$ -dimensional manifolds ( $Ω$ ) by con다지관의 ( $n - 1$ )차원 경계( $Ω$ )에서 반변성(Ω)을 비스듬히 배치한다.null

그래서 근본적인 정리는 다음과 같이 읽는다.

\int _{a,b]f(x)\,dx=\int _{[a,b]}\,dF=\int _{a\}^{b\}^{b\}^{+}F=F(b)-F(a)\,

경계가 있는 매끄러운 다지관의 제형

$Ω$ 은 차원 $n$ 의 경계가 있는 지향적인 부드러운 다지관이고 $α$ 는 $Ω$ 에서 콤팩트하게 지지되는 부드러운 n-차동형이다.첫째, $α$ 가 단일 방향 좌표도{ $U,$ $φ}$ 의 영역에서 콤팩트하게 지지된다고 가정하자. 이 경우 $Ω$ 에 $대한$ α의 적분을 Ω으로 정의한다.

\int _{\Oomega }\alpha =\int _{\varphi(U)}(\varphi ^{-1}^{*}\alpha \...

즉,

α

에서

R

까지의ⁿ 풀백을 통해.

보다 일반적으로 $Ω$ 이상 $α$ 의 적분은 다음과 같이 정의된다. ${ψ i}$ 을(를) 로컬로 유한한 표지 ${U i,$ $φ i}($ 일관적으로 지향) 좌표 차트와 연관된 통합의 분할로 설정한 다음, 적분을 정의하십시오.

\int _{\Oomega }\alpha \equiv \sum _{i}\int _{U_{i}}\psi _{i}\alpha \...

여기서 합계의 각 항은 위에서 설명한 대로

R

으로ⁿ 다시 당겨서 평가한다.이 양은 잘 정의되어 있다. 즉 좌표 차트의 선택이나 통합의 분할에 따라 달라지지 않는다.null

일반화된 스토크스 정리는 다음과 같이 읽는다.

Theorem (Stokes–Cartan) — If $\omega$ is a smooth $(n-1)$ -form with compact support on smooth $n$ -dimensional manifold-with-boundary $\Omega$ , $\partial \Omega$ denotes the boundary of $\Omega$ $\Omega$ 유도 방향과 $i:\partial \Omega \hookrightarrow \Omega$ : $i:\partial \Omega \hookrightarrow \Omega$ $i:\partial \Omega \hookrightarrow \Omega$ $i:\partial \Omega \hookrightarrow \Omega$ $i:\partial \Omega \hookrightarrow \Omega$ ${\displaystyle i:\partial \Oomega \hookrightarrow \Oomega$ }이 $i:\partial \Omega \hookrightarrow \Omega$ (가) 포함 맵인 경우,

\int _{\Oomega }d\omega =\int _{\partial \Oomega \i^{*}\momega.

Conventionally, ${\textstyle \int _{\partial \Omega }i^{*}\omega }$ is abbreviated as ${\textstyle \int _{\partial \Omega }\omega }$ , since the pullback of a differential form by the inclusion map is simply its restriction to its domain: ${\displaystyle i^{*}\omega =\omega$ $_{\partial \Oomega$ 여기서 $d$ $d$ 는 $d$ 다지관 구조만을 사용하여 정의되는 외부 파생물이다.그 오른쪽 가끔 ∮ ∂Ω ω{\textstyle \oint_{\partial \Omega}\omega}다는 사실이 그(n− 1){\displaystyle(n-1)}-manifold∂ Ω{\displaystyle\partial \Omega}영역을 가지지 않다는 것을 강조에 쓰여집니다.스토크스 정리의 주어진 원활한 n{\displaysty[주 2](이 사실은 또한, 함축. $le n}$ -dimensional manifold $\Omega$ , application of the theorem twice gives ${\textstyle \int _{\partial (\partial \Omega )}\omega =\int _{\Omega }d(d\omega )=0}$ for any $(n-2)$ -form $\omega$ , which implies that $\partial (\partial \Omega )=\emptyset$ $\partial (\partial \Omega )=\emptyset$ $\partial (\partial \Omega )=\emptyset$ $\partial (\partial \Omega )=\emptyset$ ) $\partial (\partial \Omega )=\emptyset$ = $\partial (\partial \Omega )=\emptyset$ ${\displaystyle \partial (\partial \Oomega )=\emptyet }.)$ 방정식의 오른쪽은 종종 통합 법칙을 공식화하는 데 사용된다. 왼쪽은 동등한 미분 제형으로 이어진다(아래 참조).null

이 정리는 종종 $\Omega$ ${\displaystyle$ \ $Oomega$ $}$ 이(가) 더 큰 다지관의 내장형 서브매니폴드인 상황에서 $\Omega$ 사용되며, $\mathbf {R} ^{k}$ $\omega$ ${\displaystyle \$ $mathbf{R} ^{k$ 이(가 $)$ 정의된다 $\omega$ .null

위상학적 예심, 체인을 통한 통합

$M$ 을 매끄러운 다지관이 되게 하라. $M$ 의 (매끄러운) 단수 k-simplex는 $R$ 의^k 표준 simplex에서 $M$ 까지의 매끄러운 지도로 정의된다. $M$ 에서 단수 k-chain의 그룹 $C k (M,$ $Z)$ 는 $M$ 에서 단수 k-simplices 집합에 있는 자유 아벨리안 그룹으로 정의된다.이들 그룹은 경계도map과 함께 체인 콤플렉스를 정의한다.해당 호몰로지(resp. cohomology) 그룹은 일반적인 단일 호몰로지 그룹 $H k (M,$ $Z)$ (resp)와 이형성이다. $M$ 에서 매끄러운 단순화보다는 연속적인 단순화를 사용하여 정의되는 단일한 코호몰로지 그룹 $H k (M,$ Z)

한편, 외부 파생상품과 $함께$ d를 연결지도로 하는 미분양식은 코체인 콤플렉스를 형성하는데, 이 콤플렉스는 de Rham cohomology 그룹 H $H_{dR}^{k}(M,\mathbf {R} )$ $H_{dR}^{k}(M,\mathbf {R} )$ k ( $H_{dR}^{k}(M,\mathbf {R} )$ , $H_{dR}^{k}(M,\mathbf {R} )$ ) ${\dR}^{$ dR}^{ $k}(M,\mathbf {R} )}$ 을 정의한다 $H_{dR}^{k}(M,\mathbf {R} )$

차동 k-폼은 $R$ 로^k 다시 당겨서 자연스럽게 k-simplex를 통해 통합될 수 있다.선형성에 의해 확장되면 사슬을 통해 통합할 수 있다.이것은 k-폼의 공간으로부터 단수 코인 k번째 그룹, $C k (M,$ $Z$ ), $C k (M,$ $Z$ )의 선형 함수에 이르는 선형 지도를 제공한다 $.$ 즉, k-폼 $Ω$ 은 기능을 정의한다.

I(\omega)=\point _{c}\omega.

k-ray에

Stokes의 정리에서는 이것이 de Rham cohomology에서 실제 계수가 있는 단수 코호몰로지까지의 체인 맵이라고 말하고 있다; 외부 파생 모델

d

는 형태에 있어서

\partial

의 이중처럼 작용한다.이것은 de Rham cohomology에서 단일한 cohomology에 이르는 동형성을 제공한다.양식 수준에서 이는 다음을 의미한다.

닫힌 형태, 즉 $dΩ$ = $0$ 은 경계, 즉 $\partialσ c$ $M$ 으로_c 기록할 수 있는 다지관 위에 0의 적분을 가진다.
정확한 형태, 즉 $Ω$ = $dσ$ 는 0의 적분 주기를 가지고 있다. 즉, 경계가 빈 집합에 합친 $경우 c$ : $c =$ M = $\emptyset.$

드 럼의 정리를 보면 이 동형성이 사실상 이형성임을 알 수 있다.따라서 위의 1과 2와의 역은 진실이다.즉, { $c i}$ 이(가) k번째 호몰로지 그룹을 생성하는 주기인 경우, 해당 실수인 { $a i}$ 에 대해 다음과 같은 폐쇄형 Ω이 $존재$ 한다.

\point _{c_{i}\omega =a_{i}\...

그리고 이 형태는 정확한 형태에 따라 독특하다.null

매끄러운 다지관에 대한 스톡스의 정리는 매끄러운 다지관의 사슬에 대한 스톡스의 정리에서 도출될 수 있으며, 그 반대의 경우도 마찬가지일 수 있다.^[13]공식적으로 언급된 후자는 다음과 같이 읽는다.^[14]

정리(사슬에 대한 Stokes의 정리) — $c$ 가 매끄러운 다지관 $M$ 의 매끄러운 k-체인이고, $Ω$ 이 매끄러운 ( $k - 1$ )형이라면 $M$ 의 매끄러운 (k - 1)형식이다.

\displaystyle \int _{\put c}\omega =\int _{c}d\omega.}

기본 원리

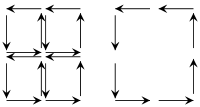
이러한 위상론적 주장을 단순화하기 위해서는 $d$ = $2차원$ 에 대한 예를 고려하여 근본 원리를 검토할 가치가 있다.본질적인 아이디어는 다지관의 방향 타일링에서 내부 경로가 반대 방향으로 교차된다는 것을 보여주는 왼쪽의 도표로 이해할 수 있다. 즉, 내부 경로가 통합된 경로에 대한 기여는 서로 쌍방향으로 취소된다.그 결과, 경계로부터의 공헌만 남는다.따라서 충분히 미세한 기울기(또는 동등하게 단순화)에 대한 스톡스의 정리를 증명하기에 충분하며, 이는 보통 어렵지 않다.null

러프 세트에 대한 일반화

매끄러운 경계가 있는 영역(여기서는

Ω

대신

D

라고 함)이것은 모서리가 있는 다지관이라 경계가 매끄러운 다지관이 아니다.

$Ω$ 이 경계를 가진 매끄러운 다지관인 위의 공식은 많은 용도에서 충분하지 않다.예를 들어, 통합의 도메인을 두 개의 x 좌표와 두 함수의 그래프 사이의 평면 영역으로 정의한다면, 도메인의 모서리가 있는 경우가 종종 발생할 것이다.그러한 경우 코너 포인트는 $Ω$ 이 경계를 가진 매끄러운 다지관이 아니라는 것을 의미하므로, 위에서 주어진 스토크스의 정리문은 적용되지 않는다.그럼에도 스토크스의 정리 결론은 여전히 사실인지 확인할 수 있다. $Ω$ 과 그 경계는 작은 점 집합(측도 0 집합)에서 떨어져서 잘 동작하기 때문이다.null

거칠기를 허용하는 스토크스의 정리 버전이 휘트니에 의해 증명되었다.^[15] $D$ 가 $R$ 의ⁿ 연결된 경계 개방 서브셋이라고 가정한다. $D$ 가 다음 속성을 만족하는 경우 D를 표준 도메인으로 호출한다. $\partial D$ 의 부분집합 $P$ 가 존재하며, $\partial D$ 의 보완에는 하우스도르프 $(n$ - 1 $)$ 측정 0이 있으며, 따라서 $P$ 의 모든 점에는 일반화된 정규 벡터가 있다.이것은 벡터 $v (x)$ 로 좌표계가 선택되어 $v (x)$ 가 제1의 기본 벡터인 경우, x $주위$ 의 열린 근방에 $P$ 가 그래프 { $x 1$ = $f (x 2, ...,$ $x n n)$ 이고 $D$ 가 영역 { $x 1$ : $f 1 (x 2, ...,$ $x n) }$ 인 부드러운 함수 $f (x 2,$ ..., x $)$ 가 존재한다.휘트니는 표준 영역의 경계는 0개의 하우스도르프 $($ $n$ - $1$ ) $측정$ 과 유한 또는 계수 가능한 매니폴드의 조합이며, 각각 한쪽 면에만 도메인을 가지고 있다고 말한다.그리고 나서 그는 $D$ 가 $R$ 의ⁿ 표준 영역이라면, $Ω$ 은 ( $n$ - 1 $)$ 형태로서 $D$ ∪ $P$ 에 정의되고 연속적이며 경계되고, $D$ 에 매끄러우며, $P$ 에 통합이 가능하며, $dΩ$ 이 $D$ 에 통합될 수 있는 형태라는 것을 증명한다. 그러면 스톡스의 정리는, 즉,

\displaystyle \int _{P}\omega =\int _{D}d\omega \,}

러프 세트의 측정-이론적 특성에 대한 연구는 기하학적 측정 이론으로 이어진다.훨씬 더 일반적인 스톡스의 정리 버전은 페더러와 해리슨에 의해 증명되었다.^[16]null

특례

미분형을 이용한 스톡스 정리의 일반적인 형태는 특수한 경우보다 강력하고 사용하기 쉽다.기존 버전은 미분 기하학의 기계 없이도 데카르트 좌표를 사용하여 제작할 수 있으므로 접근성이 높다.게다가, 그들은 나이가 더 많고 결과적으로 그들의 이름이 더 친숙하다.전통적인 형태는 종종 연습하는 과학자들과 기술자들에 의해 더 편리하다고 여겨지지만, 구면이나 원통형 좌표와 같은 친숙한 다른 좌표계를 사용할 때 전통적인 공식의 비자연성이 명백해진다.명칭의 적용 방식과 이중 제형의 사용에 혼선이 발생할 가능성이 있다.null

고전적(벡터 미적분학) 사례

표면

σ

, 경계

\partialσ

및 "정규"

벡터

n을 가진 벡터-미적분 스톡스 정리의 삽화.

이것은 1-형식(벡터장에 관한 진술이기 때문에 이중화)에 대한 (이중화)(1+1)차원 케이스다.이 특별한 경우는 흔히 많은 대학 입문 벡터 미적분학 과정에서는 스톡스의 정리라고 일컬어지며 물리학과 공학에 사용된다.컬 정리라고도 한다.null

고전적인 스톡스의 정리는 유클리드 3공간의 표면 $Ⅱ$ 에 대한 벡터장 컬의 표면 적분과 그 경계 위에 있는 벡터장 적분의 선과 관련된다.유클리드 3공간에 대한 지표를 사용하여 벡터장을 1형식으로 식별하면 일반 스톡스 정리( $n$ = $2$ )의 특별한 경우다.선 적분인 $\partialσ$ 의 곡선은 양의 방향을 가져야 하는데, 이는 표면이 정상인 $n$ 이 뷰어를 향할 때 $\partialσ이$ 시계 반대 방향으로 가리킨다는 것을 의미한다.null

이 정리의 한 가지 결과는 굴곡이 0인 벡터장의 필드 라인이 닫힌 등고선이 될 수 없다는 것이다.공식은 다음과 같이 다시 쓸 수 있다.

정리 — $F =$ ( $P (x, y, z),$ $Q (x, y, z),$ $R (x, y, z)$ 이 표면 $surface$ 이 매끄러운 지역에서 정의되며 연속적인 1차 부분파생상품을 가지고 있다고 가정한다.그러면

\iint _{\Sigma }{\Biggl (}\left({\frac {\partial R}{\partial y}}-{\frac {\partial Q}{\partial z}}\right)dy\,dz+\left({\frac {\partial P}{\partial z}}-{\frac {\partial R}{\partial x}}\right)dz\,dx+\left({\frac {\partial Q}{\partial x}}-{\frac {\partial P}{\partial y}}\right)dx\,dy{\Biggr )}=\oint _{\partial \Sigma }{\Big (}P\,dx+Q\,dy+R\,dz{\Big )}\...

여기서

P

,

Q

,

R

은

F

의 성분이며,

\partial

는 지역

σ

의 경계선이다.

그린 정리

그린의 정리는 위에서 인용한 $P$ , $Q$ , $R$ 의 측면에서 적분에서 양쪽의 제3의 통합으로 즉시 인식된다.null

전자기학에서

4개의 맥스웰 방정식 중 2개는 3-D 벡터장의 컬을 포함하며, 이들의 미분 및 적분 형태는 스톡스 정리의 특수 3차원(벡터 미적분학) 사례에 의해 관련된다.이동 경계가 있는 경우를 방지하기 위해 주의를 기울여야 한다. 부분 시간 파생상품은 그러한 경우를 제외하기 위한 것이다.이동 경계가 포함되는 경우, 통합과 분화의 교환은 아래 결과에 포함되지 않은 경계 운동과 관련된 용어를 도입한다(적분 기호 아래의 차별화 참조).null

이름	미분형	적분 형태(삼차원 스톡스 정리+상대론적 불변성 사용, ∫ $\partial/\partial t ...$ $\to$ $d / dt$ ∫ $\dots)$
맥스웰-파라데이 방정식 패러데이의 유도 법칙:	$\nabla \times \mathbf {E} =-{\frac {\partial \mathbf {B}{\partial t}}}}$	${\begin{aligned}\oint _{C}\mathbf {E} \cdot d\mathbf {l} &=\iint _{S}\nabla \times \mathbf {E} \cdot d\mathbf {A} \\&=-\iint _{S}{\frac {\partial \mathbf {B} }{\partial t}}\cdot d\mathbf {A} \end{aligned}}$ ( $C$ 와 $S$ 가 반드시 정지하지 않는 경우)
암페르의 법칙 (맥스웰의 확장자 포함):null	$\nabla \times \mathbf {H} =\mathbf {J} +{\frac {\partial \mathbf {D}{\partial t}}}}$	${\begin{aligned}\oint _{C}\mathbf {H} \cdot d\mathbf {l} &=\iint _{S}\nabla \times \mathbf {H} \cdot d\mathbf {A} \\&=\iint _{S}\mathbf {J} \cdot d\mathbf {A} +\iint _{S}{\frac {\partial \mathbf {D} }{\partial t}}\cdot d\mathbf {A} \end{aligned}}$ ( $C$ 와 $S$ 가 반드시 정지하지 않는 경우)

위에 열거된 맥스웰 방정식의 부분집합은 SI 단위로 표현되는 전자기장에 유효하다.CGS 또는 가우스 단위와 같은 다른 단위 시스템에서는 항에 대한 스케일링 계수가 다르다.예를 들어 가우스 단위에서는 패러데이의 유도의 법칙과 암페르의 법칙이 다음과 같은 형태를 취한다.^[17]^[18]

{\begin{aligned}\nabla \times \mathbf {E} &=-{\frac {1}{c}}{\frac {\partial \mathbf {B} }{\partial t}}\,,\\\nabla \times \mathbf {H} &={\frac {1}{c}}{\frac {\partial \mathbf {D} }{\partial t}}+{\frac {4\pi }{c}}\mathbf {J} \,,\end{aligned}}

여기서

c

는 각각 진공에서 빛의 속도다.null

발산정리

마찬가지로, 발산 정리.

{\displaystyle \int _{\mathrm {Vol}}\nabla \mathbf {F} \d_{\mathrm {Vol}}=\point _{\partial \operatorname {Vol}\mathbf {F} \cdot d{\bmbmbmobmobmobmbol {sma}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}.

벡터장을 유클리드 체적 양식으로 수축시켜 얻은 (

n

- 1

)

형태로 벡터장을 식별하는 특별한 경우다.이를 적용하면 사례

F

=

fc

이며 여기서

c

는 임의 상수 벡터다.제품의 다양성을 알아내면

\mathbf {c} \cdot \int _{\mathrm {Vol}\nabla f\,d_\mathbf {vol}}=\c}\cdot \partial \mathrmatrm {vol},d{\bymbol{\},}},},}\,}\,\,\,\,\,\,\,},},},.

이

모든 것이 지속되기 때문에 우리는 이 모든 것을 찾을 수 있다.

\int _{\mathrm {Vol}\nabla f\,d_{\mathrm {vol}=\point _{\partial \mathrm {vol}f\,d{\boldsymbol {\\\\\sigma},

참고 항목

찬드라세카르-웬첼 보조정리

각주

^ $γ$ 과 $γ$ 은 둘 다 루프지만, $γ$ 이 반드시 요르단 곡선인 것은 아니다.
^ 수학자들에게는 이 사실이 알려져 있기 때문에 원은 중복되고 종종 생략된다.그러나 여기서 명심해야 할 것은 $\oint{W dU total}$ 라는 표현이 자주 나타나는 열역학에서(아래 전체 파생상품에서 참조) 통합 경로 $W$ 는 훨씬 더 높은 차원 다지관의 1차원 폐쇄선이다.즉, 열역학 애플리케이션에서 $U$ 는 온도 $α 1 :=$ $T$ , 부피 $α 2 :=$ $V$ , 그리고 샘플의 전기적 양극화 $α 3$ := $P$ 의 함수인 경우, 1은 다음과 같다. ${\디스플레이 스타일 \{d_{\text{total}}U\}=\sum _{i=1}^{3}{\frac {\partial U}{\partial \alpha _{i}\,d\alpha _{i}\}}$ 그리고 원은 정말로 필요하다. 예를 들어, 통합 가정에서의 차등적인 결과를 고려하는 경우. $\point _{W}\,\{d_{\text{total}}}U\}\, {\stackrel {!}{=}}\,0\,.$

참조

^ Physics of Collisional Plasmas – Introduction to Michel Moisan Springer.
^ "2019년 11월 포트폴리오, ASIN: B07P1NNTSD" 그레고리 주커먼 "시장을 해결한 남자"
^ Cartan, Élie (1945). Les Systèmes Différentiels Extérieurs et leurs Applications Géométriques. Paris: Hermann.
^ Katz, Victor J. (1979-01-01). "The History of Stokes' Theorem". Mathematics Magazine. 52 (3): 146–156. doi:10.2307/2690275. JSTOR 2690275.
^ Katz, Victor J. (1999). "5. Differential Forms". In James, I. M. (ed.). History of Topology. Amsterdam: Elsevier. pp. 111–122. ISBN 9780444823755.
^
참조:
- Katz, Victor J. (May 1979). "The history of Stokes' theorem". Mathematics Magazine. 52 (3): 146–156. doi:10.1080/0025570x.1979.11976770.
- Thomson이 Stokes에게 보낸 편지는 다음과 같다.
- 톰슨도 스토크스도 그 정리에 대한 증거를 발표하지 않았다.1861년에 발표된 첫 번째 증거는: 한클은 정리의 저자를 언급하지 않는다.
- 각주에서 라모어는 벡터장의 컬을 표면 위에 통합시킨 초기 연구자들에 대해 언급한다.참조:
^ Darrigol, Olivier (2000). Electrodynamics from Ampère to Einstein. Oxford, England. p. 146. ISBN 0198505930.
^ ^a ^b 스피박(1965), 페이지 7, 서문.
^
참조:
- 1854년 스미스상 수상 심사는 온라인: 점원 맥스웰 재단에서 이용할 수 있다.맥스웰은 이 시험을 치르고 에드워드 존 루스와 함께 공동 1위에 올랐다.참조: 스미스의 상 또는 점원 맥스웰 재단을 참조하십시오.
- Clerk Maxwell, James (1873). A Treatise on Electricity and Magnetism. Vol. 1. Oxford, England: Clarendon Press. pp. 25–27. 27페이지의 각주에서 맥스웰은 스톡스가 1854년 스미스상시험에서 8번 문항으로 정리를 사용했다고 언급한다.이 각주는 정리가 "스톡스의 정리"로 알려지게 된 원인이었던 것으로 보인다.
^ Stewart, James (2010). Essential Calculus: Early Transcendentals. Cole.
^ 이 증거는 교수님이 주신 강의 노트에 근거한 것이다.Robert Scheichl(영국 배스 대학교 [1]), [2]를 참조하십시오.
^ "This proof is also same to the proof shown in".
^ Renteln, Paul (2014). Manifolds, Tensors, and Forms. Cambridge, UK: Cambridge University Press. pp. 158–175. ISBN 9781107324893.
^ Lee, John M. (2013). Introduction to Smooth Manifolds. New York: Springer. p. 481. ISBN 9781441999818.
^ 휘트니, 기하학적 통합 이론 III.14
^ Harrison, J. (October 1993). "Stokes' theorem for nonsmooth chains". Bulletin of the American Mathematical Society. New Series. 29 (2): 235–243. arXiv:math/9310231. Bibcode:1993math.....10231H. doi:10.1090/S0273-0979-1993-00429-4. S2CID 17436511.
^ Jackson, J. D. (1975). Classical Electrodynamics (2nd ed.). New York, NY: Wiley.
^ Born, M.; Wolf, E. (1980). Principles of Optics (6th ed.). Cambridge, England: Cambridge University Press.

추가 읽기

Grunsky, Helmut (1983). The General Stokes' Theorem. Boston: Pitman. ISBN 0-273-08510-7.
Katz, Victor J. (May 1979). "The History of Stokes' Theorem". Mathematics Magazine. 52 (3): 146–156. doi:10.2307/2690275. JSTOR 2690275.
Loomis, Lynn Harold; Sternberg, Shlomo (2014). Advanced Calculus. Hackensack, New Jersey: World Scientific. ISBN 978-981-4583-93-0.
Madsen, Ib; Tornehave, Jørgen (1997). From Calculus to Cohomology: De Rham cohomology and characteristic classes. Cambridge, UK: Cambridge University Press. ISBN 0-521-58956-8.
Marsden, Jerrold E.; Anthony, Tromba (2003). Vector Calculus (5th ed.). W. H. Freeman.
Lee, John (2003). Introduction to Smooth Manifolds. Springer-Verlag. ISBN 978-0-387-95448-6.
Rudin, Walter (1976). Principles of Mathematical Analysis. New York, NY: McGraw–Hill. ISBN 0-07-054235-X.
Spivak, Michael (1965). Calculus on Manifolds: A Modern Approach to Classical Theorems of Advanced Calculus. San Francisco: Benjamin Cummings. ISBN 0-8053-9021-9.
Stewart, James (2009). Calculus: Concepts and Contexts. Cengage Learning. pp. 960–967. ISBN 978-0-495-55742-5.
Stewart, James (2003). Calculus: Early Transcendental Functions (5th ed.). Brooks/Cole.
Tu, Loring W. (2011). An Introduction to Manifolds (2nd ed.). New York: Springer. ISBN 978-1-4419-7399-3.

외부 링크

위키미디어 커먼즈 스토크스 정리 관련 매체
"Stokes formula", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
발산정리증거와 스톡스의 정리증거
미적분 3 – Stokes Organization from lamar.edu – 설명서
"Stokes' Theorem on Manifolds". Aleph Zero. May 3, 2020. Archived from the original on 2021-12-11 – via YouTube.

[cgamma-10] $γ$ 과 $γ$ 은 둘 다 루프지만, $γ$ 이 반드시 요르단 곡선인 것은 아니다.

[14] 수학자들에게는 이 사실이 알려져 있기 때문에 원은 중복되고 종종 생략된다.그러나 여기서 명심해야 할 것은 $\oint{W dU total}$ 라는 표현이 자주 나타나는 열역학에서(아래 전체 파생상품에서 참조) 통합 경로 $W$ 는 훨씬 더 높은 차원 다지관의 1차원 폐쇄선이다.즉, 열역학 애플리케이션에서 $U$ 는 온도 $α 1 :=$ $T$ , 부피 $α 2 :=$ $V$ , 그리고 샘플의 전기적 양극화 $α 3$ := $P$ 의 함수인 경우, 1은 다음과 같다. ${\디스플레이 스타일 \{d_{\text{total}}U\}=\sum _{i=1}^{3}{\frac {\partial U}{\partial \alpha _{i}\,d\alpha _{i}\}}$ 그리고 원은 정말로 필요하다. 예를 들어, 통합 가정에서의 차등적인 결과를 고려하는 경우. $\point _{W}\,\{d_{\text{total}}}U\}\, {\stackrel {!}{=}}\,0\,.$

[1] Physics of Collisional Plasmas – Introduction to Michel Moisan Springer.

[2] "2019년 11월 포트폴리오, ASIN: B07P1NNTSD" 그레고리 주커먼 "시장을 해결한 남자"

[3] Cartan, Élie (1945). Les Systèmes Différentiels Extérieurs et leurs Applications Géométriques. Paris: Hermann.

[4] Katz, Victor J. (1979-01-01). "The History of Stokes' Theorem". Mathematics Magazine. 52 (3): 146–156. doi:10.2307/2690275. JSTOR 2690275.

[5] Katz, Victor J. (1999). "5. Differential Forms". In James, I. M. (ed.). History of Topology. Amsterdam: Elsevier. pp. 111–122. ISBN 9780444823755.

[6] 참조:
Katz, Victor J. (May 1979). "The history of Stokes' theorem". Mathematics Magazine. 52 (3): 146–156. doi:10.1080/0025570x.1979.11976770.

Thomson이 Stokes에게 보낸 편지는 다음과 같다.

톰슨도 스토크스도 그 정리에 대한 증거를 발표하지 않았다.1861년에 발표된 첫 번째 증거는: 한클은 정리의 저자를 언급하지 않는다.

각주에서 라모어는 벡터장의 컬을 표면 위에 통합시킨 초기 연구자들에 대해 언급한다.참조:

[9] Katz, Victor J. (May 1979). "The history of Stokes' theorem". Mathematics Magazine. 52 (3): 146–156. doi:10.1080/0025570x.1979.11976770.

[10] Thomson이 Stokes에게 보낸 편지는 다음과 같다.

[11] 톰슨도 스토크스도 그 정리에 대한 증거를 발표하지 않았다.1861년에 발표된 첫 번째 증거는: 한클은 정리의 저자를 언급하지 않는다.

[12] 각주에서 라모어는 벡터장의 컬을 표면 위에 통합시킨 초기 연구자들에 대해 언급한다.참조:

[7] Darrigol, Olivier (2000). Electrodynamics from Ampère to Einstein. Oxford, England. p. 146. ISBN 0198505930.

[spivak65-8] 스피박(1965), 페이지 7, 서문.

[9] 참조:
1854년 스미스상 수상 심사는 온라인: 점원 맥스웰 재단에서 이용할 수 있다.맥스웰은 이 시험을 치르고 에드워드 존 루스와 함께 공동 1위에 올랐다.참조: 스미스의 상 또는 점원 맥스웰 재단을 참조하십시오.

Clerk Maxwell, James (1873). A Treatise on Electricity and Magnetism. Vol. 1. Oxford, England: Clarendon Press. pp. 25–27. 27페이지의 각주에서 맥스웰은 스톡스가 1854년 스미스상시험에서 8번 문항으로 정리를 사용했다고 언급한다.이 각주는 정리가 "스톡스의 정리"로 알려지게 된 원인이었던 것으로 보인다.

[16] 1854년 스미스상 수상 심사는 온라인: 점원 맥스웰 재단에서 이용할 수 있다.맥스웰은 이 시험을 치르고 에드워드 존 루스와 함께 공동 1위에 올랐다.참조: 스미스의 상 또는 점원 맥스웰 재단을 참조하십시오.

[17] Clerk Maxwell, James (1873). A Treatise on Electricity and Magnetism. Vol. 1. Oxford, England: Clarendon Press. pp. 25–27. 27페이지의 각주에서 맥스웰은 스톡스가 1854년 스미스상시험에서 8번 문항으로 정리를 사용했다고 언급한다.이 각주는 정리가 "스톡스의 정리"로 알려지게 된 원인이었던 것으로 보인다.

[Jame-11] Stewart, James (2010). Essential Calculus: Early Transcendentals. Cole.

[bath-12] 이 증거는 교수님이 주신 강의 노트에 근거한 것이다.Robert Scheichl(영국 배스 대학교 [1]), [2]를 참조하십시오.

[proofwik-13] "This proof is also same to the proof shown in".

[15] Renteln, Paul (2014). Manifolds, Tensors, and Forms. Cambridge, UK: Cambridge University Press. pp. 158–175. ISBN 9781107324893.

[16] Lee, John M. (2013). Introduction to Smooth Manifolds. New York: Springer. p. 481. ISBN 9781441999818.

[17] 휘트니, 기하학적 통합 이론 III.14

[18] Harrison, J. (October 1993). "Stokes' theorem for nonsmooth chains". Bulletin of the American Mathematical Society. New Series. 29 (2): 235–243. arXiv:math/9310231. Bibcode:1993math.....10231H. doi:10.1090/S0273-0979-1993-00429-4. S2CID 17436511.

[19] Jackson, J. D. (1975). Classical Electrodynamics (2nd ed.). New York, NY: Wiley.

[20] Born, M.; Wolf, E. (1980). Principles of Optics (6th ed.). Cambridge, England: Cambridge University Press.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[note 1]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

v t 미적분학.
프레살쿨루스	이항 정리 오목함수 연속함수 요인 유한차이 자유 변수 및 경계 변수 함수의 그래프 선형함수 라디안 롤의 정리 세컨트 경사 접선
한계	불확정형 함수의 한계 단측한도 수열의 한계 근사순번 (ε, Δ)-한계의 정의
미분학	파생상품 미분 미분방정식 미분 연산자 평균값 정리 표기법 라이프니츠의 표기법 뉴턴의 표기법 차별화 규칙 직선성 힘 합계 체인 L'Hepital's girls 제품 라이프니츠 장군의 통치 지수 기타 기법 암묵적 분화 역함수와 분화 로그파생상품 관련금리 정지점 제1차 파생상품시험 2차파생성시험 극값정리 맥시마와 미니마 추가 애플리케이션 뉴턴의 방법 테일러의 정리
적분 미적분학	해독제 호 길이 기본 속성 집적 상수 미적분학의 기본 정리 통합 기호 아래 차별화 부품별 통합 대체에 의한 통합 삼각 측량 오일러 위어스트라스 적분 부분분수 2차 적분 사다리꼴 법칙 볼륨 와셔법 셸 방식
벡터 미적분학	파생상품 컬 방향파생상품 발산 그라데이션 라플라시안 기본 정리 라인 통합 그린스 스톡스 가우스
다변량 미적분학	발산정리 기하학 헤시안 행렬 야코비안 행렬과 결정인자 라그랑주 승수 라인 적분 매트릭스 다중 적분 부분파생상품 표면 적분 부피 적분 고급 주제 미분형식 외부파생상품 일반화 스톡스의 정리 텐서 미적분학
시퀀스 및 시리즈	산술-기하 시퀀스 계열의 종류 교대로 이항체 푸리에 기하학 조화 무한 힘 마클로린 테일러 텔레스코핑 수렴 시험 아벨의 교대계열 코시 응결 직접 비교 디리클레트 적분 한계비교 비율 뿌리 용어
특수 기능 와 숫자	베르누이 수 e (계속 상수) 지수함수 자연 로그 스털링의 근사치
미적분학의 역사	적정성 브룩 테일러 콜린 매클라우린 대수 일반성 고트프리트 빌헬름 라이프니즈 최소값 소수점 미적분학 아이작 뉴턴 플럭시온 연속성의 법칙 레온하르트 오일러 플럭션의 방법 기계식 이론의 방법
목록	차별화 규칙 지수함수의 통합 목록 쌍곡선 함수의 통합 목록 역 쌍곡선 함수의 통합 목록 역삼각계 함수의 통합 목록 비합리적인 기능의 통합 목록 로그 함수의 통합 목록 합리적인 기능의 통합 목록 삼각함수의 통합 목록 세컨트 큐방트 한계 목록 통합 목록
기타 항목	미분 기하학 곡면성 곡선의 표면의 오일러-마클라우린 공식 가브리엘 혼 통합 비 22/7이 π을 초과한다는 증거 레지오몬타누스의 각도 최대화 문제 스타인메츠 고체

Search