단꼬리 및 양꼬리 테스트

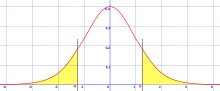
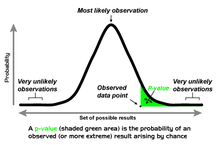
통계적 유의성 검정에서, 한쪽 꼬리 검정과 양쪽 꼬리 검사는 검정 통계량의 관점에서 데이터 집합에서 추론된 모수의 통계적 유의성을 계산하는 대체 방법입니다.예를 들어, 테스트 응시자가 특정 점수 범위를 초과하거나 밑돌 수 있는지 여부와 같이 추정 값이 특정 범위의 값보다 크거나 작을 경우 양 꼬리 테스트가 적합합니다.이 방법은 귀무 가설 검정에 사용되며 추정치가 임계 영역에 있으면 귀무 가설에 대해 대립 가설이 허용됩니다.추정된 값이 기준 값에서 왼쪽 또는 오른쪽 한 방향으로만 벗어날 수 있지만 둘 다 벗어날 수 없는 경우에는 한쪽 끝 검정이 적합합니다.예를 들어, 기계가 불량 제품을 1% 이상 생산하는지 여부를 들 수 있습니다.이 경우 추정치가 관심의 방향(보다 크거나 작음)에 따라 단측 임계 영역 중 하나에 존재하는 경우 귀무 가설에 대해 대립 가설이 허용됩니다.대체 이름은 단측 및 양면 검정입니다. "꼬리"라는 용어가 사용되는 이유는 관측치가 귀무 가설을 기각하는 원인이 되는 분포의 극단 부분이 작고 오른쪽의 노란색 또는 녹색으로 표시된 "종 곡선"과 같이 정규 분포와 같이 0을 향해 "꼬리"되는 경우가 많기 때문입니다.

적용들

단일 꼬리 검정은 적합도를 측정하는 데 공통적인 카이 제곱 분포와 같이 꼬리가 하나뿐인 비대칭 분포 또는 위치를 추정하는 데 공통적인 정규 분포와 같이 꼬리가 두 개인 분포의 한 쪽에 사용됩니다. 이는 방향을 지정하는 것과 같습니다.두 개의 꼬리가 있는 검정은 정규 분포와 같이 두 개의 꼬리가 있는 경우에만 적용 가능하며 두 방향 중 하나를 ^[1][2]유의하다고 간주하는 데 해당합니다.

Ronald Fisher의 접근법에서, 검정 통계량의 p-값이 충분히 극단적이므로(검정 통계량의 표본 분포와 비교하여) 우연의 결과일 가능성이 낮다고 판단될 때 귀무 가설₀ H는 기각됩니다.이는 보통 파라미터의 통계적 유의성을 계산할 때 결과 p-값을 α$(\displaystyle \alpha$로 $표시$된 특정 유의 수준과 비교하여 수행됩니다.한쪽 꼬리 테스트에서 "극한"은 "충분히 작다" 또는 "충분히 크다"는 뜻으로 미리 결정되며, 다른 방향의 값은 유의하지 않은 것으로 간주됩니다.왼쪽 또는 오른쪽 꼬리 확률이 궁극적으로 검정 통계가 H에서 벗어나는_0.^[3] 방향에 해당하는 단꼬리 p-값이라고 보고할 수 있다. 양 꼬리 테스트에서 "극한"은 "충분히 작거나 충분히 크다"를 의미하며, 어느 방향의 값도 ^[4]유의한 것으로 간주한다.주어진 검정 통계량의 경우 두 개의 꼬리가 있는 단일 검정과 두 개의 꼬리가 있는 두 개의 검정이 있습니다. 각 검정은 각 방향에 대해 하나씩).유의 $(\displaystyle \alpha$를 지정하면, 임계 영역은 분포의 양끝에 존재하며, 양끝 테스트의 경우 각각${\displaystyle }$α /$$(\$displaystyle \alpha / 2$)의 면적이 됩니다.또는 임계 영역은 한쪽 꼬리 테스트의 경우 α$(\displaystyle \alpha)$의 면적을 가진 단일 꼬리 끝에만 존재할 것이다.테스트 통계의 양 꼬리 테스트에서 주어진 유의 수준에 대해, 동일한 테스트 통계량에 대한 해당 한쪽 꼬리 테스트는 데이터가 테스트에 의해 지정된 방향에 있는 경우 두 배(p-값의 절반)의 유의성 또는 데이터가 다음과 같은 경우 전혀 유의하지 않은 것으로 간주됩니다($\display style$ \alpha $）$$$。테스트에 의해 지정된 임계 영역의 반대 방향으로.

예를 들어 동전을 던질 경우 앞면이 앞면으로 치우쳐 있는지 여부를 검정하는 것은 단꼬리 검정이며, "모든 앞면"의 데이터를 얻는 것은 매우 중요한 것으로 간주되지만 "모든 뒷면"의 데이터를 얻는 것은 전혀 중요하지 않습니다(p = 1).반대로, 어느 방향으로 치우쳤는지 여부를 검정하는 것은 양 꼬리 검정이며, "모든 앞면" 또는 "모든 뒷면" 모두 매우 유의한 데이터로 간주됩니다.의학 테스트에서는 일반적으로 치료가 우연보다 더 나은 결과를 초래하는지 여부에 관심이 있으며, 따라서 한쪽 꼬리 테스트를 제안한다. 더 나쁜 결과는 과학 분야에서도 흥미롭다. 따라서 치료 결과가 다음과 같은 결과를 초래하는지 여부를 테스트하는 대신 양쪽 꼬리 테스트를 사용해야 한다.좋든 ^[5]나쁘든 우연과는 다르다.피셔는 전형적인 여성이 차를 시음하는 실험에서 자신의 능력이 우연과 다른지 아닌 두 종류의 차를 시음하는 데 있어 우연보다 나은지 여부를 테스트했고, 그래서 그는 한쪽 꼬리를 이용한 테스트를 했다.

동전 던지기 예시

동전 던지기에서 귀무 가설은 확률 0.5의 베르누이 시행의 연속이며, 앞면이 1이고 뒷면이 0인 랜덤 변수 X를 산출합니다. 공통 검정 통계량은 (앞면이 $0인{\displaystyle \stackrel{}{}}$) 표본 평균 X ${\displaystyle .}$ .$$. {$display$style {$X}}$ 동전이$$앞면이$$ 한쪽 꼬리로 치우쳐 있는지 여부를 테스트합니다.테스트가 사용됩니다.대부분의 헤드만 유효합니다.이 경우 샘플 평균이 1인 5개의 헤드(HHH)로 구성된 데이터 ${\displaystyle \mathrm{세트}}$에는${\displaystyle }$1/${\displaystyle \mathrm{32\; =\; 0}}$.03125${\displaystyle 0}$ 0$.$03({$디스플레이 스타일$ 1/$32=$0$.03125\약$0.03$$$})$의 $발생{\displaystyle \mathrm{}}$ 확률이 있으며, (2개의 결과로 5회 연속 플립)^5=1/32/32이다.이 값은 p $({표시 스타일$ p$\약$0.$03)$이며, 시험이 유의 $수준$인 α ${\displaystyle =\mathrm{}}$0.$({표시$ 스타일 $\alpha = 0.05)($컷오프 경계에 해당하는 유의 수준)에서 분석될 경우 유의할 것이다(귀무 가설에 대한 추정).그러나 동전이 앞면 또는 뒷면 중 어느 쪽으로 치우쳐 있는지 검정하는 경우에는 꼬리 두 개 검정이 사용되며 앞면 다섯 개 데이터 세트(표본 평균 1)는 꼬리 다섯 개 데이터 세트(표본 평균 0)만큼 극단적입니다.그 결과 p-값은 2${\displaystyle }$/ ${\displaystyle 32}$ ${\displaystyle =0.06250}$0.$({style$ 2$/32=0.0625\approx$0.$06})$이 되며, 시험이 유의 $수준$인 α ${\displaystyle =\mathrm{}}$0.$(\display$style \$alpha = 0$.05$\})$에서 분석될 경우 유의하지 않을 수 있다.

역사

p-값은 Karl^[6] Pearson이 Pearson의 카이 제곱 검정을 통해 도입했으며, P(원래 표기법)를 통계량이 주어진 수준 이상이 될 확률로 정의했습니다.이것은 한 쪽 끝의 정의이며 카이 제곱 분포는 양수 또는 0의 값만 가정하여 비대칭이며 위쪽 끝의 꼬리만 있습니다.이 값은 이론 분포와의 정확한 일치에 해당하는 0을 사용하여 데이터의 적합도를 측정합니다. 따라서 p-값은 적합치가 이렇게 나쁘거나 더 나쁠 가능성을 측정합니다.

한 쪽 꼬리와 두 쪽 꼬리의 구별은 Ronald Fisher가 영향력 있는 책인 Statistical Methods for Research ^[7]Workers에서 널리 알려졌으며, 그는 특히 두 개의 꼬리가 같은 대칭 분포인 정규 분포에 그것을 적용했다.정규 분포는 적합도가 아닌 일반적인 위치 측도이며, 이론적인 위치(예: 이론적인 평균과 비교한 표본 평균) 위에 있거나 아래에 있는 위치의 추정치에 해당하는 두 개의 꼬리가 있습니다.정규 분포와 같은 대칭 분포의 경우 한 쪽 끝 p-값은 ^[7]두 쪽 끝 p-값의 정확히 절반입니다.

경우에 따라서는 양수로 알려진 편차가 관측치를 초과할 확률을 알고 싶은 반면, 필요한 확률은 양수와 음수가 동일한 편차가 관측치를 초과할 확률로 인해 일부 혼동이 발생할 수 있다. 후자의 확률항상 전자의 절반입니다.

--

피셔는 그의 실험 설계(^[8]1935년)에서 단순히 특정 결과의 확률보다는 꼬리 측정의 중요성, 즉 테스트 통계량의 관측값과 더욱 극단적인 값을 강조했다.그는 이를 귀무 가설에서 특정 데이터 집합이 발생할 가능성은 낮지만 더 극단적인 결과가 나타날 가능성이 높기 때문이라고 설명합니다. 따라서 이러한 관점에서 볼 때, 특정 데이터 집합은 유의하지 않은 것으로 간주해야 합니다.

특정 테스트

검정 통계량이 귀무 가설에서 학생의 t-분포를 따르는 경우(기본 변수가 스케일링 요인을 알 수 없는 정규 분포를 따르는 경우) 검정을 단꼬리 또는 양꼬리 t-검정이라고 합니다.표본의 추정치가 아닌 실제 모집단 평균과 분산을 사용하여 검정을 수행하는 경우 이를 단꼬리 또는 양꼬리 Z 검정이라고 합니다.

t 및 Z에 대한 통계 표는 단꼬리 검정과 양꼬리 검정 모두에 대한 임계 값을 제공합니다.즉, 샘플링 분포의 한쪽 또는 다른 쪽 끝에서 영역 전체를 잘라내는 임계값과 샘플링 분포의 양쪽 끝에서 영역(크기의 절반)을 잘라내는 임계값을 제공합니다.

「 」를 참조해 주세요.

• 쌍체 차이 검정(두 표본을 비교하는 경우)

레퍼런스