왜도

확률 이론과 통계학에서 왜도는 평균에 대한 실수값 랜덤 변수의 확률 분포의 비대칭성에 대한 측도입니다.왜도 값은 양수, 0, 음수 또는 정의되지 않은 값입니다.

단일 분포의 경우 일반적으로 음의 스큐는 꼬리가 분포의 왼쪽에 있음을 나타내고 양의 스큐는 꼬리가 오른쪽에 있음을 나타냅니다.한쪽 꼬리가 길고 다른 쪽 꼬리가 뚱뚱한 경우, 왜도는 단순한 규칙을 따르지 않습니다.예를 들어, 값이 0이면 평균 양쪽의 꼬리가 전체적으로 균형을 유지한다는 의미입니다. 대칭 분포의 경우이지만 한쪽 꼬리가 길고 가늘고 다른 한쪽 꼬리가 짧지만 뚱뚱한 비대칭 분포의 경우에도 해당될 수 있습니다.

서론

아래 그림의 두 가지 분포를 고려합니다.각 그래프에서 분포의 오른쪽에 있는 값은 왼쪽에 있는 값과 다르게 테이퍼됩니다.이러한 테이퍼 변을 테일이라고 하며, 분포에 다음 두 가지 종류의 왜도가 있는지 확인할 수 있는 시각적 수단을 제공합니다.

1. 음의 스큐:왼쪽 꼬리가 더 길어 분포의 질량이 그림의 오른쪽에 집중됩니다.분포는 곡선 자체가 치우치거나 오른쪽으로 기울어진 것처럼 보이지만 왼쪽으로 치우치거나 왼쪽으로 치우친다고 합니다. 대신 왼쪽 꼬리가 그려지고 종종 데이터의 일반적인 중앙에서 왼쪽으로 평균이 치우치는 것을 의미합니다.좌회전 분포는 일반적으로 우회전 ^[1]곡선으로 나타납니다.
2. 양의 스큐:오른쪽 꼬리가 더 길다. 분포의 질량은 그림의 왼쪽에 집중되어 있다.분포는 곡선 자체가 치우치거나 왼쪽으로 기울어진 것처럼 보이지만 오른쪽으로 치우치거나 오른쪽으로 치우친다고 합니다. 대신 오른쪽 꼬리가 그려지고 종종 평균이 데이터의 일반적인 중앙에서 오른쪽으로 치우치는 것을 의미합니다.오른쪽으로 기울어진 분포는 일반적으로 왼쪽 ^[1]곡선으로 나타납니다.

데이터 계열의 왜도는 그래픽뿐만 아니라 값을 단순 검사하여도 관찰될 수 있습니다.예를 들어, 값이 중앙값 50 주위에 균등하게 분포되어 있는 숫자 시퀀스(49, 50, 51)를 고려합니다.평균보다 훨씬 낮은 값(예: (40, 49, 50, 51)을 추가하여 이 시퀀스를 음의 치우침 분포로 변환할 수 있습니다.따라서 수열의 평균은 47.5가 되고 중위수는 49.5가 됩니다.($μ$- ${\displaystyle )}$) / ${\displaystyle ,}$、 { $displaystyle$( \$mu$- \ nu ) / \ $sigma$ 로$$ 정의된 비모수 스큐 공식에 따르면 스큐는 음수입니다.마찬가지로 평균보다 훨씬 높은 값(49, 50, 51, 60)을 추가하여 시퀀스가 양의 특이치(예: 평균은 52.5이고 중위수는 50.5)로 치우치게 할 수 있습니다.

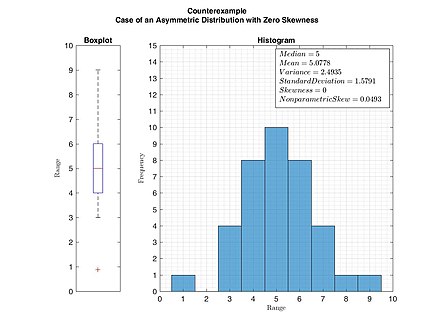
앞에서 설명한 바와 같이 왜도 값이 0인 단일 분포가 반드시 대칭인 것은 아닙니다.그러나 대칭 단일 모형 또는 다중 모형 분포의 왜도는 항상 0입니다.

평균과 중위수의 관계

치우침은 평균과 중위수 사이의 관계와 직접 관련이 없습니다. 음수 치우침이 있는 분포는 평균이 중위수보다 크거나 작을 수 있으며 양의 ^[2]치우침도 마찬가지입니다.

(${\displaystyle \mu }$- ${\displaystyle )}$) / ${\displaystyle ,}$( 、 { $displaystyle$ ( \$mu - nu$ ) / \ sigma ,$$$}$ ( μ { $displaystyle$$\$ $mu }$는 평균,$$$\mu {\displaystyle }$ { $displaystyle$\$nu$}는$$ 중위수, $（$ \ $displaystyle \sigma }$는 표준편차)로 정의되어 있는 $오래된{\displaystyle }$ 개념으로 정의되어 있습니다.n모수 스큐는 평균이 중위수보다 크다는 의미이고(오른쪽) 음수/왼쪽 비모수 스큐는 평균이 중위수보다 작다는 의미입니다(왼쪽).그러나 왜도의 현대적 정의와 전통적인 비모수적 정의가 항상 같은 부호를 갖는 것은 아닙니다. 분포의 일부 패밀리에는 일치하지만 일부 경우에는 서로 다르며, 이러한 부호를 결합하는 것은 오해를 유발할 수 있습니다.

분포가 대칭이면 평균은 중위수와 같고 분포의 ^[3]왜도는 0입니다.분포가 대칭 분포인 동시에 단일 분포인 경우 평균 = 중위수 = 모드입니다.동전 던지기나 시리즈 1,2,3,4,...그러나 그 반대가 일반적으로 참이 아니라는 점에 유의하십시오. 즉, 0 왜도(아래 정의)가 평균이 중위수와 같다는 의미는 아닙니다.

2005년 저널 기사에 ^[2]따르면 다음과 같습니다.

많은 교과서에서는 평균이 오른쪽 치우침 아래 중위수의 오른쪽이고 왼쪽 치우침 아래 중위수의 왼쪽이라는 경험 규칙을 설명합니다.이 규칙은 놀라울 정도로 빈번하게 실패한다.멀티모달 분포 또는 한쪽 꼬리가 길고 다른 쪽 꼬리가 무거운 분포에서 실패할 수 있습니다.그러나 중앙값의 왼쪽과 오른쪽 면적이 같지 않은 이산 분포에서는 규칙이 실패합니다.이러한 분포는 평균, 중위수 및 스큐 사이의 교과서적 관계와 모순될 뿐만 아니라 중위수에 대한 교과서적 해석과도 모순됩니다.

예를 들어 미국 전체 가구의 성인 거주자 분포에서 스큐는 오른쪽으로 치우쳐 있다.그러나 대부분의 경우 중위수인 모드보다 작거나 같기 때문에 평균은 더 무거운 왼쪽 꼬리에 위치합니다.그 결과, 평균이 오른쪽 치우침에서 중위수의 오른쪽이라는 경험칙이 실패했습니다.^[2]

정의.

피셔 모멘트 왜도 계수

랜덤 변수 X의 왜도는 세 번째 ${\displaystyle {표준화}_{}}$된 $모멘트\mu {\displaystyle {\stackrel{}{}}_{}}$~ 3$($ 스타일 {\$tilde {mu$}}$_{3$으로 다음과 ^[4][5]같이 정의됩니다.

${\displaystyle {\tilde {mu } =\operatorname {E} \left [\frac {X-\frac } {\fright } {\frac } {\frac } {{3}} =frac {\operatorname {E} \[3}$

여기서 μ는 평균, μ는 표준 편차, E는 기대 연산자₃, μ는 세 번째 중심 모멘트, μ는_t t번째 누적량이다.이 값을 Pearson의 ^[5]왜도 모멘트 계수 또는 단순 ^[4]왜도 모멘트 계수라고 부르기도 하지만 Pearson의 다른 왜도 통계량과 혼동해서는 안 됩니다(아래 참조).마지막 등식은 세 번째 적분률 θ와₃ 두 번째 적분률 θ의₂ 1.5제곱의 비율로 왜도를 나타냅니다.이것은 첨도를 두 번째 적분의 제곱에 의해 정규화된 네 번째 적분으로 정의하는 것과 유사하다.스큐[X]라고 하는 경우도 있습니다.

θ가 유한하면 μ도 유한하며, 왜도는 앞의 공식을 확장함으로써 비중심 모멘트 E[X³]의 관점에서 표현될 수 있다.

${\displaystyle {\tilde {\mu }}_{3}&=\operatorname {E} \left[\left\frac {X-\mu} {\display }} {\right} {{3}\right] \\&=frac {E} [X^{3}]-3\mu \operatorname {E}[X^{2}]+3\mu ^{2}\operatorname {E}-\mu ^{3}}-\fracer {E}\fracername {E}\end { aligned}}$

예

왜도는 다음과 같이 무한할 수 있습니다.

$\displaystyle \Pr \left [X>x\right]=x^{-2}{\mbox{}x>1,\Pr[X<1]=0}$

세 번째 적층체가 무한하거나, 또는 언제처럼

$\displaystyle \Pr[X]=(1-x)^{-3}/2{(음수 }}x4mbox{ 및 }}\Pr[X>x]=(1+x)^{-3}/2{\mbox{(양수 }}x}}}.$

여기서 세 번째 누적량은 정의되지 않습니다.

왜도가 유한한 분포의 예는 다음과 같습니다.

• 제3의 모멘트가 유한한 정규 분포와 다른 대칭 분포의 왜도는 0입니다.
• 반정규 분포의 왜도는 1 바로 아래입니다.
• 지수 분포의 왜도는 2입니다.
• 대수 정규 분포는 모수에 따라 모든 양의 값의 왜도를 가질 수 있습니다.

왜도의 예시

n개 값의 표본에 대해 모집단 왜도의^[6] 두 자연 추정기는 다음과 같습니다.

${\displaystyle b_{1}=black {m_{3}}{s^{3}}=black {\tfrac {1}{n}}\sum _{i=1}^{n}(x_i}-{\overline {x})^3}{\left[{\tfrac {1}{n-1}{n}{{{n}}}}{{n}}}}{{{\sum}}}}}{{{\sum}}}}}}}{{{{{{{\sum}}}}}}$

그리고.

${\displaystyle g_{1}=subfrac {m_{3}{3/2}}=subfrac {\tfrac {1}{n}}\sum _{i=1}{n}(x_{i}-{\overline {x}){3}{\left[\tfrac {1}{n}{n}_sum}_sum_sum$

$여기$서 x$¯({displaystyle$ {$x})$는 표본 평균, s는 표본 표준 편차, m은₂ (바이어스된) 표본 두 번째 중심 모멘트, m은₃ 표본 세 번째 중심 ^[6]모멘트입니다. ${\displaystyle {g\mathrm{}}_{}}$ 1 ${\$은 모멘트 추정기입니다.

샘플^[6][7] 왜도의 또 다른 일반적인 정의는 다음과 같습니다.

$디스플레이 스타일G_{1}&=snfrac {k_{3}}{k_{2}^3/2}}=snfrac {n^{2}}{(n-1)}}\;b_{1}=snfrac {n-2}}}{nfrac {n-1}}}}}{nfrac {n-2}}\g_{1}}{nfrac {n-1}}}}}{nfrac {n-1}}}}}}}}{nfrac {nfrac {n-1}}}}}}}}}}}}}}\g_{nfrac$

${\displaystyle {여기}_{}}$서 k 3$({$은 세 번째 누적액의 고유한 대칭 불편 추정치이고 ${\displaystyle {k\mathrm{}}_{}}$ 2$=$ ${\displaystyle {}^{}}$ ${\displaystyle {2\mathrm{}}^{}}$({$displaystyle k_{2$}=$s^{2}})$는 두 번째 누적액의 대칭 불편 추정치(예: 표본 분산)이다.수정된 Fisher-Pearson 표준화 모멘트 $계수{\displaystyle {}_{}}$ ${\displaystyle {G\mathrm{}}_{}}$ 1$(\$은 Excel과 Minitab, SAS 및 SPSS를 ^[7]포함한 여러 통계 패키지에 있는 버전입니다.

기본 랜덤 $변수{\displaystyle }$ X$({displaystyle$X})가 정규 분포를 따른다고 가정할 때, ${\displaystyle {3가지\mathrm{}}_{}}$ ${\displaystyle {비율\mathrm{}}_{}}$ b$$1({$displaystyle b_$$1$$}),$ g 1({$displaystyle$ g_$$${$1}),$$ 1({$displaystyle G_${1$})$ $모두$ 치우침이 없고 모집단 왜도 ${\displaystyle {}_{}}$ ${\displaystyle 0}$의 일관된 추정치이다.$$$n{\displaystyle \sqrt{}}$ ${\displaystyle b{}_{}}$ ${\displaystyle {1\mathrm{}}_{}}$ ${\displaystyle {}_{}\stackrel{}{}}$ ${\displaystyle \stackrel{}{}}$$$N (${\displaystyle 0}$$$, ${\displaystyle 6}$)$${ $display$ style \ $display$ style \ $display style$→ $dN$( \ x $rightarrow${ $d } N ( 0$ ,$6$ )$$$。$즉, 분포는 평균 0과 6의 정규 분포로 수렴됩니다(Fisher , 1930).^[6]따라서 샘플 왜도의 분산은 충분히 큰 샘플의 경우 약 $(\displaystyle$ 6$/n)$입니다.좀 더 정확히는 정규 ^[8][9]분포에서 크기가 n인 랜덤 표본에서

${\displaystyle \operatorname {var}(G_{1})=snfrac {6n(n-1)}{(n-2)(n+1)(n+3)}}.}$

일반 샘플의 경우 ${\displaystyle {b\mathrm{}}_{}}$1(\$displaystyle b_{$1$$})은 3개의 추정치 중 분산이 작습니다^[6].

$\displaystyle \operatorname {var}(b_{1}) <\operatorname {var}(g_{1}) <\operatorname {var}(G_{1}).}$

비정규 분포의 경우 $(\$ $(\$$})$ $및{\displaystyle {}_{}}$ $(\$은 일반적으로 모집단 왜도 ${\displaystyle {1\mathrm{}}_{}}$1(\$displaystyle \gamma$ _${1$의 편향된 추정치이며, 기대치는 실제 왜도와 반대 부호를 가질 수도 있습니다.예를 들어 무게가 0.01, 0.66, 0.33인 매우 얇은 Gaussians로 구성된 혼합 분포는 약 -9.77의 $(\$ \$gamma _{$1$$})이지만 $(\$})의$$ 샘플에서는 보통 약 3개의 값이 모두 032입니다.분포의 ive 값 부분(반대 방향으로 치우쳐 있음)

적용들

왜도는 히스토그램 및 정규 분위수도와 함께 데이터 또는 분포를 특성화하는 데 사용할 수 있는 기술 통계량입니다.

왜도는 정규 분포에서 편차의 방향과 상대적 크기를 나타냅니다.

현저한 왜도의 경우, 평균에 대한 신뢰 구간과 같은 표준 통계 추론 절차는 실제 적용 범위가 공칭 수준(예: 95%)과 다르다는 점에서 부정확할 뿐만 아니라, 양쪽에서 동일한 오차 확률로 귀결된다.

왜도를 사용하여 Cornish-Fisher 확장을 통해 분포의 대략적인 확률과 수량(금융 리스크 값 등)을 얻을 수 있습니다.

많은 모형은 정규 분포를 가정합니다. 즉, 데이터는 평균에 대해 대칭입니다.정규 분포의 왜도는 0입니다.그러나 실제로는 데이터 점이 완벽하게 대칭적이지 않을 수 있습니다.따라서 데이터 집합의 왜도를 이해하면 평균으로부터의 편차가 양수인지 음수인지를 알 수 있습니다.

D'Agostino의 K-제곱 검정은 표본 왜도와 표본 첨도를 기반으로 하는 적합도 정규성 검정입니다.

왜도의 기타 척도

Karl^[10] Pearson이 제안한 간단한 계산을 포함하여 왜도의 다른 측도가 사용되었습니다(Pearson의 모멘트 왜도 계수와 혼동하지 말고 위 참조).기타 척도는 다음과 같습니다.

Pearson의 첫 번째 왜도 계수(모드 왜도)

Pearson 모드 왜도 ^[11]또는 첫 번째 왜도 계수는 다음과 같이 정의됩니다.

.mw-parser-output .sfrac{white-space:nowrap}.mw-parser-output.sfrac.tion,.mw-parser-output.sfrac .tion{디스플레이:inline-block, vertical-align:-0.5em, font-size:85%;text-align:센터}.mw-parser-output.sfrac.num,.mw-parser-output.sfrac .den{디스플레이:블록, line-height:1em, 마진:00.1em}.mw-parser-output.sfrac .den{border-top:1px 고체}.mw-parser-out..sr-only{국경:0;클립:rect(0,0,0,0), 높이:1px, 마진:-1px, 오버 플로: 숨어 있었다. 패딩:0;위치:절대, 너비:1px}mean−mode/standard 편차다.

Pearson의 두 번째 왜도 계수(중간수 왜도)

Pearson 중위수 왜도 또는 두 번째 왜도 ^[12][13]계수는 다음과 같이 정의됩니다.

3(평균 - 중위수)/표준 편차입니다.

비모수 스큐의 단순한 배수입니다.

왜도는 모드, 평균 및 중위수 사이의 순서 관계와 관련이 없으므로 이러한 계수의 부호는 왜도의 유형(왼쪽/오른쪽)에 대한 정보를 제공하지 않습니다.

정량적 기준 측정

Bowley의 왜도 측정(^[14][15]1901년부터)는 Yule's 계수(^[16][17]1912년부터)라고도 불리며 다음과 같이 정의된다.

${{displaystyle {{\frac {{Q}(3/4)}+{Q}(1/4)}{2}}-{Q}(1/2)}}}{\frac {{Q}(3/4)}-{Q}}={frac {Q}(3/4)}{Q}{Q}{4}{Q}}{4}{{Q}}}}{{4}}}}$

여기서 Q는 분위수 함수(즉, 누적 분포 함수의 역함수)입니다.분자는 상위 사분위수 및 하위 사분위수 평균(위치 측도)과 중위수(위치 측도) 사이의 차이이며, 분모는 반사분위수 범위$)$ -$Q$($1$/4$)$/$({display$ style$(Q}(3/4)})}$ - {{$Q}/2$이며, 이는 대칭 분포입니다.분산의 방산

이 측정의 다른 이름으로는 골튼의 ^[18]왜도 측정, Yule-Kendall 지수^[19] 및 사분위 왜도 ^[20]측정이 있다.

마찬가지로 켈리의 왜도 측정은 다음과 같이 정의된다^[21].

${\displaystyle {{Q}(9/10)+{Q}(1/10)}-2{Q}(1/2)}}{{Q}(9/10)}-{Q}}}.}$

왜도 함수의 보다 일반적인 공식은 Groeneveld, R. A. 및 Meeden, G.(1984)^[22][23][24]에 의해 설명되었다.

$\displaystyle \display (u) = flac {Q(u)+Q(1-u)-2Q(1/2)} {Q(u)-Q(1-u)}$

함수 ((u)는 -1 ≤(u) ≤ 1을 만족하며 ^[22]분포의 모멘트가 존재하지 않고 잘 정의되어 있다.Bowley의 왜도 측정은 u = 3/4에서 평가되며 Kelly의 왜도 측정은 u = 9/10에서 평가됩니다.이 정의는 1/2 µ u < 1 범위에 걸쳐 이것의 최상위로 정의되는 해당 전체 왜도의^[23] 측정으로 이어진다.또 다른 ^[22]척도는 이 식의 분자와 분모를 적분함으로써 얻을 수 있다.

계량형 기반 왜도 측도는 언뜻 해석하기 쉽지만 모멘트 기반 방법보다 표본 변동이 상당히 큰 경우가 많습니다.즉, 대칭 분포(균등 분포와 같은)의 표본이 우연히도 분위수 기반 왜도가 크다는 것을 의미합니다.

그로네벨트와 미덴의 계수

Groeneveld와 Meeden은 ^[22]왜도의 대안으로,

${\displaystyle \mathrm {nuw}(X)=snufrac {(\mu -\nu)}{E(X-\nu)}},$

여기서 μ는 평균, μ는 중위수, ...는 절대값, E()는 기대 연산자입니다.이 값은 형식적으로 Pearson의 두 번째 왜도 계수와 밀접한 관련이 있습니다.

L-모멘트

모멘트 대신 L-모멘트를 사용하면 ^[25]L-스위니스라고 불리는 왜도를 측정할 수 있습니다.

거리 왜도

왜도 값이 0이라고 해서 확률 분포가 대칭인 것은 아닙니다.따라서 이러한 특성을 가진 비대칭성의 또 다른 측정이 필요하다. 즉,^[26] 그러한 측정이 2000년에 도입되었다.이것은 거리 왜도라고 불리며 dSkew로 나타납니다.만약 X가 d차원 유클리드 공간에서의 값을 취하는 랜덤 변수이고, X'는 유한한 기대치를 가지며, X$'$는 X의 독립적 등분포 복사이며,$θ$는 유클리드 공간에서의 노름을 나타내며, θ에$$ 대한 위치 비대칭성의 간단한 척도는 다음과 같다.

${\displaystyle \operatorname {dSkew}(X):=1-{\frac{operatorname {E}\X-X'\}{\operatorname {E}\X+X'-2\theta \}}{\text{ if }\Pr(X=\ta\ta\q} ne}1 ne}$

및 dSkew(X) : = 0(확률 1일 경우).거리왜곡은 항상 0과 1 사이이며 X가 θ에 대해 대각대칭인 경우(X와 2'-X의 확률분포가 동일), X가 확률이 ^[27]1인 상수 c( ${\displaystyle c}$ $≠$ {\ \ $display style$ c$\neq \theta$인 경우에만 1이 됩니다.따라서 표본 거리왜곡에 기초한 대각 대칭의 단순하고 일관된 통계 테스트가 있습니다.

$\displaystyle \operatorname {dSkew}_{n}(X):=1-{\frac {sum _{i,j}-x_{j}\}{\sum _{i,j}\x_{i}+x_{j}-2\theta \}}.}$

메드커플

중간 쌍은 왜도의 척도 불변 로버스트 측도로,^[28] 파손점은 25%입니다.커널 함수 값의 중앙값입니다.

${\displaystyle h(x_{i},x_{j})=paramfrac {(x_{i}-x_{m}-(x_{j})}{x_{i}-x_{j}}}}}$

모든 커플$({\displaystyle {xi}_{}}$ ${\displaystyle {xj}_{}}$$)$ {$displaystyle$${\displaystyle {}_{}{}_{}}$${i$}, ${\displaystyle {x\_}_{}}$${j})$을 인계합니다.${\displaystyle {여기}_{}}$서 x$$${\displaystyle {}_{}}$$${$displaystyle$ $x_{$$i}\geq x_{$$j$$\}$는${\displaystyle {x\mathrm{}}_{}}$ 1,${\displaystyle {}_{}}$x$2$의 ${\displaystyle {중앙값}_{}}$입니다$.$가능한 모든 백분위수 왜도 측정의 중앙값으로 사용합니다.

「 」를 참조해 주세요.

• 브래그 피크
• 코스쿠네스
• 쿠르토시스
• 형상 매개변수
• 왜곡 정규 분포
• 왜도 위험

레퍼런스

인용문

원천

외부 링크

• "Asymmetry coefficient", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
• 미셸 쁘띠장의 다변량 분포 비대칭 계수
• Kim과 White의 보다 견고한 왜도 추정 및 왜도 추정기의 첨도 비교.
• 클로즈드 스큐 분포 - 시뮬레이션, 반전 및 파라미터 추정