구조방정식 모델링

Structural equation modeling
이 글은 일반적인 구조 모델링에 관한 것입니다.계량경제학에서 구조 모형을 사용하는 방법은 구조 추정을 참조하십시오.저널에 대해서는 Structural Equation Modeling(저널)을 참조하십시오.
An example structural equation model
그림 1.추정 후 구조 방정식 모형의 예시.잠재변수는 타원형으로 표시되기도 하고 관측변수는 직사각형으로 표시되기도 합니다.잔차와 분산은 때때로 쌍두 화살표(여기에 표시됨) 또는 단일 화살표와 원(그림 2에서와 같이)으로 그려집니다.잠재 IQ 분산은 모형에 척도를 제공하기 위해 1로 고정됩니다.그림 1은 잠재 지능의 각 지표와 잠재 성취의 각 지표에 영향을 미치는 측정 오류를 보여줍니다.지표의 측정 오차나 지표의 측정 오차 [1]모두 잠재 변수에 영향을 미치는 것으로 모델링되지 않습니다.
An example structural equation model pre-estimation
그림 2.추정 전 구조 방정식 모형의 예제입니다.그림 1과 유사하지만 표준화된 값과 적은 항목이 없습니다.지능과 학업 성취도는 단지 상상된 변수이거나 이론에 근거한 변수이기 때문에, 그들의 정확한 척도 값은 알 수 없지만, 모델은 각 잠재 변수의 값이 지표 중 하나가 가지고 있는 관측 가능한 척도를 따라 어딘가에 있어야 한다고 명시합니다.잠재변수와 지표를 연결하는 1.0 효과는 잠재변수 값의 각 실제 단위 증감이 해당하는 단위 증감으로 이어진다는 것을 나타냅니다.각 잠재량에 대해 양호한 지표가 선택되었으면 좋겠지만, 이 모델은 또한 관측된 지표 측정에 원인적으로 영향을 미치는 다른 불특정 개체가 있다고 가정하여 측정 오류를 발생시키기 때문에 1.0 값은 완벽한 측정을 의미하지 않습니다.이 모델은 별도의 측정 오류가 잠재 지능의 두 지표와 잠재 성취의 각 지표에 영향을 미친다고 가정합니다.학업 성적을 가리키는 라벨이 없는 화살표는 지능 이외의 것들도 학업 성적에 영향을 미칠 수 있음을 인정합니다.

SEM(Structural Equation Modeling)은 과학자들이 관측 및 실험 연구를 수행하는 다양한 방법 집합입니다.SEM은 주로 사회 및 행동 과학 분야에서 사용되지만 역학,[2] 비즈니스 [3]및 기타 분야에서도 사용됩니다.SEM의 정의는 기술 언어를 참조하지 않으면 어렵지만 좋은 출발점은 이름 자체입니다.

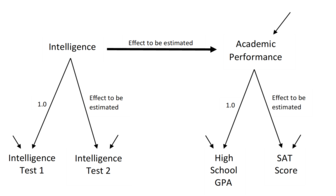
SEM은 어떤 현상의 다양한 측면이 서로 인과적으로 연결된다고 생각되는 방법을 나타내는 모델을 포함합니다.구조 방정식 모델은 종종 일부 잠재 변수(존재하는 것으로 생각되지만 직접 관찰할 수 없는 변수) 사이의 인과 관계 가정을 포함합니다.추가적인 인과관계 연결은 이러한 잠재변수를 데이터 집합에 값이 나타나는 관측변수와 연결합니다.인과적 연결은 방정식을 사용하여 표현되지만 가정된 구조는 그림 1 및 2와 같이 화살표를 포함하는 다이어그램을 사용하여 제시될 수도 있습니다.인과 구조는 관측 변수의 값 사이에 특정 패턴이 나타나야 함을 의미합니다.이를 통해 관측 변수 값 간의 연결을 사용하여 추정된 효과의 크기를 추정하고 관측 데이터가 가설된 인과 [4]구조의 요구 사항과 일치하는지 여부를 검정할 수 있습니다.

구조 방정식 모델의 존재와 존재하지 않는 것 사이의 경계는 항상 명확하지는 않지만 SE 모델은 종종 잠재 변수(존재하는 것으로 생각되지만 태도와 같이 직접 관찰할 수 없는 변수)의 집합 사이에서 가정된 인과 관계를 포함합니다.지능 또는 정신 질환) 및 일부 데이터 세트에서 값을 사용할 수 있고 관찰 가능한 변수에 가정된 잠재 변수를 연결하는 인과 관계.SEM 툴킷에서는 확인적 요인분석, 확인적 복합분석, 경로분석, 다중집단 모형화, 종단 모형화, par.를 포함한 잠재적 인과관계의 유형별 차이, 잠재적 변수를 측정하는 관측 변수별 차이, 통계적 추정 전략의 차이.최소 제곱 경로 모델링, 잠재 성장 모델링 및 계층적 또는 다단계 모델링.[5][6][7][8][9]

SEM 연구원은 컴퓨터 프로그램을 사용하여 모델링된 구조적 연결에 해당하는 계수의 강도와 부호를 추정합니다(예: 그림 1의 화살표에 연결된 숫자).그림 1과 같은 가정된 모델은 관측된 데이터 측정을 제어하는 세속적인 힘과 일치하지 않을 수 있기 때문에 프로그램은 모델 테스트와 진단 단서를 제공하여 모델과 관측된 데이터 사이에 어떤 지표 또는 어떤 모델 성분이 불일치를 초래할 수 있는지를 알려줍니다.SEM 방법에 대한 비판은 사용 가능한 모델 테스트의 무시, 모델 사양의 문제, 외적 타당성을 고려하지 않고 모델을 받아들이는 경향, 잠재적인 철학적 [10]편향을 암시합니다.

SEM의 큰 장점은 이러한 모든 측정과 테스트가 하나의 통계적 추정 절차에서 동시에 발생한다는 것입니다. 여기서 모든 모델 계수는 관측 변수의 모든 정보를 사용하여 계산됩니다.이는 연구자가 모형의 각 부분을 [11]별도로 계산하는 경우보다 추정치가 더 정확하다는 것을 의미합니다.

역사

구조 방정식 모델링(SEM)은 Sewall Wright가 관찰된 [12][13][14]변수들 사이에서 직접적이고 간접적인 효과를 생성하는 물리적이고 생리적인 메커니즘에 대한 탄탄한 이해를 바탕으로 회귀 스타일 방정식 세트에 대한 명시적인 인과 해석을 제공했을 때 상관 관계 및 회귀와 차별화하기 시작했습니다.방정식은 일반적인 회귀 방정식과 같이 추정되었지만 측정된 변수에 대한 실질적인 맥락은 단순한 예측이 아닌 명확한 인과 관계를 이해할 수 있게 했습니다.O. D. Duncan은 1975년[15] 저서에서 SEM을 사회과학에 소개했고 SEM은 컴퓨팅 능력의 증가가 실용적인 모델 추정을 허용한 1970년대 후반과 1980년대에 꽃을 피웠습니다.1987년에[6] Hayduk은 잠재변수를 가진 구조 방정식 모델링에 대한 최초의 책 길이 소개를 제공했고, 이것은 곧 Bollen의 대중적인 텍스트([16]1989)에 이어졌습니다.

심리학, 사회학, 경제학에서 다양하지만 수학적으로 관련된 모델링 접근법이 발달했습니다.초기 카울스 위원회는 컴퓨터 이전에 반복 솔루션 검색 기술이 제한되었기 때문에 최대 가능성 추정과 폐쇄형 대수 계산을 통해 운송 경제학과 최적 라우팅에서 쿠프만과 후드(1953) 알고리듬을 중심으로 동시 방정식 추정을 연구합니다.SEM의 현재 핵심은 이러한 두 가지 발전적 흐름(심리학의 요인 분석, 던컨을 통한 사회학의 경로 분석)의 융합으로 만들어졌습니다.교육[17][18][19] 테스트 서비스(Educational Testing Services)에서 개발된 여러 프로그램 중 하나인 LISREL은 잠재 변수(심리학자들이 요인 분석의 잠재 요인으로 알고 있음)를 (사회학자들이 라이트와 던컨으로부터 물려받은) 경로 분석 스타일 방정식에 포함시켰습니다.모델의 인자 구조 부분은 서로 다른 가정된 잠재 변수를 연결하는 효과의 측정 오차를 포함하여 반드시 오차가 없는 추정은 아니지만 측정 오차 조정을 허용했습니다.

요인 분석 및 경로 분석 전통의 역사적 수렴의 흔적은 모델의 측정 및 구조적 부분의 구별과 모델 테스트에 대한 지속적인 이견, 그리고 측정이 구조적 [20][21]추정보다 선행되어야 하는지 또는 동반되어야 하는지에 따라 지속됩니다.요인 분석을 데이터 감소 기법으로 보는 것은 시험을 강조하는 것인데, 이는 가정된 인과 관계를 시험하기 위한 경로 분석적 감사와 대비됩니다. 이는 시험 결과가 모델의 오규격을 나타낼 수 있습니다.요소 분석과 경로 분석 전통 사이의 마찰은 문헌과 SEMNET에서 계속 드러나고 있습니다. – 무료 목록은 앨라배마 대학교 목록 서비스의 지원을 받아 3,000명 이상의 등록자에게 SEM 게시물을 배포하는 무료 목록 서비스입니다.SEMNET 아카이브는 사용자가 지정한 주제에 대해 검색할 수 있으며, 이 위키백과 페이지에 대한 2023년 업데이트 중 많은 부분이 이전에 SEMNET에서 유용한 검토 및 코멘트를 위해 배포되었습니다.

Wright의 경로 분석은 Hermann Wold, Wold의 학생 Karl Jöreskog, Jöreskog의 학생 Claes Fornell에게 영향을 미쳤지만 SEM은 아마도 모델링 목표와 전형적인 데이터 구조의 근본적인 차이 때문에 미국 계량 경제학자들 사이에서 많은 추종자를 얻지 못했습니다.SEM의 경제 부문의 장기적인 분리는 깊은 수학적 및 통계적 연결이 남아 있지만 [22][23]절차적 및 용어적 차이로 이어졌습니다.SEM의 경제적 버전은 [4]내생성에 대한 SEMNET 논의에서 볼 수 있으며 모델링에 대한 경제적 접근 방식에 대한 DAG(directed 비순환 그래프)를 통해 유대 펄의 인과성 접근 방식으로 생성된 열에서 볼 수 있습니다.다양한 SEM 접근 방식을 비교하고 대조하는 논의는 가능하지만[24][25] 데이터 구조의 규율 차이와 경제 모델을 동기화하는 우려는 재결합을 가능하게 하지 않습니다.펄은[4] SEM을 선형 모델에서 비모수 모델로 확장하고 방정식에 대한 인과적 및 반사실적 해석을 제안했습니다.비모수 SEM은 효과의 선형성에 대한 [25]약속이나 오차항의 분포에 대한 가정 없이 총 효과, 직접 효과 및 간접 효과를 추정할 수 있습니다.

SEM 분석은 컴퓨터 프로그램이 복잡한 인과 구조를 추정하는 것을 가능하게 하기 때문에 사회 과학에서 인기가 있지만, 모델의 복잡성은 결과의 질에 상당한 변동성을 초래합니다.전부는 아니지만 일부 결과는 실험 설계,[citation needed] 통계적 통제, 표본 크기의 결과 및 기타 특성을 이해하는 "불편함" 없이 얻어집니다.


일반적인 단계 및 고려사항

많은 구조 방정식 모델의 구축 및 평가에는 다음과 같은 고려 사항이 적용됩니다.

모델 명세

모델을 구축하거나 지정하려면 다음 작업을 수행해야 합니다.

  • 사용할 변수 집합,
  • 그 변수들에 대해 알려진 것은
  • 변수들의 인과관계와 단절에 대해 추정되거나 가설화된 것.
  • 연구자가 모델링으로부터 배우려고 하는 것,
  • 그리고 변수들의 어떤 값들을 이용할 수 있을 것인가에 대한 경우(자녀?근로자?기업?국가?세포?사고?컬트(cults?

구조 방정식 모델은 인과적으로 동질적인 경우, 즉 동일한 세계적 인과 구조에 포함되어 있지만 원인에 대한 값이 다르므로 결과 변수에 대한 값이 다른 경우에 대해 작동하는 세계적 힘을 반영하려고 시도합니다.인과적 동질성은 사례 선택이나 다중 그룹 모델에서 사례를 분리함으로써 촉진될 수 있습니다.연구자가 다음을 지정하기 전에는 모델의 사양이 완성되지 않습니다.

  • 어떤 효과 및/또는 상관관계/공분산을 포함하고 추정해야 하는지,
  • 어떤 효과 및 기타 계수가 금지되거나 불필요하다고 추정되는지 여부,
  • 그리고 어떤 계수에 고정/불변 값이 주어질 것인가 (예를 들어 그림 2와 같이 잠재 변수에 대한 측정 척도를 제공하기 위해).

모형의 잠재 수준은 내생 변수와 외생 변수로 구성됩니다.내생성 잠재 변수는 적어도 하나의 다른 모형 변수로부터 효과를 받는 것으로 가정된 참-점수 변수입니다.각 내생 변수는 회귀식 방정식에서 종속 변수로 모형화됩니다.외생적 잠재변수는 하나 이상의 내생변수를 유발하는 것으로 가정된 배경변수로 회귀식 방정식의 예측변수와 같이 모델링됩니다.외생변수들 간의 인과관계는 명시적으로 모형화되지는 않지만 대개 외생변수들이 서로 자유롭게 상관관계가 있는 것으로 모형화함으로써 인정됩니다.모형에는 일부 변수에서 효과를 얻지만 다른 변수로 효과를 보내는 변수인 중간 변수가 포함될 수 있습니다.회귀 분석에서와 마찬가지로 각 내생 변수에는 사용할 수 없고 일반적으로 알려지지 않은 원인의 효과를 캡슐화하는 잔차 또는 오류 변수가 할당됩니다.외생적이든 내생적이든 각 잠재 변수는 해당 변수에 대한 사례의 참 점수를 포함하는 것으로 간주되며, 이러한 참 점수는 관측/보고된 지표 [26]변수 중 하나 이상에 유효/진성 변동을 인과적으로 기여합니다.

LISREL 프로그램은 다양한 모델 성분을 추적하기 위해 행렬 집합의 요소에 그리스 이름을 할당했습니다.이러한 이름들은 비교적 표준 표기법이 되었지만, 다양한 통계적 [19][6][16][27]고려 사항을 수용하기 위해 표기법이 확장되고 변경되었습니다.사용자가 선택한 변수 이름을 허용하는 방정식을 사용하거나 다이어그램을 통해 모델 사양을 "간소화"하는 텍스트 및 프로그램은 사용자의 모델을 배경에서 일부 표준 행렬-대수 형태로 다시 변환합니다."간소화"는 사용자가 신경 쓸 필요가 없을 것으로 추정되는 모델 기능에 대한 기본 프로그램 "가정"을 암시적으로 도입함으로써 달성됩니다.불행히도 이러한 기본 가정은 모델 구성 요소를 쉽게 모호하게 만들어 모델의 구조와 기본 행렬 내에 인식할 수 없는 문제가 잠재하게 합니다.

SEM에서는 내생적 잠재변수와 외생적 잠재변수 간의 잠재적인 인과관계를 보여주는 구조모형과 잠재변수와 지표 간의 인과관계를 보여주는 측정모형이 구분됩니다.예를 들어 탐색적 및 확인적 요인 분석 모델은 인과적 측정 연결에 초점을 맞추고, 경로 모델은 SEMs 잠재 구조적 연결에 더 밀접하게 대응합니다.

모형 제작자들은 모형의 각 계수를 자유롭게 추정하거나 일부 값으로 고정할 수 있도록 지정합니다.자유 계수는 연구자가 검정하고자 하는 효과, 외생 변수 간의 배경 상관 관계, 또는 내생 잠재 변수에 추가적인 변동을 제공하는 잔차 또는 오차 변수의 분산을 가정한 것일 수 있습니다.고정 계수는 잠재 변수에 대한 척도를 제공하는 그림 2의 1.0 값과 같은 값이거나, 학업 성취도에서 그림 1의 네 척도 중 하나를 가리키는 직접 효과가 없는 것(화살표 없음)의 주장과 같은 인과적 단절을 주장하는 0.0 값일 수 있습니다. SEM 프로그램은 fr의 추정치와 검정을 제공합니다.e 계수는 전체 모형 구조를 검정하는 데 중요한 기여를 하지만, 고정 계수는 전체 모형 구조를 검정하는 데 중요한 기여를 합니다.계수 간의 다양한 제약 조건도 [27][6][16]사용할 수 있습니다.모델 명세는 문헌에서 알려진 내용, 모델링된 지표 변수에 대한 연구자의 경험, 특정 모델 구조를 사용하여 조사되는 특징에 따라 달라집니다.

모형에서 추정할 수 있는 계수의 수에는 한계가 있습니다.추정된 계수 수보다 데이터 점의 수가 적으면 결과 모형이 "식별되지 않음"이라고 하며 계수 추정치를 얻을 수 없습니다.상호 효과 및 기타 인과 관계 고리도 [28][29][27]추정에 방해가 될 수 있습니다.

자유모델계수 추정

0, 1.0 또는 기타 값으로 고정된 모형 계수에는 이미 지정된 값이 있으므로 추정이 필요하지 않습니다.자유 모형 계수에 대한 추정 값은 자유 모형 계수가 추정 값을 차지하는 경우 데이터의 특성에 대한 적합도를 최대화하거나 데이터의 특성에 대한 차이를 최소화하여 얻을 수 있습니다.계수 값의 특정 집합에서 데이터가 어떻게 보여야 하는지에 대한 모델의 의미는 다음에 따라 달라집니다. a) 모델에서 계수의 위치(예: 어떤 변수들이 연결/연결이 끊겼는지), b) 변수들 간의 연결의 특성(공분산 또는 효과, 종종 선형으로 가정되는 효과), c) t의 특성오차 또는 잔차 변수(종종 많은 변수와 독립적이거나 인과 관계가 없는 것으로 가정됨) 및 d) 변수에 적합한 측정 척도(종종 측정값이 가정됨).

두 잠재 변수를 연결하는 더 강한 효과는 잠재 변수의 지표가 더 강한 상관 관계를 가져야 함을 의미합니다.따라서 잠재 효과의 합리적인 추정치는 해당 잠재 변수의 지표 간의 상관 관계, 즉 추정치-값이 데이터와의 일치를 최대화하거나 데이터와의 차이를 최소화하는 것입니다.최대 우도 추정을 통해 모든 자유 모형 계수의 수치 값은 표본 데이터를 관찰할 가능성을 최대화할 때까지 개별적으로 조정됩니다(초기 시작 값에서 점진적으로 증가 또는 감소). 데이터가 변수의 공분산/상관 관계인지 여부,또는 지표 변수에 대한 사례의 실제 값입니다.보통 최소 제곱 추정치는 데이터 간의 제곱 차이와 모델이 올바르게 지정된 경우 데이터가 어떻게 보이는지, 즉 모델의 추정된 모든 특징이 실제 세계적 특징과 일치하는지 여부를 최소화하는 계수 값입니다.

추정치를 얻기 위해 최대화 또는 최소화하는 적절한 통계적 특징은 변수의 측정 수준에 따라 달라집니다(공칭 측정 또는 순서 측정보다 구간 수준 측정이 일반적으로 더 용이함). 특정 변수가 모형에 나타나는 위치(예:외생적 이분법적 변수보다 내생적 이분법적 변수가 더 많은 추정상의 어려움을 야기함).대부분의 SEM 프로그램은 모형의 계수 추정치를 얻기 위해 최대화 또는 최소화할 항목에 대한 여러 가지 옵션을 제공합니다.최대 우도 추정(MLE), 완전 정보 최대 우도(FIML), 보통 최소 제곱(OLS), 가중 최소 제곱(WLS), 대각선 가중 최소 제곱(DWL) 및 2단계 최소 [27]제곱을 선택할 수 있습니다.

한 가지 일반적인 문제는 계수의 추정 값이 모형과 데이터에 의해 충분히 제약되지 않기 때문에 과소 식별될 수 있다는 것입니다.모형과 데이터가 함께 계수 값을 충분히 제약하거나 제한하지 않는 한 고유한 최적 추정치는 존재하지 않습니다.예를 들어, 두 변수 간의 단일 데이터 상관 관계의 크기는 변수 간의 모형화 효과의 상호 쌍을 추정하기에 충분하지 않습니다.상관 관계는 상호 효과 중 하나가 다른 효과보다 강하거나 다른 효과가 다른 효과보다 강하거나 동일한 크기의 효과로 설명될 수 있습니다.과소 식별된 효과 추정치는 추가 모델 및/또는 데이터 제약 조건을 도입하여 식별할 수 있습니다.예를 들어, 상호 효과는 하나의 효과 추정치를 다른 효과 [29]추정치와 동일하게 두 배, 세 배 또는 동일하게 제한함으로써 식별될 수 있지만, 결과 추정치는 추가 모형 제약 조건이 세계의 구조와 일치하는 경우에만 신뢰할 수 있습니다.상호 인과적으로 연결된 한 쌍의 변수 중 하나만 직접적으로 유발하는 제3 변수에 대한 데이터도 [28]식별에 도움이 될 수 있습니다.세 번째 변수가 상호 인과관계의 변수 중 하나를 직접적으로 야기하지 않도록 제한하면 대칭성이 깨집니다. 그렇지 않으면 그 세 번째 변수는 오직 인디에만 영향을 미치는 역수의 "다른" 끝에 있는 변수보다 직접적으로 야기하는 변수와 더 강한 상관관계가 있어야 하기 때문입니다.정확하게[28]이것은 다시 모델의 인과적 사양의 적합성을 가정합니다. 즉, 상호 효과의 끝에서 세 번째 변수에서 변수로 이어지는 직접적인 효과가 실제로 존재하며, 상호 연결된 변수 쌍의 "다른 끝"에서 변수에 직접적인 효과가 존재하지 않는다는 것에 주목하십시오.귀무/영 효과에 대한 이론적 요구는 추정에 도움이 되는 제약 조건을 제공하지만 이론에서는 어떤 효과가 존재하지 않는다고 주장하는 경우가 많습니다.

모형평가

모델 평가는 이론, 데이터, 모델 및 추정 전략에 따라 달라집니다.따라서 모델 평가는 다음을 고려합니다.

  • 데이터에 적절한 변수의 타당한 측정값이 포함되어 있는지 여부
  • 모형화된 사례가 인과적으로 동질적인지 여부(데이터 사례가 둘 이상의 서로 다른 인과관계 네트워크를 반영하는 경우 하나의 모형을 추정하는 것은 의미가 없습니다.)
  • 모형이 이론이나 관심 있는 특징을 적절하게 나타내는지 여부(이론에서 요구하는 특징을 생략하거나 해당 이론과 일치하지 않는 계수를 포함하는 경우 모형은 설득력이 없습니다.)
  • 추정치가 통계적으로 정당한지 여부 (실질적인 평가는 가정을 위반하거나 부적절한 추정치를 사용하거나 반복적인 추정치가 수렴되지 않는 경우 등으로 인해 파괴될 수 있습니다.
  • 추정치의 실질적인 합리성(음의 분산 및 1.0 또는 -1.0을 초과하는 상관 관계는 불가능합니다.이론과 일치하지 않는 통계적으로 가능한 추정도 이론과 우리의 이해에 도전할 수 있습니다.)
  • 모형과 데이터 간의 나머지 일관성 또는 불일치 (추정 과정은 모형과 데이터 간의 차이를 최소화하지만 중요한 차이와 정보적인 차이가 남을 수 있습니다.)

이론을 테스트하거나 "조사"한다고 주장하는 연구는 우연을 초월한 모델-데이터 불일치에 주의해야 합니다.추정은 데이터에 최대한 적합하도록 모형의 자유 계수를 조정합니다.SEM 프로그램의 출력에는 추정된 모형 효과가 관측 변수의 값을 실제로 제어하는 경우 관측 변수 간의 관계를 보고하는 행렬이 포함됩니다.모형 보고서의 "적합도"는 모형이 내포한 관계(종종 공분산)와 변수 간의 해당 관측 관계가 일치하거나 일치하지 않습니다.데이터와 모형의 의미 간의 크고 유의한 차이는 문제를 나타냅니다.σ2(chi-square) 검정에 수반되는 확률은 추정된 모형이 실제 기본 모집단의 힘을 구성하는 경우 데이터가 임의 표본 변동에 의해 발생할 수 있는 확률입니다.모형화된2 구조가 실제 모집단 인과력을 구성하고 나머지 차이는 무작위 표본 추출 변동으로 인한 것이라면 현재 데이터가 발생하지 않을 가능성이 작다고 보고합니다.

모형이 최적 계수 추정치를 선택했음에도 불구하고 데이터와 일관성이 없는 경우 정직한 연구 반응은 이 증거를 보고하고 이 증거에 주의를 기울입니다(종종 유의한 모형 χ 검정).기회 초과 모형-데이터 불일치는 불일치가 문제가 있는 데이터에서 발생하는지, 부적절한 통계 추정 또는 잘못된 모형 지정에 관계없이 계수 추정치와 모형의 구조를 결정하는 능력에 모두 문제가 됩니다.데이터 불일치("실패") 모델의 계수 추정치는 사용 가능한 데이터와 충돌하는 모델을 믿는 사람에게 세상이 어떻게 나타날지에 대한 보고서로 해석할 수 있습니다.데이터 불일치 모형의 추정치가 통계적으로 이상해지거나 이론에 따라 잘못된 부호를 가짐으로써 반드시 "분명히 잘못된" 것은 아닙니다.추정치는 이론의 요구 사항과 밀접하게 일치할 수도 있지만 나머지 데이터 불일치로 인해 추정치와 이론 간의 일치성이 저하됩니다.실패한 모형은 여전히 해석 가능하지만, 사용 가능한 증거와 상충되는 해석으로만 사용할 수 있습니다.

복제가 데이터에 적합하지 않은 잘못된 지정 모형을 탐지할 가능성은 낮습니다.반복실험 데이터가 원래 데이터의 랜덤 변동 내에 있으면 원래 데이터에 적합하지 않은 것과 동일한 잘못된 계수 배치도 반복실험 데이터에 적합하지 않을 가능성이 있습니다.복제는 데이터 오류와 같은 문제를 탐지하는 데는 도움이 되지만, 상반기 데이터의 탐색적 요인 분석(EFA)에 이어 무작위 하반기 데이터에 확인적 요인 분석(CFA)을 적용하는 경우와 같이 탐색적 모델 수정 후 잘못된 사양을 탐지하는 데는 특히 약합니다.

수정 지수는 현재 고정된 특정 모형 계수를 추정에 자유롭게 사용할 경우 데이터에 대한 모형의 적합도가 얼마나 "향상되는지"를 추정한 것입니다(하지만 반드시 모형의 구조가 얼마나 개선되어야 하는지는 아닙니다).데이터 불일치 모형에 직면한 연구자는 수정 지수가 적합성을 크게 개선할 가능성이 높다고 보고하는 계수를 쉽게 자유롭게 할 수 있습니다.이와 동시에, 데이터 적합도가 향상된 것은 해방된 계수가 실질적으로 합리적이거나 세계적으로 일치한다는 보장을 제공하지 않기 때문에, 인과적으로 틀리고 실패하는 모델에서 인과적으로 틀리고 적합한 모델로 이동하는 상당한 위험을 초래합니다.원래 모형에 잘못된 방향 효과 또는 사용할 수 없는 변수에 대한 잘못된 가정과 같은 인과 관계의 규격이 포함되어 있을 수 있으며, 이러한 문제는 현재 모형에 계수를 추가하여 수정할 수 없습니다.따라서 이러한 모형은 추가 계수에 의해 적합도가 더 가까워졌음에도 불구하고 여전히 잘못 지정됩니다.적합하지만 세속적이지 않은 모형은 특히 특정 모형(예: 원하는 수의 요인을 갖는 요인 모형)에 전념하는 연구자가 수정 지수에 의해 "제안된" 측정 오차 공분산을 삽입함으로써 초기에 적합하지 않은 모형을 얻을 경우 발생할 가능성이 높습니다.MacCallum(1986)은 "좋은 조건에서도 사양 검색자로부터 발생하는 모델은 [31]주의하여 보아야 합니다."라고 밝혔습니다.모델 오규격은 때때로 수정 지수에 의해 제안된 계수를 삽입함으로써 수정될 수 있지만, 유사하지만 중요하게 다른 잠재 [32]변수의 몇 가지 지표를 사용함으로써 더 많은 수정 가능성이 제기됩니다.


실패한 모델을 "충분히 근접"한 것으로 받아들이는 것도 합리적인 대안이 아닙니다.Browne, MacCallum, Kim, Anderson 및 Glaser는 χ 테스트가 (항상 그렇지는 않지만) 모델 오규격을 감지할 수 있는 상당한 힘을 가질 수 있는 이유에 대한 수학을 설명한 주의적인 사례를 제공했습니다.최적 추정치를 사용하는 현재 모형이 실제 기본 모집단의 힘을 구성하는 경우 σ2 검정에 수반되는 확률은 데이터가 임의 표본 변동에 의해 발생할 수 있는 확률입니다.현재2 모형 구조가 실제 모집단 인과력을 구성하고 나머지 차이는 무작위 표본 변동으로 인한 것이라면 현재 데이터가 발생하지 않을 가능성이 작다고 보고합니다.Browne, McCallum, Kim, Andersen, Glaser는 χ에 따라 모형이 데이터와 유의하게 일치하지 않음에도 불구하고 수용 가능하다고 판단되는 요인 모형을 제시했습니다.Hayduk, Pazkerka-Robinson, Cummings, Levers 및 Berres는[34] 실험적 특징인 Browne 등의 데이터를 통합하여 Browne 등의 데이터에 적합한 모델을 입증했습니다.눈감아 준이 고장은 지수의 산술 함수나 γ2 검정의 과민감도에 있지 않았습니다.이 문제는 Browne, MacCallum 및 다른 저자들이 [35]모델 사양의 문제의 본질, 위치 또는 심각성과 일치하는 부적합한 양을 신뢰할 수 없다는 것을 잊어버리거나 무시하거나 간과했기 때문입니다.

많은 연구자들은 γ가 표본 크기(N2)가 증가함에 따라 증가(따라서 γ2 확률이 감소)한다고 주장함으로써 모형을 검정하는 대신 적합 지수로 전환하는 것을 정당화하려고 했습니다.이를2 근거로 ①을 할인하는 것은 두 가지 잘못이 있습니다.첫째, 적절한 모형의 경우 π는2 [30]N이 증가함에 따라 증가하지 않으므로 π가2 N과 함께 증가하면 그 자체로 무언가가 감지 가능하게 문제가 있다는 신호입니다.그리고 두 번째로, 검출 가능하게 잘못된 지정을 받은 모델의 경우, N을 사용하여 증가하면2 모델의 오류를 검출할 수 있는 통계적 검정력(즉, 유형 II 오류를 검출할 수 있는 검정력)이 증가한다는 좋은 소식을 제공합니다.어떤 종류의 중요한 오규격은 χ에서 감지할 수 없기 때문에, 임의 변동에 의해 합리적으로 생성될 수 있는 이상의 부적합한 양은 보고 및 고려를 보증합니다.χ 모형 검정은 조정 가능한 가장 강력한 구조 방정식 모형 검정입니다.

여러 적합도 지수는 모형이 데이터를 얼마나 적합시키는지 수치화하지만, 모든 적합도 지수는 적합도의 크기나 양이 데이터 [35]불일치를 유발하는 문제의 심각도나 특성과 신뢰성 있게 조정되지 않는 논리적 어려움을 겪고 있습니다.데이터에 동일하게 잘 맞는 다양한 인과 구조를 가진 모형을 동등한 [27]모형이라고 부릅니다.이러한 모델은 데이터 적합 등가 모델이지만 인과적으로 동등하지는 않습니다. 따라서 소위 등가 모델 중 적어도 하나는 세계의 구조와 일치하지 않아야 합니다.X와 Y 사이에 완벽한 1.0 상관관계가 있고 X가 Y를 유발하는 것으로 모델링하면 완벽한 적합도와 0의 잔차 오차가 발생합니다.그러나 Y가 실제로 X를 유발할 수도 있고, X와 Y가 모두 공통 원인 Z에 반응할 수도 있기 때문에 모형이 세계와 일치하지 않을 수도 있으며, 세계는 이러한 효과(예: 공통 원인에 Y가 X에 미치는 영향) 또는 다른 인과 구조의 혼합을 포함할 수도 있습니다.완벽한 적합성은 모델의 구조가 세계의 구조와 일치한다는 것을 말해주지 않으며, 이는 결국 완벽한 적합성에 더 가까워지는 것이 반드시 세계의 구조에 더 가까워지는 것과 일치하는 것은 아니라는 것을 의미합니다. 어쩌면 그렇지 않을 수도 있습니다.따라서 연구자가 완벽한 모형 적합도가 모형이 정확하게 인과적으로 지정되어 있음을 의미한다고 주장하는 것은 잘못된 것입니다.중간 정도로 복잡한 모델의 경우에도 정확하게 동등하게 적합한 모델은 거의 없습니다.어떤 지수에 따라 데이터에 거의 적합한 모델은 필연적으로 잠재적으로 중요하지만 알려지지 않은 모델의 미스 사양을 추가로 도입합니다.이러한 모델들은 더 큰 연구 장애물이 됩니다.

이러한 논리적 약점은 구조 방정식 모델이 [36]데이터와 상당히 일치하지 않을 때마다 모든 적합 지수를 "도움이 되지 않는" 상태로 만들지만, 몇 가지 힘은 적합 지수 사용을 계속 전파합니다.예를 들어, Dag Sorbom은 최초의 구조 방정식 모델링 프로그램의 개발자인 Karl Joreskog에게 "그럼 왜 GFI를 추가했습니까?"라고 물었을 때, Joreskog는 "글쎄요, 사용자들은 LISREL이 항상 그렇게 큰 카이-제곱을 만들어낸다면 사용을 중단하겠다고 위협합니다.그래서 우리는 사람들을 행복하게 해줄 무언가를 발명해야만 했습니다.GFI가 그 [38]목적에 부합합니다."모델과 데이터의 불일치에 대한 ①2 증거는 통계적으로 너무 견고하여 제거하거나 폐기할 수 없었지만, 최소한 사람들은 "방해"하는 증거로부터 주의를 분산시킬 수 있는 방법을 제공받을 수 있습니다.추가 지수를 개발하고, 지수 행동에 대한 조사를 보고하며, MDI(산만한 지수 더미) 아래에 모델-데이터 불일치의 증거를 의도적으로 묻음으로써 경력 이익은 여전히 발생할 수 있습니다.연구자가 발견된 잘못된 사양을 수정하려고 시도하는 것이 아니라 원인이 있는 잘못된 모델을 "수용"해야 하는 일반적인 이유는 없는 것 같습니다.그리고 문헌의 일부는 귀무 가설의 "수용"에 적용되는 비판의 강화된 버전으로 인해 (지표 값을 "충족"하는 기준으로) "모형 수용"이 어려움을 겪는다는 것을 알아차리지 못한 것 같습니다.일반적으로 통계학 입문서에서는 유형 II 오류의 가능성을 인정하기 위해 "수용"이라는 용어를 "귀무가설을 거부하지 못함"으로 대체할 것을 권장합니다.유형 III 오류는 현재 데이터가 모형을 기각하기에 충분할 때 모형 가설을 "수용"함으로써 발생합니다.

연구자들이 세계의 구조를 찾는 데 전념할 것인가의 여부는 근본적인 관심사입니다.모델과 데이터의 불일치에 대한 테스트 증거를 허용 적합성이라는 인덱스 주장 뒤에 숨겨서 대체하면 해당 분야의 실질에 대한 구조적으로 개선된 이해를 얻기 위해 해당 분야에서 수행했을 수 있는 모든 것으로부터 주의를 분산시키는 데 드는 학문 전반의 비용이 발생합니다.이 학문은 모델 오규격의 증거를 인덱스 기반으로 교체하는 데 실질적인 비용을 지불하게 됩니다.모델 오규격 수정의 필요성에 대한 이견으로 인해 발생하는 마찰은 비요인 구조화된 모델의 사용이 증가하고 유사하지만 중요하게 [32]다른 잠재변수의 지표를 더 적게 사용함에 따라 증가할 가능성이 있습니다.

적합도 지수 사용과 관련된 고려 사항은 다음과 같습니다.

  1. 데이터 문제가 해결되었는지 여부(데이터 오류가 모델-데이터 불일치를 초래하지 않는지 확인)
  2. 연구자 모델과 같이 구조화된 모델에 대해 지수에 대한 기준 값이 조사되었는지 여부(예: 연구자 모델이 실제로 요인 구조화된 경우에만 적합한 지수 기준).
  3. 현재 모델의 잠재적인 오규격의 종류가 지수 기준의 기초가 되는 오규격의 종류에 해당하는지 여부(예: 생략된 인자 적재 시뮬레이션에 기초한 기준은 적절한 통제변수를 포함하지 않음으로 인한 오규격에 적절하지 않을 수 있음).
  4. 연구자가 의도적으로 지수 기준의 기초가 된 잘못된 사양의 종류를 가리키는 증거를 무시하는 것에 동의하는지 여부.(지수 기준이 결측 요인 부하량 한두 개를 모의실험하는 것을 기반으로 하는 경우, 이 기준을 사용하면 연구자가 결측 요인 부하량 한두 개를 포함하지 않는 모델을 받아들일 의향이 있음을 인정합니다.)
  5. (일부 지수의 기준이 시간이 지남에 따라 강화되었기 때문에) 최신 지수 기준이 사용되고 있는지 여부
  6. 지수 쌍에서 기준값을 만족시킬 필요가 있는지 여부 (예: Hu와[39] Bentler는 일부 공통 지수가 함께 평가되지 않는 한 부적절하게 기능한다고 보고합니다.
  7. 모델 테스트를 사용할 수 있는지 여부입니다.(χ 값, 자유도 및 확률은 χ을 기준으로 지수를 보고하는 모델에 사용할 수 있습니다.)
  8. 그리고 연구자가 지수 기반 의사결정을 할 때 알파(Type I)와 베타(Type II) 오류를 모두 고려했는지 여부(예를 들어, 모델이 데이터 불일치가 현저하게 심한 경우, 의료, 비즈니스, 사회 및 심리적 맥락에서 "허용 가능한" 불일치 양이 다를 가능성이 있습니다).


더 일반적으로 사용되는 적합 통계의 일부는 다음과 같습니다.

  • 카이-제곱
    • 다른 많은 적합도 측도 계산에 사용되는 적합도에 대한 기본 검정입니다.이 함수는 관측된 공분산 행렬과 모형이 의미하는 공분산 행렬 사이의 불일치 함수입니다.카이-제곱은 모형이 탐지 가능하게 잘못 [30]지정된 경우에만 표본 크기에 따라 증가합니다.
  • AIC(Akaike information criteria)
    • 상대 모형 적합도 지수:선호하는 모델은 AIC 값이 가장 낮은 모델입니다.
    • 여기서 k는 통계적 모형의 모수 수이고, L은 모형의 가능성에 대한 최대 값입니다.
  • RMSEA(근사의 평균 제곱근 오차)
    • 적합 지수 - 값이 0인 경우 가장 적합한 [40]값을 나타냅니다.RMSEA를 사용하여 "밀착 적합"을 결정하는 지침은 매우 [41]논란이 많습니다.
  • 표준화 평균 제곱 잔차(SRMR)
    • SRMR은 널리 사용되는 절대 적합 지표입니다.Hu and Bentler (1999)는 [42]양호한 착용감을 위한 지침으로 .08 이하를 제시하였습니다.
  • 비교 적합 지수(CFI)
    • 기준선 비교를 검사할 때 CFI는 데이터의 상관 관계의 평균 크기에 상당 부분 의존합니다.변수 간의 평균 상관 관계가 높지 않으면 CFI가 매우 높지 않습니다..[42]95 이상의 CFI 값이 바람직합니다.

다음 표에서는 RMSEA(Root Mean Square Error of Approximation), SRMR(Standardized Root Mean Squared Residual), CFI(Confirmatory Fit Index) 및 TLI(Tucker-Lewis Index)와 같은 일부 일반적인 인덱스에 대한 기타 기능을 문서화한 참조 자료를 제공합니다.AIC(Akaike Information Criteria)와 같은 추가 지수는 대부분의 SEM [27]소개에서 확인할 수 있습니다.각 적합도 측정에서 모델과 데이터 사이의 적합도를 나타내는 결정은 연구자의 모델링 목표를 반영합니다(다른 사람의 모델에 도전하는 경우가 있음).(또는 측정 개선); 모델이 "잘못된" 것으로 주장되는지 여부; 그리고 연구자가 지수로 제한된 부적합 [30]정도의 증거를 편안하게 "반복"하는지 여부.

적합 지수의 특징
RMSEA SRMR CFI
인덱스 이름 평균 제곱근 오차
근사
 표준화근 평균

잔차 제곱

 확인 적합 지수
공식 RMSEA = sq-root((χ - d)/(d(N-1))
기본 참고문헌 [43] [44] [45]
Factor Model 제안 문구

중요한 가치에 대하여

 .06 문구?[39]
NON-Factor Model 제안 문구

중요한 가치에 대하여
수정/변경을 제안하는 참조서,

비판적 가치관에 대한 의견 차이

 [39] [39] [39]
두 색인 또는 쌍으로 된 색인을 나타내는 참조

기준이 필요합니다.

 [39] [39] [39]
χ을 기준으로 한 지수 네. 아니요. 네.
사용하지 말 것을 권장하는 참고 자료

이 지수의

 [36] [36] [36]

[36] [45] [44] [43]

표본크기, 검정력 및 추정량

연구자들은 표본이 안정적인 계수 추정치와 합리적인 검정력을 제공할 수 있을 만큼 충분히 커야 한다는 데 동의하지만 구체적인 필요 표본 크기, 심지어 적절한 표본 크기를 결정하는 방법에 대해서도 일반적인 합의가 이루어지지 않고 있습니다.권장 사항은 추정할 계수의 수, 모델링된 변수의 수, 특정 모델 [27]계수를 다루는 몬테카를로 시뮬레이션을 기반으로 합니다.지표 수 대 잠재량의 비율에 기초한 표본 크기 권장 사항은 요인 지향적이며 측정 오차 [32]분산이 고정된 단일 지표를 사용하는 모형에는 적용되지 않습니다.전체적으로, 통계적으로 추정하기 어려운 계수가 없는 중간 크기 모델의 경우, 필요한 표본 크기(N)는 모든 지표를 사용하는 회귀에 필요한 N과 거의 유사한 것으로 보입니다.

표본 크기가 클수록 원인적으로 동질적이지 않은 경우를 포함할 가능성이 커집니다.따라서 원하는 계수를 통계적으로 유의한 것으로 보고할 수 있는 가능성을 향상시키기 위해 N을 증가시키면 모형 오규격의 위험과 오규격을 탐지할 수 있는 검정력이 동시에 증가합니다.모형화를 통해 학습하려는 연구자들은 (모형의 조정 또는 교체가 필요한 잠재적 학습을 포함하여) 자금 지원 및 모집단 기반 인과적 이질성/균질성 평가에 의해 허용되는 한 큰 표본 크기를 위해 노력할 것입니다.사용 가능한 N이 크면 사례의 하위 집합을 모형화하면 인과적 동질성을 방해할 수 있는 변수를 제어할 수 있습니다.모델의 결함을 보고해야 할 수도 있다고 우려하는 연구자들은 모델과 데이터의 불일치를 신호할 수 있는 검정력을 피하면서 더 큰 N을 사용하여 구조적인 관심 계수를 탐지하기를 원하는 것 사이에서 고민하고 있습니다.모형 구조와 데이터 특성의 큰 차이는 유사한 데이터를 사용하여 추정된 유사한 크기와 복잡성을 가진 모형에 대한 다른 연구자들의 경험(양호 및 불량)을 고려하여 적절한 표본 크기를 유용하게 찾을 수 있음을 나타냅니다.

해석

SE 모델에 대한 인과적 해석은 가장 명확하고 이해할 수 있지만 모델의 구조가 세계의 인과적 구조와 일치하지 않으면 오류/잘못된 해석이 됩니다.따라서 해석은 단순히 모델의 추정 계수만이 아니라 모델의 전체적인 상태와 구조를 다루어야 합니다.모형이 데이터를 적합시키는지 여부 및 모형이 데이터를 적합시키는지 여부는 해석에 가장 중요합니다.탐색하거나 연속적인 수정 지수를 따라 얻은 데이터 적합도는 모델이 틀렸다는 것을 보장하지는 않지만 이러한 접근 방식은 데이터 특징을 잘못 모델링하기 쉽기 때문에 심각한 의문을 제기합니다.예를 들어, 필요한 요인의 수를 확인하기 위해 탐색하는 것은 요인이 구조화되어 있지 않습니다. 특히 요인 모형이 측정 오차 공분산을 포함하여 적합하도록 "설득"된 경우에는 더욱 그렇습니다."수정 지수 제안" 효과 또는 오류 공분산이 부당하게 포함될 때마다 가정된 모델에 대해 데이터의 발언 능력이 점진적으로 저하됩니다.초기/기본 모델에 여러 [46]개의 규격 오류가 포함되어 있으면 제대로 된 모델을 복구하기가 매우 어려워집니다.

직접 효과 추정치는 회귀 방정식의 계수 해석과 병렬적으로 해석되지만 인과 관계가 있습니다.인과변수 값의 각 단위 증가는 다른 모든 작동/모형 인과적 메커니즘에 대한 통제 또는 조정이 주어지면 종속변수 값의 추정된 크기의 변화를 초래하는 것으로 간주됩니다.간접 효과는 유사하게 해석되며, 특정 간접 효과의 크기는 해당 간접 효과를 포함하는 일련의 직접 효과의 곱과 같습니다.관련된 단위는 관측 변수 값의 실제 척도와 잠재 변수에 할당된 척도 값입니다.특정 지표에 대한 잠재력의 지정된/고정된 1.0 효과는 해당 지표의 척도와 잠재 변수의 척도를 조정합니다.모형의 나머지 부분이 일정하거나 변하지 않는다는 가정은 실제 단위 증가로 인해 실제 영역에서 동시에 유발될 수 있는 간접 효과를 할인해야 할 수 있습니다.그리고 단위 증가 자체가 실제 세계에서 가능한 것과 일치하지 않을 수 있습니다. 왜냐하면 원인 변수의 값을 변경할 수 있는 알려진 방법이 없을 수 있기 때문입니다.모형에서 측정 오류를 조정하면 잠재 수준 효과를 실제 [26]점수의 변동을 참조하는 것으로 해석할 수 있습니다.

회귀에는 간접 효과의 추정치가 포함되지 않기 때문에 인과 계수 네트워크가 잠재 변수를 연결할 때 SEM 해석은 회귀 해석과 가장 근본적으로 다릅니다.SEM 해석은 배경 변수에서 개입 변수를 통해 영향을 전달하는 간접 효과 패턴의 결과를 하류 종속 변수로 전달해야 합니다.SEM 해석은 다양한 세계적 인과 경로가 조정 또는 독립적으로 작동하거나 심지어 서로 반대로 작용할 수 있는 방법을 이해하도록 합니다.직접 효과는 간접 효과에 의해 반작용(또는 강화)될 수도 있고, 상관 관계가 있는 의미가 일반적인 [15]원인의 효과에 의해 반작용(또는 강화)될 수도 있습니다.구체적인 추정의 의미와 해석은 전체 모델에서 맥락화되어야 합니다.

SE 모형 해석은 특정 모형 인과 세그먼트를 분산 및 공분산에 연결해야 합니다.단일 직접 효과는 독립 변수의 변동이 종속 변수의 값에 특정한 변동을 일으킨다는 것을 보고합니다.그러나 단일 효과 계수에는 그러한 효과가 어떻게 발생하는지에 대한 구조화된 이야기에 통합할 수 있는 하위 구성요소가 포함되지 않기 때문에 정확히 무엇이 발생하는지에 대한 인과관계 세부사항은 지정되지 않은 채로 남아 있습니다.하나의 효과가 어떻게 작동하는지에 대한 스토리를 구성하는 특징을 제공하기 위해서는 원인과 결과 사이에 개입하는 변수를 통합하는 좀 더 세분화된 SE 모델이 필요합니다.그러한 모형이 도달할 때까지 각각의 추정된 직접 효과는 미지의 색조를 유지하며, 따라서 이론의 본질을 불러일으킵니다.병렬적인 본질적 미지는 더 세분화된 모델에서 각각의 추정된 계수를 동반하므로 근본적인 신비감은 SE 모델에서 완전히 제거되지 않습니다.

각각의 모델링된 효과가 관련된 변수의 동일성과 추정된 효과의 크기 이상으로 알려지지 않더라도 여러 모델링된 효과를 연결하는 구조는 관찰된 변수를 조정하기 위해 사물이 어떻게 작동하는지를 표현할 수 있는 기회를 제공하여 유용한 해석 가능성을 제공합니다.예를 들어, 공통된 원인은 두 효과 변수 간의 공분산 또는 상관 관계에 기여하는데, 원인의 값이 올라가면 [15]각 원인의 기본이 되는 전체 이야기를 알지 못하더라도 두 효과의 값도 상승(양의 효과를 가정)해야 하기 때문입니다.(상관 관계는 분산 1.0을 갖도록 표준화된 두 변수 간의 공분산입니다.)또 다른 해석적 기여는 두 인과 변수가 종속 변수의 분산을 둘 다 설명할 수 있는 방법과 두 인과 변수 간의 공분산이 종속 변수의 설명 분산을 증가시키거나 감소시킬 수 있는 방법을 표현함으로써 이루어질 수 있습니다.즉, 해석은 효과와 공분산의 패턴이 종속 변수의 [47]분산을 감소시키는 데 어떻게 기여할 수 있는지를 설명하는 것을 포함할 수 있습니다.인과적 의미를 이해하는 것은 암묵적으로 "통제"를 이해하는 것과 연결되며,[4][48] 다른 변수가 아닌 일부 변수가 통제되어야 하는 이유를 잠재적으로 설명합니다.모델이 더욱 복잡해짐에 따라 이러한 기본 구성 요소는 변수가 0이 아닌 직접적인 인과 [15][16][6][29]효과로 연결되었음에도 불구하고 두 변수 사이에 상관 관계(공분산 0)가 없을 수 있는 방법을 설명하는 등 직관적이지 않은 방식으로 결합할 수 있습니다.

효과 추정치의 통계적 유의성이 없다는 것은 추정치가 귀무/영 효과 주변에서 임의 표본 변동으로 쉽게 발생할 수 있음을 나타냅니다. 따라서 추정치를 실제 효과로 해석하는 것은 모호해집니다.회귀 분석에서와 마찬가지로 모형화된 원인의 변동에 의해 설명되는 각 종속 변수의 분산 비율은 R에2 의해 제공되지만 종속 변수가 상호 효과 또는 루프 효과에 관련되어 있거나 예측 변수의 [49]오차 변수와 상관 관계가 있는 경우에는 Blocked-Error2 R을 사용해야 합니다.

Model Assessment(모델 평가) 섹션에 나타나는 주의 사항이 반복됩니다.모형이 데이터와 일치하는지 여부에 관계없이 해석이 가능해야 합니다.이 추정치는 모델을 믿는 사람에게 세상이 어떻게 보일지를 보고합니다. 모델이 잘못되었기 때문에 그 믿음이 근거가 없다고 해도 말입니다.해석에서는 모델 계수가 "모수"와 일치할 수도 있고 일치하지 않을 수도 있기 때문에 모델의 계수가 해당하는 세속적인 구조적 특징을 가질 수도 있기 때문에 "모수"와 일치하지 않을 수도 있음을 인정해야 합니다.

몇 개의 명확한 인과적 위치/변수에서 원래 모델에 진입하거나 나가는 새로운 잠재 변수를 추가하는 것은 그렇지 않으면 계수 해석을 망칠 수 있는 모델 규격 오류를 탐지하는 데 기여합니다.새로운 잠재 지표와 모든 원래 지표 사이의 상관 관계는 새로운 지표와 원래 지표를 조정하기 위해 소수의 새로운 효과 계수와 초점 효과 계수가 모델의 원래 직간접 효과와 함께 작동해야 하기 때문에 원래 모델의 구조를 검정하는 데 기여합니다.만약 원래 모형의 구조가 문제가 있었다면, 희박한 새로운 인과관계 연결은 새로운 지표들을 원래 지표들과 조율하기에 부족할 것이고, 이에 따라 모형-데이터 [29]불일치를 통해 원래 모형의 계수들의 부적절성을 알리게 될 것입니다.null/zero 효과 계수 및 고정된 0이 아닌 값이 할당된 계수에 근거한 상관 제약은 모델 테스트와 계수 추정에 모두 기여하므로 추정치와 [29]그 해석을 지원하는 스캐폴딩으로 인정받을 만합니다.

교호작용, 비선형성, 다중 그룹, 다중 수준 및 범주형 [27]변수가 포함된 모형의 경우 해석이 점차 복잡해집니다.교호작용을 포함하는 모형의 계수 해석은 {reference need }을(를) 참조하고, 다단계 모형은 {reference need }을(를) 참조하고, 종형 모형은 {reference need }을(를) 참조하고, 범주형 변수를 포함하는 모형은 {reference need }을(를) 참조하십시오. 인과 고리에 닿는 효과, 상호 효과,또는 상관 잔차도 [6][29]약간 수정해야 합니다.

실패한 모형과 적합한 모형 모두를 신중하게 해석하면 연구 발전을 이룰 수 있습니다.신뢰할 수 있도록 모형은 학문적으로 유익한 인과 구조를 조사하고, 해당 데이터를 이해 가능한 추정치에 적합시키고, 빈 [50]계수를 포함하지 않아야 합니다.신뢰할 수 있는 피팅 모델은 실패한 모델이나 피팅에 부적절하게 부딪힌 모델보다 드물지만 적절한 피팅 모델이 [34][51][52][53]가능합니다.

PLS[54] 모형을 개념화하는 여러 가지 방법은 PLS 모형을 복잡하게 해석합니다.PLS 모델러가 일부 존재하지만 사용할 수 없는 잠재 변수와 일치하는 방식으로 모델링된 지표가 결합되도록 노력함으로써 현실적인 관점을 채택하는 경우 위의 많은 의견이 적용됩니다.주로 R이나 표본2 외 예측력에 초점을 맞추는 PLS 모형과 같은 비원인 PLS 모형은 모형의 계수가 실제와 동일한지 여부에 대한 우려를 줄여 해석 기준을 변경합니다.모델러가 예측력을 제공하는 세계적인 구조적 힘에 관심이 없더라도 통계적으로 유의미한 예측 변수로 돈을 벌 수 있습니다.Rigdon, Sarstedt 및 Ringle에[54] 의해 논의된 다섯 가지 PLS 모델링 관점을 차별화하는 기본 특징은 PLS 모델러의 목표의 차이와 모델 특징의 해석을 보장하는 상응하는 차이를 지적합니다.

실험이나 시간 순서에 따라 조사를 진행한 경우에도 인과관계를 주장할 때는 주의해야 합니다.인과 모델이라는 용어는 반드시 검증된 인과적 결론을 도출하는 모델이 아니라 "인과적 가정을 전달하는 모델"을 의미하는 것으로 이해되어야 합니다. 어쩌면 그렇지 않을 수도 있습니다.여러 시점에서 데이터를 수집하고 실험 또는 준실험 설계를 사용하는 것은 특정 경쟁 가설을 배제하는 데 도움이 될 수 있지만 무작위 실험조차도 인과적 주장에 대한 위협을 완전히 배제할 수는 없습니다.어떤 연구 설계도 인과 구조를 [4]완벽하게 보장할 수 없습니다.


논쟁과 운동

구조 방정식 모델링은 SEMNET에 대한 논의에서 많은 부분이 표면화되었고 SEMNET의 아카이브에서 사용할 수 있습니다.SEMNET은 앨라배마 대학교에서 제공하는 무료 리스트 서비스입니다.요인 분석 전통의 연구자들은 일반적으로 경로 구조 모델에서 나중에 사용하기 위해 여러 지표 집합을 더 적게, 더 관리하기 쉬운 규모로 줄이거나 요인 점수로 줄이려고 시도합니다.이는 경로 구조 모델에서 나중에 사용될 척도 또는 인자 점수를 제공하는 초기 측정 단계와 함께 단계적 프로세스를 구성합니다.이러한 단계적 접근 방식은 분명해 보이지만 실제로는 심각한 근본적인 결함에 직면해 있습니다.단계로의 분할은 척도 또는 요인 점수가 지표를 유효하게 나타내는지 여부 및 잠재 수준 효과를 유효하게 보고하는지 여부를 철저하게 확인하는 데 방해가 됩니다.측정과 잠재수준 구조를 동시에 통합한 구조방정식 모델은 잠재요인이 지표를 적절하게 조정하는지를 확인할 뿐만 아니라,또한 동일한 잠재자가 동시에 각 잠재자의 기소자를 이론화된 원인 및/[29]또는 잠재자의 결과 지표와 적절하게 조정하는지 여부를 확인합니다.잠재 고객이 이러한 두 가지 유형의 조정을 모두 수행할 수 없는 경우 잠재 고객의 타당성에 의문이 제기되고 잠재 고객을 측정하기 위한 척도 또는 요인 점수에 의문이 제기됩니다.SEMNET의 의견 불일치는 가정된 잠재적 요인의 타당성에 도전하는 증거에 대한 존중 또는 무시를 둘러싸고 소용돌이쳤습니다.끓어오르는, 때로는 끓어오르는 SEMNET 토론은 George Marcoulides의 노력 덕분에 Hayduk and[20] Glaser의 표적 기사에 초점을 맞춘 Journal Structural Equation Modeling이라는 특별호로 이어졌고, 몇몇 논평과 답변이 [21]모두 자유롭게 제공되었습니다.

이러한 논의는 구조 방정식 모델을 데이터와 일관성 있게 테스트해야 하는지 여부에 대한 이견을 부추겼고, 모델 테스트는 SEMNET 논의의 다음 초점이 되었습니다.경로 모델링 이력이 있는 SEMNETER는 신중한 모델 테스트를 옹호하는 경향이 있는 반면, 요인 이력이 있는 사람은 적합성 테스트보다는 적합성 색인을 옹호하는 경향이 있었습니다.이러한 SEMNET 토론은 Paul[36] Barrett의 성격과 개인의 차이에 대한 목표 기사로 이어졌습니다: "사실, 저는 이제 모든 그러한 지수가 어떤 논문에서도 모델 "수용 가능성" 또는 "적합도"를 나타내는 것으로 나타나는 것을 금지할 것을 권고합니다." (821페이지).바렛의 기사에는 양쪽 [50][55]관점의 해설도 곁들여졌습니다.

SEMNET이 모델-데이터 불일치에 대한 명확한 보고를 요구함에 따라 모델 테스트에 대한 논란은 줄어들었습니다.과학자들은 증거가 [30]보고하는 것을 좋아하지 않는다고 해서 증거를 무시하거나 보고하지 않을 수 없습니다.모델 오규격을 가리키는 증거에 주의해야 한다는 요구사항은 오류/잔차 변수의 독립성 부족으로 인해 추정을 방해하는 모델 오규격 유형인 "내생성"을 해결하기 위한 보다 최근의 SEMNET 우려를 뒷받침합니다.일반적으로 요인 모형을 포함한 구조방정식 모형의 인과성에 대한 논란도 감소하고 있습니다.요인 분석에 충실한 Stan Mulaik조차 요인 [56]모형의 인과적 근거를 인정했습니다.SEM 맥락에서[25] 인과성에 대한 신화에 대한 Bollen과 Pearl의 언급은 SEM 맥락에서 인과적 사고의 중심성을 강화시켰습니다.

SEMNET 논쟁은 경쟁 모델에 초점을 맞춥니다.경쟁 모델을 비교하는 것은 큰 도움이 될 수 있지만 두 가지 모델을 만들고 더 나은 피팅 모델을 유지한다고 해서 해결될 수 없는 근본적인 문제가 있습니다.예를 들어, Levy와 Hancock(2007)[57]과 같은 발표의 통계적 정교함은 연구자가 하나의 끔찍한 모델과 하나의 끔찍한 모델로 시작하여 일부 지수가 끔찍한 모델보다 더 적합하다고 보고하기 때문에 구조적으로 끔찍한 모델을 유지하는 것으로 끝날 수 있음을 간과하기 쉽습니다.Kline(2016)[27]과 같은 강력한 SEM 텍스트조차도 모델 [58]테스트의 프레젠테이션에 불안할 정도로 약한 상태로 남아 있다는 것은 유감스러운 일입니다.전체적으로, 구조 방정식 모델링을 통해 얻을 수 있는 기여는 실패한 모델이 최선의 사용 가능한 경우에도 신중하고 상세한 모델 평가에 따라 달라집니다.

앞선 논란의 가장자리를 건드린 추가 논란이 씨엠넷에서 점화를 기다리고 있습니다.여러 지표가 있는 요인 모형과 이론이 포함된 요인 구조는 고장을 일으키는 경향이 있고 약한 지표를 떨어뜨리면 모형과 데이터의 불일치가 줄어듭니다.지표 수를 줄이면 구조 방정식 모델에서 잠재 변수를 지원하는 데 필요한 최소 지표 수에 대한 우려와 논란이 발생합니다.요인 전통에 관련된 연구자들은 잠재 변수당 지표 수를 3개로 줄이도록 설득할 수 있지만, 3개 또는 2개의 지표는 여전히 제안된 근본적인 요인 공통 원인과 일치하지 않을 수 있습니다.Hayduk and Littvay(2012)[32]는 각각의 모델링된 잠재변수에 대해 단일 지표만을 사용할 경우 측정오차에 대해 어떻게 생각하고, 방어하고, 조정해야 하는지에 대해 논의했습니다.단일 지표는 오랫동안 [51]SE 모델에서 효과적으로 사용되어 왔지만, 요인 분석 관점에서만 측정을 고려한 검토자에 대해서만 논란이 남아 있습니다.

비록 쇠퇴하고 있지만, 이러한 논란의 흔적은 SEM 문헌 곳곳에 흩어져 있으며, 여러분은 다음과 같은 질문을 함으로써 쉽게 의견 차이를 부추길 수 있습니다.데이터와 현저하게 일치하지 않는 모형은 어떻게 해야 합니까?아니면 다음을 묻습니다.모델 단순성이 데이터 불일치 증거에 대한 존중을 무시합니까?또는 일부 모형에 대해 근접하거나 근접하지 않은 데이터 적합을 보여주는 지수에 어떤 가중치를 부여해야 합니까?아니면 데이터와 일치하지 않는 인색한 모델에 대해 특히 관대해야 하며 "보상"해야 합니까?또는 RMSEA가 각 모델 자유도에 대해 실제 적합하지 않은 것을 무시하는 것을 고려할 때, RMSEA가 0이 아닌 귀무가설을 가진 모델을 테스트하는 사람들이 부족한 모델 테스트를 수행하고 있다는 것을 의미하지 않습니까?비록 응답은 연구자들이 증거를 보고하고 존중해야 하는지 여부와 관련된 비기술적인 문제에 집중될 가능성이 있지만, 그러한 질문을 적절하게 다루기 위해서는 통계적 정교성에 상당한 차이가 필요합니다.

확장, 모델링 대안 및 통계적 친족

소프트웨어

구조방정식 모델링 프로그램은 그 능력과 사용자 [60][61]요구사항이 매우 다릅니다.일반적으로, 사용자 입력이 "단순"하거나 "편리"할수록 암시적 모델 가정의 수가 증가하고, 연구 설계, 방법론, 측정, 추정 또는 모델링 문제에 대한 충분한 주의를 기울이지 않음으로써 발생하는 문제의 위험이 증가합니다.좋은 방법을 사용하려면 사용된 프로그램과 사용된 프로그램 버전을 모두 보고해야 합니다.

  • LISREL (무료가 아님) 최초의 완전한 SEM 소프트웨어로 기본 표기법 https://ssicentral.com/index.php/products/lisrel/ 도입
  • Mplus (무료) https://www.statmodel.com/
  • Stata에서 SEM (무료) https://www.stata.com/features/structural-equation-modeling/
  • sem (free R program)
  • 라반 (무료 R 프로그램) https://cran.r-project.org/web/packages/lavaan/index.html
  • OpenMX (무료 R 프로그램) https://cran.r-project.org/web/packages/OpenMx/index.html
  • AMOS (무료) https://www.ibm.com/products/structural-equation-modeling-sem
  • EQs(무료) https://www.azom.com/software-details.aspx?SoftwareID=11
  • 스타타

참고 항목

축약어

CFA = 확인적 요인분석

CFI = 비교 적합 지수

DWL = 대각선으로 가중된 최소 제곱

EFA = 탐색적 요인분석

ESEM = 탐색구조방정식 모형화

GFI = 적합도 지수

MIIV = 모형 암시적 도구 변수

OLS = 보통 최소 제곱

RMSEA = 근사치의 평균 제곱근 오차

RMSR = 제곱 평균 잔차

SRMR = 표준화된 평균 제곱 잔차

SEM = 구조 방정식 모형 또는 모형화

WLS = 가중 최소 제곱

◦ = 치 제곱

참고문헌

  1. ^ Salkind, Neil J. (2007). "Intelligence Tests". Encyclopedia of Measurement and Statistics. doi:10.4135/9781412952644.n220. ISBN 978-1-4129-1611-0.
  2. ^ Boslaugh, S.; McNutt, L-A. (2008)."구조 방정식 모델링".전염병학 백과사전.Doi 10.4135/9781412953948.n443, ISBN 978-1-4129-2816-8
  3. ^ 셸리, M.C. (2006)"구조 방정식 모델링".교육 리더십과 행정 백과사전.Doi 10.4135/9781412939584.n544, ISBN 978-0-7619-3087-7
  4. ^ a b c d e 펄, J. (2009)인과관계:모델, 추론 및 추론.세컨드 에디션.뉴욕: 캠브리지 대학 출판부.
  5. ^ Kline, Rex B. (2016). Principles and practice of structural equation modeling (4th ed.). New York. ISBN 978-1-4625-2334-4. OCLC 934184322.{{cite book}}: CS1 유지 관리: 위치 누락 게시자(링크)
  6. ^ a b c d e f Hayduk, L. (1987) LISREL을 이용한 구조방정식 모델링: Essentials and Advances볼티모어, 존스 홉킨스 대학 출판부.ISBN 0-8018-3478-3
  7. ^ Bollen, Kenneth A. (1989). Structural equations with latent variables. New York: Wiley. ISBN 0-471-01171-1. OCLC 18834634.
  8. ^ Kaplan, David (2009). Structural equation modeling: foundations and extensions (2nd ed.). Los Angeles: SAGE. ISBN 978-1-4129-1624-0. OCLC 225852466.
  9. ^ Curran, Patrick J. (2003-10-01). "Have Multilevel Models Been Structural Equation Models All Along?". Multivariate Behavioral Research. 38 (4): 529–569. doi:10.1207/s15327906mbr3804_5. ISSN 0027-3171. PMID 26777445. S2CID 7384127.
  10. ^ Tarka, Piotr (2017). "An overview of structural equation modeling: Its beginnings, historical development, usefulness and controversies in the social sciences". Quality & Quantity. 52 (1): 313–54. doi:10.1007/s11135-017-0469-8. PMC 5794813. PMID 29416184.
  11. ^ 맥컬럼 & 오스틴 2000, 페이지 209.
  12. ^ 라이트, 시월 (1921) "상관과 인과관계"Journal of Agricultural Research. 20:557-585
  13. ^ Wright, Sewall. (1934) "경로계수의 방법"수학통계연보 5(3): 161-215. 도이: 10.1214/aoms/1177732676
  14. ^ Wolfle, L.M. (1999) "경로 계수 방법에 관한 Sewall Wright:주석이 달린 참고 문헌" 구조 방정식 모델링: 6(3):280-291
  15. ^ a b c d 던컨, 오티스 더들리 (1975)구조 방정식 모델 소개.뉴욕: 학술 출판사.ISBN 0-12-224150-9.
  16. ^ a b c d 볼렌, K. (1989)잠재 변수가 있는 구조 방정식.뉴욕, 와일리.ISBN 0-471-01171-1.
  17. ^ Jöreskog, Karl; Gruvaeus, Gunnar T.; van Thillo, Marielle. (1970) ACOVS: 공분산 구조 분석을 위한 일반 컴퓨터 프로그램프린스턴, 뉴저지; 교육 테스트 서비스.
  18. ^ Jöreskog, Karl Gustav; van Thillo, Mariella (1972). "LISREL: A General Computer Program for Estimating a Linear Structural Equation System Involving Multiple Indicators of Unmeasured Variables" (PDF). Research Bulletin: Office of Education. ETS-RB-72-56 – via US Government.
  19. ^ a b Jöreskog, Karl; Sorbom, Dag. (1976) LISTREL III: 최대우도법에 의한 선형구조방정식 시스템의 추정시카고:미국 국립 교육 자원 주식회사
  20. ^ a b Hayduk, L.; Glaser, D.N. (2000) "4단계 부여, Waltzing Around Factor Analysis, and Other Serious Fun."구조 방정식 모델링. 7 (1): 1-35
  21. ^ a b Hayduk, L.; Glaser, D.N. (2000) "4단계 하기, Right-2-3, Wrong-2-3: Mulaik and Millsap; Bollen; Bentler; and Herting and Costner에 대한 간략한 답변"구조 방정식 모델링. 7 (1): 111-123
  22. ^ 웨스트랜드, J.C. (2015)구조 방정식 모델링:경로에서 네트워크로.뉴욕, 스프링어.
  23. ^ Christ, Carl F. (1994). "The Cowles Commission's Contributions to Econometrics at Chicago, 1939-1955". Journal of Economic Literature. 32 (1): 30–59. ISSN 0022-0515. JSTOR 2728422.
  24. ^ 임벤스, G.W. (2020)"잠재적인 결과와 지시된 비순환 그래프는 인과관계에 접근합니다.경제학에서의 경험적 실천과의 관련성".경제문학지. 58(4): 11-20-1179
  25. ^ a b c 볼렌, K.A.펄, J. (2013) "인과성과 구조방정식 모형에 관한 8가지 신화"S.L. Morgan(ed.)에서 사회연구를 위한 인과분석 핸드북, 15장, 301-328, Springer. Doi:10.1007/978-94-007-6094-3_15
  26. ^ a b Borsboom, D.; Mellenberg, G.J.; van Herden, J. (2003)."잠재변수의 이론적 상태"심리학적 검토, 110 (2): 203–219https://doi.org/10.1037/0033-295X.110.2.203 }
  27. ^ a b c d e f g h i Kline, Rex. (2016) 구조방정식 모델링의 원리와 실천 (4차)뉴욕, 길포드 출판사.ISBN 978-1-4625-2334-4
  28. ^ a b c Rigdon, E. (1995)."실제로 추정되는 구조 모형에 대한 필요충분한 식별 규칙"다변량 행동 연구. 30(3): 359-383
  29. ^ a b c d e f g Hayduk, L. (1996) LISREL 이슈, 토론 및 전략볼티모어, 존스 홉킨스 대학 출판부.ISBN 0-8018-5336-2
  30. ^ a b c d e f Hayduk, L.A. (2014b) "증거를 무시하는 것은 수치스러운 일입니다.구조 방정식 모델 테스트에 대한 충분한 존중이 부족한 개인적인 결과.BMC: 의학 연구 방법론, 14(124): 1-10 DOI 10.1186/1471-2288-14-24 http://www.biomedcentral.com/1471-2288/14/124
  31. ^ MacCallum, Robert (1986). "Specification searches in covariance structure modeling". Psychological Bulletin. 100: 107–120. doi:10.1037/0033-2909.100.1.107.
  32. ^ a b c d Hayduk, L. A.; Littvay, L. (2012) "연구자들은 구조방정식 모형에서 단일지표, 최상지표, 또는 다중지표를 사용해야 하는가?" BMC 의학연구방법론, 12(159): 1-17. Doi: 10,1186/1471-2288-12-159
  33. ^ Browne, M.W.; MacCallum, R.C.; Kim, C.T.; Andersen, B.L.; Glaser, R. (2002) "적합 지수와 잔차가 호환되지 않을 때."심리학적 방법.7: 403-421.
  34. ^ a b Hayduk, L. A.; Pazderka-Robinson, H.; Cummings, G.G.; Levers, M-J. D.; Beres, M. A. (2005) "구조 방정식 모델 테스트 및 자연 살해 세포 활성 측정의 품질" BMC 의학 연구 방법론. 5 (1): 1-9. Doi: 10.1186/1471-2288-5-1.Hayduk 등에서 .922에서 .992로, 그리고 .944에서 .994로 수정한 것을 주목합니다.표 1.
  35. ^ a b c L.A. Hayduk(2014a) "원인적으로 잘못 지정된 완벽한 적합 요인 모델 보기:몸에 꼭 맞는 모델을 이해하는 것은 더 나쁠 수 있습니다."교육 및 심리측정. 74(6): 905-926. 도이: 10.1177/00131644145274449
  36. ^ a b c d e f g h 바렛, P. (2007)"구조 방정식 모델링:모델 적합 판정."성격과 개인차. 42(5): 815-824
  37. ^ Satorra, A.; and Bentler, P. M. (1994) "공분산 구조 분석에서 검정 통계 및 표준 오류에 대한 수정"A. von Eye and C. C. C. Clockg(Eds.)에서 잠재변수 분석:개발연구용 출원(pp. 399-419)사우전드 오크스, 캘리포니아: 세이지.
  38. ^ Sorbom, D. "xxxxxx" in Cudeck, R; du Toit R.; Sorbom, D. (편집자) (2001) 구조 방정식 모델링: 현재와 미래:카를 요레스코그를 기리는 페스트슈리프트.Scientific Software International:링컨우드, 일리노이주
  39. ^ a b c d e f g h Hu, L.; Bentler, P.M. (1999) "공분산 구조 분석에서 적합 지수에 대한 컷오프 기준:기존 기준과 새로운 대안."구조 방정식 모델링.6: 1-55.
  40. ^ Kline 2011, 페이지 205.
  41. ^ Kline 2011, 페이지 206.
  42. ^ a b Hu & Bentler 1999, p. 27.
  43. ^ a b Steiger, J. H.; 및 Lind, J. (1980) "공통 인자 수에 대한 통계적 기반 검정"아이오와 시의 사이코메트릭 학회 연례 회의에서 발표된 논문.
  44. ^ a b Steiger, J. H. (1990) "구조 모형 평가 및 수정:간격 추정 접근법".다변량 행동 연구 25:173-180
  45. ^ a b Browne, M.W.; Cudeck, R. (1992) "모델 적합성을 평가하는 대안적인 방법"사회학적 방법 및 연구. 21(2): 230-258
  46. ^ Herting, R.H.; Costner, H.L. (2000) "적절한 요소 수"와 적절한 단계 수에 대한 또 다른 관점."구조 방정식 모델링. 7 (1): 92-110
  47. ^ Hayduk, L. (1987) LISREL을 이용한 구조방정식 모델링 : Essentials and Advances, 20페이지볼티모어, 존스 홉킨스 대학 출판부.ISBN 0-8018-3478-3 20페이지
  48. ^ Hayduk, L. A.; Cummings, G.; Stratkotter, R.; Nimmo, M.; Grugoryev, K.; Dosman, D.; Gillespie, M.; Pazderka-Robinson, H. (2003) "펄스의 D-분리:인과적 사고로 한 걸음 더."구조 방정식 모델링. 10 (2): 289-311
  49. ^ Hayduk, L.A. (2006) "Blocked-Error-R2: 루프 또는 상관 잔차를 포함하는 모델에서 설명된 분산의 비율에 대한 개념적으로 개선된 정의."품질과 수량.40: 629-649.
  50. ^ a b Millsap, R.E. (2007) "구조방정식 모델링이 어려워졌습니다."성격과 개인차.42: 875-881.
  51. ^ a b Entwisle, D.R.; Hayduk, L.A.; Reilly, T.W. (1982) 조기교육: 인지적 및 정의적 결과.볼티모어: 존스 홉킨스 대학 출판부.
  52. ^ 헤이덕, L.A. (1994)"개인 공간:심플렉스 모델을 이해하고 있습니다."비언어 행동학 저널(Journal of Nonveral Behavior.
  53. ^ Hayduk, L.A.; Stratkotter, R.; R.; Robers, M.W. (1997) "가톨릭 신학생들의 성적 지향과 교회의 가르침에 순응하려는 의지"종교의 과학적 연구를 위한 저널 36(3): 455-467
  54. ^ a b Rigdon, E.E.; Sarstedt, M.; Ringle, M. (2017) "CB-SEM과 PLS-SEM의 결과 비교에 관하여: 다섯 가지 관점과 다섯 가지 권장사항"마케팅ZFP. 39(3): 4-16. Doi: 10.15358/0344-1369-2017-3-4
  55. ^ Hayduk, L.A.; Cummings, G.; Boadu, K.; Pazderka-Robinson, H.; Boulianne, S. (2007) "Testing! testing! one, two, three – 구조 방정식 모델에서 이론을 테스트!"성격과 개인차. 42(5): 841-850
  56. ^ Mulaik, S.A. (2009) Foundations of Factor Analysis (제2판)채프먼과 홀/CRC.보카 라톤, 130-131쪽
  57. ^ Levy, R.; Hancock, G.R. (2007) "평균과 공분산 구조 모델을 비교하기 위한 통계 테스트의 프레임워크"다변량 행동 연구. 42(1): 33-66
  58. ^ Hayduk, L.A. (2018) "렉스 B. 클라인의 구조방정식 모형 원리와 실천에 관한 에세이 검토:5판을 장려합니다."캐나다 인구 연구. 45 (3-4): 154-178. DOI 10.25336/csp29397
  59. ^ Hayduk, L.A.; Establooks, C.A.; Hoben, M. (2019)"융합 유효성:인과구조방정식 모델링을 통한 이론기반 척도평가"심리학 프론티어즈, 10:1139. 도이:10.3389/psyg.2019.01139
  60. ^ Narayanan, A. (2012-05-01). "A Review of Eight Software Packages for Structural Equation Modeling". The American Statistician. 66 (2): 129–138. doi:10.1080/00031305.2012.708641. ISSN 0003-1305. S2CID 59460771.
  61. ^ Narayanan, A. (2012-05-01). "A Review of Eight Software Packages for Structural Equation Modeling". The American Statistician. 66 (2): 129–138. doi:10.1080/00031305.2012.708641. ISSN 0003-1305. S2CID 59460771.
  62. ^ Rosseel, Yves (2012-05-24). "lavaan: An R Package for Structural Equation Modeling". Journal of Statistical Software. 48 (2): 1–36. doi:10.18637/jss.v048.i02. Retrieved 27 January 2021.
  63. ^ 인용 오류:명명된 참조Bollen18호출되었지만 정의되지 않았습니다(도움말 페이지 참조).

서지학

추가열람

외부 링크