표현 이론

표현 이론은 대수적 구조가 물체에 어떻게 작용하는지 연구한다.간단한 예는 반사 및 회전으로 구성된 일반 폴리곤의 대칭이 폴리곤을 변환하는 방법입니다.

표현 이론은 추상 대수 구조를 벡터 공간의 선형 변환으로 표현하여 연구하고 이러한 추상 대수 ^[1]^[2]구조에 대한 모듈을 연구하는 수학의 한 분야이다.본질적으로, 표현은 추상 대수적 대상을 행렬과 그 대수적 연산(예를 들어 행렬 덧셈, 행렬 곱셈)에 의해 그 요소를 설명함으로써 더 구체적으로 만든다.행렬과 선형 연산자의 이론은 잘 이해되고 있기 때문에, 친숙한 선형 대수 객체의 관점에서 보다 추상적인 객체의 표현은 특성을 수집하고 때로는 보다 추상적인 이론에 대한 계산을 단순화하는 데 도움이 됩니다.

이러한 서술에 적응할 수 있는 대수적 객체에는 군, 연관대수 및 리 대수가 포함된다.이들 중 가장 두드러진 것은 (그리고 역사적으로 최초의) 그룹의 요소들이 행렬 ^[3]^[4]곱셈이 되도록 가역 행렬로 표현되는 그룹의 표현 이론이다.

표현 이론은 추상대수의 문제를 잘 ^[5]이해되는 과목인 선형대수의 문제로 줄이기 때문에 유용한 방법이다.또, 군(예를 들면)이 표현되는 벡터 공간은 무한 차원일 수 있고, 이를 예를 들면 힐버트 공간이라고 하는 것으로써,^[6]^[7] 군 이론에 해석 방법을 적용할 수 있다.표현 이론은 또한 물리학에서 중요하다. 왜냐하면, 예를 들어, 그것은 물리적 시스템의 대칭 그룹이 ^[8]그 시스템을 설명하는 방정식의 해법에 어떻게 영향을 미치는지 설명하기 때문이다.

표현 이론은 두 가지 이유로 수학의 전 분야에 널리 퍼져 있다.첫째, 표현 이론의 응용은 다양합니다.^[9] 대수에 미치는 영향 외에도, 표현 이론은 다음과 같습니다.

조화 ^[10]분석을 통해 푸리에 분석을 조명하고 일반화합니다.
불변 이론과 에를랑겐 프로그램을 ^[11]통해 기하학과 연결된다.
는 자기형태와 랭글랜드 프로그램을 ^[12]통해 수이론에 영향을 미칩니다.

둘째, 대표이론에 대한 다양한 접근법이 있다.동일한 물체는 대수기하학, 모듈 이론, 해석수 이론, 미분 기하학, 연산자 이론, 대수 조합론 및 ^[13]위상학의 방법을 사용하여 연구될 수 있다.

대표이론의 성공은 수많은 일반화를 가져왔다.가장 일반적인 것 중 하나는 범주 ^[14]이론이다.표현 이론이 적용되는 대수적 객체는 특정한 종류의 범주로 볼 수 있고, 표현은 객체 범주에서 벡터 ^[4]공간의 범주로 볼 수 있다.이 설명은 두 가지 분명한 일반화를 가리키고 있습니다. 첫째, 대수적 객체는 보다 일반적인 범주로 대체될 수 있고 둘째, 벡터 공간의 목표 범주는 잘 이해된 다른 범주로 대체될 수 있습니다.

정의 및 개념

V를 필드 ^[5]F 위의 벡터 공간이라고 합니다.예를 들어, V가ⁿ R 또는ⁿ C라고 가정하면, 각각 실수 또는 복소수 위의 열 벡터의 표준 n차원 공간입니다.이 경우, 표현 이론의 개념은 실수 또는 복소수의 n × n 행렬을 사용하여 추상 대수를 구체적으로 하는 것이다.

이것을 할 수 있는 대수적 오브젝트에는 크게 세 종류가 있다: 그룹, 연관대수, 리 대수.^[15]^[4]

모든 가역 n × n 행렬의 집합은 행렬 곱셈 하의 군이며, 그룹의 표현 이론은 가역 행렬의 관점에서 그 원소를 설명함으로써 군을 분석한다.
행렬 덧셈과 곱셈은 모든 n × n 행렬의 집합을 연관대수로 만들고, 따라서 연관대수의 대응하는 표현 이론이 있다.
행렬 곱셈 MN을 행렬 정류자 MN - NM으로 대체하면, n × n 행렬은 대신 Lie 대수가 되어 Lie 대수의 표현 이론으로 이어진다.

이것은 선형 맵이 행렬 곱셈을 대체하고 구성이 행렬 곱셈을 대체하면서 모든 필드 F와 벡터 공간 V over F로 일반화된다: V의 자기 동형의 그룹 GL(V,F), V의 모든 내형 형상의 연관 대수_F End(V) 및 대응하는 Lie 대수 gl(V,F)가 있다.

정의.

표현이란 ^[16]두 가지 방법이 있습니다.첫 번째는 행렬이 행렬 곱셈에 의해 열 벡터에 작용하는 방식을 일반화하면서 작용의 개념을 사용합니다.벡터 공간 V 위의 군 G 또는 (관련 또는 Lie) 대수 A의 표현은 지도이다.

\displaystyle \Phi \colon G\times V\quad \text {or}\quad \Phi \colon A\times V\to V

두 가지 특성이 있습니다.첫째, G의 임의의 g(또는 A의 a)에 대해 맵은

(\displaystyle\begin{aligned}\Phi(g)\colon V&\v&\mapsto\Phi(g,v)\end {aligned})

선형(F 위)입니다.둘째, $\Phi$ \ $displaystyle \Phi$ }( $\Phi$ g, v)에 대해 g · v 표기법을 도입하면 G의 g와₂ V의 v에₁ 대해 다음과 같이 됩니다.

(1)\cdot v=v

(2)\cdot g_{1}\cdot (g_{2}\cdot v)=(g_{1}g_{2})\cdot v

여기서 e는 G의 아이덴티티 요소이고 gg는₁₂ G의 곱이다.연관 대수에 대한 요구사항은 유사하지만, 연관 대수가 항상 항등식을 갖는 것은 아니며, 이 경우 등식 (1)은 무시된다.식 (2)는 행렬 곱셈의 연관성에 대한 추상적 표현이다.이것은 행렬 정류자에 적용되지 않으며 정류자에 대한 식별 요소도 없습니다.따라서 리 대수의 경우, 유일한 요건은 A의 x, x₂ 및 V의 경우₁ 다음과 같다.

(2')\cdot (x_{2}\cdot v)-x_{2}\cdot (x_{1}\cdot v)=[x_{2}]\cdot v

여기서 [x₁, x₂]는 행렬 정류자 MN - NM을 일반화하는 Lie 브래킷입니다.

표현을 정의하는 두 번째 방법은 G 내의 g를 선형 맵으로 전송하는 맵에 초점을 맞춥니다.V → V, 다음을 만족합니다.

\displaystyle \varphi (g_{1}g_{2})=\varphi (g_{1})\display \varphi (g_{2})\display {g_{1}, g_{2}\in G}

다른 경우도 마찬가지입니다.이 접근방식은 보다 간결하고 추상적입니다.이 관점에서 보면:

벡터 공간 V 위의 군 G의 표현은 군 동형사상 θ: G → GL(V,F)^[7]이다.
벡터 공간 V 위의 연관 대수 A의 표현은 대수 동형사상 θ: A → 끝_F(V)^[7]이다.
벡터 공간 V 위의 리 대수 θ의 표현은 리 대수 동형사상 θ: θ → gl(V,F)이다.

용어.

벡터 공간 V를 θ의 표현 공간이라고 하고, 그 차원(유한 경우)을 표현의 차원이라고 한다(때로는 에서와 같이 도).또한 문맥에서 동형사상 θ가 명확할 때 V 자체를 표현이라고 부르는 것이 일반적이다. 그렇지 않을 경우 표기법(V, θ)을 사용하여 표현을 나타낼 수 있다.

V가 유한 차원 n인 경우 V가 F와ⁿ V를 식별할 수 있는 근거를 선택할 수 있으므로 필드 F에 항목이 있는 행렬 표현을 복구할 수 있습니다.

유효 표현 또는 충실한 표현은 동형사상 θ가 주입된 표현(V,θ)이다.

등변지도와 등변형

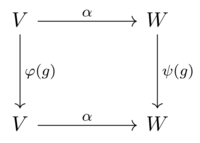
만약 V와 W가 F 위의 벡터 공간이고, 군 G의 표현 θ와 θ를 갖춘다면, V에서 W로의 등변수 맵은 선형 맵 α: V → W이다.

\displaystyle \alpha (g\cdot v)=g\cdot \alpha (v)}

G와 V의 모든 g에 대해.θ: G → GL(V) 및 θ: G → GL(W)의 관점에서 이는 다음을 의미한다.

\displaystyle \alpha \varphi (g)=\psi (g)\displaystyle \alpha }

G의 모든 g에 대해, 즉 다음 다이어그램이 정류한다.

연관대수나 리 대수의 표현에 대한 등변량 지도도 비슷하게 정의된다.만약 α가 반전가능하다면, 그것은 동형사상이라고 하며, 이 경우 V와 W(더 정확히는 β와 θ)는 동형사상이며, 동등한 표현으로도 표현된다.등변 지도는 종종 뒤엉킨 표현 지도라고 불린다. $또$ , 그룹 G의 경우는, G맵이라고 불리는 경우도 있습니다.

동형 표현은 실제 목적상 "동일하다"며, 표현되는 군이나 대수에 대한 동일한 정보를 제공한다.그러므로 표현 이론은 표현을 동형사상까지 분류하려고 한다.

하위 표현, 견적 및 축소할 수 없는 표현

$(V,\psi )$ $(V,\psi )$ , $(V,\psi )$ ) $(V,\psi )$ { $style$ ( V , \ $psi )$ 이 $(V,\psi )$ $그룹$ G {\ $displaystyle$ G $G$ 의 표현이고 $,$ $W$ {\ $displaystyle$ W $}$ 가 $W$ 모든 $w\in W$ $g\in G$ W $style$ W $\in$ 에 $w\in W$ 대해G {\ $displaystyle$ G $}$ 의 $G$ 작용에 의해 보존되는V {\ $displaystyle$ V $}$ 의 $V$ 선형 부분 공간인 경우 $yle$ g $\in$ G $g\in G$ $g\cdot w\in W$ w $w$ W $($ 세레는 이러한 $W$ 를 G $(\displaystyle$ G $)$ ^[17]에서 $W$ 안정적이라고 부릅니다). $W$ (\ $displaystyle$ W $)$ 는 $W$ 서브 표현이라고 부릅니다.

\displaystyle\phi:G에서\text로Aut}}(W)}

\phi (g)

서

\phi (g)

\phi (g)

( g

\phi (g)

) {

displaystyle

\

phi ( g

)

\psi (g)

（

\psi (g)

)

\psi (g)

{

displaystyle

\

psi ( g

)

W

W

}

(W,\phi )

(W,\phi )

(W,\phi )

, \

phi ）

a

(W,\phi )

、

W\hookrightarrow V

displaystyle VARROW

W\hookrightarrow V

을 포함하는 것을

나타냅니다

.

V/W

V

({displaystyle

V

/W})

는

V/W

G

({

displaystyle

G

G

의 표현으로도 만들 수 있습니다

.

V({displaystyle V

})

에

V

2개의 하위공간

,

즉 V({

displaystyle

V})의

V

V

표현

자체가 정확히 2개일

경우

, V({

displaystyle V({

displaystyle V})그 표현은 축소할 ^[18]수 있다고 한다.

축소할 수 없는 표현의 정의는 슈어의 보조를 암시한다: 등변 지도

\displaystyle \alpha : (V,\psi)\to (V',\psi ')

그 커널과 이미지가 하위 표현이기 때문에 축소할 수 없는 표현은 제로 맵 또는 동형사상 중 하나입니다.특히, V

V=V'

V=V'

{\

{

displaystyle

V =

V

'

일 때

,

이는

V

의

V

등변수 내형상이 기초 필드 F에 대한 연관 분할 대수를 형성함을 나타낸다.F가 대수적으로 닫힌 경우, 축소할 수 없는 표현의 등변 내형사상은 항등식의 스칼라 배수뿐이다.

환원 불가능한 표현은 많은 그룹의 표현 이론의 구성 요소이다. $표현$ V $({displaystyle$ V})가 $V$ 환원 불가능한 경우, 표현 V({displaystyle V})는 어떤 의미에서는 "단순한" 부분 표현과 몫수로 구축된다. 예를 들어 $,$ V({ $displaystyle$ V $V$ })가 유한 $V$ 인 경우, 두 부분 표현 V(substylation)는 모두 유한한 표현이다.tation과 quotient는 차원이 작습니다.표현에 하위 표현이 있지만, 단순하지 않은 구성 요소 하나만 있는 반례가 있습니다.예를 들어, 덧셈 그룹 $(\mathbb {R} ,+)$ , $(\mathbb {R} ,+)$ + $(\mathbb {R} ,+)$ )(\ $displaystyle (\mathbb {R} ,+})$ 은 $(\mathbb {R} ,+)$ 2차원 표현입니다.

\displaystyle \phi (a) = param {bmatrix}1&a\\0&1\end {bmatrix}

이 그룹은 이 동형사상에 의해 고정된 벡터

{\begin{bmatrix}1&0\end{bmatrix}}^{\mathsf {T}}

[

{\begin{bmatrix}1&0\end{bmatrix}}^{\mathsf {T}}

{\begin{bmatrix}1&0\end{bmatrix}}^{\mathsf {T}}

{\

를

{\begin{bmatrix}1&0\end{bmatrix}}^{\mathsf {T}}

가지지만, 보완 부분 공간은 다음과 같이 매핑됩니다.

{bmatrix} 0\1\end {bmatrix}\mapto {bmatrix} a\1\end {bmatrix

한 가지 축소할 수 없는 하위 표현만 제공합니다.이것은 모든 전능하지 않은 ^[19]^{: 112}그룹에게 해당된다.

직접 합계 및 분해할 수 없는 표현

만약 (V,θ)와 (W,θ)가 군 G의 표현이라면, V와 W의 직합은 다음 방정식을 통해 표준적인 방법으로 표현된다.

g\cdot (v,w)=(g\cdot v,g\cdot w).

두 표현의 직접합은 그룹 G에 대한 정보를 두 표현이 개별적으로 전달하는 것보다 더 많이 포함하지 않는다.표현이 두 개의 적절한 중요하지 않은 하위 표현의 직접 합계일 경우, 분해할 수 있다고 한다.그렇지 않으면 분해할 수 없다고 한다.

완전한 삭감

유리한 상황에서는 모든 유한 차원 표현은 축소할 수 없는 표현의 직접적인 합이다: 그러한 표현은 반단순이라고 한다.이 경우 축소할 수 없는 표현만 이해하면 됩니다.이 "완전 환원성" 현상이 발생하는 예로는 유한군(마슈케의 정리 참조), 콤팩트군, 반단순 리 대수가 있다.

완전한 환원성이 유지되지 않는 경우, 분해할 수 없는 표현이 하위대표에 의한 지분의 확장으로서 어떻게 구성될 수 있는지를 이해해야 한다.

표현 텐서 곱

$\phi _{1}:G\rightarrow \mathrm {GL} (V_{1})$ 를 들어 $\phi _{1}:G\rightarrow \mathrm {GL} (V_{1})$ $\phi _{1}:G\rightarrow \mathrm {GL} (V_{1})$ : $\phi _{1}:G\rightarrow \mathrm {GL} (V_{1})$ $\phi _{1}:G\rightarrow \mathrm {GL} (V_{1})$ $\phi _{1}:G\rightarrow \mathrm {GL} (V_{1})$ $\phi _{1}:G\rightarrow \mathrm {GL} (V_{1})$ ( V $\phi _{1}:G\rightarrow \mathrm {GL} (V_{1})$ ) \ $displaystyle$ \ $phi$ _ { $\phi _{1}:G\rightarrow \mathrm {GL} (V_{1})$ 1 : $G\rightarrow \mathrm {GL}(V_{1})$ 및 $\phi _{1}:G\rightarrow \mathrm {GL} (V_{1})$ § $\phi _{2}:G\rightarrow \mathrm {GL} (V_{2})$ : $\phi _{2}:G\rightarrow \mathrm {GL} (V_{2})$ $\phi _{2}:G\rightarrow \mathrm {GL} (V_{2})$ $\phi _{2}:G\rightarrow \mathrm {GL} (V_{2})$ L $\phi _{2}:G\rightarrow \mathrm {GL} (V_{2})$ \ $displaystyle \phi$ _ ${2}:$ $G\rightarrow \mathrm {GL}(V_{2})$ 는 $\phi _{2}:G\rightarrow \mathrm {GL} (V_{2})$ 군 $G$ {{ $displaystyle$ G $G$ 의 표현으로, 텐서 $\phi _{1}\otimes \phi _{2}$ 곱 벡터 $V_{1}\otimes V_{2}$ $V_{1}\otimes V_{2}$ $V_{1}\otimes V_{2}$ V2 ⊗ V2 $the 1$ 2 \phi $_$ { $1}$ \ $otimes \phi$ _ { $2}$ $\phi _{1}\otimes \phi _{2}$ 2 $\phi _{1}\otimes \phi _{2}$ 1 1 2 a 2 form 2 form 2 form 2 $V_{1}\otimes V_{2}$ form 2 form 2 g 2 g 2 $\phi _{1}\otimes \phi _{2}$ g 2 g 2 g 2 g 2 g 2 g 2 g 2 g 1 g g $\phi _{1}\otimes \phi _{2}$ g 2 g 2 。

(\phi _{1}\otimes \phi _{2})(g)=\phi _{1}(g)\otimes \phi _{2}(g)

(\phi _{1}\otimes \phi _{2})(g)=\phi _{1}(g)\otimes \phi _{2}(g)

(\phi _{1}\otimes \phi _{2})(g)=\phi _{1}(g)\otimes \phi _{2}(g)

(\phi _{1}\otimes \phi _{2})(g)=\phi _{1}(g)\otimes \phi _{2}(g)

(\phi _{1}\otimes \phi _{2})(g)=\phi _{1}(g)\otimes \phi _{2}(g)

) (

(\phi _{1}\otimes \phi _{2})(g)=\phi _{1}(g)\otimes \phi _{2}(g)

g )

=

(\phi _{1}\otimes \phi _{2})(g)=\phi _{1}(g)\otimes \phi _{2}(g)

1

(\phi _{1}\otimes \phi _{2})(g)=\phi _{1}(g)\otimes \phi _{2}(g)

(

(\phi _{1}\otimes \phi _{2})(g)=\phi _{1}(g)\otimes \phi _{2}(g)

(\phi _{1}\otimes \phi _{2})(g)=\phi _{1}(g)\otimes \phi _{2}(g)

2

(\phi _{1}\otimes \phi _{2})(g)=\phi _{1}(g)\otimes \phi _{2}(g)

(

(\phi _{1}\otimes \phi _{2})(g)=\phi _{1}(g)\otimes \phi _{2}(g)

)\

display

style ( \

phi

_ {

1}\otimes

\

phi

_ {

2}

( g )=\

phi

_ {1} (

g

)\

phi _

{

2}

(

g

(\phi _{1}\otimes \phi _{2})(g)=\phi _{1}(g)\otimes \phi _{2}(g)

)

$\phi _{1}$ 1 $\phi _{1}$ \ $displaystyle$ \ $phi _$ { $}$ 및 $\phi _{1}$ $\phi _{2}$ 2 \ $displaystyle$ \ $phi$ _ { $2$ }가 $\phi _{2}$ Lie 대수의 표현일 경우 사용하는^[21] 올바른 공식은 다음과 같습니다.

(\phi _{1}\otimes \phi _{2})(X)=\phi _{1}(X)\otimes I+I\otimes \phi _{2}(X)

(\phi _{1}\otimes \phi _{2})(X)=\phi _{1}(X)\otimes I+I\otimes \phi _{2}(X)

1

(\phi _{1}\otimes \phi _{2})(X)=\phi _{1}(X)\otimes I+I\otimes \phi _{2}(X)

(\phi _{1}\otimes \phi _{2})(X)=\phi _{1}(X)\otimes I+I\otimes \phi _{2}(X)

) (

(\phi _{1}\otimes \phi _{2})(X)=\phi _{1}(X)\otimes I+I\otimes \phi _{2}(X)

)

(\phi _{1}\otimes \phi _{2})(X)=\phi _{1}(X)\otimes I+I\otimes \phi _{2}(X)

1 (

(\phi _{1}\otimes \phi _{2})(X)=\phi _{1}(X)\otimes I+I\otimes \phi _{2}(X)

)

(\phi _{1}\otimes \phi _{2})(X)=\phi _{1}(X)\otimes I+I\otimes \phi _{2}(X)

I +

(\phi _{1}\otimes \phi _{2})(X)=\phi _{1}(X)\otimes I+I\otimes \phi _{2}(X)

(\phi _{1}\otimes \phi _{2})(X)=\phi _{1}(X)\otimes I+I\otimes \phi _{2}(X)

(

(\phi _{1}\otimes \phi _{2})(X)=\phi _{1}(X)\otimes I+I\otimes \phi _{2}(X)

) \

displaystyle

( \

phi _

{1} \

phi

_ {

2}

( X ) = \

phi

_

{1

} ( X ) \

phi

_ { 1 ( X ) \

times I

+ I

\

phi

( X ) _ 2 . 2

}

이 제품은 석탄 대차에서의 공동 생산물로 인식될 수 있다.일반적으로, 환원 불가능한 표현의 텐서 곱은 환원 불가능한 것이 아니다. 환원 불가능한 표현의 직접 합으로 텐서 곱을 분해하는 과정은 클렙시-고단 이론으로 알려져 있다.

군 SU(2)의 표현 이론(또는 그 복소화된 라이 $\mathrm {sl} (2;\mathbb {C} )$ $\mathrm {sl} (2;\mathbb {C} )$ l( $\mathrm {sl} (2;\mathbb {C} )$ $)$ 의 경우({displaystyle $\mathrm {sl}(2;\mathbb {C})})$ 의 경우, 분해는 쉽게 풀 ^[22]수 있다.축소할 수 없는 표현에는 음이 아닌 정수 또는 반정수인 $파라미터$ l $\displaystyle$ l $\$ displaystyle l로 $l$ $라벨$ 이 붙여집니다.이 경우 표현은 $2l+1$ $2l+1$ $2l+1$ $(\displaystyle 2l+$ 1 $2l+1$ 이 됩니다. $l_{1}\geq l_{2}$ $l_{1}$ $displaystyle$ $l_{1})$ 과 $l_{1}$ $l_{2},$ $l_{1}\geq l_{2}$ 2({ $displaystyle$ $l_{$ 2 $l_{2},$ $l_{1}\geq l_{2}$ 의 두 표현 표현 텐서 곱을 취한다고 $l_{1}\geq l_{2}$ 합니다.그러면 텐서 곱은 라벨이 있는 각 표현의 복사본의 직접 합으로 분해됩니다. $l$ { $display$ $style$ l $}$ $l$ 。 $l$ 서l { $display$ $style$ l _ { $l_{1}-l_{2}$ 1 $l_{1}+l_{2}$ } $l_{1}-l_{2}$ - $l$ _ { } - l _ { $l_{1}-l_{2}$ } 。 $l_{1}+l_{2}$ 를 $l_{1}=l_{2}=1$ $l_{1}=l_{2}=1$ $=$ $l_{1}=l_{2}=1$ $l_{1}+l_{2}$ $=$ 1 { $displaystyle l_{1$ } - $l_$ ${2$ } $l_{1}+l_{2}$ $l$ $l_{1}=l_{2}=1$ $l_{1}-l_{2}$ 、 1 $=$ $l_2$ $l_{1}=l_{2}=1$ 。2. 따라서 $(2l_{1}+1)\times (2l_{2}+1)=3\times 3=9$ 2 l 1 $(2l_{1}+1)\times (2l_{2}+1)=3\times 3=9$ + $(2l_{1}+1)\times (2l_{2}+1)=3\times 3=9$ ) $(2l_{1}+1)\times (2l_{2}+1)=3\times 3=9$ × ( $(2l_{1}+1)\times (2l_{2}+1)=3\times 3=9$ $(2l_{1}+1)\times (2l_{2}+1)=3\times 3=9$ 2 + $(2l_{1}+1)\times (2l_{2}+1)=3\times 3=9$ ) $(2l_{1}+1)\times (2l_{2}+1)=3\times 3=9$ $(2l_{1}+1)\times (2l_{2}+1)=3\times 3=9$ × $(2l_{1}+1)\times (2l_{2}+1)=3\times 3=9$ $=$ $(2l_{1}+1)\times (2l_{2}+1)=3\times 3=9$ ( $2 l$ _ {1 $}$ + 1 ) \ times ( $2$ l _ { $2$ } + 1 $(2l_{1}+1)\times (2l_{2}+1)=3\times 3=9$ = 3 \ $times$ 3 $=$ 9 )의 텐서 곱은 1차원 표현 $(l=0),$ $l$ $(l=0),$ 의 $(l=0),$ 직합으로 분해된다 $(2l_{1}+1)\times (2l_{2}+1)=3\times 3=9$ $.$ $(l=1),$ 및 5차원 표현 $(l=2)$ $(l=2)$ $(l=2)$ $(l=2)$ ) $(l=2)$ { $displaystyle (l=2$

지점 및 토픽

표현 이론은 가지는 가지 수와 군과 대수의 표현을 연구하는 접근법의 다양성으로 유명하다.비록 모든 이론들이 이미 논의된 기본 개념을 공통적으로 가지고 있지만, 세부적으로 상당히 다르다.차이는 3배 이상입니다.

표현 이론은 표현되는 대수적 객체의 유형에 따라 달라진다.그룹에는 여러 가지 다른 클래스가 있는데, 연상 대수와 리 대수가 있으며, 그들의 표현 이론은 모두 개별적인 맛을 가지고 있다.
표현 이론은 대수적 객체가 표현되는 벡터 공간의 특성에 따라 달라진다.가장 중요한 차이점은 유한 차원 표현과 무한 차원 표현 사이의 차이입니다.무한 차원에서는 추가 구조가 중요합니다(예를 들어 공간이 힐베르트 공간인지 여부, 바나흐 공간인지 여부 등).추가적인 대수 구조는 유한 차원 사례에서도 부과될 수 있다.
표현 이론은 벡터 공간이 정의되는 필드의 유형에 따라 달라집니다.가장 중요한 경우는 복소수 필드, 실수 필드, 유한 필드 및 p-adic 수 필드입니다.양의 특성을 가진 분야와 대수적으로 닫히지 않은 분야에는 추가적인 어려움이 발생한다.

유한군

그룹 표현은 유한 ^[23]그룹의 연구에서 매우 중요한 도구이다.그것들은 또한 기하학과 ^[24]결정학에 대한 유한군 이론의 적용에서 발생한다.유한 그룹의 표현은 일반 이론의 많은 특징들을 나타내며 표현 이론의 다른 분기들과 주제들로 가는 길을 가리킵니다.

특성 0의 장에 걸쳐 유한군 G의 표현은 다수의 편리한 특성을 가진다.첫째, G의 표현은 반단순(완전 환원 가능)이다.이것은 G-표현 W의 모든 하위 표현 V가 G-불변 보형을 갖는다는 마슈케의 정리의 결과이다.예를 들어 W에서 V까지의 임의의 투영 †을 선택하고, 그 평균 †로_G 치환하는 것이 있습니다.

\displaystyle \pi _{G}(x)=sum _{g\in G}g\cdot \pi (g^{-1}\cdot x)}

θ는 등변수이며, 그 커널은 필수 보완체입니다_G.

유한 차원 G 표현은 특성 이론을 사용하여 이해할 수 있다: 표현의 특성 θ: G → GL(V)은 클래스 함수 θ_φ: G → F에 의해 정의된다.

\displaystyle \chi _{\varphi }(g)=\mathrm {Tr}(\varphi (g))}

$\mathrm {Tr}$ 서 $\mathrm {Tr}$ \ $displaystyle \mathrm {Tr}$ 은 $\mathrm {Tr}$ 트레이스입니다.G의 환원 불가능한 표현은 그 특성에 의해 완전히 결정된다.

마슈케의 정리는 소수 p가 G의 차수와 공역하는 한 유한장과 같은 양의 특성 p의 장에 대해 더 일반적으로 적용된다.p와 G가 공통인자를 가질 때, 반단순이 아닌 G-표현이 있는데, 모듈러 표현 이론이라고 불리는 하위 분기에서 연구된다.

평균화 기법은 또한 F가 실수 또는 복소수인 경우, 모든 G 표현은 다음과 같은 의미에서 V의 내부 곱 $\langle \cdot ,\cdot \rangle$ 、 $display$ 、（ \ $displaystyle$ \ $langle$ \ $cdot$ ; \ $cdot$ \ rangle $\langle \cdot ,\cdot \rangle$ }을 $\langle \cdot ,\cdot \rangle$ 보존한다는 것을 보여준다.

\displaystyle \cdot v,g\cdot w\rangle =\cdl v,w\rangle }

G 및 V의 모든 g, W의 모든 w에 대해.따라서 모든 G-표현은 통일적이다.

Maschke의 결과는 하위 표현의 직교 보형을 취함으로써 증명될 수 있기 때문에 단일 표현은 자동으로 반단순이다.유한하지 않은 그룹의 표현을 연구할 때, 유니터리 표현은 유한 그룹의 실제적이고 복잡한 표현에 대한 좋은 일반화를 제공한다.

마슈케의 정리나 평균에 의존하는 유니터리 특성과 같은 결과는 적분의 적절한 개념을 정의할 수 있다면 평균을 적분으로 대체함으로써 더 일반적인 그룹으로 일반화할 수 있다.이것은 Haar 측도를 사용하여 콤팩트 위상군(콤팩트 리 군 포함)에 대해 수행될 수 있으며, 그 결과 이론이 추상 조화 분석으로 알려져 있다.

임의의 장에 걸쳐, 좋은 표현 이론을 가진 유한군의 또 다른 클래스는 리 유형의 유한군이다.중요한 예로는 유한장 위의 선형 대수군이 있다.선형 대수군과 리 군의 표현 이론은 이러한 예시를 무한 차원 군으로 확장하며, 후자는 라이 대수 표현과 밀접하게 관련된다.유한 그룹에 대한 성격 이론의 중요성은 리 그룹과 리 대수의 표현에 대한 가중치 이론과 유사하다.

유한군 G의 표현은 또한 군 연산, 선형성 및 군 연산과 스칼라 곱셈이 통근하는 요건에 의해 정의된 곱셈 연산을 갖춘 F 위의 벡터 공간인 군 대수 F[G]를 통해 대수 표현에 직접 링크된다.

모듈러 표현

유한군 G의 모듈러 표현은 특성이 G와 동일하지 않은 장에 대한 표현이다. 그래서 마슈케의 정리가 더 이상 유지되지 않는다(G는 F에서 반전할 수 없기 때문에 ^[25]G로 나눌 수 없기 때문이다).그럼에도 불구하고, Richard Brauer는 특성 이론의 많은 부분을 모듈식 표현으로 확장했고, 이 이론은 유한한 단순 그룹의 분류를 향한 초기 진전에 중요한 역할을 했다, 특히 그들의 Sylow 2-subgroups가 "너무 sm"이었기 때문에 순수하게 그룹 이론적인 방법에 따라 특성화가 조정되지 않은 단순 그룹의 경우.모두"^[26]라고 표시됩니다.

모듈러 표현은 그룹 이론에 응용할 수 있을 뿐만 아니라 대수 기하학, 부호화 이론, 조합론, 숫자 이론과 같은 수학의 다른 분야에서도 자연스럽게 발생합니다.

유니터리 표현

G의 또는(보통)진짜 복잡한 힐베르트 공간에서 단체 G의 일원화된 표현은 선형 표현 φ V은 φ(g)은 단일 사업자마다 g∈ G. 그 진술이 널리 적용에 양자 역학 이후 1920년대, 덕분에 각론에 영향이 헤르만 Weyl,[27], 이 영감을 받는 developm.멤머는가장 주목할 만한 것은 ^[28]유진 위그너의 푸앵카레 그룹의 표현 분석을 통해서이다.George Mackey는 (어플리케이션에서 유용한 특정 그룹뿐만 아니라 모든 그룹 G를 위한) Unitary 표현의 일반 이론을 구축한 선구자 중 한 명으로, 1950년대와 1960년대에 ^[29]Harish-Chandra와 다른 사람들에 의해 광범위한 이론이 개발되었습니다.

주요 목표는 ^[30]G의 환원 불가능한 유니터리 표현 공간인 "유니터리 이중"을 설명하는 것이다.이 이론은 G가 국소적으로 콤팩트한(하우스도르프) 위상군이고 표현은 강하게 ^[10]연속적인 경우에 가장 잘 개발되었습니다.G 아벨리안의 경우, 유니터리 쌍대는 단지 글자의 공간인 반면, G 콤팩트형의 경우, 피터-와일 정리는 환원 불가능한 유니터리 표현은 유한 차원이고 유니터리 쌍대는 ^[31]이산적이라는 것을 보여준다.예를 들어 G가 원군¹ S일 경우 정수로 문자가 지정되고 유니터리 쌍수는 Z가 됩니다.

비콤팩트 G의 경우, 어떤 표현이 단일인지에 대한 질문은 미묘한 것이다.환원 불가능한 유니터리 표현은 (Harish-Chandra 모듈로서) "허용"되어야 하며, 어떤 허용 표현이 비퇴행성 불변세사선형 형태를 가지는지 쉽게 검출할 수 있지만, 이 형태가 정의일 때 결정하기는 어렵다.실제 환원적 Lie 그룹(아래에서 논의됨)과 같이 비교적 잘 동작하는 그룹에서도 유니터리 이중에 대한 효과적인 설명은 표현 이론에서 중요한 미해결 문제로 남아 있다.SL(2,R) 및 로렌츠 ^[32]군과 같은 많은 특정 그룹에 대해 해결되었습니다.

고조파 분석

원군¹ S와 정수 Z 사이의 쌍대성, 혹은 보다 일반적으로 토러스ⁿ T와ⁿ Z 사이의 쌍대성은 푸리에 급수의 이론으로 잘 알려져 있으며, 푸리에 변환은 실제 벡터 공간 상의 문자 공간이 이중 벡터 공간이라는 사실을 비슷하게 표현한다.따라서 단일 표현 이론과 조화 분석은 밀접하게 관련되어 있으며, 추상 조화 분석은 국소적으로 콤팩트한 위상군 및 관련 공간에 ^[10]대한 함수 분석을 전개함으로써 이 관계를 이용한다.

주요 목표는 푸리에 변환과 플랜체렐 정리의 일반 형식을 제공하는 것입니다.이것은 G 위의 제곱 적분 가능 함수의 공간² L(G) 상의 G의 정규 표현과 L 위의 L 함수의 공간에서의² 표현 사이에 유니터리 듀얼에 대한 측도를 구성함으로써 이루어진다.폰트랴긴 이중성과 피터-바일 정리는 각각 ^[31]^[33]아벨리안과 콤팩트 G에 대해 이것을 달성한다.

또 다른 접근법은 축소할 수 없는 표현뿐만 아니라 모든 단일 표현을 고려하는 것이다.이들은 하나의 카테고리를 형성하며, Tannaka-Krein 이중성은 단일 표현 범주에서 콤팩트 그룹을 회복하는 방법을 제공한다.

알렉산더 그로텐디크는 탄나카-크레인 이중성을 선형 대수군과 탄나키아 범주 사이의 관계로 확장시켰지만, 만약 그 그룹이 아벨 군도 아니고 콤팩트 군도 아니라면, 플랑체렐 정리나 푸리에 반전의 유사체로 알려진 일반 이론은 없다.

고조파 해석도 군 G의 함수 분석에서 G의 균질 공간 함수로 확장되었다.이 이론은 대칭 공간을 위해 특히 잘 개발되었으며, 자기 형태 이론을 제공한다(아래에서 논의).

거짓말 그룹

Lie 그룹은 매끄러운 다양체이기도 한 그룹입니다.실수 또는 복소수에 대한 많은 고전적인 행렬 그룹은 Lie ^[34]그룹입니다.물리학과 화학에서 중요한 많은 그룹들은 라이 그룹이고, 그들의 대표 이론은 그 ^[8]분야에서의 그룹 이론의 적용에 매우 중요하다.

리 군의 표현 이론은 먼저 콤팩트 표현 이론의 결과가 ^[30]적용되는 콤팩트 군을 고려함으로써 발전될 수 있다.이 이론은 Weyl의 단일 트릭을 사용하여 반단순 Lie 그룹의 유한 차원 표현으로 확장될 수 있다. 각 반단순 실제 Lie 그룹 G는 복소수 Lie 그룹^c G인 복소수를 가지며, 이 복소수 Lie 그룹은 최대 콤팩트 부분군 K를 가진다.G의 유한 차원 표현은 K의 표현과 밀접하게 일치한다.

일반 Lie 그룹은 분해 가능한 Lie 그룹과 반단순 Lie 그룹의 반직접적(Levi 분해)^[35]이다.해결 가능한 Lie 그룹의 표현 분류는 일반적으로 다루기 어렵지만, 실제적인 경우에는 종종 쉽다.반직접 제품의 표현은 맥키 이론이라고 불리는 일반적인 결과를 통해 분석할 수 있다. 맥키 이론은 위그너의 푸앵카레 그룹 표현 분류에 사용된 방법의 일반화이다.

리 대수

필드 F 위의 Lie 대수는 Jacobi 항등식을 만족시키는 Lie 브래킷이라고 하는 스큐 대칭 쌍선형 연산을 갖춘 F 위의 벡터 공간입니다.리 대수는 특히 항등원소에서 리 군과 접하는 공간으로 발생하며, "최초 대칭"^[35]으로 해석됩니다.리 군의 표현 이론에 대한 중요한 접근법은 리 대수의 해당 표현 이론을 연구하는 것이지만, 리 대수의 표현 또한 본질적인 관심을 ^[36]가지고 있다.

리 대수는 리 군과 마찬가지로 리바이 분해가 반단순하고 해결 가능한 부분으로 이루어지며, 일반적으로 해결 가능한 리 대수의 표현 이론은 다루기 어렵다.반대로, 반단순 리 대수의 유한 차원 표현은 엘리 카르탕의 작업을 거쳐 완전히 이해된다.기본적으로 리 괄호가 0인 θ의 총칭 최대 서브대수 θ인 카르탄 서브대수를 선택하여 반단 리 대수 θ의 표현을 해석한다(벨리안).can의 표현은 and의 동작을 위한 eigenspace인 무게공간과 문자의 극소유사공간으로 분해할 수 있다.반단순 리 대수의 구조는 발생할 ^[35]수 있는 가능한 무게의 조합론을 쉽게 이해할 수 있도록 표현 분석을 감소시킨다.

무한 차원 리 대수

표현에 대해 연구된 무한 차원 리 대수학에는 많은 클래스가 있습니다.이들 중 중요한 클래스는 Kac-Moody ^[37]대수이다.그것들은 독립적으로 그들을 발견한 빅터 카크와 로버트 무디스의 이름을 따서 붙여졌다.이러한 대수는 유한 차원 반단순 리 대수의 일반화를 형성하고 많은 조합 특성을 공유합니다.이것은 그들이 반단순 리 대수의 표현과 같은 방식으로 이해할 수 있는 표현 클래스를 가지고 있다는 것을 의미합니다.

아핀 리 대수는 수학과 이론 물리학, 특히 등각장 이론과 정확히 해결 가능한 모델의 이론에서 특히 중요한 카크-무디 대수의 특별한 경우이다.Kac은 아핀 Kac-Moody 대수의 표현 이론에 기초한 맥도날드 동일성에 대한 우아한 증거를 발견했습니다.

라이 슈퍼 대게브라

리 초대칭은 기본 벡터 공간이 Z-격자를₂ 갖는 리 대수의 일반화이며, 리 괄호의 스큐 대칭성과 자코비 항등성은 부호에 의해 수정된다.그들의 표현 이론은 리 ^[38]대수의 표현 이론과 유사하다.

선형 대수군

선형 대수군(또는 더 일반적으로 아핀 군 체계)은 리 군의 대수 기하학에서 유사하지만, 단순히 R이나 C보다 더 일반적인 필드에 걸쳐 있다.특히, 유한한 장에 걸쳐, 그들은 유한한 리 유형의 그룹을 발생시킨다.선형 대수군은 리 군과 매우 유사한 분류를 가지고 있지만, 그들의 표현 이론은 다소 다르고(그리고 훨씬 덜 잘 이해됨) 다른 기술을 필요로 한다. 왜냐하면 자리스키 위상이 상대적으로 약하고, 더 이상 분석의 기술을 이용할 ^[39]수 없기 때문이다.

불변 이론

불변 이론은 대수적 다양성에 대한 작용이 함수에 미치는 영향의 관점에서 그룹의 표현을 형성하는 작용을 연구한다.고전적으로, 이 이론은 주어진 선형 군으로부터의 변환 하에서 변하지 않거나 불변하는 다항식 함수의 명시적 기술 문제를 다루었다.현대적 접근법은 이러한 표현들을 환원 불가능한 ^[40]것으로 분해하는 것을 분석한다.

무한 그룹의 불변 이론은 선형 대수의 발달, 특히 2차 형식과 결정식의 이론과 불가분의 관계에 있다.상호 영향력이 강한 또 다른 과목은 사영 기하학으로, 불변 이론이 주제를 구성하기 위해 사용될 수 있으며, 1960년대 동안 데이비드 멈포드에 의해 그의 기하학적 불변 ^[41]이론의 형태로 주제에 새로운 생명이 불어넣어졌다.

반단순 리 군의 표현 이론은 불변 이론에^[34] 뿌리를 두고 있으며 표현 이론과 대수 기하학 사이의 강한 연결은 기하학의 중심에 군과 대칭을 배치하는 펠릭스 ^[42]클라인의 에를랑겐 프로그램과 엘리 카르탕의 연결에서 시작하여 미분 기하학에 많은 유사점을 가지고 있습니다.현대의 발전은 표현 이론과 불변 이론을 홀로노믹, 미분 연산자 및 여러 복잡한 변수의 이론과 같은 다양한 영역으로 연결시킨다.

자기 형태와 수 이론

자기형태는 모듈러 형식을 유사한 변환 ^[43]특성을 가진 여러 복잡한 변수와 같은 보다 일반적인 분석 함수로 일반화한 것입니다.일반화에는 모듈러 그룹 PSL₂(R)과 선택된 일치 서브그룹을 반단순 Lie 그룹 G와 이산 서브그룹 δ로 대체하는 것이 포함된다.모듈러 형태는 상부 공간 H = PSL₂(R)/SO(2)의 몫에서 미분 형태로 볼 수 있듯이, 자기동형 형태는 δ\G/K의 미분 형식(또는 유사한 객체)으로 볼 수 있다. 여기서 K는 (일반적으로) G의 최대 콤팩트 부분군이지만, 일반적으로는 특이점이 있다.콤팩트 부분군에 의한 반단순 리 군의 몫은 대칭 공간이기 때문에 자기 형태 이론은 대칭 공간에서의 조화 분석과 밀접하게 관련되어 있다.

일반 이론이 발전하기 전에, 힐베르트 모듈러 형식과 시겔 모듈러 형식을 포함하여 많은 중요한 특수 사례가 상세하게 검토되었다.이 이론의 중요한 결과는 셀버그 추적 공식과 Robert Langlands가 리만-로흐 정리가 자기 형태 공간의 차원을 계산하는데 적용될 수 있다는 것을 깨달은 것을 포함한다."자동형 표현"의 후속 개념은 G가 아델릭 대수군으로 취급되는 대수군인 경우를 다루는 데 큰 기술적 가치가 있는 것으로 입증되었다.그 결과, 전체 철학인 랭글랜드 프로그램은 자기형태의 ^[44]표현과 수의 이론적 특성 사이의 관계를 중심으로 발전해 왔다.

연상 대수

어떤 의미에서, 연관 대수 표현은 군과 리 대수 표현 모두를 일반화한다.군의 표현은 대응하는 군환 또는 군대수의 표현을 유도하는 반면, 리 대수의 표현은 그것의 보편적 포락대수의 표현에 생물적으로 대응한다.그러나 일반 연상 대수의 표현 이론은 군과 리 대수의 표현 이론의 모든 훌륭한 특성을 가지고 있는 것은 아니다.

모듈 이론

연관대수의 표현을 고려할 때, 기초적인 장은 잊어버리고, 연관대수는 링으로, 그 표현은 모듈로 간주할 수 있다.이 접근방식은 놀라울 정도로 효과적입니다.표현 이론의 많은 결과는 링을 통해 모듈에 대한 특별한 결과로 해석될 수 있습니다.

호프 대수와 양자군

홉프 대수는 군과 리 대수의 대표이론을 특수한 경우로 유지하면서 연상 대수의 대표이론을 개선하는 방법을 제공한다.특히, 두 표현의 텐서 곱은 이중 벡터 공간과 마찬가지로 표현이다.

그룹과 연관된 홉프 대수는 교환 대수 구조를 가지고 있고, 그래서 일반적인 홉프 대수는 양자 그룹으로 알려져 있다. 그러나 이 용어는 종종 그룹의 변형이나 그 보편적 포섭 대수로 발생하는 특정 홉프 대수로 제한된다.양자군의 대표이론은 예를 들어 가시와라의 결정적 기초를 통해 리 군과 리 대수군의 대표이론에 놀라운 통찰력을 더했다.

일반화

집합 이론 표현

집합 X 위의 군 G의 집합 이론 표현(군 작용 또는 치환 표현이라고도 함)은 G에서^X X로, X에서 X로, 모든₁ g에서₂ g로, X에서 모든 x에 대해 다음과 같이 함수에 의해 주어진다.

\displaystyle \rho (1)[x]=x}

\displaystyle \rho(g_{1}g_{2})[x]=\rho(g_{1}[x]}

이 조건과 그룹에 대한 공리는 γ(g)가 G의 모든 g에 대한 바이젝션(또는 치환)임을 의미한다.따라서 우리는 G에서 X의 대칭군_X S까지의 군 동형사상으로 치환 표현을 동등하게 정의할 수 있다.

기타 카테고리의 표현

모든 그룹 G는 단일 객체를 가진 범주로 볼 수 있습니다. 이 범주의 형태론은 G의 요소일 뿐입니다. 임의의 범주 C가 주어졌을 때, C의 G의 표현은 G에서 C로의 함수입니다.이러한 함수는 C 내의 객체 X와 그룹 동형성을 G에서 X의 자기동형군인 Aut(X)로 선택한다.

C가 필드 F 위의 벡터 공간의 범주인 Vect인_F 경우, 이 정의는 선형 표현과 동일합니다.마찬가지로 집합이론 표현은 집합의 범주에서 G의 표현일 뿐이다.

또 다른 예로는 위상 공간의 범주인 상단을 고려합니다.상단의 표현은 위상 공간 X의 G에서 동형군까지의 동형사이다.

선형 표현과 밀접하게 관련된 두 가지 유형의 표현은 다음과 같습니다.

투영 표현: 투영 공간의 범주에서.이를 "스칼라 변환까지의 선형 표현"이라고 설명할 수 있습니다.
아핀 표현: 아핀 공간의 범주에 있습니다.예를 들어, 유클리드 그룹은 유클리드 공간에 친근하게 작용한다.
단일 및 반비하수체 그룹의 핵심 표현: 선형 또는 반비하수체 변환 형태와 함께 복잡한 벡터 공간의 범주에서.

카테고리의 표현

그룹은 범주이기 때문에 다른 범주의 표현도 고려할 수 있습니다.가장 간단한 일반화는 하나의 객체가 있는 범주인 모노이드에 대한 것입니다.그룹은 모든 형태소가 반전 가능한 모노이드이다.일반 모노이드는 어떤 범주에서도 표현됩니다.집합의 범주에서, 이것들은 모노이드 작용이지만, 벡터 공간 및 다른 물체에 대한 모노이드 표현을 연구할 수 있다.

보다 일반적으로, 표현되는 범주가 하나의 객체만을 가지고 있다는 가정을 완화할 수 있다.전체 일반론에서, 이것은 단지 범주 간의 함수 이론일 뿐이며, 거의 말할 수 없다.

한 가지 특별한 경우는 표현 이론, 즉 ^[14]흔들림의 표현 이론에 중요한 영향을 미쳤다.떨림은 단순한 방향 그래프(루프와 여러 화살표가 허용됨)이지만 그래프 내의 경로를 고려하여 범주(및 대수)로 만들 수 있습니다.그러한 범주/대수의 표현은 표현 이론의 여러 측면을 조명했다. 예를 들어, 그룹에 대한 반단순 표현 이론 질문을 경우에 따라 떨림에 대한 반단순 표현 이론 질문으로 줄일 수 있다.

「」를 참조해 주세요.

메모들

^ 대표이론에 관한 고전서로는 Curtis & Reiner(1962년)와 Serre(1977년)가 있다.다른 뛰어난 소스로는 Fulton & Harris(1991년)와 Goodman & Wallach(1998년)가 있다.
^ "representation theory in nLab". ncatlab.org. Retrieved 2019-12-09.
^ 유한군의 표현 이론의 역사는 Lam(1998)을 참조한다.대수 및 Lie 그룹에 대해서는 Borel(2001)을 참조하십시오.
^ ^a ^b ^c Etingof, Pavel; Golberg, Oleg; Hensel, Sebastian; Liu, Tiankai; Schwendner, Alex; Vaintrob, Dmitry; Yudovina, Elena (January 10, 2011). "Introduction to representation theory" (PDF). www-math.mit.edu. Retrieved 2019-12-09.
^ ^a ^b 벡터 공간과 선형 대수에 관한 많은 교과서들이 있다.고도의 치료에 대해서는, 「Kostrikin & Manin」(1997)을 참조해 주세요.
^ Sally & Vogan 1989.
^ ^a ^b ^c Teleman, Constantin (2005). "Representation Theory" (PDF). math.berkeley.edu. Retrieved 2019-12-09.
^ ^a ^b 스턴버그 1994년
^ 램 1998, 372페이지
^ ^a ^b ^c 1995년 폴랜드.
^ Goodman & Wallach 1998, Olver 1999, 샤프 1997.
^ 1979년 보렐 카셀만 겔바트 1984년
^ 이전 각주와 보렐(2001)을 참조하십시오.
^ ^a ^b Simson, Scowronski 및 Asem 2007.
^ Fulton & Harris 1991, Simson, Skowronski & Asem 2007, Humpreys 1972 harvnb 오류: 대상 없음: CITREFHumphreys 1972 (도움말)
^ 이 자료는 Curtis & Reiner(1962년 ), Fulton & Harris(1991년), Goodman & Wallach(1998년 ), Gordon & Liebeck(1993년) harvts 오류: 대상 없음: CITREFGordonLiebeck1993(도움말), Humphreys(1972년) 등 표준 교과서에서 찾을 수 있다.
^ ^a ^b 1977년 세레
^ 숫자 1이 합성도 아니고 소수도 아닌 것처럼 차원 0의 표현 {0}은(는) 환원도 아니고 환원도 불가능한 것으로 간주됩니다.
^ Humphreys, James E. (1975). Linear Algebraic Groups. New York, NY: Springer New York. ISBN 978-1-4684-9443-3. OCLC 853255426.
^ 홀 2015 섹션 4.3.2
^ Hall 2015 Proposition 4.18 및 정의 4.19
^ 홀 2015 부록 C
^ 1986년 알페린, 1998년 람, 1977년 세르
^ Kim 1999.
^ 1977년 Serre 3부
^ 1986년 알페린
^ Weyl 1928을 참조하십시오.
^ 위그너 1939년
^ 보렐 2001.
^ ^a ^b Knapp 2001.
^ ^a ^b 피터 & 와일 1927.
^ 바르그만 1947년
^ 폰트랴긴 1934년
^ ^a ^b 와일 1946년
^ ^a ^b ^c Fulton & Harris 1991.
^ 험프리스 1972a
^ Kac 1990.
^ Kac 1977.
^ 험프리스 1972b, Jantzen 2003.
^ 올버 1999년
^ 맘포드, 포가티 & 키르완 1994.
^ 샤프 1997.
^ 1979년 보렐 카셀만
^ 겔바트 1984년

레퍼런스

를 클릭합니다Alperin, J. L. (1986), Local Representation Theory: Modular Representations as an Introduction to the Local Representation Theory of Finite Groups, Cambridge University Press, ISBN 978-0-521-44926-7.
를 클릭합니다Bargmann, V. (1947), "Irreducible unitary representations of the Lorenz group", Annals of Mathematics, 48 (3): 568–640, doi:10.2307/1969129, JSTOR 1969129.
를 클릭합니다Borel, Armand (2001), Essays in the History of Lie Groups and Algebraic Groups, American Mathematical Society, ISBN 978-0-8218-0288-5.
를 클릭합니다Borel, Armand; Casselman, W. (1979), Automorphic Forms, Representations, and L-functions, American Mathematical Society, ISBN 978-0-8218-1435-2.
를 클릭합니다Curtis, Charles W.; Reiner, Irving (1962), Representation Theory of Finite Groups and Associative Algebras, John Wiley & Sons (Reedition 2006 by AMS Bookstore), ISBN 978-0-470-18975-7.
를 클릭합니다Gelbart, Stephen (1984), "An Elementary Introduction to the Langlands Program", Bulletin of the American Mathematical Society, 10 (2): 177–219, doi:10.1090/S0273-0979-1984-15237-6.
를 클릭합니다Folland, Gerald B. (1995), A Course in Abstract Harmonic Analysis, CRC Press, ISBN 978-0-8493-8490-5.
를 클릭합니다Fulton, William; Harris, Joe (1991). Representation theory. A first course. Graduate Texts in Mathematics, Readings in Mathematics. Vol. 129. New York: Springer-Verlag. doi:10.1007/978-1-4612-0979-9. ISBN 978-0-387-97495-8. MR 1153249. OCLC 246650103..
를 클릭합니다Goodman, Roe; Wallach, Nolan R. (1998), Representations and Invariants of the Classical Groups, Cambridge University Press, ISBN 978-0-521-66348-9.
를 클릭합니다James, Gordon; Liebeck, Martin (1993), Representations and Characters of Groups, Cambridge: Cambridge University Press, ISBN 978-0-521-44590-0.
Hall, Brian C. (2015), Lie Groups, Lie Algebras, and Representations: An Elementary Introduction, Graduate Texts in Mathematics, vol. 222 (2nd ed.), Springer, ISBN 978-3319134666
Helgason, Sigurdur (1978), Differential Geometry, Lie groups and Symmetric Spaces, Academic Press, ISBN 978-0-12-338460-7
를 클릭합니다Humphreys, James E. (1972a), Introduction to Lie Algebras and Representation Theory, Birkhäuser, ISBN 978-0-387-90053-7.
Humphreys, James E. (1972b), Linear Algebraic Groups, Graduate Texts in Mathematics, vol. 21, Berlin, New York: Springer-Verlag, ISBN 978-0-387-90108-4, MR 0396773
를 클릭합니다Jantzen, Jens Carsten (2003), Representations of Algebraic Groups, American Mathematical Society, ISBN 978-0-8218-3527-2.
를 클릭합니다Kac, Victor G. (1977), "Lie superalgebras", Advances in Mathematics, 26 (1): 8–96, doi:10.1016/0001-8708(77)90017-2.
를 클릭합니다Kac, Victor G. (1990), Infinite Dimensional Lie Algebras (3rd ed.), Cambridge University Press, ISBN 978-0-521-46693-6.
를 클릭합니다Knapp, Anthony W. (2001), Representation Theory of Semisimple Groups: An Overview Based on Examples, Princeton University Press, ISBN 978-0-691-09089-4.
를 클릭합니다Kim, Shoon Kyung (1999), Group Theoretical Methods and Applications to Molecules and Crystals: And Applications to Molecules and Crystals, Cambridge University Press, ISBN 978-0-521-64062-6.
를 클릭합니다Kostrikin, A. I.; Manin, Yuri I. (1997), Linear Algebra and Geometry, Taylor & Francis, ISBN 978-90-5699-049-7.
를 클릭합니다Lam, T. Y. (1998), "Representations of finite groups: a hundred years", Notices of the AMS, 45 (3, 4): 361–372 (Part I), 465–474 (Part II).
유리이 1세류비치.바나흐 집단 표현 이론 소개1985년 러시아어판(우크라이나 하르코프)에서 번역.Birkhauser Verlag.1988.
Mumford, David; Fogarty, J.; Kirwan, F. (1994), Geometric invariant theory, Ergebnisse der Mathematik und ihrer Grenzgebiete (2) [Results in Mathematics and Related Areas (2)], vol. 34 (3rd ed.), Berlin, New York: Springer-Verlag, ISBN 978-3-540-56963-3, MR 0214602; MR0719371 (제2판), MR1304906 (제3판)
를 클릭합니다Olver, Peter J. (1999), Classical invariant theory, Cambridge: Cambridge University Press, ISBN 978-0-521-55821-1.
를 클릭합니다Peter, F.; Weyl, Hermann (1927), "Die Vollständigkeit der primitiven Darstellungen einer geschlossenen kontinuierlichen Gruppe", Mathematische Annalen, 97 (1): 737–755, doi:10.1007/BF01447892, S2CID 120013521.
를 클릭합니다Pontrjagin, Lev S. (1934), "The theory of topological commutative groups", Annals of Mathematics, 35 (2): 361–388, doi:10.2307/1968438, JSTOR 1968438.
를 클릭합니다Sally, Paul; Vogan, David A. (1989), Representation Theory and Harmonic Analysis on Semisimple Lie Groups, American Mathematical Society, ISBN 978-0-8218-1526-7.
를 클릭합니다Serre, Jean-Pierre (1977), Linear Representations of Finite Groups, Springer-Verlag, ISBN 978-0387901909.
를 클릭합니다Sharpe, Richard W. (1997), Differential Geometry: Cartan's Generalization of Klein's Erlangen Program, Springer, ISBN 978-0-387-94732-7.
를 클릭합니다Simson, Daniel; Skowronski, Andrzej; Assem, Ibrahim (2007), Elements of the Representation Theory of Associative Algebras, Cambridge University Press, ISBN 978-0-521-88218-7.
를 클릭합니다Sternberg, Shlomo (1994), Group Theory and Physics, Cambridge University Press, ISBN 978-0-521-55885-3.
Tung, Wu-Ki (1985). Group Theory in Physics (1st ed.). New Jersey·London·Singapore·Hong Kong: World Scientific. ISBN 978-9971966577.
를 클릭합니다Weyl, Hermann (1928), Gruppentheorie und Quantenmechanik (The Theory of Groups and Quantum Mechanics, translated H.P. Robertson, 1931 ed.), S. Hirzel, Leipzig (reprinted 1950, Dover), ISBN 978-0-486-60269-1.
를 클릭합니다Weyl, Hermann (1946), The Classical Groups: Their Invariants and Representations (2nd ed.), Princeton University Press (reprinted 1997), ISBN 978-0-691-05756-9.
를 클릭합니다Wigner, Eugene P. (1939), "On unitary representations of the inhomogeneous Lorentz group", Annals of Mathematics, 40 (1): 149–204, Bibcode:1939AnMat..40..149W, doi:10.2307/1968551, JSTOR 1968551, S2CID 121773411.

외부 링크

"Representation theory", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
Alexander Kirillov Jr., Lie 그룹과 Lie 대수에 대한 소개(2008).교과서, 예비판 pdf는 저자 홈페이지에서 다운로드 할 수 있습니다.
Kevin Hartnett, (2020), Quanta 잡지의 표현 이론에 관한 기사

[1] 대표이론에 관한 고전서로는 Curtis & Reiner(1962년)와 Serre(1977년)가 있다.다른 뛰어난 소스로는 Fulton & Harris(1991년)와 Goodman & Wallach(1998년)가 있다.

[2] "representation theory in nLab". ncatlab.org. Retrieved 2019-12-09.

[3] 유한군의 표현 이론의 역사는 Lam(1998)을 참조한다.대수 및 Lie 그룹에 대해서는 Borel(2001)을 참조하십시오.

[:0-4] Etingof, Pavel; Golberg, Oleg; Hensel, Sebastian; Liu, Tiankai; Schwendner, Alex; Vaintrob, Dmitry; Yudovina, Elena (January 10, 2011). "Introduction to representation theory" (PDF). www-math.mit.edu. Retrieved 2019-12-09.

[linalg-5] 벡터 공간과 선형 대수에 관한 많은 교과서들이 있다.고도의 치료에 대해서는, 「Kostrikin & Manin」(1997)을 참조해 주세요.

[6] Sally & Vogan 1989.

[:1-7] Teleman, Constantin (2005). "Representation Theory" (PDF). math.berkeley.edu. Retrieved 2019-12-09.

[Sternberg-8] 스턴버그 1994년

[9] 램 1998, 372페이지

[Folland-10] 1995년 폴랜드.

[11] Goodman & Wallach 1998, Olver 1999, 샤프 1997.

[12] 1979년 보렐 카셀만 겔바트 1984년

[13] 이전 각주와 보렐(2001)을 참조하십시오.

[SSA-14] Simson, Scowronski 및 Asem 2007.

[15] Fulton & Harris 1991, Simson, Skowronski & Asem 2007, Humpreys 1972 harvnb 오류: 대상 없음: CITREFHumphreys 1972 (도움말)

[16] 이 자료는 Curtis & Reiner(1962년 ), Fulton & Harris(1991년), Goodman & Wallach(1998년 ), Gordon & Liebeck(1993년) harvts 오류: 대상 없음: CITREFGordonLiebeck1993(도움말), Humphreys(1972년) 등 표준 교과서에서 찾을 수 있다.

[Serre_1977-17] 1977년 세레

[18] 숫자 1이 합성도 아니고 소수도 아닌 것처럼 차원 0의 표현 {0}은(는) 환원도 아니고 환원도 불가능한 것으로 간주됩니다.

[19] Humphreys, James E. (1975). Linear Algebraic Groups. New York, NY: Springer New York. ISBN 978-1-4684-9443-3. OCLC 853255426.

[20] 홀 2015 섹션 4.3.2

[21] Hall 2015 Proposition 4.18 및 정의 4.19

[22] 홀 2015 부록 C

[23] 1986년 알페린, 1998년 람, 1977년 세르

[24] Kim 1999.

[25] 1977년 Serre 3부

[26] 1986년 알페린

[27] Weyl 1928을 참조하십시오.

[28] 위그너 1939년

[29] 보렐 2001.

[Knapp-30] Knapp 2001.

[Peter–Weyl-31] 피터 & 와일 1927.

[32] 바르그만 1947년

[33] 폰트랴긴 1934년

[Weyl-34] 와일 1946년

[Fulton-Harris-35] Fulton & Harris 1991.

[36] 험프리스 1972a

[37] Kac 1990.

[38] Kac 1977.

[39] 험프리스 1972b, Jantzen 2003.

[40] 올버 1999년

[41] 맘포드, 포가티 & 키르완 1994.

[42] 샤프 1997.

[43] 1979년 보렐 카셀만

[44] 겔바트 1984년

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[21]

[22]

[23]

[24]

[25]

[26]

[28]

[29]

[30]

[31]

[32]

[33]

[34]

[35]

[36]

[37]

[38]

[39]

[40]

[41]

[42]

[43]

[44]

v t 수학 분석의 주요 주제
미적분:통합 차별화 미분 방정식(일반 - 부분 - 확률적) 미적분의 기본 정리 변분법 벡터 미적분 텐서 미적분 행렬 미적분 적분 목록 파생상품표
실제 분석 복잡한 분석 초복소 분석 (4분위 분석) 기능 분석 푸리에 분석 최소 제곱 스펙트럼 분석 고조파 분석 P-adic 분석(P-adic 수) 측정 이론 표현 이론 기능들 연속 함수 특수 기능 제한. 시리즈 Infinity
수학 포털

Search

표현 이론

네임스페이스

더

목차

정의 및 개념

정의.

용어.

등변지도와 등변형

하위 표현, 견적 및 축소할 수 없는 표현

직접 합계 및 분해할 수 없는 표현

완전한 삭감

표현 텐서 곱

지점 및 토픽

유한군

모듈러 표현

유니터리 표현

고조파 분석

거짓말 그룹

리 대수

무한 차원 리 대수

라이 슈퍼 대게브라

선형 대수군

불변 이론

자기 형태와 수 이론

연상 대수

모듈 이론

호프 대수와 양자군

일반화

집합 이론 표현

기타 카테고리의 표현

카테고리의 표현

「」를 참조해 주세요.

메모들

레퍼런스

외부 링크

Search

표현 이론

정의 및 개념

정의.

용어.

등변지도와 등변형

하위 표현, 견적 및 축소할 수 없는 표현

직접 합계 및 분해할 수 없는 표현

완전한 삭감

표현 텐서 곱

지점 및 토픽

유한군

모듈러 표현

유니터리 표현

고조파 분석

거짓말 그룹

리 대수

무한 차원 리 대수

라이 슈퍼 대게브라

선형 대수군

불변 이론

자기 형태와 수 이론

연상 대수

모듈 이론

호프 대수와 양자군

일반화

집합 이론 표현

기타 카테고리의 표현

카테고리의 표현

「 」를 참조해 주세요.

메모들

레퍼런스

외부 링크

「」를 참조해 주세요.