주문통계

통계에서 통계 표본의 k차 통계량은 k번째-최소값과 ^[1]같습니다.순서 통계량은 순위 통계량과 함께 비모수 통계량 및 추론의 가장 기본적인 도구 중 하나입니다.

순서 통계량의 중요한 특수한 경우는 표본의 최소값과 최대값, 표본 중위수 및 기타 표본 분위수입니다.

확률론을 사용하여 연속형 분포에서 랜덤 표본의 순서 통계량을 분석할 때 누적 분포 함수를 사용하여 분석을 균등 분포의 순서 통계량으로 축소합니다.

표기법 및 예시

예를 들어, 네 개의 숫자가 관측되거나 기록되어 크기가 4인 표본이 있다고 가정합니다.샘플 값이 다음과 같은 경우

6, 9, 3, 8,

순서 통계는 다음과 같이 표시됩니다.

${\displaystyle x_{(1)}=3,\ x_{(2)=6,\ x_{(3)}=8,\ x_{(4)}=9,}$

여기서 괄호로 둘러싸인 첨자(i)는 표본의 i번째 순서 통계량을 나타냅니다.

1차 통계량(또는 최소차 통계량)은 항상 표본의 최소값입니다.

${\displaystyle X_{(1)}=\min\{,X_{1},\ldots,X_{n},\}$

여기서는 일반적인 규칙에 따라 랜덤 변수를 나타낼 때 대문자를 사용하고 실제 관측 값을 나타낼 때 소문자를 사용합니다.

마찬가지로 크기가 n인 표본의 경우 n차 통계량(또는 가장 큰 차수 통계량)이 최대값입니다.

${\displaystyle X_{(n)}=\max\{,X_{1},\ldots,X_{n},\}.}$

표본 범위는 최대값과 최소값의 차이입니다.이는 주문 통계의 함수입니다.

${\displaystyle {Range}\{,X_{1},\ldots,X_{n},\}=X_{(n)}-X_{(1)}.$

순서 통계량과 단순히 관련된 탐색적 데이터 분석에서 유사한 중요한 통계량은 표본 사분위간 범위입니다.

관측치 n개가 홀수인 경우에만 단일 중간 값이 존재하므로 표본 중위수는 순서 통계량일 수도 있고 아닐 수도 있습니다.보다 정확히는 n = 2m+1인 정수 m일 경우 표본 중위수는 X${\displaystyle {}_{}}$(${\displaystyle m_{}}$ +${\displaystyle 1_{}}$ $){$ $display style$ X_${(m+1)}$이고 순서 통계량도 마찬가지입니다.한편, n이 짝수인 경우 n = 2m이고 X${\displaystyle {}_{}}$( ${\displaystyle m_{}}$ )${\displaystyle {}_{}}$\$$$display style$ X _ { ($$$m$ )$$} $and$ X (${\displaystyle m_{}}$+$1$) }$$, $2개$의 중간값이 존재하며 샘플 중앙값은 2개의 함수(통상 평균)이므로 순서 통계량이 아니다.모든 표본 분위수에도 유사한 설명이 적용됩니다.

확률론적 분석

임의의 랜덤 변수₁ X, X₂..., X에서_n 순서 통계₍₁₎ X, X₍₂₎, ..., X도_(n) 랜덤 변수이며, X, ..., X의_n 값₁(실현)을 오름차순으로 정렬하여 정의합니다.

랜덤 변수₁ X, X₂..., X가_n 표본을 구성하면 서로 독립적이고 균등하게 분포됩니다.이하에 나타내는 케이스입니다.일반적으로 랜덤 변수₁ X, ..., X는_n 둘 이상의 모집단에서 표본을 추출하여 발생할 수 있습니다.그 후 이들은 독립적이지만 반드시 동일한 분포는 아니며, 이들의 공동 확률 분포는 바파트-베그 정리에 의해 주어진다.

지금부터 검토 중인 랜덤 변수가 연속형이라고 가정하고, 편리한 경우 확률밀도함수(PDF)가 있다고 가정한다. 즉, 절대 연속형이다.점(특히 이산 분포)에 질량을 할당하는 분포 분석의 특수성에 대해 마지막에 논의한다.

주문 통계량의 누적 분포 함수

위와 같은 랜덤샘플의 경우 ${\displaystyle {누적분포}_{}}$ ${\displaystyle F{}_{}}$X${\displaystyle }$( x$$)\$displaystyle F_${X$}($x$)\backslash$displaystyle F_{X^[2]$}(x$)\displaystyle의 누적분포는 다음과 같습니다(r은 어떤 순서통계정보를 지정합니다).

${\displaystyle F_{X_{(r)}}=\sum _{j=r}^{n}{\binom {n}{j}}[F_{X}(x)]^{j}[1-F_{X}(x)]^{n-j}$

해당 확률 밀도 함수는 이 결과로부터 도출될 수 있으며, 다음과 같은 것으로 확인된다.

${\displaystyle f_{(r)}}(x)=flac {n!}{(r-1)!(n-r)!}}f_{X}(x)[F_{X}(x)]^{r-1} [1-F_{X}(x)]^{n-r}.}$

게다가 CDF가 계산하기 쉬운 특별한 경우가 두 가지 있습니다.

${\displaystyle F_{(n)}}(x)=\operatorname {Prob}(\max\{,X_{1},\ldots,X_{n},\}\leq x)=[F_{X}(x)]^{n}}$

${\displaystyle F_{(1)}}(x)=\operatorname {Prob}(\min\{,X_{1},\ldots,X_{n},\}\leq x)=1-[1-F_{X}(x)]^{n}}$

그것은 확률을 신중하게 고려함으로써 도출될 수 있다.

순서 통계량의 확률 분포

균등 분포에서 표본 추출된 순서 통계량

이 섹션에서는 단위 간격에 대한 균일한 분포의 순서 통계량이 베타 분포군에 속하는 한계 분포를 갖는다는 것을 보여 줍니다.우리는 또한 임의의 수의 주문 통계량의 공동 분포를 도출하고 마지막으로 CDF를 사용하여 이러한 결과를 임의의 연속 분포로 변환하는 간단한 방법을 제공한다.

이 섹션에서는 ${\displaystyle {X1\mathrm{}}_{}}$ ${\displaystyle {X2\mathrm{}}_{}}$ ${\displaystyle ...,}$ $(\$이 ${\displaystyle {CDF}_{}}$X(\$displaystyle F_{X$에서 연속적으로 추출된 랜덤 샘플이라고 가정합니다. 즉, ${\displaystyle {Ui}_{}}$ ${\displaystyle {}_{}}$ $display$ I$)$를 $나타냅니다{\displaystyle {}_{}}$.${\displaystyle {}_{}}$U 1,${\displaystyle \dots ,}$ ${\displaystyle U_{}}$ n$$\$style$ U_${1},\ldots, U_{n}$ 표준$$ 균등 분포의 U_{n}.주문 통계도 U${\displaystyle {(i)}_{}}$ ${\displaystyle {}_{}}$ ${\displaystyle F_{}}$ X$)$ {$style$ U_${(i)}$를 충족합니다.$=F_{X}(X_{($i$)\})\}.$

${\displaystyle {\mathrm{주문}}_{}}$ $통계{\displaystyle {}_{}}$ U${\displaystyle {}_{}}$( k$$) \ $displaystyle U_{$ ( k$$) } 의$$ 확률 밀도 함수는 다음과 같습니다^[3].

${\displaystyle f_{U_{(k)}}(u)={n!\over(k-1)!(n-k)!}u^{k-1}(1-u)^{n-k}$

즉, 균등 분포의 k차 통계량은 베타 분포 랜덤 ^[3][4]변수입니다.

${\displaystyle U_{(k)}\sim \operatorname {Beta}(k,n+1\mathbf {-}k).}$

이러한 진술의 증거는 다음과 같습니다.U ${\displaystyle {(}_{}}$ ${\displaystyle k_{}}$)$${ $displaystyle$ U _ { ($k$ ) } u + du } 이 $되려면{\displaystyle {}_{}}$ 시료의 k - 1 원소가 u보다 작고 u + du 사이여야 한다.이 후자 간격에 여러 개 있을 확률은 $이미{\displaystyle }$ O$($$du$2)이므로 k - 1, 1, 1, n - k 관측치가 간격(0,$u)\displaystyle$(0$,u$$)\backslash ,$ (${\displaystyle u,u}$ + $)\display$ style$($${\displaystyle u}$$, du)\$${\displaystyle \mathrm{du}}$(u$$${\displaystyle ,}$ du$)\backslash {\displaystyle }$du에 ${\displaystyle \mathrm{정확히}}$ $포함$될 확률을 계산해야 합니다.displaystyle$(u+du,1)}$을 클릭합니다.이는 같습니다(자세한 내용은 다항 분포 참조).

$\displaystyle {n!\over (k-1)!(n-k)!}u^{k-1}\cdot du\cdot(1-u-du)^{n-k}$

결과는 다음과 같습니다.

이 분포의 평균은 k / (n + 1)입니다.

균등 분포의 순서 통계량에 대한 공동 분포

마찬가지로, i < j의 경우, 2차 통계_(i) U < U의_(j) 결합 확률 밀도 함수는 다음과 같이 나타낼 수 있다.

${\displaystyle f_{(i)}, U_{(j)}}(u,v)=n!{u^{i-1} \over (i-1)!}{(v-u)^{j-i-1} \over(j-i-1)!}{(1-v)^{n-j} \over (n-j)!}}$

($O{\displaystyle }$( ${\displaystyle du}$ d${\displaystyle v}$ ) {$displaystyle$ O $( du$ , $dv$ )$$} ${$ $display$ style ( 0 $, u$ )$$、 u + ${\displaystyle \mathrm{du}}\}$$$${\displaystyle 、}$ i - 1, j - i, 1 및 n - j 샘플 요소가 ( 0${\displaystyle }$, ${\displaystyle u}$ ,${\displaystyle u}$ )$、$ ${\displaystyle u}$ +$display$ ${\displaystyle \mathrm{style}}$ ($u$ , du )${\displaystyle }$、 du )${\displaystyle }$、 ${\displaystyle \mathrm{du}}$ 、 ${\displaystyle \mathrm{du}}$ ) 、 du 、 du 、 du 。$displaystyle ( v$ ,$v$ + ${\displaystyle \mathrm{dv}}$$$)$$$\}{\displaystyle }$ ,${\displaystyle }$( v +${\displaystyle d}$ ${\displaystyle \mathrm{v}}$ ,${\displaystyle 1}$) {$displaystyle ( v$ + dv ,$1$ ) 。

한 가지 이유는 전적으로 유사한 방법으로 고차 공동분포를 도출하는 것이다.놀랍게도 n차 통계량의 결합 밀도는 일정합니다.

$\displaystyle f_{U_{(1)},U_{(2)},\ldots,U_{n}}}(u_{1},u_{2},\ldots,u_{n}=n!}$

이를 이해하는 한 가지 방법은 무질서 표본의 밀도가 1과 동일하고 동일한 순서 통계량에 대응하는 표본의 배열이 n!개 있다는 것입니다.이는 1/n!이 0 < 1 < n < \ $displaystyle$0 < $u$_ { $1$} <\$cdots$< $u _$ { n }<1}의부피라는 사실과 관련이 있습니다.또, 균일한 랜덤 변수의 순서 통계의 또 다른 특수성과도 관련이 있습니다.그것은 BRS-inequality에서 균일 U(0,1하는 확률 변수의 사람 크기 n은 의 합을 0<>를 초과하지 않는 방안 인간 표본에서 선택할 수 있는 최대 예상 번호의<>n/2{0<, s<, n/2\displaystyle}위의 2sn{\displaystyle{\sqrt{2sn}에 의해}을 다스릴 수 있는},에 따라서 모든 s의 세트장에 불변이다 다음 n.{\displa$ystyle$ s$,n}$ (상수 $제품{\displaystyle }$ $\displaystyle$sn$\backslash )$을 사용합니다.

위의 공식을 사용하면 주문 통계 정보의 범위 분포, 즉${\displaystyle {}_{}}$U (${\displaystyle n_{}}$) -${\displaystyle {}_{}}$ ( ${\displaystyle 1_{}}$)$$\ $displaystyle$ U _ { ( n ) - U$_$ { (1)$$}의 분포를 $도출$할 수 있습니다.즉, 최대값에서 최소값을 뺀 값입니다.보다 일반적으로 nk > j1 {${\displaystyle {\mathrm{displaystyle}}_{}{}_{}}$ \$$ k $> j$ \ $geq$ 1의 경우 U ( k ) - U ( j ) { $displaystyle$ U _ { ( k${\displaystyle {}_{}}$) } - U _ { ( j$$)${\displaystyle {}_{}}$에는 베타 분포도 있습니다.

이러한 공식으로부터 두 순서 통계량 사이의 공분산을 도출할 수 있습니다.이 공식은 을 언급하는 것으로부터 시작된다.그걸 비교해서$여기$서 U ${\displaystyle ~}$ ${\displaystyle \mathrm{베타}}$( (${\displaystyle k}$ -${\displaystyle j}$ ,${\displaystyle n}$- (${\displaystyle k}$ -${\displaystyle j}$) +${\displaystyle 1}$ $){$ $displaystyle$ U$\sim \operatorname {Beta}(k-j,n-(k-j)+1$는 차이의 실제 분포입니다.

지수 분포에서 추출한 순서 통계량

X${\displaystyle {}_{}}$1, ${\displaystyle {X\mathrm{}}_{}}$2,${\displaystyle .,}$ ${\displaystyle X_{}}$n { $displaystyle X_{1}, X_{2},$ ..,$X_{n}$개의$$ 랜덤 샘플에 $대해{\displaystyle {}_{}}$ i = 1,2,3,...,n의 순서 통계 X는_(i) 각각 분포를 가진다.

${\displaystyle X_{i}{\stackrel {d}{=}{\frac {1}{j=1}^{i}{\frac {Z_{j+1}}\right}$

여기서 Z는_j iid 표준 지수 랜덤 변수(즉, 속도 매개변수 1)이다.이 결과는 Alfréd Rényi에 ^[5][6]의해 처음 출판되었다.

Erlang 분포에서 추출한 주문 통계량

순서 통계량의 Laplace 변환은 경로 카운트^{[clarification needed] [7]}방법을 통해 Erlang 분포에서 샘플링할 수 있습니다.

절대 연속형 분포의 순서 통계량에 대한 공동 분포

F가 절대 연속이라면 d ${\displaystyle F_{}}$_X X (${\displaystyle x}$ ) ${\displaystyle =}$ ${\displaystyle f_{}}$X (${\displaystyle x}$ ) ${\displaystyle d}$ x$$( x ) d x { displaystyle $dF_{X}$ (x) =$f_${X} (x), $dx$ 와 $같은{\displaystyle }$ 밀도를 가지며 치환을 사용할 수 있습니다.

${\displaystyle u=F_{X}(x)}$

그리고.

${\displaystyle du=f_{X}(x),dx}$

X 분포에서 추출한 크기 n 표본의 순서 통계량에 대한 다음과 같은 확률 밀도 함수를 도출합니다.

${\displaystyle f_{X_{(k)}}(x)=flac {n!}{(k-1)!(n-k)!}[F_{X}(x)]^{k-1}[1-F_{X}(x)]^{n-k}f_{X}(x)}$

${\displaystyle {f{}_{}}_{}}$$}[F_{X}($x)]^{$j-1}[F_{X}(y)-F_{X}($x)]^{$k-1-j}[1-F_{X}($y)]^{$n-k}f_${X$}(x)$$\_{\displaystyle }$${x$}(y$$$)}$여기서${\displaystyle }$x는 y$\le$ style y$\$l로 $표시$됩니다.

${\displaystyle {{}_{}{}_{}}_{}}$X ( ${\displaystyle {1_{}}_{}}$) , ${\displaystyle {...}_{}}$ ,${\displaystyle {{}_{}}_{}{}_{}}$ (${\displaystyle {}_{}{n_{}}_{}}$) ( ${\displaystyle {}_{}{1\mathrm{}}_{}}$) ${\displaystyle =n}$ ! ${\displaystyle f_{}}$X ( ${\displaystyle {x\mathrm{}}_{}{1}_{}}$ ) ${\displaystyle {}_{}}$ f${\displaystyle {}_{}{X}_{}}$ ( ${\displaystyle x_{}}$ n$){$ $display$ style f _ { X _ ${ 1$} , \$ldots , x _$ { n }$=$n !$f$_ {$X }$ ( X )$}$

용도: 분위수에 대한 신뢰 구간

흥미로운 질문은 순서 통계량이 기본 분포의 분위수 추정치로 얼마나 잘 수행되는지입니다.

작은 표본 크기의 예제

가장 간단한 경우는 표본 중위수가 모집단 중위수를 얼마나 잘 추정하느냐입니다.

예를 들어 크기가 6인 랜덤 표본을 고려해 보십시오.이 경우 표본 중위수는 일반적으로 3차 통계량과 4차 통계량으로 구분된 구간의 중간점으로 정의됩니다.그러나 이전 논의에서 이 구간이 실제로 모집단 중위수를^{[clarification needed]} 포함할 확률은 다음과 같습니다.

${\displaystyle {6\choose 3)(1/2)^6}={5 \over 16}\약 31\%}$

표본 중위수가 모집단 중위수의 분포에 의존하지 않는 최선의 점 추정치 중 하나일지라도 이 예제는 표본 중위수가 절대적인 측면에서 특별히 좋은 것은 아니라는 것을 보여 줍니다.이 경우 중위수에 대한 더 나은 신뢰 구간은 2차 통계와 5차 통계로 구분된 신뢰 구간이며, 이는 확률로 모집단 중위수를 포함합니다.

$\displaystyle \left [{6 \choose 2)+{6 \choose 3}+{6 \choose 4}\right](1/2)^6}={25 \over 32}\약 78\%}$

표본 크기가 작을 경우 95% 이상의 신뢰를 원한다면 중위수가 확률 31/32 또는 약 97%의 6개 관측치 중 최소값과 최대값 사이에 있다고 말할 수 있습니다.크기 6은 실제로 최소값과 최대값에 의해 결정된 구간이 모집단 중위수에 대한 95% 신뢰 구간이 되도록 가장 작은 표본 크기입니다.

샘플 사이즈가 크다

균일한 분포의 경우, n은 무한대 경향이 있으므로 p^th 표본 분위수는 점근 정규 분포입니다. 왜냐하면 다음과 같이 근사하기 때문입니다.

$\displaystyle U_{\lceil np\rceil}\sim AN\left(p, {\frac {p(1-p)}{n}}\right).}$

F(p)에서 ⁻¹ 연속적으로 0이 아닌 밀도를 갖는 일반 분포 F의 경우 유사한 점근 정규성이 적용됩니다.

${\displaystyle X_{(\lceil np\rceil)}\sim AN\left(F^{-1)(p),\frac {p(1-p)}{n[f(F^{-1}(p)}}}\right}$

여기서 f는 밀도 함수이고 ⁻¹ F는 F와 관련된 분위수 함수입니다.이 결과를 언급하고 증명한 최초의 사람 중 하나는 1946년 ^[8]프레데릭 모스텔러였다.1960년대에 더 많은 연구가 진행되어 오류 발견에 대한 정보를 제공하는 바하두르 표현으로 이어졌다.

분포가 대칭이고 모집단 중위수가 모집단 평균과 동일한 경우 흥미로운 관찰을 할 수 있습니다.이 경우 중심 한계 정리에 의해 표본 평균도 점근 정규 분포를 따르지만 분산 δ²/n을 가진다.이러한 점근 분석은 첨도가 낮은 경우 평균이 중위수보다 성능이 우수하며, 첨도가 낮은 경우 평균이 중위수보다 성능이 우수하다는 것을 나타냅니다.예를 들어, 중위수는 Laplace 분포에 대해 더 나은 신뢰 구간을 달성하고 평균은 정규 분포에 있는 X에 대해 더 나은 성능을 발휘합니다.

증명

라는 것을 알 수 있다

${\displaystyle B(k,n+1-k)\{stackrel {mathrm {d}{=}\{frac {X+Y}},$

어디에

${{displaystyle X=\sum _{i=1}^{k}Z_{i},\quad Y=\sum _{i=k+1}^{n+1}Z_{i}}$

Z는_i 비율이 1인 동일한 지수 랜덤 변수입니다.X/n과 Y/n은 CLT에 의해 점근적으로 정규 분포를 따르므로, 결과는 델타 방법을 적용한다.

용도: 비모수 밀도 추정

1차 통계량의 분포 모멘트를 사용하여 비모수 밀도 추정기를 ^[9]개발할 수 있습니다.예를 들어, x$$δ(\$displaystyle$ $f_{X$$\})$ $지점$에서 $밀도{\displaystyle {}_{}}$ f $(\$displaystyle f_{X$})$를 추정한다고 가정합니다. 랜덤 $변수{\displaystyle {}_{}}$ ${\displaystyle {Yi}_{}}$ ${\displaystyle {}_{}}$ ${\displaystyle X_{}}$i - ${\displaystyle {}^{}{}^{}}$δ (\$displaystyle Y_{i$} =$X_{i}-x^{*}$ $\}$ }, 즉 ${\displaystyle {분포}_{}}$ ${\displaystyle \mathrm{함수}}$ ${\displaystyle {}_{}=}$ Y = )의 i.id를 가정합니다.${\displaystyle -}$ ${\displaystyle y}$ $)({displaystyle g_{Y}(y)=f_{X}(y+$x^{*})+$f_{X}(x^{*}-y$ 특히 ${\displaystyle f_{}}$ X${\displaystyle {}_{}}$(${\displaystyle {}^{}}$†)= ${\displaystyle g\frac{{}_{}{Y}_{}}{}}$ (${\displaystyle \frac{0}{}}$ )$$ {$displaystyle f_{X}(x$^{*}-$y{\displaystyle {}_{}}$})$= frac0_G}$

$1차$ $통계{\displaystyle {}_{}}$ Y ( 1$$)${\displaystyle {}_{}}$\ $displaystyle Y_{$ (1$)$} 의$$ $예상값$은$$N \ $displaystyle$N 의 총$$ 수율입니다.

${\displaystyle E(Y_{(1)}=black {1}{(N+1)g(0)}+{\frac {1}{(N+2)}}\int _{0}{1}Q'(z)\delta _{N+1}(z)},dz}$

$여기$서 Q$(\displaystyle$ Q$)$는 $분포{\displaystyle {}_{}}$ $(\$와 관련된 분위수 함수입니다.$Y$ 및 ${\displaystyle n_{}N}$( z )${\displaystyle =}$( ${\displaystyle \mathrm{N}}$ +${\displaystyle 1}$ ) (${\displaystyle 1{}^{}}$- z )$$( \ $display$ \ $display$ _ { $N$} ( z ) = ($N$ +$1$ ) ( $1$- z )^$N$} 。잭나이프 기술과 조합된 이 방정식은 다음과 같은 밀도 추정 알고리즘의 기초가 된다.

입력: $샘플{\displaystyle }$ N개$(\displaystyle$ N$$$).$${\displaystyle \{}$ ${\displaystyle {}_{}}$ } ${\displaystyle {}_{}{}_{}^{}}$ ${\displaystyle {=}_{}^{}}$ ${\displaystyle {}_{}^{}}$ M {$displaystyle$\ { x _ { \ $ell$} \ } $_${ \ $ell$=$1$}^{ $M$} } ${\displaystyle {eval}_{}^{}}$ eval eval 。조정 $파라미터{\displaystyle }$ a ${\displaystyle (}$ ( ${\displaystyle 0}$,${\displaystyle 1}$ $){$ $displaystyle$a \ $in ( 0$ ,$1$ ) $$（ 통상 1/3 ） 。출력$:{\displaystyle }$ { ${\displaystyle {\stackrel{}{}}_{}}$^ ${\displaystyle {\ell }_{}}$ ${\displaystyle {}_{}{}_{}^{}}$ ${\displaystyle {\mathrm{\ell }}_{}^{}}$ ${\displaystyle {=}_{}^{}}$ ${\displaystyle {}_{}^{}}${ $displaystyle \{\hat {f}_{\ell }\}_$${\ell =1}^{M}$ 。 

1: $set{\displaystyle {}_{}}$ ${\displaystyle m_{}}$ ${\displaystyle N}$ ${\displaystyle {}_{}}$ round ${\displaystyle (}$ ( ${\displaystyle {N\mathrm{}}^{}}$1 -${\displaystyle {}^{}{a}^{}}$) { $displaystyle m$_ { N } = \$operatorname { round$} ( $N$$^$ { 1 - a$$) 2: ${\displaystyle s_{}}$ ${\displaystyle {}_{}}$ ${\displaystyle \frac{{}_{}}{}}$ ${\displaystyle \frac{{mN}_{}}{}}${ $displaystyle s_{N$} =$frac {N}$ {$m_{$n}$N$$}}}}$ 3: ${\displaystyle {N개}_{}}$의$$샘플이 $각각{\displaystyle {}_{}}$ ${\displaystyle {있는}_{}}$ m개의 서브셋$$$({$$displaystyle$ $m_$${N$})을 ${\displaystyle {보유}_{}}$하는${\displaystyle {}_{}}$s ${\displaystyle {}_{}}$ × m$$ ({$displaystyle$ $s_{$$N}\times m_{N$}) ${\displaystyle {매트릭스}_{}}$ M ${\displaystyle i_{}}$j ({$displaystyle M_ij})$를 $작성$합니다.4: 밀도 평가를 수행할 $벡터{\displaystyle \stackrel{}{}}$f$^(\$를 만듭니다.5: ${\displaystyle \mathrm{\ell }}$ ${\displaystyle =}$ 1 ${\displaystyle \to }$ ( \ $displaystyle$ \ell$= 1$ \ $to$ M )$$${\displaystyle =}$ ${\displaystyle 1}$ ${\displaystyle \to }$ ${\displaystyle m_{}}$N ( \ $displaystyle$ k$$$= 1$ \ $to$ $m$_ { $N$} 7$$ 7: 현재 $포인트{\displaystyle }$ x$$ \ $displaystyle$ x $_${ \ \ $ell$$$$$k$$$$} } the$$ $thestylestyle$ k$$k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k${\displaystyle {}_{}}$의 서브셋 평균을 x${\displaystyle {}_{}}$: : d ${\displaystyle {\ell }_{}}$ ${\displaystyle \underset{}{\overset{\mathrm{k}}{=}}}$ = 1 ${\displaystyle \underset{}{\overset{}{{}_{}}}}$ ${\displaystyle \underset{}{\overset{}{n_{}}}}$ ${\displaystyle \underset{}{\overset{}{{}_{}}}\frac{{}_{}}{}}$ ${\displaystyle \frac{{}_{}}{{}_{}}}$ k m$$ { \ $displaystyle$x _ { \ $ell$} = \ $sum$_ { k$$=$1$}^{ $m$_ {$N}}{\frac {d_{\ell k}}{m_{$$N}}}}$ 10$$: x ${\displaystyle {}_{}}$ : f${\displaystyle {\stackrel{}{}}_{}}$^ ${\displaystyle {\ell }_{}}$ ${\displaystyle {}_{}}$ ${\displaystyle 1\frac{\mathrm{}}{2\mathrm{}}}$ ( ${\displaystyle \frac{1}{}}$+ ${\displaystyle \frac{{}_{}{N}_{}}{}}$ ) ${\$ { \$hat$ { $f$} $_${ \ $el$ } =$sprac${ $1$} {$2$ ($1$ + s$_$ { $N$} ) d $_${ \ \ $el }}}:$ 11: $return{\displaystyle \stackrel{}{}}$ f${\displaystyle \stackrel{}{}}$style { { f style $^$ }} { { { { 1 : display }}}}}}}}}}}}}}}}: $12{\displaystyle {}_{}}$: return : fstyle { { { { { {

히스토그램 및 커널 기반 접근법에 대한 대역폭/길이 기반 튜닝 파라미터와 달리 순서 통계 기반 밀도 추정기의 튜닝 파라미터는 샘플 서브셋의 크기입니다.이러한 추정치는 히스토그램 및 커널 기반 접근법보다 강력합니다. 예를 들어 코시 분포와 같은 밀도(유한 모멘트가 결여됨)는 IQR 기반 대역폭과 같은 특수한 수정 없이 추론할 수 있습니다.이는 기본 분포의 기대값이 존재하는 경우 순서 통계량의 첫 번째 모멘트가 항상 존재하지만 그 반대가 반드시 ^[10]참인 것은 아니기 때문입니다.

이산 변수 처리

${\displaystyle {X\mathrm{}}_{}}$1, ${\displaystyle {}_{}{2\mathrm{}}_{}}$,${\displaystyle \dots ,}$ ${\displaystyle X_{}}$n(\$displaystyle$ $X_{1},X_{2},\ldots,X_{n})$이 $누적분포함수{\displaystyle }$F$(x)$와 $확률질량함수{\displaystyle }$ f$(x$의 이산분포에서 i.i.d. 랜덤변수라고 $합니다{\displaystyle {}_{}}$.$le$ k$^{\text{th}}$ 순서 통계$$, 먼저 세 가지 값이 필요합니다.

$\displaystyle p_{1}=P(X<x)=F(x),\p_{2}=P(X=x)=f(x),{\text{ 및 }}p_{3}=P(X>x)=1-F(x)}$

${\displaystyle {\text{k}}^{}}$ th$${\$displaystyle k^{\text{$th}}} 주문 통계량의 누적 분포 함수는 다음과 같이 계산될 수 있습니다.

${\displaystyle {begin{aligned}P(X_{(k)}\leq x)&=P({\text{}x보다 작거나 같은 관측치가 }}k개 이상 있음),\&=P({\text{\text{보다 큰 관측치가 }개소}개 이상 있음),\\={{}개소}개소}개소}개소}개소}개소\end { aligned}}$

마찬가지로 P( ( $){$ $displaystyle$ P$(X_{(k)}<x)}$는 다음과 같이 표시됩니다.

${\displaystyle {begin{aligned}P(X_{(k)}<x)&=P({\text{}x보다 작은 관측치가 }}개 이상 있음),\\&=P({\text{\text{\}x보다 크거나 같은 관측치가 }개소 있음),\\&=\\sum={n^{{{}_n}개소}개소}개소}개소}개소}개소}개소\end { aligned}}$

Note that the probability mass function of ${\displaystyle X_{(k)}}$ is just the difference of these values, that is to say

${\displaystyle {begin {(k)}=x)&=P(X_{(k)}\leq x)-P(X_{(k)}<x),\&={j=0}^n-k}{n \choose j}\left(p_{3}^{j+}p}{1}p_1}^{j}(F(x)-f(x))^{n-j}\right).\end { aligned}}$

주문 통계 계산

리스트에서 k번째로 작은(또는 가장 큰) 요소를 계산하는 문제는 선택 문제라고 불리며 선택 알고리즘에 의해 해결됩니다.이 문제는 매우 큰 목록에서는 어렵지만 목록이 완전히 정렬되지 않은 경우에도 목록 내의 요소 수에 비례하여 이 문제를 시간 내에 해결할 수 있는 정교한 선택 알고리즘이 작성되었습니다.데이터가 특정 특수 데이터 구조에 저장되어 있으면 이 시간을 O(log n)로 낮출 수 있습니다.많은 응용 프로그램에서는 모든 순서 통계가 필요하며, 이 경우 정렬 알고리즘을 사용할 수 있으며 소요 시간은 O(n log n)입니다.

「 」를 참조해 주세요.

• 랭킷
• 상자 그림
• BRS-불균등
• 병용(통계)
• 피셔-티펫 분포
• 독립적이지만 반드시 동일하지는 않은 랜덤 변수의 순서 통계량에 대한 Bapat-Beg 정리
• 번스타인 다항식
• L-추정자 – 순서 통계량의 선형 조합
• 랭크 사이즈 분포
• 선택 알고리즘

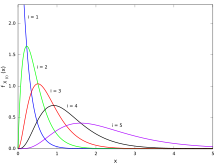
순서 통계의 예

• 샘플 최대값과 최소값
• 양분위수
• 백분위수
• 십진수
• 사분위수
• 중앙값

이 문서에는 일반적인 참조 목록이 포함되어 있지만 대응하는 충분한 인라인 인용이 없습니다. 좀 더 정밀한 인용문을 도입하여 이 기사의 개선에 협조해 주십시오.(2010년 12월) (이 템플릿메시지의 삭제 방법과 삭제 타이밍에 대해 알아보기)

레퍼런스

외부 링크

• PlanetMath에서 통계정보를 정렬합니다.2005년 2월 2일 취득
• Weisstein, Eric W. "Order Statistic". MathWorld. 2005년 2월 2일 취득
• C++ 소스 다이내믹 오더 통계 정보