고전역학

이 기사는 검증을 위해 추가 인용이 필요합니다. 신뢰할 수 있는 출처에 인용을 추가하여 이 기사를 개선하는 데 도움을 주세요. 출처가 없는 재료는 문제가 발생하여 제거될 수 있습니다. 출처 찾기 : "Classical mechanics" – 뉴스 · 신문 · 책 · 학자 · JSTOR (2022년 7월) (본 템플릿 메시지 제거 방법 및 시기에 대해 알아보기)

시리즈의 일부
고전역학
${\displaystyle {\textbf {F}}={\frac {d}{dt}}}(m{\textbf {v}})}$ 운동 제2법칙
역사 타임라인 교재
나뭇가지 응용의 천상 연속체 역학 운동학 동역학 통계학 통계역학
펀더멘털 가속도 각운동량 커플 달랑베르 원리 에너지 운동의 잠재적인 힘. 기준틀 관성 기준틀 충동 관성/관성 모멘트 덩어리 기계력 기계작업 순간. 운동량 공간 스피드 시간을 토크 속도 가상작업
제형 뉴턴의 운동 법칙 해석역학 라그랑주 역학 해밀턴 역학 루시아 역학 해밀턴-야코비 방정식 아펠의 운동방정식 쿱만-본 노이만 역학
핵심주제 감쇠 변위 운동방정식 오일러 운동 법칙 가공의 힘 마찰 고조파 발진기 관성/비관성 기준틀 평면입자운동의 역학 움직임(선형) 뉴턴의 만유인력 법칙 뉴턴의 운동 법칙 상대속도 강체 동역학 오일러 방정식 단순 고조파 운동 진동
회전 원운동 회전기준틀 구심력 원심력 반응성이 있는 코리올리스 힘 진자 접선 속도 회전주파수 각가속도/변위/주파수/속도
사이언티스트 케플러 갈릴레오 호이겐스 뉴턴 경이다. 호록스 핼리 모페르투이스 다니엘 베르누이 요한 베르누이 오일러 달랑베르 클라우로 라그랑주 라플라스 해밀턴 포아송 코시 루스 리우빌 아펠 깁스 쿠프만 폰 노이만
물리 포털 카테고리
v t

고전역학은 발사체에서 우주선, 행성, 별, 은하 등 기계와 천문학적인 물체의 일부에 이르기까지 거시적인 물체의 운동을 설명하는 물리 이론입니다. "고전 역학"에서 "고전"은 예를 들어, 고전 건축에서 말하는 것처럼 고전 고대를 가리키는 것이 아닙니다. 반대로, 고전역학의 발전은 물리학의 방법과 철학에 상당한 변화를 수반했습니다.^[1] 대신 수식어는 고전역학의 한계를 드러낸 20세기 초 혁명 이후 발전한 물리학과 고전역학을 구분합니다.^[2]

고전 역학의 가장 초기 공식은 종종 뉴턴 역학이라고 불립니다. 아이작 뉴턴 경의 17세기 기초적인 작업에 기초한 물리적 개념과 고트프리트 빌헬름 라이프니츠, 레온하르트 오일러 등이 발명한 수학적 방법으로 힘의 영향을 받는 물체의 운동을 설명합니다. 이후 에너지를 기반으로 한 방법들이 오일러, 조셉 루이 라그랑주, 윌리엄 로완 해밀턴 등에 의해 개발되어 라그랑주 역학과 해밀턴 역학을 포함한 해석역학으로 이어졌습니다. 이러한 발전은 주로 18세기와 19세기에 이루어졌으며, 이전의 작품들을 훨씬 뛰어넘어 확장되고 있습니다. 현대 물리학의 모든 분야에서 약간의 수정을 거쳐 사용되고 있습니다.

고전역학에 의하여 지배되는 물체에 대하여, 현재의 상태를 절대적인 정밀도로 알 수 있다면, 앞으로 어떻게 움직일 것인지를 예측할 수 있고(결정론), 그리고 그것이 과거에 어떻게 움직였는지(revers 가능성). 실제로 절대 정밀도는 가능하지 않으며 혼돈 이론은 고전 역학의 장기 예측이 신뢰할 수 없다는 것을 보여줍니다. 고전역학은 극도로 무겁지 않고 속도가 빛의 속도에 접근하지 않는 큰 물체를 연구할 때 정확한 결과를 제공합니다. 검사 대상 물체가 원자 지름 정도의 크기를 가질 때, 역학의 또 다른 주요 하위 분야인 양자역학을 도입하는 것이 필요하게 됩니다. 빛의 속도에 비해 작지 않은 속도를 설명하려면 특수 상대성 이론이 필요합니다. 물체가 극도로 거대해지는 경우에는 일반 상대성 이론이 적용될 수 있습니다. 그러나 현대의 많은 출처에는 고전 물리학의 상대론적 역학이 포함되어 있으며, 이는 그들의 관점에서 가장 발전되고 정확한 형태로 고전 역학을 나타냅니다.

나뭇가지

전통분업

고전 역학은 전통적으로 세 가지 주요 갈래로 나누어져 있었습니다. 정적은 가속을 경험하지 않고 오히려 환경과 평형을 이루는 물리적 시스템에 작용하는 힘과 토크의 분석과 관련된 고전 역학의 한 분야입니다.^[3] 운동학은 움직이는 힘을 고려하지 않고 점, 물체(물체), 물체의 계(물체군)의 운동을 설명합니다.^[4][5][3] 운동학은 흔히 "운동의 기하학"이라고 불리며 수학의 한 분야로 여겨지기도 합니다.^[6][7][8] 역학은 단순히 물체의 행동을 설명하는 것을 넘어 그것을 설명하는 힘도 고려합니다. 일부 저자(예: Taylor(2005)^[9]와 Greenwood(1997)^[10]는 고전 역학 내의 특수 상대성 이론을 포함합니다.

힘 대 에너지

또 다른 구분은 수학적 형식주의의 선택에 기반을 두고 있습니다. 고전 역학은 수학적으로 여러 가지 다른 방식으로 제시될 수 있습니다. 이러한 다른 제형의 물리적 내용은 동일하지만 다른 통찰력을 제공하고 다른 유형의 계산을 용이하게 합니다. "뉴턴 역학"이라는 용어는 비상대론적 고전 물리학의 동의어로 사용되기도 하지만, 뉴턴의 운동 법칙에 기초한 특정한 형식주의를 가리킬 수도 있습니다. 이런 의미에서 뉴턴 역학은 힘을 벡터량으로 강조합니다.^[11]

이와 대조적으로 해석역학은 시스템 전체를 나타내는 스칼라 운동 특성(보통 운동 에너지와 위치 에너지)을 사용합니다. 운동 방정식은 스칼라의 변화에 대한 몇 가지 기본 원칙에 의해 스칼라 양에서 파생됩니다. 해석 역학의 두 가지 주요 분야는 구성 공간에서 일반화된 좌표와 해당 일반화된 속도를 사용하는 라그랑지안 역학과 위상 공간에서 좌표와 해당 운동량을 사용하는 해밀턴 역학입니다. 두 공식 모두 일반화된 좌표, 속도 및 운동량에 대한 레전드르 변환에 의해 동등합니다. 따라서 두 공식은 시스템의 역학을 설명하는 데 동일한 정보를 포함합니다. 해밀턴-자코비 이론, 루션 역학, 아펠의 운동 방정식과 같은 다른 공식들이 있습니다. 입자와 장에 대한 모든 운동 방정식은 어떤 형식주의에서도 최소 작용의 원리라고 불리는 널리 적용 가능한 결과에서 도출될 수 있습니다. 한 가지 결과는 보존 법칙과 관련된 대칭을 연결하는 진술인 Nother's theorem입니다.

신청지역별

또는 애플리케이션 영역별로 구분할 수 있습니다.

• 별, 행성 및 기타 천체와 관련된 천체 역학
• 연속체 역학, 연속체로 모델링된 재료, 예를 들어 고체 및 유체(즉, 액체 및 기체).
• 상대론적 역학(즉, 특수 상대성 이론과 일반 상대성 이론을 포함)은 속도가 빛의 속도에 가까운 물체를 위한 것입니다.
• 개별 원자와 분자의 미시적 특성을 물질의 거시적 또는 벌크 열역학적 특성과 연관시키는 프레임워크를 제공하는 통계역학.

물체와 물체의 움직임에 대한 설명

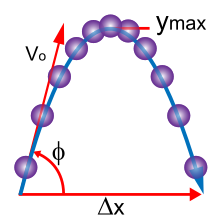
단순화를 위해 고전역학에서는 현실 세계의 물체를 점입자, 즉 무시할 수 있는 크기의 물체로 모델링하는 경우가 많습니다. 점입자의 운동은 소수의 매개변수, 즉 위치, 질량, 그리고 점입자에 가해지는 힘에 의해 결정됩니다. 고전역학은 또한 확장된 비점과 같은 물체의 더 복잡한 운동을 설명합니다. 오일러 법칙은 이 영역에서 뉴턴 법칙의 확장을 제공합니다. 각운동량의 개념은 1차원 운동을 설명하는 데 사용되는 것과 같은 미적분학에 의존합니다. 로켓 방정식은 물체의 운동량 변화율의 개념을 확장하여 물체 "잃어가는 질량"의 영향을 포함합니다. (이러한 일반화/확장은 예를 들어, 고체를 점들의 집합으로 분해함으로써 뉴턴의 법칙에서 유도됩니다.)

실제로는 고전역학이 묘사할 수 있는 물체의 종류는 항상 0이 아닌 크기를 가지고 있습니다. (전자와 같은 매우 작은 입자의 행동은 양자역학에 의해 더 정확하게 설명됩니다.) 크기가 0이 아닌 물체는 예를 들어 야구공이 움직이는 동안 회전할 수 있는 추가적인 자유도 때문에 가상의 점입자보다 더 복잡한 행동을 합니다. 그러나 점 입자에 대한 결과는 이러한 물체를 복합 물체로 취급하여 연구하는 데 사용할 수 있으며, 이는 다수의 집합적으로 작용하는 점 입자로 구성됩니다. 복합 물체의 질량 중심은 점입자처럼 행동합니다.

고전 역학은 물질과 에너지가 공간에서의 위치와 속도와 같은 확실하고 알 수 있는 속성을 가지고 있다고 가정합니다. 또한 비상대론적 역학은 힘이 순간적으로 작용한다고 가정합니다(거리에서의 작용도 참조).

운동학

SI에서 파생된 "기계적"
(즉, 전자기 또는 열적이 아님)
kg, m, s 단위

위치	m
각진 위치/각도	유니트리스(라디안)
속도	m·s−1
각속도	ㅅ−1
가속도	m·s−2
각가속도	ㅅ−2
얼간이	m·s−3
"angular 저크"	ㅅ−3
비에너지	m2·s−2
흡수 선량률	m2·s−3
관성 모멘트	kg·m2
기세	kg·m·s−1
각운동량	kg·m2·s−1
힘.	kg·m·s−2
토크	kg·m2·s−2
에너지	kg·m2·s−2
힘	kg·m2·s−3
압력과 에너지 밀도	kg·m−1·s−2
표면 장력	kg·s−2
용수철 상수	kg·s−2
복사와 에너지 흐름	kg·s−3
운동학적 점성	m2·s−1
동적 점성	kg·m−1·s−1
밀도(질량밀도)	kg·m−3
비중(비중밀도)	kg·m−2·s−2
수밀도	m−3
액션.	kg·m2·s−1

점입자의 위치는 원점 O라고 불리는 공간의 임의의 고정된 기준점을 중심으로 하는 좌표계와 관련하여 정의됩니다. 단순 좌표계는 원점 O에서 점 P를 가리키는 화살표 r로 표시된 벡터로 입자 P의 위치를 설명할 수 있습니다. 일반적으로 점입자는 O에 대해 정지해 있을 필요가 없습니다. P가 O에 대해 상대적으로 움직이는 경우 r은 t, 시간의 함수로 정의됩니다. 아인슈타인 이전의 상대성 이론(Galilean 상대성 이론으로 알려져 있음)에서 시간은 절대적인 것으로 간주됩니다. 즉, 주어진 한 쌍의 사건 사이에서 경과하는 것으로 관찰되는 시간 간격은 모든 관찰자에게 동일합니다.^[12] 절대 시간에 의존하는 것 외에도 고전역학은 공간의 구조에 대해 유클리드 기하학을 가정합니다.^[13]

속도와 속도

속도 또는 시간에 따른 변위 변화율은 시간에 대한 위치의 도함수로 정의됩니다.

${\displaystyle \mathbf{}\mathbf{v}}$ = $drd$t {\displaystyle \mathbf${\displaystyle \mathbf{}}${v} = {\mathrm {d} \mathbf {r} \over \mathrm {d} t}\,\!}.

고전 역학에서 속도는 직접 가산 및 감산입니다. 예를 들어, 한 자동차가 60km/h로 동쪽으로 이동하고 50km/h로 같은 방향으로 이동하는 다른 자동차를 지나간다면, 느린 자동차는 더 빠른 자동차를 60 - 50 = 10km/h로 동쪽으로 이동하는 것으로 인식합니다. 그러나 더 빠른 차의 관점에서 볼 때, 더 느린 차는 서쪽으로 10km/h를 이동하고 있으며, 종종 표지판이 반대 방향을 암시하는 -10km/h로 표시됩니다. 속도는 벡터 양으로 직접 가산됩니다. 벡터 분석을 사용하여 처리해야 합니다.

수학적으로 앞의 논의에서 제1객체의 속도를 벡터 u = ud로, 제2객체의 속도를 벡터 v = v로 표기하면, u는 제1객체의 속도, v는 제2객체의 속도, d와 e는 각각 각 물체의 운동 방향의 단위 벡터, 그러면 두 번째 물체가 보는 첫 번째 물체의 속도는 다음과 같습니다.

${\displaystyle \mathbf {u} '=\mathbf {u} -\mathbf {v} \,}$

마찬가지로 첫 번째 물체는 두 번째 물체의 속도를 다음과 같이 봅니다.

${\displaystyle \mathbf {v'} =\mathbf {v} -\mathbf {u} \,}$

두 물체가 같은 방향으로 움직일 때 이 방정식은 다음과 같이 단순화할 수 있습니다.

${\displaystyle \mathbf {u} '=(u-v)\mathbf {d} \,}$

또는 방향을 무시함으로써 속도로만 차이를 부여할 수 있습니다.

${\displaystyle u'=u-v\,}$

가속도

가속도 또는 속도 변화율은 시간에 대한 속도의 도함수(시간에 대한 위치의 2차 도함수)입니다.

${\displaystyle \mathbf {a} = {\mathrm {d} \mathbf {v} \over \mathrm {d} t} = {\mathrm {d^{2}} \mathbf {r} \over \mathrm {d} t^{2}}}$

가속도는 시간에 따른 속도의 변화를 나타냅니다. 속도는 크기, 방향 또는 둘 다 변할 수 있습니다. 때때로 속도 "v"의 크기가 감소하는 것을 감속이라고 하지만 일반적으로 감속을 포함하여 시간에 따른 속도의 변화를 가속도라고 합니다.

기준틀

입자의 위치, 속도 및 가속도는 운동 상태에 있는 모든 관찰자에 대해 설명할 수 있지만 고전 역학은 자연의 기계적 법칙이 비교적 간단한 형태를 취하는 특별한 기준 프레임 계열의 존재를 가정합니다. 이러한 특별한 기준 프레임을 관성 프레임이라고 합니다. 관성 프레임은 0의 알짜 힘이 작용하는 물체가 일정한 속도로 움직이는 이상적인 기준 프레임입니다. 즉, 정지 상태이거나 직선으로 균일하게 움직이는 것입니다. 관성 프레임에서 뉴턴의 운동 법칙인 $F$ = ${\displaystyle \mathrm{ma}}$ ${\$displaystyle F = ma}는 유효합니다.

비 관성 기준 프레임은 다른 관성 프레임과 관련하여 가속됩니다. 관성 프레임을 기준으로 회전하는 몸체는 관성 프레임이 아닙니다.^[14] 관성 프레임에서 볼 때 비 관성 프레임의 입자는 기준 프레임의 기존 장으로부터의 힘에 의해 설명되지 않는 방식으로 움직이는 것으로 보입니다. 따라서 상대가속도에 의해서만 운동방정식에 들어가는 다른 힘들이 있는 것처럼 보입니다. 이 힘들을 가상의 힘, 관성력, 또는 유사한 힘이라고 합니다.

두 개의 기준 프레임을 고려합니다. S'. 각 참조 프레임의 관측자에 대해 이벤트는 프레임 S 및 (x,y,z,t)의 시공간 좌표를 갖습니다.x',y',z',t') 틀 안에서 S'. 시간이 모든 기준 프레임에서 동일하게 측정된다고 가정할 때, t = 0일 때 x = 를 필요로 할 경우, 기준 프레임에서 관찰된 동일한 이벤트의 시공간 좌표 사이의 관계 S' x방향으로 상대속도 u로 움직이는 S는 다음과 같습니다.

${\displaystyle {aligned}x'&=x-tu,\y'&=y,\z'&=z,\t'&=t.\end{align}}}$

이 공식 집합은 갈릴레이 변환(비공식적으로는 갈릴레이 변환)으로 알려진 군 변환을 정의합니다. 이 군은 특수 상대성 이론에서 사용되는 푸앵카레 군의 제한적인 경우입니다. 제한적인 경우는 속도 u가 빛의 속도인 c에 비해 매우 작을 때 적용됩니다.

변환의 결과는 다음과 같습니다.

• v' = v - u (S'의 관점에서 입자의 속도 v'는 S의 관점에서 입자의 속도 v보다 u만큼 느림)
• a' = a (입자의 가속도는 어떤 관성 기준틀에서도 동일)
• F' = F (입자에 대한 힘은 어떤 관성 기준틀에서도 동일)
• 빛의 속도는 고전역학에서 상수가 아니며, 상대론적 역학에서 빛의 속도에 주어진 특별한 위치는 고전역학에서 그에 대응하지 않습니다.

일부 문제의 경우 회전 좌표(기준 프레임)를 사용하는 것이 편리합니다. 따라서 편리한 관성 프레임에 대한 매핑을 유지하거나 가상의 원심력과 코리올리 힘을 추가로 도입할 수 있습니다.

뉴턴 역학

물리학에서의 힘은 물체의 속도를 변화시키는, 즉 가속시키는 모든 작용입니다. 힘은 정전기장(정전하에 의한), 전자기장(움직이는 전하에 의한) 또는 중력장(질량에 의한)과 같은 필드 내에서 발생합니다.

뉴턴은 힘과 운동량 사이의 관계를 수학적으로 표현한 최초의 사람입니다. 어떤 물리학자들은 뉴턴의 운동 제2법칙을 힘과 질량의 정의로 해석하는 반면, 다른 사람들은 뉴턴의 운동 제2법칙을 기본적인 가정, 자연의 법칙으로 간주합니다.^[15] 두 해석 모두 역사적으로 "뉴턴의 제2법칙"으로 알려진 수학적 결과를 가지고 있습니다.

${\displaystyle \mathbf {F} = {\mathrm {d} \mathbf {p} \over \mathrm {d} t} = {\mathrm {d} (m\mathbf {v}) \over \mathrm {d} t}}$

수량 mv를 (정규) 운동량이라고 합니다. 따라서 입자에 대한 알짜 힘은 시간에 따른 입자의 운동량 변화율과 같습니다. 가속도의 정의는 = dv/dt이므로 두 번째 법칙은 단순화되고 더 친숙한 형태로 작성될 수 있습니다.

${\displaystyle \mathbf {F} = m\mathbf {a} \,}$

입자에 작용하는 힘을 알기만 하면, 뉴턴의 제2법칙으로 입자의 운동을 설명할 수 있습니다. 일단 입자에 작용하는 각 힘에 대한 독립적인 관계를 이용할 수 있게 되면 뉴턴의 제2법칙에 대입하여 일반적인 미분방정식을 얻을 수 있는데, 이를 운동방정식이라고 합니다.

예를 들어, 마찰은 입자에 작용하는 유일한 힘이며, 다음과 같이 입자의 속도에 대한 함수로 모델링될 수 있다고 가정합니다.

${\displaystyle \mathbf {F} _{\rm {R}}=-\lambda \mathbf {v,}$

여기서 λ는 양의 상수이고, 음의 부호는 힘이 속도의 감각과 반대라는 것을 나타냅니다. 그러면 운동방정식은

${\displaystyle -\lambda \mathbf {v} =m\mathbf {a} =m{\mathrm {d} \mathbf {v} \over \mathrm {d} t}\,}$

이를 통합하여 다음을 얻을 수 있습니다.

${\displaystyle \mathbf {v} =\mathbf {v} _{0}e^{-\lambda t}/{m}}$

여기서₀ v는 초기 속도입니다. 이것은 이 입자의 속도가 시간이 지남에 따라 지수 함수적으로 0으로 감소한다는 것을 의미합니다. 이 경우, 입자의 운동 에너지가 마찰에 의해 흡수되어(에너지 보존에 따라 열 에너지로 변환됨) 입자가 느려지는 것이 동등한 관점입니다. 이 식을 더 적분하여 입자의 위치 r을 시간의 함수로 구할 수 있습니다.

중요한 힘에는 중력과 전자기력에 대한 로렌츠 힘이 포함됩니다. 또한 뉴턴의 제3법칙은 때때로 입자에 작용하는 힘을 추론하는 데 사용될 수 있습니다. 만약 입자 A가 다른 입자 B에 F의 힘을 작용한다고 알려지면, B는 A에 대해 동등하고 반대의 반력인 -F를 작용해야 합니다. 뉴턴의 제3법칙의 강한 형태는 F와 -F가 A와 B를 잇는 선을 따라 작용할 것을 요구하지만 약한 형태는 그렇지 않습니다. 뉴턴의 제3법칙의 약한 형태에 대한 삽화는 종종 자기력에 대해 발견됩니다.^{[clarification needed]}

일과 에너지

변위 δRr을 만드는 입자에 일정한 힘 F가 가해지면 힘에 의해 수행되는 일은 힘과 변위 벡터의 스칼라 곱으로 정의됩니다.

${\displaystyle W=\mathbf {F} \cdot \Delta \mathbf {r} \,}$

더 일반적으로 입자가 경로 C를 따라 r에서₁ r로₂ 이동할 때 위치 함수에 따라 힘이 변하면 입자에 대한 일은 선분적분에 의해 주어집니다.

${\displaystyle W=\int_{C}\mathbf {F}(\mathbf {r})\cdot \mathrm {d} \mathbf {r} \,}$

입자를 r에서₁ r로₂ 이동시키는 작업이 어떤 경로를 택하든 동일하다면 힘은 보수적이라고 합니다. 후크의 법칙에 의해 주어진 이상화된 용수철에 의한 힘과 마찬가지로 중력은 보존력입니다. 마찰로 인한 힘은 비보존적입니다.

속력 v로 이동하는 질량 m의 입자의 운동에너지 E는_k 다음과 같이 주어집니다.

${\displaystyle E_{\mathrm {k} }={\tfrac {1}{2}}mv^{2}\,.}$

많은 입자로 구성된 확장된 물체의 경우 합성체의 운동 에너지는 입자의 운동 에너지의 합입니다.

일-에너지 정리는 일정한 질량 m의 입자에 대해 위치 r에서₁ r로₂ 이동할 때 입자에 대해 행해지는 총 일 W는 입자의 운동 에너지 E의_k 변화와 같다는 것을 말합니다.

${\displaystyle W=\Delta E_{\mathrm {k} }=E_{\mathrm {k_{2}} }-E_{\mathrm {k_{1}} }={\tfrac {1}{2}}m\left(v_{2}^{\,2}-v_{1}^{\,2}\right).}$

보존력은 위치 에너지로 알려져 있고 E로_p 표시되는 스칼라 함수의 기울기로 표현할 수 있습니다.

${\displaystyle \mathbf {F} = -\mathbf {\nabla } E_{\mathrm {p} }\,.}$

입자에 작용하는 모든 힘이 보존적이고, E가_p 각 힘에 해당하는 퍼텐셜 에너지를 합산하여 얻은 총 퍼텐셜 에너지(체의 상호 위치를 재배열하는 관련 힘의 작용으로 정의됨)라면,

${\displaystyle \mathbf {F} \cdot \Delta \mathbf {r} =-\mathbf {\nabla } E_{\mathrm {p} }\cdot \Delta \mathbf {r} =-\Delta E_{\mathrm {p} }\,.}$

퍼텐셜에너지의 감소는 운동에너지의 증가와 같습니다.

${\displaystyle -\Delta E_{\mathrm {p} }=\Delta E_{\mathrm {k} }\Rightarrow \Delta (E_{\mathrm {k} }+E_{\mathrm {p} })=0\,.}$

이 결과는 에너지 보존으로 알려져 있으며 총 에너지는

${\displaystyle \sum E=E_{\mathrm {k}}+E_{\mathrm {p}\,}$

시간은 일정합니다. 흔히 접하는 많은 힘이 보수적이기 때문에 유용한 경우가 많습니다.

라그랑주 역학

라그랑주 역학은 정지 작용 원리(최소 작용 원리라고도 함)에 기초한 고전 역학의 공식입니다. 이탈리아계 프랑스인 수학자이자 천문학자인 조제프 루이 라그랑주가 1760년^[16] 토리노 과학 아카데미에 발표한 발표에서 소개한 것으로, 1788년 대작인 메카니크 분석 기법이 절정에 달했습니다. 라그랑지안 역학은 기계 시스템을 라그랑지안이라고 불리는 공간 내에서$$ 구성 $공간$ $M$ ${\textstyle$$$M$}$과 매끄러운 함수 $L$ ${\textstyle L}$으로 구성된$$ 쌍$$($M, L)$으로 설명합니다. 많은 시스템에서 $L$ = $T$- $,$ {\$textstyle$ L = T-V,} 여기서 T {\textstyle T$}$ 및 V {\displaystyle V}는 각각 시스템의 운동 및 위치 에너지입니다. 정지 작용 원리는 $L$ ${\textstyle L}$에서 파생된 시스템의 작용 함수가 시스템의 시간 진화 동안 정지된 점(최대, 최소 또는 안장)에 유지되어야$$ 함을 요구합니다. 이 제약은 라그랑주 방정식을 사용하여 시스템의 운동 방정식을 계산할 수 있게 해줍니다.^[17]

해밀턴 역학

해밀턴 역학은 1833년 라그랑주 역학의 재구성으로 등장했습니다. 윌리엄 로완 해밀턴 경에 의해 소개된 해밀턴 역학은 라그랑주 역학에서 사용되는 (일반화된) $속도$ $q$˙i ${\displaystyle${\dot {q}}^{i}}를 (일반화된) 모멘트로 대체합니다. 두 이론 모두 고전 역학에 대한 해석을 제공하고 동일한 물리적 현상을 설명합니다. 해밀턴 역학은 기하학(특히 단순 기하학 및 포아송 구조)과 밀접한 관계를 가지며 고전 역학과 양자 역학의 연결고리 역할을 합니다.

이 형식주의에서 계의 동역학은 해밀턴 방정식에 의해 지배됩니다. 해밀턴 방정식은 위치와 운동량 변수의 시간 도함수를 해밀턴 방정식이라고 불리는 함수의 편도함수로 표현합니다.

해밀토니안은 라그랑지안의 레전드르 변환이며, 많은 물리적 관심 상황에서 계의 총 에너지와 동일합니다.

유효성의 한계

고전역학의 많은 분야는 더 정확한 형태의 단순화 또는 근사화입니다. 가장 정확한 두 가지는 일반 상대성 이론과 상대론적 통계역학입니다. 기하광학은 빛의 양자 이론에 대한 근사치이며, 우월한 "고전적" 형태를 가지고 있지 않습니다.

자유도가 많은 양자 수준과 같이 양자역학과 고전역학이 모두 적용될 수 없을 때 양자장이론(QFT)이 사용됩니다. QFT는 상호작용 전반에 걸쳐 입자 수에 변화가 있을 가능성뿐만 아니라 많은 자유도를 가진 작은 거리와 큰 속도를 다룹니다. 거시적 차원에서 큰 자유도를 다룰 때 통계역학이 유용해집니다. 통계역학은 거시적 수준에서 많은 수의 입자의 행동과 전체적인 상호작용을 설명합니다. 통계역학은 주로 고전적인 열역학의 가정의 한계를 벗어난 계에 열역학에서 사용됩니다. 빛의 속도에 접근하는 고속 물체의 경우 특수 상대성 이론에 의해 고전 역학이 강화됩니다. 물체가 극도로 무거워지는 경우(즉, 주어진 응용 프로그램에 대해 슈바르츠실트 반경이 무시할 정도로 작지 않음), 뉴턴 역학으로부터의 편차는 명백해지고 매개변수화된 포스트 뉴턴 형식주의를 사용하여 정량화될 수 있습니다. 그 경우 일반 상대성 이론(GR)이 적용됩니다. 하지만 지금까지는 물체가 극도로 작아지고 무거워질 때 사용할 수 있다는 의미에서 GR과 QFT를 통합하는 양자중력 이론은 없었습니다.^[4][5]

특수 상대성 이론에 대한 뉴턴의 근사치

특수 상대성 이론에서 입자의 운동량은 다음과 같이 주어집니다.

${\displaystyle \mathbf {p} ={\frac {m\mathbf {v} }{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}}\,,}$

여기서 m은 입자의 정지 질량, 속도, v는 v의 모듈러스, c는 빛의 속도입니다.

v가 c에 비해 매우 작으면 v²/c는² 대략 0이므로,

${\displaystyle \mathbf {p} \approx m\mathbf {v} \,}$

따라서 뉴턴 방정식 p = mv는 빛의 속도와 비교하여 저속으로 움직이는 물체에 대한 상대론적 방정식의 근사치입니다.

예를 들어, 사이클로트론, 자이로트론 또는 고전압 마그네트론의 상대론적 사이클로트론 주파수는 다음과 같이 주어집니다.

${\displaystyle f=f_{\mathrm {c} }{\frac {m_{0}}{m_{0}+{\frac {T}{c^{2}}}}}\,,}$

여기서_c f는 자기장에서 운동에너지 T와 (정지) 질량₀ m을 가진 전자(또는 다른 하전입자)의 고전적 진동수입니다. 전자의 (정지된) 질량은 511 keV입니다. 따라서 주파수 보정은 5.11kV 직류 가속 전압을 가진 자기 진공관의 경우 1%입니다.

양자역학에 대한 고전적 근사치

고전역학의 광선 근사는 드브로이 파장이 시스템의 다른 차원보다 훨씬 작지 않을 때 분해됩니다. 상대론적이지 않은 입자의 경우, 이 파장은

${\displaystyle \lambda ={\frac {h}{p}}$

여기서 그의 플랑크 상수와 p는 운동량입니다.

다시 말하지만, 이것은 더 무거운 입자에서 발생하기 전에 전자에서 발생합니다. 예를 들어 1927년 클린턴 데이비슨과 레스터 저머가 54V 가속하여 사용한 전자의 파장은 0.167nm로 원자간 거리가 0.215nm인 니켈 결정의 면에서 반사할 때 하나의 회절 측엽을 나타낼 수 있을 정도로 길었습니다. 더 큰 진공 챔버를 사용하면 각도 분해능이 라디안 주변에서 밀리라디안으로 증가하고 집적 회로 컴퓨터 메모리의 주기적 패턴에서 양자 회절을 보는 것이 비교적 쉬워 보입니다.

엔지니어링 규모에서 고전 역학의 실패의 더 실제적인 예로는 터널 다이오드에서 양자 터널링에 의한 전도와 집적 회로에서 매우 좁은 트랜지스터 게이트가 있습니다.

고전역학은 기하광학과 같은 극초단파 고주파 근사치입니다. 휴식 질량을 가진 입자와 신체를 묘사하기 때문에 더 자주 정확합니다. 이들은 동일한 운동 에너지를 가진 빛과 같은 질량 없는 입자보다 운동량이 많고 따라서 더 짧은 드브로이 파장을 갖습니다.

역사

신체의 운동에 대한 연구는 고대의 것으로 고전역학을 과학, 공학, 기술 분야에서 가장 오래되고 큰 주제 중 하나로 만듭니다. 고전역학의 발전은 수학의 많은 영역의 발전으로 이어집니다.^{[19]: 54}

고대 그리스 철학자들, 그들 중, 아리스토텔레스는 "모든 일은 이유가 있어서 일어난다" 그리고 이론적인 원리가 자연에 대한 이해를 도울 수 있다는 생각을 최초로 유지했을지도 모릅니다. 현대 독자들에게 이러한 보존된 많은 아이디어들은 대단히 합리적인 것으로 나오지만, 우리가 알고 있는 바와 같이 수학 이론과 통제된 실험 모두가 눈에 띄게 부족합니다. 이것들은 나중에 현대 과학을 형성하는 데 결정적인 요소가 되었고, 그들의 초기 적용은 고전 역학으로 알려지게 되었습니다. 중세 수학자 요르다누스 드 네모어는 그의 엘레멘타 초실증 논문에서 "위치 중력"의 개념과 구성 요소 힘의 사용을 소개했습니다.

행성의 운동에 대한 최초의 출판된 인과적 설명은 1609년에 출판된 요하네스 케플러의 천문학 노바입니다. 그는 화성의 궤도에 대한 타이코 브라헤의 관찰을 바탕으로 행성의 궤도가 타원형이라는 결론을 내렸습니다. 고대 사상과의 이러한 단절은 갈릴레오가 물체의 운동에 대한 추상적인 수학 법칙을 제안하던 때와 비슷한 시기에 일어나고 있었습니다. 그는 피사의 탑에서 무게가 다른 두 개의 대포알을 떨어뜨리는 유명한 실험을 수행했을 수도 있고, 그것들이 동시에 땅에 부딪혔다는 것을 보여주었을 수도 있습니다. 그 특정한 실험의 현실은 논란의 여지가 있지만, 그는 경사면에서 공을 굴려서 정량적인 실험을 수행했습니다. 그의 가속 운동 이론은 그러한 실험의 결과로부터 파생되었고 고전 역학의 초석을 형성합니다. 1673년 크리스티아누 호이겐스는 그의 호롤기움 오실라토리엄에서 운동의 첫 두 법칙을 설명했습니다.^[20] 이 연구는 물리적 문제(낙하하는 물체의 가속 운동)가 일련의 매개 변수에 의해 이상화된 다음 수학적으로 분석되는 응용 수학의 중요한 작업 중 하나를 구성하는 최초의 현대 논문이기도 합니다.^[21]

뉴턴은 세 가지 제안된 운동 법칙, 관성 법칙, 가속도 제2 법칙(위에서 언급한), 작용과 반작용 법칙에 기초하여 자연 철학의 원리를 확립했습니다. 따라서 고전 역학의 기초를 마련했습니다. 뉴턴의 철학 æ 자연주의 원리 수학에서는 뉴턴의 제2법칙과 제3법칙 모두 적절한 과학적, 수학적 취급을 받았습니다. 여기서 그것들은 불완전하거나, 부정확하거나, 정확한 수학적 표현이 거의 주어지지 않았던 유사한 현상을 설명하려는 초기의 시도들과 구별됩니다. 뉴턴은 운동량과 각운동량의 보존 원리도 설명했습니다. 역학에서 뉴턴은 최초로 만유인력에 관한 뉴턴의 법칙에서 최초로 정확한 과학적, 수학적 중력 공식을 제공했습니다. 뉴턴의 운동 법칙과 중력 법칙의 결합은 고전 역학에 대한 가장 완벽하고 정확한 설명을 제공합니다. 그는 이러한 법칙들이 천체뿐만 아니라 일상적인 물체에도 적용된다는 것을 증명했습니다. 특히, 그는 행성들의 운동에 대한 케플러의 법칙에 대한 이론적인 설명을 얻었습니다.

뉴턴은 이전에 미적분학을 발명했지만, 프린시피아는 전적으로 유클리드의 에뮬레이션에서 오랫동안 확립된 기하학적 방법의 관점에서 공식화되었습니다. 호이겐스를 제외한 뉴턴과 대부분의 동시대 사람들은 고전역학이 빛을 포함한 모든 현상을 기하광학의 형태로 설명할 수 있을 것이라는 가정하에 일했습니다. 이른바 뉴턴의 고리(파장 간섭 현상)를 발견할 때도 그는 자신만의 빛의 미립자 이론을 유지했습니다.

뉴턴 이후 고전역학은 물리학뿐만 아니라 수학의 주요 학문 분야가 되었습니다. 수학 공식화는 훨씬 더 많은 수의 문제에 대한 해결책을 찾을 수 있게 해주었습니다. 최초의 주목할 만한 수학적 처리는 1788년 조셉 루이스 라그랑주에 의해 이루어졌습니다. 라그랑주 역학은 윌리엄 로완 해밀턴에 의해 1833년에 다시 공식화되었습니다.

19세기 후반에 좀 더 현대적인 물리학에 의해서만 해결될 수 있는 몇 가지 어려움이 발견되었습니다. 이러한 어려움 중 일부는 전자기 이론과의 호환성, 유명한 마이컬슨-몰리 실험과 관련이 있습니다. 이러한 문제의 해결은 여전히 고전 역학의 일부로 간주되는 특수 상대성 이론으로 이어졌습니다.

두 번째 어려움은 열역학과 관련이 있습니다. 열역학과 결합하면 고전역학은 엔트로피가 잘 정의된 양이 아닌 고전 통계역학의 깁스 역설로 이어집니다. 흑체복사는 양자의 도입 없이는 설명되지 않았습니다. 실험이 원자 수준에 도달함에 따라 고전역학은 원자의 에너지 수준과 크기, 광전 효과와 같은 기본적인 것들을 설명하지 못했습니다. 이러한 문제를 해결하기 위한 노력은 양자역학의 발전으로 이어졌습니다.

20세기 말부터 물리학의 고전역학은 더 이상 독립적인 이론이 아니었습니다. 대신, 고전역학은 이제 더 일반적인 양자역학의 근사 이론으로 여겨집니다. 강조점은 표준 모델에서와 같이 자연의 근본적인 힘을 이해하고 모든 것에 대한 통일된 이론으로 현대적인 확장을 이해하는 것으로 옮겨졌습니다. 고전역학은 약한 중력장에서 양자가 아닌 기계적, 저에너지 입자의 운동을 연구하는 데 유용한 이론입니다.

참고 항목

메모들

참고문헌

더보기

• Alonso, M.; Finn, J. (1992). Fundamental University Physics. Addison-Wesley.
• Feynman, Richard (1999). The Feynman Lectures on Physics. Perseus Publishing. ISBN 978-0-7382-0092-7.
• Feynman, Richard; Phillips, Richard (1998). Six Easy Pieces. Perseus Publishing. ISBN 978-0-201-32841-7.
• Goldstein, Herbert; Charles P. Poole; John L. Safko (2002). Classical Mechanics (3rd ed.). Addison Wesley. ISBN 978-0-201-65702-9.
• Kibble, Tom W.B.; Berkshire, Frank H. (2004). Classical Mechanics (5th ed.). Imperial College Press. ISBN 978-1-86094-424-6.
• Kleppner, D.; Kolenkow, R.J. (1973). An Introduction to Mechanics. McGraw-Hill. ISBN 978-0-07-035048-9.
• Landau, L.D.; Lifshitz, E.M. (1972). Course of Theoretical Physics, Vol. 1 – Mechanics. Franklin Book Company. ISBN 978-0-08-016739-8.
• Morin, David (2008). Introduction to Classical Mechanics: With Problems and Solutions (1st ed.). Cambridge: Cambridge University Press. ISBN 978-0-521-87622-3.
• Gerald Jay Sussman; Jack Wisdom (2001). Structure and Interpretation of Classical Mechanics. MIT Press. ISBN 978-0-262-19455-6.
• O'Donnell, Peter J. (2015). Essential Dynamics and Relativity. CRC Press. ISBN 978-1-4665-8839-4.
• Thornton, Stephen T.; Marion, Jerry B. (2003). Classical Dynamics of Particles and Systems (5th ed.). Brooks Cole. ISBN 978-0-534-40896-1.

외부 링크

• 크로웰, 벤자민. 빛과 물질(개론 텍스트, 미적분학과 관련된 선택적 섹션이 있는 대수학 사용)
• 피츠패트릭, 리처드 고전역학(미적분학 사용)
• 호일랜드, 폴(2004). 선호하는 기준 및 상대성틀
• 호르바치, 마르코, "고전역학 과정 노트"
• 로수, 하렛 C, "고전역학" 물리 교육. 1999. [arxiv.org : 물리/9909035]
• 샤피로, 조엘 A. (2003) 고전역학
• Sussman, Gerald Jay & Wisdom, Jack & Mayer, Meinhard E. (2001) 고전역학의 구조와 해석
• 통, 데이빗. 고전동역학 (Cambridge 강의 노트 중 라그랑지안과 해밀턴 형식주의)
• 디지털 도서관 설계를 위한 운동학적 모델
  코넬 대학의 수백 개의 작동하는 기계 시스템 모델의 영화와 사진. 또한 기계 설계 및 엔지니어링에 대한 고전 텍스트의 전자책 라이브러리도 포함되어 있습니다.
• MIT OpenCourseWare 8.01: Classical Mechanics 강의 노트, 과제 및 시험 링크가 포함된 실제 코스 강의 동영상을 무료로 제공합니다.
• 알레한드로 A. 토라사, 고전역학에 대하여