특수상대성이론

특수상대성이론
상대성 원리 상대성이론 제형
기초 아인슈타인의 가설 관성기준틀 광속 맥스웰 방정식 로런츠 변환
결과들 시간확장 길이수축 상대론적 질량 질량-에너지 등가성 동시성 상대성 상대론적 도플러 효과 토마스 세차운동 상대론적 원반 벨의 우주선 역설 에렌페스트 역설
시공간 민코프스키 시공간 시공간도 월드 라인 라이트콘
다이나믹스 적정시간 적정 질량 포모멘트
역사 전구물질 갈릴레이 상대성 이론 갈릴레오 변환 에테르설
사람 아인슈타인 소머펠트 마이컬슨 몰리 피츠제럴드 헤르글로츠 로렌츠 푸앵카레 민코프스키 피조 아브라함 태어난 플랑크 폰 라우에 에렌페스트 톨만 디랙
물리학 포털 카테고리
v t

물리학에서 특수상대성이론, 또는 줄여서 특수상대성이론은 공간과 시간의 관계에 대한 과학적 이론입니다.알베르트 아인슈타인의 1905년 연구에서 이론은 단 두 가지 가설에 근거한 것으로 제시됩니다.^{[p 1][1][2]}

1. 물리 법칙은 모든 관성 기준 프레임(즉 가속도가 없는 기준 프레임)에서 불변(동일)합니다.
2. 진공에서의 빛의 속도는 광원이나 관측자의 움직임에 관계없이 모든 관측자에게 동일합니다.

원산지 및 의의

특수상대성이론은 아인슈타인이 1905년 9월 26일에 발표한 "움직이는 물체의 전기역학에 관하여"라는 제목의 논문에서 설명했습니다.^{[p 1]}맥스웰의 전자기 방정식은 뉴턴 역학과 양립할 수 없는 것으로 보였고, 마이컬슨-모리 귀무 결과는 가정된 발광 에테르에 대한 지구의 움직임을 감지하는 데 실패했습니다.이것은 움직이는 물체의 거리와 시간을 조정하는 로렌츠 변환의 발전으로 이어졌습니다.특수상대성이론은 모든 운동을 포함하는 상황과 특히 빛의 속도에 가까운 속도(상대론적 속도로 알려짐)를 처리하기 위해 역학의 지금까지의 법칙을 수정합니다.오늘날 특수상대성이론은 중력과 양자효과가 무시될 정도일 때 어떤 속도에서도 가장 정확한 운동 모델임이 입증되었습니다.^[3][4]그럼에도 불구하고, 뉴턴 모델은 지구에서의 일상적인 움직임과 같은 낮은 속도(빛의 속도에 상대적인)에서의 단순하고 정확한 근사치로서 여전히 유효합니다.

특수 상대성 이론은 실험적으로 검증된 광범위한 결과를 가져옵니다.^[5]그것들은 동시성의 상대성, 길이 수축, 시간 팽창, 상대론적 속도 가산 공식, 상대론적 도플러 효과, 상대론적 질량, 보편적 속도 한계, 질량-에너지 등가성, 인과성의 속도와 토마스 세차운동을 포함합니다.^[1][2]예를 들어, 그것은 절대적인 보편적인 시간의 개념을 기준 프레임과 공간적 위치에 의존하는 시간의 개념으로 대체했습니다.두 사건 사이에는 불변의 시간 간격이 아닌 불변의 시공간 간격이 있습니다.다른 물리 법칙과 결합하여, 두 특수 상대성 이론의 가정은 질량-에너지 등가 공식 $E$ = ${\displaystyle {mc}^{}}$ 2 ${\displaystyle$E = $mc^{2}$로 표현된 것처럼 질량과 에너지의 등가성을 예측합니다$.$ $여기$서 c ${\displaystyle c}$는 진공에서의 빛의 속도입니다.또한 전기와 자기의 현상이 어떻게 연관되어 있는지 설명합니다.^[1][2]

특수 상대성 이론의 정의적 특징은 뉴턴 역학의 갈릴레이 변환을 로렌츠 변환으로 대체하는 것입니다.시간과 공간은 서로 분리되어 정의될 수 없습니다(이전에 생각했던 것처럼).오히려, 시공간과 시간은 시공간으로 알려진 단일 연속체로 엮여 있습니다.한 관측자에 대해 동시에 발생하는 이벤트는 다른 관측자에 대해 다른 시간에 발생할 수 있습니다.

몇 년 후 아인슈타인이 중력을 통합하기 위해 곡선 시공간을 도입한 일반 상대성 이론을 개발할 때까지 "특수 상대성"이라는 문구는 사용되지 않았습니다.때때로 사용되는 번역은 "제한된 상대성 이론"이고, "특별한"은 실제로 "특별한 경우"를 의미합니다.^{[p 2][p 3][p 4][note 1]}특수 상대성 이론에서 알버트 아인슈타인의 연구 중 일부는 헨드릭 로렌츠와 앙리 푸앵카레에 의한 초기 연구에 기초하고 있습니다.이론은 1907년 헤르만 민코프스키의 시공간에 관한 논문들과 함께 본질적으로 완성되었습니다.^[4]

이 이론은 시공간이 "평탄한" 경우, 즉 시공간의 곡률(에너지-운동량 텐서와 중력을 나타내는 결과)이 무시할 수 있는 특수한 경우에만 적용된다는 점에서 "특별한" 이론입니다.^{[8][note 2]}중력을 정확하게 수용하기 위해, 아인슈타인은 1915년에 일반상대성이론을 공식화했습니다.특수 상대성 이론은 일부 역사적 기술과 달리 가속 기준 프레임뿐만 아니라 가속을 수용합니다.^[9][10]

갈릴레이 상대성 이론이 저속에서 유효한 특수 상대성 이론의 근사치로 받아들여지는 것처럼, 특수 상대성 이론은 약한 중력장, 즉 충분히 작은 규모(조력이 무시할 수 있는 경우)와 자유 낙하 조건에서 유효한 일반 상대성 이론의 근사치로 여겨집니다.그러나 일반 상대성 이론은 중력 효과를 시공간의 기하학적 곡률로 나타내기 위해 비유클리드 기하학을 포함합니다.특수 상대성 이론은 민코프스키 공간으로 알려진 평평한 시공간에 국한됩니다.우주가 의사-리만 다양체로 모델링될 수 있는 한, 특수 상대성 이론을 준수하는 로렌츠 불변 프레임은 이 곡선 시공간의 각 점의 충분히 작은 이웃에 대해 정의될 수 있습니다.

갈릴레오 갈릴레이는 현재 갈릴레오의 상대성 원리라고 불리는 원리인 절대적이고 명확한 휴식 상태가 존재하지 않는다고 이미 가정했습니다.아인슈타인은 마이컬슨-모리 실험에서 관찰되었던 현상인 일정한 빛의 속도를 설명하도록 이 원리를 확장했습니다.^[11]그는 또한 이것이 역학과 전기역학의 법칙을 포함한 모든 물리학 법칙을 지지한다고 가정했습니다.^[12]

특수 상대성 이론에 대한 전통적인 "두 개의 가설" 접근법

아인슈타인은 역학이나 전기역학의 법칙의 정확한 타당성에 관계없이 가장 확실해 보이는 두 가지 기본적인 명제를 발견했습니다.이러한 명제는 진공에서의 빛의 속도의 일정성과 관성계의 선택으로부터 물리적 법칙(특히 빛의 속도의 일정성)의 독립성이었습니다.1905년 그의 최초의 특수 상대성 이론 발표에서 그는 다음과 같은 가설을 제시했습니다.^{[p 1]}

• 상대성 이론의 원리 – 물리적 시스템의 상태가 변화를 겪는 법칙은, 이러한 상태의 변화가 서로에 대해 균일한 병진운동을 하는 두 시스템 중 하나 또는 다른 하나로 언급되든 간에 영향을 받지 않습니다.^{[p 1]}
• 광속 불변의 원리 – "... 빛은 항상 방출체의 운동 상태와 무관한 일정한 속도 [속도] c로 빈 공간에서 전파됩니다."^{[p 1]} (서두에서)즉, 진공 내의 빛은 광원의 운동 상태에 관계없이 적어도 하나의 관성 좌표계("정지 시스템")에서 속도 c(고정 상수, 방향에 관계없이)와 함께 전파됩니다.

빛의 속도의 일정성은 맥스웰의 전자기^{[citation needed]} 이론과 발광 에테르에 대한 증거의 부족에서 비롯되었습니다.아인슈타인이 마이컬슨-모리 실험의 무효 결과에 영향을 받은 정도에 대해서는 상반된 증거가 있습니다.^[13][14]어쨌든, 마이컬슨-모리 실험의 무효 결과는 빛의 속도의 일정성에 대한 개념이 광범위하고 빠르게 받아들여지는 데 도움이 되었습니다.

특수 상대성 이론의 유도는 이 두 개의 명시적인 가정뿐만 아니라 공간의 등방성과 동질성, 과거 역사로부터의 측정 막대와 시계의 독립성 등 몇 가지 암묵적 가정(거의 모든 물리학 이론에서 만들어진)에도 의존합니다.^{[p 6]}

1905년 아인슈타인의 특수 상대성 이론에 대한 최초의 발표 이후, 다양한 대안적 파생에서 많은 다른 가정들이 제안되었습니다.^[15]그러나 가장 일반적인 가설들의 집합은 아인슈타인이 그의 원래 논문에서 사용한 가설들로 남아있습니다.아인슈타인에 의해 나중에 만들어진 상대성 원리에 대한 더 수학적인 진술은 위에 언급되지 않은 단순성의 개념을 소개합니다.

특수 상대성 원리:만약 그것과 관련하여, 물리적 법칙들이 가장 간단한 형태로 좋은 상태를 유지하도록 좌표 K의 체계를 선택한다면, 같은 법칙들은 K에 대해 균일한 번역으로 움직이는 다른 좌표 K'의 체계와 관련하여 좋은 상태를 유지합니다.^[16]

앙리 푸앵카레는 로렌츠 변환이 그의 푸앵카레 대칭 변환 그룹의 부분집합이라는 것을 증명함으로써 상대성 이론의 수학적 틀을 제공했습니다.아인슈타인은 나중에 그의 공리로부터 이러한 변형을 유도했습니다.

아인슈타인의 많은 논문들은 이 두 가지 원리에 기초한 로렌츠 변환의 파생을 제시합니다.^{[p 7]}

상대성 원리

기준 프레임 및 상대 운동

기준 프레임은 상대성 이론에서 중요한 역할을 합니다.여기서 사용되는 참조 프레임이라는 용어는 3개의 공간 축(정지 상태 또는 등속)을 따라 위치를 측정할 수 있는 움직임(가속도)의 변화를 겪지 않는 공간에서의 관측적 관점입니다.또한, 기준 프레임은 "클럭"(주기성이 균일한 임의의 기준 장치)을 사용하여 이벤트의 시간의 측정을 결정할 수 있습니다.

이벤트는 참조 프레임에 대한 공간 내의 단일 고유 모멘트와 위치를 할당할 수 있는 발생입니다. 시공간의 "점"입니다.기준 프레임에 관계없이 빛의 속도가 상대성 이론에서 일정하기 때문에, 이벤트가 발생한 후 시계에 도달하는 데 시간이 걸리더라도, 빛의 펄스는 거리를 명확하게 측정하고 이벤트가 발생한 시간을 시계로 되돌리는 데 사용될 수 있습니다.

예를 들어, 폭죽의 폭발은 "사건"으로 간주될 수 있습니다.4개의 시공간 좌표로 사건을 완전히 지정할 수 있습니다.발생 시점과 그 3차원 공간적 위치는 기준점을 정의합니다.이 참조 프레임을 S라고 합니다.

상대성 이론에서, 우리는 종종 다른 기준 프레임으로부터 사건의 좌표를 계산하려고 합니다.서로 다른 프레임에서 측정한 값을 변환 방정식이라고 합니다.

표준구성

서로 다른 참조 프레임에서 관찰자에 의해 측정된 시공간 좌표가 서로 어떻게 비교되는지에 대한 통찰력을 얻기 위해서는 표준 구성에서 프레임을 사용하여 단순화된 설정으로 작업하는 것이 유용합니다.^{[17]: 107} 이를 통해 수학을 단순화하고 결론에 도달하는 일반성을 잃지 않도록 주의해야 합니다.도 2-1에서는, 2개의 갈릴레이 기준 프레임(즉, 종래의 3 공간 프레임)이 상대 운동으로 표시되어 있습니다.프레임 S는 첫 번째 관측자 O에 속하며, 프레임 S'("Sprime" 또는 "Sash"로 발음됨)는 두 번째 관측자 O'에 속합니다.

• 프레임 S의 x, y, z 축은 프레임 S'의 각각의 프라이밍된 축과 평행하게 배향됩니다.
• 프레임 S'는, 단순화를 위해, 프레임 S에서 측정된 것과 같은 일정한 속도 v를 갖는 프레임 S의 x 방향으로 이동합니다.
• 프레임 S와 프레임 S'의 원점은 프레임 S의 시간 t = 0이고 프레임 S'의 시간 t' = 0일 때 일치합니다.

상대성 이론에는 절대적인 기준 틀이 없기 때문에, 모든 것이 다른 기준 틀에 대해 움직일 수 있기 때문에 "움직이는" 개념은 엄밀하게 존재하지 않습니다.대신, 동일한 방향으로 동일한 속도로 움직이는 임의의 두 프레임은 이동한다고 합니다.따라서 S와 S'는 움직이지 않습니다.

절대기준틀부족

물리 법칙들이 각각의 관성 기준 틀에서 같은 형태를 갖는다는 상대성의 원리는 갈릴레오까지 거슬러 올라가 뉴턴 물리학에 통합되었습니다.그러나 19세기 후반 전자기파의 존재로 인해 일부 물리학자들은 우주가 "에테르"라고 불리는 물질로 가득 차 있다고 주장했습니다. 그들은 이러한 파동, 즉 진동이 전파되는 매개체 역할을 할 것이라고 가정했습니다(많은 측면에서 소리가 공기를 통해 전파되는 방식과 유사합니다).에테르는 모든 속도를 측정할 수 있는 절대적인 기준 프레임으로 간주되었으며, 지구 또는 다른 고정된 기준점에 대해 고정되고 움직이지 않는 것으로 간주될 수 있습니다.에테르는 전자기파를 지지할 수 있을 만큼 충분히 탄성이 있어야 하는 반면, 그러한 파동은 물질과 상호작용할 수 있지만, 통과하는 물체에는 저항을 제공하지 않습니다(그것의 한 가지 특성은 전자기파가 전파될 수 있게 한다는 것이었습니다).1887년 마이컬슨-모리 실험을 포함한 다양한 실험의 결과는 에테르가 존재하지 않는다는 것을 보여줌으로써 특수 상대성 이론으로 이어졌습니다.^[18]아인슈타인의 해결책은 에테르의 개념과 절대적인 휴식 상태를 버리는 것이었습니다.상대성 이론에서, 균일한 운동으로 움직이는 어떤 기준 프레임도 같은 물리 법칙을 관찰할 것입니다.특히, 진공에서의 빛의 속도는 항상 c로 측정되며, 이는 서로 다른(그러나 일정한) 속도로 움직이는 여러 시스템에 의해 측정될 때에도 마찬가지입니다.

두 번째 공준이 없는 상대성 이론

빛의 속도의 일정성을 가정하지 않고 상대성 원리만으로 (즉, 공간의 등방성과 특수 상대성 원리에 의해 암시된 대칭을 사용하여) 관성 프레임 사이의 시공간 변환이 유클리드, 갈릴레이 또는 로렌츠임을 알 수 있습니다.로렌츠의 경우 상대론적 구간 보존과 일정한 유한 한계 속도를 얻을 수 있습니다.실험 결과, 이 속도는 진공 속에서 빛의 속도임을 알 수 있습니다.^{[p 8][19]}

특수상대성이론의 핵심으로서의 로렌츠 불변성

특수 상대성 이론에 대한 대안적 접근법

아인슈타인은 상대성 이론과 광속 불변의 두 가지 기본 원칙에 의거하여 로렌츠 불변성(특수 상대성 이론의 본질적인 핵심)의 유도에 일관되게 기초했습니다.그는 이렇게 썼습니다.

특수상대성이론의 기본적인 통찰력은 다음과 같습니다.좌표와 사건의 시간의 변환을 위해 새로운 유형("로렌츠 변환")의 관계를 가정하면 가정 상대성 이론과 광속 불변성은 양립할 수 있습니다.특수상대성이론의 보편적 원리는 다음과 같이 가정합니다.물리학의 법칙은 로렌츠 변환(한 관성계에서 임의로 선택된 다른 관성계로의 전환)과 관련하여 불변합니다.이것은 자연법에 대한 제한적인 원칙입니다.^{[p 5]}

따라서 특수 상대성 이론의 많은 현대적인 처리는 보편적인 로렌츠 공분산의 단일 공준에 기초하거나, 동등하게 민코프스키 시공간의 단일 공준에 기초합니다.^{[p 9][p 10]}

이 글은 보편적 로렌츠 공분산을 파생 원리로 간주하기보다는 특수 상대성 이론의 기본적인 전제로 간주합니다.특수 상대성 이론에 대한 전통적인 두 개의 가설 접근법은 수많은 대학 교과서와 대중적인 발표에 제시되어 있습니다.^[20]민코프스키 시공간의 단일 공준으로 시작하는 교과서에는 테일러와 휠러^[21], 캘러핸의 교과서가 있습니다.^[22]이것은 또한 위키피디아 기사 스페이스타임과 민코프스키 다이어그램에 이어지는 접근법이기도 합니다.

로렌츠 변환과 그 역

시스템 S의 시공간 좌표(t, x, y, z)와 해당 프레임 S'에 대해 속도 v로 이동하는 기준 프레임(t', x', y', z')을 갖도록 이벤트를 정의합니다.그런 다음 로렌츠 변환은 이 좌표들이 다음과 같은 방식으로 연관되어 있음을 지정합니다.

어디에는 로렌츠 계수이고 c는 진공에서의 빛의 속도이며, S에 대한 S'의 속도 v는 x축과 평행합니다.단순화를 위해 y와 z 좌표는 영향을 받지 않으며 x와 t 좌표만 변환됩니다.이러한 로렌츠 변환은 선형 매핑의 하나의 매개 변수 그룹을 형성하며, 그 매개 변수는 신속성이라고 불립니다.

프리밍되지 않은 좌표에 대해 위의 네 가지 변환 방정식을 풀면 역 로렌츠 변환이 생성됩니다.

이는 프라이밍되지 않은 프레임이 프라이밍된 프레임에서 측정된 속도 -v로 움직이고 있음을 보여줍니다.^[23]

x축에 대해서는 특별한 것이 없습니다.변환은 y축 또는 z축에 적용될 수 있으며, 실제로는 운동과 평행하고 수직인 모든 방향에 적용될 수 있습니다. 자세한 내용은 로렌츠 변환 기사를 참조하십시오.

로런츠 변환 하에서 불변량은 로런츠 스칼라로 알려져 있습니다.

로런츠 변환과 그 역을 좌표 차이로 표기하면, 한 사건은 좌표 (x₁, t₁)와 (x',₁ t')₁를 가지며, 다른 사건은 좌표 (x₂, t)와₂ (x',₂ t')₂를 가지며, 그 차이는 다음과 같이 정의됩니다.

• 식 1: ${\displaystyle \Delta x'=x'_{2}-x'_{1}\,\\Delta t'=t'_{2}-t'_{1}\.}$
• 등식 2: ${\displaystyle \Delta x=x_{2}-x_{1}\,\ \Delta t=t_{2}-t_{1}\.}$

우리가 얻는

• 등식 3: ${\displaystyle \Delta x'=\gamma \ (\Delta x-v\,\Delta)\,\ \}$ ${\displaystyle \Delta t'=\gamma \left(\Delta t-v\ \Delta x/c^{2}\right)\.}$
• 등식 4: ${\displaystyle \Delta x=\gamma \(\Delta x'+v\,\Delta t')\,\}$ ${\displaystyle \Delta t=\gamma \left(\Delta t'+v\ \Delta x'/c^{2}\right)\.}$

우리가 차이를 취하는 대신에 차이를 취하면

• 식 5: ${\displaystyle dx'=\gamma \(dx-v\,dt)\,\ \ }$ ${\displaystyle dt'=\gamma \left(dt-v\dx/c^{2}\right)\ .}$
• 식 6: ${\displaystyle dx=\gamma \(dx'+v\,dt')\,\}$ ${\displaystyle dt=\gamma \left(dt'+v\dx'/c^{2}\right)\ .}$

로렌츠 변환의 그래픽 표현

시공간 다이어그램(민코프스키 다이어그램)은 서로 다른 참조 프레임 간의 좌표 변환 방법을 시각화하는 데 매우 유용합니다.로렌츠 변환을 직접 호출하는 것만큼 정확한 계산을 수행하는 것이 쉽지는 않지만, 그들의 주요 능력은 상대론적 시나리오의 결과를 직관적으로 파악할 수 있는 능력입니다.^[19]

시공간 다이어그램을 그리기 위해서는 그림 2-1과 같이 표준 구성에서 두 개의 갈릴레이 기준 프레임인 S와 S'를 고려하는 것으로 시작합니다.^{[19][24]: 155–199}

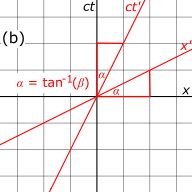
그림 3-1a.프레임 S의 $x{\displaystyle }$ ${\displaystyle x}$ 축과$$ $t{\displaystyle }$ ${\displaystyle t}$ 축을$$ 그립니다.$x{\displaystyle }$ ${\displaystyle x}$ 축은$$ 수평이고 $t{\displaystyle }$ ${\displaystyle$ t$}($실제로 ${\displaystyle \mathrm{ct}}$ ${\displaystyle ct})$축은 수직이며, 이는 운동학의 일반적인 관례와 반대입니다.${\displaystyle c}$ ${\displaystyle c}$ 축은$$ $c{\displaystyle }$ ${\displaystyle c}$의 인자로 축의 크기가 조정되어$$ 두 축 모두 공통된 길이 단위를 갖습니다.그림에서 격자선은 한 단위 거리만큼 떨어져 있습니다.45° 대각선은 시간 $t$ = $.{\displaystyle$t = $0.}$에서 원점을 통과하는 두 광자의 세계선을 나타냅니다.$$ 광자가 시간 단위당 공간에서 한 단위씩 진행하기 때문에 이러한 세계선의 기울기는 1입니다.$두{\displaystyle }$ 이벤트,$$A {\$displaystyle$ {\$text{$$A}}$ 및$$ $B{\displaystyle ,}$ ${\displaystyle {\text{$$B}},}$은(는) S와 S의 프레임에서 좌표를 비교할 수 있도록 이 그래프에 표시되었습니다.

그림 3-1b.프레임 S'의 $x{\displaystyle {}^{\text{'}}}$ ${\$ x$'}$ ${\displaystyle {}^{}}$과 c${\displaystyle {\text{'}}^{}}${\$displaystyle ct'}$ 축을$$ 그립니다.${\displaystyle {}^{\text{'}}}$ ${\$ 축은$$ 프레임 S에서 측정한 S' 좌표계 원점의 세계선을 나타냅니다.이 그림에서 $v$ = ${\displaystyle c}$/ ${\displaystyle 2\mathrm{.}}$ ${\displaystyle v$= $c/2$.$}$c ${\displaystyle {\text{'}}^{}}$ ${\displaystyle ct'}$ 및 $x{\displaystyle {\text{'}}^{}}$ ${\displaystyle$ x$'}$ 축은 모두 비프림 축에서 각도 $\alpha$ $=$ ${\displaystyle {\tan }^{}}$- ${\displaystyle 1^{}}$$⁡$${\displaystyle (\beta ),}$ ${\displaystyle \alpha$ $=$\$tan ^{-1}(\$$beta$$)$만큼 기울어져 있으며, 여기서 $\beta$ $=$ ${\displaystyle v}$/ ${\displaystyle c.}$ ${\displaystyle$\$beta =$$$v$/c.}$$$ 프레임 S와 S'가 표준 구성으로 설정되었기 때문에 primed 축과 unprimed 축은 공통 원점을 공유하므로 $t$ ${\displaystyle =}$ ${\displaystyle \mathrm{0일}}$ 때 t = $0$ ${\displaystyl$e t$=0$$}.$ {\$displaystyle$ t'= $0.}$

그림 3-1c.프라이밍 축의 단위는 프라이밍되지 않은 축의 단위와 척도가 다릅니다.로렌츠 변환으로부터, 우리는 프라이밍 좌표계에서$$(${\displaystyle \mathrm{x}\text{'},}$ $')$ {\$displaystyle$ ($x',$ct$')}$ {\$displaystyle (0,1)}$의 좌표가 비프라이밍 좌표계에서$$(${\displaystyle \beta }$ γ,${\displaystyle }$γ${\displaystyle )}$ ${\displaystyle (\beta \gamma,\gamma )}$로 변환됨을 관찰합니다.마찬가지로$,$ 프라이밍 좌표계에서${\displaystyle }$($) {\displaystyle$($x',$ ${\displaystyle {}^{}\text{'})\}}$의 ${\$displaystyle (x', $ct')}$ 좌표가 비 프라이밍 시스템에서 ($$γ,${\displaystyle \beta }$ γ${\displaystyle )}$ ${\displaystyle (\gamma,\beta \gamma )}$로 변환됩니다.$점$(k γ${\displaystyle ,}$ k $β$γ$) {\displaystyle$$ct'}$ 축과 평행한 격자선을 비프림 프레임에서 측정한 $대로$$$$그립니다$(k {\$displaystyle$ k}는$$정수입니다$).$마찬가지로, 프리밍되지 않은 프레임에서 $측정$된 x${\displaystyle {\text{'}}^{}}$ ${\displaystyle$ x$'}$ 축과 평행한 격자선을 그립니다$({\displaystyle k}$ ${\displaystyle \beta }$ γ${\displaystyle ,}$ ${\displaystyle k}$ γ${\displaystyle )}$ ${\displaystyle (k\beta \gamma,k\gamma )}.$피타고라스 정리를 사용하여, ${\displaystyle {}^{}}$는 프레임 S에서 ${\displaystyle \mathrm{측정}}$한 ct$${\$displaystyle ct'}$개$$ 단위$$ 사이의 간격이 $(\sqrt{1}$ +$\sqrt{{\beta \mathrm{}}^{}}$ 2$\sqrt{{}^{}}$)$\sqrt{}$/$\sqrt{}$($\sqrt{1}$ -$\sqrt{{}^{}}$ $\sqrt{{2\mathrm{}}^{}}$) ${\$배임을$$ 관찰합니다$.$이 비율은 항상 1보다 크며, 궁극적으로는 $\beta {\displaystyle }$→ $.{\displaystyle \$beta$\to$ 1$.}$로 무한대에 가까워집니다.

그림 3-1d.빛의 속도는 불변하기 때문에, $시간$ t${\displaystyle {\text{'}}^{}}$= ${\displaystyle 0}$ ${\displaystyle$t' = $0}$에서 원점을 지나는 두 광자의 세계선은 여전히 45° 대각선으로 표시됩니다.$A{\displaystyle }$ ${\$의 프라이밍된 좌표$A}}$ 및$$ $B{\displaystyle }$ ${\$$B}}}$은(충분히 정확하게 플롯되었다고 가정할 때) 로렌츠 변환을 통해 프라이밍되지 않은 좌표와 관련이 있으며 그래프에서 대략적으로 측정할 수 있지만 민코프스키 다이어그램의 실제 장점은 시나리오에 대한 기하학적 시각을 제공한다는 것입니다.예를 들어, 이 그림에서, 우리는 프라이밍되지 않은 프레임에서 서로 다른 x 좌표를 가졌던 두 개의 시간적으로 분리된 사건이 이제 공간에서 같은 위치에 있다는 것을 관찰합니다.

프라이밍되지 않은 프레임은 직각으로 만나는 공간 및 시간 축으로 그려지는 반면, 프라이밍된 프레임은 예각 또는 둔각으로 만나는 축으로 그려집니다.이러한 비대칭성은 시공간 좌표가 데카르트 평면에 매핑되는 방법의 불가피한 왜곡 때문이지만, 프레임은 실제로 동일합니다.

로런츠 변환에 의한 결과

특수 상대성 이론의 결과는 로렌츠 변환 방정식에서 도출될 수 있습니다.^[25]이러한 변환과 특수 상대성 이론은 모든 상대 속도에서 뉴턴 역학의 물리적 예측과 다른 물리적 예측을 유도하며, 상대 속도가 빛의 속도와 비슷해질 때 가장 두드러집니다.빛의 속도는 대부분의 인간들이 마주치는 그 어떤 것보다 훨씬 커서 상대성 이론에 의해 예측된 효과들 중 일부는 처음에는 직관에 어긋납니다.

불변구간

갈릴레이 상대성 이론에서, 물체의 길이( δ ${\displaystyle r}$ ${\displaystyle \Delta$와 두 사건 사이의 시간적 분리( δ ${\displaystyle t}$ ${\displaystyle \Delta$는 독립적인 불변량이며, 서로 다른 기준 프레임에서 관측될 때 값이 변하지 않습니다.

그러나 특수상대성이론에서 공간좌표와 시간좌표의 상호 직조는 δ ${\displaystyle {}^{}}$ {\$displaystyle$ \$Delta s^{2}}$로 표시되는 불변의 간격 개념을 생성합니다$.$

공간과 시간의 상호 직조는 비이동 프레임 간의 절대적 동시성과 동기화라는 암묵적으로 가정된 개념을 취소합니다.

시간 경과 제곱과 공간 거리 제곱의 차이인 δ ${\displaystyle 2^{}}$ ${\displaystyle \Delta s^{2}}$의 형태는 유클리드와 시공간 거리 사이의 근본적인 불일치를 보여줍니다.이 간격의 불변성은 일반적인 로렌츠 변환(푸앵카레 변환이라고도 함)의 특성이며, 시공간의 등각입니다.일반적인 로렌츠 변환은 데카르트 관성 프레임 사이의 다른 모든 변환, 반사 및 회전과 함께 표준 로렌츠 변환(회전 없이 변환, 즉, 로렌츠 부스팅)을 확장합니다.^{[29]: 33–34}

시공간 다이어그램과 같은 단순화된 시나리오의 분석에서 불변 구간의 축소된 차원 형태가 종종 사용됩니다.

간격이 불변임을 증명하는 것은 축소된 차원의 경우와 표준 구성의 프레임에 대해 간단합니다.^[19]

$따라서$ δs ${\displaystyle 2^{}}$ ${\displaystyle \Delta s^{2}}$의 값은 측정되는 프레임과 무관합니다.

δ 2 ${\displaystyle$ \$Delta$ s$^{2}}$의 ${\displaystyle {}^{}}$ 의미를 고려할 때, 주목해야 할 세 가지 경우가 있습니다$.$

• δ > 0: 이 경우, 두 사건은 공간보다 시간적으로 더 많이 분리되므로 시간적으로 분리된다고 합니다.이는 δ /δ < ${\displaystyle$\$Delta$ $x$${\displaystyle {/\backslash }^{}}$$Delta t$< $c,}$를 의미하며, 로런츠 변환 δ x'${\displaystyle }$= γ${\displaystyle }$(δ ${\displaystyle x}$ - ${\displaystyle V}$gamma${\displaystyle }$t$),$ {\$displaystyle$ \$Delta$ x' =$\$δ \ (\$Delta$ $x-v\,\Delta$ t)가 주어졌을 때,$$δ ${\displaystyle {\text{'}}^{}}$ =$0인$c {\$displaystyle$ $c}$보다 작은$$v {\$displaystyle v}$가 존재함이 명백합니다. (특히$,$${\displaystyle v}$ $=$ ${\displaystyle \delta }$ ${\displaystyle x}$ /${\displaystyle }$δ ${\displaystyle t}$ ${\displaysty$ v=\$Delta$ x$/\Delta$ t$}).$즉, 시간적으로 분리된 두 사건을 고려할 때, 두 사건이 같은 장소에서 일어나는 프레임을 찾을 수 있습니다.이 프레임에서는 시간의 분리, δ ${\displaystyle s}$/ ${\displaystyle c,}$ ${\displaystyle \Delta$ s / c$,}$를 적절한 시간이라고 합니다.
• δ < 0: 이 경우, 두 사건은 시간보다 더 많은 공간에 의해 분리되므로, 분리된 공간과 같다고 할 수 있습니다.이는 δ /δ δ t> ${\displaystyle \Delta$x$/\Delta$ t > c$,}$ 로런츠 변환 γ ${\displaystyle {\text{'}}^{}}$ = δ${\displaystyle }$(δ t${\displaystyle }$- ${\displaystyle v}$ gamma x${\displaystyle }$/ ${\displaystyle c^{}}$ 2${\displaystyle {}^{}),}$ ${\displaystyle \Delta$t' =\δ$$\ $(\Delta$ t - $v\Delta x$/ c$^{2}),$ $c$ ${\displaystyle c}$ 보다 작은 $v$ ${\displaystyle v}$가 존재하며, 이에 대해 δ ${\displaystyle {\text{'}}^{}}$ = ${\displaystyle 0}$ ${\displaystyle \Delta$t' = 0$}(특히$,${\displaystyle v}$ $=$ ${\displaystyle c}$ ${\displaystyle 2^{}}$ ${\displaystyle \delta }$ ${\displaystyle t}$ /${\displaystyle }$δ ${\displaystyle x}$ ${\displaysty$v$=c^{2}\Deltaat/\Deltax})$입니다.즉, 공간처럼 분리된 두 사건을 고려할 때, 두 사건이 동시에 발생하는 프레임을 찾을 수 있습니다.이 프레임에서는 ${\displaystyle \sqrt{\mathrm{공간}}}$의 구분인 -$$δ${\displaystyle \sqrt{{}^{}}}$ ${\displaystyle \sqrt{2^{}}}$ ${\displaystyle {\sqrt {-\Deltas^{2}}}$을(를) 적절한 거리 또는 적절한 길이라고 합니다.$v$ ${\displaystyle v}$의 값이 c ${\displaystyle 2^{}}$ δ t /${\displaystyle }$δ ${\displaystyle x}$보다 크고 작은 경우${\displaystyle$ c$^{2}\Delta t/\Delta$ x$,}$ δ ${\displaystyle {\text{'}}^{}}$ ${\displaystyle \Delta t'}$의 부호가 변경되며, 이는 이벤트가 표시되는 프레임에 따라 공간과 유사하게 분리된 이벤트의 시간 순서가 변경됨을 의미합니다.$그러나$ v ${\displaystyle v}$이(가) $c$ ${\displaystyle 2^{}}$ δ t /${\displaystyle }$δ x ${\displaystyle c^{2}\Delta$ t$/\Delta x}$보다 클 수 있는 유일한 방법은 > c${\displaystyle v>c$인 경우뿐이므로 시간으로 구분된 이벤트의 시간 순서는 절대적입니다$.$$}$
• δ = 0: 이 경우 두 사건은 서로 분리된 것처럼 가볍다고 합니다.이는 δ ${\displaystyle x}$ /${\displaystyle }$δ ${\displaystyle t}$ = c${\displaystyle ,}$ ${\displaystyle \Delta x/\Delta$t = c$,}$를 의미하며 이 관계는 s ${\displaystyle 2^{}}$의 불변성 때문에 프레임 독립적입니다.${\displaystyle$ s$^{2}}$ 이로부터 모든 관성 프레임에서 빛의 속도가 $c$ ${\displaystyle c}$임을 알 수 있습니다.즉, 보편적 로렌츠 공분산의 가정에서 출발하여 빛의 일정한 속도는 특수 이론의 두 개의 가설에서와 같은 가설이 아니라 유도된 결과입니다.

동시성 상대성

한 관성 관찰자의 기준 프레임에서 동시에 발생하는 두 개의 다른 위치에서 발생하는 두 가지 사건을 고려합니다.이들은 다른 관성 관찰자의 기준 프레임에서 비동시적으로 발생할 수 있습니다(절대 동시성 결여).

식 3으로부터(좌표차의 관점에서 정방향 로렌츠 변환)

프레임 S(satisf링 δt = 0)에서 동시인 두 이벤트가 반드시 다른 관성 프레임 S'(satisf링 δt' = 0)에서 동시인 것은 아님을 알 수 있습니다.프레임 S(satisf링 δx = 0)에서 이러한 이벤트가 추가적으로 공동 로컬인 경우에만, 다른 프레임 S'에서 동시에 발생합니다.

사냐크 효과는 동시성의 상대성의 발현으로 간주될 수 있습니다.^[31]$v{\displaystyle }$ ${\displaystyle v}$에서는 동시성의 상대성이 1차 효과이므로 링 레이저 자이로스코프 및 광섬유 자이로스코프와 같이 작동을 위해 Sagnac 효과를 기반으로 하는 기기는 극도의 감도가 가능합니다$.$^{[19][p 14]}

시간확장

두 사건 사이의 시간 경과는 한 관찰자에서 다른 관찰자로 불변하지 않고 관찰자의 참조 프레임의 상대 속도에 따라 달라집니다.

비프림 시스템 S에 시계가 정지되어 있다고 가정합니다.그러면 두 개의 서로 다른 눈금에서 시계의 위치는 δx = 0으로 표시됩니다.두 시스템에서 측정된 이러한 눈금 사이의 시간 관계를 찾기 위해 식 3을 사용하여 다음을 찾을 수 있습니다.

${\displaystyle \mathrm{}}$$\delta$${\displaystyle \mathrm{}t\mathrm{\text{'}}=}$$$γ${\displaystyle \mathrm{}}$ ${\displaystyle x}$ ${\displaystyle =}$ ${\displaystyle 0}$을$$만족하는 이벤트에${\displaystyle \mathrm{}}$대${\displaystyle \mathrm{한\; \delta \; g}}$amma t {\displaystyle \$Delt$ $'=\$δ \,\$Delta$ t$}.$$${\$displaystyle$ \$Delt$${\displaystyle \mathrm{a}}$ x = 0$\.}$

이는 클럭이 이동하는 프레임(S')에서 볼 수 있는 두 눈금 사이의 시간( δt')이 클럭의 나머지 프레임(S')에서 측정한 눈금 사이의 시간( δt)보다 길다는 것을 보여줍니다.시간 지연은 많은 물리적 현상을 설명합니다. 예를 들어, 우주선이 지구 외부 대기의 입자와 충돌하여 표면으로 이동하면서 생성된 고속 뮤온의 수명은 실험실에서 생성되고 붕괴되는 뮤온의 수명보다 큽니다.^[32]

"움직이는 시계는 느리게 돌아간다"는 취지의 말을 들을 때마다, 사람들은 동일한 동기화된 시계들로 빽빽하게 채워진 관성 기준 프레임을 상상해야 합니다.움직이는 시계가 이 배열을 통과할 때, 특정 지점의 시계는 같은 지점의 정지 시계와 비교됩니다.^{[33]: 149–152}

만약 우리가 실제로 움직이는 시계를 본다면 우리가 얻을 수 있는 측정값은 일반적으로 전혀 같지 않을 것입니다. 왜냐하면 보는 시간이 빛의 유한한 속도에 의해 지연될 것이기 때문입니다. 즉, 우리가 보는 시간이 도플러 효과에 의해 왜곡될 것이기 때문입니다.상대론적 효과의 측정은 항상 유한한 광속 효과를 고려한 후에 이루어진 것으로 이해되어야 합니다.^{[33]: 149–152}

랑주뱅의 빛시계

상대성 이론의 초기 지지자인 폴 랑게빈은 아인슈타인의 혁명적인 개념에 대한 많은 물리학자들의 저항에 직면하여 이론을 대중화시키기 위해 많은 일을 했습니다.특수 상대성 이론의 기초에 대한 그의 수많은 공헌들 중에는 질량-에너지 관계에 대한 독립적인 연구, 쌍둥이 역설에 대한 철저한 연구, 그리고 회전 좌표계에 대한 연구들이 있었습니다.그의 이름은 그가 로렌츠 변환의 새로운 파생을 수행하기 위해 사용했던 (1909년^[34] 루이스와 톨만에 의해 원래 개발된) "빛 시계"라고 불리는 가상의 구조에 자주 붙여집니다.^[35]

빛시계는 빛의 신호가 서로 반대쪽 면에서 앞뒤로 반사되는 완벽한 반사 벽의 상자라고 생각됩니다.두 거울을 연결하는 선에 수직인 균일한 관성운동으로 진행하는 빛시계를 이용하여 시간확장의 개념을 자주 가르칩니다.^{[36][37][38][39]} (랑주뱅 자신은 빛시계를 그 운동선과 평행하게 배열한 것을 사용했습니다.)^[35]

그림 4-3a에 예시된 시나리오를 고려합니다.관찰자 A는 $빛시계$를 따라 위아래로 왕복하는 데 펄스가 걸리는 시간을 측정하는 전자 타이머와 함께$$$$길이 L {\$displaystyle L}$의 빛시계를 들고 있습니다.관찰자 A는 기차를 따라 빠르게 이동하고 있지만, 그녀의 관점에서 펄스의 방출과 수신은 같은 장소에서 발생하고, 그녀는 이 두 사건의 정확한 위치에 위치한 하나의 시계를 이용하여 간격을 측정합니다.이 두 이벤트 사이의 간격에 대해 관찰자 A는 ${\displaystyle {tA}_{}}$ = ${\displaystyle \mathrm{2L}}$/ ${\displaystyle c}$를 찾습니다${\displaystyle .}$ ${\displaystyle t_{A$} = $2L/c}$ 특정 참조 프레임에서 움직임이 없는 단일 클럭을 사용하여 측정한 시간 간격을 적절한 시간 간격이라고 합니다.

그림 4-3b는 기차가 $displaystyle v.}$의 속도로 지나갈 때 선로 옆에 주차되어 있는 관찰자 B의 입장에서 동일한 두 사건을 보여줍니다. ${\$displaystyle v.} 관찰자 B는 상하로 직선 운동을 하는 대신$$ 지그재그 라인을 따라 움직이는 펄스를 볼 수 있습니다.그러나 빛의 속도의 일정성에 대한 가정 때문에, 이 대각선을 따른 펄스의 속도는 관찰자 A가 그녀의 상하 펄스에 대해 본 것과$$ $동일$한 c ${\displaystyle c}$입니다.B는 펄스의 총 왕복 시간이 t ${\displaystyle B_{}}$ = ${\displaystyle 2}$ ${\displaystyle \mathrm{L}}$/ ${\displaystyle c}$ 2${\displaystyle \sqrt{{}^{}}}$-${\displaystyle \sqrt{{}^{}}}$v {\$displaystyle {\sqrt {c$$^{$$2}$ - v$^{2}},$$${\${\displaystyle displaystyle}$ {${\displaystyle \sqrt{{t\_}^{}}}$${$${\displaystyle \sqrt{B^{}}}$} = $2L$ / {\$sqrt$ {c${\displaystyle ^\{}$${\displaystyle 2_{}}$ -${\displaystyle \sqrt{}}$${\displaystyle \sqrt{{}^{}}}$${\displaystyle \sqrt{{}^{}2{}^{}}}$ = t A / 1 - v 2 / c 2 .$$${\displaystyle$ = $t_{$$A}/{\sqrt {1-v^{2}/c^{2}}}.$ 관찰자$$ B의 경우 빛 펄스의 방출과 수신이 서로 다른 위치에서 발생했고, 참조 프레임의 서로 다른 두 위치에 위치한 두 개의 정지 시계와 동기 시계를 사용하여 간격을 측정했습니다.따라서 B가 측정한 시간 간격은 정지 시계 하나로 측정하지 않았기 때문에 적절한 시간 간격이 아니었습니다.^[40]

상호 시간 지연

랑게뱅 빛시계에 대한 위의 설명에서, 한 관찰자는 정지해 있고 다른 관찰자는 정지해 있다고 표시하는 것은 완전히 자의적이었습니다.관찰자 B가 빛 시계를 들고 왼쪽으로$$ ${\displaystyle v}$의 속도로 움직이게 할 수 있는데, 이 경우 관찰자 A는 B의 시계가 자신의 로컬 시계보다 느리게 움직인다고 인식할 것입니다.

A와 B 둘 다에 동의할 독립적인 관찰자 C가 없기 때문에 여기에는 역설이 없습니다.관측자 C는 반드시 자신의 기준 프레임에서 측정을 수행합니다.만약 그 기준 프레임이 A의 기준 프레임과 일치한다면, C는 A의 시간 측정에 동의할 것입니다.만약 C의 기준 프레임이 B의 기준 프레임과 일치한다면, C는 B의 시간 측정에 동의할 것입니다.C의 기준 프레임이 A의 프레임이나 B의 프레임 모두와 일치하지 않으면 C의 시간 측정은 A와 B의 시간 측정과 일치하지 않습니다.^[41]

쌍둥이 역설

별개의 관성 프레임에서 두 관측자 사이의 시간 팽창의 상호성은 1911년 랑게빈에 의해 현재 형태로 명시된 소위 쌍둥이 역설로 이어집니다.^[42]Langevin은 지구의 미래를 탐험하고 싶어하는 모험가를 상상했습니다.이 여행자는 빛의 속도의 99.995%로 이동할 수 있는 발사체에 탑승합니다.자신의 일생 중 단 2년만에 가까운 별을 왕복한 후, 그는 200년 이상 된 지구로 돌아옵니다.

이 결과는 여행자와 지구로 향하는 관찰자 모두가 다른 사람을 움직이는 것으로 볼 것이기 때문에 혼란스럽게 보입니다. 그래서 시간 지연의 상호성 때문에 처음에는 서로가 덜 늙었다는 것을 발견했어야 한다고 예상할 수 있기 때문입니다.사실 역설은 전혀 없습니다. 왜냐하면 두 관찰자가 적절한 시간을 비교하기 위해서는 상황의 대칭성이 깨져야 하기 때문입니다.두 관찰자 중 적어도 한 명은 다른 관찰자와 일치하도록 동작 상태를 변경해야 합니다.^[43]

그러나 역설의 일반적인 해결책을 안다고 해서 정확한 정량적 결과를 계산할 수 있는 능력이 즉각적으로 나오는 것은 아닙니다.이 퍼즐에 대한 많은 해결책이 문헌에 제시되었고 트윈 패러독스 기사에서 검토되었습니다.우리는 역설에 대한 그러한 해결책을 다음의 하나에서 검토할 것입니다.

우리의 기본적인 목표는 여행 후에, 두 쌍둥이가 서로 다른 경험에 관계없이 누가 얼마나 늙었는지에 대해 완전히 일치한다는 것을 보여주는 것입니다.도 4-4는 주행중인 쌍둥이가 0.6 c로 3 거리의 항성을 왕복하는 시나리오를 나타낸 것입니다.여행 중에, 각각의 쌍둥이는 다른 쌍둥이에게 연간 시간 신호를 보냅니다. (적절한) 시간으로 측정됨)를 보냅니다.여행 후에는 누적 횟수가 비교됩니다.트립의 바깥쪽 위상에서 각 쌍둥이는 f${\displaystyle {\text{'}}^{}}$ = f ${\displaystyle (\sqrt{1}}$ -${\displaystyle \sqrt{\beta }}$)${\displaystyle \sqrt{}}$/${\displaystyle \sqrt{}}$(${\displaystyle \sqrt{1}}$ +${\displaystyle \sqrt{\beta }}$ ${\displaystyle \sqrt{)}}$의 낮은 $비율$로 다른 쌍둥이의 신호를 받습니다${\displaystyle .}$ ${\displaystyle$f'=$f{\sqrt {(1-\$beta$)/(1+\$beta $)}.$$}$처음에는$$, 상황이 완벽하게 대칭적입니다: 각각의 쌍둥이가 자신의 시계로 측정된 2년에 다른 쌍둥이의 1년 신호를 받는다는 것에 주목하세요.이 대칭은 쌍둥이가 시계로 측정한 4년 단위로 돌 때 깨집니다.여행의 남은 4년 동안, 그녀는 향상된 $속도$의 f${\displaystyle {}^{}}$″ = ${\displaystyle f\sqrt{}}$(${\displaystyle \sqrt{1}}$ +${\displaystyle \sqrt{}}$β${\displaystyle \sqrt{)}}$ /${\displaystyle \sqrt{}}$(1 -${\displaystyle \sqrt{\beta }}$ ) .${\displaystyle$f"=$f{\sqrt {(1+\$beta$)/(1-\$beta $)}$로 신호를 받습니다.$}$고정 쌍둥이의 경우는 상황이$$ 상당히 다릅니다.광속 지연 때문에, 그는 8년이 지나서야 그의 여동생이 돌아서는 것을 볼 수 있습니다.따라서 그는 비교적 짧은 기간 동안만 여동생으로부터 향상된 속도의 신호를 받습니다.쌍둥이는 각각의 총 시간에 대한 측정에 동의하지 않지만, 다음 표와 민코프스키 다이어그램의 간단한 관찰을 통해 각 쌍둥이가 한 쌍에서 다른 쌍으로 보내는 신호의 총 수에 대해 서로 완전히 일치한다는 것을 알 수 있습니다.따라서 역설은 없습니다.^{[33]: 152–159}

아이템	측정값: 집콕의	그림 4-4	측정: 나그네	그림 4-4
총이동시간	${\displaystyle T={\frac {2L}{v}}$	10년	${\displaystyle T'={\frac {2L}{\gamma v}}$	8년
전송된 총 펄스 수	${\displaystyle fT={\frac {2fL}{v}}}$	10	${\displaystyle fT'={\frac {2fL}{\gamma v}}$	8
여행자 회차가 감지된 시간	${\displaystyle t_{1}={\frac {L}{v}}+{\frac {L}{c}}}$	8년	${\displaystyle t_{1}'={\frac {L}{\gamma v}}$	4년
초기 $f{\displaystyle {}^{\text{'}}}$ ${\$ f$'}$ 속도에서$$ 수신된 펄스 수	${\displaystyle ft_{1}}$ ${\displaystyle = {\frac {fL}{v}}(1+\beta )\left ({\frac {1-\beta }{1+\beta }\right)^{1/2}$ ${\displaystyle = {\frac {fL}{v}}(1-\beta^{2})^{1/2}}$	4	${\displaystyle ft_{1}'}$ ${\displaystyle = {\frac {fL}{v}}(1-\beta^{2})^{1/2}\left ({\frac {1-\beta }{1+\beta }}\right)^{1/2}}$ ${\displaystyle = {\frac {fL}{v}}(1-\beta )}$	2
남은여행시간	${\displaystyle t_{2}={\frac {L}{v}}-{\frac {L}{c}}}$	2년	${\displaystyle t_{2}'={\frac {L}{\gamma v}}$	4년
최종 $f$ ″ ${\displaystyle$ f$"}$ 속도에서 수신된 신호 수	${\displaystyle f`t_{2}}$ ${\displaystyle = {\frac {fL}{v}}(1-\beta )\left ({\frac {1+\beta }{1-\beta }\right)^{1/2}$ ${\displaystyle = {\frac {fL}{v}}(1-\beta^{2})^{1/2}}$	4	${\displaystyle f"t_{2}'}$ ${\displaystyle = {\frac {fL}{v}}(1-\beta^{2})^{1/2}\left ({\frac {1+\beta }{1-\beta }\right)^{1/2}}$ ${\displaystyle = {\frac {fL}{v}}(1+\beta )}$	8
총 수신 펄스 수	${\displaystyle {\frac {2fL}{v}}(1-\beta^{2})^{1/2}}$ ${\displaystyle = {\frac {2fL}{\gamma v}}$	8	${\displaystyle {\frac {2fL}{v}}$	10
다른 쌍둥이가 얼마나 늙었어야 했는지에 대한 쌍둥이의 계산	${\displaystyle T'={\frac {2L}{\gamma v}}$	8년	${\displaystyle T={\frac {2L}{v}}$	10년

길이수축

한 관측자에 의해 측정된 물체의 치수(예: 길이)는 다른 관측자에 의해 측정된 동일한 물체의 측정 결과보다 작을 수 있습니다(예: 사다리 역설은 빛의 속도에 근접하여 더 작은 차고 내에 포함되는 긴 사다리를 포함합니다).

마찬가지로, 비프림 시스템 S에서 측정 막대가 정지해 있고 x축을 따라 정렬되어 있다고 가정합니다.이 시스템에서 이 막대의 길이는 δx로 표시됩니다.로드가 이동하는 시스템 S'에서 이 로드의 길이를 측정하려면 로드의 끝점까지의 거리 x'를 해당 시스템 S'에서 동시에 측정해야 합니다.즉, 측정값은 δt' = 0인 것을 특징으로 하며, 이는 수학식 4와 결합하여 길이 δx와 δx' 사이의 관계를 구할 수 있습니다.

${\displaystyle \mathrm{}}$${\displaystyle {}^{}}$${\displaystyle \mathrm{\text{'}}{}^{}=}$$$${\displaystyle \mathrm{\delta }}$ γ $δ$t'${\displaystyle }$= 0을 ${\displaystyle \mathrm{만족}}$하는 이벤트의 ${\$$displaystyle$ \Delta${\displaystyle \mathrm{}}$x' = {\$frac${\$Delta$ x$mma$ }}. ${\displaystyle$ \$Delta$${\displaystyle \mathrm{}}$t' = $0\.}$

이는 이동 중인 프레임(S')에서 측정한 로드의 길이( δx')가 자체 정지 프레임(S)에서 로드의 길이( δx)보다 짧음을 보여줍니다.

시간 지연과 길이 수축은 단순한 외형이 아닙니다.시간 지연은 주어진 좌표계에서 동일한 위치에서 발생하는 이벤트 사이의 시간 간격을 측정하는 우리의 방법("공동 로컬" 이벤트라고 함)과 명백하게 관련되어 있습니다.이러한 시간 간격(관련 관측자에 의해 실제로 실험적으로 측정될 수 있고 실제로 측정될 수 있는)은 사건이 동시에 발생하지 않는 한 첫 번째 좌표계에 대해 이동하는 다른 좌표계에서는 다릅니다.마찬가지로, 길이 수축은 지정된 좌표계에서 분리된 이벤트 사이의 측정된 거리와 관련이 있습니다.이러한 이벤트가 공국적이 아니라 거리(공간)로 분리된 경우 다른 이동 좌표계에서 볼 때 서로 동일한 공간적 거리에서 발생하지 않습니다.

속도의 로런츠 변환

표준 구성에서 두 프레임 S와 S'를 고려합니다.S의 입자는 속도 벡터 $u$를 사용하여 x 방향으로 이동합니다${\displaystyle .}$ ${\displaystyle \mathbf {u}.}$ 프레임 S'에서 속도 $u{\displaystyle {\mathbf{}}^{\text{'}}}$ ${\$얼마입니까$$?

우리는 쓸 수 있습니다.

$${\displaystyle \mathbf {u} =u= dx/dt\,}$$

(7)

$${\displaystyle \mathbf {u'} =u'=dx'/dt'\",}$$

(8)

식 5의 d$$ ${\$ 및$$ ${\displaystyle {}^{}}$ t${\$을 식 8로 대체한 다음, 식 7의 간단한 수학적 조작 및 역대체를 통해 속도 $u{\displaystyle }$ ${\displaystyle$ $u$$}$을(를) $u{\displaystyle {}^{}}$' ${\$ u$'$로 로런츠 변환$:$

$${\displaystyle u'={\frac {dx'}{dt'}={\frac {\gamma(dx-vdt)}{\gamma \left(dt-{\frac {vdx}{c^{2}}\right)}}={\frac {{\frac {dx}{dt}-v}{1-\left ({\frac {v}{c^{2}}\right)\left ({\frac {dx}{dt}\right)}}}={\frac {u-v}{1-uv/c^{2}}}.$$

(9)

역 관계는 프라이밍 기호와 프라이밍되지 않은 기호를 바꾸고 v {\$displaystyle v}$을$({\displaystyle }$를) $.$ {\$displaystyle -v\}($으)로 바꿈으로써 얻어집니다.

$${\displaystyle u={\frac {u'+v}{1+u'v/c^{2}}}.$$

(10)

x축을 따라 정렬되지 $않은$ u ${\$의 경우 다음과 같이 적습니다.^{[12]: 47–49}

$${\displaystyle \mathbf {u} =(u_{1},\u_{2},\u_{3})=(dx/dt,\dy/dt,\dz/dt)\.}$$

(11)

$${\displaystyle \mathbf {u'} =(u_{1}',\u_{2}',\u_{3}'=(dx'/dt',\dy'/dt',\dz'/dt')\.}$$

(12)

이 경우의 정방향 변환과 역방향 변환은 다음과 같습니다.

$${\displaystyle u_{1}'={\frac {u_{1}-v}{1-u_{1}v/c^{2}}\,\qquad u_{2}'={\frac {u_{2}}{\gamma \left(1-u_{1}v/c^{2}\right)}},\qquad u_{3}'={\frac {u_{3}}{\left(1-u_{1}v/c^{2}\right)}\.}$$

(13)

$${\displaystyle u_{1}={\frac {u_{1}'+v}{1+u_{1}'v/c^{2}}\,\qquad u_{2}={\frac {u_{2}}{\gamma \left(1+u_{1}'v/c^{2}\right)}},\qquad u_{3}={\frac {u_{3}}{\left(1+u_{1}'v/c^{2}\right)}\.}$$

(14)

식 10과 식 14는 두 개의 $속도$v {\$displaystyle$ \$mathbf$ {v$}}$와 u$',$ {\$displaystyle$ \$mathbf {u'},$의 $u${\$displaystyle$ \$mathbf {u}}$를 주는 것으로 해석할 수 있으며, 이들은 갈릴레이 상대성 이론에서 유효한 공식 $u$ = ${\displaystyle {}^{}}$'${\displaystyle }$+ ${\displaystyle \mathbf{v}}$ ${\displaystyle \mathbf {$u=$u'+v}를$대체합니다.이러한 방식으로 해석하면, 일반적으로 상대론적 속도 덧셈(또는 조성) 공식이라고 하며, S와 S'의 세 축이 서로 정렬되는 데 유효합니다(표준 구성에서는 아니지만).^{[12]: 47–49}

다음 사항에 유의합니다.

• 물체(예: 광자)가 한 프레임(즉, u = ±c 또는 u' = ±c)에서 빛의 속도로 움직이고 있다면, 다른 프레임에서도 빛의 속도로 움직이고 있을 것이며, v < c로 움직일 것입니다.
• 크기가 c보다 작은 두 속도의 결과 속도는 항상 크기가 c보다 작은 속도입니다.
• 만약 u와 v(그리고 u'와 v')가 빛의 속도에 대하여 모두 작다면(예를 들어 u/c ≪ 1), 직관적인 갈릴레이 변환은 특수 상대성 이론에 대한 변환 방정식으로부터 회복됩니다.
• (아인슈타인이 고려하는 것처럼 광선을 타는) 광자에 프레임을 부착하는 것은 변환에 대한 특별한 처리가 필요합니다.

표준 구성에서 x 방향에 대해서는 특별한 사항이 없습니다.위의 형식주의는 모든 방향에 적용되며, 세 개의 직교 방향은 속도 벡터를 이러한 방향의 성분으로 분해함으로써 공간의 모든 방향을 다룰 수 있습니다.자세한 내용은 Velocity-addition 공식을 참조하십시오.

토머스 로테이션

두 개의 비공선 로렌츠 부스트(즉, 회전을 수반하지 않는 두 개의 비공선 로렌츠 변환)의 구성은 순수 부스트가 아니라 부스트와 회전의 구성인 로렌츠 변환을 초래합니다.

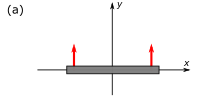
토마스 회전은 동시성의 상대성에서 비롯됩니다.도 4-5a에서, 정지 프레임에서 $길이$ L ${\$$displaystyle L}$의 로드($즉{\displaystyle }$, L {\$displaystyle$ L}의$$적절한 길이를 갖는$)$는 지면 프레임에서 y축을 따라 수직으로 상승합니다.

도 4-5b에서는 $속도{\displaystyle }$ v ${\displaystyle v}$로 이동하는 로켓의 프레임에서 오른쪽으로 동일한 막대가 관찰됩니다.막대의 왼쪽 끝과 오른쪽 끝에 위치한 두 개의 시계가 막대의 프레임에서 동기화되는 것을 상상하면, 동시성의 상대성 이론으로 인해 로켓 프레임의 관찰자는 막대의 오른쪽 끝에 있는 $시계$가 $/$ {\$displaystyle Lv/c^{$$2$만큼 시간이 지남에 따라 관찰(안 보임)하게 됩니다.$}$로드가$$ 기울어짐에 따라 관찰됩니다.^{[30]: 98–99}

길이 수축이나 시간 팽창과 같은 2차 상대론적 효과와는 달리, 이 효과는 상당히 낮은 속도에서도 상당히 크게 나타납니다.예를 들어, 이것은 움직이는 입자의 스핀에서 볼 수 있는데, 토마스 세차운동은 기본 입자의 스핀이나 거시 자이로스코프의 회전에 적용되는 상대론적 보정이며, 곡선 궤도를 따르는 입자의 스핀의 각속도와 궤도 운동의 각속도를 연관시킵니다.^{[30]: 169–174}

토마스 회전은 잘 알려진 "미터 막대와 구멍 역설"에 대한 해상도를 제공합니다.^{[p 15][30]: 98–99}

인과관계와 빛보다 빠른 운동의 금지

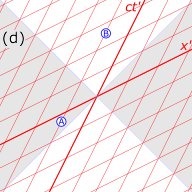
그림 4-6에서, 사건 A("원인")와 사건 B("효과") 사이의 시간 간격은 '시간과 같다' 즉, 사건 A와 사건 B가 공간의 동일한 위치에서 서로 다른 시간에 발생하는 것만으로 분리되는 기준 프레임이 존재합니다.해당 프레임에서 A가 B보다 앞에 있으면 로렌츠 변환으로 액세스할 수 있는 모든 프레임에서 A가 B보다 앞에 있습니다.물질(또는 정보)이 갑의 위치에서 을의 위치까지 광속 이하로 이동(광속 이하)하여 을의 위치에 도달하여 을의 위치까지 이동하는 것이 가능하므로 인과관계(갑의 원인과 을의 효과)가 존재할 수 있습니다.

다이어그램에서 AC 간격은 '공간 유사'입니다. 즉, 이벤트 A와 C가 동시에 발생하고 공간에서만 분리되는 참조 프레임이 있습니다.A가 C 앞에 있는 프레임(그림 참조)과 C가 A 앞에 있는 프레임도 있습니다.그러나 이벤트 A와 C가 동일한 위치에서 발생하는 로렌츠 변환으로 접근할 수 있는 프레임은 없습니다.사건 A와 사건 C 사이에 인과관계가 존재할 수 있다면 인과관계의 역설이 발생할 것입니다.

예를 들어, 신호가 빛보다 더 빨리 전송될 수 있다면, 신호는 전송자의 과거(그림에서 관찰자 B)로 전송될 수 있습니다.^{[44][p 16]}그러면 다양한 인과적 역설이 구축될 수 있습니다.

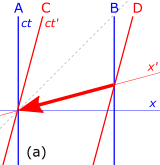
그림 4-7의 시공간 도표를 생각해 보자. 고속열차가 지나갈 때 A와 B는 철로를 따라 서 있는데, C는 열차의 마지막 칸에, D는 선두칸에 타고 있습니다.A와 B의 세계선은 수직(ct)으로 지상에서 관측된 관측자의 정지 위치를 구분하는 반면 C와 D의 세계선은 전방(ct')으로 기울어져 있어 지상에서 관측된 관측자 C와 D의 정지된 움직임을 반영합니다.

1. 그림 4-7a.선두차가 지나갈 때 "B가 D에게 메시지를 전달한다"는 이벤트가 D의 프레임의 기원이 됩니다.D는 가상의 "즉각 통신기"를 사용하여 기차를 따라 메시지를 뒷좌석의 C에게 보냅니다.이 메시지의 월드 라인은${\displaystyle {}^{}}$' ${\$ 축을$$ 따라 있는 굵은 빨간색 화살표이며, 이는 C와 D의 프라이밍된 프레임에서 동시성 라인입니다.(프림되지 않은) 접지 프레임에서는 신호가 전송된 것보다 더 일찍 도착합니다.
2. 그림 4-7b.기찻길 옆에 서 있는 A에게 메시지를 전달하는 'C'의 사건이 그들의 프레임의 기원이 되고 있습니다.이제 A는 트랙을 따라 "즉각 통신기"를 통해 메시지를 B에게 보냅니다.이 메시지의 월드 라인은${\displaystyle }$+${\displaystyle x}$ ${\displaystyle +x}$ 축을$$ 따라 있는 파란색 지방 화살표이며, 이는 A와 B의 프레임에 대한 동시성 라인입니다.시공간 도표에서 볼 수 있듯이, B는 메시지를 보내기 전에 수신할 것이며, 이는 인과관계 위반입니다.^[45]

신호가 즉각적으로 인과관계를 위반할 필요는 없습니다.D에서 C로의 신호가 $x{\displaystyle {}^{\text{'}}}$ ${\$ x$'}$ 축보다$$ 약간 낮더라도(그리고 A에서 B로의 $신호$가 x ${\displaystyle x$} 축보다$$ 약간 가파르다), B가 메시지를 보내기 전에 수신하는 것은 여전히 가능할 것입니다.열차의 속도를 광속에 가깝게 증가시킴으로써, ${\displaystyle {}^{\text{'}}}$ ${\$ 및$$ $x{\displaystyle {}^{\text{'}}}$ ${\$ 축을$$ 광속을 나타내는 파선에 매우 가깝게 압착할 수 있습니다.이 수정된 설정을 사용하면 빛의 속도보다 약간 빠른 신호라도 인과관계 위반을 초래한다는 것을 증명할 수 있습니다.^[46]

따라서 인과관계가 보존되어야 한다면, 특수상대성이론의 결과 중 하나는 어떤 정보신호나 물질적인 물체도 진공에서 빛보다 더 빠르게 이동할 수 없다는 것입니다.

광속보다 빠른 모든 것이 불가능하다는 것은 아닙니다.(실제 물질이나 에너지가 아닌) 어떤 "물"들이 빛보다 더 빠르게 움직이는 다양한 사소한 상황들이 묘사될 수 있습니다.^[47]예를 들어, 탐조등의 빔이 구름의 바닥에 닿은 위치는 탐조등이 빠르게 회전할 때 빛보다 더 빠르게 이동할 수 있습니다(이는 인과관계나 다른 상대론적 현상에 위배되지 않음).^[48][49]

광학효과

드래그 효과

1850년, 히폴리테 피조와 레옹 푸코는 독립적으로 빛이 공기보다 물에서 더 느리게 움직인다는 것을 확립했고, 따라서 프레넬의 빛의 파동 이론에 대한 예측을 타당화하고 뉴턴의 근육 이론에 대한 대응하는 예측을 무효화했습니다.^[50]빛의 속도는 정적인 물에서 측정되었습니다.흐르는 물의 빛의 속도는 얼마일까요?

1851년, 피조는 이 질문에 답하기 위한 실험을 수행했고, 그 단순화된 표현은 그림 5-1에 나와 있습니다. 한 줄기의 빛은 빔 스플리터에 의해 분리되고, 분리된 빔은 흐르는 물의 관을 통해 서로 반대 방향으로 전달됩니다.이들은 재결합되어 간섭무늬를 형성하는데, 이는 관찰자가 볼 수 있는 광경로 길이의 차이를 나타냅니다.실험은 흐르는 물에 의해 빛이 끌리는 것이 가장자리의 변위를 일으켜 물의 움직임이 빛의 속도에 영향을 미쳤다는 것을 보여주었습니다.

그 당시에 널리 퍼져 있던 이론에 따르면, 빛이 움직이는 매질을 통과하는 속도와 매질의 속도를 합하면 빛은 매질을 통과하는 속도의 단순한 합이 될 것입니다.예상과 달리, 피조는 빛이 물에 끌려가는 것처럼 보이지만, 끌리는 크기가 예상보다 훨씬 낮다는 것을 발견했습니다.$u$'${\displaystyle {}^{}}$= ${\displaystyle c}$/ n ${\$$displaystyle$ u' = c / $n}$ 가 $정지수$에서의 빛의 속도이고 v {\$displaystyle v}$ 가 물의 속도이고 $u{\displaystyle {}_{}}$± ${\displaystyle u_{\pm }$ 가 물의 흐름이 빛의 속도에 가감되는 실험실 프레임에서의 빛의 수적 속도라면,

피조의 결과는 부분 에테르 드래그라는 프레넬의 초기 가설과 일치하지만 당시 물리학자들에게는 매우 혼란스러웠습니다.무엇보다도, 굴절률이 존재한다는 것은 n ${\displaystyle n}$은 파장에 의존하기$$ 때문에 에테르는 동시에 다른 움직임을 유지할 수 있어야 한다는 것을 의미합니다.^{[note 8]}서로 완전히 대립하는 프레넬의 항력계수를 설명하기 위해 다양한 이론적 설명이 제안되었습니다.마이컬슨-모리 실험 전에도 피조의 실험 결과는 움직이는 물체의 광학을 설명하는 데 중요한 상황을 만든 여러 관측 중 하나였습니다.^[51]

특수상대성이론의 관점에서 피조의 결과는 속도의 구성에 대한 상대론적 공식인 식 10에 대한 근사치에 불과합니다.^[29]

${\displaystyle u_{\pm }={\frac {u'\pm v}{1\pm u'v/c^{2}}=}$ ${\displaystyle {\frac {c/n\pm v}{1\pm v/cn}\approx }$ ${\displaystyle c\left ({\frac {1}{n}}\pm {\frac {v}{c}\right)\left(1\mp {\frac {v}{cn}\right)\approx }$ ${\displaystyle {\frac {c}{n}}\pm v\left(1-{\frac {1}{n^{2}}}\right)}$

상대론적 빛의 수차

빛의 속도가 유한하기 때문에, 소스와 수신기의 상대적인 움직임이 가로 성분을 포함하는 경우, 수신기에 도달하는 빛의 방향은 수신기에 대한 소스의 공간의 기하학적 위치로부터 이동됩니다.변위의 고전적인 계산은 두 가지 형태를 가지며, 매질에 대해 수신기, 공급원, 또는 둘 다 움직임에 따라 다른 예측을 합니다. (1) 수신기가 움직임에 있다면, 변위는 빛의 수차의 결과일 것입니다.수신기에 대한 빔의 입사각은 수신기 움직임의 벡터 합과 입사광의 속도로부터 계산될 수 있습니다.^[52] (2) 소스가 움직이고 있다면, 변위는 광시 보정의 결과가 될 것입니다.소스의 겉보기 위치가 기하학적 위치에서 이동하는 것은 빛이 수신기에 도달하는 데 걸리는 시간 동안 소스의 움직임의 결과일 것입니다.^[53]

고전적인 설명은 실험 테스트에 실패했습니다.수차각은 수신기의 속도와 입사광의 속도 사이의 관계에 의존하기 때문에, 입사광이 굴절매체를 통과하는 것은 수차각을 변화시켜야 합니다.1810년, 아라고는 이 예상된 현상을 빛의 속도를 측정하기 위한 실패한 시도로 사용했고,^[54] 1870년, 조지 에어리는 물이 채워진 망원경을 사용하여 이 가설을 시험했고, 예상과 달리 측정된 수차는 공기가 채워진 망원경으로 측정된 수차와 동일하다는 것을 발견했습니다.^[55]이러한 결과를 설명하기 위한 "어설픈" 시도는 부분 에테르 항력의 가설을 사용했지만,^[56] 명백하게 완전한 에테르 항력을 요구하는 마이컬슨-모리 실험의 결과와 양립할 수 없었습니다.^[57]

관성 프레임을 가정할 때, 빛의 수차에 대한 상대론적 표현은 수신기 이동 및 소스 이동 케이스 모두에 적용할 수 있습니다.다양한 삼각형 등가 공식이 발표되었습니다.그림 5-2의 변수로 표현하면 다음과^{[29]: 57–60} 같습니다.

${\displaystyle \cos \theta'={\frac {\cos \theta +v/c}{1+(v/c)\cos \theta}}}$ 오어 ${\displaystyle \sin \theta'={\frac {\sin \theta}{\gamma [1+(v/c)\cos \theta ]}}}$ 오어 ${\displaystyle \tan {\frac {\theta'}{2}}=\left ({\frac {c-v}{c+v}\right)^{1/2}\tan {\frac {\theta}{2}}$

상대론적 도플러 효과

상대론적 종도플러 효과

고전적인 도플러 효과는 매질에 대해 소스, 수신기, 또는 둘 다 움직임이 있는지 여부에 따라 달라집니다.상대론적 도플러 효과는 어떤 매개체와도 무관합니다.그럼에도 불구하고, 소스와 수신기가 서로를 향해 또는 멀리 이동하는 종적인 경우에 대한 상대론적 도플러 이동은 고전적인 현상인 것처럼 유도될 수 있지만, 시간 확장 항을 추가함으로써 수정될 수 있으며, 그것이 여기에 설명된 처리입니다.^[58][59]

수신기 또는 소스에서 관찰자가 측정한 상대$$ $속도{\displaystyle }$ v ${\$을(를) 사용하여 수신기와 소스가 서로 멀어지고 있다고 가정합니다(여기서 채택된 부호 규칙은 수신기와 소스가 서로를 향해 이동하는 $경우{\displaystyle }$ v$${\$displaystyle v}$이(가) 음수입니다).공급원이 매체에 고정되어 있다고 가정합니다.그리고나서

${\displaystyle {여기}_{}}$서 c ${\$는 음속입니다.

빛과 수신기가 상대론적 속도로 움직이는 경우 수신기의 시계는 소스의 시계에 비해 시간이 확장됩니다.수신기가 수신 주파수를 측정합니다.

어디에

• ${\displaystyle \beta }$ =$v$ /${\displaystyle c}$ ${\displaysty$ta =v/$c} 및$
• ${\displaystyle }$γ ${\displaystyle =}$ ${\displaystyle \frac{\sqrt{11}}{}}$ -${\displaystyle \frac{\sqrt{{\beta }^{}}}{}}$ 2 ${\displaysty$ ={\$frac {1}{\sqrt$ ^{$2}}}}}$는 로렌츠 계수입니다.

이동 소스를 사용하여 수신기의 참조 프레임에서 분석을 수행할 때 상대론적 도플러 이동에 대한 동일한 표현식이 얻어집니다.^[60][19]

횡도플러 효과

가로 도플러 효과는 특수 상대성 이론의 주요한 새로운 예측 중 하나입니다.

고전적으로 소스와 수신기가 상대적인 움직임에 대해 종적 성분이 없는 상태에서 서로에 대해 횡방향으로 움직이고 있다면 수신기에 도달하는 빛에 도플러 이동이 없어야 한다고 예상할 수 있습니다.

특수 상대성 이론은 그렇지 않을 것으로 예측합니다.그림 5-3은 이 시나리오의 두 가지 일반적인 변형을 보여줍니다.두 변형 모두 간단한 시간 확장 인수를 사용하여 분석할 수 있습니다.^[19]그림 5-3a에서, 수신기는 소스로부터의 빛이 γ ${\displaystyle \gamma}$의 인자에 의해 청색 시프트된 것을 관찰하고$,$ 그림 5-3b에서, 빛은 동일한 인자에 의해 적색 시프트된 것을 관찰합니다.

측정 대 시각적 외관

시간 지연과 길이 수축은 착시가 아니라 진정한 효과입니다.이러한 효과의 측정은 도플러 이동의 아티팩트가 아니며, 빛이 사건에서 관찰자까지 이동하는 데 걸리는 시간을 고려하지 않은 결과도 아닙니다.

과학자들은 한편으로 측정이나 관찰, 시각적인 모습, 또는 사람이 보는 것을 근본적으로 구분합니다.측정된 개체의 모양은 개체의 점이 한 순간에 존재하기 때문에 개체의 모든 점에 대한 가상 스냅샷입니다.그러나 물체의 시각적인 모습은 빛이 물체의 다른 지점에서 사람의 눈까지 이동하는 데 걸리는 다양한 시간에 영향을 받습니다.

여러 해 동안, 그 둘의 구별은 일반적으로 인정되지 않았고, 일반적으로 관찰자를 지나는 길이 수축된 물체는 실제로 길이 수축된 것으로 보일 것이라고 여겨져 왔습니다.1959년, 제임스 테렐과 로저 펜로즈는 독립적으로 움직이는 물체의 다른 부분에서 관측자에게 도달하는 신호의 시차 효과가 측정된 모양과 매우 다른 결과를 가져온다고 지적했습니다.예를 들어, 후퇴하는 물체는 수축된 것처럼 보이고, 다가오는 물체는 길게 보이며, 지나가는 물체는 회전에 비유된 꼬불꼬불한 모습을 가질 것입니다.^{[p 19][p 20][61][62]}움직이는 구는 모든 속도, 거리 및 모든 시야각에 대해 원형 윤곽선을 유지하지만, 구의 표면과 그 위의 이미지는 왜곡되어 보입니다.^[63][64]

도 5-4 및 도 5-5는 모두 시선 방향으로 횡방향으로 이동하는 물체를 나타낸 것입니다.도 5-4에서는 정육면체를 변의 4배 길이의 거리에서 바라본 모습을 보여주고 있습니다.고속에서는 큐브의 움직임 방향과 수직인 측면이 쌍곡선 모양으로 나타납니다.큐브는 실제로 회전되지 않습니다.오히려, 정육면체의 뒤쪽에서 오는 빛은 앞에서 오는 빛에 비해 사람의 눈에 도달하는 데 더 오랜 시간이 걸리며, 이 시간 동안 정육면체는 오른쪽으로 이동합니다.그림 5-5의 구체는 빠른 속도에서 시야선으로부터 최대 45°까지 기울어진 평평한 원반의 모습을 하고 있습니다.물체의 움직임이 엄격하게 횡적인 것이 아니라 종적인 요소를 포함하는 경우, 관점에서 과장된 왜곡이 나타날 수 있습니다.^[65]이 환상은 테렐 회전 또는 테렐-펜로즈 효과로 알려지게 되었습니다.^{[note 9]}

시각적 외관이 측정과 상충되는 또 다른 예는 다양한 전파 은하, BL Lac 천체, 퀘이사 및 관찰자에 대해 좁은 각도로 물질의 상대론적 속도 제트를 방출하는 다른 천체들에서 명백한 초광성 운동을 관찰하는 것에서 비롯됩니다.겉보기 착시 현상은 가벼운 여행보다 빠른 것처럼 보입니다.^[66][67][68]그림 5-6에서 은하 M87은 아원자 입자의 고속 분출을 거의 직접적으로 우리 쪽으로 분출하지만, 펜로즈-그림 5-4의 정육면체 모양이 늘어져 있는 것과 같은 방식으로 제트가 옆으로 움직이는 것처럼 보이게 하는 것이 테렐 회전입니다.^[69]

다이나믹스

섹션 로렌츠 변환에서 도출된 결과는 운동학, 운동을 일으키는 힘을 고려하지 않고 점, 물체 및 물체의 시스템의 운동에 대한 연구를 엄격하게 다루었습니다.이 절에서는 질량, 힘, 에너지 등에 대해 논의하므로 로렌츠 변환 자체가 포함하는 물리적 효과 이상의 물리적 효과를 고려해야 합니다.

질량과 에너지의 등가성

물체의 속도가 관찰자의 관점에서 빛의 속도에 가까워지면 상대론적 질량이 증가하여 관찰자의 기준 범위 내에서 물체를 가속하는 것이 점점 더 어려워집니다.

질량 m인 정지 물체의 에너지 함량은 mc와² 같습니다.에너지 보존은 어떤 반응에서도 입자의 질량 합의 감소는 반응 후 입자의 운동 에너지의 증가를 수반해야 함을 의미합니다.마찬가지로, 물체의 질량은 운동 에너지를 흡수함으로써 증가할 수 있습니다.

아인슈타인은 위에서 언급한 로런츠 변환의 유도와 특수 상대성 이론의 기초를 설명하는 논문 외에도 E=mc에 대해 질량과 에너지의 동등성(및 투과성)에 대한 발견적 논쟁을 제공하는 논문을 최소 4편 썼습니다.

질량-에너지 등가성은 특수 상대성 이론의 결과입니다.뉴턴 역학에서 분리된 에너지와 운동량은 상대성 이론에서 4개의 벡터를 형성하며, 이것은 시간 성분(에너지)과 공간 성분(운동량)을 사소한 방식으로 연관시킵니다.정지한 물체의 경우, 에너지-운동량 4벡터는 (E/c, 0, 0, 0): 에너지인 시간 성분과 0인 공간 성분 3개를 갖습니다.속도 v의 값이 작은 x 방향으로 로렌츠 변환을 갖는 프레임을 변경함으로써 에너지 운동량 4벡터는 (E/c, Ev/c², 0, 0)이 됩니다.운동량은 에너지에 속도를 c로² 나눈 것과 같습니다.따라서 물체의 뉴턴 질량은 느린 속도에 대한 운동량과 속도의 비율로 E/c와² 같습니다.

에너지와 운동량은 물질과 방사선의 성질이며, 두 개의 특수상대성이론의 기본적인 가정만으로 네 개의 벡터를 형성한다는 것을 추론하는 것은 불가능합니다. 왜냐하면 이것들은 물질이나 방사선에 대해 이야기하는 것이 아니라 공간과 시간에 대해서만 이야기하기 때문입니다.따라서 유도에는 몇 가지 추가적인 물리적 추론이 필요합니다.아인슈타인은 1905년 논문에서 뉴턴 역학이 느린 속도에 대해 유지해야 할 추가적인 원리를 사용하여 느린 속도에서 에너지 스칼라와 3벡터 운동량이 하나 존재하고 에너지와 운동량에 대한 보존 법칙이 상대성 이론에서 정확히 맞는다는 것을 발견했습니다.또한, 그는 맥스웰 방정식을 기반으로 이전에 사실로 보여주었던 빛의 에너지가 주파수와 동일한 도플러 쉬프트 인자에 의해 변형된다고 가정했습니다.^{[p 1]}이 주제에 관한 아인슈타인의 논문 중 첫 번째는 1905년의 "한 물체의 관성은 그것의 에너지 내용물에 의존하는가?"였습니다.^{[p 21]}이 논문에서 아인슈타인의 주장은 물리학자들에 의해 거의 보편적으로 옳으며, 심지어 자명한 것으로 받아들여지고 있지만, 수년에 걸쳐 많은 저자들은 그것이 틀렸다고 제안했습니다.^[70]다른 저자들은 논쟁이 단지 일부 암묵적인 가정에 의존했기 때문에 결론을 내리지 못했다고 주장합니다.^[71]

아인슈타인은 1907년 특수 상대성 이론에 관한 조사 논문에서 자신의 파생에 대한 논란을 인정했습니다.거기서 그는 휴리스틱 질량-에너지 논쟁을 맥스웰 방정식에 의존하는 것은 문제가 있다고 지적합니다.그의 1905년 논문의 주장은 질량이 없는 입자의 방출로 수행될 수 있지만, 맥스웰 방정식은 특히 빛의 방출이 오직 일을 해야만 달성될 수 있다는 것을 분명히 하기 위해 암묵적으로 사용됩니다.전자기파를 방출하기 위해서는 대전된 입자를 흔들기만 하면 됩니다. 그리고 이것은 분명히 일을 하고 있기 때문에 방출은 에너지입니다.^{[p 22][note 10]}

아인슈타인의 1905년 E=mc 시연

아인슈타인은 1905년 아누스 미라빌리스 논문 중 네 번째 논문에서 질량과 에너지의 동등성에 대한 발견론적 주장을 제시했습니다.^{[p 21]}비록 위에서 논의된 바와 같이, 후속 학문은 그의 주장이 광범위하게 확정적인 증거에 미치지 못한다는 것을 확립했지만, 이 논문에서 그가 도달한 결론은 시간의 시험대에 섰습니다.

아인슈타인은 맥스웰 방정식이 암시하는 상대론적 도플러 이동에 대한 그의 최근 발견된 공식, 에너지 보존과 운동량 보존 법칙, 그리고 빛의 진동수와 에너지 사이의 관계를 초기 가정으로 삼았습니다.

그림 6-1(상단)참조 프레임 S의 x축에 대해 ϕ ${\displaystyle \phi}$ 방향으로 진행하는 주파수 $f$ ${\displaystyle$ f$}$의 빛의 평면파 시스템을 고려합니다.속도 $v{\displaystyle }$ ${\displaystyle v}$로 x축을 따라 움직이는 프레임 S'에서 측정된 파동의 진동수(따라서 에너지)는$$ 아인슈타인이 1905년 특수 상대성 이론에 관한 논문에서 개발한 상대론적 도플러 이동 공식에 의해 주어집니다.^{[p 1]}

${\displaystyle {\frac {f'}{f}={\frac {1-{\tfrac {v}{c}}\cos {\phi}}{{\sqrt {1-v^{2}/c^{2}}}}$

그림 6-1(하단)참조 프레임 S에서 정지해 있는 임의의 물체를 생각합니다.이 물체가 x축에 대해 각도 ϕ ${\displaystyle \phi}$에서 한 쌍의 등에너지 광 펄스를 서로 반대 방향으로 방출하도록 합니다.각 펄스는 에너지 $L{\displaystyle /2\mathrm{}}$ ${\displaystyle$ L$/2}$을(를) 갖습니다$.$ 운동량 보존 때문에 몸체는 두 펄스가 방출된 후에도 S에서 정지 상태로 유지됩니다.${\displaystyle {두\mathrm{}}_{}}$ 펄스가 방출되기 전에는 $E0$ {\displaystyle $E_{0},$ 방출 후에는$$ ${\displaystyle {E1\mathrm{}}_{}}$ ${\$라고 합니다$$.

다음으로 프레임 S에 대한$$ $속도{\displaystyle }$v {\$displaystyle v}$에서 x축을 따라 이동하는 프레임 S'에서 관찰된 동일한 시스템을 고려합니다.이 프레임에서는 순방향 펄스와 역방향 펄스의 빛이 상대적으로 도플러 쉬프트됩니다.H ${\displaystyle {0\mathrm{}}_{}}$ ${\$를 두 펄스의 방출 전 참조 프레임 S'에서 측정한 신체의 에너지라고 하고$$ 방출 후 H$$ ${\displaystyle {1\mathrm{}}_{}}$ ${\$라고 합니다.우리는 다음과 같은 관계를 얻습니다.^{[p 21]}

${\displaystyle E_{0}=E_{1}+{\tfrac {1}{2}}L+{\tfrac {1}{2}}L=E_{1}+L}$

${\displaystyle {\begin{aligned}H_{0}&=H_{1}+{\tfrac {1}{2}}L{\tfrac {1-{\tfrac {v}{c}}\cos {\phi}}}{\sqrt {1-v^{2}/c^{2}}}+{\tfrac {1}{c}}\cos {\phi}}{\sqrt {1-v^{2}}\&=H_{1}+{\tfrac {L}{\sqrt {1-v^{2}/c^{2}}}\end{aligned}}$

위의 식들로부터 우리는 다음을 얻습니다.

${\displaystyle \quad \quad(H_{0}-E_{0})-(H_{1}-E_{1})=L\left({\frac {1}{\sqrt {1-v^{2}/c^{2}}}}-1\right)}$

(6-1)

$위{\displaystyle }$ 식에서 본 H$$ - E ${\displaystyle$ H -$E}$의 두 가지 차이점은 간단한 물리적 해석을 갖습니다.$H{\displaystyle }$ ${\displaystyle H}$ 및$$ $E{\displaystyle }$ ${\displaystyle E}$는 이동프레임 및 정지프레임에서 임의체의 에너지이므로,${\displaystyle H_{}}$ ${\displaystyle {0\mathrm{}}_{}}$- ${\displaystyle {}_{}}$ ${\displaystyle {0\mathrm{}}_{}}$ ${\$ - ${\displaystyle {}_{}}$${0}},$ ${\displaystyle H_{}}$ ${\displaystyle {1\mathrm{}}_{}{}_{}}$-$$E 1 {\$displaystyle H_{1}$ - E_{$1}}$는 빛의 방출 전후 신체의 운동 에너지를 나타냅니다$$(에너지의 영점을 고정하고 관례적으로 0으로 설정된 가산 상수는 제외).이런 이유로,

${\displaystyle \quad \quad K_{0}-K_{1}=L\left({\frac {1}{\sqrt {1-v^{2}/c^{2}}}}-1\right)}$

(6-2)

테일러 시리즈 확장을 선택하고 더 높은 차수의 조건을 무시함으로써 그는

${\displaystyle \quad \quad K_{0}-K_{1}={\frac {1}{2}}{\frac {L}{c^{2}}}v^{2}}}$

(6-3)

그리고 나서 아인슈타인은 위의 표현을 운동 에너지에 대한 고전적인 표현인 K.E. = 1/2mv와 비교하면서 다음과 같이 언급했습니다: "만약 물체가 복사의 형태로 에너지 L을 방출한다면, 질량은 L/c만큼 감소합니다."

린들러는 아인슈타인의 휴리스틱 이론이 단지 에너지가 질량에 기여한다는 것을 암시하는 것을 관찰했습니다.1905년, 아인슈타인의 질량-에너지 관계의 신중한 표현은 물체의 모든 에너지가 제거된 후에도 남아있을 "휴면" 질량이 존재할 가능성을 가능하게 했습니다.그러나 1907년까지 아인슈타인은 모든 관성 질량이 에너지 비축을 나타낸다고 주장할 준비가 되어 있었습니다."모든 질량과 에너지를 동일시하기 위해서는 아인슈타인의 특징적인 미적 믿음이 필요했습니다."^{[12]: 81–84} 아인슈타인의 대담한 가설은 그의 원래 제안 이후 수년간 충분히 확인되었습니다.

여러 가지 이유로, 아인슈타인의 독창적인 파생은 현재 거의 가르쳐지지 않고 있습니다.그의 원래 유도의 공식적인 정확성에 대해 오늘날까지 계속되는 격렬한 논쟁 외에도, 특수 상대성 이론을 아인슈타인이 "원리 이론"이라고 불렀던 것으로 인식하는 것은 전자기 현상에 의존하는 것에서 순수하게 동적인 증명 방법으로 전환하게 만들었습니다.^[72]

탄성충돌

전 세계의 입자 가속기에 의해 생성된 충돌 생성물에 대한 조사는 과학자들에게 아원자 세계의 구조와 그것을 지배하는 자연 법칙에 대한 증거를 제공합니다.충돌 생성물의 총합이 충돌 입자의 총합을 크게 초과할 수 있으므로 특수 상대성 이론이 필요합니다.^[73]

뉴턴 역학에서 충돌의 분석은 질량, 운동량, 에너지에 대한 보존 법칙의 사용을 포함합니다.상대론적 역학에서 질량은 독립적으로 보존되지 않는데, 이는 질량이 전체 상대론적 에너지에 포섭되었기 때문입니다.우리는 질량이 같은 두 개의 완전 탄성 충돌 입자의 단순한 경우를 조사함으로써 입자 충돌에 대한 뉴턴식과 상대론적 처리 사이에 발생하는 차이를 설명합니다. (비탄성 충돌은 시공간 #보존 법칙에서 논의됩니다.방사성 붕괴는 일종의 시간 역전 비탄성 충돌로 간주될 수 있습니다.)^[73]

브렘스스트랄룽 방사선의 생성으로 인해 하전된 기본 입자의 탄성 산란이 이상성을 벗어납니다.^[74][75]

뉴턴 해석학

그림 6-2는 당구 선수들에게 친숙한 결과인데, 고정된 공이 동일한 질량의 다른 공에 의해 탄성적으로 부딪히면(사이드 스핀이 없다고 가정할 때), 충돌 후 두 공의 발산 경로가 직각을 이루게 된다는 것을 보여줍니다. (a) 고정된 프레임에서, 2v st로 이동하는 입사구정지된 구와 충돌합니다. (b) 운동량의 중심에서 두 구는 ±v로 서로 대칭적으로 접근합니다. 탄성 충돌 후 두 구는 동일한 속도와 반대 속도 ±u로 서로 반등합니다.에너지 절약을 위해서는 u = v. (c) 정지 프레임으로 되돌아가면 반발속도는 v ± u입니다.점곱 (v + u) • (v - u) = v - u = 0으로 벡터가 직교함을 나타냅니다.

상대론적 분석

그림 6-3에서 동일 질량의 정지 입자와 충돌하는 이동 입자의 탄성 충돌 시나리오를 고려합니다.뉴턴의 경우와는 달리 충돌 후 두 입자 사이의 각도는 90° 미만이며, 산란각에 따라 달라지며, 입사하는 입자의 속도가 광속에 가까워질수록 점점 작아집니다.

입자의 상대론적 운동량과 총 상대론적 에너지는 다음과 같이 주어집니다.

${\displaystyle \quad \quad {\vec {p}}=\gamma m{\vec {v}}\quad {\text{and}}\quad E=\gamma mc^{2}}$

(6-4)

운동량 보존은 들어오는 입자와 정지하는 입자의 운동량의 합(처음에는 운동량 = 0)이 발생하는 입자의 운동량의 합과 같다는 것을 나타냅니다.

${\displaystyle \quad \quad \gamma \gamma _{1}m{\vec {v_{1}}+0=\gamma _{2}m{\vec {v_{2}}}+\+ _{3}m{\vec {v_{3}}}$

(6-5)

마찬가지로, 들어오는 입자와 정지된 입자의 총 상대론적 에너지의 합(초기에는 총 에너지 mc를² 가짐)은 발생하는 입자의 총 에너지의 합과 같습니다.

${\displaystyle \quad \quad \gamma \gamma _{1}mc^{2}+mc^{2}=\gamma _{2}mc^{2}+\gamma _{3}mc^{2}}$

(6-6)

(6-5)를 해당 구성 요소로 분해하고 $v{\displaystyle }${\$displaystyle v}$을(를) 무차원 $\beta {\displaystyle }${\$displaystyle \beta}($으)로$$대체하고 (6-5) 및 (6-6)에서 공통 항을 인수분해하면 다음과 같은 결과를 얻을 수 있습니다.^{[p 23]}

${\displaystyle \quad \quad \beta \gamma _{1}\beta _{1}=\gamma _{2}\cos {\theta}+\beta _{3}\cos {\phi}}$

(6-7)

${\displaystyle \quad \quad \beta \gamma _{2}\beta _{2}\sin {\theta}=\gamma _{3}\sin {\phi}}$

(6-8)

${\displaystyle \quad \quad \gamma _{1}+1=\gamma _{2}+\gamma _{3}}$

(6-9)

이를 통해 다음과 같은 관계를 얻습니다.^{[p 23]}

${\displaystyle \quad \quad \beta _{2}={\frac {\beta _{1}\sin {\phi}}}{\{\beta _{1}^{2}}\sin^{2}{\phi }+\sin^{2}(\phi +\theta )/\gamma _{1}^{2}^{1/2}}}}.$

(6-10)

${\displaystyle \quad \quad \beta _{3}={\frac {\beta _{1}\sin {\theta}}}{\{\beta _{1}^{2}\sin ^{2}{\theta}}+\sin ^{2}(\phi +\theta )/\gamma _{1}^{2}^{1/2}}}}.$

(6-11)

${\displaystyle \quad \cos {(\phi +\theta )} = {\frac {(\gamma _{1}-1)\sin {\theta }}\cos {\theta }}{\{(\gamma _{1}+1)^{2}\sin ^{2}\theta +4\cos ^{2}\theta \}}}$

(6-12)

ϕ =${\displaystyle {}_{}}$θ ${\displaystyle$ \$phi$ =\$theta$ }와$$$\beta$ 2 =$$ ${\displaystyle {3인}_{}}$ 대칭형의 경우 ${\displaystyle$ \beta $_{2}$=$\$beta _{$3}}($6-12)는 다음과 같은 간단한 형태를 취합니다.

${\displaystyle \quad \quad \cos {\theta}={\frac {\beta _{1}}{\{2/\gamma _{1}+3\beta _{1}^{2}-2\}^{1/2}}}}$

(6-13)

지구에서 얼마나 멀리 여행할 수 있습니까?

빛보다 더 빠르게 이동할 수 있는 것은 없기 때문에, 사람은 ~100광년보다 더 멀리 지구를 여행할 수 없다고 결론지을 수도 있습니다.당신은 여행자가 지구로부터 100광년 이내에 존재하는 몇 안 되는 태양계에 결코 도달할 수 없을 것이라고 쉽게 생각할 것입니다.하지만, 시간 지연 때문에 가상의 우주선은 승객의 일생 동안 수천 광년을 여행할 수 있습니다.만약 일정한 1g의 속도로 가속하는 우주선이 만들어질 수 있다면, 1년 후에 그것은 지구에서 봤을 때 거의 빛의 속도로 이동할 것입니다.이를 다음과 같이 설명합니다.

여기서 v(t)는 시간 t에서의 속도이고, a는 우주선의 가속도이며, t는 지구인에 의해 측정된 좌표 시간입니다.^{[p 24]}따라서 9.81m/s로 1년간 가속한 후 우주선은 지구와 비교하여 3년 후 v = 0.712c, 0.946c로 이동하게 됩니다.이 가속이 시작된 지 3년이 지난 후, 우주선은 지구에 대한 빛의 속도의 94.6%의 속도를 달성하게 되며, 시간 지연은 우주선에서 경험하는 매 초를 지구로 되돌아오는 3.1초에 해당합니다.여행하는 동안, 지구인들은 그들의 시계(모든 물리적 현상)가 우주선의 시계보다 3.1배 더 빠르게 똑딱거릴 것이기 때문에, 그들의 여행 동안 그들보다 더 많은 시간을 경험할 것입니다.여행자가 5년 동안 왕복하는 데는 6.5년의 지구 시간이 소요되며 6광년 이상의 거리를 주행할 수 있습니다.20년간 왕복(가속 5년, 감속 5년, 각각 2회)하면 지구 335년, 거리 331광년을 여행한 후 지구에 착륙하게 됩니다.^[76]1g으로 40년을 여행하는 완전한 여행은 58,000년을 지속하고 55,000광년의 거리를 커버하는 지구상에 나타날 것입니다.1.1g으로 40년을 여행하는 것은 148,000년의 지구년이 걸리며 약 140,000광년을 커버할 것입니다.안드로메다 은하까지 1g 가속으로 편도 28년(14년 가속, 14년 감속) 여행하면 안드로메다 은하까지 200만 광년에 이를 수 있습니다.^[76]이와 같은 시간 지연으로 인해 c 가까이 이동하는 뮤온은 반감기의 c배보다 훨씬 더 멀리 이동하는 것으로 관측됩니다.^[77]

상대성 이론과 통합 전자기학

고전 전자기학의 이론적 연구는 파동 전파의 발견으로 이어졌습니다.전자기 효과를 일반화하는 방정식은 E와 B장의 유한한 전파 속도가 하전 입자에 대한 특정한 행동을 필요로 한다는 것을 발견했습니다.이동 전하에 대한 일반적인 연구는 리나르를 형성합니다.특수상대성이론으로 나아가는 위허트 잠재력.

움직이는 전하의 전기장을 움직이지 않는 관찰자의 기준 프레임으로 로런츠 변환하면 흔히 자기장이라고 불리는 수학 용어가 나타납니다.반대로, 움직이는 전하에 의해 생성된 자기장은 사라지고 움직이는 기준 프레임에서 순수하게 정전기장이 됩니다.그러므로 맥스웰 방정식은 우주의 고전적인 모델에서 특별한 상대론적 효과에 단순히 경험적으로 적합합니다.전기장과 자기장은 기준 프레임에 의존적이어서 서로 얽혀 있기 때문에 전자기장에 대해 이야기합니다.특수 상대성 이론은 한 관성 프레임의 전자기장이 다른 관성 프레임에서 어떻게 나타나는지에 대한 변환 규칙을 제공합니다.

3D 형태의 맥스웰 방정식은 이미 특수 상대성 이론의 물리적 내용과 일치하지만, 명백하게 공변적인 형태, 즉 텐서 미적분학의 언어로 조작하기가 더 쉽습니다.^[78]

상대성이론과 양자역학

특수상대성이론은 양자역학과 결합하여 상대론적 양자역학과 양자전기역학을 형성할 수 있습니다.일반상대성이론과 양자역학이 어떻게 통일될 수 있는지는 물리학에서 해결되지 않은 문제 중 하나입니다. 양자중력과 일반상대성이론을 포함한 통일이 필요한 "만물의 이론"은 이론적 연구에서 활발하고 지속적인 분야입니다.

초기의 보어-소머펠트 원자 모형은 특수 상대성 이론과 당시의 양자역학에 대한 예비 지식을 모두 사용하여 알칼리 금속 원자의 미세한 구조를 설명했습니다.^[79]

1928년 폴 디랙은 현재 그를 기리기 위해 디랙 방정식으로 알려진 영향력 있는 상대론적 파동 방정식을 만들었고,^{[p 25]} 이 방정식은 특수 상대성 이론과 1926년 이후 존재하는 양자 이론의 최종 버전과 완전히 양립할 수 있습니다.이 방정식은 스핀이라고 불리는 전자의 고유 각운동량을 설명했을 뿐만 아니라 전자의 반입자(양전자)를 예측하게 했고,^{[p 25][p 26]} 미세한 구조는 특수상대성이론으로만 충분히 설명할 수 있었습니다.그것은 상대론적 양자역학의 첫번째 토대였습니다.

반면에, 반입자의 존재는 상대론적 양자역학이 입자 상호작용의 더 정확하고 완전한 이론에 충분하지 않다는 결론으로 이어집니다.대신, 양자장 이론이라고 불리는 양자화된 장으로 해석되는 입자 이론이 필요하게 되는데, 이 이론에서 입자는 시공간을 통해 생성되고 소멸될 수 있습니다.

상황

민코프스키 시공간의 특수 상대성 이론은 중력 퍼텐셜의 절대값이 관심 영역의 c보다² 훨씬 작을 때만 정확합니다.^[80]강한 중력장에서는 일반 상대성 이론을 사용해야 합니다.일반상대성이론은 약한 장의 한계에서 특수상대성이론이 됩니다.플랑크 길이 이하와 같은 매우 작은 규모에서는 양자 중력을 발생시키는 양자 효과를 고려해야 합니다.그러나 거시적인 규모와 강력한 중력장이 없는 상황에서 특수 상대성 이론은 극도로 높은 정확도(10⁻²⁰)^[81]로 실험적으로 테스트되어 물리학계에 받아들여집니다.이와 모순되는 것으로 보이는 실험 결과는 재현성이 없으므로 실험 오류로 인한 것으로 널리 추정됩니다.

특수 상대성 이론은 수학적으로 자기 일관성이 있으며, 특히 양자장 이론, 끈 이론, 일반 상대성 이론의 유기적인 부분입니다.

뉴턴 역학은 수학적으로 작은 속도(광속과 비교)로 특수 상대성 이론을 따릅니다. 따라서 뉴턴 역학은 느리게 움직이는 물체의 특수 상대성 이론으로 간주될 수 있습니다.보다 자세한 논의는 고전역학을 참조하십시오.

아인슈타인의 1905년 논문 이전의 여러 실험들은 상대성 이론에 대한 증거로 해석됩니다.이 중 아인슈타인이 1905년 이전에 피조 실험을 알고 있었다는 것은 알려져 있으며,^[82] 역사학자들은 아인슈타인이 말년에 이론의 발전에 아무런 역할을 하지 못했다고 주장했음에도 불구하고 적어도 1899년에 마이컬슨-모리 실험을 알고 있었다고 결론 내렸습니다.^[14]

• 피조 실험(1851년, 1886년에 마이컬슨과 몰리가 반복)은 움직이는 매체에서 빛의 속도를 측정했고, 결과는 공선 속도의 상대론적 추가와 일치했습니다.
• 유명한 Michelson-Morley 실험(1881, 1887)은 절대 기준 속도를 검출할 수 없다는 가정을 더욱 뒷받침했습니다.여기서 많은 대안적인 주장과는 달리, 소스와 관찰자 모두 항상 같은 속도로 함께 이동하고 있었기 때문에 소스와 관찰자의 속도에 대한 빛의 속도의 불변성에 대해 거의 언급하지 않았다는 것을 밝혀야 합니다.
• Trouton-Noble 실험(1903)에서 커패시터의 토크는 위치 및 관성 기준 프레임과 무관함을 보여주었습니다.
• 레일리와 브레이스의 실험(1902, 1904)은 상대성 원리에 따라 길이 수축이 동시에 움직이는 관찰자의 복굴절로 이어지지 않는다는 것을 보여주었습니다.

입자가속기는 통상적으로 빛의 속도에 가까운 속도로 움직이는 입자의 특성을 가속하고 측정합니다. 여기서 그들의 행동은 상대성 이론과 완전히 일치하고 초기 뉴턴 역학과 일치하지 않습니다.이 기계들은 상대론적 원리에 따라 설계되지 않았다면 작동하지 않았을 것입니다.게다가, 특수 상대성 이론을 시험하기 위해 많은 현대적인 실험들이 수행되었습니다.몇 가지 예:

• 상대론적 에너지 및 운동량 테스트 – 입자의 한계 속도 테스트
• Ives-Stilwell 실험 – 상대론적 도플러 효과 및 시간 지연 테스트
• 시간지연의 실험적 실험 - 빠르게 움직이는 입자의 반감기에 대한 상대론적 영향
• Kennedy–Thorndike 실험 – 로렌츠 변환에 따른 시간 지연
• Hughes-Driver 실험 – 공간과 질량의 등방성 시험
• 로렌츠 위반에 대한 현대적 검색 – 다양한 현대적 테스트
• 방출 이론을 시험하기 위한 실험은 빛의 속도가 방출자의 속도와 무관하다는 것을 증명했습니다.
• 에테르 항력 가설을 검정하기 위한 실험 - "에테르 흐름 방해물" 없음.

시공간의 기술적 논의

시공간의 기하학

평평한 유클리드 공간과 민코프스키 공간의 비교

특수 상대성 이론은 시공간의 예인 "평탄한" 4차원 민코프스키 공간을 사용합니다.민코프스키 시공간은 표준 3차원 유클리드 공간과 매우 유사한 것으로 보이지만, 시간과 관련하여 결정적인 차이가 있습니다.

3D 공간에서 거리(선 요소) ds의 차분은 다음과 같이 정의됩니다.

여기서 dx = (dx, dx, dx)는 세 공간 차원의 미분입니다.민코프스키 기하학에서는 시간에서 파생된 좌표 X로⁰ 거리 미분이 다음을 만족시키는 추가 차원이 있습니다.

여기서 dX = (dX, dX, dX, dX)는 4개 시공간 차원의 미분입니다.이것은 깊은 이론적 통찰을 암시합니다. 특수 상대성 이론은 단순히 유클리드 공간의 회전 대칭과 유사한 시공간의 회전 대칭입니다(그림 10-1 참조).^[84]유클리드 공간이 유클리드 메트릭을 사용하는 것처럼 시공간도 민코프스키 메트릭을 사용합니다.기본적으로 특수 상대성 이론은 관성 기준 프레임에서 볼 때 모든 시공간 간격(즉, 임의의 두 사건 사이의 4D 거리)의 불변성으로 나타낼 수 있습니다.특수 상대성 이론의 모든 방정식과 효과는 민코프스키 시공간의 이러한 회전 대칭(푸앵카레 군)으로부터 유도될 수 있습니다.

위 ds의 실제 형태는 메트릭과 X 좌표에⁰ 대한 선택에 따라 달라집니다.시간 좌표를 공간 좌표처럼 보이게 하려면 가상: X = ICT로 처리할 수 있습니다(이를 윅 회전이라고 합니다).Misner, Thorne and Wheeler(1971, § 2.3)에 따르면, 궁극적으로 특수 상대성 이론과 일반 상대성 이론 모두에 대한 더 깊은 이해는 민코프스키 메트릭(아래 설명됨)에 대한 연구에서 비롯될 것이며, ICT를 시간 좌표로 사용하는 "disguised" 유클리드 메트릭이 아니라 X = ct를 취할 것입니다.

일부 저자들은 X = t를 사용하며, 보상하기 위해 c의 인자를 다른 곳에 사용합니다. 예를 들어 공간 좌표를 c로 나누거나 c의 인자를 메트릭 텐서에 포함합니다.이러한 수많은 규약들은 c = 1인 자연 단위를 사용함으로써 대체될 수 있습니다.그러면 공간과 시간은 동등한 단위를 가지며, c의 인자는 어디에도 나타나지 않습니다.

3차원 시공간

우리가 3차원 공간에서 물리학을 표현할 수 있도록 공간 차원을 2로 줄이면

널 측지선은 방정식으로 정의된 듀얼 원뿔(그림 10-2 참조)을 따라 놓여 있음을 알 수 있습니다.

아니면 간단히

이것은 반지름 cdt의 원의 방정식입니다.

4차원 시공간

이를 세 공간 차원으로 확장하면 널 측지선은 4차원 원뿔입니다.

그렇게

그림 10-3에 나타낸 바와 같이, 널 측지선은 반지름이 = cdt인 연속 동심원의 집합으로 시각화할 수 있습니다.

이 널 듀얼 원뿔은 공간에 있는 점의 "시선"을 나타냅니다.즉, 우리가 별들을 보고 "내가 받고 있는 저 별에서 나오는 빛은 X년 된 것이다"라고 말할 때, 우리는 이 시선, 즉 널 측지선을 내려다보고 있는 것입니다.우리는 사건 a 거리 $d$ = x $1$ $\sqrt{{}_{}^{}}$+ x $\sqrt{{}_{}^{}}$+ x $\sqrt{{}_{}^{}}$ ${\textstyle$d = {\$sqrt {x_{1}^{2}$ + $x_{2$$}^{2}+x_{3$$}^{2}}}}:$ 떨어져$$ 있고 과거 d/c 시간입니다.이러한 이유로 널 듀얼 콘은 "라이트 콘"이라고도 합니다. (그림 10-2의 왼쪽 아래에 있는 점은 별, 원점은 관측자, 선은 널 측지선 "시선"을 나타냅니다.)

-t 영역의 원뿔은 점이 "수신"하고 있다는 정보이고, +t 영역의 원뿔은 점이 "전송"하고 있다는 정보입니다.

민코프스키 공간의 기하학은 특수 상대성 이론의 많은 사고 실험을 이해하는 데 유용한 민코프스키 다이어그램을 사용하여 묘사될 수 있습니다.

시공간에서의 물리학

기준 프레임간 물리량 변환

위에서 시간 좌표와 세 개의 공간 좌표에 대한 로렌츠 변환은 이들이 서로 얽혀 있음을 보여줍니다.이것은 더 일반적으로 사실입니다. "시간적"과 "공간적" 양의 특정 쌍은 동일한 로렌츠 변환 하에서 동일한 기반에서 자연스럽게 결합합니다.

위의 표준 구성에서 로렌츠 변환, 즉 x 방향의 증가를 위해 다음과 같이 행렬 형태로 재캐스팅할 수 있습니다.

뉴턴 역학에서 크기와 방향을 갖는 양은 수학적으로 유클리드 공간에서 3차원 벡터로 설명되며, 일반적으로 시간에 따라 매개변수화됩니다.특수 상대성 이론에서, 이 개념은 공간과 같은 벡터 양에 적절한 시간 유사량을 더함으로써 확장되고, 우리는 민코프스키 시공간에서 4d 벡터, 즉 "4-벡터"를 갖습니다.벡터의 구성 요소는 텐서 인덱스 표기법을 사용하여 작성되는데, 이것은 많은 장점을 가지고 있습니다.표기법은 푸앵카레 그룹 아래에서 방정식이 명백하게 공변적임을 분명히 하여 이 사실을 확인하기 위해 지루한 계산을 우회합니다.그러한 방정식을 구성할 때, 우리는 종종 이전에 관련이 없다고 생각되었던 방정식들이 실제로 같은 텐서 방정식의 일부로 밀접하게 연결되어 있다는 것을 발견합니다.다른 물리량을 텐서로 인식하면 변환 법칙이 단순해집니다.전체적으로 상위 지수(첨자)는 제곱을 나타내는 경우를 제외하고 지수가 아닌 변동 지수이고 하위 지수(첨자)는 공변 지수입니다.단순화와 이전 방정식과의 일관성을 위해 데카르트 좌표가 사용됩니다.

4개 vector의 가장 간단한 예는 시공간에서의 사건의 위치로, 시간과 유사한 성분 ct와 공간과 유사한 성분 x = (x, y, z)를 구성하며, 성분이 있는 반변형 위치 4개 vector:

여기서 X = ct를 정의하여 시간 좌표가 다른 공간 차원과 동일한 거리 차원을 갖도록 함으로써 공간과 시간이 동일하게 취급되도록 합니다.이제 위치 4-벡터의 변형 성분의 변환은 다음과 같이 압축적으로 작성할 수 있습니다.

ν ${\displaystyle$ \$nu}에$대해 0부터 3까지 암시적 합이 있고, ν $\mu {\displaystyle {{\text{'}}^{}}^{}}$λ$${\$displaystyle ^{\mu'}{{\nu$}}는 행렬입니다.

일반적으로, 4벡터 $T$ ν ${\displaystyle$ T$^{\nu }}$의 모든 반변 성분은 로렌츠 변환에 의해 한 프레임에서 다른 프레임으로 변환됩니다.

다른 4-벡터들의 예들은 적절한 시간에 관하여 위치 4-벡터의 도함수로서$$ 정의된 ${\displaystyle {4-속도}^{}}$ U${\displaystyle {}^{}}$μ$,$ {\$displaystyle$ U$^{\mu }$를 포함합니다:

여기서 로렌츠 계수는 다음과 같습니다.

물체의 상대론적 에너지 $E$ = γ${\displaystyle }$(${\displaystyle v)}$ ${\displaystyle {mc}^{}}$ 2 ${\displaystyle$E =\$gamma (v)mc^{2}$와 상대론적 운동량 $p$ =$$γ ${\displaystyle (v)}$ ${\displaystyle mv}$ ${\displaystyle \mathbf {p}$ =\gamma $(v)m\mathbf {v} }$는 각각 반변형 4momentum 벡터의 시간적, 공간적 성분입니다.

여기서 m은 불변 질량입니다.

4가속도는 4가속도의 적절한 시간 도함수입니다.

3차원 속도와 가속도에 대한 변환 규칙은 매우 어색합니다. 표준 구성 위에서도 속도 방정식은 비선형성 때문에 상당히 복잡합니다.반면에, 4-속도와 4-가속의 변환은 로렌츠 변환 행렬에 의해 더 간단합니다.

스칼라 필드 φ의 4구배는 다음과 같이 변형되지 않고 공변적으로 변환합니다.

이는 다음의 전치입니다.

데카르트 좌표에서만 가능합니다.명확한 공분산에서 변환하는 것은 공변 도함수이며, 데카르트 좌표에서는 부분 도함수로 감소하지만 다른 좌표에서는 감소하지 않습니다.

일반적으로 4-벡터의 공변 성분은 역 로렌츠 변환에 따라 다음과 같이 변환됩니다.

여기서 λ ${\displaystyle {\mu }_{}}$'${\displaystyle {{}^{}}_{}}$ν ${\displaystyle \Lambda$ _${\mu'}^{\nu }}$는 λ μ'${\displaystyle {{}^{}}^{}}$ν$${\$displaystyle \Lambda$^{\$mu'}_{\nu }}$의 역행렬입니다$.$

특수 상대성 이론의 가설은 로렌츠 변환 행렬이 취하는 정확한 형태를 제약합니다.

일반적으로, 대부분의 물리량은 텐서(tensor)의 성분으로 가장 잘 설명됩니다.따라서 한 프레임에서 다른 프레임으로 변환하기 위해 우리는 잘 알려진 텐서^[89] 변환 법칙을 사용합니다.

여기서 λ χ ' ψ ${\displaystyle \Lambda _{\chi'}^{\psi }}$는 λ χ ' ψ ${\displaystyle \Lambda ^{\chi'}{}_{\psi }}$의 역행렬입니다$.$ 모든 텐서는 이 규칙에 의해 변환됩니다.

4차원 2차 반대칭 텐서의 예는 상대론적 각운동량이며, 6개의 성분을 가지고 있습니다: 3개는 고전 각운동량이고, 나머지 3개는 계의 질량 중심의 상승과 관련이 있습니다.적절한 시간에 대한 상대론적 각운동량의 도함수는 상대론적 토크이며, 2차 반대칭 텐서입니다.

전자기장 텐서는 또 다른 2차 반비대칭 텐서장으로, 6개의 성분이 있습니다: 전기장 3개와 자기장 3개.전자기장에 대한 스트레스 에너지 텐서, 즉 전자기 스트레스 에너지 텐서가 있습니다.

미터법

메트릭 텐서를 통해 두 벡터의 내부 곱을 정의할 수 있으며, 이를 통해 벡터에 크기를 할당할 수 있습니다.시공간의 4차원 특성을 고려할 때 민코프스키 미터법 η에는 4×4 행렬로 배열할 수 있는 성분(적당히 선택된 좌표로 유효)이 있습니다.

이는 해당 프레임에서 $역수$인 η α ${\displaystyle {\beta }^{}}$ ${\displaystyle$ \$eta^{\alpha$ \beta $}}$와 같습니다.위와 같은 기호를 사용하는 동안 저자마다 다른 규칙을 사용합니다. 민코프스키 미터법 대체 기호 참조.

푸앵카레 군은 민코프스키 메트릭을 보존하는 가장 일반적인 변환 군입니다.

이것이 특수상대성이론의 기초가 되는 물리적 대칭입니다.

이 메트릭은 벡터 및 텐서의 인덱스를 높이거나 낮추는 데 사용할 수 있습니다.불변량은 메트릭을 사용하여 구성할 수 있으며, 다른 4벡터 S가 있는 4벡터 T의 내부 곱은 다음과 같습니다.

불변성은 스칼라(0 랭크 텐서)이기 때문에 모든 관성 프레임에서 동일한 값을 가져간다는 것을 의미하며, 따라서 사소한 변환에서 λ이 나타나지 않습니다.4벡터 T의 크기는 내부 제품 자체의 양의 제곱근입니다.

이 아이디어를 더 높은 차수의 텐서로 확장할 수 있으며, 2차 텐서의 경우 불변량을 형성할 수 있습니다.

고차 텐서의 경우도 마찬가지입니다.불변식, 특히 자신이 있는 4벡터의 내적은 불변량을 결정하기 위해 로렌츠 변환을 수행할 필요가 없기 때문에 계산에 유용한 방정식을 제공합니다.

상대론적 운동학과 불변성

좌표 미분 변환은 또한 모순적으로 변환됩니다.

따라서 다음을 사용하여 구성된 위치 4벡터 dX의^μ 미분 길이 제곱 는 불변입니다.선 요소 dX가 음수이면 √-dX가 적절한 시간의 미분이고 dX가 양수이면 √dX가 적절한 거리의 미분입니다.

4-속도 U는^μ 불변의 형태를 갖습니다.

모든 속도 4 vectors의 크기가 c임을 의미합니다.이것은 상대성 이론에 있어서 조화로운 휴식이라는 것은 존재하지 않는다는 사실의 표현입니다: 적어도 당신은 항상 시간을 통해 전진하고 있습니다.위 식을 τ으로 미분하면 다음과 같은 결과가 나옵니다.그래서 특수상대성이론에서 가속도 4벡터와 속도 4벡터는 직교합니다.

상대론적 동역학과 불변성

운동량 4-벡터의 불변 크기는 에너지- 운동량 관계를 생성합니다.

우리는 먼저 스칼라이기 때문에 어떤 참조 프레임에서 스칼라를 계산하는지는 중요하지 않다고 주장한 다음 총 운동량이 0인 프레임으로 변환함으로써 이 불변량이 무엇인지 알 수 있습니다.

우리는 나머지 에너지가 독립적인 불변성임을 알 수 있습니다.정지 에너지는 운동량이 0인 프레임으로 변환하여 움직이는 입자와 시스템에 대해서도 계산할 수 있습니다.

휴식 에너지는 위에서 논의한 공식에 따라 질량과 관련이 있습니다.

운동량 중심 프레임(총 운동량이 0인 경우)에서 측정된 시스템의 질량은 이 프레임에서 시스템의 총 에너지로 표시됩니다.이 값은 다른 프레임에서 측정된 개별 시스템 질량의 합과 동일하지 않을 수 있습니다.

뉴턴의 운동 제3법칙을 사용하려면 두 힘 모두 동일한 시간 좌표에 대한 운동량의 변화율로 정의되어야 합니다.즉, 위에서 정의한 3D 힘이 필요합니다.불행히도 4D에는 구성 요소 중 3D 힘 벡터의 구성 요소를 포함하는 텐서가 없습니다.

만약 입자가 c로 이동하지 않는다면, 3차원 힘을 입자의 공동 이동 기준 프레임에서 관찰자의 기준 프레임으로 변환할 수 있습니다.이렇게 하면 4개의 벡터를 얻을 수 있습니다.적절한 시간에 대한 위의 에너지 운동량 4벡터의 변화율입니다.4력의 공변 버전은 다음과 같습니다.

물체의 나머지 프레임에서, 물체의 "불변 질량"이 변하지 않는 한, 4중력의 시간 성분은 0입니다. (이것은 에너지/질량이 물체로부터 직접 추가되거나 제거되는 비폐쇄 시스템을 필요로 합니다.) 이 경우 질량 변화율인 c의 음수입니다.그러나 일반적으로 세 힘은 좌표 시간에 대한 운동량 변화율, 즉 dp/dt에 의해 정의되는 반면, 네 힘은 적절한 시간에 대한 운동량 변화율, 즉 dp/d τ에 의해 정의되기 때문에 네 힘의 성분은 세 힘의 성분과 동일하지 않습니다.

연속 매체에서 힘의 3D 밀도는 힘의 밀도와 결합하여 공변 4-벡터를 형성합니다.공간 부분은 작은 셀(3-공간)에 가해지는 힘을 해당 셀의 부피로 나눈 결과입니다.시간 성분은 해당 셀에 전달되는 전력을 셀의 부피로 나눈 -1/c배입니다.이는 전자기학 섹션에서 아래에 사용됩니다.

참고 항목

• 사용자:
  • 맥스 플랑크
  • 헤르만 민코프스키
  • 막스 폰 라우에
  • 아놀드 소머펠트
  • 맥스 본
• 상대성 이론:
  • 특수상대성이론의 역사
  • 이중특수상대성이론
  • 본디크-캘큘러스
  • 아인슈타인 동기화
  • 리에다이크-퍼트넘 논법
  • 특수상대성이론(대체 제형)
  • 상대성 우선권 분쟁
• 물리학:
  • 아인슈타인의 사고 실험
  • 물리 우주론
  • 상대론적 오일러 방정식
  • 로렌츠 에테르 이론
  • 움직이는 자석과 도체 문제
  • 모양파
  • 상대론적 열전도
  • 상대론적 원반
  • 모태강직
  • 태생좌표
• 수학:
  • 로렌츠 군
  • APS 형식주의의 상대성 이론
• 철학:
  • 실재론
  • 인습주의
• 역설:
  • 에렌페스트 역설
  • 벨의 우주선 역설
  • 속도 조성 역설
  • 등대 역설

메모들

일차출처

참고문헌

추가열람

아인슈타인의 글과 특수상대성이론의 역사에 관한 글

• 아인슈타인, 알버트 (1920).상대성 이론: 특수 이론과 일반 이론.
• 아인슈타인, 알버트 (1996).상대성의 의미.커뮤니케이션즈가 좋아요.ISBN 1-56731-136-9
• 로구노프, 아나톨리 A. (2005)앙리 푸앵카레와 상대성 이론 (번역)폰토코르보와 V.O. 솔로비예프의 러시아어 가사, V.A. 페트로프 편집).나우카, 모스크바.

교재

• 찰스 미스너, 킵 손, 존 아치볼드 휠러 (1971) 중력.W.H. 프리먼사ISBN 0-7167-0334-3
• 포스트, E.J., 1997 (1962) 전자기학의 공식 구조: 일반 공분산과 전자기학.도버 출판사입니다.
• 볼프강 린들러 (1991).특수상대성이론 개론 (제2판), 옥스퍼드 대학교 출판부ISBN 978-0-19-853952-0; ISBN 0-19-853952-5
• 하비 R.브라운 (2005).물리 상대성 이론 : 동적 관점의 시공간 구조, 옥스포드 대학 출판부, ISBN 0-19-927583-1; ISBN 978-0-19-927583-0
• Qadir, Asghar (1989). Relativity: An Introduction to the Special Theory. Singapore: World Scientific Publications. p. 128. Bibcode:1989rist.book.....Q. ISBN 978-9971-5-0612-4.
• French, A. P. (1968). Special Relativity (M.I.T. Introductory Physics) (1st ed.). W. W. Norton & Company. ISBN 978-0393097931.
• 실버스타인, 루드윅 (1914).상대성 이론.
• Lawrence Sklar (1977). Space, Time and Spacetime. University of California Press. ISBN 978-0-520-03174-6.
• Lawrence Sklar (1992). Philosophy of Physics. Westview Press. ISBN 978-0-8133-0625-4.^{[영구 데드링크]}
• Sergey Stepanov (2018). Relativistic World. De Gruyter. ISBN 9783110515879.
• 테일러, 에드윈, 존 아치볼드 휠러 (1992).시공간 물리학 (제2판).W.H. 프리먼사ISBN 0-7167-2327-1.
• 티플러, 폴, 르웰린, 랄프 (2002).현대 물리학 (제4회).W.H. 프리먼사ISBN 0-7167-4345-0.

저널기사

• Alvager, T.; Farley, F. J. M.; Kjellman, J.; Wallin, L.; et al. (1964). "Test of the Second Postulate of Special Relativity in the GeV region". Physics Letters. 12 (3): 260–262. Bibcode:1964PhL....12..260A. doi:10.1016/0031-9163(64)91095-9.
• Darrigol, Olivier (2004). "The Mystery of the Poincaré–Einstein Connection". Isis. 95 (4): 614–26. doi:10.1086/430652. PMID 16011297. S2CID 26997100.
• Wolf, Peter; Petit, Gerard (1997). "Satellite test of Special Relativity using the Global Positioning System". Physical Review A. 56 (6): 4405–09. Bibcode:1997PhRvA..56.4405W. doi:10.1103/PhysRevA.56.4405.
• 특수상대성이론 스콜라피디아
• Rindler, Wolfgang (2011). "Special relativity: Kinematics". Scholarpedia. 6 (2): 8520. Bibcode:2011SchpJ...6.8520R. doi:10.4249/scholarpedia.8520.

외부 링크

원작

• Zur Elektrodynamic begter Körper 아인슈타인의 독일어 원저, Annalender Physik, Bern 1905
• 운동체의 전기역학에 관하여 1923년 저서 상대성의 원리에 출판된 영문 번역.

일반 청중을 위한 특수 상대성 이론(수학적 지식 필요 없음)

• 아인슈타인 라이트 수학이 있든 없든 간에 수십 페이지의 추가 설명과 애니메이션으로 뒷받침되는 수상 경력에 빛나는 비기술적인 소개(필름 클립 및 시연).
• 아인슈타인 온라인 2010-02-01 맥스 플랑크 중력 물리학 연구소의 상대성 이론에 대한 웨이백 머신 소개에서 보관.
• 오디오: Cain/Gay (2006) – Astronomy Cast.아인슈타인의 특수상대성이론

특수 상대성 이론 설명(단순 또는 고급 수학 사용)

• Bondi K-Calculus – 특수 상대성 이론에 대한 간단한 소개.
• 그레그 이건 재단입니다
• 특수 상대성에 대한 호그 노트 미적분학을 사용하는 학부 수준의 특수 상대성에 대한 좋은 소개.
• 상대성 계산기: 특수 상대성 이론 – E = mc에 대한 대수적 및 적분적분학 유도.
• 수학 페이지 – 상대성에 대한 성찰 광범위한 참고 문헌과 함께 상대성에 대한 완전한 온라인 책.
• 특수상대성이론 학부 수준의 특수상대성이론에 대한 소개.
• 상대성 이론: 알베르트 아인슈타인의 구텐베르크 프로젝트의 특수 이론과 일반 이론
• 특수 상대성 강의 노트는 버지니아 폴리테크닉 대학교와 주립 대학교의 도면과 시공간 도표에 기초한 설명을 포함하는 특수 상대성에 대한 표준 소개입니다.
• 특수상대성이론의 이해 쉽게 이해할 수 있는 방법으로 특수상대성이론.
• 로버트 카츠(Robert Katz)의 "일반 물리학에 대한 소개와 미적분학에 대해 약간 알고 있는 학생이라면 누구나 접근할 수 있는 소개..."(130 pp; pdf 형식).
• JD크레서 물리학과 맥쿼리대학의 특수상대성이론 강의노트
• SpecialRelativity.net – 시각화와 최소한의 수학이 포함된 개요입니다.
• 상대성 이론이 4번이나?초광운동의 문제는 재미있는 방식으로 논의됩니다.

시각화

• 특수 상대성의 영향을 받아 여러 시나리오를 시각화하는 광선 추적 특수 상대성 소프트웨어.
• Real Time Relativity Archive 2013-05-08 Wayback Machine The Australian National University.대화형 프로그램을 통해 경험하는 상대론적 시각 효과.
• 시공간 여행 상대론적 운동에서 블랙홀에 이르기까지 상대론적 효과의 다양한 시각화.
• 아인슈타인의 눈을 통해 2013-05-14 호주 국립 대학교 웨이백 머신에서 보관.상대론적 시각 효과는 영화와 이미지로 설명됩니다.
• 경사 특수 상대성 시뮬레이터 빛의 속도에 가깝게 이동하는 효과를 보여주는 컴퓨터 프로그램.
• 로런츠 변환을 시각화한 유튜브 애니메이션 클립
• 존 드 필의 오리지널 인터랙티브 플래시 애니메이션은 로렌츠와 갈릴레이 프레임, 기차와 터널 역설, 쌍둥이 역설, 파동 전파, 시계 동기화 등을 보여줍니다.
• 광속 특수 상대성 이론이 움직이는 물체의 외관에 미치는 영향을 설명하기 위해 개발된 OpenGL 기반 프로그램.
• 광속으로 빠르게 가속하는 우주선에서 볼 수 있는 지구 근처의 별들을 보여주는 애니메이션.