회의 행렬

수학에서 컨퍼런스 매트릭스(C-매트릭스라고도 함)는 대각선 상에 0이 있고 대각선으로부터 +1과 -1이 떨어져 있는 정사각형 매트릭스 C로 CC는^T ID 매트릭스 I의 배수인 것이다. 따라서 행렬의 순서가 n이면 CC^T = (n-1)I이다. 일부 저자는 보다 일반적인 정의를 사용하며, 이는 각 행과 열에 0이 있어야 하지만 반드시 대각선 상에 있을 필요는 없다.^[1][2]

회의 매트릭스는 처음에 전화 통신의 문제와 관련하여 발생하였다.^[3] 그것들은 처음에 비톨드 벨레비치(Vitold Belevitch)에 의해 묘사되었는데, 그는 또한 그들에게 그들의 이름을 주었다. 벨레비치는 이상적인 변압기로부터 이상적인 전화 회의 네트워크를 구축하는 데 관심이 있었고, 그러한 네트워크가 회의 매트릭스로 대표된다는 것을 알게 되었고, 따라서 이름이 붙여졌다.^[4] 다른 애플리케이션은 통계에 있고,^[5] 다른 애플리케이션은 타원형 기하학에 있다.^[6]

n > 1의 경우, 회의 매트릭스의 두 종류가 있다. 먼저 (더 일반적인 정의를 사용할 경우) C를 정규화하여 모든 0이 대각선에 오도록 행을 재조정하고, 그 다음 첫 번째 항목이 음의 행이나 열을 부정하도록 하자. (이러한 연산은 행렬이 회의 행렬인지 여부를 변경하지 않는다.) 따라서 정규화된 회의 행렬은 첫 번째 행과 열에 모두 1이 있고 왼쪽 상단 모서리에 0이 있고 대각선에 0이 된다. C의 첫 번째 행과 열을 제거할 때 남아 있는 행렬이 S가 되도록 한다. 그러면 n은 균등하게 (4의 배수), S는 대칭성이거나(첫 번째 행이 부정된 경우 정규화된 C와 같음), 또는 n은 이상하게도 짝수(2모듈로 4에 해당), S는 대칭(정규화된 C와 같음)이다.

대칭 회의 행렬

C가 순서 n > 1의 대칭적인 회의 행렬이라면 n은 2 (모드 4)에 합치되어야 할 뿐만 아니라 n - 1도 두 제곱 정수의 합이어야 한다;^[7] 반 린트와 세이델에는 기초 행렬 이론에 의한 교묘한 증거가 있다.^[6] n - 1이 원시적인 힘이라면 n은 항상 두 제곱의 합이 될 것이다.^[8]

대칭적인 회의 행렬이 주어진 경우, 행렬 S는 그래프의 Seel 인접 행렬로 볼 수 있다. 그래프에는 S의 행과 열에 해당하는 n - 1 정점이 있으며, S의 해당 항목이 음수일 경우 두 정점이 인접해 있다. 이 그래프는 (매트릭스 뒤에) 회의 그래프라고 불리는 유형의 매우 규칙적이다.

상기 제한사항에서 허용하는 주문의 회의 행렬의 존재는 n의 일부 값에 대해서만 알려져 있다. 예를 들어, n = q + 1 여기서 q가 1(모드 4)에 해당하는 주요 전력이라면, Paley 그래프는 S를 Paley 그래프의 Seel 행렬로 취함으로써 순서 n의 대칭적인 회의 행렬의 예를 제공한다. The first few possible orders of a symmetric conference matrix are n = 2, 6, 10, 14, 18, (not 22, since 21 is not a sum of two squares), 26, 30, (not 34 since 33 is not a sum of two squares), 38, 42, 46, 50, 54, (not 58), 62 (sequence A000952 in the OEIS); for every one of these, it is known that a symmetric conference matrix of that order exists. 주문 66은 공개적인 문제인 것 같다.

예

순서 6의 본질적으로 고유한 회의 매트릭스는 다음과 같다.

(0+1+1+1+1+1+10+1− 1− 1+1+1+10+1− 1− 1+1− 1+10+1− 1+1− 1− 1+10+1+1+1− 1− 1+10){\displaystyle{\begin{pmatrix}0&, +1&, +1&, +1&, +1&, +1\\+1&, 0&, +1&, -1&, -1&, +1\\+1&, +1&, 0&a.융점, +1&, -1&, -1\\+1&, -1&, +1&, 0&, +1&, -1\\+1&, -1&, -1&, +1&, 0&,+$1\\\+1&#1&-1&#1&#1&#0\end${pmatrix

순서 6의 다른 모든 회의 행렬은 일부 행 및/또는 열의 표지를 뒤집어서(그리고 사용 중인 정의에 따라 행 및/또는 열의 순열을 취함으로써) 이 행렬에서 얻는다.

비대칭 회의 행렬

비대칭 행렬은 또한 Paley 구성에 의해 생성될 수 있다. q를 잔류물 3(모드 4)이 있는 주력이 되도록 한다. 그리고 q 순서의 Paley digraph가 있어 n = q + 1 순서의 대칭 회의 행렬로 이어진다. 행렬은 i에서 j까지 디그그래프의 호가 있을 경우 위치(i,j)에 +1과 위치(j,i)에 -1이 있는 × q 행렬을 S에 대해 취함으로써 얻는다. 그 후 C는 S에서 위와 같이 구성되었지만 첫 번째 행은 모두 음의 대칭 회의 행렬이다.

이 구조는 n 순서의 대칭적 회의 행렬이 존재하는 짝수 n을 결정하는 문제의 극히 일부만 해결한다.

일반화

때로는 순서 n의 회의 행렬이 W(n, n-1) 형식의 무게 행렬로 정의될 뿐이며, 여기서 W(n,w)는 무게 w>0이라고 하며, 크기 n의 제곱 행렬이며 W W^t = W = W를 만족하는 {-1, 0, +1}의 항목이 있으면 n을 정렬한다.^[2] 이 정의를 사용하면 제로 원소가 더 이상 대각선에 있을 필요가 없지만, 여전히 각 행과 열에 정확히 하나의 제로 원소가 있어야 한다는 것을 쉽게 알 수 있다. 예를 들어, 행렬

${\displaystyle {\pmatrix}1&0&1&1\\0&-1&-1&1\\1&1&1&1&0\end{pmatrix}}}$

이러한 완화된 정의를 만족시키겠지만, 0원소가 대각선 상에 있어야 하는 보다 엄격한 정의는 충족시키지 못한다.

회의 설계는 회의 행렬을 직사각형이 아닌 행렬로 일반화하는 것이다. 회의 설계 C는 ${\displaystyle N}$ ${\displaystyle \times }$ k ${\displaystyle N\time k}$ 행렬로$$, {-1${\displaystyle ,}$ ${\displaystyle 0}$, +1}의 항목이 $W{\displaystyle {}^{}}$ ${\displaystyle {}^{}}$ W${\displaystyle }$= (${\displaystyle }$N${\displaystyle }$- ${\displaystyle 1}$) I ${\displaystyle k_{}}$ ${\$)를 만족한다$.$$I_{k$ 여기서 I ${\displaystyle k_{}}$ ${\$은(는${\displaystyle )}$ ${\displaystyle k}$ $×$ k {\$displaystyle$k$\times$ k$}$ ID$$ 행렬이며$$, 각 행에 최대 1 0이다. 컨퍼런스 설계의 폴드오버 설계는 최종 선별 설계로 사용될 수 있다.^[9][10]

전화 회의 회로

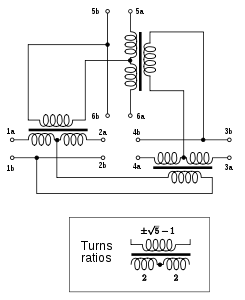
Berlevitch는 n 최대 38까지의 모든 값에 대한 회의 매트릭스에 대한 완전한 해결책을 얻었고 일부 소형 매트릭스에 회로를 제공했다. 이상적인 회의 네트워크는 신호 손실이 전적으로 여러 회의 가입자 포트 간에 신호가 분할되어 있기 때문에 발생하는 네트워크다. 즉, 네트워크 내에는 소산 손실이 없다. 네트워크는 저항 없이 이상적인 변압기만을 포함해야 한다. n-포트 이상적인 회의 네트워크는 n 순서의 회의 매트릭스가 존재하는 경우에만 존재한다. 예를 들어, 3포트 컨퍼런스 네트워크는 전화 핸드셋과 회선 리피터에서 2와이어에서 4와이어 변환에 사용되는 잘 알려진 하이브리드 변압기 회로를 사용하여 구성할 수 있다. 그러나, 순서 3 회의 매트릭스는 없으며, 이 회로는 이상적인 회의 네트워크를 생성하지 않는다. 일치를 위해 신호가 소멸되거나 불일치로 신호가 손실되는 저항이 필요하다.^[11]

위에서 언급한 바와 같이, 회의 매트릭스가 존재하기 위해 필요한 조건은 n-1이 두 제곱의 합이어야 한다는 것이다. n-1에 대해 두 칸의 가능한 합계가 두 개 이상인 경우 해당 회의 네트워크에 대해 본질적으로 서로 다른 여러 가지 해결책이 존재할 것이다. 이러한 상황은 26, 66의 n에서 발생한다. n-1이 완벽한 사각형일 때 네트워크는 특히 간단하다(n = 2, 10, 26, ...).^[12]

메모들

참조

• Belevitch V (1950). "Theory of 2n-terminal networks with applications to conference telephony". Electrical Communication. 27: 231–244.
• Goethals J.M., Seidel J.J. (1967). "Orthogonal matrices with zero diagonal". Canadian Journal of Mathematics. 19: 1001–1010. doi:10.4153/cjm-1967-091-8.
• Lili Xiao and Dennis K. J. Lin and Fengshan Bai (2012). "Constructing Definitive Screening Designs Using Conference Matrices". Journal of Quality Technology. 44 (1): 2–8. doi:10.1080/00224065.2012.11917877.
• 세이델, JJ(1991), 에드 D.G. 코네일, R. 마튼, 보스턴: 학술 출판사. 몇몇 기사들은 회의 매트릭스와 그들의 그래프와 관련이 있다.
• Colbourn, Charles J.; Dinitz, Jeffrey H. (2007) 플로리다 주 보카 라튼의 조합 설계 핸드북: 채프먼과 홀/CRC 프레스, ISBN 1-58488-506-8.
• 판 린트, 야코부스 헨드리커스; 윌슨, 리처드 마이클(2001) 캠브리지 주 콤비네이터릭스의 과정: 케임브리지 대학 출판부, ISBN 0-521-00601-5.
• Stinson, Douglas Robert (2004) 조합 설계: 시공 및 분석, 뉴욕: 스프링거, ISBN 0-387-95487-2.
• Eric D. Schoen, Pieter T. Eendebak, Peter Goos (2018). "A Classification Criterion for Definitive Screening Designs". Annals of Statistics.{{cite journal}}: CS1 maint : 복수이름 : 작성자 목록(링크)

추가 읽기

• N. A. 발로닌, 제니퍼 세베리, "A Review and New Symmetric Conference Matrice", 2014년 월롱공 대학교 리서치 온라인. 부록은 1002까지 모든 알려진 가능한 회의 매트릭스를 열거한다.