접촉공정(수학)

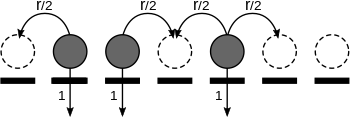
접촉 과정은 그래프의 $S$ ${\displaystyle S}$ 사이트에서 인구 증가를 일정한 비율로 모형화하는 데 사용되는 확률적 과정으로, 빈 부지는 인접한 부지의 수에 비례하는 비율로 점유된다. $따라서{\displaystyle }$, 비례$$ 상수 ${\displaystyle \lambda }$을(를) 기준으로 표시하면, 각 사이트는 기하급수적으로 분산된 매개변수 1인 임의 시간 동안 점유된 상태로 유지되며, 이 기간 동안$$ 포아송 프로세스 $매개변수{\displaystyle }$ { ${\displaystyle \lambda }$의 이벤트 시간에 모든 빈 인접 사이트에 하위 사이트를 배치한다.od. 모든 프로세스는 서로 독립적이며 무작위 기간 동안 현장이 점유된 상태로 유지된다. 접촉 과정은 입자를 $S{\displaystyle }$ ${\displaystyle S}$의 부지에 위치한 개인에 퍼지는 박테리아로 생각함으로써 감염 확산의 모델로 해석할 수 있으며$,$ 점유된 사이트는 감염된 개인에 해당하고, 빈 공간은 건강한 개인에 해당한다.

주요 관심량은 공정의 입자 수(예: N ${\displaystyle t_{}}$ ${\$로$,$ 첫 번째 해석에서는 두 번째 해석의 감염 부위 수에 해당한다. 따라서 이 과정은 입자 수가 항상 양수일 때마다 생존하는데, 이는 두 번째 입자에는 항상 감염자가 있는 경우에 해당한다. 어떤 무한한 그래프 S{S\displaystyle}동안 물과 한정된 긍정적인 임계값 λ c{\displaystyle \lambda_{c}}도록 만약λ<>만약λ>λ c{\displaystyle \lambda>\lambda_{c}}는 프로세스 입자들을 한정에서 시작해 생존 긍정적인 확률과 발생하고,;λ 존재한다. c{$\디스플레이$ 스타일 \styleda $<\lambda _{c}} 이들$의 소멸은 거의 확실하다. Note that by reductio ad absurdum and the infinite monkey theorem, survival of the process is equivalent to ${\displaystyle N_{t}\to \infty }$, as ${\displaystyle t\to \infty }$, whereas extinction is equivalent to ${\displaystyle N_{t}\to 0}$, as ${\displaystyle t\to \infty }$, and there${\displaystyle {따라서}_{}}$ 프로세스가 존속할 때 $N$ t${\displaystyle {}_{}}$→ ∞${\displaystyle N_{t}\property }$에 대한 비율을 묻는 것은 당연하다.

수학적 정의

If the state of the process at time ${\displaystyle t}$ is ${\displaystyle \xi _{t}}$, then a site ${\displaystyle x}$ in ${\displaystyle S}$ is occupied, say by a particle, if ${\displaystyle \xi _{t}(x)=1}$ and vacant if ${\displaystyle \xi _{t}(x)=0}$. The contact 공정은 상태 공간${\displaystyle }${${\displaystyle 0,}$ ${\displaystyle 1}$ ${\displaystyle {}^{}}$ ${\displaystyle S^{}}$ ${\$을(를) 가진 연속 시간 Markov 공정이며$,$ $여기$서 S ${\d}은($는) 유한하거나 카운트 가능한 그래프이며$$, $일반적$으로 Z ${\displaystyle {}^{}}${\$displaystyle \mathb{Z} ^{d$ 상호작용하는 입자 시스템의 특수한 경우. 좀 더 구체적으로, 기본 접촉 프로세스의 역학관계는 다음과 같은 전환율로 정의된다: $현장{\displaystyle }$x {\$displaystyle$ x$\},$

${\displaystyle 1\rightarrow 0\put {\text{text{time},}$

${\displaystyle 0\rightarrow 1\cHB {\text{at rate}\\cHBDA \sum _{y\\,y\\\\\sim \,x}\xi _{t}(y),}$

여기서 합계는 $S{\displaystyle }$ ${\displaystyle S}$에 $있는{\displaystyle }$ x$${\$displaystyle$x}의$$ 모든 $인접{\displaystyle }$ y$${\$displaystyle y}$에 걸쳐 있다$.$ 이는 각 사이트가 해당 속도로 지수 시간을 기다린 다음 flip(그러므로 0은 1이 되고 그 반대는 1이 됨)을 의미한다.

퍼콜레이션 연결

접촉 과정은 과대포장 이론과 밀접하게 연결된 확률적인 과정이다. Ted Harris(1974)는 감염과 회복이 이산 시간$\{{\displaystyle 1,}$ ${\displaystyle 2}$,${\displaystyle }$…,${\displaystyle \}}$ ${\displaystyle \{1,2,\ldots ,\}$에서만 발생할 수 있는 Ⅱ의^d 접촉 프로세스는 Ⅱ의 각^{d + 1} 가장자리를 좌표-값 상승 방향으로 방향을 설정하여 얻은 그래프에서 한 번에 한 단계씩의 결합 과시에 해당한다는$$ 점에 주목했다.

정수의 법칙

정수에 대한 공정의 입자 수에 대한 많은 수의 법칙은 모든 큰 $t{\displaystyle }$ ${\displaystyle t}$에 대해$$$N{\displaystyle {}_{}}$ t ${\$이 일부 양의 상수 $c{\displaystyle }$= ${\displaystyle c(}$ ${\displaystyle \lambda }$ )${\displaysty c=c(\lambda )}$에 대해 $c{\displaystyle }$ ${\$ {\displaysty$}$과 거의 같다는 것을 의미한다$.$t, 공정이 존속할 $경우{\displaystyle {}_{}}$ N ${\displaystyle t_{}}$ ${\$의 성장률은 기껏해야 선형이며$$, 적어도 시간적으로는 선형이다. (공정이 확률로 수렴된다는) 대수의 약한 법칙은 듀렛(1980)에 의해 나타났다. 몇 년 후, 더렛과 그리페스(1983)는 이것을 대수의 강력한 법칙으로 개선하여, 그 과정의 거의 확실한 정합성을 부여했다.

위독하게 죽다.

모든 정수 격자에서의 접촉 과정의 경우, 1990년 베즈덴하우트와 그림메트가 접촉 과정 또한 거의 확실히 임계치에서 소멸한다는 것을 보여주었을 때 주요한 돌파구가^{[citation needed]} 왔다.^{[citation needed]}

더렛의 추측과 중심 한계 정리

더렛은 해리스의 접촉 과정인 viz에 대한 중앙 한계 정리(central limit organization)에 대해 80년대와 90년대 초의 조사 논문과 강의 노트에서 그 과정이 살아남으면 모든 큰 $t{\displaystyle }$ ${\displaystyle t$ $N{\displaystyle {}_{}}$ ${\displaystyle t_{}}$ ${\$은 $c{\displaystyle }$ ${\$ t$}$이고 오차는 $\sigma {\displaystyle }$ ${\displaystyle t\sqrt{}}$ {\$displayt$${\displaystyle \}}$과 동일하다고 추측했다.$\displaystyle \sigma {\sqrt{t}}$에 표준 가우스 분포에 따라 분포된 (랜덤) 오차를 곱한 값.^[1][2][3]

듀렛의 추측은 2018년에 증명된 바와 같이$$ ${\displaystyle \sigma}$의 다른 값에 대한 것으로 밝혀졌다.^[4]

참조

• C. Bezuidenhout과 G. R. Grimett, 중요한 접촉 과정이 사라진다, 앤. 프로밥. 18 (1990), 1462–1482.
• Durrett, Richard (1980). "On the Growth of One Dimensional Contact Processes". The Annals of Probability. 8 (5): 890–907. doi:10.1214/aop/1176994619.
• 더렛, 리처드(1988) Wadsworth의 "입자 시스템과 퍼콜레이션에 대한 선택 노트".
• 더렛, 리처드(1991) "접촉 과정, 1974–1989." 코넬 대학, 수리 과학 연구소.
• Durrett, Richard (1984). "Oriented Percolation in Two Dimensions Number". The Annals of Probability. 12 (4): 999–1040. doi:10.1214/aop/1176993140.

• Durrett, Richard; David Griffeath (1983). "Supercritical Contact Processes on Z". The Annals of Probability. 11 (1): 1–15. doi:10.1214/aop/1176993655.
• Grimmett, Geoffrey (1999), Percolation, Springer

• Liggett, Thomas M. (1985). Interacting Particle Systems. New York: Springer Verlag. ISBN 978-0-387-96069-2.
• 토마스 M. 리겟 "스토크스틱 인터랙티브 시스템: 접촉, 유권자 및 배제 프로세스", Springer-Verlag, 1999.