콕스-잉거솔-로스 모형

수학 금융에서 콕스-잉거솔-로스(CIR) 모델은 이자율의 진화를 설명합니다. 금리 움직임을 시장 위험의 단 하나의 원천에 의해 움직이는 것으로 설명하기 때문에 "원 팩터 모델"(단기 금리 모델)의 한 유형입니다. 이 모델은 이자율 파생상품의 평가에 사용될 수 있습니다. 1985년 [1] 존 C에 의해 소개되었습니다. 콕스, 조나단 E. 잉거솔과 스티븐 A. 로스는 바시섹 모델의 연장선상에 있습니다.

모델이

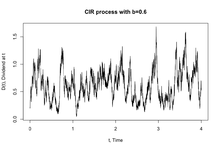
CIR 모델은 확률적 미분 방정식인 Feller 제곱근 프로세스를 $r_{t}$ 사용하여 순간 이자율 $r_{t}$ ${\$ 를 설명합니다.

dr_{t}=a(b-r_{t})\,dt+\sigma {\sqrt {r_{t}}}\,dW_{t},

여기서 $W_{t}$ $W_{t}$ 는 Wiener 프로세스(랜덤 시장 위험 요소 모델링)이며 ${\displaystyle$ a $a$ b ${\displaystyle$ b $}$ 및 $\sigma \,$ σ ${\displaystyle$ \sigma \,}가 매개 변수입니다. 매개 $a$ a{\ $displaystyle$ a}는 $b$ b{\ $displaystyle$ b $}$ 에 대한 조정 속도에 해당하고 $\sigma \,$ σ {\displaystyle $\sigma \,$ \sigma \,}는 변동성에 해당합니다. 드리프트 인자 $a(b-r_{t})$ - r $a(b-r_{t})$ ) ${\displaystyle$ a $(b$ - r_ ${t$ 는 Vasicek 모형에서와 정확히 같습니다. 조정 속도는 엄격하게 양의 파라미터 $a$ ${\displaystyle$ a $}$ 에 의해 제어되며 $b$ 장기 값 $b$ ${\displaystyle$ b $}$ 를 향한 이자율의 평균 복귀를 보장합니다 $a$

표준 편차 $\sigma {\sqrt {r_{t}}}$ 인 $\sigma {\sqrt {r_{t}}}$ σrt ${\displaystyle \sigma {\sqrt {$ r_ $\sigma {\sqrt {r_{t}}}$ t}}}은(는 $)$ {\ $b$ a $}$ 및b ${\$ displaystyle b $b$ 의 모든 양의값에 대해 마이너스 금리가 발생할 가능성을 방지합니다. 또한 조건이 발생하면 0의 금리도 배제됩니다.

2ab\geq \ sigma ^{2}\,

충족됩니다. 보다 일반적으로 속도( $r_{t}$ ${\displaystyle r_{t$ 가 0에 가까우면 $\sigma {\sqrt {r_{t}}}$ 편차 $($ σrt ${\displaystyle \sigma {\sqrt$ {r_ $\sigma {\sqrt {r_{t}}}$ t}}})도 매우 작아져서 속도에 대한 무작위 충격의 영향이 줄어듭니다. 결과적으로 속도가 0에 가까워지면 속도를 (평형을 향해) 위로 밀어 올리는 드리프트 팩터에 의해 진화가 지배됩니다.

케이스 $2ab=\sigma ^{2}\,$ $2ab=\sigma ^{2}\,$ b = $2ab=\sigma ^{2}\,$ σ 2 {\displaystyle 2ab=\ sigma ^{2}\,}의 경우, 펠러 제곱근 과정은 오른슈타인의 제곱으로부터 구할 수 있습니다.울렌벡 과정. 에르고딕이며 고정 분포를 가지고 있습니다. Heston 모형에서 확률적 변동성을 모형화하는 데 사용됩니다.

분배

미래분포

CIR 프로세스의 미래 값 분포는 폐쇄형으로 계산할 수 있습니다.

r_{t+T}={\frac {Y}{2c}}

where

c={\frac {2a}{(1-e^{-aT})\sigma ^{2}}}

, and Y is a non-central chi-squared distribution with

{\frac {4ab}{\sigma ^{2}}}

degrees of freedom and non-centrality parameter

2cr_{t}e^{-aT}

. 공식적으로 확률 밀도 함수는 다음과 같습니다.

f(r_{t+T};r_{t},a,b,\sigma )=c\,e^{-u-v}\left({\frac {v}{u}}\right)^{q/2}I_{q}(2{\sqrt {uv}}),

여기서

q={\frac {2ab}{\sigma ^{2}}}-1

=

q={\frac {2ab}{\sigma ^{2}}}-1

a

b

u=cr_{t}e^{-aT}

σ 2 - 1 {\displaystyle q =

{\

frac {2ab}{\sigma ^{2}}-1}, u = cr - a T {\display u = cr_{t}e^{-aT}}, v = cr + T {\displaystyle v = cr_{t+

T

I_{q}(2{\sqrt {uv}})

I_{q}(2{\sqrt {uv}})

(

I_{q}(2{\sqrt {uv}})

{\displaystyle I_{q}(2{\sqrt {uv}})

는

I_{q}(2{\sqrt {uv}})

첫 번째 종류의

q

q

의 수정된 베셀 함수입니다

q

점근분포

r_{\infty }

반전으로 인해 시간이 길어질수록 r

r_{\infty }

∞ {\displaystyle

r_{\

infty}} 분포는 다음과 같은 확률 밀도를 갖는 감마 분포에 접근합니다.

f(r_{\infty};a,b,\sigma)={\frac {\beta ^{\alpha}}{\Gamma(\alpha )}}{\infty}}r_{\alpha -1}e^{-\beta r_{\infty}}

여기서

\beta =2a/\sigma ^{2}

= 2

\beta =2a/\sigma ^{2}

\alpha =2ab/\sigma ^{2}

/

\alpha =2ab/\sigma ^{2}

σ 2 {\displaystyle \beta = 2a/\sigma ^{2}} 및 α = 2 a / σ 2 {\displaystyle \alpha = 2ab/\sigma ^{2}}입니다.

점근분포의 유도

CIR 모델에 대한 점근 분포 $p$ ∞ {\displaystyle $p_{\$ infty }}를 도출하려면 Fokker-Planck 방정식을 사용해야 합니다.

{\partial p \over {\partial t}}+{\partial \over {\partial r}}[a(b-r)p]={1 \over {2}}\sigma ^{2}{\partial ^{2} \over {\partial r^{2}}(rp)

$\partial _{t}p\rightarrow 0$ 의 $\partial _{t}p\rightarrow 0$ 은 ∂ t p $\partial _{t}p\rightarrow 0$ → $\partial _{t}p\rightarrow 0$ 0 {\ $displaystyle$ \partial _{ $t$ p\rightarrow 0}일 때 단순화된 방정식으로 이어지는 특별한 경우에 있습니다.

a(b-r)p_{\infty}={1 \over {2}}\sigma ^{2}\left(p_{\infty}+r{dp_{\infty} \over {dr}}\right)

$\alpha =2ab/\sigma ^{2}$ = $\alpha =2ab/\sigma ^{2}$ / $\beta =2a/\sigma ^{2}$ σ 2 ${\$ displaystyle \ $alpha$ = 2ab/\sigma ^{2}} 및 β = 2 a / σ 2 {\displaystyle \beta = 2a/\sigma ^{2}를 정의하고 항을 재정렬하면 다음과 같은 방정식이 나타납니다.

{\alpha -1 \over {r}}-\beta ={d \over {dr}}\log p_{\infty}

통합하면 다음과 같은 이점을 얻을 수 있습니다.

p_{\infty}\proptor^{\alpha-1}e^{-\beta r}

$p_{\infty }\in (0,\infty ]$ p ∞ ∈ $0$ , ∞) ${\displaystyle p_{\infty$ }\in $p_{\infty }\in (0,\infty ]$ 0,\infty]}에서 이 밀도는 감마 분포를 설명합니다. 따라서 CIR 모형의 점근 분포는 감마 분포입니다.

특성.

평균 복귀,
수준에 따른 변동성 $($ σ rt ${\displaystyle \sigma {\sqrt {$ r_{t}}}),
주어진 $r_{0}$ 의 $r_{0}$ 0 $r_{0}$ {\ $displaystyle r_{0}$ 에 대해 2 $2ab\geq \sigma ^{2}$ ≥ σ 2 {\displaystyle 2ab\geq \sigma ^{2}}인 경우 프로세스는 영점에 닿지 않습니다. 그렇지 않으면 영점에 가끔 닿을 수 있습니다.
$\operatorname {E} [r_{t}\mid r_{0}]=r_{0}e^{-at}+b(1-e^{-at})$ $\operatorname {E} [r_{t}\mid r_{0}]=r_{0}e^{-at}+b(1-e^{-at})$ [ $\operatorname {E} [r_{t}\mid r_{0}]=r_{0}e^{-at}+b(1-e^{-at})$ t ∣ r $\operatorname {E} [r_{t}\mid r_{0}]=r_{0}e^{-at}+b(1-e^{-at})$ ] $\operatorname {E} [r_{t}\mid r_{0}]=r_{0}e^{-at}+b(1-e^{-at})$ r $\operatorname {E} [r_{t}\mid r_{0}]=r_{0}e^{-at}+b(1-e^{-at})$ e - $at$ + b (1 - e - at ) {\displaystyle \operatorname {E} [r_{t}\mid r_{ $\operatorname {E} [r_{t}\mid r_{0}]=r_{0}e^{-at}+b(1-e^{-at})$ }] = r_{0}e^{-at} + b(1-e^{-at})}이므로 장기 평균은 b {\displaystyle b},
$\operatorname {Var} [r_{t}\mid r_{0}]=r_{0}{\frac {\sigma ^{2}}{a}}(e^{-at}-e^{-2at})+{\frac {b\sigma ^{2}}{2a}}(1-e^{-at})^{2}.$

눈금 매기기

보통최소제곱

연속 SDE는 다음과 같이 이산화할 수 있습니다.

r_{t+\Delta t}-r_{t}=a(b-r_{t})\,\Delta t+\sigma \,{\sqrt {r_{t}\Delta t}}\varepsilon _{t},

에 해당하는 것.

{\frac {r_{t+\Delta t}-r_{t}}{{\sqrt {r}}_{t}}}={\frac {ab\Delta t}{{\sqrt {r}}_{t}}}-a{\sqrt {r}}_{t}\Delta t+\sigma \,{\sqrt {\Delta t}}\varepsilon _{t},

제공되는

\varepsilon _{t}

ε t

{\displaystyle

\

varepsilon

_{t}}는 n.i.i.d. (0,1)입니다. 이 식은 선형 회귀 분석에 사용할 수 있습니다.

마팅게일추정
최대우도

시뮬레이션

CIR 프로세스의 확률적 시뮬레이션은 다음 두 가지 변형을 사용하여 달성할 수 있습니다.

이산화
정확한

채권가격결정

무차익 거래 가정 하에서 채권은 이 이자율 프로세스를 사용하여 가격이 책정될 수 있습니다. 채권 가격은 이자율의 지수적 아핀입니다.

P(t,T)=A(t,T)e^{-B(t,T)r_{t}}\!

어디에

A(t,T)=\left({\frac {2he^{(a+h)(T-t)/2}}{2h+(a+h)(e^{h(T-t)}-1)}}\right)^{2ab/\sigma ^{2}}

B(t,T)={\frac {2(e^{h(T-t)}-1)}{2h+(a+h)(e^{h(T-t)}-1)}}

h={\sqrt {a^{2}+2\sigma ^{2}}}

확장

CIR 모델은 기본 아핀 점프 확산의 특수한 경우를 사용하며, 이는 여전히 채권 가격에 대한 폐쇄형 표현을 허용합니다. 계수를 대체하는 시간 가변 함수를 모형에 도입하여 미리 할당된 이자율 및 변동성 기간 구조와 일치시킬 수 있습니다. 가장 일반적인 접근법은 Maghsoodi(1996)입니다.^[2] 더 다루기 쉬운 접근법은 Brigo and Mercurio(2001b)^[3]에서 요금의 입력 기간 구조와의 일관성을 위해 외부 시간 의존적 이동이 모델에 추가되는 것입니다.

CIR 모델을 확률적 평균과 확률적 변동성의 경우로 크게 확장한 것이 Lin Chen(1996)에 의해 주어졌으며 Chen 모델로 알려져 있습니다. 클러스터 변동성, 마이너스 금리 및 다양한 분포를 처리하기 위한 보다 최근의 확장은 올란도, 미니 및 부팔로(2018,^[4] 2019,^[5]^[6] 2020,^[7] 2021,^[8] 2023^[9])의 소위 "CIR #"이며, 마이너스 금리에 초점을 맞춘 보다 간단한 확장은 Di Francesco 및 Kamm(2021,^[10] 2022^[11])에 의해 제안되었습니다. CIR- 및 CIR- 모델이라고 합니다.

참고 항목

참고문헌

^ "A Theory of the Term Structure of Interest Rates - The Econometric Society". www.econometricsociety.org. Retrieved 2023-10-14.
^ Maghsoodi, Yoosef (January 1996). "SOLUTION OF THE EXTENDED CIR TERM STRUCTURE AND BOND OPTION VALUATION". Mathematical Finance. 6 (1): 89–109. doi:10.1111/j.1467-9965.1996.tb00113.x. ISSN 0960-1627.
^ Brigo, Damiano; Mercurio, Fabio (2001-07-01). "A deterministic–shift extension of analytically–tractable and time–homogeneous short–rate models". Finance and Stochastics. 5 (3): 369–387. doi:10.1007/PL00013541. ISSN 0949-2984.
^ Orlando, Giuseppe; Mininni, Rosa Maria; Bufalo, Michele (2018). "A New Approach to CIR Short-Term Rates Modelling". New Methods in Fixed Income Modeling. Contributions to Management Science. Springer International Publishing: 35–43. doi:10.1007/978-3-319-95285-7_2. ISBN 978-3-319-95284-0.
^ Orlando, Giuseppe; Mininni, Rosa Maria; Bufalo, Michele (1 January 2019). "A new approach to forecast market interest rates through the CIR model". Studies in Economics and Finance. 37 (2): 267–292. doi:10.1108/SEF-03-2019-0116. ISSN 1086-7376. S2CID 204424299.
^ Orlando, Giuseppe; Mininni, Rosa Maria; Bufalo, Michele (19 August 2019). "Interest rates calibration with a CIR model". The Journal of Risk Finance. 20 (4): 370–387. doi:10.1108/JRF-05-2019-0080. ISSN 1526-5943. S2CID 204435499.
^ Orlando, Giuseppe; Mininni, Rosa Maria; Bufalo, Michele (July 2020). "Forecasting interest rates through Vasicek and CIR models: A partitioning approach". Journal of Forecasting. 39 (4): 569–579. arXiv:1901.02246. doi:10.1002/for.2642. ISSN 0277-6693. S2CID 126507446.
^ Orlando, Giuseppe; Bufalo, Michele (2021-05-26). "Interest rates forecasting: Between Hull and White and the CIR#—How to make a single‐factor model work". Journal of Forecasting. 40 (8): 1566–1580. doi:10.1002/for.2783. ISSN 0277-6693.
^ Orlando, Giuseppe; Bufalo, Michele (2023-07-14). "Time series forecasting with the CIR# model: from hectic markets sentiments to regular seasonal tourism". Technological and Economic Development of Economy. 29 (4): 1216–1238. doi:10.3846/tede.2023.19294. ISSN 2029-4921.
^ Di Francesco, Marco; Kamm, Kevin (4 October 2021). "How to handle negative interest rates in a CIR framework". SeMa Journal. 79 (4): 593–618. arXiv:2106.03716. doi:10.1007/s40324-021-00267-w. S2CID 235358123.
^ Di Francesco, Marco; Kamm, Kevin (2022). "On the Deterministic-Shift Extended CIR Model in a Negative Interest Rate Framework". International Journal of Financial Studies. 10 (2): 38. doi:10.3390/ijfs10020038. hdl:11585/916048.

추가 참조

Hull, John C. (2003). Options, Futures and Other Derivatives. Upper Saddle River, NJ: Prentice Hall. ISBN 0-13-009056-5.
Cox, J.C., J.E. Ingersoll and S.A. Ross (1985). "A Theory of the Term Structure of Interest Rates". Econometrica. 53 (2): 385–407. doi:10.2307/1911242. JSTOR 1911242.{{cite journal}}: CS1 maint: 다중 이름: 저자 목록 (링크)
Maghsoodi, Y. (1996). "Solution of the extended CIR Term Structure and Bond Option Valuation". Mathematical Finance. 6 (6): 89–109. doi:10.1111/j.1467-9965.1996.tb00113.x.
Damiano Brigo; Fabio Mercurio (2001). Interest Rate Models — Theory and Practice with Smile, Inflation and Credit (2nd ed. 2006 ed.). Springer Verlag. ISBN 978-3-540-22149-4.
Brigo, Damiano; Fabio Mercurio (2001b). "A deterministic-shift extension of analytically tractable and time-homogeneous short rate models". Finance & Stochastics. 5 (3): 369–388. doi:10.1007/PL00013541. S2CID 35316609.
파이썬에서 CIR 프로세스를 구현하는 오픈 소스 라이브러리
Orlando, Giuseppe; Mininni, Rosa Maria; Bufalo, Michele (2020). "Forecasting interest rates through Vasicek and CIR models: A partitioning approach". Journal of Forecasting. 39 (4): 569–579. arXiv:1901.02246. doi:10.1002/for.2642. ISSN 1099-131X. S2CID 126507446.

[1] "A Theory of the Term Structure of Interest Rates - The Econometric Society". www.econometricsociety.org. Retrieved 2023-10-14.

[2] Maghsoodi, Yoosef (January 1996). "SOLUTION OF THE EXTENDED CIR TERM STRUCTURE AND BOND OPTION VALUATION". Mathematical Finance. 6 (1): 89–109. doi:10.1111/j.1467-9965.1996.tb00113.x. ISSN 0960-1627.

[3] Brigo, Damiano; Mercurio, Fabio (2001-07-01). "A deterministic–shift extension of analytically–tractable and time–homogeneous short–rate models". Finance and Stochastics. 5 (3): 369–387. doi:10.1007/PL00013541. ISSN 0949-2984.

[4] Orlando, Giuseppe; Mininni, Rosa Maria; Bufalo, Michele (2018). "A New Approach to CIR Short-Term Rates Modelling". New Methods in Fixed Income Modeling. Contributions to Management Science. Springer International Publishing: 35–43. doi:10.1007/978-3-319-95285-7_2. ISBN 978-3-319-95284-0.

[5] Orlando, Giuseppe; Mininni, Rosa Maria; Bufalo, Michele (1 January 2019). "A new approach to forecast market interest rates through the CIR model". Studies in Economics and Finance. 37 (2): 267–292. doi:10.1108/SEF-03-2019-0116. ISSN 1086-7376. S2CID 204424299.

[6] Orlando, Giuseppe; Mininni, Rosa Maria; Bufalo, Michele (19 August 2019). "Interest rates calibration with a CIR model". The Journal of Risk Finance. 20 (4): 370–387. doi:10.1108/JRF-05-2019-0080. ISSN 1526-5943. S2CID 204435499.

[7] Orlando, Giuseppe; Mininni, Rosa Maria; Bufalo, Michele (July 2020). "Forecasting interest rates through Vasicek and CIR models: A partitioning approach". Journal of Forecasting. 39 (4): 569–579. arXiv:1901.02246. doi:10.1002/for.2642. ISSN 0277-6693. S2CID 126507446.

[8] Orlando, Giuseppe; Bufalo, Michele (2021-05-26). "Interest rates forecasting: Between Hull and White and the CIR#—How to make a single‐factor model work". Journal of Forecasting. 40 (8): 1566–1580. doi:10.1002/for.2783. ISSN 0277-6693.

[9] Orlando, Giuseppe; Bufalo, Michele (2023-07-14). "Time series forecasting with the CIR# model: from hectic markets sentiments to regular seasonal tourism". Technological and Economic Development of Economy. 29 (4): 1216–1238. doi:10.3846/tede.2023.19294. ISSN 2029-4921.

[10] Di Francesco, Marco; Kamm, Kevin (4 October 2021). "How to handle negative interest rates in a CIR framework". SeMa Journal. 79 (4): 593–618. arXiv:2106.03716. doi:10.1007/s40324-021-00267-w. S2CID 235358123.

[11] Di Francesco, Marco; Kamm, Kevin (2022). "On the Deterministic-Shift Extended CIR Model in a Negative Interest Rate Framework". International Journal of Financial Studies. 10 (2): 38. doi:10.3390/ijfs10020038. hdl:11585/916048.

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

v t 채권시장
유대 사채 고정수입
발행자별채권종류	대리채권 회사채 선순위채무 후순위채무 부실채권 국채 인프라채권 지방채 글로벌본드
지급채권의 종류	발생채권 경매요율담보 콜가능채권 상업용지 콘솔 조건부전환사채 전환사채 교환사채 신축채권 고정금리채권 변동금리어음 고수익채무 인플레이션지수채권 역변동금리주 복권채권 영구채 풋가능채권 역전환증권 제로쿠폰본드
채권평가	청정가격 볼록성 쿠폰 신용 스프레드 현재수익률 더티프라이스 지속 아이 스프레드 주택담보대출수익률 명목수익률 옵션조정스프레드 무위험채권 가중평균수명 수익률곡선 수익률스프레드 만기수익률 Z스프레드
증권화상품	자산담보부증권 담보부채무 담보부저당채무 상업용 근저당증권 저당담보부증권
채권옵션	콜가능채권 전환사채 내장옵션 교환사채 신축채권 풋가능채권
기관	상업용 모기지 증권 협회 국제자본시장협회 증권산업금융시장협회

v t 확률적 과정
이산시간	베르누이 과정 분기공정 중식당과정 갈턴-왓슨 과정 독립적이고 동일한 분산 랜덤 변수 마르코프 체인 모란과정 임의 보행 루프가 지워진 자기기피 편향된 최대 엔트로피
연속시간	덧셈공정 베셀과정 출생-사망과정 순산 브라운 운동 다리 익스포크 분수 기하학적 미앤더 코시공정 연락과정 연속 시간 랜덤 워크 콕스 과정 확산과정 다이슨 브라운 운동 경험적 과정 펠러공정 플레밍-비오트 과정 감마 과정 기하학적 과정 호크 공정 헌트과정 상호작용하는 입자계 Itô 확산 Itô process 점프 확산 점프 과정 레비 과정 현지시간 마르코프 덧셈 과정 맥킨-블라소프 과정 오른슈타인-울렌벡 과정 포아송 과정 컴파운드 비균질적 슈람-로너 진화 세미마팅게일 시그마마팅게일 안정공정 수퍼프로세스 전신과정 분산 감마 과정 위너공정 위너 소시지
둘다요.	분기공정 갤브스–뢰처바흐 모형 가우스 과정 은닉 마르코프 모형(HMM) 마르코프 과정 마르팅게일 차이점. 현지의 서브- 슈퍼- 임의동역학계 재생과정 갱신과정 가변 길이의 메모리를 갖는 확률적 사슬 백색소음
필드 및 기타	디리클레 과정 가우스 랜덤 필드 깁스 측도 홉필드 모형 아이싱모델 포츠 모형 부울 네트워크 마르코프 랜덤 필드 퍼콜레이션 피트먼-요르프로세스 점공정 콕스 포아송 랜덤 필드 랜덤그래프
시계열 모형	자기회귀 조건부 이분산성(ARCH) 모형 자기회귀식 통합이동평균(ARIMA) 모형 자기회귀모형 자기회귀-이동평균(ARMA) 모형 일반화 자기회귀 조건부 이분산성(GARCH) 모형 이동평균(MA)모델
재무모형	이항옵션가격결정모형 블랙-더만–토이 블랙-카라신스키 블랙-스쿨즈 찬-카롤리-롱스태프-샌더스(CKLS) 첸 등분산탄력성(CEV) 콕스-잉거솔-로스(CIR) Garman–Kohlhagen 히스-재로우-모턴(HJM) 헤스턴 호이-리 헐-화이트 리보 시장 렌들맨 – 바터 SABR 변동성 바시체크 윌키
보험수리모형	ü만 크라머-룬드베르크 리스크프로세스 스페어-앤더슨
대기열 모델	벌크 유동적 일반화 대기열망 M/G/1 M/M/1 M/M/c
특성.	까들랑길 계속되는 연속경로 에르고딕 교환가능 펠러 연속 가우스마르코프 마르코프 믹싱 조각적 결정론적 예측가능 점진적으로 측정 가능 셀프시밀러 정지된 시간 가역
리미트 정리	중심 극한 정리 돈스커 정리 두브의 마팅게일 수렴 정리 에르고딕 정리 피셔-티펫-그네덴코 정리 대편차원리 대수의 법칙(약함/강함) 반복 로그의 법칙 최대 에르고딕 정리 사노프 정리 0-1 법칙 (블루멘탈 , 보렐-칸텔리, 엥겔베르트-슈미트, 휴이트-새비지, 콜모고로프, 레비)
부등식	부르크홀더-다비스-건디 두브마팅게일 두브 업크로스 구니타와타나베 마르킨키에비치-지그문트
도구들	캐머런-마틴 공식 랜덤 변수의 수렴 돌레앙-데이드 지수 두브분해정리 두브마이어 분해 정리 두브의 선택적 정지 정리 딘킨 공식 파인만-카크 공식 여과 기르사노프 정리 무한소 생성기 Itô 적분 Itmma's 보조개 카르후넨-뢰브 정리 콜모고로프 연속성 정리 콜모고로프 확장 정리 레비-프로코로프 계량 맬리아빈 미적분학 마르팅게일 표현정리 선택적 정지 정리 프로호로프 정리 이차 변동 반사원리 스코로호드 적분 스코로호드의 표현 정리 스코로호드 공간 스넬 봉투 확률미분방정식 다나카 정지시간 스트라토노비치 적분 균일한 통합성 일반적인 가설 위너 공간 고전적인 추상적인
규율	보험수리수학 제어이론 계량경제학 에르고딕 이론 극값 이론(EVT) 대이동설 수리금융 수학통계학 확률론 대기열 이론 갱신설 파멸론 신호처리 통계학 확률적 분석 시계열 분석 기계학습
토픽 목록 카테고리

Search