홉필드 네트워크

홉필드 네트워크(혹은 신경망의 이싱 모델 또는 이싱-렌츠-리틀 모델)는 존 홉필드가 이싱 모델에서 에른스트 이싱이 빌헬름 렌츠와 함께 한 작업을 바탕으로^[2] 1974년 리틀이 앞서 설명한 대로 1982년에^[1] 대중화한 인공 신경망의 일종이자 스핀 글라스 시스템의 일종이다.^[3] 홉필드 네트워크는 이진 임계값 노드가 있거나 연속 변수가 있는 컨텐츠 주소 지정("관련") 메모리 시스템 역할을 한다.^[4] 홉필드 네트워크는 인간의 기억을 이해하는 모델도 제공한다.^[5][6]

오리진스

신경망의 이싱 모델을 메모리 모델로 하는 것은 윌리엄 A에 의해 처음 제안되었다. 홉필드가 1982년 논문에서 인정한 1974년의 일은 거의 없다.^[2][1] 지속적인 역학을 가진 네트워크들은 홉필드가 1984년 논문에서 개발했다.^[4] 메모리 저장 용량의 주요 진보는 2016년^[7] 네트워크 역학 및 에너지 기능의 변화를 통해 Krotov와 Hopfield에 의해 개발되었다. 이 아이디어는 2017년 데미킬과 협력자들에 의해 더욱 확장되었다.^[8] 대용량 메모리 용량 모델의 지속적인 역학 관계는 2016년부터 2020년까지 일련의 논문에서 개발되었다.^[7][9][10] 대용량 메모리 스토리지 용량인 Hopfield Networks는 현재 조밀 연상 메모리 또는 현대적인 Hopfield 네트워크라고 불린다.

구조

Hopfield nets의 단위는 2진수 임계값 단위로서, 즉, 단위는 2개의 서로 다른 값만을 자신의 상태에 대해 취하며, 단위의 입력이 임계 ${\$를 초과하는지 여부에 따라 값이 결정된다$.$ 이산 Hopfield nets는 2진수(발화 또는 불발화되지 않는) 뉴런 $1{\displaystyle \mathrm{}}$,${\displaystyle \mathrm{2개}}$ 사이의 관계를 기술한다${\displaystyle .}$${\displaystyle \dots ,}$ ${\displaystyle i,}$ ${\displaystyle j,}$…${\displaystyle N}$ ${\displaystyle$1$,2,\ldots, i,j,\ldots,N$^[1] 특정 시간에 신경망의 상태는 벡터 $V{\displaystyle }$ ${\\displaystyle V}$에 의해 설명되는데$,$ 이 벡터 V {\displaystytle V}에 의해 어떤 뉴런이 N비트의 이진어로 발사되고 있는지를 기록한다.

뉴런들 간의$$ $상호작용{\displaystyle {}_{}}$ ${\displaystyle {wi}_{}}$ ${\displaystyle j_{}}$ ${\$는 보통 1 또는 -1의 값을 갖는 단위를 가지며, 이 관행이 이 글 전반에 걸쳐 사용될 것이다. 그러나 다른 문헌은 0과 1의 값을 갖는 단위를 사용할 수 있다. 이러한 상호작용은 특정 상태 V {\$displaystyle V^{s}$에 대해 Hebb의 연관 법칙을 통해 "학습"된다.

${\displaystyle w_{ij}=V_{i}^{s}V_{j}^{s}}}}}}$

그러나 $w{\displaystyle {}_{}}$ ${\displaystyle i_{}}$= ${\displaystyle 0}$ ${\displaystyle w_{i}=0$

(Hebbian 학습 규칙은 단위들이 {0, 1의 값을 가정할 때$$ $w{\displaystyle {}_{}}$ ${\displaystyle i_{}}$ ${\displaystyle j_{}}$=${\displaystyle }$( 2 ${\displaystyle {}_{}^{}}$ ${\displaystyle i_{}^{}}$ ${\displaystyle {}_{}^{}}$- ${\displaystyle 1}$)${\displaystyle }$(${\displaystyle {}_{}^{}}$ V ${\displaystyle {}_{}^{}}$- ${\displaystyle 1}$) ${\displaystyle w_{i}=(2V_{i}^{s}-1)$ $(2V_{j}^{s}-1$)의 형식을 취한다는 점에 유의한다.)

일단 네트워크 훈련을 받는다, 나는{\displaystyle w_{ij}}더 이상 진화하 j w. 만약 뉴런 V는 새로운 열심인({\displaystyle V^{s'}}은 신경 네트워크에, 신경 세포에 최종적인 행위는 다음과 같게 된다.

• ${\displaystyle V_{i}^{s'}\rightarrow 1}$ if ${\displaystyle \sum _{j}w_{ij}V_{j}^{s'}>$U_{나는}}
• V나는′→ − 1{\displaystyle V_{나는}^{s'}\rightarrow-1}만약∑ jwij Vj신규′<>열심인, U나는{\displaystyle \sum_{j}w_{ij}V_{j}^{s'}&lt을 말한다.U_{나는}}

그i'th 뉴런(종종 0을 찍)어디 U나는}{\displaystyle U_{나는}은 임계값이.[11] 그러나 만약 새로운 상태 Vs({\displaystyle V^{s'}}의 상호 작용 매트릭스에 노출될 때까지 원상 Vs{\displaystyle V^{s}}(아래의 업데이트 섹션을 참조하십시오)과 일치하기 때문에, 각각의 뉴런을 바꿀 것 이러한 방법으로 Hopfield 네트워크 능력은 주들이 상호 작용. 기질에 저장되"기억하"야 한다.

Hopfield net의 연결에는 일반적으로 다음과 같은 제한이 있다.

• ${\displaystyle w_{}}$ ${\displaystyle i_{}}$= ${\displaystyle 0,}$ ${\displaystyle \mathrm{\forall }}$ ${\displaystyle i}$ ${\displaystyle w_{i}=0,\all i}($단위가 자체와 연결되지 않음)
• ${\displaystyle w_{}}$ ${\displaystyle i_{}}$ ${\displaystyle j_{}}$= ${\displaystyle {}_{}}$ j ${\displaystyle i_{}}$ ${\displaystyle \mathrm{\forall }}$ ${\displaystyle i,}$ j ${\displaystyle w_{ij}=w_{ji},\all i,j}($대칭)

가중치가 대칭이라는 제약조건은 활성화 규칙을 따르는 동안 에너지 기능이 단조롭게 감소함을 보장한다.^[12] 비대칭 가중치를 가진 네트워크는 일부 주기적 또는 혼돈적 행동을 보일 수 있지만, Hopfield는 이러한 동작이 위상 공간의 상대적으로 작은 부분에 국한되며 콘텐츠 주소 지정 연상 기억 시스템으로서 작용하는 네트워크의 능력을 손상시키지 않는다는 것을 발견했다.

홉필드는 또한 연속적인 값을 위해 신경망을 모델링했는데, 여기서 각 뉴런의 전기 출력은 이진이 아니라 0과 1 사이의 어떤 값이다.^[4] 그는 이러한 유형의 네트워크가 암기된 상태를 저장하고 재생산할 수 있다는 것을 발견했다.

Notice that every pair of units i and j in a Hopfield network has a connection that is described by the connectivity weight ${\displaystyle w_{ij}}$. In this sense, the Hopfield network can be formally described as a complete undirected graph ${\displaystyle G=\langle V,f\rangle }$, where ${\displaystyle V$$}}$은(는) McCulloch-Pitts $뉴런$과${\displaystyle }$f : ${\displaystyle {V\mathrm{}}^{}2\mathbb{}}$ → R ${\$$V^{2}\rightarrow \mathb$ {$R} }$은(는) 단위 쌍을 실제 값인 연결 무게에 연결하는 함수다$$.

업데이트 중

홉필드 네트워크에서 하나의 단위(인공 뉴런을 시뮬레이션하는 그래프의 노드)를 업데이트하는 작업은 다음 규칙을 사용하여 수행된다.

${\displaystyle s_{i}\leftarrow \좌측\{\n1}{\loss{\text}}}}}}{j}{w_{ij}s_{j}}}\j}\geq \theta _{i}\-1&}\text{\text{data.}}}\end{array}\오른쪽.}$

여기서:

• ${\displaystyle w_{}}$ ${\displaystyle i_{}}$ ${\displaystyle j_{}}$ ${\$는 단위 j에서 단위 i까지 연결 중량의 강도(연결 중량)이다$$.
• ${\displaystyle s_{}}$ ${\displaystyle i_{}}$ ${\$는 단위 i의 상태를 말한다.
• ${\displaystyle {\theta }_{}}$ ${\displaystyle i_{}}$ ${\$는 단위 i의 임계값이다$$.

Hopfield 네트워크에서 업데이트는 다음과 같은 두 가지 방법으로 수행될 수 있다.

• 비동기식: 한 번에 하나의 유닛만 업데이트된다. 이 단위는 무작위로 고를 수도 있고, 아니면 처음부터 미리 정해진 순서를 부과할 수도 있다.
• 동기식: 모든 유닛이 동시에 업데이트된다. 이것은 동기화를 유지하기 위해 시스템에 대한 중앙 시계가 필요하다. 일부 사람들은 유사한 생물학적 또는 물리적 관심 시스템에 영향을 미치는 관찰된 글로벌 시계의 부재를 근거로 이 방법을 현실성이 떨어지는 것으로 본다.

뉴런은 주 공간에서 "서로 애착을 갖거나 밀어낸다"

두 단위 사이의 무게는 뉴런의 값에 강력한 영향을 미친다. 두 뉴런 i와 j 사이의$$ 연결 $중량$은 w ${\displaystyle i_{}}$ ${\displaystyle j_{}}$ ${\$ > 0 ${\displaystyle w_{ij}>0$인 경우 업데이트 규칙은 다음을 암시한다.

• ${\displaystyle s_{}}$= ${\displaystyle 1}$ ${\displaystyle s_{j}=1}$인$$경우 가중치 합계에서 j의 기여는 양의 값이다. 따라서 $s{\displaystyle {}_{}}$ ${\displaystyle i_{}}$ ${\$은(는) 값$$ ${\displaystyle i_{}}$= 1 {\$displaystyle s_{i$}=1}을$($를) 향해 j에 의해 당겨진다$$.
• ${\displaystyle s_{}}$=${\displaystyle }$- ${\displaystyle 1}$ ${\displaystyle s_{j}=-1$ 가중치 합계에서 j의 기여는 음수가 된다. 한편, $s{\displaystyle {}_{}}$ ${\displaystyle i_{}}$ ${\$은(는) 값 $s{\displaystyle {}_{}}$ ${\displaystyle i_{}}$=${\displaystyle }$- ${\displaystyle 1}$ ${\displaystyle s_{i}=-1}$을(를) 향해 j에 의해 밀린다$$.

따라서 뉴런 i와 j 사이의 무게가 양성이면 뉴런 i와 j의 가치는 수렴하게 된다. 마찬가지로 무게가 음성이면 분리가 된다.

이산형 및 연속형 Hopfield 네트워크의 작동 원리

브루크는 1990년 자신의 논문에서 뉴런의 융합을 증명하면서 이산 홉필드 네트워크에서 뉴런의 행동을 조명했다.^[13] 후속 논문은^[14] 최적화 프로세스 동안 해당 에너지 기능이 최소화되었을 때 이산 시간 및 연속 시간 홉필드 네트워크에서 뉴런의 동작을 추가로 연구했다. Bruck은 뉴런 j가 다음과 같은 편향된 사이비 컷을 더 줄여야만 상태가 바뀐다는 것을 보여준다^[13]. 이산 홉필드 네트워크는 홉필드 네트워크의 시냅스 중량 매트릭스에 대해 다음과 같은 편향된 사이비 컷을^[14] 최소화한다.

${\displaystyle J_{pseudo-cut}(k)=\sum _{i\in C_{1}(k)\sum _{j\in C_{2}w_{ij}+\sum _{j\in C_{1}(k){j}{\ta _{j}}}}}}}}$

여기서 $C{\displaystyle {}_{}}$ ${\displaystyle {1\mathrm{}}_{}}$( ${\displaystyle k}$) ${\displaystyle C_{1}($${\displaystyle k}$$)}$ 및 ${\displaystyle C_{}}$ $2{\displaystyle {}_{}}$( k${\displaystyle }$) ${\$$displaystyle C_$${2}(k$$)}$는 $각각{\displaystyle }$ -1 및 +1인 뉴런 집합을 나타내며$$$,$ 자세한 내용은 최근 문서를 참조하십시오.^[14]

이산 시간 홉필드 네트워크는 항상 다음과 같은 사이비^[13][14] 컷을 최소화한다.

${\displaystyle U(k)=\sum _{i=1}^{N}\sum _{j=1}{j=1}^{n}w_{n}(k){ij}(s_{i}-s_{j})(k)^{2}+2\sum _{j=1}{j}^{j}}k}}}}}}}}}}}}}}}}}}$

연속 시간 Hopfield 네트워크는 항상 다음과 같은 가중 컷에^[14] 대한 상한선을 최소화한다.

${\displaystyle V(t)=\sum _{i=1}^{N}\sum _{j=1}^{N}w_{ij}(f(s_{i}(t))-f(s_{j}(t))^{2}+2\sum _{j=1}^{N}\theta _{j}f(s_{j}(t))}$

여기서 $f{\displaystyle }$ (${\displaystyle \cdot }$) ${\displaystyle$ f$(\cdot )}$는 제로 중심 s자형 함수다.

반면에 복잡한 호프필드 네트워크는 일반적으로 망의 복잡한 중량 매트릭스의 이른바 섀도 컷을 최소화하는 경향이 있다.^[15]

에너지

홉필드 네트는 네트워크의 각 상태와 관련된 스칼라 값을 가지며, 여기서 다음과 같은 경우 네트워크의 "에너지" E라고 한다.

${\displaystyle E=-{\frac {1}{1}:{2}}\sum _{i,j}w_{ij}s_{ij}s_{i}s_{j}+\sum _{i}\theta_{i}s_{i}s_{i}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}$

이 양은 네트워크 단위가 업데이트될 때 감소하거나 그대로 유지되기 때문에 "에너지"라고 불린다. 더욱이, 반복적인 업데이트 하에서 네트워크는 결국 에너지 함수의 국소 최소값인 상태(Lyapunov 함수로 간주됨)^[1]로 수렴될 것이다. 그러므로 어떤 상태가 에너지 함수의 국소 최소치인 경우 그것은 네트워크의 안정적 상태가 된다. 이 에너지 함수는 Ising 모델이라는 이름으로 물리학의 일반적인 모델 등급에 속한다는 점에 유의하십시오. 관련 확률 측정인 Gibbs 측정은 Markov 속성을 가지고 있기 때문에 Markov 네트워크의 특수한 경우입니다.

최적화 중인 Hopfield 네트워크

Hopfield와 Tank는 1985년에 고전적인 여행-영업자 문제를 해결하는데 있어서 Hopfield 네트워크 애플리케이션을 제시했다.^[16] 그 이후로, Hopfield 네트워크는 최적화를 위해 널리 이용되었다. 최적화 문제에서 Hopfield 네트워크를 사용하는 아이디어는 간단하다. 제약/제약되지 않은 비용 함수를 Hopfield 에너지 함수 E의 형태로 작성할 수 있는 경우, 평형 지점이 제약/제약되지 않은 최적화 문제에 대한 해결책을 나타내는 Hopfield 네트워크가 존재한다. Hopfield 에너지 함수를 최소화하면, 제약조건이 네트워크의 시냅스 가중치에 "내포"될 때 또한 객관적인 기능을 최소화하고 제약조건을 만족시킨다. 최적 제약을 가능한 최선의 방법으로 시냅스 가중치에 포함시키는 것은 어려운 작업이지만, 실제로 여러 분야의 제약조건과 함께 여러 가지 어려운 최적화 문제들이 Hopfield 에너지 함수로 변환되었다. 연상 메모리 시스템, 아날로그-디지털 변환, 작업-샵 스케줄링 문제, 2차 배정 및 기타 관련 NP-완전 문제, 무선 네트워크의 채널 할당 문제, 모바일 애드호크 네트워크 라우팅 문제, 이미지 복원, 시스템 식별, 조합 최적화 등 몇 가지를 예로 들 수 있다. 자세한 내용은 예를 들어 논문에서 확인할 수 있다.^[14]

초기화 및 실행

Hopfield 네트워크의 초기화는 장치의 값을 원하는 시작 패턴으로 설정함으로써 이루어진다. 그런 다음 네트워크가 유인기 패턴으로 수렴될 때까지 반복적인 업데이트가 수행된다. 이 비선형 동적 시스템의 유인기가 다른 시스템처럼^{[citation needed]} 주기적이거나 혼란스럽지 않고 안정적이라는 것을 Hopfield가 증명했듯, 수렴은 일반적으로 보장된다. 그러므로, 호프필드 네트워크의 맥락에서, 유인자 패턴은 최종 안정 상태로서, 업데이트^{[citation needed]} 중에 그 안에서 어떠한 값도 변경할 수 없는 패턴이다.

트레이닝

홉필드 네트 훈련은 네트가 "기억해야 한다"는 주의 에너지를 낮추는 것을 포함한다. 이를 통해 넷이 컨텐츠 어드레스 가능한 메모리 시스템 역할을 할 수 있게 되는데, 즉, 네트워크는 국가의 일부분만 주어진다면 "기억된" 상태로 수렴하게 된다. 그물은 그 입력과 가장 유사한 훈련된 상태로의 왜곡된 입력으로부터 회복하는 데 사용될 수 있다. 이것은 유사성을 기초로 기억을 회복하기 때문에 연상기억이라고 불린다. 예를 들어, 상태(1, -1, 1, -1, 1)가 에너지 최소가 되도록 5단위로 홉필드망을 훈련시키고, 네트워크에 상태(1, -1, -1, -1, -1, -1, 1)를 부여하면 (1, -1, 1, -1, 1)로 수렴된다. 그러므로 네트워크는 네트워크가 기억해야 할 상태의 에너지가 국소 미니마일 때 적절하게 훈련된다. 페르셉트론 훈련과는 대조적으로 뉴런의 문턱은 결코 갱신되지 않는다는 점에 유의한다.

학습규칙

홉필드 네트워크의 기억 속에 정보를 저장하는 데 사용할 수 있는 다양한 학습 규칙이 있다. 학습 규칙은 다음 두 가지 특성을 모두 갖는 것이 바람직하다.

• Local: 각각의 체중이 특정 체중에 관련된 연결의 양쪽에 있는 뉴런이 이용할 수 있는 정보를 사용하여 업데이트되는 경우 학습 규칙은 로컬이다.
• 증분: 새로운 패턴은 훈련에도 사용되었던 옛 패턴의 정보를 사용하지 않고도 학습할 수 있다. 즉, 훈련에 새로운 패턴을 사용할 때, 가중치에 대한 새로운 값은 낡은 값과 새로운 패턴에만 의존한다.^[17]

이러한 특성은 이를 만족시키는 학습 규칙이 생물학적으로 더 그럴듯하기 때문에 바람직하다. 예를 들어 인간의 뇌는 항상 새로운 개념을 배우고 있기 때문에 인간의 학습이 증분이라고 추론할 수 있다. 증분적이지 않은 학습 시스템은 일반적으로 한 번만 교육되며, 방대한 양의 교육 데이터가 제공된다.

Hopfield 네트워크에 대한 Hebbian 학습 규칙

헤비안 이론은 1949년 도널드 헵이 뉴런 세포의 동시 활성화가 이들 세포 사이의 시냅스 강도의 확연한 증가로 이어지는 '연관적 학습'을 설명하기 위해 도입했다.^[18] 흔히 '함께 발사하는 신경, 함께 전선을 연결한다'로 요약된다. 뉴런은 동기화되지 않은 상태로 발화하지만 연결되지 않는다"고 말했다.

헤비안 규칙은 국부적이고 증분적이다. Hopfield 네트워크의 경우, $n{\displaystyle }$ ${\displaystyle n}$ 이진$$ 패턴을 학습할 때 다음과 같은 방법으로 구현된다.

${\displaystyle w_{ij}={\frac {1}{n}\sum _{\mu =1}^{n}\epsilon _{i}^{\mu }\epsilon _{j}^{j}}}}{\mu }}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}$

여기서 $ϵ{\displaystyle {}_{}^{}}$ ${\displaystyle i_{}^{}}$ ${\displaystyle {}_{}^{}}$ ${\$는 패턴 $\mu {\displaystyle }$ ${\displaystyle \mu }$의 비트 i를 나타낸다$$$.$

뉴런$$ i와 j에 해당하는 비트가 패턴 $[\displaystyle \mu$ $\}\}$에서 같다면, ${\displaystyle {ϵ}_{}^{}}$ ${\displaystyle {}_{}^{}}$ ${\displaystyle {\mu }_{}^{}}$ j ${\displaystyle {}_{}^{}}${\$displaystyle \epsilon _{i}^{}\mu _{j}^{$j}^{\$mu }}}}}}}}.$ 이는 다시 w ${\displaystyle i_{}}$ ${\displaystyle j_{}}$ ${\$의 무게에 긍정적인 영향을 미치고$$, i와 j의 값이 같아지는 경향이 있다. 뉴런 i와 j에 해당하는 비트가 다를 경우 그 반대 현상이 일어난다.

스토키 학습 규칙

이 규칙은 1997년 Amos Storkey에 의해 도입되었으며, 지역적이면서도 증분적이다. Storkey는 또한 이 규칙을 사용하여 훈련된 Hopfield 네트워크가 Hebbian 규칙을 사용하여 훈련된 해당 네트워크보다 더 큰 용량을 가지고 있다는 것을 보여주었다.^[19] 끌어당기는 신경망의^{[clarification needed]} 중량 매트릭스는 다음과 같은 경우에 스토키 학습 규칙을 따른다고 한다.

${\displaystyle w_{ij}^{\nu }=w_{ij}^{\nu -1}+{\frac {1}{n}}\epsilon _{i}^{\nu }\epsilon _{j}^{\nu }-{\frac {1}{n}}\epsilon _{i}^{\nu }h_{ji}^{\nu }-{\frac {1}{n}}\epsilon _{j}^{\nu }h_{ij}^{\nu }}$

where ${\displaystyle h_{ij}^{\nu }=\sum _{k=1~:~i\neq k\neq j}^{n}w_{ik}^{\nu -1}\epsilon _{k}^{\nu }}$ is a form of local field^[17] at neuron i.

이 학습 규칙은 시냅스들이 그들의 측면에 있는 뉴런만을 고려하기 때문에 지역적이다. 이 규칙은 지역 영역의 영향으로 일반화된 헤비안 규칙보다 패턴과 가중치로부터 더 많은 정보를 사용한다.

스퓨러 패턴

네트워크가 훈련을 위해 사용하는 패턴(검색 상태라고 함)이 시스템의 유인자가 되는 패턴. 반복적인 업데이트는 결국 검색 상태 중 하나로 통합될 것이다. 그러나, 때때로 네트워크는 (훈련 패턴과는 다른) 가상의 패턴으로 수렴할 것이다.^[20] 이러한 가짜 패턴의 에너지 또한 국소 최소치다. 저장된 각 패턴 x에 대해 부정 -x도 가짜 패턴이다.

가짜 상태는 또한 홀수의 검색 상태의 선형 결합일 수 있다. 예를 들어 3가지 패턴 ${\displaystyle {\mu 1\mathrm{}}_{}}$,${\displaystyle {}_{}{\mu 2\mathrm{}}_{}}$,${\displaystyle {}_{}{\mu 3\mathrm{}}_{}}$ ${\$을 사용하면 다음과 같은 모의 상태를 얻을 수 있다$.$

${\displaystyle \epsilon _{i}^{\rm}=\pm \sgnname {sgn}(\pm \pm \epsilon _{i}^{1}pm \ipsilon _{2}}:00 \i}^{i}{i}^{{{}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}pmo_{{{{{3}}}}}}}}})}$

짝수 상태를 가진 가짜 패턴은 0까지^[20] 합칠 수 있으므로 존재할 수 없다.

역량

Hopfield 네트워크 모델의 네트워크 용량은 주어진 네트워크 내의 뉴런 양과 연결에 의해 결정된다. 따라서 저장할 수 있는 기억의 수는 뉴런과 연결에 따라 달라진다. 더욱이 벡터와 노드 사이의 회수 정확도는 0.138(매 1,000개 노드마다 저장소에서 약 138개 벡터를 회수할 수 있음)인 것으로 나타났다(Hertz et al., 1991). 따라서 벡터를 많이 저장하려고 하면 많은 실수가 발생할 것이 분명하다. Hopfield 모델이 올바른 패턴을 기억하지 못할 때, 의미론적으로 관련된 항목은 개인을 혼란스럽게 하는 경향이 있고, 잘못된 패턴에 대한 기억이 발생하기 때문에 침입이 일어났을 가능성이 있다. 따라서, 호프필드 네트워크 모델은 검색 시 저장된 항목과 다른 항목의 모델을 혼동하는 것으로 나타난다. 완벽한 리콜과 대용량인 >0.14는 Storkey 학습 방법에 의해 네트워크에 로딩될 수 있으며, ETAM,^[21][22] ETAM 실험도 에 포함된다.^[23] 나중에 Hopfield 네트워크에서 영감을 받은 전위 모델들은 저장 한도를 높이고 검색 오류율을 줄이기 위해 고안되었는데, 일부는 원샷 학습이 가능하다.^[24]

스토리지 용량은 $C{\displaystyle }$ ${\displaystyle \cong \frac{n\mathrm{}}{}}$ 2 ${\displaystyle \frac{{\log }_{}}{}}$ ${\displaystyle \frac{{2\mathrm{}}_{}}{}}$ ${\displaystyle \frac{{}_{}n}{}}$ ${\$}n$}}}$로 지정할 수 있으며$, 여기$서 n은 네트$$ 내의$$뉴런 $수입니다$.

인간기억

Hopfield 모델은 메모리 벡터의 통합을 통해 연관 메모리를 설명한다. 메모리 벡터는 약간 사용될 수 있으며, 이것은 네트워크에서 가장 유사한 벡터의 검색을 촉발할 것이다. 그러나 이러한 과정으로 인해 침입이 발생할 수 있다는 것을 알게 될 것이다. Hopfield 네트워크의 연결 메모리에는 자동 연결과 헤테로 연결의 두 가지 운영 유형이 있다. 첫 번째는 벡터가 자신과 연관되었을 때, 후자는 저장소에서 서로 다른 두 벡터가 연관되었을 때 입니다. 더욱이, 두 가지 유형의 운영은 하나의 메모리 매트릭스 내에 저장할 수 있지만, 주어진 표현 매트릭스가 운영의 하나 또는 다른 하나가 아니라, 오히려 둘의 조합(자동 연관성 및 이성 연관성)인 경우에만 가능하다. 홉필드의 네트워크 모델은 헵의 (1949년) 학습 규칙과 동일한 학습 규칙을 활용하는데, 기본적으로 학습은 활동이 발생할 때쯤 가중치를 강화한 결과로 발생한다는 것을 보여주려고 노력했다는 점에 유의할 필요가 있다.

리즈토와 카하나(2001)는 확률론적 학습 알고리즘을 통합함으로써 신경망 모델이 리콜 정확도에 대한 반복을 설명할 수 있다는 것을 보여줄 수 있었다. 검색 과정 중에는 학습이 일어나지 않는다. 그 결과, 네트워크의 가중치는 고정된 상태로 유지되어, 모델이 학습 단계에서 회수 단계로 전환할 수 있음을 보여 준다. 상황별 표류를 추가함으로써, 그들은 대기 중인 리콜 작업 동안 Hopfield 모델에서 발생하는 빠른 망각을 보여줄 수 있었다. 전체 네트워크는 모든 단일 노드의 활성화 변화에 기여한다.

뉴런의 행동을 기술한 맥컬로치와 피츠'(1943)의 역동적 법칙은 다중 뉴런의 활성화가 어떻게 새로운 뉴런의 발화율의 활성화에 매핑되는지, 뉴런의 무게가 어떻게 새로운 활성화된 뉴런(그리고 그것을 활성화시킨 뉴런들) 사이의 시냅스 연결을 강화하는지 보여주는 방식으로 그렇게 한다. 홉필드는 홉필드 네트워크에서 검색이 어떻게 가능한지 보여주기 위해 맥컬로치-피트스의 역동적인 규칙을 사용할 것이다. 그러나, 홉필드는 반복적으로 그렇게 할 것이라는 것을 주목하는 것이 중요하다. 홉필드는 선형 함수를 사용하는 대신 비선형 활성화 함수를 사용할 것이다. 따라서 이것은 Hopfield 동적 규칙을 만들 것이며, 이를 통해 Hopfield는 비선형 활성화 함수를 통해 동적 규칙이 저장된 패턴 중 하나의 방향으로 상태 벡터의 값을 항상 수정한다는 것을 보여줄 수 있었다.

밀도 높은 연관 메모리 또는 현대적인 Hopfield 네트워크

홉필드 네트워크는^[1][4] 동적 궤적이 고정된 지점 유치기 상태로 수렴되고 에너지 함수로 설명되는 반복 신경 네트워크다. 각 모델 뉴런 $i$ ${\textstyle i}$의 상태는 시간 의존 변수 $V{\displaystyle {}_{}}$ ${\displaystyle i_{}}$ ${\$에 의해 정의되며$,$ 이는 이산형 또는 연속형으로 선택할 수 있다. 완전한 모델은 각 뉴런의 미래 활동 상태가 모든 뉴런의 알려진 현재 또는 이전의 활동에 어떻게 의존하는지에 대한 수학을 설명한다.

연상기억의 원래 호프필드 모델에서는 변수가 2진수였고, 뉴런의 상태를 한 번에 한 번씩 업데이트하는 것으로 역학을 기술했다.^[1] $V{\displaystyle {}_{}}$ ${\displaystyle i_{}}$ ${\$에서 에너지 함수가 2차적으로 정의되었으며$$, 역학 관계는 시스템의 총 에너지를 낮추는 경우에만$$ 각 단일 뉴런 $i{\displaystyle }$ ${\displaystyle i}$의 활성도를 변경하는 것으로 구성되었다. $이러한{\displaystyle {}_{}}$ 생각은 V i ${\$의 출력을 나타내는 연속형 $변수$인 V i ${\displaystyle$ i$\}$와 입력 전류의 단조함수인$$ ${\displaystyle {Vi}_{}}$ ${\$의 경우에 확장되었다. 역학은 시스템의 "에너지"가 항상 감소하는 1차 미분 방정식의 집합으로 표현되었다.^[4] 연속 케이스의 에너지는 ${\displaystyle V_{}}$ i ${\$이진 모델과 동일)에서 2차적인 한 항과 게인 함수(네우론의 활성화 함수)에 따라 달라지는 두 번째 항을 가진다. 이러한 고전적 시스템들은 연관 메모리의 바람직한 특성들을 많이 가지고 있지만, 입력 특징의 수에 따라 선형적으로 확장되는 작은 메모리 저장 용량에 시달린다.^[1]

고밀도 연상기억^[7](현대식 홉필드 네트워크라고도^[9] 함)은 입력 특징 수와 저장된 메모리 수 사이의 선형 스케일링 관계를 끊는 고전적인 홉필드 네트워크의 일반화다. 이는 형상 뉴런 수의 함수로써 더 강한 비선형성(에너지함수나 뉴런의 활성화함수 중 하나)을 도입하여 초선형^[7](수치수까지^[8]) 메모리 저장 용량을 유도함으로써 달성된다. 네트워크는 여전히 충분한 수의 숨겨진 뉴런을 필요로 한다.^[10]

현대 홉필드 네트워크의 핵심 이론적 발상은 고전적인 홉필드 네트워크와 비교하여 뉴런의 구성 공간에서 저장된 기억을 중심으로 더욱 첨예하게 정점을 이루는 에너지 함수와 업데이트 규칙을 사용하는 것이다.^[7]

이산형 변수

현대적인 홉필드 네트워크의 간단한 예는^[7] 모델 $뉴런{\displaystyle }$ i ${\displaystyle i$의 활성 ${\displaystyle {Vi}_{}}$=${\displaystyle }$+ 1 ${\displaystyle V_{i}=+1}$ 및$$ 비활성 ${\displaystyle {Vi}_{}}$=${\displaystyle }$- ${\displaystyle 1}$ ${\displaystyle V_{i}=-1}$ 상태를$$ 나타내는 이진$$ 변수 $V{\displaystyle {}_{}}$ ${\displaystyle i_{}}$ ${\$ i$}$의 관점에서 작성할 수 있다.

이 공식에서 가중치 ${\mathrm{\mu i}}_{}$ ${\$ i$}$는 메모리 벡터의 행렬(지수 $\mu {\displaystyle }$= 1${\displaystyle \mathrm{...)}}$을 나타낸다$$.${\$$N_{\text{mem}}}$은(는) 서로 다른 메모리를$$ 열거하며, $인덱스{\displaystyle }$ i${\displaystyle }$= ${\displaystyle \mathrm{1...}}$${\$$N_{f}}$는 $i{\displaystyle }$ ${\displaystyle i}$ -th$$ feature neuron)에 해당하는 각 메모리의 내용을 열거하며$$, $F{\displaystyle (x}$ $){\displaystyf F(x)}$ 함수는 빠르게$$ 성장하는 비선형함수다. (비동기 사례에서) 개별 뉴런에 대한 업데이트 규칙은 다음과 같은 형태로 작성될 수 있다. 즉, $네트워크$는 i ${\textstyle i}$ -th$$ 뉴런의 업데이트된 상태를 계산하기 위해 두 가지 에너지를 비교한다. 즉, 잔류 상태의 경우 네트워크의 에너지와 $ON{\displaystyle }$ 상태의 i ${\displaystyle$ i$}$ -th$$ 뉴런의 네트워크 에너지와 OFF 상태의 $i{\displaystyle }$ ${\displaystyle$ i$}$ -th$$ 뉴런의 에너지를 비교한다.ng 뉴런 $i{\displaystyle }$ ${\displaystyle i}$ -th$$ 뉴런의 업데이트된 상태는 두 에너지 중 가장 낮은 상태를 선택한다.^[7]

비선형 에너지 함수가 2차 $F{\displaystyle (x}$ ${\displaystyle )}$= ${\displaystyle {}^{}}$ ${\displaystyle {2\mathrm{}}^{}}$ ${\$인 경우 이러한 방정식은$$ 고전적인 이진 Hopfield Network에 대한 익숙한 에너지 함수와 업데이트 규칙으로 감소한다.^[1]

이러한 네트워크의 메모리 저장 용량은 임의의 이진 패턴에 대해 계산할 수 있다. ${\displaystyle \mathrm{전력}}$ 에너지 함수 $F{\displaystyle (}$ x${\displaystyle }$)${\displaystyle }$= ${\displaystyle x^{}}$ ${\displaystyle {}^{}}$ ${\$에 대해 오류 없이 이 네트워크에서 저장 및 검색할 수 있는 최대$$ 메모리 수는 다음과 같다^[7].

$\mathrm{지수}$ 에너지 함수 $F($ x$$)$$= e $x^{}$ ${\\$의 경우 메모리$$ 저장 용량은 피쳐 뉴런^[8] 수가 기하급수적이다.

연속형 변수

현대의 Hopfield 네트워크나 밀도 높은 연상기억은 연속변수와 연속시간에서 가장 잘 이해할 수 있다.^[9][10] 그림 1과 같은 네트워크 구조와 뉴런 상태 진화^[10] 방정식을 고려하십시오.

$${\displaystyle {\begin}\tau _{f}{f}{f}{frac {dx_{i}}}=\sum \limits _{\mu =1}^{{h}\i_{i\mu }f_{}-x_{i}+++++++++++++++++++++++++++++++++++++++++++++++++++++I_{i}\\\tau _{h}{dh_{\mu }}}}{dt}}=\sum \limits _{i=1}^{f}\xi _{\mu i}g_{i}-h_{\case}}}}}}}}}}}}}$$

(1)

여기서 피쳐 뉴런의 $전류$는 x $i_{}${\$textstyle x_{i$로 표시되고 메모리 뉴런의 전류는 $h{\displaystyle {}_{}}$ ${\displaystyle {\mu }_{}}$ ${\$${\displaystyle }$ ${\displaystyle h}$은 숨겨진 뉴런을 의미한다$$). 형상 뉴런이나 기억 뉴런 사이에는 시냅스 연결이 없다. 매트릭스 ${\displaystyle {\mathrm{\mu i}}_{}}$ ${\$는 특징 뉴런 $i{\displaystyle }$ ${\displaystyle i}$에서 기억 뉴런 $[\$$displaystyle$ $\$$mu$ $}}$까지의 시냅스의 강도를$$ 나타낸다. 시냅스는 대칭으로 가정하여 동일한 값이 메모리 뉴런$\mu s$와 다른 물리적 시냅스의 특성을 나타낸다$.$$$기능$$$뉴런{\displaystyle }$ i ${\displaystyle i}$에 $\}.$ 메모리 뉴런과 형상 뉴런의 출력은 $해당{\displaystyle {}_{}}$ 전류의 비선형 함수인 f ${\displaystyle {\mu }_{}}$ ${\$와 ${\displaystyle g_{}}$ $i{\displaystyle {}_{}}$ ${\$로 표시된다. In general these outputs can depend on the currents of all the neurons in that layer so that ${\displaystyle f_{\mu }=f(\{h_{\mu }\})}$ and ${\textstyle g_{i}=g(\{x_{i}\})}$. It is convenient to define these activation function as derivatives of the Lagrangian functions for the two 뉴런의 집단

$${\displaystyle f_{\mu }={\frac {\partial L_{h}}{\partial h_{\mu }}}\\\ \ \{\prac}={\partial L_{v}}{partial x_{i}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}\\\\\\\\\$$

(2)

이렇게 해서 뉴런 상태에 대한 방정식의 구체적인 형태는 일단 라그랑비아 함수가 지정되면 완전히 정의된다. 마지막으로, 두 신경세포 그룹에 대한 시간 상수는 ${\displaystyle {\tau }_{}}$ f ${\$ ${\displaystyle h_{}}$ h ${\$ ${\displaystyle I_{}}$ ${\$로 표시되며, 이는$$ 제시된 데이터에 의해 구동될 수 있는 네트워크 입력 전류다.

비선형 미분 방정식의 일반 시스템은 비선형성과 초기 조건의 선택에 따라 달라질 수 있는 많은 복잡한 동작을 가질 수 있다. 그러나, Hopfield Networks의 경우, 이것은 그렇지 않다 - 역동적인 궤도는 항상 고정된 지점 유치기 상태로 수렴된다. 이 특성은 이러한 방정식이 에너지 함수의 기초가^[10] 되도록 특별히 설계되었기 때문에 달성된다.

$${\displaystyle E(t)={\Big [}\sum \limits _{i=1}^{N_{f}}(x_{i}-I_{i})g_{i}-L_{x}{\Big ]}+{\Big [}\sum \limits _{\mu =1}^{N_{h}}h_{\mu }f_{\mu }-L_{h}{\Big ]}-\sum \limits _{\mu ,i}f_{\mu }\xi _{\mu i}g_{i}}$$

(3)

대괄호로 묶인 용어는 뉴런의 상태에 관한 라그랑지안 함수의 레전드르 변환을 나타낸다. 라그랑지안 함수의 헤시안 행렬이 양의 반정확한 값일 경우, 에너지 함수는 동적 궤적에서^[10] 감소할 것을 보장한다.

$${\displaystyle {\frac {dE(t)}{dt}}=-\tau _{f}\sum \limits _{i,j=1}^{N_{f}}{\frac {dx_{i}}{dt}}{\frac {\partial ^{2}L_{x}}{\partial x_{i}\partial x_{j}}}{\frac {dx_{j}}{dt}}-\tau _{h}\sum \limits _{\mu ,\nu =1}^{N_{h}}{\frac {dh_{\mu }}{dt}}{\frac {\partial ^{2}L_{h}}{\partial h_{\mu }\partial h_{\nu }}}{\frac {dh_{\nu }}{dt}}\leq 0}$$

(4)

이 특성은 뉴런의 활동 시간적 진화를 기술하는 동적 방정식의 시스템이 결국 고정된 지점 유치기 상태에 도달할 것이라는 것을 증명하는 것을 가능하게 한다.

$어떤$ 상황에서는 피쳐 뉴런에${}_{}{비해}_{}$ 숨겨진 ${뉴런}_{}$의 역학 관계가 훨씬 $빠른$ 시간 척도로 안정화된다고 가정할 수 있다$.$ 이 경우 시스템 (1)의 두 번째 방정식의 안정적 상태 솔루션을 사용하여 숨겨진 단위 진통의 전류를 표현할 수 있다.uh 특징 뉴런의 출력물. 이로써 피쳐 뉴런에 대해서만 일반론(1)을 효과적인 이론으로 줄일 수 있게 되었다. 결과적인 유효 업데이트 규칙과 라그랑지안 함수의 다양한 공통 선택에 대한 에너지는 그림.2에 나타나 있다. log-sum-exponential Lagrangian 함수의 경우 형상 뉴런 상태에 대한 업데이트 규칙(한 번 적용되는 경우)은 현대의 많은 AI 시스템에서 일반적으로 사용되는 주의 메커니즘이다^[9](연속 시간 공식에서 이 결과를 도출하는 방법은 참조).^[10]

연속형 변수를 갖는 고전적 Hopfield 네트워크와의 관계

연속 홉필드 네트워크의^[4] 고전적인 공식화는 하나의 숨겨진 계층을 가진 현대 홉필드 네트워크의 특별한 제한 사례로 이해할^[10] 수 있다. 등급이 매겨진 뉴런을 위한 연속 홉필드 네트워크는 일반적으로 동적 방정식으로 설명된다^[4].

$${\displaystyle \tau_{f}{f}{\frac {dx_{i}}}=\sum \limits _{j=1}^{N_{f}}}}T_{ij}V_{j}-x_{i}+I_{i}}$$

(5)

그리고 에너지 기능

$${\displaystyle E=-{\frac {1}{1}:{2}}\sum \limits _{i,j=1}^{N_{f}}}T_{ij}V_{i}V_{j}-\sum \limits _{i=1}^{N_{f}V_{i}I_{i}+\sum \limits _{i=1}^{N_{f}}\int \limits ^{V_{i}g^{-1}(z)\,dz}$$

(6)

where ${\textstyle V_{i}=g(x_{i})}$, and ${\displaystyle g^{-1}(z)}$ is the inverse of the activation function ${\displaystyle g(x)}$. This model is a special limit of the class of models that is called models A,^[10] with the following choice of the Lagrangian functions

$${\displaystyle L_{v}=\sum \limits _{i=1}^{N_{f}}\int \limits ^{x_{i}}g(x)dx,\ \ \ \ \ {\text{and}}\ \ \ \ \ L_{h}={\frac {1}{2}}\sum \limits _{\mu =1}^{N_{h}}h_{\mu }^{2}}$$

(7)

정의(2)에 따라 활성화 기능으로 이어짐

$${\displaystyle V_{i}=g(x_{i}),\\ \ \\\\\\\\\ \ \ \ \ \ \ \ \ \ \{\mu }}}}}$$

(8)

If we integrate out the hidden neurons the system of equations (1) reduces to the equations on the feature neurons (5) with ${\displaystyle T_{ij}=\sum \limits _{\mu =1}^{N_{h}}\xi _{\mu i}\xi _{\mu j}}$, and the general expression for the energy (3) reduces to the effective energy

$${\displaystyle E=-{\frac {1}{1}:{2}}\sum \limits _{i,j=1}^{N_{f}}}T_{ij}V_{i}V_{j}-\sum \limits _{i=1}^{N_{f}V_{i}I_{i}+\sum \limits _{i=1}^{N_{f}}{\Big (}x_{i}V_{i}-\int \limits ^{x_{i}g(x)dx{\Big )}}}}}}}}}}}}$$

(9)

방정식 (6)의 처음 두 항은 방정식 (9)의 항과 같지만, 세 번째 항은 피상적으로 다르게 보인다. 방정식 (9)에서는 형상 뉴런에 대한 라그랑지안의 레전드르 변환인 반면, (6)에서는 제3항은 역활성화 함수의 적분이다. 그럼에도 불구하고, 한 함수의 파생상품과 그것의 레전드르 변환은 서로 역함수이기 때문에, 이 두 표현은 사실상 동등하다. 이 두 용어가 명시적으로 동일하다는 것을 알 수 있는 가장 쉬운 ${\displaystyle {방법}_{}}$은$$x i {\$displaystyle x_{$i}}에 대해 각 용어를 구별하는 것이다$.$ 두 식에 대한 이러한 차이점의 결과는 $x{\displaystyle {}_{}}$ ${\displaystyle i_{}}$ ${\displaystyle {}_{}}$( ${\displaystyle x_{}}$ i${\displaystyle {}_{}{}^{}}$) ${\displaystyle {\prime }^{}}$ ${\$과 같다$.$ 따라서 두 표현은 가법 상수까지 같다. 이로써 연속적인 상태를^[4] 가지는 고전적인 호프필드 네트워크가 에너지 (3)을 가진 현대적인 호프필드 네트워크(1)의 특별한 제한 사례라는 증거가^[10] 완성되었다.

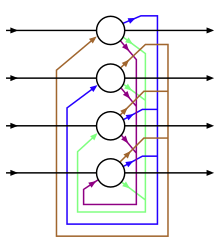
현대 Hopfield 네트워크의 일반적 공식화

생물학적 신경망은 서로 다른 세포의 종류에 있어서 이질성이 크다. 이 절에서는 극도의 이질성을 가정하는 완전히 연결된 현대 홉필드 네트워크의 수학 모델을 설명한다. 즉, 모든 뉴런은 다르다.^[25] 구체적으로 에너지 함수와 그에 상응하는 동적 방정식은 각 뉴런이 고유의 활성화 함수와 운동 시간 척도를 가지고 있다고 가정하여 기술한다. 네트워크는 완전하게 연결되어 있다고 가정하여 모든 뉴런이 ${\displaystyle W_{}}$ I ${\displaystyle J_{}}$ ${\$ 무게의 대칭 행렬을 사용하여 다른 모든 뉴런과 연결된다.$IJ}$색인 $I{\displaystyle }$ ${\displaystyle I}$ 및 $J$ ${\displaystyle J}$은 네트워크의 서로 다른 뉴런을 열거한다(그림$$ 3 참조). 이 문제를 수학적으로 공식화하는 가장 쉬운 방법은 네트워크에 있는 모든 뉴런들의 활동에 의존하는$$ 라그랑비아 함수 $L{\displaystyle }$ ${I}\}){\displaystyle L(\{x_{I}\}})$을 통해 아키텍처를 정의하는 것이다. 각 뉴런에 대한 활성화 함수는 그 뉴런의 활동과 관련하여 라그랑지안의 부분적 파생물로 정의된다.

$${\displaystyle g_{I}={\frac {\partial L}{\partial x_{I}}}$$

(10)

${\displaystyle {생물학적}_{}}$ 관점에서 보면 $g{\displaystyle {}_{}}$ I ${\$에 대해 생각할 수 있다.$I}}}}$ $뉴런{\displaystyle }$ I${\displaystyle I$}의 축출력으로$.$ 가장 간단한 경우 라그랑지안이 다른 뉴런에 첨가되어 있을 때, 이 정의는 그 뉴런의 활동에서 비선형 함수인 활성화를 초래한다. 비중독성 래그랑지아의 경우 이 활성화 기능은 뉴런 그룹의 활동에 따라 달라질 수 있다. 예를 들어, 대조(소프트맥스) 또는 분열 정규화를 포함할 수 있다. 주어진 뉴런의 시간적 진화를 설명하는 동적 방정식은 다음과 같다^[25].

$${\displaystyle \tau _{I}{\frac {dx_{I}{dt}}=\sum \limits _{J=1}^{{N}W_{{{}}}IJ}g_{J}-x_{I}}$$

(11)

이 방정식은 신경과학에서 발화율 모델이라 불리는 모델의 등급에 속한다. 각 뉴런 $I{\displaystyle }$ ${\displaystyle I}$은(는) 모든 뉴런으로부터$$ 축 출력 ${\displaystyle g_{}}$ ${\$를 수집하여$$ 시냅스 계수 $W{\displaystyle {}_{}}$ ${\displaystyle I_{}}$ J ${\$로 가중치를 부여한다.$IJ}}$을(를) 생성하며 자체 시간 의존 활동 ${\displaystyle x_{}}$ I${\$을(를) 생산한다$.$ 시간적 진화는 시간 상수 ${\displaystyle {\tau }_{}}$ I ${\$를 가지는데$,$ 일반적으로 모든 뉴런에 대해 다를 수 있다. 이 네트워크는 글로벌 에너지 기능을^[25] 가지고 있다.

$${\displaystyle E=\sum \limits _{I=1}^{N}x_{{{N}x_{{I=1}}I}g_{I}-L-{\frac {1}{1}:{2}}\sum \limits _{I,J=1}^{N}g_{{{}g_{{}}}}}I}W_{IJ}g_{{J}$$

(12)

여기서 처음 두 용어는 뉴런의 전류 ${\displaystyle x_{}}$ I ${\$와 관련하여 라그랑지안 함수의 레전드르 변환을 나타낸다$.$ 이 에너지 함수의 시간적 파생물은 (자세한 내용은 참조)로 이어지는 동적 궤도에 따라 계산할 수 있다.

$${\displaystyle {\frac {dE}{dt}=-\sum \limits_{I,K=1}^{N}{\frac {dx_{{}I}{dt}M_{IK}{\frac {dx_{K}}}}{dt}}\leq 0,\\\\\\\\\\\\ \ \ \ M_{IK}=\tau_{{I}{\frac {\partial ^{2}L}{\partial x_{{{{}}}}}}}}}}}}}}}}}}}}}}{\partial x_{\}}}}}}}}}}}}{\partial x_{\I}\partial x_{K}}}}$$

(13)

마지막 불평등 부호는 행렬 M $I{\displaystyle {}_{}}$ ${\displaystyle K_{}}$ ${\$또는 그 대칭 부분)가 양의 반정확한 값이라는 것을 전제로 한다. 이와 더불어 에너지 함수가 비선형 동적 방정식 아래에서 경계되어 고정된 점 유치기 상태로 수렴할 것을 보장할 경우. 라그랑지안 함수의 관점에서 이 네트워크를 형성하는 이점은 활성화 함수의 서로 다른 선택과 뉴런의 다른 구조적 배열로 쉽게 실험할 수 있게 한다는 것이다. 그러한 모든 유연한 선택에 대해 수렴 조건은 $매트릭스{\displaystyle {}_{}}$ M ${\displaystyle I_{}}$ ${\displaystyle J_{}}$ ${\$의 특성과 에너지$$ 함수에 대한 하한값의 존재에 의해 결정된다.

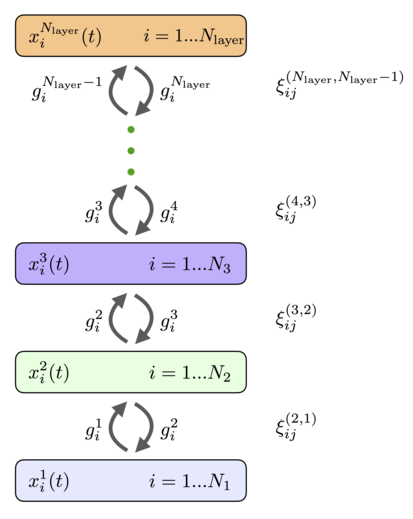
계층적 연관 메모리 네트워크

뉴런은 층별로 구성하여 주어진 층의 모든 뉴런이 동일한 활성화 기능과 동일한 동적 시간 스케일을 갖도록 할 수 있다. 만약 우리가 층 내의 뉴런들 사이에 수평적 연결이 없고 (측면 연결) 스킵레이어 연결이 없다고 가정한다면, 일반적인 완전 연결 네트워크 (11), (12)는 그림.4에 나타낸 구조로 감소한다. $연속{\displaystyle {}_{}}$ 변수 x ${\displaystyle {}_{}^{}}$ ${\$에 의해 설명되는 상태와 함께 N $레이어 {\$ x_{i}^{A}}을$($를) 가지고 있으며 활성화$$ 함수 $g{\displaystyle {}_{}^{}}$ ${\displaystyle I_{}^{}}$ ${\$$displaystystyle g_$${i}^{A$ 색인 $}$가 네트워크의 레이어를 열거하고$$ i를 표시한다.ndex $i{\displaystyle }$ ${\displaystyle i}$은(는) 해당 층의 개별 뉴런을 열거한다$$. 활성화 기능은 층에 있는 모든 뉴런의 활동에 따라 달라질 수 있다. 각 층마다 뉴런 ${\displaystyle {수}_{}}$가 다를 수 있다$.$ $N_{A}$의 개수가 다를 수 있다$.$ 이 뉴런들은 앞의 층과 이후의 층에 있는 뉴런들과 반복적으로 연결되어 있다. 레이어 $A{\displaystyle }$ ${\displaystyle A}$과 $B{\displaystyle }$ ${\displaystyle B}$의 뉴런을 연결하는 가중치 행렬은 $\xi {\displaystyle {}_{}^{}}$ ${\displaystyle i_{}^{}}$ ${\displaystyle j_{}^{}}$(${\displaystyle A_{}^{}}$, B${\displaystyle {}_{}^{}}$) ${\$}^{(A$,$B)}}}}}}}}}}}}로 표시된다$$($$체중량에 대한 상위 지수 순서는 $지수$ ${\}$을 의미한다.$style i}$은(는$)$ $A{\displaystyle }$ 레이어의 뉴런을 열거하고$,$ 인덱스 $j{\displaystyle }$ ${\displaystyle j}$은(는) $레이어$의 뉴런을 열거한다$({\displaystyle$ B$}$ $$$레이어$의 뉴런을 열거한다$$. 피드포워드 웨이트와 피드백 웨이트가 동일하다. 뉴런 상태에 대한 동적 방정식은 다음과^[25] 같이 쓰여질 수 있다.

$${\displaystyle \tau _{A}{\frac {dx_{i}^{A}}{dt}}=\sum \limits _{j=1}^{N_{A-1}}\xi _{ij}^{(A,A-1)}g_{j}^{A-1}+\sum \limits _{j=1}^{N_{A+1}}\xi _{ij}^{(A,A+1)}g_{j}^{A+1}-x_{i}^{A}$$

(14)

경계조건으로.

$${\displaystyle g_{i}^{0}=0,\ \ \ \ \ \ \ \ \\{i}^{N_{\text}}+1}=0}$$

(15)

기존의 피드포워드 네트워크와 이러한 방정식의 주요 차이점은 상위 계층의 피드포워드 네트워크로부터 피드백을 담당하는 두 번째 기간의 존재에 있다. 이러한 하향 신호는 하위 계층의 뉴런들이 제시된 자극에 대한 반응을 결정하는 데 도움을 준다. 일반적인 레시피에 따라 라그랑지안 함수 L ${\displaystyle A^{}}$(${\displaystyle }${ x ${\displaystyle i_{}^{}}$ ${\displaystyle {}_{}^{}}$ $){\displaystyle L^{A}(\{x_{i}^)$를 도입하는 것이 편리하다.$A{\displaystyle }$ ${\displaystyle A}$ - 세$$ 번째 숨겨진 레이어에 대한$$${A}\}.$ 이 레이어는 해당 레이어에 있는 모든 뉴런의 활동에 따라 달라진다.^[25] 그 계층의 활성화 기능은 라그랑고의 부분파생상품으로 정의될 수 있다.

$${\디스플레이 스타일 g_{i}^{A}={\frac {\partial L^{A}}{\partial x_{i}^{{partial l^}{partial l^}{partial x_{i}}}A}}}$$

(16)

이러한 정의로 에너지(Lyapunov) 함수는 다음과 같다^[25].

$${\displaystyle E=\sum \limits _{A=1}^{N_{\text{layer}}}{\Big [}\sum \limits _{i=1}^{N_{A}}x_{i}^{A}g_{i}^{A}-L^{A}{\Big ]}-\sum \limits _{A=1}^{N_{\text{layer}}-1}\sum \limits _{i=1}^{N_{A+1}}\sum \limits _{j=1}^{N_{A}}g_{i}^{A+1}\xi _{ij}^{(A+1,A)}g_{j}^{A}$$

(17)

각 계층에 대한 헤사인이 양의 반확정성이며 전체적인 에너지가 아래에서 경계되는 방식으로 라그랑비아 함수 또는 동등하게 활성화 함수를 선택하는 경우, 이 시스템은 고정된 지점 유치기 상태로 수렴할 것을 보장한다. 이 에너지 함수의 시간적 파생물은 다음과^[25] 같다.

$${\dplaystyle {\frac {dE}{dt}=-\sum \limits _{A=1}{\text{layer}}}}\au _{A}\i,j=1}^{N}}{\frac {dx_{j}^{j}^{}}^{A}}}}}}{{{}}}}}}}}}}}}}}}}}}}}}}}}}}}}}A}{dt}}{\frac {\partial ^{2}L^{A}}{\partial x_{j}^{}}}{{partial x_{partial ^}}}{{partial ^}}}{A}\partial x_{i}^{{}^A}}{\frac {dx_{i}^{A}{dt}}\leq 0}$$

(18)

그러므로 계층적 계층화된 네트워크는 실로 글로벌 에너지 기능을 가진 유인 네트워크다. 이 네트워크는 각 특정 문제에 대해 학습할 수 있는 계층적 시냅스 가중치 집합에 의해 설명된다.

참고 항목

• 연상기억(동음이의)
• 자동 연관 메모리
• 볼츠만 기계 - 호프필드 네트와 유사하지만 경사로 하강 대신 아닐레드 Gibbs 샘플링을 사용한다.
• 동적 인식 시스템 모델
• 이싱 모형
• 헤비안 이론

참조

외부 링크

위키미디어 커먼즈에는 홉필드 네트와 관련된 미디어가 있다.

• Rojas, Raul (12 July 1996). "13. The Hopfield model" (PDF). Neural Networks – A Systematic Introduction. ISBN 978-3-540-60505-8.
• 홉필드 네트워크 자바스크립트
• 이동 중인 세일즈맨 문제 – Hopfield Neural Network JAVA 애플릿
• Hopfield, John (2007). "Hopfield network". Scholarpedia. 2 (5): 1977. doi:10.4249/scholarpedia.1977.
• Fletcher, Tristan. "Hopfield Network Learning Using Deterministic Latent Variables" (PDF) (Tutorial). Archived from the original (PDF) on 2011-10-05.
• Neural Lab 그래픽 인터페이스 – Hopfield Neural Network 그래픽 인터페이스(Python & gtk)