반인륜주의

획일적 반권위주의
유형	반규칙 타일링
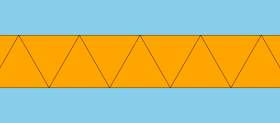
정점 구성	3.3.3.∞
슐레플리 기호	sr { 2, } $또는{\displaystyle }$s {${\displaystyle \begin{array}{c}\mathrm{}2\\ \mathrm{}\end{array}}$ 2$}$ { $displaystyle$ s { \ $begin${ $Bmatrix$} \ $infty$\ \$2$ \$end$ { $Bmatrix$} }
위토프 기호	2 2 ∞
콕서터 다이어그램
대칭	[param,2+], (param22)
회전 대칭	[param,2],+ (param22)
Bowers 약자	아자프
듀얼	편평면체
특성.	정점-이행

기하학에서, 반대칭 또는 무한^[1] 반대칭은 반대칭 계열의 산술적 한계이다; 그것은 무한 다면체 또는 평면의 타일로 간주될 수 있다.

변이 정삼각형이면 균일한 타일링입니다.일반적으로 두 개의 반평면으로 둘러싸인 두 세트의 합동 이등변 삼각형을 가질 수 있습니다.

관련 타일링 및 다면체

p가 무한대 경향이 있기 때문에 반비례는 반비례 계열의 산술 한계 sr{2, p} 또는 p.3.3이다. 따라서 반비례는 유클리드 타일링으로 변한다.

• 

  무직선 프리즘에 교대 연산을 적용함으로써 무직선 안티프리즘을 구성할 수 있다.

• 

  편평형 반작용의 이중 타일은 편평형 삼각면체이다.

균일한 다면체 및 균일한 타일링과 마찬가지로 8개의 균일한 타일링은 정규적인 아페이로곤 타일링에 기초할 수 있다.정류된 형태와 알 수 있는 형태가 중복되고, 2배의 무한도 무한이므로, 잘린 형태와 전치된 형태도 중복되어 독특한 형태의 수가 4개로 감소한다. 즉, 편평면 타일링, 편평면 호소면체, 편평면 프리즘 및 편평면 안티프리즘이다.

2차 정규 또는 균일한 수평 타일링

(∞ 2 2)	부모	잘렸다	수정 완료	비트런컷	양방향 (표준)	할 수 있다	옴니트런 (칸티트런컷)	스너브
위토프 기호	2 ∞ 2	2 2 ∞	2 ∞ 2	2 ∞ 2	∞ 2 2	∞ 2 2	∞ 2 2	∞ 2 2
슐레플리 기호	{∞,2}	t{buffic,2}	r{syslog,2}	t{2,169}	{2,∞}	rr{syslog,2}	tr {syslog,2}	sr {sr,2}
콕서터-딘킨 도표
정점 설정	∞.∞	∞.∞	∞.∞	4.4.∞	2개∞	4.4.∞	4.4.∞	3.3.3.∞
타일링 이미지
타일링명	편평 이면체	편평 이면체	편평 이면체	편평 프리즘	정평면 호소면체	편평 프리즘	편평 프리즘	반인륜주의

메모들

레퍼런스

• The Symmetries of Things 2008, John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, ISBN978-1-56881-220-5
• Grünbaum, Branko; Shephard, G. C. (1987). Tilings and Patterns. W. H. Freeman and Company. ISBN 0-7167-1193-1.
• T. 고셋:N차원 공간의 정칙 및 반정규 도형에 대하여, 맥밀런, 1900