재파일

Rep-tile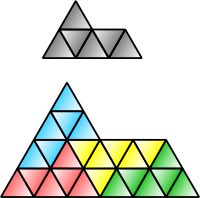
"스핑크스" 폴리아몬드 리필일.그림과 같이 4개의 스핑크스 복사본을 함께 사용하여 더 큰 스핑크스를 만들 수 있습니다.

테셀레이션의 기하학에서, 파충류는 같은 모양의 작은 복사본으로 해부될 수 있는 모양입니다.이 용어는 레크리에이션 수학자 솔로몬 골롬에 의해 동물 파충류에 대한 말장난으로 만들어졌고 1963년 사이언티픽 아메리칸 [1]5월호에서 마틴 가드너에 의해 "수학 게임" 칼럼에서 대중화되었습니다.2012년에 리 살로우는 수학 [2]잡지에 자기 타일 세트라고 불리는 반복 타일의 일반화를 소개했습니다.

스핑크스, 물고기 두 마리, 5-삼각형을 포함한 반복 타일 선택

용어.

의자 대체(왼쪽) 및 의자 타일링의 일부(오른쪽)

해부에서 n개의 복사본을 사용하는 경우 rep-n으로 레이블이 지정됩니다.이러한 모양은 많은 경우 비주기적 타일링과 같이 평면 타일링의 프로토타일을 형성합니다.원래 모양의 다른 크기를 사용하는 반복실험을 비정규 반복실험 또는 반복실험이라고 합니다.해부에서 n개의 복사본을 사용하는 경우 모양은 irrep-n이라고 합니다.모든 하위 타일의 크기가 서로 다를 경우 타일링은 완벽한 것으로 추가로 설명됩니다.rep-n 또는 irrep-n인 모양은 rep-n 구획에서 가장 작은 타일을 n개 더 작은 타일로 대체함으로써 k > 1에 대해 irrep-(kn - k + n) 또한 사소한 것입니다.반복 타일을 사용하든 비반복 타일을 사용하든 모양의 순서는 가능한 최소 타일 수로 [3]충분합니다.

예

반복 타일을 반복적으로 해부하고 팽창시켜 비주기 타일링(바람개비 타일링)을 정의합니다.

모든 정사각형, 직사각형, 평행사변형, 마름모꼴 또는 삼각형은 rep-4입니다.스핑크스 헥시아몬드(위 그림)는 rep-4 및 rep-9이며, 몇 안 되는 자기 복제 오각형 중 하나입니다.고스퍼 섬은 rep-7입니다.코흐 눈송이는 irrep-7입니다: 같은 크기의 작은 눈송이 여섯 개와 작은 눈송이의 세 배 면적을 가진 또 다른 눈송이가 합쳐져 하나의 더 큰 눈송이를 형성할 수 있습니다.

측면 길이가 1:2인 직각 삼각형은 rep-5이며, rep-5 단면은 비주기적 바람개비 타일링의 기초를 형성합니다.피타고라스의 정리에 따르면, rep-5 삼각형의 빗변 또는 경사진 변의 길이는 π5입니다.

국제 표준 ISO 216은 √2를 사용하여 종이의 크기를 정의합니다. 여기서 직사각형 종이의 긴 면은 종이의 짧은 면의 두 배의 제곱근입니다.이 모양의 직사각형은 rep-2입니다.직사각형(또는 평행사변형)의 가로 세로 비율이 √n:1이면 rep-n입니다.이등변 직각 삼각형도 rep-2입니다.

반복 타일 및 대칭

사각형과 등변 삼각형과 같은 일부 반복 타일은 대칭이고 거울에 반사될 때 동일하게 유지됩니다.스핑크스와 같은 다른 것들은 비대칭이며 거울 반사에 의해 관련된 두 가지 다른 형태로 존재합니다.스핑크스와 다른 비대칭 반복 타일을 해부하려면 원래 모양과 거울 이미지를 모두 사용해야 합니다.

반복 타일 및 폴리폼

일부 반복 타일은 폴리아몬드 및 폴리오미노와 같은 폴리폼 또는 정삼각형과 사각형을 가장자리에서 가장자리로 배치하여 만든 모양을 기반으로 합니다.

사각형

폴리오미노가 수정 가능한 경우, 즉 직사각형에 타일을 붙일 수 있는 경우, 직사각형은 변 길이 비율이 정수이므로 정사각형에 타일을 붙이기 때문에 반복 타일이 됩니다.이것은 여덟 개의 정사각형으로 만들어진 팔색조에서 볼 수 있습니다.일부 문어체의 복사본 두 개는 정사각형 타일을 붙이기 때문에 이러한 문어체도 rep-16 반복 타일입니다.

수정 가능한 옥토미노를 기반으로 한 반복 타일

일부 노노미노 및 노나킹의 4개 복사본은 정사각형 타일링이므로 이러한 폴리폼도 rep-36 반복 타일링입니다.

수정 가능한 노노미노 및 9-폴리킹(노노킹)에서 생성된 리프타일

정삼각형

마찬가지로, 폴리아몬드가 정삼각형에 타일을 붙이면, 그것은 또한 반복 타일이 될 것입니다.

등변 삼각형에서 작성된 반복실험 타일


세 개의 정삼각형을 기반으로 한 물고기 모양의 반복실험
도데시아몬드 또는 12개의 정삼각형이 모서리와 모서리를 맞대고 배치된(그리고 모서리와 모서리를 맞대고 배치된) 로켓과 같은 리필일.

직각삼각형

직각삼각형은 90°의 직각을 하나 포함하는 삼각형입니다.오른쪽 삼각형의 두 가지 특정 형태, 즉 45°-90°-45° 삼각형과 30°-60°-90° 삼각형이 반복 타일 연구자들의 관심을 끌었습니다.

45°-90°-45° 삼각형

이등변 직각삼각형에 기초한 다면체는 변의 비율이 1:1:√2인 다면체를 폴리아볼로(polyabolos)라고 합니다.그들 중 무한한 수가 반복 타일입니다.실제로, 모든 반복 타일 중 가장 단순한 것은 이등변 직각 삼각형 하나입니다.빗변에 대한 직각을 이등분하는 단일 선으로 나누면 rep-2입니다.Rep-2 반복 타일도 rep-2이며n, rep-4,8,16+ 삼각형은 추가 반복 타일을 생성합니다.이것들은 하위 복사본의 절반을 버리고 나머지를 직각 삼각형 내에서 대칭이 될 때까지 순열함으로써 발견됩니다.즉, 두 개의 복사본이 직각 삼각형에 타일을 붙입니다.이 새로운 반복 타일 중 하나는 세 개의 정삼각형으로 형성된 물고기를 연상시킵니다.

오른쪽 삼각형을 기준으로 다시 타일 표시
4개의 이등변 직각 삼각형을 기준으로 한 물고기 모양의 반복실험 파일

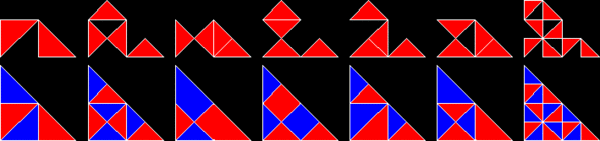
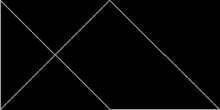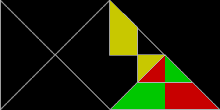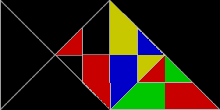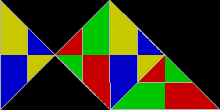
30°-60°-90° 삼각형

30°-60°-90° 직각 삼각형을 기반으로 한 다각형은 변의 비율이 1:θ3:2인 다각형이라고 합니다.어떤 것들은 폴리미노와 폴리 다이아몬드와 동일하고, 다른 것들은 별개입니다.[4]

세 개의 30-60-90° 삼각형으로 만들어진 삼각형 또는 모양입니다.
파충류로서의 삼류 서까래.
네 개의 30-60-90° 삼각형으로 만든 사행기 또는 모양입니다.
파충류로서의 네발동물.
육각형 서까래 또는 30-60-90° 삼각형 여섯 개로 만든 모양입니다.
파충류로서의 육각형 서까래.

다중 및 변형 리필링

대부분의 일반적인 반복실험은 n의 모든 양의 정수 값에 대해2 rep-n입니다.특히 이것은 세 개의 정삼각형으로 형성된 것, 세 개의 축 평행 육각형(L-트로미노, L-테트로미노, P-펜토미노) 및 스핑크스 헥사몬드를 [5]포함한 세 개의 사다리꼴에 대해 사실입니다.또한 특히 rep-n이 높은 많은 반복 타일은 다양한 방법으로 자체 타일링할 수 있습니다.예를 들어, rep-9 L-테트라미노는 적어도 14개의 서로 다른 리필링을 가지고 있습니다.rep-9 스핑크스 헥시아몬드는 다른 방식으로 타일을 붙일 수도 있습니다.

rep-9 L-테트로미노의 다양한 리필링
rep-9 스핑크스 헥사몬드의 변형 리필링

면이 무한대인 반복 타일

뿔 달린 삼각형 또는 삼각형

가장 친숙한 반복실험 타일은 변의 수가 유한한 다각형이지만, 변의 수가 무한한 일부 도형도 반복실험 타일일 수 있습니다.예를 들어, 삼각형 또는 뿔 달린 삼각형은 rep-4입니다.프랙탈 반복 타일의 예이기도 합니다.

오각형 반타일

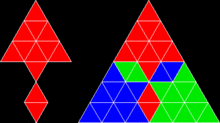
삼각형 및 사각형(사면체) 반복 타일은 일반적이지만 오각형 반복 타일은 거의 없습니다.오랫동안, 스핑크스가 알려진 유일한 예라고 널리 믿어져 왔지만, 독일/뉴질랜드 수학자 칼 셰어와 미국 수학자 조지 시허먼은 이중 피라미드와 긴 스핑크스 버전을 포함한 더 많은 예를 발견했습니다.이 오각형 반복 타일은 미국 수학자 에리히 프리드먼이 [6]감독하는 수학 마법 페이지에 설명되어 있습니다.그러나 스핑크스와 확장 버전은 동일한 복사본으로 다시 타일링할 수 있는 유일한 알려진 오각형입니다.클라크의 파충류 페이지를 참조하십시오.

칼 셰어가 발견한 오각형의 재파일

반복 타일 및 프랙탈

타일을 프랙탈로 반복

반복 타일을 사용하여 프랙탈 또는 더 작은 스케일에서 자체 유사한 모양을 만들 수 있습니다.반복 타일 프랙탈은 반복 타일을 세분화하고, 세분화된 모양의 복사본을 하나 이상 제거한 다음 재귀적으로 계속함으로써 형성됩니다.예를 들어, 시에르핀스키 카펫은 정사각형의 재 타일링에서 27개의 더 작은 정사각형으로, 시에르핀스키 삼각형은 정삼각형의 재 타일링에서 네 개의 더 작은 삼각형으로 형성됩니다.하나의 하위 복사본이 폐기되면 rep-4 L-트리오미노를 사용하여 네 개의 프랙탈을 만들 수 있으며, 그 중 두 개는 방향을 제외하고 동일합니다.

L-트리오미노의 기하학적 해부(rep-4)
L-트리오미노를 기반으로 한 프랙탈(rep-4)
L-트리오미노를 기반으로 한 또 다른 프랙탈
L-트리오미노를 기반으로 한 또 다른 프랙탈

반복 타일로서의 프랙탈

프랙탈은 종종 더 작은 스케일에서 자체적으로 유사하기 때문에 많은 프랙탈은 재파일처럼 자신의 복사본으로 분해될 수 있습니다.그러나 프랙탈의 내부가 비어 있으면 이 분해로 인해 전체 평면이 타일링되지 않을 수 있습니다.예를 들어, 시에르핀스키 삼각형은 3개의 복사본으로 타일링되어 있고, 시에르핀스키 카펫은 8개의 복사본으로 타일링되어 있지만, 이러한 분해의 반복은 타일링을 형성하지 않습니다.반면에, 용 곡선은 비어 있지 않은 내부를 가진 공간을 채우는 곡선입니다; 그것은 rep-4이고 타일링을 형성합니다.마찬가지로, 고스퍼 섬은 공간을 채우는 고스퍼 곡선에서 형성된 rep-7이고 다시 타일링을 형성합니다.

구성에 의해, 동일한 비율의 n개의 수축 맵의 반복 함수 시스템에 의해 정의된 프랙탈은 rep-n입니다.

시에르핀스키 삼각형의 세 개의 작은 복사본을 기반으로 한 시에르핀스키 삼각형
시어핀스키 카펫의 8개의 작은 복사본을 기반으로 한 시어핀스키 카펫
용 곡선의 4개의 작은 복사본을 기반으로 한 용 곡선

무한 타일링

일반 다각형 중에서 삼각형과 정사각형만 더 작은 크기의 동일한 크기의 복사본으로 해부할 수 있습니다.그러나, 정육각형은 6개의 정삼각형으로 해부될 수 있고, 각 정삼각형은 정육각형과 세 개의 정삼각형으로 해부될 수 있습니다.이것은 육각형과 육각형의 무한 타일링의 기초입니다.따라서 육각형은 불연속적이거나 불연속적입니다.


  • Regular hexagon tiled with infinite copies of itself

    무한한 자체 복사본으로 타일링된 일반 육각형

  • Fractal elongated Koch snowflake (Siamese) tiled with infinite copies of itself[7]

    자신의[7] 무한한 복제품으로 타일을 붙인 프랙탈 길쭉한 코흐 눈송이(시암)

참고 항목

메모들

  1. ^ 가드너의 12가지—Martin의 과학적인 미국 커버 스토리
  2. ^ Salows(2012).
  3. ^ 가드너(2001).
  4. ^ 폴리드래프터 역침형
  5. ^ 니시치 (2003).
  6. ^ 수학 마술, 이달의 문제 (2002년 10월)
  7. ^ Pietrocola, Giorgio (2005). "Tartapelago. Arte tassellazione". Maecla.

레퍼런스

  • Gardner, M. (2001), "Rep-Tiles", The Colossal Book of Mathematics: Classic Puzzles, Paradoxes, and Problems, New York: W. W. Norton, pp. 46–58
  • Gardner, M. (1991), "Chapter 19: Rep-Tiles, Replicating Figures on the Plane", The Unexpected Hanging and Other Mathematical Diversions, Chicago, IL: Chicago University Press, pp. 222–233
  • Langford, C. D. (1940), "Uses of a Geometric Puzzle", The Mathematical Gazette, 24 (260): 209–211, doi:10.2307/3605717
  • Niţică, Viorel (2003), "Rep-tiles revisited", MASS selecta, Providence, RI: American Mathematical Society, pp. 205–217, MR 2027179
  • Sallows, Lee (2012), "On self-tiling tile sets", Mathematics Magazine, 85 (5): 323–333, doi:10.4169/math.mag.85.5.323, MR 3007213
  • Scherer, Karl (1987), A Puzzling Journey to the Reptiles and Related Animals
  • Wells, D. (1991), The Penguin Dictionary of Curious and Interesting Geometry, London: Penguin, pp. 213–214

외부 링크

리프타일

Wikimedia Commons에는 Rep-tiles와 관련된 미디어가 있습니다.

이리프타일