그래픽 모델

시리즈의 일부
기계 학습 및 데이터 마이닝
문제 분류 클러스터링 회귀 이상 검출 데이터 클리닝 자동 ML 어소시에이션 규칙 강화 학습 구조화된 예측 기능 엔지니어링 기능 학습 온라인 학습 준지도 학습 비지도 학습 순위 매기기 학습 문법 유도
지도 학습 (분류 • 회귀) 의사결정 트리 앙상블 배깅 부스팅 랜덤 포레스트 k-NN 선형 회귀 네이비 베이즈 인공신경망 로지스틱 회귀 분석 퍼셉트론 관련 벡터 머신(RVM) 서포트 벡터 머신(SVM)
클러스터링 버치 치유하다 계층적 k자형 기대 최대화(EM) DBSCAN 광학 평균 이동
치수 축소 인자 분석 CCA ICA LDA NMF PCA PGD t-SNE
구조화된 예측 그래픽 모델 베이즈 네트 조건부 랜덤 필드 히든 마르코프
이상 검출 k-NN 국소 특이치 계수
인공신경망 자동 인코더 인지 컴퓨팅 딥 러닝 딥 드림 다층 퍼셉트론 RNN LSTM GRU ESN 저장고 계산 제한 볼츠만 기계 GAN somerset. 컨볼루션 뉴럴 네트워크 유넷 트랜스포머 비전. 스파이킹 뉴럴 네트워크 메모리 트랜지스터 전기화학 RAM(ECRAM)
강화 학습 Q-러닝 사사 시간차(TD) 멀티 에이전트 셀프 플레이
인간과의 학습 액티브 러닝 크라우드 소싱 휴먼 인 더 루프
모델 진단 학습 곡선
이론. 커널 머신 바이어스-분산 트레이드오프 컴퓨터 학습 이론 경험적 리스크 최소화 오컴 러닝 PAC 학습 통계학 학습 VC 이론
기계학습장 NeurolIPS ICML ML JMLR ArXiv:cs.LG
관련 기사 인공지능 용어집 기계 학습 연구를 위한 데이터 세트 목록 기계학습의 개요
v t

이 문서에는 일반적인 참조 목록이 포함되어 있지만 대응하는 충분한 인라인 인용이 없습니다. 좀 더 정밀한 인용문을 도입하여 이 글의 개선에 도움을 주시기 바랍니다.(2017년 5월) (이 템플릿메시지 삭제 방법 및 삭제 시기 확인)

그래픽 모델, 확률론적 그래픽 모델(PGM) 또는 구조화된 확률론적 모델은 그래프가 랜덤 변수 간의 조건부 의존 구조를 나타내는 확률론적 모델이다.확률론, 통계학, 특히 베이지안 통계학 및 기계 학습에서 일반적으로 사용됩니다.

그래픽 모델의 종류

일반적으로 확률론적 그래픽 모델은 다차원 공간에 걸친 분포를 부호화하기 위한 기초로서 그래프 기반 표현을 사용하고 특정 분포에 유지되는 일련의 독립성을 압축 또는 인수분해한 표현인 그래프를 사용한다.분포의 두 가지 그래픽 표현, 즉 베이지안 네트워크와 마르코프 랜덤 필드가 일반적으로 사용됩니다.두 패밀리는 인수분해와 독립성의 속성을 포함하지만 부호화할 수 있는 독립성 집합과 유도하는 분포의 인수분해에서 서로 다릅니다.^[1]

무방향 그래픽 모델

표시된 무방향 그래프에는 몇 가지 해석 중 하나가 있을 수 있습니다.일반적인 특징은 에지의 존재는 대응하는 랜덤 변수 간에 일종의 의존성을 의미한다는 것입니다.이 그래프에서$$A를$$ $알게$ $되면{\displaystyle }$ B${\displaystyle ,}$ ${\displaystyle C,}$ $(\$$displaystyle$B,$C, D)$는 모두 상호 독립적이라는 $것$을 알 수 있습니다.또는 (이 경우 동등하게)

${\displaystyle P[A,B,C,D]=f_{AB}[A,B]\cdot f_{AC}[A,C]\cdot f_{AD}[A,D]}$

일부 음이 아닌 함수 ${\displaystyle f_{}}$ ${\displaystyle A_{}}$ B${\displaystyle {}_{}}$ ${\displaystyle f_{}}$ ${\displaystyle A_{}}$ C${\displaystyle {}_{}}$ ${\displaystyle f_{}}$ ${\displaystyle A_{}}$ D$${\$displaystyle f_{AB}, f_{AC}, f_{$$AD$

베이지안 네트워크

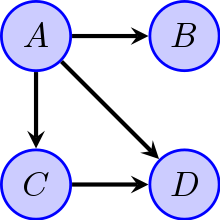
모델의 네트워크 구조가 유도 비순환 그래프인 경우, 모델은 모든 랜덤 변수의 결합 확률의 인수분해를 나타냅니다.보다 정확하게는 이벤트가 ${\displaystyle {X1\mathrm{}}_{}\dots ,}$ $(\$인 경우 결합 확률은 다음을 만족합니다.

$({displaystyle P[X_{1},\ldots,X_{n}=\prod _{i=1}^{n}P[X_{i}{text{pa}}(X_{i})]})$

${\displaystyle \text{여기}}$서${\displaystyle }$pa ( ${\displaystyle {Xi}_{}}$ ${\displaystyle${pa$}(X_{i})$$$는 $노드{\displaystyle {}_{}}$ $($를 $(\$ $X_$${i$})$$의 부모 세트입니다.즉, 조건부 분포의 곱에 대한 공동 분포 요인입니다.예를 들어, 그림에 표시된 방향 비순환 그래프에서 이 인수분해는 다음과 같습니다.

${\displaystyle P}$[ ${\displaystyle A}$,${\displaystyle B}$ ,${\displaystyle C}$ , ${\displaystyle D}$] ${\displaystyle =P}$ [ ${\displaystyle A}$]${\displaystyle 、}$ ${\displaystyle P}$[ B A${\displaystyle ]}$ 、${\displaystyle P}$ [ C ${\displaystyle A}$] 、 P [ D A${\displaystyle }$, $C$] $、$ \ $display style$P [$A$ ] $= P$ [ $A ]\ CD P$ [ $A ]$

부모 값을 지정하면 2개의 노드는 조건부로 독립적입니다.일반적으로 d-separation이라고 하는 기준이 그래프에 포함되는 경우 세 번째 세트가 주어지면 두 개의 노드 세트는 조건적으로 독립적입니다.베이지안 네트워크에서는 로컬 독립성과 글로벌 독립성이 동등합니다.

이러한 유형의 그래픽 모델은 유도 그래픽 모델, 베이지안 네트워크 또는 믿음 네트워크로 알려져 있습니다.숨겨진 마르코프 모델, 신경 네트워크 및 가변 차수 마르코프 모델과 같은 새로운 모델과 같은 고전적인 기계 학습 모델은 베이지안 네트워크의 특별한 경우로 간주될 수 있다.

순환 지향 그래픽 모델

다음 그림은 주기가 있는 그래픽 모델을 보여 줍니다.이것은 각 변수의 관점에서 상위 변수의 값에 따라 어떤 식으로든 해석될 수 있습니다.표시된 특정 그래프는 다음과 같은 인자를 갖는 결합 확률 밀도를 나타냅니다.

${\displaystyle P}$[ ${\displaystyle A}$,${\displaystyle B}$ ,${\displaystyle C}$ , ${\displaystyle D}$] ${\displaystyle =P}$ [ ${\displaystyle A}$]${\displaystyle p}$P [ ${\displaystyle B}$]${\displaystyle }$p P${\displaystyle }$[ ${\displaystyle C}$, $D$ , $B ]$ ${\displaystyle \mathrm{display}}$ [ $display style$P [ $A$、 B , D ] $= P$ [ A$$] \ $cdot$P [ $B$] \ $CDOT$P [$B$$]$

다른 해석도 가능합니다.^[2]

기타 타입

• 단일 루트를 가진 트리를 사용하는 Naigive Bayes 분류자
• 어디 순환이 허용된다 의존성 네트워크이다.
• Tree-augmented 선형 분급기 또는 TAN 모델이다.
• A인자 그래프는 지도자 없는 양분 그래프 변수와 요인들을 연결한다.각 요소가 연결될 변수에 대한 함수., 시행하도록 믿음을 전파를 이해하기 위한 이것은 도움이 되는 표현입니다.
• 파벌이 한 패거리 나무나 접합 나무는 나무, 그 교차로 트리 알고리즘에서 사용했다.
• 며 지도자 없는 가장자리 연출할 수 있는 체인 그래프 그래프는, 어떠한 직접적인 주기 없이(만약 우리가 화살 통과 한다면 어느 꼭짓점에 서든며 그래프는 어떤 화살의 방향을 존중하는 것을 함께 실행하기 시작하 i.e., 우리가부터 시작된 꼭지점에 돌아오지 못하).둘 다와 체인을 그래프의 이것은 통합하고 일반화하고 마르코프 네트워크 베이즈의 방법을 제공할 수 있무방향 그래프다 특별한 케이스, 비순환 그래프라고 지시했다.[3]
• 조상 그래프는 방향성, 양방향성 및 무방향성을 ^[4]가진 추가 확장입니다.
• 랜덤 필드 기술
  • 마르코프 랜덤 필드는 마르코프 네트워크라고도 하며 무방향 그래프 상의 모델입니다.반복된 서브유닛이 많은 그래픽 모델은 플레이트 표기법으로 나타낼 수 있습니다.
  • 조건부 랜덤 필드는 무방향 그래프에 대해 지정된 차별 모델입니다.
• 제한 볼츠만 기계는 무방향 그래프에 대해 지정된 초당 생성 모델이다.

적용들

복잡한 분포에서 구조를 발견 및 분석하여 간결하게 기술하고 구조화되지 않은 정보를 추출하는 알고리즘을 제공하는 모델의 프레임워크는 모델을 효과적으로 ^[1]구성하고 활용할 수 있도록 한다.그래픽 모델의 적용에는 인과 추론, 정보 추출, 음성 인식, 컴퓨터 비전, 저밀도 패리티 체크 코드의 디코딩, 유전자 조절 네트워크의 모델링, 질병의 유전자 발견과 진단 및 단백질 구조를 위한 그래픽 모델이 포함된다.

「 」를 참조해 주세요.

• 믿음의 전파
• 구조 방정식 모형

메모들

추가 정보

서적 및 서적

• Barber, David (2012). Bayesian Reasoning and Machine Learning. Cambridge University Press. ISBN 978-0-521-51814-7.

• Bishop, Christopher M. (2006). "Chapter 8. Graphical Models" (PDF). Pattern Recognition and Machine Learning. Springer. pp. 359–422. ISBN 978-0-387-31073-2. MR 2247587.
• Cowell, Robert G.; Dawid, A. Philip; Lauritzen, Steffen L.; Spiegelhalter, David J. (1999). Probabilistic networks and expert systems. Berlin: Springer. ISBN 978-0-387-98767-5. MR 1697175. 보다 고도의 통계적 지향의 책
• Jensen, Finn (1996). An introduction to Bayesian networks. Berlin: Springer. ISBN 978-0-387-91502-9.
• Pearl, Judea (1988). Probabilistic Reasoning in Intelligent Systems (2nd revised ed.). San Mateo, CA: Morgan Kaufmann. ISBN 978-1-55860-479-7. MR 0965765. 그래프와 확률 사이의 관계가 공식적으로 소개된 계산 추론 접근법.

저널 기사

• Edoardo M. Airoldi (2007). "Getting Started in Probabilistic Graphical Models". PLOS Computational Biology. 3 (12): e252. arXiv:0706.2040. Bibcode:2007PLSCB...3..252A. doi:10.1371/journal.pcbi.0030252. PMC 2134967. PMID 18069887.
• Jordan, M. I. (2004). "Graphical Models". Statistical Science. 19: 140–155. doi:10.1214/088342304000000026.
• Ghahramani, Zoubin (May 2015). "Probabilistic machine learning and artificial intelligence". Nature. 521 (7553): 452–459. Bibcode:2015Natur.521..452G. doi:10.1038/nature14541. PMID 26017444. S2CID 216356.

다른.

• Heckerman's Bayes 넷 러닝 튜토리얼
• 그래픽 모델과 베이지안 네트워크의 개요
• 확률론적 그래픽 모델에 관한 Sargur Srihari의 강의 슬라이드

외부 링크

• 그래픽 모델 및 조건부 랜덤 필드
• CMU에서 Eric Xing이 학습한 확률론적 그래픽 모델