인자 분석

요인 분석은 관측된 상관 변수 간의 변동성을 요인이라고 하는 관측되지 않은 변수의 수가 적을 수 있다는 관점에서 설명하는 데 사용되는 통계 방법입니다.예를 들어, 관측된 6개의 변수의 변동은 주로 관측되지 않은(기본적인) 두 변수의 변동을 반영할 수 있습니다.인자 분석은 관측되지 않은 잠재 변수에 대한 반응으로 이러한 접합 변동을 검색합니다.관측된 변수는 잠재적 요인과 "오차" 항의 선형 조합으로 모형화되므로 요인 분석은 변수 오차 ^[1]모형의 특수한 경우로 간주할 수 있습니다.

간단히 말해, 변수의 인자 적재는 변수가 주어진 ^[2]인자와 관련된 정도를 수량화합니다.

요인 분석 방법 뒤에 있는 공통 근거는 관측된 변수 간의 상호의존성에 대해 얻은 정보를 나중에 데이터 집합의 변수를 줄이는 데 사용할 수 있다는 것이다.인자 분석은 심리학, 성격 심리학, 생물학, 마케팅, 제품 관리, 운영 연구, 금융 및 기계 학습에서 일반적으로 사용됩니다.관측 변수가 많고 기초 변수/잠재 변수 수가 적을 경우 데이터 세트를 처리하는 데 도움이 될 수 있습니다.이것은 가장 일반적으로 사용되는 상호의존성 기법 중 하나이며, 관련 변수 집합이 체계적인 상호의존성을 나타낼 때 사용되며, 공통성을 만드는 잠재 요인을 찾는 것이 목적이다.

통계 모형

정의.

이 모델은 단위당 인자가 단위당 관측치( $<\displaystyle k>)$ 보다 $k$ 적은 k개의 공통 $요인$ ( $f_{i,j}$ $\$ 을 사용하여 각 $n개$ 의 \ $displaystyle$ n개인의 $n$ 관측치 $p$ $p$ 를 설명하려고 합니다.개인마다 공통인자k개(\ $displaystyle$ k $)$ 가 $k$ $있으며$ , 이는 단일 관측에 대해 인자 부하 행렬(\ $displaystyle$ $\in \mathbb {R}^{p\times$ k}) $L\in \mathbb {R} ^{p\times k}$ 을 통해 관측과 관련된다.

\displaystyle x_{i,m}-\mu _{i,1}f_{1,m}+\display +l_{i,k}f_{k,m}+\varepsilon _{i,m}

그래서

$x_{i,m}$ i $x_{i,m}$ {\ $displaystyle$ $x_{i,m$ $}}$ 은 $x_{i,m}$ $i$ $m번째$ $i$ 의 $i번째$ 관찰값입니다.
$\mu _{i}$ i $\mu _{i}$ { $display$ style \ $mu$ _ { $\mu _{i}$ i } $\mu _{i}$ 、 idisplay 、 $display style$ i $obs$ 관측 평균입니다.
$l_{i,j}$ $($ 는 $l_{i,j}$ j $(displaystyle$ j $)$ 인자의 i $(displaystyle$ i $)$ 관측에 대한 부하입니다.
$f_{j,m}$ j $f_{j,m}$ {\ $displaystyle f_{j,m}$ 은 $f_{j,m}$ m{\ $displaystyle$ m $}$ $j$ 의j{ $displaystyle$ j $}$ 번째 $j$ 계수의 값입니다.
$\varepsilon _{i,m}$ , m \ $\varepsilon _{i,m}$ $displaystyle$ \ $varepsilon _$ { $i$ , $(i,m)$ $m$ $}$ 은 평균 0 및 유한 분산을 $(i,m)$ ( $(i,m)$ i $(i,m)$ , $m$ )번째 $(i,m)$ 비관측 확률 오차항입니다 $(i,m)$

행렬 표기법

X-\mathrm {M} = LF+\varepsilon

여기서 $X\in \mathbb {R} ^{p\times n}$ X $X\in \mathbb {R} ^{p\times n}$ R $X\in \mathbb {R} ^{p\times n}$ × n \ $displaystyle$ $X$ \ $in$ \ $mathbb$ { $L\in \mathbb {R} ^{p\times k}$ $R$ } $^$ { p \ $times$ n $X\in \mathbb {R} ^{p\times n}$ $로드행렬 L {\$ R × k \ $in$ $L\in \mathbb {R} ^{p\times k}$ \ $mathbb$ { $R }$ { p \ $times$ k $L\in \mathbb {R} ^{p\times k}$ $F\in \mathbb {R} ^{k\times n}$ F $F\in \mathbb {R} ^{k\times n}$ R $F\in \mathbb {R} ^{k\times n}$ × $F\in \mathbb {R} ^{k\times n}$ \ $displaystyle$ F \ $times$ { K $}$ $^$ { $K}$ $hbb {R}$ ^{ $p\times$ n $}$ 및 $\varepsilon \in \mathbb {R} ^{p\times n}$ $\mathrm {M} \in \mathbb {R} ^{p\times n}$ M $\mathrm {M} _{i,m}=\mu _{i}$ $\mathrm {M} \in \mathbb {R} ^{p\times n}$ $×$ n \ $in \mathbb {R}$ \in \ $mathbb$ {R $} ^{p$ $\times$ n}. 여기서 $(i,m)$ ( $(i,m)$ m $)$ { $display$ style ( $i$ $,$ $m)}$ $번째$ 요소는 단순 $\mathrm {M} _{i,m}=\mu _{i}$ $\mathrm {M} _{i,m}=\mu _{i}$ $=$ $,$ $mu} _mu,$

또한F {\ $displaystyle$ F $F$ 에 대해 다음과 같은 전제조건을 부과합니다.

$\varepsilon$ {\ $displaystyle$ F $}$ 및 $F$ ${\$ {\ $displaystyle \varepsilon}$ 은 $\varepsilon$ (는 $)$ 독립적입니다.
$\mathrm {E} (F)=0$ ( $\mathrm {E} (F)=0$ ) $=$ {\ $style \mathrm {E}$ (F)= $0$ ; $\mathrm {E}$ 서 E $(\$ 는 $\mathrm {E}$ 예상값입니다.
$\mathrm {Cov} (F)=I$ $\mathrm {Cov}$ 서 I $}$ 은 $\mathrm {Cov} (F)=I$ C $\mathrm {Cov}$ v $\displaystyle \mathrm$ { $Cov$ 인자가 상관관계가 $I$ 을 확인하기 위한 공분산 행렬이며, I $\displaystyle$ I는 $I$ 항등 행렬입니다.

$\mathrm {Cov} (X-\mathrm {M} )=\Sigma$ $\mathrm {Cov} (X-\mathrm {M} )=\Sigma$ v ( $\mathrm {Cov} (X-\mathrm {M} )=\Sigma$ - $\mathrm {Cov} (X-\mathrm {M} )=\Sigma$ ) $\mathrm {Cov} (X-\mathrm {M} )=\Sigma$ \ $displaystyle$ \ $mathrm$ { $Cov$ } ( X - \ $mathrm$ { $M$ } ) = \ $Sigma }$ 。

\displaystyle \Sigma =\mathrm {Cov}(X-\mathrm {M})=\mathrm {Cov}(LF+\varepsilon ),}

따라서 위의 F $(\displaystyle$ F $)$ 에 $F$ 부과된 조건에 따라

(\displaystyle \Sigma = L\mathrm {Cov} (F)L^{T}+\mathrm {Cov}(\varepsilon ),}

또는 $\Psi :=\mathrm {Cov} (\varepsilon )$ : $\Psi :=\mathrm {Cov} (\varepsilon )$ $\Psi :=\mathrm {Cov} (\varepsilon )$ $\Psi :=\mathrm {Cov} (\varepsilon )$ v ( $\Psi :=\mathrm {Cov} (\varepsilon )$ $){$ $displaystyle \Psi$ : = \ $mathrm {Cov}(\varepsilon )$ 를 설정합니다 $\Psi :=\mathrm {Cov} (\varepsilon )$

(\displaystyle \Sigma = LLL^{T}+\Psi ., )

직교 $행렬$ Q $(\displaystyle$ Q $Q$ 에 대해 L $=$ $L^{\prime }=\ LQ$ Q $(\displaystyle$ L $^{\prime$ }=\ $LQ}$ 및 $L^{\prime }=\ LQ$ $F^{\prime }=Q^{T}F$ $=$ $F^{\prime }=Q^{T}F$ $F^{\prime }=Q^{T}F$ F $(\displaystyle$ F $^{\prime$ }= $Q^{T}F$ 를 $L^{\prime }=\ LQ$ 하면 인자 및 부하 유지에 대한 기준이 됩니다.따라서 일련의 요인 및 인자 적재는 직교 변환까지만 고유합니다.

예

심리학자가 "언어 지능"과 "수학 지능"이라는 두 가지 종류의 지능이 있지만, 둘 다 직접적으로 관찰되지 않는다고 가정해 보자.그 가설에 대한 증거는 1000명의 학생들로 구성된 10개의 다른 학문 분야의 시험 점수에서 구한다.각 학생이 많은 모집단에서 랜덤으로 선택되면 각 학생의 10점 만점은 랜덤 변수가 됩니다.심리학자의 가설은 10개의 학문 분야 각각에 대해 언어 지능과 수학적 지능에 대한 몇 가지 공통된 가치 쌍을 공유하는 모든 학생들의 그룹에 대한 평균 점수는 어떤 일정한 수준의 언어 지능과 또 다른 일정한 수준의 수학 지능을 곱한 것이라고 말할 수 있다.이 두 개의 "직선"의 선형 조합입니다.두 종류의 지능을 곱하여 예상 점수를 얻는 특정 피험자의 숫자는 모든 지능 수준 쌍에 대해 동일하다는 가설에 의해 배치되며, 이 ^{[clarification needed]}피험자에 대해 "인자 부하"라고 불립니다.예를 들어, 그 가설은 천문학 분야에서 예측된 평균 학생의 적성은 다음과 같다고 주장할 수 있다.

{10 × 학생의 언어 지능} + {6 × 학생의 수학적 지능}

숫자 10과 6은 천문학과 관련된 인자 적재입니다.다른 학문적 과목에 따라 인자 적재가 다를 수 있습니다.

언어 지능과 수학적 지능의 수준이 같다고 가정한 두 학생은 천문학에서 측정된 적성이 다를 수 있습니다. 왜냐하면 개별 적성은 평균 적성과 다르며(위에서 예측한) 측정 오류 그 자체 때문입니다.이러한 차이는 집합적으로 "오류"라고 불리는 것을 구성한다.이 통계 용어는 측정 시 개인이 지능 수준에 따라 평균이 다르거나 예측되는 양을 의미한다(통계학에서 오류 및 잔차 참조).

요인 분석에 들어가는 관측 가능한 데이터는 1000명의 학생 각각에 대해 10점씩 총 10,000개의 숫자가 됩니다.각 학생의 두 가지 지능의 요인 적재 및 수준은 데이터에서 추론해야 합니다.

동일한 예제의 수학적 모형

다음에서 행렬은 색인화된 변수로 표시됩니다."Subject" 인덱스는 $문자$ a $\displaystyle$ a $\,$ $c$ \ $displaystyle$ b $\$ 및 c $\displaystyle$ c $c$ displaystyle p $\,$ 즉 위의 예에서 10 $\displaystyle$ 10 $\$ 에 $1$ $p$ $10$ 해당하는 $값$ 을 사용하여 $표시$ 됩니다."Factor" 인덱스는 문자 $\displaystyle$ $p$ $p$ q\ $displaystyle$ q $r$ r $\displaystyle$ r을 사용하여 표시됩니다.위의 예에서는 값이 $1$ $(\displaystyle$ 1 $1$ $)$ ~ $k$ $displaystyle$ 2)입니다 $k$ $2$ ."인스턴스" 또는 "샘플 $"$ 인덱스는 문자 $i$ (\ $displaystyle$ i $i$ $(\$ $displaystyle$ j $),$ k $(\$ $displaystyle$ k $N$ 를 $j$ $1$ 사용하여 $1$ 됩니다 $.$ 위의 예에서는 N $N=1000$ $(\displaystyle$ N $=1000)$ 의 $N=1000$ $N=1000$ 이 p에 $p=10$ 한 경우 $=$ $10회$ ( $displaystyle$ $p=$ 10 $p=10$ ) $시험$ $,$ $1회($ $style$ a $a$ )시험 점수는 $i$ $x$ $($ ai})로 매겨집니다 $p=10$ 인자 분석의 목적은 변수 $x_{a}$ a $x_{ai}$ (x a _ display $style$ x _ { $a$ $x_{a}$ } )의 $x_{a}$ 상관관계를 파악하는 것입니다.x a $x_{ai}$ x $x_{ai}$ (x a _ $display$ style $x$ _ { a $x_{ai}$ } )는 $x_{ai}$ 특정 인스턴스 또는 관측치 집합입니다.변수가 동일한 위치에 있도록 표준 $점수$ z $displaystyle$ z로 정규화됩니다.

({displaystyle z_{ai}=black {x_{ai}-\mu _{a}}{\displaystyle _{a}}})

여기서 표본 평균은 다음과 같습니다.

\mu _{a}=tfrac {1}{N}}\sum _{i}x_{ai

표본 분산은 다음과 같습니다.

_{a}^{2}=tfrac {1}{N-1}\sum _{i}(x_{ai}-\mu _{a}^2

이 특정 표본에 대한 인자 분석 모형은 다음과 같습니다.

{\displaystyle {dots}z_{1,i}&={1,1}F_{1,i}&\ell_{2,i}F_{2,i}&+&\varepsilon_{1,i}\vdots&\vdots&\dots,\dots}F_{2,i}F_{2,i}F_{2,i}&+\varepsilon}&\dots,

또는 보다 간결하게:

z_{ai}=\sum _{p}\ell _{ap}F_{pi}+\varepsilon _{ai

어디에

$($ F_ ${1i})$ 는 $F_{1i}$ I $(디스플레이 스타일$ i $)$ 의 $i$ "언어 지능"입니다.
$F_{2i}$ $($ F_ ${2i})$ 는 $F_{2i}$ I $(디스플레이 스타일$ I $)$ 의 $i$ "수학 지능"입니다.
$p(\displaystyle$ \ $ell _{$ ap $\ell _{ap}$ })는 p $p=1,2$ = $p=1,2$ , $2$ (\ $displaystyle p=1$ 2)의 $p=1,2$ p $(\displaystyle$ a $a$ $)$ 번째 피험자에 $대한$ 인자 로딩입니다.

행렬 표기법에서, 우리는

Z=LF+\varepsilon

F $(\displaystyle$ F $F$ 의 각 열에 있는 첫 번째 구성요소인 "언어 인텔리전스"를 측정하는 척도를 두 배로 늘리고 동시에 언어 인텔리전스에 대한 요소 로딩을 절반으로 줄임으로써 모델에 차이가 없음을 관찰하십시오.따라서 언어 지능에 대한 요인의 표준 편차를 1 $displaystyle$ 1)로 가정하면 일반성이 손실되지 않습니다. 수리 지능에 대해서도 마찬가지입니다.또한, 유사한 이유로 두 요인이 서로 상관관계가 없다고 가정하여 일반성을 잃지 않는다.즉, 다음과 같습니다.

\displaystyle \sum _{i}F_{pi}F_{qi}=\delta_{pq}

여기서 $\delta _{pq}$ $\delta _{pq}$ q \ $displaystyle _$ { $pq$ $}$ $p=q$ 는 $\delta _{pq}$ $0$ $p\neq q$ Kronecker 델타( $p$ $q$ 일 $p\neq q$ 0 \ $displaystyle$ 0 ), $p$ $p=q$ $q$ 일 경우1 \ $displaystyle$ p $=q$ 일 $1$ 경우 1)입니다.오차는 인자와 무관하다고 가정합니다.

\displaystyle \sum _{i}F_{pi}\varepsilon _{ai}=0}

용액의 회전도 해결책이기 때문에 요인을 해석하기가 어렵습니다.아래 단점을 참조하십시오.이 예에서 두 가지 유형의 지능이 상관관계가 없다는 것을 사전에 알지 못하면 두 가지 요소를 두 가지 유형의 지능으로 해석할 수 없습니다.비록 그들이 상관관계가 없다고 해도, 우리는 어떤 요소가 언어 지능에 해당하고 어떤 요소가 수학 지능에 해당하는지 외부의 주장 없이 구별할 수 없다.

관측된 $데이터$ X $(\$ $displaystyle$ X $)$ 및 $X$ $F$ (\ $displaystyle$ F $)$ 에 기초하여 $부하$ L(\ $displaystyle$ L $L$ $\mu$ $\varepsilon$ (\ $displaystyle \mu$ 및 "오류" $\varepsilon$ {\(\ $displaystyle \varepsilon)$ 의 $\varepsilon$ 분산 값을 추정해야 합니다(요인자의 수준에 대한 가정은 $F$ 에 대해 고정됨). $(\displaystyle$ F}) $F$ "기본 정리"는 위의 조건에서 도출할 수 있다.

\displaystyle \sum _{i}z_{bi}=\sum _{j}\ell _{aj}+\sum _{i}\varepsilon _{ai}\varepsilon _{bi}

왼쪽 항은 관측된 데이터의 ( $(a,b)$ $)$ \ $displaystyle$ ( $p\times N$ $,$ b) \displaystyle (a, b $)$ \displaystyle (a, b) \displaystyle (a, $p\times p$ ) \ $displaystyle p\$ $times$ p $\$ times p $)$ $p\times N$ 의 $(a,b)$ $p\times p$ $p\times N$ $p$ $(a,b)$ $p$ 다 $.$ $(디스플레이 스타일$ 1) $1$ 입니다 $1$ .오른쪽의 두 번째 항은 항이 통일성보다 작은 대각 행렬입니다.오른쪽의 첫 번째 항은 "감소 상관 행렬"이며 대각선 값이 통일보다 작다는 점을 제외하고 상관 행렬과 동일합니다.감소된 상관 행렬의 이러한 대각선 요소를 "공통성"이라고 합니다(이것은 인자에 의해 설명되는 관측 변수의 분산 비율을 나타냅니다).

h_{a}^{2}=1-\psi_{a}=\sum_{j}\ell_{aj}\ell_{aj

샘플 $z_{ai}$ $z_{ai}$ $z_{ai}$ i $z_{ai}$ {\ $displaystyle z_{ai$ }}는 $z_{ai}$ 샘플 오차, 모델의 부적합 등으로 인해 위에 제시된 기본 방정식을 따르지 않습니다.위 모델의 분석의 목적은 데이터에 "최적합"을 부여하는 $F_{pi}$ $($ F_ ${pi$ })와 $F_{pi}$ 적재 $\ell _{ap}$ p $($ 스타일 $\ell$ _ ${ap})$ 를 $\ell _{ap}$ 찾는 것입니다.인자 분석에서 최적 적합치는 상관 ^[3]행렬의 오프 대각 잔차에서 평균 제곱 오차의 최소값으로 정의됩니다.

\displaystyle \varepsilon ^{2}=\sum _{a\neq b}\left[\sum _{i}z_{bi}-\sum _{j}\ell _{a}\ell _{right}^2}}

이는 모형 방정식에서 기대값이 0인 오차 공분산의 엇대각 성분을 최소화하는 것과 같습니다.이는 모든 ^[3]잔차의 평균 제곱 오차를 최소화하려는 주성분 분석과 대조됩니다.고속 컴퓨터가 등장하기 전에는 특히 다른 수단을 통한 공동체성 추정에 있어 문제에 대한 대략적인 해결책을 찾는 데 상당한 노력을 기울였으며, 이는 알려진 감소된 상관 행렬을 산출함으로써 문제를 상당히 단순화시켰다.그런 다음 이를 사용하여 인자와 하중을 추정했다.고속컴퓨터의 등장으로 최소화 문제를 적절한 속도로 반복적으로 해결할 수 있게 되었고, 그 과정에서 미리 필요한 것이 아니라 커뮤니티를 계산하게 되었다.MinRes 알고리즘은 이 문제에 특히 적합하지만 해결책을 찾는 유일한 반복 수단이 아닙니다.

솔루션 요인의 상관 관계가 허용되는 경우(예: 'oblimin' 회전) 해당 수학적 모형은 직교 좌표 대신 스큐 좌표를 사용합니다.

기하학적 해석

3명의 응답자가 "a" 질문을 하기 위한 요인 분석 모수의 기하학적 해석."답변"은 단위

\mathbf {z} _{a}

z

\mathbf {z} _{a}

\

displaystyle \mathbf {z} _{a

로 표현되며

\mathbf {F} _{1}

, 두 개의 직교 정규

\mathbf {F} _{1}

(\

{F

}

\mathbf {F} _{2}

{

1})

\mathbf {F} _{2}

displaystyle \

mathbf {F} _{

2

\mathbf {F} _{2}

에 의해 정의된 평면에 투영됩니다.투영 벡터는

{\hat {\mathbf {z} }}_{a}

^

{\hat {\mathbf {z} }}_{a}

\

style {\mathbf {z}}

_{

a}

입니다

{\hat {\mathbf {z} }}_{a}

.

{\boldsymbol {\varepsilon }}_{a}

^

displaystyle

{\

boldsymbol {varepsilon }}

_{

a}

는

{\boldsymbol {\varepsilon }}_{a}

평면에 수직이므로

\mathbf {z} _{a}={\hat {\mathbf {z} }}_{a}+{\boldsymbol {\varepsilon }}_{a}

\mathbf {z} _{a}={\hat {\mathbf {z} }}_{a}+{\boldsymbol {\varepsilon }}_{a}

\mathbf {z} _{a}={\hat {\mathbf {z} }}_{a}+{\boldsymbol {\varepsilon }}_{a}

^

\mathbf {z} _{a}={\hat {\mathbf {z} }}_{a}+{\boldsymbol {\varepsilon }}_{a}

+

= displaystyle \mathbf {z} _

{

a}

{a}

는 평면에 수직입니다

.

a

{\hat {\mathbf {z} }}_{a}

벡터

{\hat {\mathbf {z} }}_{a}

^

a

{\displaystyle {\

mathbf

{z

}}_{

a

{\hat {\mathbf {z} }}_{a}

}는 인자 벡터의 관점에서 z

{\hat {\mathbf {z} }}_{a}=\ell _{a1}\mathbf {F} _{1}+\ell _{a2}\mathbf {F} _{2}

^

{\hat {\mathbf {z} }}_{a}=\ell _{a1}\mathbf {F} _{1}+\ell _{a2}\mathbf {F} _{2}

{\hat {\mathbf {z} }}_{a}=\ell _{a1}\mathbf {F} _{1}+\ell _{a2}\mathbf {F} _{2}

{\hat {\mathbf {z} }}_{a}=\ell _{a1}\mathbf {F} _{1}+\ell _{a2}\mathbf {F} _{2}

{\hat {\mathbf {z} }}_{a}=\ell _{a1}\mathbf {F} _{1}+\ell _{a2}\mathbf {F} _{2}

1 +

f

2 F

{\hat {\mathbf {z} }}_{a}=\ell _{a1}\mathbf {F} _{1}+\ell _{a2}\mathbf {F} _{2}

2

{\displaystyle

{\

mathbf {z}}}}_

{a} = \

ell

_1 F {

1}

로

{\hat {\mathbf {z} }}_{a}=\ell _{a1}\mathbf {F} _{1}+\ell _{a2}\mathbf {F} _{2}

수 있습니다

.

투영 벡터 길이의 제곱은

||{\hat {\mathbf {z} }}_{a}||^{2}=h_{a}^{2}

입니다

||{\hat {\mathbf {z} }}_{a}||^{2}=h_{a}^{2}

z ^

||{\hat {\mathbf {z} }}_{a}||^{2}=h_{a}^{2}

||{\hat {\mathbf {z} }}_{a}||^{2}=h_{a}^{2}

||{\hat {\mathbf {z} }}_{a}||^{2}=h_{a}^{2}

||{\hat {\mathbf {z} }}_{a}||^{2}=h_{a}^{2}

a

||{\hat {\mathbf {z} }}_{a}||^{2}=h_{a}^{2}

{ {

displaystyle

}

_

{

a } ^

{ 2 } ^ {

2

} =

||{\hat {\mathbf {z} }}_{a}||^{2}=h_{a}^{2}

h _ {

a

\mathbf {z} _{a}

}^ { 2

||{\hat {\mathbf {z} }}_{a}||^{2}=h_{a}^{2}

。다른 데이터

\mathbf {z} _{b}

z \

\mathbf {z} _{a}

\

mathbf { z }

_ { b } _ { b

\mathbf {z} _{b}

}

\mathbf {z} _{a}

, , , , , , \ mathsty \

mathstyloth

_

{ displaystyle \

mathb

。

bf {z} _{a}

\mathbf {z} _{b}

z

\mathbf {z} _{b}

{{

displaystyle \mathbf {z} _{b}}

는

\mathbf {z} _{b}

r_{ab}

r_{ab}

{

displaystyle r_{ab}}

: 상관 매트릭스의

(a,b)

b

)

{

displaystyle (a, b)}

- entry가

(a,b)

r_{ab}

.(Harman 그림 4.^[3]3에서 인용).

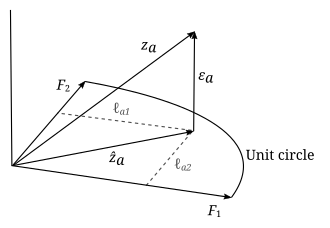
인자 분석의 모수 및 변수는 기하학적 해석을 제공할 수 있습니다. $\mathbf {z} _{a}$ ( $z_{ai}$ $z_{ai}$ {\ $displaystyle z_{$ $ai$ }), $z_{ai}$ $F_{pi}$ ( $F_{pi}$ $F_{pi}$ { $displaystyle F_{$ pi $F_{pi}$ 및 오류( $\varepsilon _{ai}$ {\ $displaystyle \$ $varepsilon$ _ ${ai$ $\mathbf {z} _{a}$ 는 N ${\$ N $}$ 유클리드 공간(샘플 공간)의 벡터로 볼 수 있습니다 $.$ $($ ${\boldsymbol {\varepsilon }}_{a}$ 스타일 $)_mathbf {F}$ $_$ ${j}$ 및 $($ 스타일 $)_{a}).$ 데이터가 표준화되었기 때문에 데이터 벡터는 단위 길이( $||\mathbf {z} _{a}||=1$ a $||\mathbf {z} _{a}||=1$ \ $displaystyle \mathbf {z} _{a} = 1$ ) $||\mathbf {z} _{a}||=1$ 입니다.인자 벡터는 이 공간에서 데이터 벡터가 직교로 투영되는 k $(\displaystyle$ k $)$ 차원 $k$ 선형 부분 공간(즉, 하이퍼 플레인)을 정의합니다.이것은 모형 방정식에서 나온 것이다.

\mathbf {z}_{a}=\sum _{j}\ell _{aj}\mathbf {F}_{j}+{\boldsymbol {varepsilon }}}_{a}}

요인 및 오류의 독립성: $\mathbf {F} _{j}\cdot {\boldsymbol {\varepsilon }}_{a}=0$ j $\mathbf {F} _{j}\cdot {\boldsymbol {\varepsilon }}_{a}=0$ $\mathbf {F} _{j}\cdot {\boldsymbol {\varepsilon }}_{a}=0$ $\mathbf {F} _{j}\cdot {\boldsymbol {\varepsilon }}_{a}=0$ \ $displaystyle$ \ $mathbf$ { $F$ } $_$ { $j$ } \ $cdot$ { bold $symbol$ \ $varepsilon$ } $} _$ { a $\mathbf {F} _{j}\cdot {\boldsymbol {\varepsilon }}_{a}=0$ = $0$ }위의 예에서 하이퍼플레인은 2개의 요인 벡터에 의해 정의된 2차원 평면일 뿐입니다.하이퍼플레인에 대한 데이터 벡터의 투영법은 다음과 같습니다.

{\hat {z}}_{a}=\sum _{j}\ell _{aj}\mathbf {F}_{j

오류는 투영된 지점에서 데이터 지점까지의 벡터이며 하이퍼플레인에 수직입니다.인자 분석의 목적은 데이터에 "최적"인 하이퍼플레인을 찾는 것입니다.따라서 하이퍼플레인을 정의하는 인자 벡터가 독립적이고 하이퍼플레인에 존재하는 한 이 하이퍼플레인을 정의하는 인자 벡터가 어떻게 선택되는지는 중요하지 않습니다.우리는 그것들을 일반성의 손실 없이 직교 및 정규( $\mathbf {F} _{j}\cdot \mathbf {F} _{q}=\delta _{pq}$ j $\mathbf {F} _{j}\cdot \mathbf {F} _{q}=\delta _{pq}$ $\mathbf {F} _{j}\cdot \mathbf {F} _{q}=\delta _{pq}$ q $\mathbf {F} _{j}\cdot \mathbf {F} _{q}=\delta _{pq}$ $\mathbf {F} _{j}\cdot \mathbf {F} _{q}=\delta _{pq}$ $\mathbf {F} _{j}\cdot \mathbf {F} _{q}=\delta _{pq}$ p $\mathbf {F} _{j}\cdot \mathbf {F} _{q}=\delta _{pq}$ \ $displaystyle \mathbf {F} _{j}\cdot \mathbf {F} _{q}$ \ $mathbf$ {F} )로 지정할 수 있다.적절한 인자가 발견되면 하이퍼플레인 내에서 임의로 회전하여 인자 벡터의 회전이 동일한 하이퍼플레인으로서 동시에 솔루션이 되도록 할 수도 있습니다.그 결과, 적합한 하이퍼플레인이 2차원인 위의 예에서 두 가지 유형의 지능이 상관관계가 없음을 사전에 알지 못하면 두 가지 요소를 두 가지 유형의 지능으로 해석할 수 없습니다.비록 상관관계가 없다고 해도, 우리는 어떤 요소가 언어 지능에 해당하고 어떤 요소가 수학적 지능에 해당하는지, 또는 외부 논거 없이 두 요소의 선형 조합인지 구별할 수 없다.

데이터 $\mathbf {z} _{a}$ $\mathbf {z} _{a}$ a $\mathbf {z} _{a}$ \ $displaystyle \mathbf {z} _{a}$ 에는 $\mathbf {z} _{a}$ 단위 길이가 있습니다.데이터에 대한 상관 행렬의 엔트리는 $r_{ab}=\mathbf {z} _{a}\cdot \mathbf {z} _{b}$ $r_{ab}=\mathbf {z} _{a}\cdot \mathbf {z} _{b}$ b $=$ $r_{ab}=\mathbf {z} _{a}\cdot \mathbf {z} _{b}$ ${\$ $r_{ab}=\mathbf {z} _{a}\cdot \mathbf {z} _{b}$ b { $displaystyle r_{ab$ }=\ $mathbf$ {z $} _{a}\cdot \mathbf {z} _{b$ 로 표시됩니다.상관행렬은 두 데이터 $\mathbf {z} _{a}$ z $\mathbf {z} _{a}$ {\ $displaystyle \mathbf {z} _{a}}$ 와 $\mathbf {z} _{a}$ $\mathbf {z} _{b}$ b {\ $displaystyle \mathbf {z} _{b$ 사이의 각도의 코사인으로서 기하학적으로 해석할 수 있습니다.대각선 요소는 1초 $(\style$ 1)가 $1$ $되며$ 오프 대각선 요소는 절대값이 통일 이하가 됩니다."reduced correlation matrix"는 다음과 같이 정의됩니다.

{\hat {r}}_{ab}={\hat {\mathbf {z} }}_{a}\cdot {\hat {\mathbf {z} }}_{b}

^

{\hat {r}}_{ab}={\hat {\mathbf {z} }}_{a}\cdot {\hat {\mathbf {z} }}_{b}

{\hat {r}}_{ab}={\hat {\mathbf {z} }}_{a}\cdot {\hat {\mathbf {z} }}_{b}

{\hat {r}}_{ab}={\hat {\mathbf {z} }}_{a}\cdot {\hat {\mathbf {z} }}_{b}

{\hat {r}}_{ab}={\hat {\mathbf {z} }}_{a}\cdot {\hat {\mathbf {z} }}_{b}

^

{\hat {r}}_{ab}={\hat {\mathbf {z} }}_{a}\cdot {\hat {\mathbf {z} }}_{b}

{\hat {r}}_{ab}={\hat {\mathbf {z} }}_{a}\cdot {\hat {\mathbf {z} }}_{b}

z

{\hat {r}}_{ab}={\hat {\mathbf {z} }}_{a}\cdot {\hat {\mathbf {z} }}_{b}

^

{\hat {r}}_{ab}={\hat {\mathbf {z} }}_{a}\cdot {\hat {\mathbf {z} }}_{b}

^ b {

displaystyle {r} _

{

ab

} =

cdot

{

mathbf { z

} } }

_

{

a }

\

cdot

{

mathbf

{

z }

} } _ {

b

} }

인자 분석의 목적은 단위 값을 갖는 것으로 알려진 상관 행렬의 대각 요소를 제외하고, 감소된 상관 행렬이 상관 행렬을 가능한 한 가깝게 재현하도록 적합한 초평면을 선택하는 것입니다.즉, 데이터의 교차 상관 관계를 최대한 정확하게 재현하는 것이 목표입니다.특히, 적합 초평면의 경우, 비대각 성분의 평균 제곱 오차

\displaystyle \varepsilon ^{2}=\sum _{a\neq b}\left(r_{ab}-{\hat {r}_{ab}\right}^{2}}

최소화해야 하며, 이는 일련의 직교 정규 요인 벡터에 대해 최소화함으로써 달성됩니다.라는 것을 알 수 있다

{displaystyle r_{ab}-{\hat {r}}_{ab}=cdot {bold symbol {varepsilon }}_{a}\cdot {boldsymbol {varepsilon}_{b}

오른쪽 항은 오차의 공분산일 뿐입니다.모형에서 오차 공분산은 대각 행렬로 명시되므로 위의 최소화 문제는 사실상 모형에 "최적 적합"을 산출합니다.평균 제곱 의미에서 비대각 성분을 최소화한 오차 공분산의 표본 추정치를 산출합니다.z ${\hat {z}}_{a}$ $(\$ 는 ${\hat {z}}_{a}$ 데이터 벡터의 직교 투영이므로 그 길이는 투영된 데이터 벡터의 길이 이하인 통일성을 나타냅니다.이 길이의 제곱은 축소된 상관 행렬의 대각 요소일 뿐입니다.감소된 상관 행렬의 대각 요소는 "커뮤니티"로 알려져 있습니다.

{displaystyle {h_{a}}^2}= {hat {mathbf {z}}_{a}^{2}=\sum _{j}{\ell _{aj}}^2}

커뮤니티의 큰 값은 적합 하이퍼플레인이 상관 행렬을 정확하게 재현하고 있음을 나타냅니다.요인의 평균 값도 0으로 제한해야 하며, 따라서 오차 평균 값도 0이 됩니다.

실용적인 구현

인자 분석 유형

탐색적 요인 분석

탐색적 요인 분석(EFA)은 통합 ^[4]개념의 일부인 항목과 그룹 항목 간의 복잡한 상호 관계를 식별하기 위해 사용된다.연구자는 ^[4]요인 간의 관계에 대해 선험적 가정을 하지 않습니다.

확인인자분석

확인 요인 분석(CFA)은 항목이 특정 ^[4]요인과 연관되어 있다는 가설을 검정하는 더 복잡한 방법입니다.CFA는 구조 방정식 모델링을 사용하여 인자에 부하를 가하면 관측 변수와 관측되지 않은 ^[4]변수 간의 관계를 평가할 수 있는 측정 모델을 테스트합니다.구조 방정식 모델링 접근법은 측정 오차를 수용할 수 있으며 최소 제곱 ^[4]추정보다 덜 제한적입니다.가설 모델은 실제 데이터에 대해 테스트되며, 분석을 통해 잠복 변수(요인)에 관측된 변수가 적재되는 것뿐만 아니라 잠복 ^[4]변수 간의 상관 관계도 확인할 수 있습니다.

인자 추출 유형

주성분분석(PCA)은 EFA의 ^[4]첫 단계인 인자 추출에 널리 사용되는 방법이다.인자 가중치는 가능한 최대 분산을 추출하기 위해 계산되며, 유의한 분산이 ^[4]더 이상 남아 있지 않을 때까지 연속 인수분산이 계속됩니다.그런 다음 분석을 ^[4]위해 요인 모형을 회전해야 합니다.

Rao의 정준 인자 분석이라고도 불리는 정준 인자 분석은 주축 방법을 사용하는 PCA와 동일한 모델을 계산하는 다른 방법입니다.표준 요인 분석은 관측된 변수와 표준 상관 관계가 가장 높은 요인을 찾습니다.표준 요인 분석은 데이터의 임의 재스케일링에 영향을 받지 않습니다.

주 요인 분석(PFA) 또는 주축 인수 분석(PAF)이라고도 하는 공통 요인 분석은 변수 집합의 공통 분산(상관 관계)을 설명할 수 있는 가장 적은 요인을 찾습니다.

이미지 팩터링은 실제 변수가 아닌 예측 변수의 상관 행렬을 기반으로 합니다. 여기서 각 변수는 다중 회귀 분석을 사용하여 다른 변수로부터 예측됩니다.

알파 인자 배율은 변수가 여러 변수에서 랜덤하게 추출된다고 가정할 때 요인의 신뢰도를 극대화하는 데 기초합니다.다른 모든 방법은 사례를 추출하고 변수를 고정하는 것으로 가정합니다.

요인 회귀 모형은 요인 모형과 회귀 모형의 조합 모형입니다. 또는 요인이 부분적으로 알려진 교잡 ^[5]요인 모형으로 볼 수도 있습니다.

용어.

Factor loadings: 공통성은 항목의 표준화된 외부 하중의 제곱입니다.Pearson의 r-제곱과 유사하게 인자 적재 제곱은 인자에 의해 설명되는 해당 지시 변수의 분산 백분율입니다.각 요인이 설명하는 모든 변수의 분산 비율을 얻으려면 해당 요인(열)에 대한 인자 적재 제곱의 합을 더한 다음 변수 수로 나눕니다.(표준화 변수의 분산은 1이므로 변수의 수는 분산의 합과 같습니다.이는 요인의 고유값을 변수 수로 나눈 것과 같습니다.
확증적 요인 분석에서 경험칙 하나를 사용하여 해석할 때, 인자에 의해 설명되는 지표의 분산의 약 절반에 해당한다는 근거에 따라 선험적으로 식별된 독립 변수가 특정 인자에 의해 표현된다는 것을 확인하기 위해 인자 적재가 0.7 이상이어야 한다.그러나 .7 표준은 높은 수준이며 실제 데이터는 이 기준을 충족하지 못할 수 있다. 따라서 일부 연구자는 특히 탐색 목적으로 중심 인자에 .4, 기타 인자에 .25와 같은 낮은 수준을 사용할 것이다.어떤 경우에도 인자 적재는 임의 컷오프 레벨이 아닌 이론적인 관점에서 해석해야 합니다.
사선회전에서는 패턴매트릭스와 구조매트릭스를 모두 조사할 수 있다.구조 행렬은 단순히 직교 회전과 같이 요인 적재 행렬로, 고유한 기여도와 공통 기여도 기준으로 인자에 의해 설명되는 측정된 변수의 분산을 나타냅니다.반면 패턴 행렬에는 고유한 기여도를 나타내는 계수가 포함되어 있습니다.요인이 많을수록 분산에 대한 일반적인 기여가 더 많아지므로 일반적으로 패턴 계수가 낮아집니다.경사 회전의 경우 연구자는 인자에 레이블을 지정할 때 구조와 패턴 계수를 모두 조사합니다.사선 회전의 원리는 교차 엔트로피와 그것의 이중 ^[6]엔트로피에서 모두 도출될 수 있다.
Communality: 주어진 변수(행)에 대한 모든 인자에 대한 인자 적재의 제곱합은 모든 인자가 설명하는 해당 변수의 분산입니다.공통성은 모든 요인에 의해 공동으로 설명되는 주어진 변수의 분산 비율을 측정하며, 배치되는 요인의 맥락에서 지표의 신뢰성으로 해석될 수 있습니다.
Spurious solutions: 군집성이 1.0을 초과하면 표본이 너무 작거나 요인을 너무 많이 또는 너무 적게 추출할 수 있는 스플리어스 솔루션이 있을 수 있습니다.
Uniqueness of a variable: 변수의 변동에서 해당 공통성을 뺀 값입니다.
Eigenvalues/characteristic roots: 고유값은 각 요인이 설명하는 총 표본의 변동량을 측정합니다.고유값의 비율은 변수에 대한 요인의 설명적 중요도 비율입니다.요인의 고유값이 낮으면 변수의 분산에 대한 설명에 거의 도움이 되지 않으며 고유값이 높은 요인보다 덜 중요한 것으로 무시될 수 있습니다.
Extraction sums of squared loadings: 추출 후의 초기 고유값과 고유값(SPSS에 의해 "Redition Sums of Squared Loadings"로 나열됨)은 PCA 추출에서는 동일하지만 다른 추출 방법에서는 추출 후의 고유값이 초기 고유값보다 낮아집니다.SPSS는 "하중의 제곱 회전합"도 출력하며 PCA의 경우에도 이러한 고유값은 총계는 동일하지만 초기 및 추출 고유값과 다릅니다.
Factor scores
Component scores (in PCA): 요인 분석의 관점이 아닌 PCA의 관점에서 설명됩니다.
각 요인(열)에 대한 각 사례(행)의 점수입니다.주어진 인자에 대한 주어진 사례에 대한 요인 점수를 계산하려면 각 변수에 대한 사례의 표준화된 점수를 취하여 주어진 인자에 대한 변수의 해당 적재를 곱한 다음 이러한 곱을 계산합니다.요인 점수를 계산하면 요인 특이치를 찾을 수 있습니다.또한 요인 점수는 후속 모형화에서 변수로 사용될 수 있습니다.

요인 수 결정 기준

연구자들은 "내게는 의미가 있었다"와 같은 주관적 또는 자의적인 요인 보존 기준을 피하고자 합니다.사용자가 조사할 ^[7]수 있는 적절한 범위의 솔루션을 결정할 수 있도록 이 문제를 해결하기 위해 많은 객관적인 방법이 개발되었습니다.그러나 이러한 다른 방법들은 종종 유지되어야 하는 요소의 수에 대해 서로 의견이 일치하지 않는다.예를 들어, 병렬 분석은 5가지 요인을 제시하고 벨리셔의 MAP는 6가지 요인을 제시하므로, 연구원은 5가지 및 6가지 요인 솔루션을 모두 요청하고 외부 데이터 및 이론과의 관계 측면에서 각각에 대해 논의할 수 있습니다.

오래된 방법

카이저 기준:카이저 규칙은 고유값이 1.0 미만인 성분을 모두 폐기하는 것입니다. 이 값은 평균 단일 ^[19]항목이 설명하는 정보와 동일합니다.카이저 기준은 SPSS 및 대부분의 통계 소프트웨어에서 기본값이지만, ^[20]인자를 과도하게 추출하는 경향이 있기 때문에 인자 수를 추정하기 위한 유일한 컷오프 기준으로 사용할 경우 권장되지 않는다.이 방법의 변형은 연구자가 각 고유값에 대한 신뢰 구간을 계산하고 전체 ^[14]^[21]신뢰 구간이 1.0보다 큰 요인만 유지하는 방식으로 생성되었습니다.

Screw 그림:^[22]Cattell 스크리 검정은 성분을 X 축으로 표시하고 해당 고유값을 Y 축으로 표시합니다.오른쪽으로 이동하면 나중에 구성 요소를 향해 고유값이 떨어집니다.하강이 멈추고 곡선이 덜 가파른 하강으로 팔꿈치를 만들 때, Cattell의 스크리 테스트에 따르면 팔꿈치에서 시작하는 부품 이후에 모든 추가 부품을 떨어뜨립니다.이 규칙은 연구자가 통제하는 "허위"에 순응한다는 비판을 받기도 한다.즉, 곡선이 여러 개의 팔꿈치를 가지고 있거나 부드러운 곡선이므로 "팔꿈치"를 선택하는 것이 주관적일 수 있으므로, 연구자는 자신의 연구 ^{[citation needed]}의제에 의해 원하는 요인 수로 컷오프를 설정하고 싶을 수 있다.

분산 설명 기준:일부 연구자들은 단순히 변동의 90%(때로는 80%)를 설명할 수 있을 만큼 충분한 인자를 유지하는 규칙을 사용합니다.연구자의 목표가 절약성을 강조하는 경우(가능한 한 적은 인자를 사용하여 분산을 설명함), 기준은 50%까지 낮을 수 있습니다.

베이지안법

인도 뷔페 프로세스에 기초한 베이지안 접근법은 그럴듯한 수의 잠재 ^[23]인자에 대한 확률 분포를 반환합니다.

회전 방식

회전하지 않은 출력은 첫 번째 요인과 후속 요인의 분산을 최대화하고 요인이 직교하도록 합니다.이 데이터 압축은 대부분의 항목을 초기 요인에 로드하는 데 따른 비용이며, 일반적으로 많은 항목을 여러 요소에 로드하는 데 따른 비용입니다.회전은 이른바 "단순 구조"를 추구함으로써 출력을 보다 이해하기 쉽게 하는 역할을 합니다. 즉, 각 항목이 한 요인에만 강하게 로드되고 다른 요인에는 훨씬 약하게 로드되는 로드 패턴입니다.회전은 직교 또는 경사(인자가 상관할 수 있음)일 수 있습니다.

베리맥스 회전은 요인 행렬의 모든 변수(행)에 대한 요인(열)의 적재 제곱 분산을 최대화하기 위해 요인 축을 직교 회전하는 것으로, 추출된 인자로 원래 변수를 미분하는 효과가 있습니다.각 요인은 특정 변수의 적재가 크거나 작은 경향이 있습니다.베리맥스 솔루션을 사용하면 각 변수를 단일 인자로 쉽게 식별할 수 있는 결과를 얻을 수 있습니다.이것은 가장 일반적인 회전 옵션입니다.그러나 요인의 직교성은 종종 비현실적인 가정입니다.사선회전은 직교회전을 포함하므로 사선회전이 바람직하다.태도, 의견, 지적 능력이 상관되는 경향이 있고,^[24] 그렇지 않다고 가정하는 것은 비현실적이기 때문에 심리측정학 연구에 특히 적용된다.

쿼티맥스 회전은 각 변수를 설명하는 데 필요한 요인의 수를 최소화하는 직교 대안입니다.이러한 유형의 회전은 대부분의 변수가 높은 정도 또는 중간 정도로 로드되는 일반 요인을 생성하는 경우가 많습니다.이러한 요인 구조는 보통 연구 목적에 도움이 되지 않습니다.

등축 회전은 정맥류 기준과 쿼티맥스 기준 사이의 절충입니다.

직접 직교(사각) 솔루션을 원하는 경우, 즉 요인이 상관될 수 있는 표준 방법은 직교(사각) 회전입니다.그러면 고유값은 더 높지만 요인의 해석 가능성은 떨어집니다.이하를 ^{[clarification needed]}참조해 주세요.

프로맥스 회전은 직접 제거 방법보다 계산 속도가 빠른 대안 비직교(사각) 회전 방법이며, 따라서 때때로 매우 큰 데이터 세트에 사용됩니다.

고차 요인 분석

고차 인자 분석은 반복 단계 인자 분석 - 경사 회전 - 회전 인자의 인자 분석으로 구성된 통계 방법입니다.그것의 장점은 연구자가 연구된 현상의 계층 구조를 볼 수 있도록 하는 것이다.그 결과들이 해석하기 위해서 수익금 중 하나가 post-multiplying의 일차적 원인 패턴에 매트릭스는higher-order 요소 패턴 매트릭스(Gorsuch, 1983년)고 아마도를 적용하는 Varimax 회전 결과로(톰슨, 1990년)또는을 이용함으로써 Schmid-Leiman 해결책(SLS슈미드 &, Leiman, 1957년, 또한 Schmid-Leiman 변환으로 알려진).에서1차 요인에서 2차 요인까지의 변동을 고려합니다.

심리 측정학

역사

찰스 스피어먼은 1904년 ^[26]발표한 논문에서 공통인자^[25] 분석을 논한 최초의 심리학자였다.그것은 그의 방법에 대한 세부사항을 거의 제공하지 않았고 단일 요인 ^[27]모델에 관한 것이었다.그는 전혀 관련이 없어 보이는 다양한 과목에 대한 학생들의 점수가 긍정적인 상관관계를 가지고 있다는 것을 발견했고, 이것은 그가 하나의 일반적인 정신 능력, 즉 g가 인간의 인지 능력의 기초가 되고 형태를 형성한다고 가정하게 만들었다.

여러 인자를 가진 공통 요인 분석의 초기 개발은 1930년대 ^[28]^[29]초 루이스 서스톤이 그의 1935년 책인 마음의 벡터(The Vector of Mind)^[30]에 요약된 두 개의 논문에서 제공하였다.Thurstone은 공통성, 고유성 및 ^[31]회전을 포함한 몇 가지 중요한 요인 분석 개념을 도입했습니다.그는 "단순한 구조"를 주창했고,^[25] 그러한 구조를 실현하기 위한 방법으로 사용할 수 있는 회전 방법을 개발했다.

Q 방법론에서 Spearman의 학생인 Stephenson은 개인 간 차이 연구를 지향하는 R 인자 분석과 주관적인 개인 간 차이를 지향하는 ^[32]^[33]Q 인자 분석을 구분합니다.

Raymond Cattell은 인자 분석과 심리 측정학의 강력한 지지자였으며 지능을 설명하기 위해 Thurstone의 다인자 이론을 사용했다.Cattell은 또한 "스크리" 검정과 유사성 계수를 개발했다.

심리학에서의 응용

인자 분석은 다양한 검정의 다양한 결과를 설명하는 "요인"을 식별하는 데 사용됩니다.예를 들어, 지능 연구는 언어 능력 테스트에서 높은 점수를 받는 사람들이 언어 능력을 필요로 하는 다른 테스트에서도 잘 한다는 것을 알아냈다.연구원들은 종종 언어 ^{[citation needed]}지능이라고 불리는 한 가지 요소를 분리하기 위해 요인 분석을 사용함으로써 이것을 설명했는데, 이것은 누군가가 언어 기술과 관련된 문제들을 해결할 수 있는 정도를 나타낸다.

심리학에서 인자 분석은 가장 자주 지능 연구와 관련이 있다.그러나, 그것은 또한 성격, 태도, 신념 등과 같은 광범위한 영역의 요소들을 찾는 데 사용되어 왔다.그것은 계측기가 실제로 가정된 ^{[citation needed]}요인을 측정하는지 여부를 찾아냄으로써 계측기의 유효성을 평가할 수 있기 때문에 심리측정학과 연계된다.

요소 분석은 이종 문화 연구에서 자주 사용되는 기법이다.그것은 문화적 차원을 추출하는 목적에 도움이 된다.가장 잘 알려진 문화적 차원 모델은 Geert Hofstede, Ronald Inglehart, Christian Welzel, Shalom Schwartz 및 Michael Minkov가 정교하게 만든 모델입니다.

이점

두 개 이상의 변수를 단일 인자로 결합하여 변수 수를 줄입니다.예를 들어, 달리기, 공 던지기, 배팅, 점프, 역도에서의 성과는 일반적인 운동 능력과 같은 단일 요소로 결합될 수 있다.일반적으로 사람별 항목 행렬에서는 관련 항목을 그룹화하여 요인을 선택합니다.Q 인자 분석 기법에서는 행렬이 전치되고 관련된 사람들을 그룹화하여 인자가 생성됩니다.예를 들어, 자유주의자, 자유주의자, 보수주의자, 사회주의자들이 별개의 그룹으로 형성될 수 있다.
상호 관련 변수 그룹을 식별하여 서로 어떻게 관련되어 있는지 확인합니다.예를 들어, Carroll은 요인 분석을 사용하여 삼층 이론을 구축했습니다.그는 "광범위한 시각적 지각"이라고 불리는 요소가 개인이 시각적인 일을 얼마나 잘하는지와 관련이 있다는 것을 발견했다.그는 또한 청각 업무 능력과 관련된 "광범위한 청각 지각" 요소도 발견했다.게다가, 그는 "광시적 지각"과 "광시적 청각 지각" 둘 다와 관련된 "g" 또는 일반 지능이라고 불리는 세계적인 요소를 발견했다.이는 높은 "g"를 가진 누군가가 높은 "시각적 지각" 능력과 높은 "청각적 지각" 능력을 모두 가지고 있을 가능성이 높음을 의미하며, 따라서 "g"는 왜 그 두 영역에서 누군가가 좋은지 나쁜지에 대한 좋은 부분을 설명해 준다.

단점들

"...각 방향은 수학적으로 동등하게 허용됩니다."그러나 다른 요인 이론은 주어진 솔루션의 요인 축 방향에서 다른 어떤 것과 마찬가지로 많은 차이가 있음이 입증되었기 때문에 모형 적합성은 이론을 구별하는 데 유용하지 않았다." (Sternberg, 1977^[34])즉, 모든 회전은 서로 다른 기본 공정을 나타내지만 모든 회전은 표준 인자 분석 최적화의 유효한 결과입니다.따라서 인자 분석만으로는 적절한 회전을 선택할 수 없습니다.
인자 분석은 데이터가 허용하는 범위 내에서만 우수할 수 있습니다.연구자들이 종종 자기 보고와 같이 덜 유효하고 신뢰할 수 있는 척도에 의존해야 하는 심리학에서, 이것은 문제가 될 수 있다.
요인 분석은 "절대 ^[35]사실이 아니더라도 편리한" 솔루션인 "휴리스틱"을 사용하는 것을 기반으로 합니다.동일한 방식으로 동일한 데이터에 대해 둘 이상의 해석을 수행할 수 있으며 요인 분석에서는 인과 관계를 식별할 수 없습니다.

탐색적 요인 분석(EFA) 대 주성분 분석(PCA)

인자 분석은 주성분 분석(PCA)과 관련이 있지만 두 가지가 ^[36]동일하지는 않습니다.이 분야에서는 두 기술의 차이에 대해 상당한 논란이 있어 왔다.PCA는 고속 컴퓨터가 등장하기 전 초기에 개발된 탐색적 요인 분석(EFA)의 보다 기본적인 버전이라고 볼 수 있습니다.PCA와 인자 분석은 모두 데이터 집합의 차원성을 줄이는 것을 목표로 하지만, 이를 위해 취해지는 접근 방식은 두 가지 기술에 대해 다릅니다.요인 분석은 관찰된 변수에서 관찰할 수 없는 특정 요소를 식별하기 위한 목적으로 명확하게 설계되지만, PCA는 이 목표를 직접 다루지 않는다. 기껏해야 PCA는 필수 ^[37]요소에 대한 근사치를 제공한다.탐색적 분석의 관점에서 PCA의 고유값은 팽창 성분 하중, 즉 오차 ^[38]^[39]^[40]^[41]^[42]^[43]분산으로 오염된 것이다.

일부 통계 분야에서는 EFA와 PCA가 동의어 기법으로 취급되지만,^[44]^[45] 이는 비판을 받아왔다.인자 분석은 "기본 원인 구조를 가정하여 처리한다: [] 관측된 변수의 공변화는 이러한 관측 변수에 인과적 영향을 미치는 하나 이상의 잠재 변수(요인)의 존재에 기인한다고 가정한다."^[46]이와는 대조적으로 PCA는 그러한 근본적인 인과관계를 가정하지도 의존하지도 않는다.연구자들은 두 기술 사이의 차이는 분석 목표에 기초하여 다른 기술보다 하나를 선호할 때 객관적인 이점이 있다는 것을 의미할 수 있다고 주장해 왔다.요인 모형이 잘못 공식화되거나 가정이 충족되지 않으면 요인 분석에서 잘못된 결과를 얻을 수 있습니다.시스템을 충분히 이해하면 우수한 초기 모형 공식이 가능한 경우 인자 분석이 성공적으로 사용되었습니다.PCA는 공분산 행렬의 형식에 대한 가정 없이 원래 데이터에 대한 수학적 변환을 사용합니다.PCA의 목적은 원래 변수의 선형 조합을 결정하고 많은 정보를 ^[47]손실하지 않고 데이터 세트를 요약하는 데 사용할 수 있는 몇 가지를 선택하는 것입니다.

PCA와 EFA를 대조하는 인수

Fabrigar et al.(^[44]1999)는 PCA가 인자 분석과 동등하지 않음을 시사하는 데 사용된 여러 가지 이유를 다룬다.

PCA는 계수 분석보다 계산 속도가 빠르고 필요한 리소스가 적다는 의견이 종종 제기되기도 합니다.Fabrigar 등은 쉽게 구할 수 있는 컴퓨터 자원이 이러한 실질적인 우려를 무관하게 만들었다고 주장한다.
PCA 및 인자 분석에서도 유사한 결과가 나올 수 있습니다.이 점은 Fabrigar 등에 의해서도 다루어지고 있다.; 공동체가 낮은 특정 경우(0.4 등) 두 가지 기술은 서로 다른 결과를 도출한다.실제로 Fabrigar 등은 데이터가 공통 요인 모델의 가정에 해당하는 경우 PCA의 결과는 부정확하다고 주장한다.
요인 분석이 '하이우드 사례'로 이어지는 경우도 있습니다.여기에는 측정된 변수의 분산 중 100% 이상이 모델에 의해 설명되는 상황이 포함됩니다.Fabrigar 등은 이러한 사례들이 실제로 연구자에게 유익하며, 이는 잘못 지정된 모델 또는 공통 요인 모델의 위반을 나타낸다.PCA 접근법에 Heywood 사례가 없다는 것은 이러한 문제가 간과된다는 것을 의미합니다.
연구자들은 PCA 접근법(특정 구성요소에 대한 개인의 점수 등)을 통해 추가 정보를 얻습니다. 이러한 정보는 요인 분석에서 얻어지는 것이 아닙니다.그러나 Fabrigar 등이 주장하는 바와 같이, 인자 분석의 전형적인 목적, 즉 측정된 변수 간의 상관관계를 설명하는 인자를 결정하는 것은 인자 점수에 대한 지식이 필요하지 않으므로 이 장점은 무효화된다.요인 분석에서 요인 점수를 계산할 수도 있습니다.

분산 대 공분산

인자 분석은 측정에 내재된 랜덤 오차를 고려하는 반면 PCA는 그렇지 않습니다.이 점은 계산에 관련된 상관 행렬과 관련하여 다음과 같이 지적한 Brown(2009)^[48]에 의해 예시된다.

"PCA에서 1.00s는 행렬의 모든 분산을 설명해야 한다는 대각선(각 변수에 고유한 분산, 변수 간에 공통적인 분산 및 오차 분산 포함)에 놓입니다.따라서 정의상 변수의 모든 분산을 포함합니다.이와는 대조적으로 EFA에서 공통성은 다른 변수와 공유되는 분산만 설명해야 한다는 대각선 의미에 놓인다(각 변수에 고유한 분산과 오차 분산 제외).따라서 정의상 변수 간에 공통적인 분산만 포함됩니다."
--

이러한 이유로 Brown(2009)은 변수 간의 관계에 대한 이론적 아이디어가 존재할 때 인자 분석을 사용할 것을 권장하는 반면, 연구자의 목표가 데이터의 패턴을 탐색하는 것이라면 PCA를 사용해야 합니다.

절차와 결과의 차이

PCA와 인자 분석(FA)의 차이는 Suhr(2009)^[45]에 의해 더욱 설명된다.

PCA는 관측 변수에 대한 최대 분산량을 설명하는 주성분을 생성합니다. FA는 데이터의 공통 분산을 설명합니다.
PCA는 상관행렬의 대각선에 1을 삽입합니다.FA는 상관행렬의 대각선을 고유한 인수로 조정합니다.
PCA는 성분 축에 대한 수직 거리 제곱의 합을 최소화합니다. FA는 관측 변수의 반응에 영향을 미치는 요인을 추정합니다.
PCA의 성분 점수는 고유 벡터에 의해 가중된 관측 변수의 선형 조합을 나타냅니다. FA의 관측 변수는 기본 요인과 고유 요인의 선형 결합입니다.
PCA에서 산출된 구성요소는 해석할 수 없다. 즉, 기본 '구조물'을 나타내지 않는다. FA에서는 정확한 모델 규격이 주어지면 기본 구조물에 라벨을 붙이고 쉽게 해석할 수 있다.

마케팅 부문

기본적인 순서는 다음과 같습니다.

소비자가 이 카테고리의 제품을 평가하기 위해 사용하는 주요 속성을 식별합니다.
양적 마케팅 조사 기법(조사 등)을 사용하여 모든 제품 속성의 등급에 대한 잠재적 고객 표본의 데이터를 수집합니다.
통계 프로그램에 데이터를 입력하고 인자 분석 절차를 실행합니다.컴퓨터는 일련의 기본 속성을 생성합니다.
이러한 요소를 사용하여 지각 지도 및 기타 제품 포지셔닝 장치를 구성합니다.

정보 수집

데이터 수집 단계는 일반적으로 마케팅 조사 전문가에 의해 수행됩니다.설문조사 질문은 응답자에게 제품 샘플 또는 제품 컨셉에 대한 설명을 다양한 속성에 따라 평가하도록 요구합니다.5 ~ 20개의 속성이 선택됩니다.사용의 용이성, 중량, 정확성, 내구성, 색채, 가격, 크기 등이 있습니다.선택한 속성은 연구 대상 제품에 따라 달라집니다.연구의 모든 제품에 대해 동일한 질문을 합니다.여러 제품에 대한 데이터는 코드화되어 R, SPSS, SAS, Stata, STATICA, JMP 및 SYSTAT와 같은 통계 프로그램에 입력됩니다.

분석.

분석에서는 연관 ^[49]행렬을 사용하여 데이터를 설명하는 기본 요인을 분리합니다.인자 분석은 상호의존성 기술이다.상호의존 관계의 완전한 세트를 조사한다.종속 변수, 독립 변수 또는 인과 관계에 대한 지정이 없습니다.요인 분석에서는 서로 다른 속성에 대한 모든 등급 데이터를 몇 가지 중요한 차원으로 줄일 수 있다고 가정합니다.이러한 감소는 일부 속성이 서로 관련되어 있을 수 있기 때문에 가능합니다.하나의 Atribute에 부여되는 등급은 부분적으로 다른 Atribute의 영향의 결과입니다.통계 알고리즘은 등급(원시 점수라고 함)을 다양한 구성요소로 분해하고 부분 점수를 기본 요인 점수로 재구성합니다.초기 원시 점수와 최종 요인 점수 간의 상관 관계를 인자 적재라고 합니다.

이점

주관적 속성을 점수로 변환할 수 있다면 객관적 속성과 주관적 속성을 모두 사용할 수 있다.
요인 분석은 직접 분석으로는 확인할 수 없는 잠재적 치수 또는 구조를 식별할 수 있습니다.
그것은 쉽고 저렴하다.

단점들

유용성은 충분한 제품 속성 집합을 수집할 수 있는 연구자의 능력에 따라 달라집니다.중요한 속성이 제외되거나 무시될 경우 절차 값이 감소합니다.
관측된 변수 집합이 서로 매우 유사하고 다른 항목과 구별되는 경우 요인 분석을 통해 단일 요인이 할당됩니다.이것은 더 흥미로운 ^{[clarification needed]}관계를 나타내는 요소들을 모호하게 할 수 있다.
유사해 보이지 않는 속성이 알려지지 않은 이유로 강한 상관관계를 가질 수 있기 때문에 명명 요인은 이론 지식을 필요로 할 수 있습니다.

물리 및 생물과학 분야

인자 분석은 지구화학, 수화학,^[50] 천체물리학, 우주론과 같은 물리과학뿐만 아니라 생태학, 분자생물학, 신경과학, 생화학 등의 생물과학에서도 널리 사용되어 왔다.

지하수 수질 관리에서 서로 다른 화학적 매개변수의 공간적 분포를 서로 다른 화학적 특성을 가진 서로 다른 가능한 선원과 관련짓는 것이 중요하다.예를 들어, 황화물 광산은 높은 산도, 용해된 황산염 및 전이 금속과 관련이 있을 수 있습니다.이러한 시그니처는 R-모드 인자 분석을 통해 인자로 식별할 수 있으며 인자 ^[51]점수를 등고선화하여 가능한 선원의 위치를 제안할 수 있습니다.

지구화학에서, 다른 인자는 다른 광물 결합에 해당할 수 있으며, 따라서 광물화에 ^[52]해당할 수 있다.

마이크로 어레이 분석 중

인자 분석은 Affymetrix GeneChips 프로브 수준에서 고밀도 올리고뉴클레오티드 DNA 마이크로어레이 데이터를 요약하기 위해 사용할 수 있다.이 경우 잠복 변수는 ^[53]샘플의 RNA 농도에 해당합니다.

실행

인자 분석은 1980년대 이후 여러 통계 분석 프로그램에서 구현되어 왔다.

BMDP
JMP(통계 소프트웨어)
Mplus(통계 소프트웨어)]
Python: 모듈 Scikit-learn^[54]
R(패키지 심리에서의 기본 함수 팩터널 또는 fa 함수 포함).회전은 GPArotation R 패키지로 구현됩니다.
SAS(PROC Factor 또는 PROC CALIS 사용)
SPSS^[55]
스타타

스탠드아론

요인 [1] - Rovira i Virgili University에서 개발한 무료 요인 분석 소프트웨어

「」를 참조해 주세요.

레퍼런스

^ Jöreskog, Karl G. (1983). "Factor Analysis as an Errors-in-Variables Model". Principals of Modern Psychological Measurement. Hillsdale: Erlbaum. pp. 185–196. ISBN 0-89859-277-1.
^ Bandalos, Deborah L. (2017). Measurement Theory and Applications for the Social Sciences. The Guilford Press.
^ ^a ^b ^c Harman, Harry H. (1976). Modern Factor Analysis. University of Chicago Press. pp. 175, 176. ISBN 978-0-226-31652-9.
^ ^a ^b ^c ^d ^e ^f ^g ^h ⁱ Polit DF Beck CT (2012). Nursing Research: Generating and Assessing Evidence for Nursing Practice, 9th ed. Philadelphia, USA: Wolters Klower Health, Lippincott Williams & Wilkins.
^ Meng, J. (2011). "Uncover cooperative gene regulations by microRNAs and transcription factors in glioblastoma using a nonnegative hybrid factor model". International Conference on Acoustics, Speech and Signal Processing. Archived from the original on 2011-11-23.
^ Liou, C.-Y.; Musicus, B.R. (2008). "Cross Entropy Approximation of Structured Gaussian Covariance Matrices" (PDF). IEEE Transactions on Signal Processing. 56 (7): 3362–3367. Bibcode:2008ITSP...56.3362L. doi:10.1109/TSP.2008.917878. S2CID 15255630.
^ ^a ^b ^c Zwick, William R.; Velicer, Wayne F. (1986). "Comparison of five rules for determining the number of components to retain". Psychological Bulletin. 99 (3): 432–442. doi:10.1037//0033-2909.99.3.432.
^ Horn, John L. (June 1965). "A rationale and test for the number of factors in factor analysis". Psychometrika. 30 (2): 179–185. doi:10.1007/BF02289447. PMID 14306381. S2CID 19663974.
^ Dobriban, Edgar (2017-10-02). "Permutation methods for factor analysis and PCA". arXiv:1710.00479v2 [math.ST].
^ * Ledesma, R.D.; Valero-Mora, P. (2007). "Determining the Number of Factors to Retain in EFA: An easy-to-use computer program for carrying out Parallel Analysis". Practical Assessment Research & Evaluation. 12 (2): 1–11.
^ Tran, U.S., & Formann, A. K. (2009년)바이너리 데이터가 존재하는 경우 단차원성을 검색하는 병렬 분석의 성능.교육 및 심리 측정, 69, 50-61
^ ^a ^b Velicer, W.F. (1976). "Determining the number of components from the matrix of partial correlations". Psychometrika. 41 (3): 321–327. doi:10.1007/bf02293557. S2CID 122907389.
^ ^a ^b 코트니, M. G. R. (2013)EFA에서 유지할 요소 수 결정: SPSS R-Menu v2.0을 사용하여 보다 현명한 추정.Practical Assessment, Research and Evaluation, 18(8)온라인으로 입수 가능 : http://pareonline.net/getvn.asp?v=18&n=8
^ ^a ^b Warne, R. T.; Larsen, R. (2014). "Evaluating a proposed modification of the Guttman rule for determining the number of factors in an exploratory factor analysis". Psychological Test and Assessment Modeling. 56: 104–123.
^ Ruscio, John; Roche, B. (2012). "Determining the number of factors to retain in an exploratory factor analysis using comparison data of known factorial structure". Psychological Assessment. 24 (2): 282–292. doi:10.1037/a0025697. PMID 21966933.
^ Garrido, L. E., & Abad, F. J. 및 폰소다, V. (2012년)순서형 변수를 사용한 Horn의 병렬 분석을 새롭게 살펴봅니다.심리학적 방법온라인 퍼블리셔를 진행하다doi: 10.1037/a0030005
^ Revelle, William (2007). "Determining the number of factors: the example of the NEO-PI-R" (PDF). {{cite journal}}:Cite 저널 요구 사항 journal=(도움말)
^ Revelle, William (8 January 2020). "psych: Procedures for Psychological, Psychometric, and PersonalityResearch".
^ Kaiser, Henry F. (April 1960). "The Application of Electronic Computers to Factor Analysis". Educational and Psychological Measurement. 20 (1): 141–151. doi:10.1177/001316446002000116. S2CID 146138712.
^ Bandalos, D.L.; Boehm-Kaufman, M.R. (2008). "Four common misconceptions in exploratory factor analysis". In Lance, Charles E.; Vandenberg, Robert J. (eds.). Statistical and Methodological Myths and Urban Legends: Doctrine, Verity and Fable in the Organizational and Social Sciences. Taylor & Francis. pp. 61–87. ISBN 978-0-8058-6237-9.
^ Larsen, R.; Warne, R. T. (2010). "Estimating confidence intervals for eigenvalues in exploratory factor analysis". Behavior Research Methods. 42 (3): 871–876. doi:10.3758/BRM.42.3.871. PMID 20805609.
^ Cattell, Raymond (1966). "The scree test for the number of factors". Multivariate Behavioral Research. 1 (2): 245–76. doi:10.1207/s15327906mbr0102_10. PMID 26828106.
^ Alpaydin (2020). Introduction to Machine Learning (5th ed.). pp. 528–9.
^ Russell, D.W. (December 2002). "In search of underlying dimensions: The use (and abuse) of factor analysis in Personality and Social Psychology Bulletin". Personality and Social Psychology Bulletin. 28 (12): 1629–46. doi:10.1177/014616702237645. S2CID 143687603.
^ ^a ^b Mulaik, Stanley A (2010). Foundations of Factor Analysis. Second Edition. Boca Raton, Florida: CRC Press. p. 6. ISBN 978-1-4200-9961-4.
^ Spearman, Charles (1904). "General intelligence objectively determined and measured". American Journal of Psychology. 15 (2): 201–293. doi:10.2307/1412107. JSTOR 1412107.
^ Bartholomew, D. J. (1995). "Spearman and the origin and development of factor analysis". British Journal of Mathematical and Statistical Psychology. 48 (2): 211–220. doi:10.1111/j.2044-8317.1995.tb01060.x.
^ Thurstone, Louis (1931). "Multiple factor analysis". Psychological Review. 38 (5): 406–427. doi:10.1037/h0069792.
^ Thurstone, Louis (1934). "The Vectors of Mind". The Psychological Review. 41: 1–32. doi:10.1037/h0075959.
^ Thurstone, L. L. (1935). The Vectors of Mind. Multiple-Factor Analysis for the Isolation of Primary Traits. Chicago, Illinois: University of Chicago Press.
^ Bock, Robert (2007). "Rethinking Thurstone". In Cudeck, Robert; MacCallum, Robert C. (eds.). Factor Analysis at 100. Mahwah, New Jersey: Lawrence Erlbaum Associates. p. 37. ISBN 978-0-8058-6212-6.
^ Mckeown, Bruce (2013-06-21). Q Methodology. ISBN 9781452242194. OCLC 841672556.
^ Stephenson, W. (August 1935). "Technique of Factor Analysis". Nature. 136 (3434): 297. Bibcode:1935Natur.136..297S. doi:10.1038/136297b0. ISSN 0028-0836. S2CID 26952603.
^ Sternberg, R. J. (1977). Metaphors of Mind: Conceptions of the Nature of Intelligence. New York: Cambridge University Press. pp. 85–111.^{[검증 필요]}
^ "Factor Analysis". Archived from the original on August 18, 2004. Retrieved July 22, 2004.
^ Bartholomew, D.J.; Steele, F.; Galbraith, J.; Moustaki, I. (2008). Analysis of Multivariate Social Science Data. Statistics in the Social and Behavioral Sciences Series (2nd ed.). Taylor & Francis. ISBN 978-1584889601.
^ Jollife I.T. 주요 컴포넌트 분석, 시리즈: Springer Series in Statistics, 2nd, Springer, NY, 2002, XXIX, 487p.28 ilus.ISBN 978-0-387-95442-4
^ 캐텔, R. B. (1952)인자 분석.뉴욕: 하퍼.
^ Fruchter, B. (1954)인자 분석 입문반 노스트랜드.
^ 캐텔, R. B. (1978)행동과학 및 생명과학에서의 인자 분석 사용.뉴욕: 플레넘.
^ Child, D. (2006)인자 분석의 요점, 제3판.블룸스베리 학술 출판사
^ Gorsuch, R. L.(1983)인자 분석, 제2판힐스데일, 뉴저지 주: 얼바움.
^ 맥도날드, R. P. (1985년)인자 분석 및 관련 방법.힐스데일, 뉴저지 주: 얼바움.
^ ^a ^b Fabrigar; et al. (1999). "Evaluating the use of exploratory factor analysis in psychological research" (PDF). Psychological Methods.
^ ^a ^b Suhr, Diane (2009). "Principal component analysis vs. exploratory factor analysis" (PDF). SUGI 30 Proceedings. Retrieved 5 April 2012.
^ SAS Statistics. "Principal Components Analysis" (PDF). SAS Support Textbook.
^ Meglen, R.R. (1991). "Examining Large Databases: A Chemometric Approach Using Principal Component Analysis". Journal of Chemometrics. 5 (3): 163–179. doi:10.1002/cem.1180050305. S2CID 120886184.
^ Brown, J. D. (January 2009). "Principal components analysis and exploratory factor analysis – Definitions, differences and choices" (PDF). Shiken: JALT Testing & Evaluation SIG Newsletter. Retrieved 16 April 2012.
^ Ritter, N. (2012).인자 분석에서 무분포 방법과 비분포 방법의 비교.논문은 LA 뉴올리언스에서 열린 Southwestern Education Research Association(SERA) Conference 2012(ED529153)에서 발표되었습니다.
^ Subbarao, C.; Subbarao, N.V.; Chandu, S.N. (December 1996). "Characterisation of groundwater contamination using factor analysis". Environmental Geology. 28 (4): 175–180. Bibcode:1996EnGeo..28..175S. doi:10.1007/s002540050091. S2CID 129655232.
^ Love, D.; Hallbauer, D.K.; Amos, A.; Hranova, R.K. (2004). "Factor analysis as a tool in groundwater quality management: two southern African case studies". Physics and Chemistry of the Earth. 29 (15–18): 1135–43. Bibcode:2004PCE....29.1135L. doi:10.1016/j.pce.2004.09.027.
^ Barton, E.S.; Hallbauer, D.K. (1996). "Trace-element and U—Pb isotope compositions of pyrite types in the Proterozoic Black Reef, Transvaal Sequence, South Africa: Implications on genesis and age". Chemical Geology. 133 (1–4): 173–199. doi:10.1016/S0009-2541(96)00075-7.
^ Hochreiter, Sepp; Clevert, Djork-Arné; Obermayer, Klaus (2006). "A new summarization method for affymetrix probe level data". Bioinformatics. 22 (8): 943–9. doi:10.1093/bioinformatics/btl033. PMID 16473874.
^ "sklearn.decomposition.FactorAnalysis — scikit-learn 0.23.2 documentation". scikit-learn.org.
^ MacCallum, Robert (June 1983). "A comparison of factor analysis programs in SPSS, BMDP, and SAS". Psychometrika. 48 (2): 223–231. doi:10.1007/BF02294017. S2CID 120770421.

추가 정보

를 클릭합니다Child, Dennis (2006), The Essentials of Factor Analysis (3rd ed.), Continuum International, ISBN 978-0-8264-8000-2.
Fabrigar, L.R.; Wegener, D.T.; MacCallum, R.C.; Strahan, E.J. (September 1999). "Evaluating the use of exploratory factor analysis in psychological research". Psychological Methods. 4 (3): 272–299. doi:10.1037/1082-989X.4.3.272.
B.T. 그레이(1997) 고차 인자 분석(회의서류)
Jennrich, Robert I., "구성 요소 손실 함수를 사용한 단순 적재로의 회전:사선상자", Psychometrika, 제71, 제1호, 173–191페이지, 2006년 3월.
캣츠, 제프리 오웬, 그리고 롤프, F. 제임스.프라이머리 제품 기능 플레인:단순한 구조로의 사선 회전.다변량행동연구, 1975년 4월, 제10권, 페이지 219–232.
캣츠, 제프리 오웬, 그리고 롤프, F. 제임스.기능 플레인:심플한 구조 회전에 대한 새로운 접근법.사이코메트리카, 1974년 3월, 제39권, 제1호, 37-51페이지
캣츠, 제프리 오웬, 그리고 롤프, F. 제임스.기능점 클러스터 분석.계통동물학, 1973년 9월, 제22권, 제3호, 295-301페이지.
를 클릭합니다Mulaik, S. A. (2010), Foundations of Factor Analysis, Chapman & Hall.
Preacher, K.J.; MacCallum, R.C. (2003). "Repairing Tom Swift's Electric Factor Analysis Machine" (PDF). Understanding Statistics. 2 (1): 13–43. doi:10.1207/S15328031US0201_02. hdl:1808/1492.
J.Schmid와 J.M. Leiman(1957).계층적 요인 솔루션의 개발.사이코메트리카, 22(1), 53~61
를 클릭합니다Thompson, B. (2004), Exploratory and Confirmatory Factor Analysis: Understanding concepts and applications, Washington DC: American Psychological Association, ISBN 978-1591470939.

Hans-Georg Wolff, Katja Preising (2005)schmid-leman 솔루션을 통한 항목 및 고차 요소 구조 탐색 : SPSS 및 SASBehavior 연구 방법, 기기 및 컴퓨터 구문 코드, 37 (1) 및 48-58

외부 링크

요인 분석 초보자 가이드
탐색적 요인 분석.Tucker, L. & MacCallum R.(1993)의 책 원고.2006년 6월 8일 취득원: [2]
Garson, G. David, 통계정보의 "요인 분석: 다변량 분석 항목.StatNotes에서 2009년 4월 13일 취득: North Carolina State University의 G. David Garson의 다변량 분석 주제, 행정 프로그램
100에서의 인자 분석 - 회의 자료
FARMS - R 패키지인 견고한 마이크로 어레이 집약을 위한 인자 분석

[1] Jöreskog, Karl G. (1983). "Factor Analysis as an Errors-in-Variables Model". Principals of Modern Psychological Measurement. Hillsdale: Erlbaum. pp. 185–196. ISBN 0-89859-277-1.

[2] Bandalos, Deborah L. (2017). Measurement Theory and Applications for the Social Sciences. The Guilford Press.

[Harman-3] Harman, Harry H. (1976). Modern Factor Analysis. University of Chicago Press. pp. 175, 176. ISBN 978-0-226-31652-9.

[Polit-4] ^ ^a ^b ^c ^d ^e ^f ^g ^h ⁱ Polit DF Beck CT (2012). Nursing Research: Generating and Assessing Evidence for Nursing Practice, 9th ed. Philadelphia, USA: Wolters Klower Health, Lippincott Williams & Wilkins.

[meng2011-5] Meng, J. (2011). "Uncover cooperative gene regulations by microRNAs and transcription factors in glioblastoma using a nonnegative hybrid factor model". International Conference on Acoustics, Speech and Signal Processing. Archived from the original on 2011-11-23.

[6] Liou, C.-Y.; Musicus, B.R. (2008). "Cross Entropy Approximation of Structured Gaussian Covariance Matrices" (PDF). IEEE Transactions on Signal Processing. 56 (7): 3362–3367. Bibcode:2008ITSP...56.3362L. doi:10.1109/TSP.2008.917878. S2CID 15255630.

[Zwick1986-7] Zwick, William R.; Velicer, Wayne F. (1986). "Comparison of five rules for determining the number of components to retain". Psychological Bulletin. 99 (3): 432–442. doi:10.1037//0033-2909.99.3.432.

[Horn1965-8] Horn, John L. (June 1965). "A rationale and test for the number of factors in factor analysis". Psychometrika. 30 (2): 179–185. doi:10.1007/BF02289447. PMID 14306381. S2CID 19663974.

[9] Dobriban, Edgar (2017-10-02). "Permutation methods for factor analysis and PCA". arXiv:1710.00479v2 [math.ST].

[10] * Ledesma, R.D.; Valero-Mora, P. (2007). "Determining the Number of Factors to Retain in EFA: An easy-to-use computer program for carrying out Parallel Analysis". Practical Assessment Research & Evaluation. 12 (2): 1–11.

[11] Tran, U.S., & Formann, A. K. (2009년)바이너리 데이터가 존재하는 경우 단차원성을 검색하는 병렬 분석의 성능.교육 및 심리 측정, 69, 50-61

[Velicer-12] Velicer, W.F. (1976). "Determining the number of components from the matrix of partial correlations". Psychometrika. 41 (3): 321–327. doi:10.1007/bf02293557. S2CID 122907389.

[pareonline.net-13] 코트니, M. G. R. (2013)EFA에서 유지할 요소 수 결정: SPSS R-Menu v2.0을 사용하여 보다 현명한 추정.Practical Assessment, Research and Evaluation, 18(8)온라인으로 입수 가능 : http://pareonline.net/getvn.asp?v=18&n=8

[Warne,_R._T._2014-14] Warne, R. T.; Larsen, R. (2014). "Evaluating a proposed modification of the Guttman rule for determining the number of factors in an exploratory factor analysis". Psychological Test and Assessment Modeling. 56: 104–123.

[Ruscio-15] Ruscio, John; Roche, B. (2012). "Determining the number of factors to retain in an exploratory factor analysis using comparison data of known factorial structure". Psychological Assessment. 24 (2): 282–292. doi:10.1037/a0025697. PMID 21966933.

[Garrido-16] Garrido, L. E., & Abad, F. J. 및 폰소다, V. (2012년)순서형 변수를 사용한 Horn의 병렬 분석을 새롭게 살펴봅니다.심리학적 방법온라인 퍼블리셔를 진행하다doi: 10.1037/a0030005

[17] Revelle, William (2007). "Determining the number of factors: the example of the NEO-PI-R" (PDF). {{cite journal}}:Cite 저널 요구 사항 journal=(도움말)

[18] Revelle, William (8 January 2020). "psych: Procedures for Psychological, Psychometric, and PersonalityResearch".

[Kaiser1960-19] Kaiser, Henry F. (April 1960). "The Application of Electronic Computers to Factor Analysis". Educational and Psychological Measurement. 20 (1): 141–151. doi:10.1177/001316446002000116. S2CID 146138712.

[20] Bandalos, D.L.; Boehm-Kaufman, M.R. (2008). "Four common misconceptions in exploratory factor analysis". In Lance, Charles E.; Vandenberg, Robert J. (eds.). Statistical and Methodological Myths and Urban Legends: Doctrine, Verity and Fable in the Organizational and Social Sciences. Taylor & Francis. pp. 61–87. ISBN 978-0-8058-6237-9.

[21] Larsen, R.; Warne, R. T. (2010). "Estimating confidence intervals for eigenvalues in exploratory factor analysis". Behavior Research Methods. 42 (3): 871–876. doi:10.3758/BRM.42.3.871. PMID 20805609.

[22] Cattell, Raymond (1966). "The scree test for the number of factors". Multivariate Behavioral Research. 1 (2): 245–76. doi:10.1207/s15327906mbr0102_10. PMID 26828106.

[23] Alpaydin (2020). Introduction to Machine Learning (5th ed.). pp. 528–9.

[24] Russell, D.W. (December 2002). "In search of underlying dimensions: The use (and abuse) of factor analysis in Personality and Social Psychology Bulletin". Personality and Social Psychology Bulletin. 28 (12): 1629–46. doi:10.1177/014616702237645. S2CID 143687603.

[:0-25] Mulaik, Stanley A (2010). Foundations of Factor Analysis. Second Edition. Boca Raton, Florida: CRC Press. p. 6. ISBN 978-1-4200-9961-4.

[26] Spearman, Charles (1904). "General intelligence objectively determined and measured". American Journal of Psychology. 15 (2): 201–293. doi:10.2307/1412107. JSTOR 1412107.

[27] Bartholomew, D. J. (1995). "Spearman and the origin and development of factor analysis". British Journal of Mathematical and Statistical Psychology. 48 (2): 211–220. doi:10.1111/j.2044-8317.1995.tb01060.x.

[28] Thurstone, Louis (1931). "Multiple factor analysis". Psychological Review. 38 (5): 406–427. doi:10.1037/h0069792.

[29] Thurstone, Louis (1934). "The Vectors of Mind". The Psychological Review. 41: 1–32. doi:10.1037/h0075959.

[30] Thurstone, L. L. (1935). The Vectors of Mind. Multiple-Factor Analysis for the Isolation of Primary Traits. Chicago, Illinois: University of Chicago Press.

[31] Bock, Robert (2007). "Rethinking Thurstone". In Cudeck, Robert; MacCallum, Robert C. (eds.). Factor Analysis at 100. Mahwah, New Jersey: Lawrence Erlbaum Associates. p. 37. ISBN 978-0-8058-6212-6.

[32] Mckeown, Bruce (2013-06-21). Q Methodology. ISBN 9781452242194. OCLC 841672556.

[33] Stephenson, W. (August 1935). "Technique of Factor Analysis". Nature. 136 (3434): 297. Bibcode:1935Natur.136..297S. doi:10.1038/136297b0. ISSN 0028-0836. S2CID 26952603.

[Sternberg-34] Sternberg, R. J. (1977). Metaphors of Mind: Conceptions of the Nature of Intelligence. New York: Cambridge University Press. pp. 85–111.^{[검증 필요]}

[35] "Factor Analysis". Archived from the original on August 18, 2004. Retrieved July 22, 2004.

[Bartholomew2008-36] Bartholomew, D.J.; Steele, F.; Galbraith, J.; Moustaki, I. (2008). Analysis of Multivariate Social Science Data. Statistics in the Social and Behavioral Sciences Series (2nd ed.). Taylor & Francis. ISBN 978-1584889601.

[Principal_Component_Analysis-37] Jollife I.T. 주요 컴포넌트 분석, 시리즈: Springer Series in Statistics, 2nd, Springer, NY, 2002, XXIX, 487p.28 ilus.ISBN 978-0-387-95442-4

[38] 캐텔, R. B. (1952)인자 분석.뉴욕: 하퍼.

[39] Fruchter, B. (1954)인자 분석 입문반 노스트랜드.

[40] 캐텔, R. B. (1978)행동과학 및 생명과학에서의 인자 분석 사용.뉴욕: 플레넘.

[41] Child, D. (2006)인자 분석의 요점, 제3판.블룸스베리 학술 출판사

[42] Gorsuch, R. L.(1983)인자 분석, 제2판힐스데일, 뉴저지 주: 얼바움.

[43] 맥도날드, R. P. (1985년)인자 분석 및 관련 방법.힐스데일, 뉴저지 주: 얼바움.

[Fabrigar-44] Fabrigar; et al. (1999). "Evaluating the use of exploratory factor analysis in psychological research" (PDF). Psychological Methods.

[Suhr-45] Suhr, Diane (2009). "Principal component analysis vs. exploratory factor analysis" (PDF). SUGI 30 Proceedings. Retrieved 5 April 2012.

[Sas-46] SAS Statistics. "Principal Components Analysis" (PDF). SAS Support Textbook.

[47] Meglen, R.R. (1991). "Examining Large Databases: A Chemometric Approach Using Principal Component Analysis". Journal of Chemometrics. 5 (3): 163–179. doi:10.1002/cem.1180050305. S2CID 120886184.

[Brown-48] Brown, J. D. (January 2009). "Principal components analysis and exploratory factor analysis – Definitions, differences and choices" (PDF). Shiken: JALT Testing & Evaluation SIG Newsletter. Retrieved 16 April 2012.

[49] Ritter, N. (2012).인자 분석에서 무분포 방법과 비분포 방법의 비교.논문은 LA 뉴올리언스에서 열린 Southwestern Education Research Association(SERA) Conference 2012(ED529153)에서 발표되었습니다.

[50] Subbarao, C.; Subbarao, N.V.; Chandu, S.N. (December 1996). "Characterisation of groundwater contamination using factor analysis". Environmental Geology. 28 (4): 175–180. Bibcode:1996EnGeo..28..175S. doi:10.1007/s002540050091. S2CID 129655232.

[51] Love, D.; Hallbauer, D.K.; Amos, A.; Hranova, R.K. (2004). "Factor analysis as a tool in groundwater quality management: two southern African case studies". Physics and Chemistry of the Earth. 29 (15–18): 1135–43. Bibcode:2004PCE....29.1135L. doi:10.1016/j.pce.2004.09.027.

[52] Barton, E.S.; Hallbauer, D.K. (1996). "Trace-element and U—Pb isotope compositions of pyrite types in the Proterozoic Black Reef, Transvaal Sequence, South Africa: Implications on genesis and age". Chemical Geology. 133 (1–4): 173–199. doi:10.1016/S0009-2541(96)00075-7.

[53] Hochreiter, Sepp; Clevert, Djork-Arné; Obermayer, Klaus (2006). "A new summarization method for affymetrix probe level data". Bioinformatics. 22 (8): 943–9. doi:10.1093/bioinformatics/btl033. PMID 16473874.

[54] "sklearn.decomposition.FactorAnalysis — scikit-learn 0.23.2 documentation". scikit-learn.org.

[55] MacCallum, Robert (June 1983). "A comparison of factor analysis programs in SPSS, BMDP, and SAS". Psychometrika. 48 (2): 223–231. doi:10.1007/BF02294017. S2CID 120770421.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[13]

[12]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]

[24]

[26]

[25]

[27]

[28]

[29]

[30]

[31]

[32]

[33]

[34]

[35]

[36]

[37]

[38]

[39]

[40]

[41]

[42]

[43]

[44]

[45]

[46]

[47]

[48]

[49]

[50]

[51]

[52]

[53]

[54]

[55]

Search