삼각수 제곱

측면 길이가 삼각형인 정사각형은 정사각형과 정사각형에 면적이 추가된 반제곱으로 분할할 수 있다.굴리(2010년) 출신이다.

숫자 이론에서, 첫 $번째$ n 큐브의 합은 n번째 삼각형 숫자의 제곱이다.그것은

1^{3}+2^{3}+3^{3}+\cdots +n^{3}}}=\왼쪽(1+2+3+\cdots +n\오른쪽)^{2}

같은 방정식은 합산을 위한 수학적 표기법을 사용하여 보다 간결하게 작성할 수 있다.

\sum \sum _{k=1}^{n}k^{3}={\bigg (}\sum _{k=1}^{n}k{\bigg )}^{2}.

이 정체성을 게라사의 니코마코스(c. 60 – c. 120 CE)의 이름을 따서 니코마쿠스의 정리라고 부르기도 한다.

역사

니코마코스(Nicomacus)는 산술 입문서 20장 말미에, 한 사람이 홀수 목록을 쓰면 첫 번째가 1의 세제곱, 다음 두 개의 합은 2의 세제곱, 다음 세 개의 합은 3의 세제곱 등이라고 지적했다.He does not go further than this, but from this it follows that the sum of the first $n$ cubes equals the sum of the first $n(n+1)/2$ odd numbers, that is, the odd numbers from 1 to $n(n+1)-1$ . The average of these numbers is obviously ${\displaystyl$ $e n(n+1)/2}$ 이 $n(n+1)/2$ $n(n+1)/2$ ) $n(n+1)/2$ n $n(n+1)/2$ 1 )/ $n(n+1)/2$ $n(n+1)/2$ 이 $n(n+1)/2$ (가) 있으므로, 합은 ${\bigl (}n(n+1)/2{\bigr )}^{2}.$ ( ${\bigl (}n(n+1)/2{\bigr )}^{2}.$ / ${\bigl (}n(n+1)/2{\bigr )}^{2}.$ ) ${\bigl (}n(n+1)/2{\bigr )}^{2}.$ . ${\displaystyle {\bigl (}n+1)/2{\bigr )^{2}.$ $}$

많은 초기 수학자들이 니코마쿠스의 정리 증거를 연구하고 제공했다.스트로커(1995)는 "숫자 이론의 모든 학생들이 틀림없이 이 기적적인 사실에 경탄했을 것"이라고 주장한다.Pengelley(2002)는 1세기 CE의 현재 요르단인 니코마쿠스의 작품뿐만 아니라 5세기 인도의 아리아브하타 작품, 페르시아의 알카라지 cerca 1000의 작품에서도 그 정체성에 대한 언급을 발견한다.브레수드(2004)는 이 공식에 관한 알카비시(10세기 아라비아), 게르손데스(1300 프랑스), 닐라칸타 소마야지(인도 1500 인도)의 초기 수학 작품들을 추가로 언급하고 있으며, 닐라칸타의 시각적 증거를 재현하고 있다.

숫자 값, 기하학적 및 확률적 해석

전체 36 [(1² + 2 + 3) ²= 1³ + 2³³² + 3²] 사각형(빨간색)을 포함하여 3×3 사각형(4×4 정점) 그리드에 있는 직사각형

삼각형 숫자의 제곱 순서는^[1]

0, 1, 9, 36, 100, 225,

441, 784, 1296, 2025, 3025, 4356, 6084, 8281,

... .

이 숫자들은 삼각형 숫자와 네모난 피라미드 숫자의 4차원 과피라미드 일반화인 구상 숫자로 볼 수 있다.

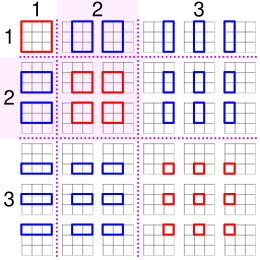
스타인(1971)이 관찰한 바와 같이, 이 숫자들은 $또한$ n × $n$ 그리드에서 형성된 수평면과 수직면을 가진 직사각형의 수를 계산한다.예를 들어, $4$ × $4$ 격자(또는 한 쪽에 세 개의 작은 정사각형으로 구성된 사각형)의 점은 36개의 다른 직사각형을 형성할 수 있다.정사각형 격자 안의 정사각형 수는 정사각형 피라미드 숫자로 비슷하게 계수된다.

그 정체성은 또한 다음과 같은 자연적인 확률론적 해석을 인정한다. $X,$ $Y,$ $Z,$ $W$ 를 $1$ 과 $n$ 사이의 임의로 선택한 네 개의 정수여야 한다.그렇다면 $W$ 가 네 숫자 중 가장 클 확률은 $Y$ 가 적어도 $X만큼$ 크고 $W$ 가 적어도 $Z만큼$ 클 확률을 의미한다.즉, $P[\max(X,Y,Z)\leq W]=P[X\leq Y\wedge Z\leq W]$ [ $P[\max(X,Y,Z)\leq W]=P[X\leq Y\wedge Z\leq W]$ ( $P[\max(X,Y,Z)\leq W]=P[X\leq Y\wedge Z\leq W]$ , Y $P[\max(X,Y,Z)\leq W]=P[X\leq Y\wedge Z\leq W]$ , $P[\max(X,Y,Z)\leq W]=P[X\leq Y\wedge Z\leq W]$ ) $P[\max(X,Y,Z)\leq W]=P[X\leq Y\wedge Z\leq W]$ $P[\max(X,Y,Z)\leq W]=P[X\leq Y\wedge Z\leq W]$ $P[\max(X,Y,Z)\leq W]=P[X\leq Y\wedge Z\leq W]$ = $P[\max(X,Y,Z)\leq W]=P[X\leq Y\wedge Z\leq W]$ [ $P[\max(X,Y,Z)\leq W]=P[X\leq Y\wedge Z\leq W]$ $P[\max(X,Y,Z)\leq W]=P[X\leq Y\wedge Z\leq W]$ Y $P[\max(X,Y,Z)\leq W]=P[X\leq Y\wedge Z\leq W]$ $P[\max(X,Y,Z)\leq W]=P[X\leq Y\wedge Z\leq W]$ $P[\max(X,Y,Z)\leq W]=P[X\leq Y\wedge Z\leq W]$ $P[\max(X,Y,Z)\leq W]=P[X\leq Y\wedge Z\leq W]$ $P[\max(X,Y,Z)\leq W]=P[X\leq Y\wedge Z\leq W]$ ${\displaystyle P[\max(X,Y,Z)\leq W]=$ $P[X\leq Y\wedge Z\leq W]}$ . For any particular value of $W$ , the combinations of $X$ , $Y$ , and $Z$ that make $W$ largest form a cube $1 \leq X, Y, Z \leq n$ so (adding the size of this cube over all choices of $W$ ) the number of combinations of $X, Y, Z, W$ for which $W$ is largest is a sum of cubes, the left hand side of the Nichomachus identity. $X$ ≤ $Y$ 를 가진 쌍 $(X, Y)$ 과 $Z$ ≤ $W$ 를 가진 쌍 $(Z, W)$ 의 집합은 직삼각형이며, 확률 방정식의 우측에 의해 계산된 집합은 이 두 삼각형의 데카르트 산물이므로 그 크기는 니코마코스 정체성의 우측에 있는 삼각형의 숫자의 제곱이다.확률 자체는 각각 니코마코스 정체성의 왼쪽과 오른쪽이며, 양쪽을 $n$ 으로⁴ 나누어 확률을 만들기 위해 정규화되었다.^{[citation needed]}

교정쇄

찰스 휘트스톤(1854)은 특히 단순한 파생법을 제시하는데, 합계의 각 입방체를 연속된 홀수 집합으로 확장시켜 준다.그는 정체성을 주는 것으로 시작한다.

n^{3}=\underbrace {\reft(n^{2}-n+1+2\right)+\reft(n^{2}-n+1+4\right)+\left(n^{2}+n-1\right)} _{n{n\text}}}}}

이 ID는 다음과 같은 방법으로

T_{n}

삼각형 숫자

T_{n}

n

{\

과(와) 관련이 있다.

n^{3}=\sum _{k=T_{n-1}+1}^{{n1}T_{n}}(2k-1),

따라서 n

{\

n

^{3}

를 형성하는 요약은 이전

1^{3}

1

{\

1

^{

(n-1)^{3}

}

까지를

1^{3}

형성하는 것이 (n

n^{3}

(n-1)^{3}

-

(n-1)^{3}

)

(n-1)^{3}

{\

까지를 형성한 후에 시작한다

(n-1)^{3}

이 속성을 다른 잘 알려진 ID와 함께 적용한다.

n^{2}=\sum _{k=1}^{n}(2k-1)

다음과 같은 파생어가 생성된다.

{\regated}\sum _{k=1}^{n^{3}&=1+8+27+64+\cdots +n^{3}}\\&,=\underbrace{1}_{1^{3}}+\underbrace(_{2^{3}}+\underbrace(_{3^{3}}+\underbrace(_{4^{3}}+\cdots+\underbrace{\left(n^{2}-n+1\right)+\cdots +\left(n^{2}+n-1\right)}_{n^{3}}\\&,=\underbrace{\underbrace{\underbrace{\underbrace{1}_{1^{2}}+3}_{2^{2}}+5}_{3^{2}}}_{\left({\fr +\left(n^{2}+n-1\right)+\cdots.교류{{2n^}}+n}{2}}\\오른쪽)^{2}}\\&=(1+2+\cdots +n)^{2}\\&={\bigg (}\sum _{k=1}^{n}k{\bigg )^{2}.\end{정렬}}

행(1893)은 두 가지 다른 방법으로 제곱 곱셈표에 숫자를 합산하여 또 다른 증거를 얻는다. $i$ $i$ 행의 합은 $i$ ${\displaystyle$ i $}$ 에 $i$ 삼각형 숫자를 곱한 것이며, 여기서 모든 행의 합은 삼각형 숫자의 제곱인 것이다.또는 표를 일련의 중첩된 Gnomon으로 분해할 수 있으며, 각 Gnomon은 두 용어 중 큰 것이 일정한 값인 제품으로 구성된다.각 gmonon 내의 합은 정육면체이므로 전체 테이블의 합은 정육면체의 합이다.

삼각형 숫자의 제곱이 입방체의 합과 같다는 것을 시각적으로 증명한다.

보다 최근의 수학 문헌에서, 에드몬드(1957)는 부품별 합계를 이용한 증거를 제공한다.스타인(1971)은 이 숫자들의 직사각형 수를 세는 해석을 사용하여 정체성에 대한 기하학적 증거를 형성한다(벤자민, 퀸 & 우르츠 2006 참조). 그는 그것이 또한 유도에 의해 쉽게(그러나 비정보적으로) 증명될 수 있다고 관찰하고, 토플리츠(1963)가 "흥미로운 오래된 아랍어 증명서"를 제공한다고 진술한다.카님(2004)은 순전히 시각적 증거를, 벤자민 & 오리슨(2002)은 2개의 증거를, 넬슨(1993)은 7개의 기하학적 증거를 제시한다.

일반화

니코마쿠스의 정리와 유사한 결과는 모든 전력 합계에 대한 것, 즉 홀수 전력 합(이상 전력의 합)이 삼각수로 된 다항식이라는 것이다.이것들은 포크하버 다항식이라고 불리는데, 그 중 큐브의 합이 가장 단순하고 우아한 예다.그러나, 다른 어떤 경우에도 하나의 권력이 다른 권력의 제곱합이 아니다.^[2]

스트로커(1995)는 연속적인 큐브 순서의 합이 정사각형을 이루는 더 일반적인 조건들을 연구한다.개럿 & 험멜(2004)과 워나르(2004)는 일련의 다항식이 다른 다항식의 제곱에 더해지는 사각 삼각수 공식의 다항식 유사점을 연구한다.

메모들

^ Sloane, N. J. A. (ed.), "Sequence A000537", The On-Line Encyclopedia of Integer Sequences, OEIS Foundation
^ 에드먼즈(1957년).

참조

Benjamin, Arthur T.; Orrison, M. E. (2002), "Two quick combinatorial proofs of $\textstyle \sum k^{3}={n+1 \choose 2}^{2}$ " (PDF), College Mathematics Journal, 33 (5): 406–408, doi:10.2307/1559017, JSTOR 1559017.
Benjamin, Arthur T.; Quinn, Jennifer J.; Wurtz, Calyssa (2006), "Summing cubes by counting rectangles" (PDF), College Mathematics Journal, 37 (5): 387–389, doi:10.2307/27646391, JSTOR 27646391.
Bressoud, David (2004), Calculus before Newton and Leibniz, Part III (PDF), AP Central.
Edmonds, Sheila M. (1957), "Sums of powers of the natural numbers", The Mathematical Gazette, 41: 187–188, doi:10.2307/3609189, JSTOR 3609189, MR 0096615
Garrett, Kristina C.; Hummel, Kristen (2004), "A combinatorial proof of the sum of $q$ -cubes", Electronic Journal of Combinatorics, 11 (1), Research Paper 9, doi:10.37236/1762, MR 2034423.
Gulley, Ned (March 4, 2010), Shure, Loren (ed.), Nicomachus's Theorem, Matlab Central.
Kanim, Katherine (2004), "Proofs without words: The sum of cubes—An extension of Archimedes' sum of squares", Mathematics Magazine, 77 (4): 298–299, doi:10.2307/3219288, JSTOR 3219288.
Nelsen, Roger B. (1993), Proofs without Words, Cambridge University Press, ISBN 978-0-88385-700-7.
Pengelley, David (2002), "The bridge between continuous and discrete via original sources", Study the Masters: The Abel-Fauvel Conference (PDF), National Center for Mathematics Education, Univ. of Gothenburg, Sweden.
Row, T. Sundara (1893), Geometric Exercises in Paper Folding, Madras: Addison, pp. 47–48.
Stein, Robert G. (1971), "A combinatorial proof that $\textstyle \sum k^{3}=(\sum k)^{2}$ ", Mathematics Magazine, 44 (3): 161–162, doi:10.2307/2688231, JSTOR 2688231.
Stroeker, R. J. (1995), "On the sum of consecutive cubes being a perfect square", Compositio Mathematica, 97 (1–2): 295–307, MR 1355130.
Toeplitz, Otto (1963), The Calculus, a Genetic Approach, University of Chicago Press, ISBN 978-0-226-80667-9.
Warnaar, S. Ole (2004), "On the $q$ -analogue of the sum of cubes", Electronic Journal of Combinatorics, 11 (1), Note 13, doi:10.37236/1854, MR 2114194.
Wheatstone, C. (1854), "On the formation of powers from arithmetical progressions" (PDF), Proceedings of the Royal Society of London, 7: 145–151, doi:10.1098/rspl.1854.0036.

외부 링크

[1] Sloane, N. J. A. (ed.), "Sequence A000537", The On-Line Encyclopedia of Integer Sequences, OEIS Foundation

[FOOTNOTEEdmonds1957-2] 에드먼즈(1957년).

[1]

[2]

Search

삼각수 제곱

네임스페이스

더

목차

역사

숫자 값, 기하학적 및 확률적 해석

교정쇄

일반화

메모들

참조

외부 링크