수신기 작동 특성

수신기 작동 특성 곡선 또는 ROC 곡선은 구별 임계값이 변화함에 따라 이항 분류기 시스템의 진단 능력을 보여주는 그래픽 그림이다. 이 방법은 원래 1941년부터 군사용 레이더 수신기의 운용자를 위해 개발되었으며, 이것이 그 명칭으로 이어졌다.

ROC 곡선은 다양한 임계값 설정에서 거짓 양성 비율(FPR)에 대한 실제 양성 비율(TPR)을 표시하여 생성된다. 참 양성률은 기계학습에서 감도, 회수 또는 검출^[9] 확률로도 알려져 있다. 거짓 양성률은 거짓 경보^[9] 확률이라고도 하며 (1 - 특수성)으로 계산할 수 있다. 또한 결정규칙의 제1종 오류의 함수로서 힘의 플롯으로 생각할 수 있다(성능을 모집단의 표본만으로 계산할 때, 이 수량의 추정자로 생각할 수 있다). 그러므로 ROC 곡선은 낙하의 함수로써의 민감도 또는 리콜이다. 일반적으로 검출 및 거짓 경보에 대한 확률 분포를 모두 알고 있는 경우, Y축 대 누적 검출 확률의 누적 분포 함수${\displaystyle -\infuly$}부터$$ 차별 임계값까지의 확률 분포에 따른 영역)를 표시하여 ROC 곡선을 생성할 수 있다.x축에 대한 거짓 확률의 ve 분포 함수.

ROC 분석은 가능한 최적 모델을 선택하고 비용 컨텍스트 또는 클래스 배포와 독립적으로 차선의 모델을 폐기하는 도구를 제공한다. ROC 분석은 진단 의사결정의 비용/효익 분석을 위한 직접적이고 자연스러운 방법으로 관련된다.

ROC 곡선은 제2차 세계 대전 중 전기 기술자와 레이더 기술자에 의해 전쟁터에서 적 물체를 탐지하기 위해 처음 개발되었으며, 곧 자극의 지각 탐지를 설명하기 위해 심리학에 도입되었다. 그 이후 ROC 분석은 수십 년 동안 의학, 방사선학, 생체 측정학, 자연 재해 예측,^[10] 기상학,^[11] 모델 성능 평가 ^[12]및 기타 분야에서 사용되었으며 기계 학습 및 데이터 마이닝 연구에 점점 더 많이 사용되고 있다.

ROC는 기준이 변경됨에 따라 두 가지 운용 특성(TPR과 FPR)을 비교한 것이기 때문에 상대 운용 특성 곡선으로도 알려져 있다.^[13]

요약하면: ROC 곡선은 모든 관련 수량을 하나의 플롯에 가질 수 있기 때문에 검출/분류 이론과 가설 시험에서 통계적 성능 측정으로서 매우 강력한 도구다.

기본개념

분류 모델(분류기 또는 진단^[14])은 특정 클래스/그룹 간의 인스턴스 매핑이다. 분류기 또는 진단 결과는 임의의 실제 값(연속 출력)이 될 수 있기 때문에, 계급 간의 분류기 경계는 임계값(예: 혈압 측정에 근거하여 고혈압이 있는지 여부를 판단하기 위해)에 의해 결정되어야 한다. 또는 클래스 중 하나를 나타내는 이산 클래스 레이블일 수 있다.

결과가 양수(p) 또는 음수(n)로 표시되는 2종류 예측 문제(이진 분류)를 고려하십시오. 이항 분류기에서 4가지 가능한 결과가 있다. 예측의 결과가 p이고 실제 값도 p이면 참양(TP)이라고 하지만 실제 값이 n이면 거짓양(FP)이라고 한다. 반대로 예측 결과와 실제 값이 모두 n일 때 참 음수(TN)가 발생했고, 거짓 음수(FN)는 예측 결과가 n일 때 실제 값이 p일 때 발생한다.

실제 문제에서 적절한 예를 들려면 특정 질병이 있는지 여부를 확인하는 진단 테스트를 고려해 보십시오. 이 경우에 잘못된 양성반응은 양성반응을 보였지만 실제로 그 병에 걸리지 않을 때 발생한다. 반면에 잘못된 음성은 음성으로 검사할 때 발생하는데, 이것은 그들이 건강하다는 것을 암시하고, 그들이 실제로 병에 걸렸을 때 발생한다.

P 양수 인스턴스로부터 실험을 정의하고 일부 조건에 대해 N개의 음수 인스턴스로부터 실험을 정의해 봅시다. 네 가지 결과는 다음과 같이 2×2 분할표 또는 혼란 행렬로 작성할 수 있다.

ROC 공간

분할표는 몇 가지 평가 "측정학"을 도출할 수 있다(인포박스 참조). ROC 곡선을 그리려면 (일부 분류기 매개변수의 함수로서) 참 양수(TPR)와 거짓 양수(FPR)만 필요하다. TPR은 시험 중 이용 가능한 모든 양성 검체 중에서 얼마나 많은 양의 정확한 양성 결과가 발생하는지를 정의한다. 반면에 FPR은 시험 중 이용 가능한 모든 음성 표본 중에서 얼마나 많은 잘못된 양성 결과가 발생하는지를 규정한다.

ROC 공간은 FPR과 TPR에 의해 각각 x축과 y축으로 정의되며, 이는 진정한 긍정(편익)과 거짓 긍정(비용) 사이의 상대적 절충을 나타낸다. TPR은 감도와 같고 FPR은 1 - 특성과 같기 때문에 ROC 그래프를 감도 대 (1 - 특수성) 그림이라고 부르기도 한다. 각 예측 결과 또는 혼동 행렬의 인스턴스는 ROC 공간의 한 점을 나타낸다.

가능한 최선의 예측 방법은 왼쪽 상단 모서리에 점을 산출하거나 ROC 공간의 좌표(0,1)를 산출하여 100% 민감도(허위 부정 없음)와 100% 특수성(허위 긍정 없음)을 나타낸다. (0,1)점을 만점 분류라고도 한다. 무작위 추측은 (긍정적이고 부정적인 기준 비율과 관계없이) 왼쪽 하단에서 오른쪽 상단 모서리로 대각선( 이른바 차별금지선)을 따라 포인트를 줄 것이다.^[23] 무작위 추측의 직관적인 예는 동전을 던져 결정하는 것이다. 표본의 크기가 증가함에 따라 랜덤 분류자의 ROC 지점은 대각선을 향한다. 균형이 잡힌 동전의 경우, 포인트(0.5, 0.5)로 기울게 된다.

대각선은 ROC 공간을 나눈다. 대각선 위의 점은 양호한 분류 결과(임의보다 우수함)를 나타내고, 선 아래의 점은 불량 결과(임의보다 좋지 않음)를 나타낸다. 일관적으로 나쁜 예측 변수의 출력은 단순히 좋은 예측 변수를 얻기 위해 반전될 수 있다는 점에 유의하십시오.

100개의 양수 및 100개의 음수 인스턴스로부터 4개의 예측 결과를 살펴보자.

ROC 공간에서 위의 네 가지 결과를 나타내는 그림은 그림에 나와 있다. 방법 A의 결과는 A, B, C 중에서 가장 우수한 예측력을 명백히 보여준다. B의 결과는 무작위 추측선(대각선)에 놓여 있으며, 표에서 B의 정확도가 50%임을 알 수 있다. 그러나 C가 중앙점(0.5,0.5)을 가로질러 미러링될 때, 결과적인 방법 C′은 A보다 훨씬 낫다. 이 미러링된 방법은 C 분할표를 작성한 어떤 방법이나 시험의 예측을 뒤집는 것일 뿐이다. 원래의 C 방법은 음의 예측력을 가지고 있지만, 단순히 결정을 번복하는 것만으로도 긍정적인 예측력을 가진 새로운 예측법 C′으로 이어진다. C 방법이 p 또는 n을 예측하는 경우, C method 방법은 각각 n 또는 p를 예측한다. 이런 방식으로 C′ 테스트가 가장 잘 수행될 것이다. 분할표의 결과가 왼쪽 위 모서리에 가까울수록 예측이 잘되지만, 두 방향의 랜덤 추측선으로부터의 거리는 한 방법이 얼마나 많은 예측력을 가지고 있는지를 나타내는 최선의 지표다. 결과가선 이하일 경우(즉, 방법이 무작위 추측보다 나쁠 경우), 그 힘을 활용하기 위해서는 방법의 예측을 모두 뒤집어야 하며, 따라서 결과가 무작위 추측선 위로 이동해야 한다.

ROC 공간의 곡선

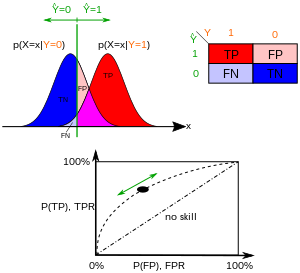
이항 분류에서 각 인스턴스의 클래스 예측은 종종 연속 랜덤 $변수{\displaystyle }$ X ${\displaystyle X}$에 기초하여 이루어지는데, 이 변수는 해당 인스턴스에 대해 계산된 "점수"이다(예: 로지스틱 회귀 분석의 추정 확률). 임계값 매개 변수 $T{\displaystyle }$ ${\displaystyle T}$을$($를) 지정하면 해당 는 X> ${\displaystyle$ X$>T$이면 "양수"로, 그렇지 않으면 "음수"로 분류된다. ${\displaystyle X}$ ${\displaystyle X}$은(는) 실제로 클래스 "양수"에 속할$$ 경우 $확률밀도{\displaystyle {}_{}}$ f ${\displaystyle {1\mathrm{}}_{}x}$ )$${\$displaystyle f_{1}(x)$을 $따르고{\displaystyle {}_{}}$, 그렇지 않을$$ 경우 f ${\displaystyle {0\mathrm{}}_{}x}$) ${\displaystystyle f_{0}(x)}$을 따른다. 따라서 TPR${\displaystyle (T_{}^{}}$ ) = ${\displaystyle )}$T${\displaystyle {\mathrm{}}_{}^{}}$ ${\displaystyle {}_{}^{}{}_{}}$ ${\displaystyle {1\mathrm{}}_{}}$( ${\displaystyle x}$) ${\displaystyle d}$d {\$displaystyle {\mbox{$$TPR}}(T)=\int _{T}^{\infty }f_{1}(x)\,dx}$ and the false positive rate is given by ${\displaystyle {\mbox{FPR}}(T)=\int _{T}^{\infty }f_{0}(x)\,dx}$. The ROC curve plots parametrically ${\displaystyle {\mbox{$$TPR}(T)$ 대$$ ${\displaystyle \text{FPR}(T}$ ${\displaystyle )}$ ${\displaystyle {\mbox{FPR}(T)}($$T{\displaystyle }$) 대 T ${\displaystyle T}$을(를) 다양한 매개 변수로$$ 사용$$.

예를 들어, 병든 사람과 건강한 사람의 혈액 단백질 수치가 각각 2 g/dL과 1 g/dL의 방법으로 분포한다고 상상해보자. 의료 검사는 혈액 샘플에서 특정 단백질의 수준을 측정하고 특정 임계값을 초과하는 숫자를 질병을 나타내는 것으로 분류할 수 있다. 실험자는 임계치(그림의 검은색 수직선)를 조정할 수 있으며, 이는 결국 거짓 양성률을 변화시킬 것이다. 임계값을 증가시키면 곡선의 좌회전 움직임에 해당하는 잘못된 긍정(및 더 많은 잘못된 부정)이 감소한다. 곡선의 실제 모양은 두 분포가 얼마나 겹치는가에 따라 결정된다.

추가 해석

때때로, ROC는 요약 통계를 생성하기 위해 사용된다. 일반 버전은 다음과 같다.

• 45도의 라인이 차별 없는 라인에 직교하는 ROC 곡선의 절편 - 민감도 = 1 - 특수성인 균형점
• 무오차점(0,1)에 가장 근접한 무차별선(0,1)에 평행한 45도 접선을 갖는 ROC 곡선의 절편 - 유덴의 J 통계량이라고도 하며 Informentity로^{[citation needed]} 일반화된다.
• ROC 곡선과 무차별선 사이에 2를 곱한 영역을 지니계수라고 한다. 지니계수라고도 하는 통계적 산포의 척도와 혼동해서는 안 된다.
• 전체 ROC 곡선과 삼각형 ROC 곡선 사이의 영역(만 포함), (1,1) 및 선택된 하나$({\displaystyle \mathrm{tp}}$ ${\displaystyle r}$, ${\displaystyle f}$ ${\displaystyle p}$ $){\displaystyle (tpr,fpr)}$ -$$ 일관성^[24]
• ROC 곡선 또는 "AUC"("커브 아래의 면적") 또는 A("a-primate"^[25]로 발음됨) 또는 "c-statistic"("컨코드 통계량")^[26] 아래에 있는 영역.
• 민감도 지수 d'("d-prime")는 소음 독립형 조건에서 시스템의 활동 분포 평균과 신호 독립형 조건에서의 분포 사이의 거리로서, 이 두 분포가 모두 동일한 표준 편차로 정규 분포라는 가정 하에 표준 편차로 나눈 값이다. 이러한 가정 하에서 ROC의 모양은 전적으로 d'에 의해 결정된다.

그러나 ROC 곡선을 단일 숫자로 요약하려는 시도는 특정 판별기 알고리즘의 트레이드오프 패턴에 대한 정보를 손실한다.

곡선 아래 영역

정규화된 단위를 사용할 때, 곡선 아래의 영역(흔히 단순하게 AUC라고 함)은 분류자가 무작위로 선택한 양의 인스턴스(instance)를 무작위로 선택한 음의 인스턴스(instance)보다 높게('양'의 순위가 '음'보다 높다고 가정)^[27]할 확률과 같다. 이는 다음과 같이 볼 수 있다: 곡선 아래의 영역은 (큰 임계값 $T{\displaystyle }$ ${\displaystyle T}$이(가) x축에 더 낮은 값을 가지므로$$ 적분 경계는 역전됨)

${\displaystyle {\mbox}TPR}(T):T\mapsto y(x)}$

${\displaystyle {\mbox{FPR}(T):T\mapsto x}$

${\displaystyle A=\int _{x=0}^{1}{\mbox{TPR}}({\mbox{F)PR}}^{-1}(x)\,dx=\int_{\int _{\infit }^{-\infit }{\mbox{TPR}(T){\mbox{FPR}}'(T)\,dT=\int _{-\infty }^{\infty }\int _{-\infty }^{\infty }I(T'>T)f_{1}(T')f_{0}(T)\,dT'\,dT=P(X_{1}>X_{0})}$

여기서 $X{\displaystyle {}_{}}$ ${\displaystyle {1\mathrm{}}_{}}$ ${\$${$$1$}는$$ 양의 인스턴스(instance)에 대한 점수, ${\displaystyle {X\mathrm{}}_{}}$ $0{\displaystyle {}_{}}$ {\$displaystyle X_{0}$은 음의 인스턴스(instance)에 대한 점수, $f{\displaystyle {}_{}}$ ${\displaystyle {0\mathrm{}}_{}}$ ${\$ 및 $f{\displaystyle {}_{}}$ ${\displaystyle {1\mathrm{}}_{}}$ ${\$1}은 $이전$절에서 정의한 확률 밀도이다$$.

AUC가 부정보다 높은 순위에 있는지 여부를 검정하는 ^[28][29]Mann-Whitney U와 밀접하게 연관되어 있음을 더욱 알 수 있다. 계급의 윌콕슨 시험과도 맞먹는다.^[29] 예측 변수 $f$ ${\textstyle f}$의 경우$,$ AUC의 편향되지 않은 추정기는 다음과 같은 Wilcoxon-Mann-Whitney 통계량으로 표현할 수 있다.^[30]

${\displaystyle AUC(f)={\frac {\sum _{t_{0}\in {\mathcal {D}}^{0}}\sum _{t_{1}\in {\mathcal {D}}^{1}}{\textbf {1}}[f(t_{0})<f(t_{1})]}{ {\mathcal {D}}^{0} \cdot {\mathcal {D}}^{1} }},}$

어디, 1[f(t 0<>f(t 1컵]{\textstyle{\textbf{1}}[f(t_{0})<>f(t_{1})]};1iff f(t 0)<>를 반환하는 지표 기능을 나타낸다 이름(t1){\displaystyle f(t_{0})<, f(t_{1})} 그렇지 않으면;부정적인 예들의 D0{\displaystyle{{D\mathcal}}^{0}}은 집합과 0을 반환하다. D1${\displaystyle {\mathcal{D}^{1}$는 양의 예시 집합이다.

AUC는 ${\displaystyle {G1\mathrm{}}_{}}$= ${\displaystyle 2}$ ${\displaystyle \text{AUC}}$- 1 ${\displaystyle G_{1}=2{\mbox{$${\displaystyle 1}$$\}$라는 공식에 의해 *지니 계수*(${\displaystyle {G1\mathrm{}}_{}}$ ${\$와 관련된다.$AUC}-1$ 여기서:

${\displaystyle G_{1}=1-\sum _{k=1}^{n}(X_{k}-X_{k-1})(Y_{k}+Y_{k-1})}$^[31]

이러한 방식으로 사다리꼴 근사치의 평균을 사용하여 AUC를 계산할 수 있다. G1{\displaystyle G_{1}는 지니계수라고도 하는 통계적 분산 측정과 혼동해서는 안 된다.

또한 두 예측 결과 사이의 선 세그먼트에서 임의의 점(ROC AUCH = ROC AUCH AUC)은 세그먼트의 반대편 구성 요소의 상대적 길이에 비례하는 확률로 한 시스템 또는 다른 시스템을 사용하여 달성할 수 있으므로 ROC 볼록스 선체 아래의 면적(ROC AUCH = ROCH AUC)을 계산하는 것이 일반적이다.^[32] 또한 빈도를 반전시킬 수도 있다 – 그림에서처럼 더 나쁜 해결책이 더 나은 해결책이 되기 위해 반영될 수 있다; 빈도는 어느 선 세그먼트에서도 반영될 수 있지만, 이 보다 극단적인 형태의 융접은 데이터를 과도하게 적합시킬 가능성이 훨씬 높다.^[33]

머신러닝 커뮤니티는 모델 비교를 위해 ROC AUC 통계를 가장 많이 사용한다.^[34] 이러한 관행은 AUC의 추정이 상당히 시끄럽고 다른 문제들로 고통 받고 있기 때문에 의문을 제기해 왔다.^[35][36][37] 그럼에도 불구하고, 통합 분류 성과의 척도로서 AUC의 일관성은 균일한 비율 분포의 관점에서 입증되었고,^[38] AUC는 브리어 점수 같은 많은 다른 성과 지표와 연계되었다.^[39]

대만 탄산 암모늄-우라닐 또 다른 문제는 단일 번호에 대만 곡선을 낮추는 것은 사실은 그 관련 대안을 마련 Informedness이 다른 시스템 또는 성능점 아니라 개별 시스템의 성능뿐만 아니라 오목한 형태 회복의 가능성을 무시하고 사울 사이의 트레이드 오프에 대해, 사태를 외면하고 있다.[표창 필요한] 또는 DeltaP가 권장된다.^[24][40] 이러한 측정은 기본적으로 DeltaP' = Informity = 2AUC-1로 단일 예측 지점에 대한 지니와 동일하며, DeltaP = Markness는 이중(실제 등급으로부터의 예측을 예측하는 viz)을 나타내며, 그 기하 평균은 Matthews 상관 계수다.^{[citation needed]}

반면에 대만 탄산 암모늄-우라닐 0과 1— 사이에 충분한 정보를 선형 분급기 0.5—은 다른 방안 Informedness,[표창 필요한]확실성[24]과 지니 계수로(단일 parameterization 또는 단일 시스템 사건에)[표창 필요한] 알려진 굴복에 따라 다양한 모든 이동하는 1완벽한 표현하 0기회를 성능을 나타내는 장점을 가진다. 성능, 그리고 −1"페를 나타냅니다.항상 잘못된 응답을 제공하는 완전한 지식의 반대" 사례.^[41] 우연한 성과를 0으로 가져오면 이러한 대체 척도를 카파 통계로 해석할 수 있다. 지식은 코헨 카파, 플라이스 카파 등 카파의 다른 일반적인 정의에 비해 머신러닝에 바람직한 특성을 가지고 있는 것으로 나타났다.^{[citation needed][42]}

때때로 전체 곡선보다는 ROC 곡선의 특정 영역을 보는 것이 더 유용할 수 있다. 부분적인 AUC를 계산하는 것이 가능하다.^[43] 예를 들어, 종종 모집단 선별 검사의 주된 관심사인 낮은 거짓 양성률로 곡선 영역에 초점을 맞출 수 있다.^[44] P common N (생물정보학 애플리케이션에서 공통)이 x축에 대한 로그 척도를 사용하는 분류 문제에 대한 또 다른 일반적인 접근법이다.^[45]

곡선 아래의 ROC 영역은 c-통계학적 또는 c 통계량이라고도 한다.^[46]

기타조치

TOC(Total Operating Personality)는 또한 ROC보다 더 많은 정보를 공개하면서 진단 능력을 특징으로 한다. 각 임계값에 대해 ROC는 TP/(TP + FN)와 FP/(FP + TN)의 두 가지 비율을 나타낸다. 즉, ROC는 적중/(히트 + 미스)와 거짓 경보/(허위 경보 + 정정 거부)를 공개한다. 반면에 TOC는 각 임계값에 대한 보정값 표의 총 정보를 보여준다.^[47] TOC 방법은 ROC 방법이 제공하는 모든 정보와 더불어 ROC가 밝히지 않는 중요한 추가 정보, 즉 각 임계값에 대한 보정표의 모든 항목의 크기를 나타낸다. TOC는 또한 ROC의 인기 있는 AUC를 제공한다.^[48]

이 수치는 동일한 데이터와 임계값을 사용하는 TOC 및 ROC 곡선이다. 임계값 74에 해당하는 점을 고려하십시오. TOC 곡선은 안타 수를 3으로 나타내고, 따라서 빗맞은 횟수는 7이다. 또한 TOC 곡선을 보면 거짓 경보의 수는 4개, 정확한 거부 횟수는 16개임을 알 수 있다. ROC 곡선의 특정 지점에서 거짓 경보/(허위 경보 + 정확한 거부) 및 히트/(히트 + 미스)의 비율 값을 수집할 수 있다. 예를 들어, 임계값 74에서는 x 좌표가 0.2이고 y 좌표가 0.3인 것이 분명하다. 그러나 이 두 값은 기초적인 2대 2 분할표의 모든 항목을 구성하기에 불충분하다.

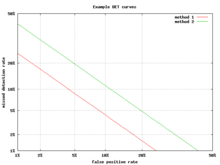
탐지 오류 트레이드오프 그래프

ROC 곡선의 대안은 검출 오류 트레이드오프(DET) 그래프로, 비선형 변환 x축과 y축에 대한 거짓 음률(실수 검출) 대 거짓 양률(허위 경보)을 표시한다. 변환 함수는 정규 분포의 계량 함수, 즉 누적 정규 분포의 역함수다. 사실 적중률의 보완, 즉 미스 레이트 또는 거짓 마이너스 레이트를 사용하는 것을 제외하면, 이하 zROC와 동일한 변환이다. 이 대안은 관심 영역에 더 많은 그래프 영역을 사용한다. 대부분의 ROC 영역은 거의 관심이 없다. 주로 y축과 왼쪽 상단 모서리에 대해 지역을 집중한다. 이 영역은 보완 요소 대신 미스 레이트를 사용하기 때문에 적중률이 DET 플롯의 왼쪽 하단 모서리가 된다. 또한 DET 그래프는 선형성의 유용한 속성과 정규 분포에 대한 선형 분계점 동작을 가지고 있다.^[49] DET 플롯은 DET라는 이름이 처음 사용된 자동 스피커 인식 커뮤니티에서 광범위하게 사용된다. 이러한 축의 뒤틀림을 이용한 그래프에서의 ROC 성능 분석은 심리학자들이 20세기 중반에 걸친 인식 연구에서 사용되었는데,^{[citation needed]} 여기서 이를 "이중 확률지"라고 불렀다.^[50]

Z-점수

ROC 곡선에 표준점수를 적용하면 곡선이 직선으로 변형된다.^[51] 이 z-점수는 평균이 0이고 표준 편차가 1인 정규 분포를 기반으로 한다. 기억력 강도 이론에서 zROC는 선형일 뿐만 아니라 경사도 1.0이라고 가정해야 한다. 대상(대상자가 리콜해야 하는 스터디 대상)과 유인(대상자가 리콜을 시도하는 비연구 대상물)의 정규 분포가 zROC를 선형화하는 요인이다.

zROC 곡선의 선형성은 목표물의 표준 편차와 강도 분포에 따라 달라진다. 표준 편차가 같을 경우 기울기는 1.0이 된다. 목표 강도 분포의 표준 편차가 미끼 강도 분포의 표준 편차보다 크면 기울기가 1.0보다 작다. 대부분의 연구에서 zROC 곡선 경사가 지속적으로 1 아래로 떨어져 있으며, 대개 0.5에서 0.9 사이인 것으로 밝혀졌다.^[52] 많은 실험에서 zROC 기울기는 0.8이었다. 기울기가 0.8이면 목표 강도 분포의 변동성이 미끼 강도 분포의 변동성보다 25% 크다는 것을 의미한다.^[53]

사용되는 또 다른 변수는 d' (d prime) (위에서 "기타 조치"에서 설명됨)로 z 값 단위로 쉽게 표현할 수 있다. d'는 일반적으로 사용되는 매개변수지만, 위에서 만들어진 강도 이론의 매우 강한 가정을 엄격히 고수할 때만 관련성이 있다는 것을 인식해야 한다.^[54]

ROC 곡선의 z-점수는 특별한 상황을 제외하고 가정된 대로 항상 선형이다. 요넬리나스의 친숙성-회수 모델은 인식기억의 2차원 계정이다. 특정 입력에 대해 단순히 예, 아니오라고 대답하는 피사체가 입력에 친숙한 느낌을 주는 대신, 피사체는 원래의 ROC 곡선처럼 작용한다. 그러나 무엇이 변하느냐는 R(Recemption)에 대한 매개변수다. 기억은 전부 혹은 아예 없는 것으로 가정되며, 그것은 친숙함을 능가한다. 기억 요소가 없다면 zROC의 예상 기울기는 1이 될 것이다. 그러나 기억 요소를 추가할 때 zROC 곡선은 위로 오목하게 되며 기울기는 감소한다. 이러한 형태와 기울기의 차이는 일부 항목이 회수되기 때문에 변동성의 추가 요소에서 비롯된다. 기억상실증 환자는 기억을 할 수 없기 때문에 요넬리나스 zROC 곡선은 1.0에 가까운 경사를 가질 수 있다.^[55]

역사

ROC 곡선은 제2차 세계대전 중 레이더 신호 분석에 처음 사용됐다.^[56] 1941년 진주만 공격 이후 미군은 레이더 신호에서 일본 항공기가 정확하게 탐지될 것이라는 예측을 높이기 위해 새로운 연구에 착수했다. 이러한 목적을 위해 그들은 이러한 중요한 구분을 할 수 있는 레이더 수신기 운영자의 능력을 측정했는데, 이를 수신기 작동 특성이라고 한다.^[57]

1950년대에 ROC 곡선은 약한 신호의 인간(그리고 때때로 인간이 아닌 동물) 탐지를 평가하기 위해 정신물리학에 사용되었다.^[56] 의학에서는 ROC 분석이 진단 테스트 평가에 광범위하게 사용되어 왔다.^[58][59] ROC 곡선은 역학 및 의학 연구에도 광범위하게 사용되며 증거 기반 의학과 함께 자주 언급된다. 방사선학에서 ROC 분석은 새로운 방사선학 기법을 평가하는 일반적인 기법이다.^[60] 사회과학에서 ROC 분석을 흔히 ROC Accuracy Ratio라고 하는데, 이는 기본 확률 모델의 정확도를 판단하는 일반적인 기법이다. ROC 곡선은 시험의 진단 정확도를 평가하고, 시험의 최적 컷오프를 선택하고, 여러 시험의 진단 정확도를 비교하기 위해 실험실 의학에서 널리 사용된다.

또한 ROC 곡선은 기계 학습 기법의 평가에 유용하다는 것이 입증되었다. 기계학습에서 ROC의 첫 번째 적용은 서로 다른 분류 알고리즘을 비교하고 평가하는 데 있어서 ROC 곡선의 가치를 입증한 Spackman에 의해서였다.^[61]

ROC 곡선은 기상학에서 예측을 검증하는 데도 사용된다.^[62]

이항 분류를 초과하는 ROC 곡선

클래스 수에 따라 자유도가 2차적으로 증가하며, ROC $공간$은 c${\displaystyle (\mathrm{c}}$ - 1${\displaystyle }$) ${\displaystyle$ c$(c-1)$치수가$$ 있으므로, 클래스 수가 2개 이상인 분류 문제에 대한 ROC 곡선의 확장은 항상 번거로웠다. 여기서 c ${\displaystyle$ c$}$은 $클래스$ 수입니다.^[63] 세 가지 등급(3방향 ROC)의 특정 사례에 대해 일부 접근방식이 이루어졌다.^[64] ROC 지표면(VUS)에 따른 부피 계산은 다중 등급 문제에 대한 성능 지표로 분석, 연구되었다.^[65] 그러나, 진정한 VUS에 근접한 복잡성 때문에, AUC의 확장에 기초한 다른 접근법은 평가 지표로 더 인기가 있다.

분류 모델 평가를 위한 ROC 곡선의 성공을 감안하여, 다른 감독 업무에 대한 ROC 곡선의 확장도 조사되었다. 회귀 문제에 대한 주목할 만한 제안은 소위 회귀 오류 특성(REC) 곡선과 회귀 ROC(Rech) 곡선이다.^[68] 후자에서 RROC 곡선은 비대칭, 우위 및 볼록 선체의 개념으로 분류에 대한 ROC 곡선과 극히 유사하게 된다. 또한 RROC 곡선 아래의 영역은 회귀 모형의 오차 분산에 비례한다.

참고 항목

• 브리어 점수
• 결정계수
• 상시 거짓 경보율
• 탐지 오류 트레이드오프
• 검출이론
• F1 점수
• 거짓 경보
• 정확성에 대한 가설 검정
• 정밀도 및 회수
• 로케트
• 민감성 및 특수성
• 총 작동 특성

참조

외부 링크

• ROC 데모
• 또 다른 ROC 데모
• ROC 비디오 설명
• 총 운영 특성 소개: 토지변경모델 평가의 효용성에 관한 연구
• R에서 TOC 패키지를 실행하는 방법
• Github의 TOC R 패키지
• TOC 원곡선 생성을 위한 Excel 통합 문서

추가 읽기

• 발라크리쉬난, 나라야나스와미(1991); 마르셀 데커, 주식회사, ISBN 978-0-8247-8587-1
• Brown, Christopher D.; Davis, Herbert T. (2006). "Receiver operating characteristic curves and related decision measures: a tutorial". Chemometrics and Intelligent Laboratory Systems. 80: 24–38. doi:10.1016/j.chemolab.2005.05.004.
• Rotello, Caren M.; Heit, Evan; Dubé, Chad (2014). "When more data steer us wrong: replications with the wrong dependent measure perpetuate erroneous conclusions" (PDF). Psychonomic Bulletin & Review. 22 (4): 944–954. doi:10.3758/s13423-014-0759-2. PMID 25384892. S2CID 6046065.
• Fawcett, Tom (2004). "ROC Graphs: Notes and Practical Considerations for Researchers" (PDF). Pattern Recognition Letters. 27 (8): 882–891. CiteSeerX 10.1.1.145.4649. doi:10.1016/j.patrec.2005.10.012.
• 고넨, 미타트(2007); SAS, SAS Press, ISBN 978-1-59994-298-8을 이용한 수신기 작동 특성 곡선 분석
• 그린, 윌리엄 H, (2003) Econometric Analysis, 5판, 프렌티스 홀, ISBN 0-13-066189-9
• Heagerty, Patrick J.; Lumley, Thomas; Pepe, Margaret S. (2000). "Time-dependent ROC Curves for Censored Survival Data and a Diagnostic Marker". Biometrics. 56 (2): 337–344. doi:10.1111/j.0006-341x.2000.00337.x. PMID 10877287. S2CID 8822160.
• 호스머, 데이비드 W., 그리고 스탠리 (2000) 레메쇼; 적용 로지스틱 회귀 분석, 2차 에드, 뉴욕: 와일리, ISBN 0-471-35632-8
• Lasko, Thomas A.; Bhagwat, Jui G.; Zou, Kelly H.; Ohno-Machado, Lucila (2005). "The use of receiver operating characteristic curves in biomedical informatics". Journal of Biomedical Informatics. 38 (5): 404–415. CiteSeerX 10.1.1.97.9674. doi:10.1016/j.jbi.2005.02.008. PMID 16198999.
• Mas, Jean-François; Filho, Britaldo Soares; Pontius, Jr, Robert Gilmore; Gutiérrez, Michelle Farfán; Rodrigues, Hermann (2013). "A suite of tools for ROC analysis of spatial models". ISPRS International Journal of Geo-Information. 2 (3): 869–887. Bibcode:2013IJGI....2..869M. doi:10.3390/ijgi2030869.
• Pontius, Jr, Robert Gilmore; Parmentier, Benoit (2014). "Recommendations for using the Relative Operating Characteristic (ROC)". Landscape Ecology. 29 (3): 367–382. doi:10.1007/s10980-013-9984-8. S2CID 15924380.
• Pontius, Jr, Robert Gilmore; Pacheco, Pablo (2004). "Calibration and validation of a model of forest disturbance in the Western Ghats, India 1920–1990". GeoJournal. 61 (4): 325–334. doi:10.1007/s10708-004-5049-5. S2CID 155073463.
• Pontius, Jr, Robert Gilmore; Batchu, Kiran (2003). "Using the relative operating characteristic to quantify certainty in prediction of location of land cover change in India". Transactions in GIS. 7 (4): 467–484. doi:10.1111/1467-9671.00159. S2CID 14452746.
• Pontius, Jr, Robert Gilmore; Schneider, Laura (2001). "Land-use change model validation by a ROC method for the Ipswich watershed, Massachusetts, USA". Agriculture, Ecosystems & Environment. 85 (1–3): 239–248. doi:10.1016/S0167-8809(01)00187-6.
• Stephan, Carsten; Wesseling, Sebastian; Schink, Tania; Jung, Klaus (2003). "Comparison of Eight Computer Programs for Receiver-Operating Characteristic Analysis". Clinical Chemistry. 49 (3): 433–439. doi:10.1373/49.3.433. PMID 12600955.
• 스윗츠, 존 A; 도스, 로빈 M; 모나한, 존(2000); 과학, 사이언티픽 아메리칸을 통한 더 나은 결정, 10월 페이지 82-87
• Zou, Kelly H.; O'Malley, A. James; Mauri, Laura (2007). "Receiver-operating characteristic analysis for evaluating diagnostic tests and predictive models". Circulation. 115 (5): 654–7. doi:10.1161/circulationaha.105.594929. PMID 17283280.
• Zhou, Xiao-Hua; Obuchowski, Nancy A.; McClish, Donna K. (2002). Statistical Methods in Diagnostic Medicine. New York, NY: Wiley & Sons. ISBN 978-0-471-34772-9.