요인

선택된 인수; 과학적 표기법의 값은 반올림됩니다.

${\displaystyle n}$	${\displaystyle n!}$
0	1
1	1
2	2
3	6
4	24
5	120
6	720
7	5040
8	40320
9	362880
10	3628800
11	39916800
12	479001600
13	6227020800
14	87178291200
15	1307674368000
16	20922789888000
17	355687428096000
18	6402373705728000
19	121645100408832000
20	2432902008176640000
25	1.551121004×1025
50	3.041409320×1064
70	1.197857167×10100
100	9.332621544×10157
450	1.733368733×101000
1000	4.023872601×102567
3249	6.412337688×1010000
10000	2.846259681×1035659
25206	1.205703438×10100000
100000	2.824229408×10456573
205023	2.503898932×101000004
1000000	8.263931688×105565708
10100	1010101.9981097754820

수학에서 음이 아닌 $정수{\displaystyle }$ n ${\displaystyle n$의 계승은 $n{\displaystyle !}$ ${\displaystyle n!}$으로 표시되며$,$ $n{\displaystyle }$ ${\displaystyle n}$보다 작거나 같은 모든 양의 정수의 곱입니다$.$ $n$ ${\displaystyle n}$의 요인도 n ${\displaystyle n}$의 곱과 같으며$$ 다음으로 작은 요인도 있습니다.

예를들면, 0!의 값은 빈 제품에 대한 관례에 따라 1입니다.^[1]

인자는 여러 고대 문화에서 발견되었으며, 특히 자인 문학의 표준 저작에서 인도 수학과 탈무드 서적 세퍼 예치라에서 유대 신비주의자들에 의해 발견되었습니다. 계승 연산은 수학의 많은 영역에서 발견되는데, 특히 조합론에서 가장 기본적인 사용은 $n개$의 ${\display$ $n$$}$개의$$ 서로 다른 객체 중 가능한 서로 다른 시퀀스(순열)를 세는 것입니다: $!{\display$ n$!}$ 수학적 분석에서$$, 요인은 지수 함수 및 기타 함수의 멱급수에 사용되며 대수학, 수론, 확률론 및 컴퓨터 과학에도 적용됩니다.

계승 함수에 대한 수학의 대부분은 18세기 말과 19세기 초에 개발되었습니다. 스털링의 근사치는 큰 수의 계승에 대한 정확한 근사치를 제공하여 지수 성장보다 더 빠르게 성장함을 보여줍니다. Legendre의 공식은 요인의 소인수분해에서 소수의 지수를 설명하고 요인의 후행 0을 계산하는 데 사용할 수 있습니다. 다니엘 베르누이와 레온하르트 오일러는 요인 함수를 (오프셋) 감마 함수인 음의 정수를 제외하고 복소수의 연속 함수로 보간했습니다.

이항 계수, 이중 인수분해, 하강 인수분해, 원시 및 하위 인수분해를 포함하여 많은 다른 주목할 만한 함수 및 숫자 시퀀스가 인수분해와 밀접하게 관련되어 있습니다. 요인 함수의 구현은 일반적으로 다양한 컴퓨터 프로그래밍 스타일의 예로 사용되며 과학 계산기 및 과학 컴퓨팅 소프트웨어 라이브러리에 포함됩니다. 곱 공식 또는 반복을 사용하여 큰 인수를 직접 계산하는 것은 효율적이지 않지만 더 빠른 알고리즘은 동일한 자릿수의 숫자에 대한 빠른 곱셈 알고리즘 시간과 일정한 인수 내에서 일치하는 것으로 알려져 있습니다.

역사

요소의 개념은 많은 문화권에서 독립적으로 생겨났습니다.

• 인도 수학에서 인자에 대한 가장 초기의 설명 중 하나는 자인 문학의 표준 작품 중 하나인 아누요가다브라-수트라(^[2]Anuyogadvāra-sutra)에서 유래하며, 기원전 300년부터 서기 400년까지 날짜가 지정되어 있습니다.^[3] 요인에 대한 일반적인 곱 공식에서 두 개를 빼서 혼합된 순서의 수를 평가하는 항목 집합의 정렬된 순서와 반대 순서를 다른 "혼합" 순서에서 분리합니다. 6세기 CE 자인 스님 지나바드라도 순열의 곱 규칙을 설명했습니다.^[2] 힌두교 학자들은 적어도 1150년에 바샤라 2세가 ī라바트 ī에서 계승을 언급한 이래로 계승 공식을 사용해 왔습니다. 이는 비슈누가 자신의 네 가지 특징적인 대상(고둥 껍질, 원반, 메이스, 연꽃)을 네 손에 잡을 수 있는 방법과 열 손을 가진 신에게도 비슷한 문제와 관련이 있습니다.
• 중동의 수학에서, 탈무드 시대 (서기 200년에서 500년)의 히브리 신비주의 창조 책인 세퍼 예찌라는 히브리 알파벳에서 형성될 수 있는 단어의 수에 대한 조사의 일환으로 7까지 계승을 나열합니다.^[5][6] 8세기 아랍 문법학자 알칼릴 이븐 아흐마드 알파라히디도 비슷한 이유로 인수분해를 연구했습니다.^[5] 아랍 수학자 이븐 알하이탐(965년경 – 1040년경)은 인수분해와 소수를 연결하는 윌슨의 정리를 처음으로 공식화했습니다.^[7]
• 유럽에서는, 비록 그리스 수학이 일부 조합론을 포함하고, 플라톤이 5,040개(인수)를 이상적인 공동체의 모집단으로 사용한 것으로 유명하지만, 부분적으로 그것의 분할 특성 때문에 고대 그리스의 인수 연구에 대한 직접적인 증거는 없습니다.^[8] 대신 유럽에서 요소에 대한 첫 번째 작업은 샤브베타이 돈놀로와 같은 유대 학자들에 의해 세퍼 예찌라 구절을 설명했습니다.^[9] 1677년, 영국의 작가 파비안 스테드먼은 몇몇 조율된 종들의 울리는 것을 포함하는 음악 예술인 벨소리를 바꾸기 위해 요소들을 적용하는 것을 묘사했습니다.^[10][11]

15세기 후반부터 인수분해는 서양 수학자들의 연구 대상이 되었습니다. 1494년 논문에서 이탈리아 수학자 루카 파치올리는 식탁 배열의 문제와 관련하여 인수를 11까지 계산했습니다.^[12] 크리스토퍼 클라비우스는 1603년에 요하네스 드 사크로보스코의 연구에 대한 논평에서 인수분해에 대해 논의했고, 1640년대에 프랑스의 다수학자 마린 메르센은 클라비우스의 연구를 바탕으로 64!까지 큰(완전히 정확하지는 않지만) 인수분해 표를 발표했습니다.^[13] 지수 함수에 대한 멱급수는 계수에 대한 계수의 역수를 가지는 지수 함수에 대한 멱급수는 1676년 아이작 뉴턴이 고트프리트 빌헬름 라이프니츠에게 보낸 편지에서 처음으로 공식화되었습니다.^[14] 인수분해에 관한 초기 유럽 수학의 다른 중요한 업적은 존 월리스의 1685년 논문에서 광범위한 범위를 포함하는데, 이 논문은 1721년 에이브러햄 드 무아브르의 $n{\displaystyle }${\$display$n}의 큰 값에 대한 근사값에 대한 연구이며, 1729년 제임스 스털링이 드 무아브르에게 보낸 편지에서 스털링의 근사값으로 알려지게 된 것을 기술한 것입니다. 그리고 동시에 Daniel Bernoulli와 Leonhard Euler에 의해 감마 함수에 대한 계승 함수의 연속 확장을 공식화합니다.^[15] Adrien-Marie Legendre는 1808년 정수론에 대한 텍스트에서 인수분해에서 소수로 지수를 설명하는 Legendre의 공식을 포함시켰습니다.^[16]

인수분해에 대한$$ $n{\displaystyle !}$ ${\displaystyle n!}$ 표기법은 1808년 프랑스 수학자 크리스티안 크람에 의해 소개되었습니다.^[17] 다른 많은 표기법도 사용되었습니다. 또 다른 나중 표기법 ${\displaystyle n\underset{}{}}$ ${\displaystyle \underset{}{}}$ ${\$요인의 인수가 상자의 왼쪽과 아래로 반쯤 둘러싸인${\,n$는 한동안 영국과 미국에서 인기를 끌었지만 타이핑이 어려워서인지 사용하지 않게 되었습니다.^[17] "factorial" (원래 프랑스어: factorielle)이라는 단어는 1800년 루이 프랑수아 앙투안 아르보가스트에 의해 최초로 사용되었는데,^{[19] [18]}이는 파 디 브루노 공식에 대한 첫 번째 연구에서 사용되었지만 산술 진행의 곱에 대한 더 일반적인 개념을 가리킵니다. 이 이름이 언급하는 "요인"은 요인에 대한 곱 공식의 항입니다.^[20]

정의.

양의 정수 $n{\displaystyle }$ ${\displaystyle$ n$}$의 계승 함수는 $n{\displaystyle }$ ${\displaystyle n}$보다 크지 않은 모든 양의 정수의 곱으로 정의됩니다$$.

이것은 제품 표기법에 다음과^[1] 같이 더 간결하게 쓰여질 수 있습니다.

이 곱 공식이 마지막 항을 제외한 모든 항을 유지하도록 변경되면 더 작은 요인에 대해 동일한 형태의 곱을 정의하게 됩니다. 따라서 요인 함수의 각 값은 이전 값에 $n{\displaystyle }$ ${\displaystyle$ n$}$을 곱하여 얻을 수 있습니다$.$^[21]

${\displaystyle \mathrm{예}}$를 들어 $5$!${\displaystyle }$= ${\displaystyle 5}$ ⋅ 4! = 5 ⋅ ${\displaystyle 24}$ = $120 {\displaystyle 5$! = 5$\cdot$ 4! = 5$\cdot$ 24 = 120}입니다.

0의 인수

$0$ ${\displaystyle 0}$의 인수는 $1$ ${\displaystyle$ 1$}$또는 ${\displaystyle \mathrm{기호}}$로 $0{\displaystyle !}$ = 1${\$displaystyle 0!= 1}입니다. 이 정의에는 다음과 같은 몇 가지 동기가 있습니다.

• $n$ = ${\$displaystyle n = 0}일 때, n!{\displaystyle n!}의 곱의 정의는 수가 전혀 없는 곱을 포함하며, 따라서 원소가 없는 곱인 빈 곱은 곱셈 항등식과 같다는 더 넓은 관례의 예도 마찬가지입니다.
• 0개의 객체에 대한 순열은 정확히 하나입니다. 순열할 것이 없고, 아무것도 하지 않는 것이 유일한 재배열입니다.^[21]
• 이 규칙은 조합론의 많은 ID를 매개 변수의 모든 유효한 선택에 유효하게 만듭니다. 예를 들어, $n$ ${\displaystyle$ n$}$ 집합에서 $n$ ${\displaystyle n}$ 요소를 모두 선택하는 방법의 수는$$($\genfrac{}{}{0ex}{}{n}{}$ n$$) = $n\frac{}{}$!$\frac{}{}$n$$! 0 ! = 1, {\textstyle {\tbinom {n}} = {\tfrac {n!$}{n!0!$}}$=1,}$ 0! $=$ 1 {\displaystyle 0!$=$ 1}에서만 유효한 이항 계수 항등식입니다.
• $0{\displaystyle !}$ = ${\$displaystyle 0! = 1}일 때 요인에 대한 반복 관계는 n = 1 {\displaystyle n = 1}에서 유효합니다. 따라서 이 규칙에서는 요인의 재귀적 계산을 기본 경우로 0에 대한 값만 있으면 계산이 간단해지고 추가적인 특수 경우가 필요하지 않습니다.
• $0{\displaystyle !}$ = ${\$displaystyle 0!=1$}$을(를) 설정하면 지수 함수와 같은 많은 공식을 $멱급수$로 압축하여 표현할 수 있습니다: x = ∑ n = 0 ∞ x n!. {\textstyle e^{x}=\sum _{n=0}^{\infty$}{\$frac {x^{n}}{\n!$}}.}$^[14]
• 이 선택은 감마 함수 $0{\displaystyle !}$ = γ${\displaystyle }$(0 + 1) = 1 {\displaystyle 0!=\Gamma (0 + 1) = 1}과 일치하며, 감마 함수가 연속 함수가 되려면 이 값을 가져야 합니다.

적용들

계승 함수의 가장 초기 사용에는 순열을 세는 것이 포함됩니다. $!{\$$displaystyle$ n$!}$$개$의 서로 다른 개체를 순서로 배열하는 방법에는 n$!{\displaystyle$ n$!}$가지가$$ 있습니다.^[26] 인수분해는 객체의 다양한 순서를 설명하기 위해 조합론의 많은 공식에서 더 광범위하게 나타납니다. For instance the binomial coefficients ${\displaystyle {\tbinom {n}{k}}}$ count the ${\displaystyle k}$-element combinations (subsets of ${\displaystyle k}$ elements) from a set with ${\displaystyle n}$ elements, and can be computed from factorials using the formula^[27]

첫 번째 종류의 스털링 수를 인수에 합한 다음, $n{\displaystyle }$ ${\displaystyle n}$개의 순열을 동일한 수의 주기를 가진 부분 집합으로 그룹화하여$$ 계산합니다.^[28] 또 다른 조합 응용 프로그램은 원소를 원래 위치에 남기지 않는 순열인 편차를 계산하는 것입니다. $n{\displaystyle }$ ${\displaystyle n}$ 항목의$$ 편차 수는 $n{\displaystyle !}$/ ${\displaystyle e}$ ${\displaystyle n!/e}$에 가장 가까운 정수입니다$.$^[29]

대수학에서 인수는 합의 거듭제곱을 확장하기 위해 이항 계수를 사용하는 이항 정리를 통해 발생합니다.^[30] 또한 대칭 다항식에 대한 뉴턴 항등식과 같이 특정 다항식의 가족을 서로 연관시키는 데 사용되는 계수에서도 발생합니다.^[31] 순열을 계산할 때 이들의 사용은 대수적으로 다시 설명될 수도 있습니다. 인수분해는 유한 대칭군의 순서입니다.^[32] 미적분학에서 인자는 Fa higher di Bruno의 상위 도함수를 연결하는 공식에서 발생합니다. 수학적 분석에서 요인은 멱급수의 분모에 자주 나타나며, 특히 지수 함수에 대한 급수에서 가장 두드러집니다.^[14]

그리고 다른 테일러 급수의 계수(특히 삼각 함수 및 쌍곡선 함수의 계수)에서는 $x{\displaystyle {}^{}}$ ${\displaystyle n^{}}$ ${\$의 $n{\displaystyle }$ ${\displaystyle n}$번째 도함수에서$$ $n{\displaystyle !}$ ${\displaystyle$ n$!}$의 인자를 취소합니다$.$^[33] 멱급수에서 인자의 이러한 사용은 지수 ${\displaystyle {생성}_{}}$ 함수를 통해 분석적 조합론으로 다시 연결되며, n ${\$크기가 ${\displaystyle$ i$}$인 조합$$ 클래스의 경우 $멱급수$로^[34] 정의됩니다$$.

수론에서 인수분해의 가장 두드러진 특성은 $n{\displaystyle }$$!{\displaystyle n!}$의 모든 양의 정수 ${\displaystyle n!}$에 의한 분할이며$,$ Legendre의 공식에 의해 소수 인자에 대해 더 정확하게 설명됩니다. 임의로 큰 소수를 $n{\displaystyle !}$± ${\displaystyle 1}$ ${\display style$n!\$pm 1}$개의 소수 인자로 찾을 수$$있어 소수의 수가 무한하다는 유클리드 정리의 증명으로 이어집니다.^[35] When ${\displaystyle n!\pm 1}$ is itself prime it is called a factorial prime;^[36] relatedly, Brocard's problem, also posed by Srinivasa Ramanujan, concerns the existence of square numbers of the form ${\displaystyle n!+1}$.^[37] In contrast, the numbers ${\displaystyle n!+2,n!+3,\dots n!$$+n}$은(는) 모두 합성이어야 하며$$, 임의로 큰 소수 간격이 존재함을 증명합니다.^[38] Paul Erd ő의$$첫 번째$$결과 중 $하나$인 [n$,$ 2 n${\displaystyle ]}$ {\displaystyle [$n,2n]}$ 형태의 임의의 간격에서 소수의 존재에 대한 Bertrand의 가정에 대한 기본적인 증거는 인수의 분할 특성에 기초했습니다$.$ 인수분해 수 체계는 각 자리의 자리 값이 인수분해인 숫자에 대한 혼합 기수 표기법입니다.^[41]

인자는 포아송 분포^[42] 및 랜덤 순열의 확률과 같은 확률 이론에서 광범위하게 사용됩니다.^[43] ${\displaystyle {컴퓨터}_{}}$ 과학에서는 순열에 대한 단순한 강제 검색 분석에 나타나는 것을 넘어 요인이 ${\displaystyle {log}_{}}$ ${\displaystyle 2}$ ⁡ n! =${\displaystyle {}_{}}$n${\displaystyle \log }$ ${\displaystyle 2}$ ⁡ n - O (n$) {\displaystyle \$log_{2}n!비교에 필요한 비교 횟수에 $대한$ $=$n\$log _{2}n-O(n$)}개의 ${\displaystyle$n}$개$ 항목 집합을 정렬하고 연결된 해시 테이블 분석에서 셀당 키 분포를 포아송 분포로 정확하게 근사할 수 있습니다. 게다가 인자들은 양자 물리학과 통계 물리학의 공식에 자연스럽게 나타나는데, 여기서 사람들은 종종 입자 집합의 가능한 모든 순열을 고려합니다. 통계역학에서 볼츠만의 엔트로피 공식이나 사쿠르와 같은 엔트로피의 계산은 다음과 같습니다.Tetrode 방정식은 Gibbs 역설을 피하기 위해 각 유형의 구별할 수 없는 입자의 수의 인수로 나누어 미시 상태의 수를 수정해야 합니다. 양자 물리학은 이러한 보정이 필요한 근본적인 이유를 제공합니다.^[47]

특성.

성장 및 근사

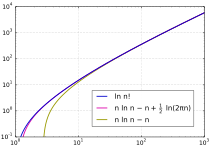
$n{\displaystyle }$ ${\displaystyle n}$의 함수로서 요인의 성장 속도는 지수 함수보다 빠르지만 이중 지수 함수보다는 느리게 성장합니다$.$^[48] 성장 속도는 ${\displaystyle n^{}}${\$displaystyle n^{n}}$과$$비슷하지만 지수 함수만큼 느립니다. 이 결과에 접근하는 한 가지 방법은 곱 공식을 합으로 바꾸는 요인의 자연로그를 취한 다음 적분으로 합을 추정하는 것입니다.

결과를 지수화하면(그리고 무시할 수 있는${\displaystyle }$+${\displaystyle 1}$ ${\displaystyle +1}$ 항은$$ 무시함) $!{\displaystyle$ n$!}$을${\displaystyle }$(${\displaystyle n}$/ e${\displaystyle {}^{}}$) n ${\$과 같이 근사합니다$.$^[49] 사다리꼴 규칙을 사용하여 위와 아래의 합을 적분으로 더 조심스럽게 묶으면, 는 이 추정치가 n ${\$에 비례하는 보정 계수가 필요함을 보여줍니다$.$ 이 보정에 대한 비례 상수는$$π${\$displaystyle \pi}을(를) 2의 인수와 거듭제곱의 제한 비율로 표현하는 Wallis 제품에서 찾을 수 있습니다. 이러한 보정의 결과는 스털링의 근사치입니다.^[50] 여기서${\displaystyle }$~ ${\displaystyle \sim }$ 기호는$$ $n{\displaystyle }$ ${\displaystyle n}$이 무한대로 갈수록$$ 좌우의 비율이 한계 내에서 1에 가까워짐을 의미합니다. 스털링의 공식은 더 많은 항을 고려할 때 훨씬 더 정확해지는 점근 급수의 첫 번째 항을 제공합니다.^[51] 대체 버전은 수정 항에서 홀수 지수만 사용합니다.^[51] Srinivasa Ramanujan, Bill Gosper 등에 의해 이러한 공식의 다른 많은 변형도 개발되었습니다.^[51]

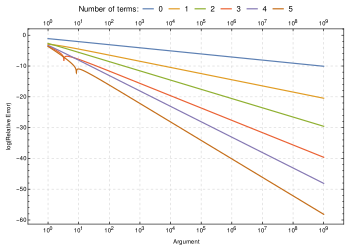
비교 정렬을 분석하는 데 사용되는 요인의 이진 로그는 스털링의 근사를 사용하여 매우 정확하게 추정할 수 있습니다. 아래 공식에서 $O{\displaystyle (1)}$ ${\displaystyle O(1)}$ 항은$$ 빅 O 표기법을 호출합니다.^[45]

나눗셈과 숫자

요인에 대한 곱 공식은 $n{\displaystyle !}$ ${\displaystyle$ n$!}$이(가) $최대{\displaystyle }$ n ${\displaystyle n}$인 모든 소수와$$더 이상의 소수로 구분되지 않음을 의미합니다.^[52] 나눗셈에 대한 더 정확한 정보는 $!{\displaystyle n!}$의 소인수분해에서$$ 각 소수 $p{\displaystyle }$ ${\displaystyle p}$의 지수를 제공하는$$^[53][54] Legendre 공식에 의해 제공됩니다.

${\displaystyle {여기}_{}}$서 p${\displaystyle {}_{}n)}$ ${\displaystyle s_{p}(n)}$는 $n{\displaystyle }$ ${\displaystyle$ $n$$}$의 기본 ${\displaystyle }$ ${\displaystyle$ p$}$자리의$$ 합을 나타내며$$$,$ 이 공식에 의해 주어진 지수는 고급 수학에서도 요인의 p-adic 값으로 해석될 수 있습니다.^[54] Legendre의 공식을 이항 계수의 곱 공식에 적용하면 Kummer의 정리가 생성되며, 이는 이항 계수의 인수분해에서 각 소수의 지수에 대한 결과와 유사합니다.^[55] 요인의 소수 요인을 여러 가지 방법으로 소수 거듭제곱으로 그룹화하면 요인의 곱셈 분할이 생성됩니다.^[56]

$p$ = ${\displaystyle 5}$ ${\$displaystyle p = 5}에 대한 Legendre의 공식의 특수한 경우는 인수의 10진수 표현에서 뒤에 오는 0의 수를 제공합니다. $이{\displaystyle }$ 공식에 따르면 0의 수는 n ${\displaystyle n}$에서 n ${\displaystyle$ n$}$의 밑-5자리를 뺀$$후 결과를 4로 나누면 구할 수 있습니다.^[58] Legendre의 공식은 소수 $p$ = ${\$displaystyle p = 2}의 지수가 항상 p = 5 {\displaystyle p = 5}의 지수보다 크다는 것을 의미합니다. 따라서 5의 각 인자는 2의 인자와 쌍을 이루어 이러한 후행 0 중 하나를 생성할 수 있습니다. 인수의 선두 자리 수는 벤포드 법칙에 따라 분포됩니다.^[59] 모든 숫자의 모든 순서는 모든 숫자의 기본 숫자에 있는 어떤 요인 번호의 초기 숫자의 순서입니다.^[60]

인수 분해에 대한 또 다른 결과인 윌슨의 정리는${\displaystyle }$(${\displaystyle \mathrm{n}}$ -${\displaystyle 1)!}$ + 1$${\$displaystyle (n-1)!$$n{\displaystyle }$ {\$displaystyle n}$이 소수인 경우에만$$ $+1}$^[52]을 n ${\displaystyle n}$으로 나눕니다. For any given integer ${\displaystyle x}$, the Kempner function of ${\displaystyle x}$ is given by the smallest ${\displaystyle n}$ for which ${\displaystyle x}$ divides ${\displaystyle n!}$.^[61] For almost all numbers (all but a subset of exceptions with asymptotic density zero), $x{\displaystyle }$ ${\displaystyle x}$의 가장 큰 소인수와 일치합니다$.$^[62]

${\displaystyle 두}$ 인수의 곱인 $m{\displaystyle !}$ ⋅ $n! {\displaystyle$m!\cdot n!}은 항상 ${\displaystyle \mathrm{균등}}$하게${\displaystyle }$나눕니다$!$ ${\displaystyle$(m+n)!}. 다른 $인수$의 곱과 동일한 인수는 무한히 많습니다$:$ $만약$ n ${\displaystyle$ n}이 그 자체로 $인수$의 곱이라면$,$ n! ${\displaystyle$ n!$}$동일한 제품에 요인을 하나 더 곱한 것과 같습니다$$$.{\displaystyle }$ (${\displaystyle \mathrm{n}}$ ${\displaystyle -}$1 ${\displaystyle )!}${\$displaystyle (n-1$ ${\displaystyle \mathrm{다른}}$ 요인의 제품이지만 이러한 "trivial" 형태가 아닌 요인의 알려진 유일한 예는 9${\displaystyle !}$ =${\displaystyle }$7${\displaystyle !}$⋅ 3! ⋅ 3! ⋅ 2! {\display 9!= 7!\$cdot$3!\cdot 2!}, 10! = 7! ⋅ 6! = 7! ⋅ 5! ⋅ 3! {\display 10!$=$${\displaystyle 7}$$!\$cdot 6!$=$7$!\cdot$ 5$!\cdot 3$ ${\displaystyle \mathrm{그리고}}$ 16${\displaystyle !}$ $=$ 14${\displaystyle !}$ $⋅$$5$! $⋅$ 2! {\displaystyle 16!$=$14!\cdot 5!\cdot 2!}. 아주 사소한 예들이 많이 있다는 것은 abc 추측으로부터 따를 것입니다.

정수에 대한$$ $차수{\displaystyle }$ d$${\$displaystyle$ d$}$의 원시 다항식 값의 최대 공약수는 $균등$하게 나누어져 있습니다${\displaystyle !}$ ${\displaystyle$ d$!\}.$^[63]

연속 보간 및 비-정수 일반화

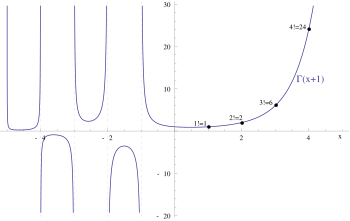
인수를 연속 함수로 확장하는 방법은 무한히 많습니다.^[66] 이^[67] 중 가장 널리 사용되는 것은 감마 함수를 사용하는데, 감마 함수는 양의 실수에 대해 적분으로 정의될 수 있습니다.

결과 함수는 음수가 아닌 $정수{\displaystyle }$ n ${\displaystyle n}$의 계승과 관계가$$ 있습니다. integer가 아닌 인수에 대한 요인의 정의로 사용할 수 있습니다. γ$(x$) ${\displaystyle$ \$Gamma($x)} 및 γ(x - 1) {\displaystyle \Gamma(x-1)}가 모두 정의된 모든 $값$ x ${\displaystyle$ x$}$에서 감마 함수는 함수 방정식을 따릅니다. 요인에 대한 재발 관계를 일반화합니다.^[66]

실수 부분이$$ 양수인 복소수 $z{\displaystyle }$ ${\displaystyle z}$에 대해서는 동일한 적분이 더 일반적으로 수렴합니다. 이는 오일러의 반사 공식을 풀어서 복소평면의 나머지 부분의 비-정수점까지 확장될 수 있습니다.

그러나 정수에서는 ${\displaystyle \sin }$⁡ π z {\displaystyle \sin \piz} 항이 0으로 나눗셈을 생성하므로 이 공식을 사용할 수 없습니다. 이 확장 과정의 결과는 분석 함수, 즉 감마 함수에 대한 적분 공식의 분석 연속입니다. 단순 극값을 갖는 양이 아닌 정수를 제외한 모든 복소수에서 0이 아닌 값을 갖습니다. 이에 따라 음의 정수를 제외한 모든 복소수에서 요인에 대한 정의가 제공됩니다.^[67] 감마 함수의 한 특성은 인자의 다른 연속 보간과 구별되며, 감마 함수(1로 오프셋)가 인자를 보간하고 동일한 함수 방정식을 따르는 양의 실수에 대한 유일한 로그 변환 함수라는 보어-몰럽 정리에 의해 제공됩니다. Helmut Wielandt의 관련 유일성 정리는 복소 감마 함수와 그 스칼라 배수가 함수 방정식을 따르고 실수 부분이 1과 2 사이인 복소수에 대해 경계를 유지하는 양의 복소 반평면에서 유일한 홀로모픽 함수라고 말합니다.^[68]

요인 값을 보간하는 다른 복소수 함수에는 양이 아닌 정수를 포함한 모든 복소수에 대한 전체 함수인 하다마드의 감마 함수가 포함됩니다.^[69][70] p-아딕 수에서는 큰 정수(p-아딕의 조밀한 부분 집합)의 인수분해가 Legendre의 공식에 따라 0으로 수렴하여 값에 가까운 연속 함수가 모든 곳에서 0이 되도록 만들기 때문에 요인 함수를 직접 연속적으로 보간할 수 없습니다. 대신 p-아딕 감마 함수는 요인의 수정된 형태의 연속 보간을 제공하여 요인에서 p로 나눌 수 있는 요인을 생략합니다.^[71]

디감마 함수는 감마 함수의 로그 도함수입니다. 감마 함수가 인자의 연속 보간을 1로 오프셋하는 것과 마찬가지로 디감마 함수는 오일러-마스케로니 상수에 의해 오프셋되는 조화수의 연속 보간을 제공합니다.^[72]

연산

요인 함수는 과학 계산기의 일반적인 특징입니다.^[73] 파이썬 수학 함수 모듈^[74], 부스트 C++ 라이브러리와 같은 과학 프로그래밍 라이브러리에도 포함되어 있습니다.^[75] 효율성이 문제가 되지 않으면 계산 요소는 사소한 것입니다. $1{\displaystyle \mathrm{}}$ ${\displaystyle 1}$로 초기화된 변수에$$ n ${\displaystyle n}$까지의 정수를 연속적으로 곱하면 됩니다$.$ 이 계산의 단순성으로 인해 다양한 컴퓨터 프로그래밍 스타일과 방법을 사용하는 일반적인 예가 됩니다.^[76]

$n{\displaystyle !}$ ${\displaystyle n!}$의 계산은 반복을^[77] 사용하여 의사 코드로 표현할$$ 수 있습니다.

요인(n) 정의: i:= 1, 2, 3, ..., n: f:= f * i는 f를 반환합니다. 

또는 재발 관계에 기반한 재귀를^[78] 사용합니다.

요인(n)을 정의합니다. (n = 0) 1 반환 n * 요인(n - 1) 

계산에 적합한 다른 방법으로는 메모화,^[79] 동적 프로그래밍 ^[80]및 기능 프로그래밍이 있습니다.^[81] 이러한 알고리즘의 계산 복잡도는 각 산술 연산에 일정한 시간이 소요되고 각 숫자가 일정한 양의 저장 공간을 사용하는 계산의 단위 비용 랜덤 액세스 기계 모델을 사용하여 분석될 수 있습니다. 이 모델에서 이러한 방법은 $시간{\displaystyle }$ $O{\displaystyle (n)}$ ${\displaystyle O(n)}$에서 n$!{\displaystyle$ n$!}$을 계산할 수$$있으며 반복 버전은 $공간{\displaystyle }$ O${\displaystyle (1)}$ ${\displaystyle$ O$(1)}$을 사용합니다$.$ 꼬리 재귀에 최적화되지 않은 경우 재귀 버전은 콜 스택을 저장하기 위해 선형 공간을 사용합니다.^[82] 그러나 이 계산 모델은 $n{\displaystyle }$ ${\displaystyle n}$이(가) $!{\displaystyle n!}$을(를) 기계어에 넣을$$ 수 있을 정도로 작을 때만 적합합니다.^[83] 값 12!과 20!은 각각 32비트와^[84] 64비트 정수에 저장할 수 있는 가장 큰 인수입니다.^[85] 부동 소수점은 더 큰 인수를 나타낼 수 있지만 정확하게는 아니지만 ${\displaystyle 170}$보다 큰 인수의 경우에도 여전히 넘칠${\displaystyle }$것입니다$.$ {\$display 170$^[84]

더 큰 인수의 정확한 계산에는 빠른 성장과 정수 오버플로우로 인해 임의의 정밀도 산술이 포함됩니다. 계산 시간은 결과의 자릿수나 비트 수에 대한 함수로 분석할 수 있습니다.^[85] 스털링 공식에 따라 $n{\displaystyle !}$ ${\displaystyle$ n$!}$은(는) $b$ = O ${\displaystyle (n}$log ⁡ n) {\displaystyle b = O(n\log n)} 비트입니다. Schönhage-Strassen 알고리즘은 시간 $O$에서 $b$ ${\displaystyle b}$ 비트 제품을 생성할 수 있으며${\displaystyle (}$$blog$⁡${\displaystyle }$b ${\displaystyle \mathrm{로그}}$ ⁡ $b$) {\displaystyle O(b\log b\log \log b)}, 시간 O(blog ⁡ b) {\displaystyle O(b\log b)}이 소요되는 더 빠른 곱셈 알고리즘이 알려져 있습니다. 그러나 요인 계산에는 단일 곱이 아닌 반복되는 곱이 포함되므로 이러한 시간 한계가 직접 적용되지 않습니다. $이$ 설정에서 n! ${\displaystyle$ $n!}$을${\displaystyle (}$를) $1$부터 n {\displaystyle $n$$}$까지의 숫자를 순차적으로 곱하여 계산하는 것은$n$ {\$displaystyle$ n$}$ 곱하기를 포함하고, 그 중 일정한 분수는 각각 $($ ${\displaystyle {\log }^{}}$ ${\displaystyle 2}$ ⁡ n) ${\displaystyle$ O$(n\log$ ^{2}n)} 시간이 걸리기 때문에 비효율적입니다. 총 시간 $O{\displaystyle ({}^{}}$ ${\displaystyle 2^{}}$ ${\displaystyle {\log }^{}}$ ${\displaystyle 2}$ ⁡ n) ${\displaystyle$O($n^{2}\log$2}n)}를 제공합니다. 더 나은 접근 방식은 i ${\displaystyle$ i}$숫자$의 시퀀스를$$i / 2${\displaystyle$ i/2} ${\displaystyle 숫자}$의 두${\displaystyle }하위$ 시퀀스로 분할하여 곱셈을 곱하는 분할정복 알고리즘으로 수행하는 것입니다. 는 각 하위 시퀀스를 곱하고 결과를 마지막 곱셈 하나와 결합합니다. 요인에 대한 이 접근 방식은 총 시간 $O{\displaystyle (n^{}}$ ${\displaystyle {\log }^{}}$ ${\displaystyle 3}$ ⁡ n) ${\displaystyle O(n\log$^{3}n)}: 하나의 로그는 요인의 비트 수에서 나오고, 두 번째 로그는 곱셈 알고리즘에서 나오고, 세 번째 로그는 분할 및 정복에서 나옵니다.

제곱에 의한 지수화는 지수를 곱으로 확장하는 것보다 더 빠르다는 원리에 기초하여 소인수분해로부터 n!을 계산함으로써 훨씬 더 나은 효율성을 얻을 수 있습니다.^[86][89] 이에 대한 알고리즘은 예를 들어 에라토스테네스의 체를 사용하여$$$n{\displaystyle }$ ${\display$ n$}$까지의 $소수$의 목록을 찾는 것으로 시작되며, 각 소수의 지수를 계산하기 위해 레전드레의 공식을 사용합니다. 그런 다음 재귀적 알고리즘을 사용하여 다음과 같이 소수의 거듭제곱의 곱을 계산합니다.

• 나눗셈과 정복을 사용하여 지수가 홀수인 소수의 곱을 계산합니다.
• 모든 지수를 2로 나누고(정수로 반올림), 이 작은 지수로 소수의 거듭제곱의 곱을 재귀적으로 계산하고 결과를 제곱합니다.
• 이전 두 단계의 결과를 곱합니다.

$n$ ${\displaystyle n}$까지의 모든 소수의 곱은 소수 정리에 의해 $O{\displaystyle (n)}$ ${\displaystyle O(n)}$ 비트 수이므로 첫 번째 단계의 $시간$은 O${\displaystyle (n^{}}$ ${\displaystyle {\log }^{}}$ ${\displaystyle 2}$ ⁡ n) {\$displaystyle$ O$(n\log$^{2}n)}이며, 하나의 로그는 분할 및 정복에서 오고 다른 하나는 곱셈 알고리즘에서 나옵니다. 알고리즘에 대한 재귀적 호출에서 소수 정리를 다시 호출하여 각 재귀 수준에서 해당 곱의 비트 수가 일정한 인자만큼 감소한다는 것을 증명할 수 있습니다. 따라서 모든 수준의 재귀에서 이러한 단계의 총 시간은 $O{\displaystyle (n}$ ${\displaystyle {\log }^{}}$ ${\displaystyle 2}$ ⁡$n$) ${\displaystyle O(n\log$ $^\{$2}n)}에 기하급수를 추가합니다. 두 번째 단계의 제곱 시간과 세 번째 단계의 곱셈은 $다시$ O$($${\displaystyle n}$ ${\displaystyle {\log }^{}}$ ${\displaystyle 2}$ ⁡ n) ${\displaystyle$ O(n$\$log ^{2}n)}입니다. 각각은 O(n log ⁡ n) {\displaystyle O(n\log n)} 비트를 갖는 숫자의 단일 곱셈이기 때문입니다. 다시 각 재귀 수준에서 관련된 숫자는 비트 수만큼 일정한 분수를 갖습니다(그렇지 않으면 반복적으로 제곱하면 최종 결과가 너무 커지기 때문에). 따라서 재귀 호출에서 이러한 단계의 시간은 $n$ ${\displaystyle {\log }^{}}$ ${\displaystyle 2}$ ⁡ n) ${\display$ O$(n\log$^{2}n)}에 기하급수를 추가합니다. 결과적으로, 전체 알고리즘은 $O{\displaystyle (n}$ ${\displaystyle {log}^{}}$ ${\displaystyle 2}$ ⁡ $n){\displaystyle O(n\log$^{2}n)} 시간이 소요되며, 결과가 동일한 비트 수를 갖는 단일 곱셈에 비례합니다.

관련 시퀀스 및 기능

다음과 같은 몇 가지 다른 정수 시퀀스가 인수분해와 유사하거나 관련되어 있습니다.

교대 요인

교대 요인은 첫 $번째$ n개$${\$displaystyle$ n$}$ 요인의 $\underset{}{\overset{}{교대}}$ 합인 ∑ i = 1$\underset{}{\overset{}{\mathrm{n}}}$( - 1 ) n - i ! {\textstyle \sum _{i=1}^{n}(-1)^{n-i}i!}의 절대값입니다. 이것들은 주로 그것들의 기본성과 관련하여 연구되어 왔습니다; 그것들 중 오직 유한하게 많은 것들만이 기본이 될 수 있지만, 이러한 형태의 기본들의 완전한 목록은 알려져 있지 않습니다.^[90]

바르가바 요인

바르가바 인수분해는 인자 자체를 특수한 경우로 포함하여 인수분해와 유사한 수론적 특성을 가진 만줄 바르가바에 의해 정의된 정수 시퀀스 계열입니다.^[63]

이중 요인

어떤 홀수 양의 $정수{\displaystyle }$ n ${\displaystyle$ $n$$}$까지의 모든 홀수 정수의 곱을 $n{\displaystyle }$ ${\displaystyle$ n$}$의 이중 계승이라고 하며$$${\displaystyle ,<img\; alt="n"\; aria-hidden="true"\; class="mwe-math-fallback-image-inline\; mw-invert"\; src="https://wikimedia.org/api/rest\_v1/media/math/render/svg/a601995d55609f2d9f5e233e36fbe9ea26011b3b"\; style="vertical-align:\; -0.338ex;\; width:1.395ex;\; height:1.676ex;">}$ $n{\displaystyle }$!로 표시합니다${\displaystyle .}$ ${\displaystyle n!!$$}$^[91] 즉.

$${\displaystyle (2k-1)!!=\prod _{i=1}^{k}(2i-1)={\frac {(2k)!}{2^{k}k!}}.}$$

예를 들면 9!!= 1 × 3 × 5 × 7 × 9 = 945. 이중 인수분해는 삼각함수 적분,^[92] 반정수에서의 감마 함수와 초구의 부피에 대한 표현,^[93] 이진 트리와 완벽한 일치를 계산하는 데 사용됩니다.^[91][94]

지수적 요인

삼각형 숫자가 $1{\displaystyle \mathrm{}}$ ${\displaystyle$ $1$$}$에서 $n{\displaystyle }$ ${\displaystyle$ $n$$}$까지의 숫자를 합한$$것과 같이 요인의 곱을 취하면 지수 요인이 지수화됩니다. 지수 계승은 ${\displaystyle 0}$ = 1${\displaystyle ,{{}_{}}^{}}$ =$n$- 1 {\display a_{0} = 1,\ a_{n} = n^{a_{n-1}}로 재귀적으로 정의됩니다. 예를 들어, 4의 지수 계승은 다음과 같습니다.

$${\displaystyle 4^{3^{2^{1}}=262144.}$$

이 숫자들은 일반적인 인수보다 훨씬 더 빨리 증가합니다.^[95]

낙수 요인

The notations ${\displaystyle (x)_{n}}$ or ${\displaystyle x^{\underline {n}}}$ are sometimes used to represent the product of the ${\displaystyle n}$ integers counting up to and including ${\displaystyle x}$, equal to ${\displaystyle x!/(x-n)!}$. 이를 하강 요인 또는 역 요인이라고도 하며$,{\displaystyle }$ (${\displaystyle x{}_{}}$ ${\displaystyle n_{}}$ ${\$ 표기법은$$ Pochammer 기호입니다.^[96] 하강 요인은 $x{\displaystyle }$ ${\displaystyle x}$개$$ 항목의 우주에서 그릴 수 있는 $n{\displaystyle }$ ${\displaystyle n}$개 항목의$$ 서로 다른 시퀀스의 수를 계산합니다.^[97] 이들은 다항식의 상위 도함수와 랜덤 변수의 요인 모멘트에서 계수로 발생합니다.^[98][99]

초요소

$n {\displaystyle$ n$}$의 하이퍼팩터는 제품 ${\displaystyle {}^{}}$ ⋅ $22$ ⋯ n ${\displaystyle$1^{1}\$cdot 2^{$2$\}\backslash$cdots n^{n}입니다. 이 숫자들은 에르미트 다항식의 판별식을 형성합니다.^[100] 이들은 K-함수에 의해 연속적으로 보간될 수 있으며,^[101] 스털링의 공식과^[102] 윌슨의 정리와 유사한 것을 따를 수 있습니다.^[103]

조던-폴랴 수

요르단-폴랴 수는 반복을 허용하는 인수의 산물입니다. 모든 나무는 대칭의 수가 조던인 대칭군을 가지고 있습니다.폴랴, 그리고 모든 요르단 사람들은..폴랴 수는 어떤 나무의 대칭을 세어요.^[104]

원시의

기본 ${\displaystyle n\#}$은 $n{\displaystyle }$ ${\displaystyle$ n$}$보다 작거나 같은 소수의 곱입니다$.$ 이 구성은 인수분해와 유사한 분할 특성을 ^[36]제공하지만 인수분해와 달리 제곱이 없습니다.^[105] ${\displaystyle \mathrm{요인}}$ 소수 $n{\displaystyle !}$± 1 ${\displaystyle n!\pm$ 1$}$과 마찬가지로$$연구자들은 ${\displaystyle \mathrm{n번}\mathrm{\pm }}$ 1 ${\displaystyle n\#\pm$ 1$}$의 기본 소수를 연구했습니다$.$^[36]

하위 요인

하위 요인은 $n개{\displaystyle }${\$displaystyle$n}개$$ 개체 집합의 이탈 횟수를 산출합니다. $!{\displaystyle }$ ${\displaystyle n}$ ${\displaystyle !n}$로 표시되기도 하며$,$ $n{\displaystyle !}$/ ${\displaystyle e}$ ${\displaystyle n!/e}$에 가장 가까운 정수와 같습니다$.$^[29]

슈퍼팩터럴

$n{\displaystyle }$ ${\displaystyle$ $n$$}$의 초계수는 첫 번째 $n{\displaystyle }$ ${\displaystyle$ n$}$개의$$ 인수의 곱입니다$$. 초요인들은 반스 G-함수에 의해 연속적으로 보간됩니다.^[106]

참고문헌

외부 링크

• OEIS 시퀀스 A000142 (공장 번호)
• "Factorial". Encyclopedia of Mathematics. EMS Press. 2001 [1994].
• Weisstein, Eric W. "Factorial". MathWorld.